Lift (force)

A fluid flowing around the surface of a solid object applies a force on it. It does not matter whether the object is moving through a stationary fluid (e.g. an aircraft flying through the air) or whether the object is stationary and the fluid is moving (e.g. a wing in a wind tunnel) or whether both are moving (e.g. a sailboat using the wind to move forward). Lift is the component of this force that is perpendicular to the oncoming flow direction.^[1] Lift is always accompanied by a drag force, which is the component of the surface force parallel to the flow direction.

Lift is mostly associated with the wings of fixed-wing aircraft, although it is more widely generated by many other streamlined bodies such as propellers, kites, helicopter rotors, racing car wings, maritime sails, wind turbines, and by sailboat keels, ship's rudders, and hydrofoils in water. Lift is also used by flying and gliding animals, especially by birds, bats, and insects, and even in the plant world by the seeds of certain trees.^[2] While the common meaning of the word "lift" assumes that lift opposes weight, lift can be in any direction with respect to gravity, since it is defined with respect to the direction of flow rather than to the direction of gravity. When an aircraft is cruising in straight and level flight, the lift opposes gravity. However, when an aircraft is climbing, descending, or banking in a turn the lift is tilted with respect to the vertical.^[3] Lift may also act as downforce on the wing of a fixed-wing aircraft at the top of an aerobatic loop, and on the horizontal stabiliser of an aircraft. Lift may also be largely horizontal, for instance on a sailing ship.

The lift discussed in this article is mainly in relation to airfoils; marine hydrofoils and propellers share the same physical principles and work in the same way, despite differences between air and water such as density, compressibility, and viscosity.

The flow around a lifting airfoil is a fluid mechanics phenomenon that can be understood on essentially two levels: There are mathematical theories, which are based on established laws of physics and represent the flow accurately, but which require solving equations. And there are physical explanations without math, which are less rigorous.^[4] Correctly explaining lift in these qualitative terms is difficult because the cause-and-effect relationships involved are subtle.^[5] A comprehensive explanation that captures all of the essential aspects is necessarily complex. There are also many simplified explanations, but all leave significant parts of the phenomenon unexplained, while some also have elements that are simply incorrect.^{[4][6][7][8][9][10]}

An airfoil is a streamlined shape that is capable of generating significantly more lift than drag.^[11] A flat plate can generate lift, but not as much as a streamlined airfoil, and with somewhat higher drag. Most simplified explanations follow one of two basic approaches, based either on Newton's laws of motion or on Bernoulli's principle.^{[4][12][13][14]}

An airfoil generates lift by exerting a downward force on the air as it flows past. According to Newton's third law, the air must exert an equal and opposite (upward) force on the airfoil, which is lift.^{[15][16][17][18]}

As the airflow approaches the airfoil it is curving upward, but as it passes the airfoil it changes direction and follows a path that is curved downward. According to Newton's second law, this change in flow direction requires a downward force applied to the air by the airfoil. Then Newton's third law requires the air to exert an upward force on the airfoil; thus a reaction force, lift, is generated opposite to the directional change. In the case of an airplane wing, the wing exerts a downward force on the air and the air exerts an upward force on the wing.^[19][20] The downward turning of the flow is not produced solely by the lower surface of the airfoil, and the air flow above the airfoil accounts for much of the downward-turning action.^{[21][22][23][24]}

This explanation is correct but it is incomplete. It does not explain how the airfoil can impart downward turning to a much deeper swath of the flow than it actually touches. Furthermore, it does not mention that the lift force is exerted by pressure differences, and does not explain how those pressure differences are sustained.^[4]

Some versions of the flow-deflection explanation of lift cite the Coandă effect as the reason the flow is able to follow the convex upper surface of the airfoil. The conventional definition in the aerodynamics field is that the Coandă effect refers to the tendency of a fluid jet to stay attached to an adjacent surface that curves away from the flow, and the resultant entrainment of ambient air into the flow.^[25][26][27]

More broadly, some consider the effect to include the tendency of any fluid boundary layer to adhere to a curved surface, not just the boundary layer accompanying a fluid jet. It is in this broader sense that the Coandă effect is used by some popular references to explain why airflow remains attached to the top side of an airfoil.^[28][29] This is a controversial use of the term "Coandă effect"; the flow following the upper surface simply reflects an absence of boundary-layer separation, thus it is not an example of the Coandă effect.^{[30][31][32][33]} Regardless of whether this broader definition of the "Coandă effect" is applicable, calling it the "Coandă effect" does not provide an explanation, it just gives the phenomenon a name.^[34]

The ability of a fluid flow to follow a curved path is not dependent on shear forces, viscosity of the fluid, or the presence of a boundary layer. Air flowing around an airfoil, adhering to both upper and lower surfaces, and generating lift, is accepted as a phenomenon in inviscid flow.^[35]

There are two common versions of this explanation, one based on "equal transit time", and one based on "obstruction" of the airflow.

The "equal transit time" explanation starts by arguing that the flow over the upper surface is faster than the flow over the lower surface because the path length over the upper surface is longer and must be traversed in equal transit time.^[36][37][38] Bernoulli's principle states that under certain conditions increased flow speed is associated with reduced pressure. It is concluded that the reduced pressure over the upper surface results in upward lift.^[39]

While it is true that the flow speeds up, a serious flaw in this explanation is that it does not correctly explain what causes the flow to speed up.^[4] The longer-path-length explanation is incorrect. No difference in path length is needed, and even when there is a difference, it is typically much too small to explain the observed speed difference.^[40] This is because the assumption of equal transit time is wrong when applied to a body generating lift. There is no physical principle that requires equal transit time in all situations and experimental results confirm that for a body generating lift the transit times are not equal.^{[41][42][43][44][45][46]} In fact, the air moving past the top of an airfoil generating lift moves much faster than equal transit time predicts.^[47] The much higher flow speed over the upper surface can be clearly seen in this animated flow visualization.

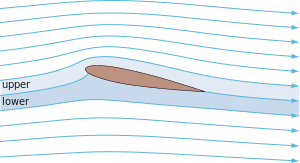
Like the equal transit time explanation, the "obstruction" or "streamtube pinching" explanation argues that the flow over the upper surface is faster than the flow over the lower surface, but gives a different reason for the difference in speed. It argues that the curved upper surface acts as more of an obstacle to the flow, forcing the streamlines to pinch closer together, making the streamtubes narrower. When streamtubes become narrower, conservation of mass requires that flow speed must increase.^[48] Reduced upper-surface pressure and upward lift follow from the higher speed by Bernoulli's principle, just as in the equal transit time explanation. Sometimes an analogy is made to a venturi nozzle, claiming the upper surface of the wing acts like a venturi nozzle to constrict the flow.^[49]

One serious flaw in the obstruction explanation is that it does not explain how streamtube pinching comes about, or why it is greater over the upper surface than the lower surface. For conventional wings that are flat on the bottom and curved on top this makes some intuitive sense, but it does not explain how flat plates, symmetric airfoils, sailboat sails, or conventional airfoils flying upside down can generate lift, and attempts to calculate lift based on the amount of constriction or obstruction do not predict experimental results.^{[50][51][52][53]} Another flaw is that conservation of mass is not a satisfying physical reason why the flow would speed up. Effectively explaining the acceleration of an object requires identifying the force that accelerates it.^[54]

A serious flaw common to all the Bernoulli-based explanations is that they imply that a speed difference can arise from causes other than a pressure difference, and that the speed difference then leads to a pressure difference, by Bernoulli's principle. This implied one-way causation is a misconception. The real relationship between pressure and flow speed is a mutual interaction.^[4] As explained below under a more comprehensive physical explanation, producing a lift force requires maintaining pressure differences in both the vertical and horizontal directions. The Bernoulli-only explanations do not explain how the pressure differences in the vertical direction are sustained. That is, they leave out the flow-deflection part of the interaction.^[4]

Although the two simple Bernoulli-based explanations above are incorrect, there is nothing incorrect about Bernoulli's principle or the fact that the air goes faster on the top of the wing, and Bernoulli's principle can be used correctly as part of a more complicated explanation of lift.^[55]

Lift is a result of pressure differences and depends on angle of attack, airfoil shape, air density, and airspeed.

Pressure is the normal force per unit area exerted by the air on itself and on surfaces that it touches. The lift force is transmitted through the pressure, which acts perpendicular to the surface of the airfoil. Thus, the net force manifests itself as pressure differences. The direction of the net force implies that the average pressure on the upper surface of the airfoil is lower than the average pressure on the underside.^[56]

These pressure differences arise in conjunction with the curved airflow. When a fluid follows a curved path, there is a pressure gradient perpendicular to the flow direction with higher pressure on the outside of the curve and lower pressure on the inside.^[57] This direct relationship between curved streamlines and pressure differences, sometimes called the streamline curvature theorem, was derived from Newton's second law by Leonhard Euler in 1754:

${\displaystyle {\frac {\operatorname {d} p}{\operatorname {d} R}}=\rho {\frac {v^{2}}{R}}}$

The left side of this equation represents the pressure difference perpendicular to the fluid flow. On the right side of the equation, ρ is the density, v is the velocity, and R is the radius of curvature. This formula shows that higher velocities and tighter curvatures create larger pressure differentials and that for straight flow (R → ∞), the pressure difference is zero.^[58]

The angle of attack is the angle between the chord line of an airfoil and the oncoming airflow. A symmetrical airfoil generates zero lift at zero angle of attack. But as the angle of attack increases, the air is deflected through a larger angle and the vertical component of the airstream velocity increases, resulting in more lift. For small angles, a symmetrical airfoil generates a lift force roughly proportional to the angle of attack.^[59][60]

As the angle of attack increases, the lift reaches a maximum at some angle; increasing the angle of attack beyond this critical angle of attack causes the upper-surface flow to separate from the wing; there is less deflection downward so the airfoil generates less lift. The airfoil is said to be stalled.^[61]

The maximum lift force that can be generated by an airfoil at a given airspeed depends on the shape of the airfoil, especially the amount of camber (curvature such that the upper surface is more convex than the lower surface, as illustrated at right). Increasing the camber generally increases the maximum lift at a given airspeed.^[62][63]

Cambered airfoils generate lift at zero angle of attack. When the chord line is horizontal, the trailing edge has a downward direction and since the air follows the trailing edge it is deflected downward.^[64] When a cambered airfoil is upside down, the angle of attack can be adjusted so that the lift force is upward. This explains how a plane can fly upside down.^[65][66]

The ambient flow conditions which affect lift include the fluid density, viscosity and speed of flow. Density is affected by temperature, and by the medium's acoustic velocity – i.e. by compressibility effects.

Lift is proportional to the density of the air and approximately proportional to the square of the flow speed. Lift also depends on the size of the wing, being generally proportional to the wing's area projected in the lift direction. In calculations it is convenient to quantify lift in terms of a lift coefficient based on these factors.

No matter how smooth the surface of an airfoil seems, any surface is rough on the scale of air molecules. Air molecules flying into the surface bounce off the rough surface in random directions relative to their original velocities. The result is that when the air is viewed as a continuous material, it is seen to be unable to slide along the surface, and the air's velocity relative to the airfoil decreases to nearly zero at the surface (i.e., the air molecules "stick" to the surface instead of sliding along it), something known as the no-slip condition.^[67] Because the air at the surface has near-zero velocity but the air away from the surface is moving, there is a thin boundary layer in which air close to the surface is subjected to a shearing motion.^[68][69] The air's viscosity resists the shearing, giving rise to a shear stress at the airfoil's surface called skin friction drag. Over most of the surface of most airfoils, the boundary layer is naturally turbulent, which increases skin friction drag.^[69][70]

Under usual flight conditions, the boundary layer remains attached to both the upper and lower surfaces all the way to the trailing edge, and its effect on the rest of the flow is modest. Compared to the predictions of inviscid flow theory, in which there is no boundary layer, the attached boundary layer reduces the lift by a modest amount and modifies the pressure distribution somewhat, which results in a viscosity-related pressure drag over and above the skin friction drag. The total of the skin friction drag and the viscosity-related pressure drag is usually called the profile drag.^[70][71]

An airfoil's maximum lift at a given airspeed is limited by boundary-layer separation. As the angle of attack is increased, a point is reached where the boundary layer can no longer remain attached to the upper surface. When the boundary layer separates, it leaves a region of recirculating flow above the upper surface, as illustrated in the flow-visualization photo at right. This is known as the stall, or stalling. At angles of attack above the stall, lift is significantly reduced, though it does not drop to zero. The maximum lift that can be achieved before stall, in terms of the lift coefficient, is generally less than 1.5 for single-element airfoils and can be more than 3.0 for airfoils with high-lift slotted flaps and leading-edge devices deployed.^[72]

The flow around bluff bodies – i.e. without a streamlined shape, or stalling airfoils – may also generate lift, in addition to a strong drag force. This lift may be steady, or it may oscillate due to vortex shedding. Interaction of the object's flexibility with the vortex shedding may enhance the effects of fluctuating lift and cause vortex-induced vibrations.^[73] For instance, the flow around a circular cylinder generates a Kármán vortex street: vortices being shed in an alternating fashion from the cylinder's sides. The oscillatory nature of the flow produces a fluctuating lift force on the cylinder, even though the net (mean) force is negligible. The lift force frequency is characterised by the dimensionless Strouhal number, which depends on the Reynolds number of the flow.^[74][75]

For a flexible structure, this oscillatory lift force may induce vortex-induced vibrations. Under certain conditions – for instance resonance or strong spanwise correlation of the lift force – the resulting motion of the structure due to the lift fluctuations may be strongly enhanced. Such vibrations may pose problems and threaten collapse in tall man-made structures like industrial chimneys.^[73]

In the Magnus effect, a lift force is generated by a spinning cylinder in a freestream. Here the mechanical rotation acts on the boundary layer, causing it to separate at different locations on the two sides of the cylinder. The asymmetric separation changes the effective shape of the cylinder as far as the flow is concerned such that the cylinder acts like a lifting airfoil with circulation in the outer flow.^[76]

As described above under "Simplified physical explanations of lift on an airfoil", there are two main popular explanations: one based on downward deflection of the flow (Newton's laws), and one based on pressure differences accompanied by changes in flow speed (Bernoulli's principle). Either of these, by itself, correctly identifies some aspects of the lifting flow but leaves other important aspects of the phenomenon unexplained. A more comprehensive explanation involves both downward deflection and pressure differences (including changes in flow speed associated with the pressure differences), and requires looking at the flow in more detail.^[77]

The airfoil shape and angle of attack work together so that the airfoil exerts a downward force on the air as it flows past. According to Newton's third law, the air must then exert an equal and opposite (upward) force on the airfoil, which is the lift.^[17]

The net force exerted by the air occurs as a pressure difference over the airfoil's surfaces.^[78] Pressure in a fluid is always positive in an absolute sense,^[79] so that pressure must always be thought of as pushing, and never as pulling. The pressure thus pushes inward on the airfoil everywhere on both the upper and lower surfaces. The flowing air reacts to the presence of the wing by reducing the pressure on the wing's upper surface and increasing the pressure on the lower surface. The pressure on the lower surface pushes up harder than the reduced pressure on the upper surface pushes down, and the net result is upward lift.^[78]

The pressure difference which results in lift acts directly on the airfoil surfaces; however, understanding how the pressure difference is produced requires understanding what the flow does over a wider area.

An airfoil affects the speed and direction of the flow over a wide area, producing a pattern called a velocity field. When an airfoil produces lift, the flow ahead of the airfoil is deflected upward, the flow above and below the airfoil is deflected downward leaving the air far behind the airfoil in the same state as the oncoming flow far ahead. The flow above the upper surface is sped up, while the flow below the airfoil is slowed down. Together with the upward deflection of air in front and the downward deflection of the air immediately behind, this establishes a net circulatory component of the flow. The downward deflection and the changes in flow speed are pronounced and extend over a wide area, as can be seen in the flow animation on the right. These differences in the direction and speed of the flow are greatest close to the airfoil and decrease gradually far above and below. All of these features of the velocity field also appear in theoretical models for lifting flows.^[80][81]

The pressure is also affected over a wide area, in a pattern of non-uniform pressure called a pressure field. When an airfoil produces lift, there is a diffuse region of low pressure above the airfoil, and usually a diffuse region of high pressure below, as illustrated by the isobars (curves of constant pressure) in the drawing. The pressure difference that acts on the surface is just part of this pressure field.^[82]

The non-uniform pressure exerts forces on the air in the direction from higher pressure to lower pressure. The direction of the force is different at different locations around the airfoil, as indicated by the block arrows in the pressure field around an airfoil figure. Air above the airfoil is pushed toward the center of the low-pressure region, and air below the airfoil is pushed outward from the center of the high-pressure region.

According to Newton's second law, a force causes air to accelerate in the direction of the force. Thus the vertical arrows in the accompanying pressure field diagram indicate that air above and below the airfoil is accelerated, or turned downward, and that the non-uniform pressure is thus the cause of the downward deflection of the flow visible in the flow animation. To produce this downward turning, the airfoil must have a positive angle of attack or have sufficient positive camber. Note that the downward turning of the flow over the upper surface is the result of the air being pushed downward by higher pressure above it than below it. Some explanations that refer to the "Coandă effect" suggest that viscosity plays a key role in the downward turning, but this is false. (see above under "Controversy regarding the Coandă effect").

The arrows ahead of the airfoil indicate that the flow ahead of the airfoil is deflected upward, and the arrows behind the airfoil indicate that the flow behind is deflected upward again, after being deflected downward over the airfoil. These deflections are also visible in the flow animation.

The arrows ahead of the airfoil and behind also indicate that air passing through the low-pressure region above the airfoil is sped up as it enters, and slowed back down as it leaves. Air passing through the high-pressure region below the airfoil is slowed down as it enters and then sped back up as it leaves. Thus the non-uniform pressure is also the cause of the changes in flow speed visible in the flow animation. The changes in flow speed are consistent with Bernoulli's principle, which states that in a steady flow without viscosity, lower pressure means higher speed, and higher pressure means lower speed.

Thus changes in flow direction and speed are directly caused by the non-uniform pressure. But this cause-and-effect relationship is not just one-way; it works in both directions simultaneously. The air's motion is affected by the pressure differences, but the existence of the pressure differences depends on the air's motion. The relationship is thus a mutual, or reciprocal, interaction: Air flow changes speed or direction in response to pressure differences, and the pressure differences are sustained by the air's resistance to changing speed or direction.^[83] A pressure difference can exist only if something is there for it to push against. In aerodynamic flow, the pressure difference pushes against the air's inertia, as the air is accelerated by the pressure difference.^[84] This is why the air's mass is part of the calculation, and why lift depends on air density.

Sustaining the pressure difference that exerts the lift force on the airfoil surfaces requires sustaining a pattern of non-uniform pressure in a wide area around the airfoil. This requires maintaining pressure differences in both the vertical and horizontal directions, and thus requires both downward turning of the flow and changes in flow speed according to Bernoulli's principle. The pressure differences and the changes in flow direction and speed sustain each other in a mutual interaction. The pressure differences follow naturally from Newton's second law and from the fact that flow along the surface follows the predominantly downward-sloping contours of the airfoil. And the fact that the air has mass is crucial to the interaction.^[85]

Producing a lift force requires both downward turning of the flow and changes in flow speed consistent with Bernoulli's principle. Each of the simplified explanations given above in Simplified physical explanations of lift on an airfoil falls short by trying to explain lift in terms of only one or the other, thus explaining only part of the phenomenon and leaving other parts unexplained.^[86]

When the pressure distribution on the airfoil surface is known, determining the total lift requires adding up the contributions to the pressure force from local elements of the surface, each with its own local value of pressure. The total lift is thus the integral of the pressure, in the direction perpendicular to the farfield flow, over the airfoil surface.^[87]

${\displaystyle L=\oint p\mathbf {n} \cdot \mathbf {k} \;\mathrm {d} S,}$

where:

• S is the projected (planform) area of the airfoil, measured normal to the mean airflow;
• n is the normal unit vector pointing into the wing;
• k is the vertical unit vector, normal to the freestream direction.

The above lift equation neglects the skin friction forces, which are small compared to the pressure forces.

By using the streamwise vector i parallel to the freestream in place of k in the integral, we obtain an expression for the pressure drag D_p (which includes the pressure portion of the profile drag and, if the wing is three-dimensional, the induced drag). If we use the spanwise vector j, we obtain the side force Y.

${\displaystyle {\begin{aligned}D_{p}&=\oint p\mathbf {n} \cdot \mathbf {i} \;\mathrm {d} S,\\Y&=\oint p\mathbf {n} \cdot \mathbf {j} \;\mathrm {d} S.\end{aligned}}}$

The validity of this integration generally requires the airfoil shape to be a closed curve that is piecewise smooth.

Lift depends on the size of the wing, being approximately proportional to the wing area. It is often convenient to quantify the lift of a given airfoil by its lift coefficient ${\displaystyle C_{L}}$, which defines its overall lift in terms of a unit area of the wing.

If the value of ${\displaystyle C_{L}}$ for a wing at a specified angle of attack is given, then the lift produced for specific flow conditions can be determined:^[88]

${\displaystyle L={\tfrac {1}{2}}\rho v^{2}SC_{L}}$

where

• ${\displaystyle L}$ is the lift force
• ${\displaystyle \rho }$ is the air density
• ${\displaystyle v}$ is the velocity or true airspeed
• ${\displaystyle S}$ is the planform (projected) wing area
• ${\displaystyle C_{L}}$ is the lift coefficient at the desired angle of attack, Mach number, and Reynolds number^[89]

Mathematical theories of lift are based on continuum fluid mechanics, assuming that air flows as a continuous fluid.^[90][91][92] Lift is generated in accordance with the fundamental principles of physics, the most relevant being the following three principles:^[93]

• Conservation of momentum, which is a consequence of Newton's laws of motion, especially Newton's second law (which relates the net force on an element of air to its rate of momentum change) and third law.
• Conservation of mass, including the assumption that the airfoil's surface is impermeable for the air flowing around, and
• Conservation of energy, which says that energy is neither created nor destroyed.

Because an airfoil affects the flow in a wide area around it, the conservation laws of mechanics are embodied in the form of partial differential equations combined with a set of boundary condition requirements which the flow has to satisfy at the airfoil surface and far away from the airfoil.^[94]

To predict lift requires solving the equations for a particular airfoil shape and flow condition, which generally requires calculations that are so voluminous that they are practical only on a computer, through the methods of computational fluid dynamics (CFD). Determining the net aerodynamic force from a CFD solution requires "adding up" (integrating) the forces due to pressure and shear determined by the CFD over every surface element of the airfoil as described under "pressure integration".

The Navier–Stokes equations (NS) provide the potentially most accurate theory of lift, but in practice, capturing the effects of turbulence in the boundary layer on the airfoil surface requires sacrificing some accuracy, and requires use of the Reynolds-averaged Navier–Stokes equations (RANS). Simpler but less accurate theories have also been developed.

These equations represent conservation of mass, Newton's second law (conservation of momentum), conservation of energy, the Newtonian law for the action of viscosity, the Fourier heat conduction law, an equation of state relating density, temperature, and pressure, and formulas for the viscosity and thermal conductivity of the fluid.^[95][96]

In principle, the NS equations, combined with boundary conditions of no through-flow and no slip at the airfoil surface, could be used to predict lift with high accuracy in any situation in ordinary atmospheric flight. However, airflows in practical situations always involve turbulence in the boundary layer next to the airfoil surface, at least over the aft portion of the airfoil. Predicting lift by solving the NS equations in their raw form would require the calculations to resolve the details of the turbulence, down to the smallest eddy. This is not yet possible, even on the most powerful computer.^[97] So in principle the NS equations provide a complete and very accurate theory of lift, but practical prediction of lift requires that the effects of turbulence be modeled in the RANS equations rather than computed directly.

These are the NS equations with the turbulence motions averaged over time, and the effects of the turbulence on the time-averaged flow represented by turbulence modeling (an additional set of equations based on a combination of dimensional analysis and empirical information on how turbulence affects a boundary layer in a time-averaged average sense).^[98][99] A RANS solution consists of the time-averaged velocity vector, pressure, density, and temperature defined at a dense grid of points surrounding the airfoil.

The amount of computation required is a minuscule fraction (billionths)^[97] of what would be required to resolve all of the turbulence motions in a raw NS calculation, and with large computers available it is now practical to carry out RANS calculations for complete airplanes in three dimensions. Because turbulence models are not perfect, the accuracy of RANS calculations is imperfect, but it is adequate for practical aircraft design. Lift predicted by RANS is usually within a few percent of the actual lift.

The Euler equations are the NS equations without the viscosity, heat conduction, and turbulence effects.^[100] As with a RANS solution, an Euler solution consists of the velocity vector, pressure, density, and temperature defined at a dense grid of points surrounding the airfoil. While the Euler equations are simpler than the NS equations, they do not lend themselves to exact analytic solutions.

Further simplification is available through potential flow theory, which reduces the number of unknowns to be determined, and makes analytic solutions possible in some cases, as described below.

Either Euler or potential-flow calculations predict the pressure distribution on the airfoil surfaces roughly correctly for angles of attack below stall, where they might miss the total lift by as much as 10–20%. At angles of attack above stall, inviscid calculations do not predict that stall has happened, and as a result they grossly overestimate the lift.

In potential-flow theory, the flow is assumed to be irrotational, i.e. that small fluid parcels have no net rate of rotation. Mathematically, this is expressed by the statement that the curl of the velocity vector field is everywhere equal to zero. Irrotational flows have the convenient property that the velocity can be expressed as the gradient of a scalar function called a potential. A flow represented in this way is called potential flow.^{[101][102][103][104]}

In potential-flow theory, the flow is assumed to be incompressible. Incompressible potential-flow theory has the advantage that the equation (Laplace's equation) to be solved for the potential is linear, which allows solutions to be constructed by superposition of other known solutions. The incompressible-potential-flow equation can also be solved by conformal mapping, a method based on the theory of functions of a complex variable. In the early 20th century, before computers were available, conformal mapping was used to generate solutions to the incompressible potential-flow equation for a class of idealized airfoil shapes, providing some of the first practical theoretical predictions of the pressure distribution on a lifting airfoil.

A solution of the potential equation directly determines only the velocity field. The pressure field is deduced from the velocity field through Bernoulli's equation.

Applying potential-flow theory to a lifting flow requires special treatment and an additional assumption. The problem arises because lift on an airfoil in inviscid flow requires circulation in the flow around the airfoil (See "Circulation and the Kutta–Joukowski theorem" below), but a single potential function that is continuous throughout the domain around the airfoil cannot represent a flow with nonzero circulation. The solution to this problem is to introduce a branch cut, a curve or line from some point on the airfoil surface out to infinite distance, and to allow a jump in the value of the potential across the cut. The jump in the potential imposes circulation in the flow equal to the potential jump and thus allows nonzero circulation to be represented. However, the potential jump is a free parameter that is not determined by the potential equation or the other boundary conditions, and the solution is thus indeterminate. A potential-flow solution exists for any value of the circulation and any value of the lift. One way to resolve this indeterminacy is to impose the Kutta condition,^[105][106] which is that, of all the possible solutions, the physically reasonable solution is the one in which the flow leaves the trailing edge smoothly. The streamline sketches illustrate one flow pattern with zero lift, in which the flow goes around the trailing edge and leaves the upper surface ahead of the trailing edge, and another flow pattern with positive lift, in which the flow leaves smoothly at the trailing edge in accordance with the Kutta condition.

This is potential-flow theory with the further assumptions that the airfoil is very thin and the angle of attack is small.^[107] The linearized theory predicts the general character of the airfoil pressure distribution and how it is influenced by airfoil shape and angle of attack, but is not accurate enough for design work. For a 2D airfoil, such calculations can be done in a fraction of a second in a spreadsheet on a PC.

When an airfoil generates lift, several components of the overall velocity field contribute to a net circulation of air around it: the upward flow ahead of the airfoil, the accelerated flow above, the decelerated flow below, and the downward flow behind.

The circulation can be understood as the total amount of "spinning" (or vorticity) of an inviscid fluid around the airfoil.

The Kutta–Joukowski theorem relates the lift per unit width of span of a two-dimensional airfoil to this circulation component of the flow.^{[80][108][109]} It is a key element in an explanation of lift that follows the development of the flow around an airfoil as the airfoil starts its motion from rest and a starting vortex is formed and left behind, leading to the formation of circulation around the airfoil.^{[110][111][112]} Lift is then inferred from the Kutta-Joukowski theorem. This explanation is largely mathematical, and its general progression is based on logical inference, not physical cause-and-effect.^[113]

The Kutta–Joukowski model does not predict how much circulation or lift a two-dimensional airfoil produces. Calculating the lift per unit span using Kutta–Joukowski requires a known value for the circulation. In particular, if the Kutta condition is met, in which the rear stagnation point moves to the airfoil trailing edge and attaches there for the duration of flight, the lift can be calculated theoretically through the conformal mapping method.

The lift generated by a conventional airfoil is dictated by both its design and the flight conditions, such as forward velocity, angle of attack and air density. Lift can be increased by artificially increasing the circulation, for example by boundary-layer blowing or the use of blown flaps. In the Flettner rotor the entire airfoil is circular and spins about a spanwise axis to create the circulation.

The flow around a three-dimensional wing involves significant additional issues, especially relating to the wing tips. For a wing of low aspect ratio, such as a typical delta wing, two-dimensional theories may provide a poor model and three-dimensional flow effects can dominate.^[114] Even for wings of high aspect ratio, the three-dimensional effects associated with finite span can affect the whole span, not just close to the tips.

The vertical pressure gradient at the wing tips causes air to flow sideways, out from under the wing then up and back over the upper surface. This reduces the pressure gradient at the wing tip, therefore also reducing lift. The lift tends to decrease in the spanwise direction from root to tip, and the pressure distributions around the airfoil sections change accordingly in the spanwise direction. Pressure distributions in planes perpendicular to the flight direction tend to look like the illustration at right.^[115] This spanwise-varying pressure distribution is sustained by a mutual interaction with the velocity field. Flow below the wing is accelerated outboard, flow outboard of the tips is accelerated upward, and flow above the wing is accelerated inboard, which results in the flow pattern illustrated at right.^[116]

There is more downward turning of the flow than there would be in a two-dimensional flow with the same airfoil shape and sectional lift, and a higher sectional angle of attack is required to achieve the same lift compared to a two-dimensional flow.^[117] The wing is effectively flying in a downdraft of its own making, as if the freestream flow were tilted downward, with the result that the total aerodynamic force vector is tilted backward slightly compared to what it would be in two dimensions. The additional backward component of the force vector is called lift-induced drag.

The difference in the spanwise component of velocity above and below the wing (between being in the inboard direction above and in the outboard direction below) persists at the trailing edge and into the wake downstream. After the flow leaves the trailing edge, this difference in velocity takes place across a relatively thin shear layer called a vortex sheet.

The wingtip flow leaving the wing creates a tip vortex. As the main vortex sheet passes downstream from the trailing edge, it rolls up at its outer edges, merging with the tip vortices. The combination of the wingtip vortices and the vortex sheets feeding them is called the vortex wake.

In addition to the vorticity in the trailing vortex wake there is vorticity in the wing's boundary layer, called 'bound vorticity', which connects the trailing sheets from the two sides of the wing into a vortex system in the general form of a horseshoe. The horseshoe form of the vortex system was recognized by the British aeronautical pioneer Lanchester in 1907.^[118]

Given the distribution of bound vorticity and the vorticity in the wake, the Biot–Savart law (a vector-calculus relation) can be used to calculate the velocity perturbation anywhere in the field, caused by the lift on the wing. Approximate theories for the lift distribution and lift-induced drag of three-dimensional wings are based on such analysis applied to the wing's horseshoe vortex system.^[119][120] In these theories, the bound vorticity is usually idealized and assumed to reside at the camber surface inside the wing.

Because the velocity is deduced from the vorticity in such theories, some authors describe the situation to imply that the vorticity is the cause of the velocity perturbations, using terms such as "the velocity induced by the vortex", for example.^[121] But attributing mechanical cause-and-effect between the vorticity and the velocity in this way is not consistent with the physics.^{[122][123][124]} The velocity perturbations in the flow around a wing are in fact produced by the pressure field.^[125]

The flow around a lifting airfoil must satisfy Newton's second law regarding conservation of momentum, both locally at every point in the flow field, and in an integrated sense over any extended region of the flow. For an extended region, Newton's second law takes the form of the momentum theorem for a control volume, where a control volume can be any region of the flow chosen for analysis. The momentum theorem states that the integrated force exerted at the boundaries of the control volume (a surface integral), is equal to the integrated time rate of change (material derivative) of the momentum of fluid parcels passing through the interior of the control volume. For a steady flow, this can be expressed in the form of the net surface integral of the flux of momentum through the boundary.^[126]

The lifting flow around a 2D airfoil is usually analyzed in a control volume that completely surrounds the airfoil, so that the inner boundary of the control volume is the airfoil surface, where the downward force per unit span ${\displaystyle -L'}$ is exerted on the fluid by the airfoil. The outer boundary is usually either a large circle or a large rectangle. At this outer boundary distant from the airfoil, the velocity and pressure are well represented by the velocity and pressure associated with a uniform flow plus a vortex, and viscous stress is negligible, so that the only force that must be integrated over the outer boundary is the pressure.^{[127][128][129]} The free-stream velocity is usually assumed to be horizontal, with lift vertically upward, so that the vertical momentum is the component of interest.

For the free-air case (no ground plane), the force ${\displaystyle -L'}$ exerted by the airfoil on the fluid is manifested partly as momentum fluxes and partly as pressure differences at the outer boundary, in proportions that depend on the shape of the outer boundary, as shown in the diagram at right. For a flat horizontal rectangle that is much longer than it is tall, the fluxes of vertical momentum through the front and back are negligible, and the lift is accounted for entirely by the integrated pressure differences on the top and bottom.^[127] For a square or circle, the momentum fluxes and pressure differences account for half the lift each.^{[127][128][129]} For a vertical rectangle that is much taller than it is wide, the unbalanced pressure forces on the top and bottom are negligible, and lift is accounted for entirely by momentum fluxes, with a flux of upward momentum that enters the control volume through the front accounting for half the lift, and a flux of downward momentum that exits the control volume through the back accounting for the other half.^[127]

The results of all of the control-volume analyses described above are consistent with the Kutta–Joukowski theorem described above. Both the tall rectangle and circle control volumes have been used in derivations of the theorem.^[128][129]

An airfoil produces a pressure field in the surrounding air, as explained under "The wider flow around the airfoil" above. The pressure differences associated with this field die off gradually, becoming very small at large distances, but never disappearing altogether. Below the airplane, the pressure field persists as a positive pressure disturbance that reaches the ground, forming a pattern of slightly-higher-than-ambient pressure on the ground, as shown on the right.^[130] Although the pressure differences are very small far below the airplane, they are spread over a wide area and add up to a substantial force. For steady, level flight, the integrated force due to the pressure differences is equal to the total aerodynamic lift of the airplane and to the airplane's weight. According to Newton's third law, this pressure force exerted on the ground by the air is matched by an equal-and-opposite upward force exerted on the air by the ground, which offsets all of the downward force exerted on the air by the airplane. The net force due to the lift, acting on the atmosphere as a whole, is therefore zero, and thus there is no integrated accumulation of vertical momentum in the atmosphere, as was noted by Lanchester early in the development of modern aerodynamics.^[131]

• Drag coefficient
• Flow separation
• Fluid dynamics
• Foil (fluid mechanics)
• Küssner effect
• Lift-to-drag ratio
• Lifting-line theory
• Spoiler (automotive)