Perfect fluid

In classical mechanics, ideal fluids are described by Euler equations. Ideal fluids produce no drag according to d'Alembert's paradox. If a fluid produced drag, then work would be needed to move an object through the fluid and that work would produce heat or fluid motion. However, a perfect fluid can not dissipate energy and it can't transmit energy infinitely far from the object.^[4]: 34

A flock of birds in the medium of air is an example of a perfect fluid; an electron gas is also modeled as a perfect fluid.^[1]

Superfluids are fluids with zero viscosity, however in practice superfluids cannot be accurately described as a perfect fluid.^[5][6] In the two-fluid model, superfluids are macroscopically considered as having two-coexisting phases, a mixture between a normal fluid and a perfect fluid.^[6]

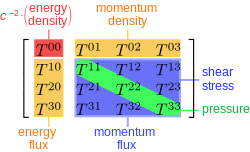
Perfect fluids are a fluid solution used in general relativity to model idealized distributions of matter, such as the interior of a star or an isotropic universe. In the latter case, the symmetry of the cosmological principle and the equation of state of the perfect fluid lead to Friedmann equation for the expansion of the universe.^[7]

In space-positive metric signature tensor notation, the stress–energy tensor of a perfect fluid can be written in the form

${\displaystyle T^{\mu \nu }=\left(\rho _{m}+{\frac {p}{c^{2}}}\right)\,U^{\mu }U^{\nu }+p\,\eta ^{\mu \nu },}$

where U is the 4-velocity vector field of the fluid and where ${\displaystyle \eta _{\mu \nu }=\operatorname {diag} (-1,1,1,1)}$ is the metric tensor of Minkowski spacetime.

The case where p=0 describes a dust solution. When ${\displaystyle p=\rho _{m}c^{2}/3}$, it describes a photon gas (radiation).

In time-positive metric signature tensor notation, the stress–energy tensor of a perfect fluid can be written in the form

${\displaystyle T^{\mu \nu }=\left(\rho _{\text{m}}+{\frac {p}{c^{2}}}\right)\,U^{\mu }U^{\nu }-p\,\eta ^{\mu \nu },}$

where ${\displaystyle U}$ is the 4-velocity of the fluid and where ${\displaystyle \eta _{\mu \nu }=\operatorname {diag} (1,-1,-1,-1)}$ is the metric tensor of Minkowski spacetime.

This takes on a particularly simple form in the rest frame

${\displaystyle \left[{\begin{matrix}\rho _{e}&0&0&0\\0&p&0&0\\0&0&p&0\\0&0&0&p\end{matrix}}\right]}$

where ${\displaystyle \rho _{\text{e}}=\rho _{\text{m}}c^{2}}$ is the energy density and ${\displaystyle p}$ is the pressure of the fluid.

Perfect fluids admit a Lagrangian formulation, which allows the techniques used in field theory, in particular, quantization, to be applied to fluids.

Relativistic Euler equations read

${\displaystyle \partial _{\nu }T^{\mu \nu }=0}$

in the non relativistic limit, these equations reduce to the usual Euler equations.^[8]

• Equation of state
• Ideal gas
• Fluid solutions in general relativity
• Potential flow