Hubbry Logo
BijectionBijectionMain
Open search
Bijection
Community hub
Bijection
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Bijection
Bijection
Bijection
View on Wikipedia
from Wikipedia

A bijective function, f: X → Y, where set X is {1, 2, 3, 4} and set Y is {A, B, C, D}. For example, f(1) = D.
Function
x ↦ f (x)
History of the function concept
Types by domain and codomain
 Classes/properties 
  Constructions
  Generalizations  
  List of specific functions

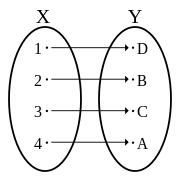
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set (the codomain) is the image of exactly one element of the first set (the domain). Equivalently, a bijection is a relation between two sets such that each element of either set is paired with exactly one element of the other set.

A function is bijective if it is invertible; that is, a function is bijective if and only if there is a function the inverse of f, such that each of the two ways for composing the two functions produces an identity function: for each in and for each in

For example, the multiplication by two defines a bijection from the integers to the even numbers, which has the division by two as its inverse function.

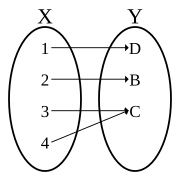
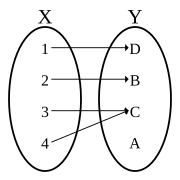
A function is bijective if and only if it is both injective (or one-to-one)—meaning that each element in the codomain is mapped from at most one element of the domain—and surjective (or onto)—meaning that each element of the codomain is mapped from at least one element of the domain. The term one-to-one correspondence must not be confused with one-to-one function, which means injective but not necessarily surjective.

The elementary operation of counting establishes a bijection from some finite set to the first natural numbers (1, 2, 3, ...), up to the number of elements in the counted set. It results that two finite sets have the same number of elements if and only if there exists a bijection between them. More generally, two sets are said to have the same cardinal number if there exists a bijection between them.

A bijective function from a set to itself is also called a permutation,[1] and the set of all permutations of a set forms its symmetric group.

Some bijections with further properties have received specific names, which include automorphisms, isomorphisms, homeomorphisms, diffeomorphisms, permutations, and most geometric transformations. Galois correspondences are bijections between sets of mathematical objects of apparently very different nature.

Definition

[edit]

For a binary relation pairing elements of set X with elements of set Y to be a bijection, four properties must hold:

  1. each element of X must be paired with at least one element of Y,
  2. no element of X may be paired with more than one element of Y,
  3. each element of Y must be paired with at least one element of X, and
  4. no element of Y may be paired with more than one element of X.

Satisfying properties (1) and (2) means that a pairing is a function with domain X. It is more common to see properties (1) and (2) written as a single statement: Every element of X is paired with exactly one element of Y. Functions which satisfy property (3) are said to be "onto Y " and are called surjections (or surjective functions). Functions which satisfy property (4) are said to be "one-to-one functions" and are called injections (or injective functions).[2] With this terminology, a bijection is a function which is both a surjection and an injection, or using other words, a bijection is a function which is both "one-to-one" and "onto".[3]

Examples

[edit]

Batting line-up of a baseball or cricket team

[edit]

Consider the batting line-up of a baseball or cricket team (or any list of all the players of any sports team where every player holds a specific spot in a line-up). The set X will be the players on the team (of size nine in the case of baseball) and the set Y will be the positions in the batting order (1st, 2nd, 3rd, etc.) The "pairing" is given by which player is in what position in this order. Property (1) is satisfied since each player is somewhere in the list. Property (2) is satisfied since no player bats in two (or more) positions in the order. Property (3) says that for each position in the order, there is some player batting in that position and property (4) states that two or more players are never batting in the same position in the list.

Seats and students of a classroom

[edit]

In a classroom there are a certain number of seats. A group of students enter the room and the instructor asks them to be seated. After a quick look around the room, the instructor declares that there is a bijection between the set of students and the set of seats, where each student is paired with the seat they are sitting in. What the instructor observed in order to reach this conclusion was that:

  1. Every student was in a seat (there was no one standing),
  2. No student was in more than one seat,
  3. Every seat had someone sitting there (there were no empty seats), and
  4. No seat had more than one student in it.

The instructor was able to conclude that there were just as many seats as there were students, without having to count either set.

More mathematical examples

[edit]
n mod 2 + (-1)^(n+1) n
Bijection from the natural numbers to the integers, which maps 2n to −n and 2n + 1 to n+1, for n ≥ 0.
  • For any set X, the identity function 1X: X → X, 1X(x) = x is bijective.
  • The multiplicative inverse function gives a bijection of the unit interval (0, 1) with the semi-infinite interval (1, +∞).
  • The function f: R → R, f(x) = 2x + 1 is bijective, since for each y there is a unique x = (y − 1)/2 such that f(x) = y. More generally, any linear function over the reals, f: R → R, f(x) = ax + b (where a is non-zero) is a bijection. Each real number y is obtained from (or paired with) the real number x = (y − b)/a.
  • The function f: R → (−π/2, π/2), given by f(x) = arctan(x) is bijective, since each real number x is paired with exactly one angle y in the interval (−π/2, π/2) so that tan(y) = x (that is, y = arctan(x)). If the codomain (−π/2, π/2) was made larger to include an integer multiple of π/2, then this function would no longer be onto (surjective), since there is no real number which could be paired with the multiple of π/2 by this arctan function.
  • The exponential function, g: R → R, g(x) = ex, is not bijective: for instance, there is no x in R such that g(x) = −1, showing that g is not onto (surjective). However, if the codomain is restricted to the positive real numbers , then g would be bijective; its inverse (see below) is the natural logarithm function ln.
  • The function h: R → R+, h(x) = x2 is not bijective: for instance, h(−1) = h(1) = 1, showing that h is not one-to-one (injective). However, if the domain is restricted to , then h would be bijective; its inverse is the positive square root function.
  • By Schröder–Bernstein theorem, given any two sets X and Y, and two injective functions f: X → Y and g: Y → X, there exists a bijective function h: X → Y.

Inverses

[edit]

A bijection f with domain X (indicated by f: X → Y in functional notation) also defines a converse relation starting in Y and going to X (by turning the arrows around). The process of "turning the arrows around" for an arbitrary function does not, in general, yield a function, but properties (3) and (4) of a bijection say that this inverse relation is a function with domain Y. Moreover, properties (1) and (2) then say that this inverse function is a surjection and an injection, that is, the inverse function exists and is also a bijection. Functions that have inverse functions are said to be invertible. A function is invertible if and only if it is a bijection.

Stated in concise mathematical notation, a function f: X → Y is bijective if and only if it satisfies the condition

for every y in Y there is a unique x in X with y = f(x).

Continuing with the baseball batting line-up example, the function that is being defined takes as input the name of one of the players and outputs the position of that player in the batting order. Since this function is a bijection, it has an inverse function which takes as input a position in the batting order and outputs the player who will be batting in that position.

Composition

[edit]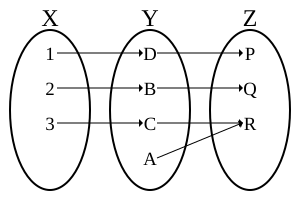
A bijection composed of an injection (X → Y) and a surjection (Y → Z).

The composition of two bijections and is a bijection, whose inverse is given by is .

Conversely, if the composition of two functions is bijective, it only follows that f is injective and g is surjective.

Cardinality

[edit]

If X and Y are finite sets, then there exists a bijection between the two sets X and Y if and only if X and Y have the same number of elements. Indeed, in axiomatic set theory, this is taken as the definition of "same number of elements" (equinumerosity), and generalising this definition to infinite sets leads to the concept of cardinal number, a way to distinguish the various sizes of infinite sets.

Properties

[edit]
  • A function f: R → R is bijective if and only if its graph meets every horizontal and vertical line exactly once.
  • If X is a set, then the bijective functions from X to itself, together with the operation of functional composition (), form a group, the symmetric group of X, which is denoted variously by S(X), SX, or X! (X factorial).
  • Bijections preserve cardinalities of sets: for a subset A of the domain with cardinality |A| and subset B of the codomain with cardinality |B|, one has the following equalities:
    |f(A)| = |A| and |f−1(B)| = |B|.
  • If X and Y are finite sets with the same cardinality, and f: X → Y, then the following are equivalent:
    1. f is a bijection.
    2. f is a surjection.
    3. f is an injection.
  • For a finite set S, there is a bijection between the set of possible total orderings of the elements and the set of bijections from S to S. That is to say, the number of permutations of elements of S is the same as the number of total orderings of that set—namely, n!.

Category theory

[edit]

Bijections are precisely the isomorphisms in the category Set of sets and set functions. However, the bijections are not always the isomorphisms for more complex categories. For example, in the category Grp of groups, the morphisms must be homomorphisms since they must preserve the group structure, so the isomorphisms are group isomorphisms which are bijective homomorphisms.

Generalization to partial functions

[edit]

The notion of one-to-one correspondence generalizes to partial functions, where they are called partial bijections, although partial bijections are only required to be injective. The reason for this relaxation is that a (proper) partial function is already undefined for a portion of its domain; thus there is no compelling reason to constrain its inverse to be a total function, i.e. defined everywhere on its domain. The set of all partial bijections on a given base set is called the symmetric inverse semigroup.[4]

Another way of defining the same notion is to say that a partial bijection from A to B is any relation R (which turns out to be a partial function) with the property that R is the graph of a bijection f:A′→B′, where A′ is a subset of A and B′ is a subset of B.[5]

When the partial bijection is on the same set, it is sometimes called a one-to-one partial transformation.[6] An example is the Möbius transformation simply defined on the complex plane, rather than its completion to the extended complex plane.[7]

[edit]
  • An injective non-surjective function (injection, not a bijection)
    An injective non-surjective function (injection, not a bijection)
  • An injective surjective function (bijection)
    An injective surjective function (bijection)
  • A non-injective surjective function (surjection, not a bijection)
    A non-injective surjective function (surjection, not a bijection)
  • A non-injective non-surjective function (also not a bijection)
    A non-injective non-surjective function (also not a bijection)

See also

[edit]

Notes

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Bijection

View on Grokipedia
from Grokipedia
In , particularly in and function theory, a bijection is a function between two sets that is both injective (one-to-one, meaning distinct elements in the domain map to distinct elements in the ) and surjective (onto, meaning every element in the is mapped to by at least one element in the domain), thereby establishing a perfect one-to-one correspondence between the elements of the two sets. Bijections play a fundamental role in determining the cardinality of sets, where two sets are considered to have the same size or if and only if there exists a bijection between them, allowing for the comparison of infinite sets as well, such as the natural numbers and the integers. This property underpins the concept of set equivalence in and Zermelo-Fraenkel set theory, enabling proofs of results like the uncountability of the real numbers via diagonalization, which shows no bijection exists between the reals and the naturals. Furthermore, every bijection is invertible, with its inverse function also being a bijection, which facilitates in mappings and is essential in areas like for isomorphisms between structures. Examples of bijections include the on a set, which maps each element to itself, and linear functions like f(x)=x+cf(x) = x + c over the real numbers, both of which preserve the one-to-one correspondence. In , bijections are often used in bijective proofs to establish equalities between quantities by directly pairing elements, avoiding or induction. These mappings are not only theoretical but also appear in practical contexts, such as encoding schemes in where data structures require reversible transformations.

Fundamentals

Definition

In mathematics, a set is a well-defined collection of distinct objects, often denoted by capital letters such as AA or BB. A function f:A→Bf: A \to B is a mapping that assigns to each element aa in the domain set AA exactly one element f(a)f(a) in the set BB. A function f:A→Bf: A \to B is a bijection if for every element bb in BB, there exists exactly one element aa in AA such that f(a)=bf(a) = b. This establishes a one-to-one correspondence between the elements of AA and BB. Equivalently, a bijection is a function that is both injective (one-to-one), meaning f(a1)=f(a2)f(a_1) = f(a_2) implies a1=a2a_1 = a_2 for all a1,a2∈Aa_1, a_2 \in A, and surjective (onto), meaning for every b∈Bb \in B, there exists at least one a∈Aa \in A such that f(a)=bf(a) = b. As a consequence, every bijection has an . Bijections are often denoted using a standard function arrow f:A→Bf: A \to B qualified as bijective, or symbolically with a double-headed arrow A↔BA \leftrightarrow B to indicate the existence of such a correspondence, which preserves the structure of the sets in terms of their elements.

Examples

A bijection can be illustrated through simple everyday scenarios where there is a perfect one-to-one matching between two collections without any omissions or duplicates. For instance, consider the batting line-up of a team, where each of the nine players is uniquely assigned to one specific position in the order, and every position is filled by exactly one player. Similarly, in a , the assignment of seats to students establishes a bijection if each seat is occupied by precisely one student and every student has a unique seat, ensuring no empty seats or shared assignments. In , bijections appear in fundamental constructions on sets. The on any set XX, defined by f(x)=xf(x) = x for all x∈Xx \in X, maps each element to itself and is thus both injective and surjective, making it a bijection. For finite sets, any rearranges the elements such that each is mapped uniquely to another, preserving the set's structure; for example, swapping two elements in a set of three items like {a,b,c}\{a, b, c\} to {b,a,c}\{b, a, c\} via a specific mapping yields a bijection. Another classic example is the function f:N→2Nf: \mathbb{N} \to 2\mathbb{N} given by f(n)=2nf(n) = 2n, where N\mathbb{N} is the set of and 2N2\mathbb{N} is the set of even natural numbers, pairing each natural number with a unique even number and covering all even numbers exactly once. To visualize a bijection, imagine two finite sets represented as rows of dots, such as five dots for and five dots for seats; lines connecting each student dot to a unique seat dot without overlaps or loose ends demonstrate the matching, where arrows can indicate the direction of the function while ensuring every dot on both sides is connected precisely once. For the natural numbers to even numbers bijection, a might show a sequence of pairs like 1 to 2, 2 to 4, 3 to 6, extending infinitely to the right, illustrating the exhaustive pairing without gaps.

Structural Properties

Inverses

A bijection f:A→Bf: A \to B possesses a unique f−1:B→Af^{-1}: B \to A that satisfies the conditions f−1(f(a))=af^{-1}(f(a)) = a for all a∈Aa \in A and f(f−1(b))=bf(f^{-1}(b)) = b for all b∈Bb \in B. This existence and uniqueness follow directly from the bijectivity of ff, as injectivity ensures that no two elements in AA map to the same element in BB, while surjectivity guarantees that every element in BB is reached exactly once. The is constructed by defining f−1(b)f^{-1}(b) to be the unique element a∈Aa \in A such that f(a)=bf(a) = b, for each b∈Bb \in B. This definition is well-founded because surjectivity provides the of at least one such aa, and injectivity ensures its uniqueness, thereby establishing f−1f^{-1} as a total function from BB to AA. The inverse f−1f^{-1} is itself bijective, as applying the same reasoning shows that ff serves as its inverse, satisfying the round-trip identity conditions. Consequently, the compositions f∘f−1f \circ f^{-1} and f−1∘ff^{-1} \circ f both equal the respective identity functions idB:B→B\mathrm{id}_B: B \to B and idA:A→A\mathrm{id}_A: A \to A, where idX(x)=x\mathrm{id}_X(x) = x for all x∈Xx \in X. This uniqueness of the inverse implies that no other function can serve in this role for ff.

Composition

The composition of two functions f:A→Bf: A \to B and g:B→Cg: B \to C is the function g∘f:A→Cg \circ f: A \to C defined by (g∘f)(a)=g(f(a))(g \circ f)(a) = g(f(a)) for all a∈Aa \in A. If ff and gg are bijections, then their composition g∘fg \circ f is also a bijection. To see this, first consider injectivity: suppose (g∘f)(a1)=(g∘f)(a2)(g \circ f)(a_1) = (g \circ f)(a_2) for a1,a2∈Aa_1, a_2 \in A. Then g(f(a1))=g(f(a2))g(f(a_1)) = g(f(a_2)). Since gg is injective, it follows that f(a1)=f(a2)f(a_1) = f(a_2), and since ff is injective, a1=a2a_1 = a_2. Thus, g∘fg \circ f is injective. For surjectivity, let c∈Cc \in C. Since gg is bijective, there exists b∈Bb \in B such that g(b)=cg(b) = c, namely b=g−1(c)b = g^{-1}(c). Since ff is bijective, there exists a∈Aa \in A such that f(a)=bf(a) = b, namely a=f−1(b)a = f^{-1}(b). Then (g∘f)(a)=g(f(a))=g(b)=c(g \circ f)(a) = g(f(a)) = g(b) = c, so g∘fg \circ f is surjective. The composition of bijections is associative: for bijections f:A→Bf: A \to B, g:B→Cg: B \to C, and h:C→Dh: C \to D, we have (h∘g)∘f=h∘(g∘f)(h \circ g) \circ f = h \circ (g \circ f). This follows from the general associativity of function composition, where ((h∘g)∘f)(a)=h(g(f(a)))((h \circ g) \circ f)(a) = h(g(f(a))) and (h∘(g∘f))(a)=h((g∘f)(a))=h(g(f(a)))(h \circ (g \circ f))(a) = h((g \circ f)(a)) = h(g(f(a))) for all a∈Aa \in A. For a finite set SS with nn elements, the set of all bijections from SS to itself, equipped with composition as the group operation, forms the symmetric group SnS_n, which contains exactly n!n! elements and is generated by compositions of its members.

Additional Properties

In the context of ordered sets, a bijection that additionally preserves the order relation—such that if x≤yx \leq y in the domain, then f(x)≤f(y)f(x) \leq f(y) in the codomain—is termed an order isomorphism. For sets endowed with algebraic structures, such as groups or vector spaces, a bijection that preserves the relevant operations (e.g., f(a+b)=f(a)+f(b)f(a + b) = f(a) + f(b) for addition in vector spaces) qualifies as an isomorphism, maintaining the operational integrity of the structure. However, arbitrary bijections between unstructured sets do not inherently preserve order or algebraic properties. In infinite sets, bijections to itself similarly provide one-to-one correspondences that extend the concept, though the may involve additional considerations like choice axioms for explicit construction. Bijections possess strong cancellation properties under . If f:A→Bf: A \to B is a bijection and g,h:C→Ag, h: C \to A satisfy f∘g=f∘hf \circ g = f \circ h, then g=hg = h (left cancellation law). Analogously, for r,s:B→Dr, s: B \to D, if r∘f=s∘fr \circ f = s \circ f, then r=sr = s (right cancellation law). These properties stem from the invertibility of bijections, allowing the "cancellation" of ff by composing with its inverse. Particular bijections, especially permutations of finite sets, may lack fixed points, where no element maps to itself (f(x)≠xf(x) \neq x for all xx). Such mappings are derangements, which are bijections with no fixed points and play a key role in for counting rearrangements without stabilizers. While derangements are typically discussed for finite permutations, the absence of fixed points can analogously characterize certain infinite bijections.

Theoretical Contexts

Cardinality

In set theory, two sets AA and BB have the same , denoted ∣A∣=∣B∣|A| = |B|, there exists a bijection f:A→Bf: A \to B, establishing a one-to-one correspondence between their elements. This definition extends the intuitive notion of size equality from finite collections to arbitrary sets, allowing precise comparisons even when direct enumeration is impossible. For finite sets, a bijection directly implies equal sizes, as the correspondence pairs each element uniquely without leftovers. For example, the sets {1,2,3}\{1, 2, 3\} and {a,b,c}\{a, b, c\} satisfy ∣{1,2,3}∣=∣{a,b,c}∣=3|\{1, 2, 3\}| = |\{a, b, c\}| = 3 via the bijection f(1)=af(1) = a, f(2)=bf(2) = b, f(3)=cf(3) = c. In contrast, infinite cardinalities exhibit counterintuitive behaviors, where proper subsets can match the original set's size through bijections. Consider the natural numbers N={1,2,3,… }\mathbb{N} = \{1, 2, 3, \dots\} and N∪{0}={0,1,2,3,… }\mathbb{N} \cup \{0\} = \{0, 1, 2, 3, \dots\}; the function f:N→N∪{0}f: \mathbb{N} \to \mathbb{N} \cup \{0\} defined by f(1)=0f(1) = 0 and f(n)=n−1f(n) = n - 1 for n>1n > 1 is a bijection, so ∣N∣=∣N∪{0}∣|\mathbb{N}| = |\mathbb{N} \cup \{0\}|. This equivalence illustrates how infinite sets can "absorb" additional elements without increasing , as popularized by Hilbert's hotel paradox: a fully occupied infinite hotel accommodates a new guest by shifting occupant nn to room n+1n+1, freeing room 1—a bijection between the original and expanded guest sets. Bijections also play a key role in distinguishing infinite cardinalities, such as in Cantor's diagonal argument, which proves the uncountability of the real numbers by assuming a bijection f:N→(0,1)f: \mathbb{N} \to (0,1) exists and constructing a real number in (0,1)(0,1) not in the image, yielding a contradiction; thus, no such bijection exists, and ∣R∣>∣N∣|\mathbb{R}| > |\mathbb{N}|. The Schröder–Bernstein theorem further refines cardinality comparisons: if there exist injections g:A→Bg: A \to B and h:B→Ah: B \to A, then a bijection A→BA \to B exists. One proof constructs the bijection by iteratively defining nested subsets A0=AA_0 = A, B0=BB_0 = B, An+1=h(Bn)A_{n+1} = h(B_n), Bn+1=g(An)B_{n+1} = g(A_n), forming decreasing chains, and partitioning into differences where bijections are defined via gg and h−1h^{-1} on appropriate components, with the intersection handled separately to ensure surjectivity and injectivity.

Category Theory

In category theory, the concept of a bijection from generalizes to the notion of an , which captures invertible s between objects in any category. In the , denoted Set, where objects are sets and s are functions, a f:A→Bf: A \to B is an if and only if it is a bijection, meaning it is both injective and surjective, and possesses an inverse g:B→Ag: B \to A such that g∘f=idAg \circ f = \mathrm{id}_A and f∘g=idBf \circ g = \mathrm{id}_B. This equivalence holds because the identity s in Set are bijections, and the composition of bijections preserves this property, ensuring two-sided invertibility. More broadly, in an arbitrary category C\mathcal{C}, an is defined as a f:X→Yf: X \to Y that admits an inverse g:Y→Xg: Y \to X satisfying the same composition conditions with the identity morphisms on XX and YY. Thus, bijections in Set exemplify isomorphisms, but the categorical definition extends the idea of two-sided inverses to structured settings beyond mere sets, emphasizing equivalence of objects up to invertible arrows rather than strict equality. This abstraction allows to unify diverse mathematical domains by focusing on relational properties preserved under inversion. In other categories, isomorphisms take forms tailored to the structure of the objects and morphisms. For instance, in the category Vect of vector spaces over a field (with linear maps as morphisms), an isomorphism is an invertible linear map, which is necessarily bijective on underlying sets but also preserves the vector space operations, such as scalar multiplication and addition. Similarly, in the category Top of topological spaces (with continuous functions as morphisms), an isomorphism is a : a continuous bijection with a continuous inverse, ensuring that the topological —open sets and continuity—is preserved bidirectionally. Automorphisms arise as a special case of isomorphisms, namely those from an object to itself, forming the automorphism group Aut(X)\mathrm{Aut}(X) under composition, which encodes the symmetries of XX. In Set, these are precisely the bijections f:A→Af: A \to A, with the symmetric group Sym(A)\mathrm{Sym}(A) as the automorphism group for finite sets AA. This group structure highlights how isomorphisms generate algebraic insights into object equivalences within categories.

Generalizations

A partial bijection, also known as a , is a f:A⇀Bf: A \rightharpoonup B between sets AA and BB such that the restriction of ff to its domain dom⁡(f)⊆A\operatorname{dom}(f) \subseteq A induces a onto its image im⁡(f)⊆B\operatorname{im}(f) \subseteq B. This means ff is injective on dom⁡(f)\operatorname{dom}(f) and surjective onto im⁡(f)\operatorname{im}(f), ensuring a one-to-one correspondence between these subsets. Partial bijections extend the concept of total bijections to scenarios where functions may be undefined on parts of the domain, preserving bijectivity where defined. They form a category under composition, where the composition of two partial bijections is defined only where domains overlap appropriately. In , partial bijections play a key role in modeling the semantics of recursive and computable functions within partially ordered sets (domains), where they represent embeddings and projections that maintain structural continuity. This framework, foundational to in programming languages, uses partial bijections to approximate infinite computations via finite approximations in Scott domains. Bijections also induce important relations on collections of sets. Specifically, the relation ∼\sim on the class of all sets, defined by A∼BA \sim B if there exists a bijection between AA and BB, is an : it is reflexive (via the identity bijection), symmetric (via the inverse bijection), and transitive (via composition of bijections). This equivalence partitions the universe of sets into classes, where equivalent sets share the same "size" in the sense of Dedekind. Equivalence relations in general correspond bijectively to partitions of a set, with each relation defining a partition into equivalence classes and vice versa. In and programming languages, bijections manifest as type isomorphisms, providing invertible mappings between types that preserve computational structure. For instance, in , a type isomorphism between types AA and BB consists of functions to:A→Bto: A \to B and from:B→Afrom: B \to A such that to∘from=idBto \circ from = id_B and from∘to=idAfrom \circ to = id_A, enabling seamless conversion without information loss. Similarly, in Coq's dependently typed framework, isomorphisms are bijections equipped with proofs of invertibility, facilitating modular reasoning about data representations. The Curry-Howard correspondence further links these isomorphisms to logical equivalences, interpreting type equalities as provable bijections between proof terms. The concept of one-to-one correspondences, central to bijections, traces back to Gottlob Frege's late 19th-century work in Grundlagen der Arithmetik (1884), where he used them to logically define cardinal numbers as equivalence classes under such mappings, laying groundwork for modern set theory. In contemporary computer science, bijections underpin applications like database schema mappings, ensuring invertible transformations between relational structures to maintain data integrity during migrations.

References

  1. https://www.siue.edu/~jloreau/courses/math-223/notes/sec-injective-surjective.html
  2. https://sites.millersville.edu/bikenaga/math-proof/cardinality/cardinality.html
  3. https://www.whitman.edu/mathematics/higher_math_online/section04.06.html
  4. https://mathresearch.utsa.edu/wiki/index.php?title=Functions:Bijective
  5. https://www.math.fsu.edu/~pkirby/mad2104/SlideShow/s4_2.pdf
  6. https://math.mit.edu/~rstan/bij.pdf
  7. https://pi.math.cornell.edu/~karola/dimex/bijections.pdf
  8. https://www.math.ucdavis.edu/~hunter/intro_analysis_pdf/ch1.pdf
  9. https://mathworld.wolfram.com/Bijective.html
  10. https://www.sciencedirect.com/topics/mathematics/bijection
  11. https://www.cs.virginia.edu/~robins/cs6160/basics.pdf
  12. http://stanford.edu/~dntse/classes/cs70_fall09/n20_fall09.pdf
  13. https://math.colorado.edu/~kstange/has-inverse-is-bijective.pdf
  14. https://users.cs.duke.edu/~brd/Teaching/dm/F2025/handouts/bb-bijection.pdf
  15. https://ecroot.math.gatech.edu/2406_2012/cantor2.pdf
  16. https://sites.math.washington.edu/~arms/m300A17/InvFunc.pdf
  17. https://dummit.cos.northeastern.edu/teaching_fa23_1365/1365_lecture_24_inverse_functions.pdf
  18. https://math.libretexts.org/Bookshelves/Combinatorics_and_Discrete_Mathematics/Applied_Discrete_Structures_%28Doerr_and_Levasseur%29/07%253A_Functions/7.03%253A_Function_Composition
  19. https://www.cs.cornell.edu/courses/cs2800/2015fa/lectures/lec06-proofs.html
  20. https://math.libretexts.org/Courses/Mount_Royal_University/Abstract_Algebra_I/Chapter_3%253A_Permutation_Groups/3.1%253A_Symmetric_Groups
  21. https://www.math.wustl.edu/~freiwald/ch8.pdf
  22. https://people.willamette.edu/~jlaison/algebra-isomorphisms.pdf
  23. https://people.tamu.edu/~yvorobets/MATH433-2010B/Lect2-01web.pdf
  24. https://faculty.etsu.edu/gardnerr/3000/notes-MR/Gerstein-3-3.pdf
  25. https://www.math.emory.edu/~rg/derangements.pdf
  26. https://math.libretexts.org/Bookshelves/Mathematical_Logic_and_Proof/Proofs_and_Concepts_-_The_Fundamentals_of_Abstract_Mathematics_(Morris_and_Morris)/09%3A_Cardinality/9.01%3A_Counting_and_Infinite_Sets
  27. https://math.libretexts.org/Bookshelves/Mathematical_Logic_and_Proof/Proofs_and_Concepts_-_The_Fundamentals_of_Abstract_Mathematics_(Morris_and_Morris)/09%3A_Cardinality/9.04%3A_Hotel_infinity_and_the_cardinality_of_infinite_sets
  28. https://web.williams.edu/Mathematics/lg5/CanBer.pdf
  29. http://math.uchicago.edu/~womp/2004/guilskiad04.pdf
  30. http://math.uchicago.edu/~may/REU2022/REUPapers/Stern.pdf
  31. https://ocw.mit.edu/courses/18-s996-category-theory-for-scientists-spring-2013/b84f9d8840db0c745c75ab23c89851bb_MIT18_S996S13_chapter4.pdf
  32. https://www.ucl.ac.uk/~ucahmto/0005_2021/Ch4.S22.html
  33. https://math.uchicago.edu/~may/REU2016/SalazarNotes.pdf
  34. https://arxiv.org/pdf/0903.1017
  35. https://dl.acm.org/doi/pdf/10.1145/3236796
  36. https://www3.cs.stonybrook.edu/~cse213/slides/4equ.pdf
  37. https://kseo.github.io/posts/2016-12-25-type-isomorphism.html
  38. https://drops.dagstuhl.de/storage/00lipics/lipics-vol269-types2022/LIPIcs.TYPES.2022.11/LIPIcs.TYPES.2022.11.pdf
  39. https://richardzach.org/wp-content/uploads/2019/11/Zach-2019-The-Significance-of-the-Curry-Howard-Isomorphism.pdf
  40. https://rkheck.frege.org/pdf/published/Originals/FregesPrinciple.pdf
  41. https://docs.oracle.com/cd/B32110_01/web.1013/b28218/relmapun.htm
Add your contribution
Related Hubs
Contribute something
User Avatar
No comments yet.