Hubbry Logo
Line codeLine codeMain
Open search
Line code
Community hub
Line code
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Line code
Line code
Line code
View on Wikipedia
from Wikipedia
An example of coding a binary signal using rectangular pulse-amplitude modulation with polar non-return-to-zero code
An example of bipolar encoding, or AMI.
Encoding of 11011000100 in Manchester encoding
An example of differential Manchester encoding
An example of biphase mark code
An example of MLT-3 encoding
Passband modulation
Analog modulation
Digital modulation
Hierarchical modulation
Spread spectrum
See also

In telecommunications, a line code is a pattern of voltage, current, or photons used to represent digital data transmitted down a communication channel or written to a storage medium. This repertoire of signals is usually called a constrained code in data storage systems.[1] Some signals are more prone to error than others as the physics of the communication channel or storage medium constrains the repertoire of signals that can be used reliably.[2]

Common line encodings are unipolar, polar, bipolar, and Manchester code.

Transmission and storage

[edit]

After line coding, the signal is put through a physical communication channel, either a transmission medium or data storage medium.[3][4] The most common physical channels are:

Some of the more common binary line codes include:

Signal Comments 1 state 0 state
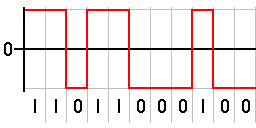
NRZ–L Non-return-to-zero level. This is the standard positive logic signal format used in digital circuits. forces a high level forces a low level
NRZ–M Non-return-to-zero mark forces a transition does nothing (keeps sending the previous level)
NRZ–S Non-return-to-zero space does nothing (keeps sending the previous level) forces a transition
RZ Return to zero goes high for half the bit period and returns to low stays low for the entire period
Biphase–L Manchester. Two consecutive bits of the same type force a transition at the beginning of a bit period. forces a negative transition in the middle of the bit forces a positive transition in the middle of the bit
Biphase–M Variant of Differential Manchester. There is always a transition halfway between the conditioned transitions. forces a transition keeps level constant
Biphase–S Differential Manchester used in Token Ring. There is always a transition halfway between the conditioned transitions. keeps level constant forces a transition
Differential Manchester (Alternative) Need a Clock, always a transition in the middle of the clock period is represented by no transition. is represented by a transition at the beginning of the clock period.
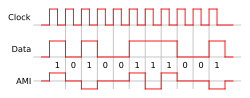
Bipolar The positive and negative pulses alternate. forces a positive or negative pulse for half the bit period keeps a zero level during bit period
An arbitrary bit pattern in various binary line code formats

Each line code has advantages and disadvantages. Line codes are chosen to meet one or more of the following criteria:

  • Minimize transmission hardware
  • Facilitate synchronization
  • Ease error detection and correction
  • Achieve a target spectral density
  • Eliminate a DC component

Disparity

[edit]

Most long-distance communication channels cannot reliably transport a DC component. The DC component is also called the disparity, the bias, or the DC coefficient. The disparity of a bit pattern is the difference in the number of one bits vs the number of zero bits. The running disparity is the running total of the disparity of all previously transmitted bits.[5] The simplest possible line code, unipolar, gives too many errors on such systems, because it has an unbounded DC component.

Most line codes eliminate the DC component – such codes are called DC-balanced, zero-DC, or DC-free. There are three ways of eliminating the DC component:

  • Use a constant-weight code. Each transmitted code word in a constant-weight code is designed such that every code word that contains some positive or negative levels also contains enough of the opposite levels, such that the average level over each code word is zero. Examples of constant-weight codes include Manchester code and Interleaved 2 of 5.
  • Use a paired disparity code. Each code word in a paired disparity code that averages to a negative level is paired with another code word that averages to a positive level. The transmitter keeps track of the running DC buildup, and picks the code word that pushes the DC level back towards zero. The receiver is designed so that either code word of the pair decodes to the same data bits. Examples of paired disparity codes include alternate mark inversion, 8b/10b and 4B3T.
  • Use a scrambler. For example, the scrambler specified in RFC 2615 for 64b/66b encoding.

Polarity

[edit]

Bipolar line codes have two polarities, are generally implemented as RZ, and have a radix of three since there are three distinct output levels (negative, positive and zero). One of the principal advantages of this type of code is that it can eliminate any DC component. This is important if the signal must pass through a transformer or a long transmission line.

Unfortunately, several long-distance communication channels have polarity ambiguity. Polarity-insensitive line codes compensate in these channels.[6][7][8][9] There are three ways of providing unambiguous reception of 0 and 1 bits over such channels:

Run-length limited codes

[edit]

For reliable clock recovery at the receiver, a run-length limitation may be imposed on the generated channel sequence, i.e., the maximum number of consecutive ones or zeros is bounded to a reasonable number. A clock period is recovered by observing transitions in the received sequence, so that a maximum run length guarantees sufficient transitions to assure clock recovery quality.

RLL codes are defined by four main parameters: m, n, d, k. The first two, m/n, refer to the rate of the code, while the remaining two specify the minimal d and maximal k number of zeroes between consecutive ones. This is used in both telecommunications and storage systems that move a medium past a fixed recording head.[10]

Specifically, RLL bounds the length of stretches (runs) of repeated bits during which the signal does not change. If the runs are too long, clock recovery is difficult; if they are too short, the high frequencies might be attenuated by the communications channel. By modulating the data, RLL reduces the timing uncertainty in decoding the stored data, which would lead to the possible erroneous insertion or removal of bits when reading the data back. This mechanism ensures that the boundaries between bits can always be accurately found (preventing bit slip), while efficiently using the media to reliably store the maximal amount of data in a given space.

Early disk drives used very simple encoding schemes, such as RLL (0,1) FM code, followed by RLL (1,3) MFM code which were widely used in hard disk drives until the mid-1980s and are still used in digital optical discs such as CD, DVD, MD, Hi-MD and Blu-ray using EFM and EFMPLus codes.[11] Higher density RLL (2,7) and RLL (1,7) codes became the de facto standards for hard disks by the early 1990s.[citation needed]

Synchronization

[edit]
Main article: Clock recovery

Line coding should make it possible for the receiver to synchronize itself to the phase of the received signal. If the clock recovery is not ideal, then the signal to be decoded will not be sampled at the optimal times. This will increase the probability of error in the received data.

Biphase line codes require at least one transition per bit time. This makes it easier to synchronize the transceivers and detect errors, however, the baud rate is greater than that of NRZ codes.

Other considerations

[edit]

A line code will typically reflect technical requirements of the transmission medium, such as optical fiber or shielded twisted pair. These requirements are unique for each medium, because each one has different behavior related to interference, distortion, capacitance and attenuation.[12]

Common line codes

[edit]

Optical line codes

[edit]

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Line code

View on Grokipedia
from Grokipedia
A line code, also known as line coding, is a technique used in digital communications to convert sequences into a physical or sequence of electrical pulses suitable for transmission over a , such as a wire or fiber optic line. This encoding process maps binary 0s and 1s to distinct signal levels or transitions, ensuring reliable data transfer by addressing challenges like signal , , and over distances where effects are significant. Line codes serve critical functions in digital transmission systems, including minimizing required transmission bandwidth, optimizing power efficiency for a given rate and error probability, and providing favorable to avoid DC components that could saturate transformers or amplifiers. They also incorporate timing content for at the receiver, enable error detection or correction (such as single-error detection in bipolar formats), and ensure transparency by supporting arbitrary binary sequences without long runs of identical bits that might disrupt . Common categories include unipolar schemes like on-off keying (with or variants), polar formats that use positive and negative levels for better immunity, bipolar or alternate mark inversion codes that alternate polarity for 1s to eliminate , and more advanced or biphase codes that guarantee transitions per bit for robust timing extraction. These methods are foundational in applications ranging from and Ethernet networking to high-speed links, where selecting an appropriate line code balances trade-offs in complexity, performance, and hardware requirements.

Fundamentals of Line Coding

Definition and Purpose

Line coding refers to the process of transforming sequences of into digital signals suitable for transmission over physical communication channels, such as metallic wires or optical fibers, or for storage on media like magnetic tapes. This conversion ensures that the digital information can be reliably propagated while accommodating the limitations of the . The primary purposes of line coding include enabling accurate signal detection at the receiver by shaping the to distinguish bits clearly, maintaining DC balance to avoid baseline wander that could distort long sequences of identical bits, facilitating for timing recovery without separate clock lines, and optimizing spectral properties to minimize required bandwidth and control power distribution across frequencies. These functions address key challenges in digital transmission, such as signal degradation over distance and interference from the channel. Line coding techniques originated in the 19th century with early systems using basic on-off keying schemes such as . They evolved in the through the development of for in 1937 by Alec Reeves, leading to more efficient handling of voice and data signals. By the mid-20th century, it advanced into standardized digital systems, with the (ITU) issuing recommendations such as G.703 in 1972 (and subsequent revisions) that specify line coding formats for synchronous digital hierarchy interfaces to ensure interoperability in global networks. Effective line codes must meet key requirements including to utilize bandwidth economically, power efficiency to reduce for a given rate and error performance, and robustness to and interference for reliable operation in adverse environments. These attributes prioritize the balance between transmission reliability and resource constraints in practical deployments.

Basic Encoding Principles

Line coding fundamentally involves the process of mapping sequences—typically represented as streams of 0s and 1s—into analog waveforms suitable for transmission over a physical medium, such as a twisted-pair cable or . This mapping transforms digital bits into voltage levels, pulses, or transitions that propagate along the while preserving the information content. The encoder at the transmitter side converts each bit into a corresponding signal element, often using to control the waveform's duration and amplitude, ensuring compatibility with the channel's bandwidth limitations and characteristics. Waveforms in line coding are classified based on their polarity and timing behavior. Unipolar formats employ only positive voltage levels (or a single polarity), where a logical 1 might be represented by a positive voltage and a 0 by zero voltage, as seen in unipolar (NRZ) schemes. Bipolar formats, in contrast, utilize both positive and negative voltage levels to encode bits, enhancing signal detection by providing greater contrast; for example, in bipolar NRZ, a 1 could alternate between +V and -V, while a 0 remains at zero. Additionally, (RZ) formats return the signal to a zero level during a portion of each bit period (typically mid-bit), which aids in clock extraction but doubles the required bandwidth compared to NRZ formats that maintain the level throughout the bit interval without returning to zero. In transmission, line coding adapts basic modulation principles such as shifts, where bit values determine the pulse height, or phase transitions for encoding changes between levels. These techniques operate at low frequencies near DC, avoiding carrier modulation to minimize complexity; for instance, (PAM) assigns discrete levels to bits, shaping the power to suppress low-frequency components that could cause baseline wander. Frequency shifts are less common in pure line coding but may involve rate adjustments to embed timing information. A simple binary encoding example illustrates these principles: in unipolar NRZ, a logical 1 is mapped to a (+V) sustained for the entire bit duration, while a 0 is mapped to low voltage (0V), producing a rectangular sequence. is evaluated using eye patterns, which overlay multiple bit transitions to visualize the received signal's clarity; a wide-open eye indicates low and noise margins, whereas closure suggests degradation from bandwidth constraints or distortions in the line-coded .

Essential Properties

Disparity and DC Balance

In line codes, disparity refers to the running count of the difference between the number of 1s and 0s (or positive and negative pulses in bipolar schemes) accumulated over a sequence of codewords, serving as a measure of signal imbalance. This running disparity tracks the cumulative deviation to monitor and control the overall balance in the encoded stream. DC balance, characterized by maintaining an average disparity of zero, is essential in transmission systems to eliminate the DC component of the signal, thereby preventing distortion in AC-coupled circuits where capacitors block steady-state voltages. Without balance, prolonged sequences of identical bits can cause baseline wander—a gradual shift in the signal's reference level due to high-pass filtering effects—leading to errors in receiver detection thresholds. The disparity for a given sequence is often normalized as D=number of 1s−number of 0stotal bitsD = \frac{\text{number of 1s} - \text{number of 0s}}{\text{total bits}}, where a value of D=0D = 0 indicates perfect balance and corresponds to a spectral null at DC frequency. To achieve DC balance, block coding techniques partition data into fixed-length groups and map them to codewords selected based on the current running disparity, ensuring the transmitted symbols have an equal or compensating number of 1s and 0s. For instance, the seminal 8b/10b code, developed by Widmer and Franaszek, encodes 8-bit data into 10-bit symbols with individual disparities of 0, +2, or -2; the encoder alternates symbol polarity to invert the disparity when necessary, keeping the running disparity bounded and the long-term average at zero. methods, such as those used in Ethernet standards, apply pseudo-random sequences to data before encoding, statistically distributing 1s and 0s to suppress low-frequency components without fixed block structures. As an example, consider a simplified sequence in an 8b/10b-like scheme starting with running disparity RD = 0: a codeword with four 1s and six 0s yields a block disparity of -2, updating RD to -2; the next codeword is then chosen or complemented to have +2 disparity, restoring RD to 0 and demonstrating cumulative control. Over long-term sequences, maximum allowable disparity limits—such as ±4 in certain —constrain excursions to guarantee bounded low-frequency content and maintain the DC spectral null, minimizing wander even in extended transmissions.

Polarity Considerations

In line coding, polarity refers to the assignment of voltage levels to represent binary states, where unipolar schemes employ a single polarity—typically zero for one state and a positive voltage for the other—while bipolar schemes utilize both positive and negative voltages alongside zero. Unipolar encoding, such as unipolar NRZ, maps binary 0 to 0 V and binary 1 to +V, resulting in a persistent DC component that can cause baseline wander and ambiguity in decoding if the received signal drifts due to channel imperfections or . This ambiguity heightens error susceptibility, as a gradual DC offset might flip perceived 0s into 1s or vice versa without violating timing constraints. Bipolar schemes mitigate these issues by alternating polarities for successive 1s, enhancing rejection through differential-like properties that cancel common-mode interference, particularly effective in balanced transmission media. The alternating nature suppresses low-frequency and improves overall by distributing energy across positive and negative domains, reducing the impact of induced from external sources. A prominent example is Alternate Mark Inversion (AMI), a bipolar format where binary 0s (spaces) are encoded as 0 V and binary 1s (marks) as pulses alternating between +V and -V on successive occurrences. This strict alternation rule enables inherent error detection: a bipolar violation—such as two consecutive marks sharing the same polarity—signals a transmission error, allowing receivers to flag and potentially correct or discard affected bits without additional overhead. In transmission over twisted-pair lines, bipolar polarity schemes like AMI reduce crosstalk by minimizing unbalanced electromagnetic coupling between adjacent pairs, as the zero-mean signal limits near-end and far-end interference. This balanced approach also boosts (SNR) by rejecting common-mode noise more effectively than unipolar signals. These polarity strategies complement DC balance objectives by inherently limiting long-term voltage offsets through alternation.

Run-Length Limitations

Run-length limited (RLL) codes, denoted as (d,k)-RLL, are binary encoding schemes that constrain the lengths of consecutive identical , specifically limiting runs of zeros between successive ones to a minimum of d and a maximum of k. This notation defines a constrained channel where sequences violating the run-length bounds are invalid, ensuring controlled symbol patterns in line-coded signals. The primary purpose of these constraints in line coding is to optimize timing recovery and properties of the transmitted signal. The d enforces a minimum separation between transitions to mitigate inter-symbol interference, while the k caps the maximum run length to prevent prolonged absence of transitions that could hinder clock extraction; together, they shape the power spectrum by reducing low-frequency energy, which minimizes baseline wander and interference in bandwidth-limited channels. Mathematically, the constraints dictate a minimum transition density of 1k+1\frac{1}{k+1} transitions per bit, as the longest allowable run of k zeros followed by a one yields this periodic lower bound. The channel capacity, analogous to Shannon's limit but for constrained inputs, is log⁡2λ\log_2 \lambda, where λ\lambda is the largest eigenvalue of the adjacency matrix representing the finite-state model of valid transitions; this bound quantifies the supremum of achievable rates in bits per symbol for the (d,k)-RLL system. For example, a (0,3)-RLL code allows zero to three consecutive zeros between ones, promoting a high transition density for robust timing in high-speed links. In block implementations, the coding overhead manifests as a rate of log⁡2Mn\frac{\log_2 M}{n}, where M is the number of valid n-bit codewords, reducing the effective data throughput relative to uncoded binary transmission. Some (d,k)-RLL designs further integrate disparity controls to achieve DC balance alongside run-length constraints.

Synchronization Aspects

Clock Recovery Mechanisms

Clock recovery is essential in line-coded digital communication systems, where timing information must be embedded within the data signal itself due to the absence of a dedicated clock line. This embedded approach allows for efficient single-channel transmission but introduces challenges such as , which arises from and distortions in the channel, and , caused by differences in oscillator frequencies between transmitter and receiver. These impairments can lead to sampling errors if the recovered clock phase deviates significantly from the data transitions. Common techniques for clock recovery include phase-locked loops (PLLs) for continuous phase alignment and methods for signals with frequent transitions. In PLL-based recovery, a (VCO) adjusts its phase to match the incoming data edges, using a to compare timing and a loop filter to stabilize the response; this method effectively tracks ongoing data streams while suppressing high-frequency . For line codes like Manchester encoding, which guarantee a transition in every bit period, simpler circuits can extract the clock by identifying mid-bit transitions, enabling robust without complex analog components. Quantitative analysis of clock recovery performance often focuses on jitter tolerance, defined as the maximum allowable phase error before bit errors occur. For binary signaling, the maximum phase error is typically limited to π\pi radians to ensure the sampling point remains within the eye opening, preventing decision errors at the receiver. PLL lock time, the duration required for the loop to settle within a specified error band after initial acquisition, can be estimated using the second-order system settling time approximation tlock≈4ζωnt_{\text{lock}} \approx \frac{4}{\zeta \omega_n}, where ζ\zeta is the damping factor and ωn\omega_n is the natural frequency; this highlights the trade-off between loop bandwidth and acquisition speed. The choice of line code significantly influences clock recovery efficacy, as higher transition density provides more reference edges for phase locking, thereby reducing the probability of clock slips during long sequences of identical bits. Preamble patterns, consisting of alternating bits or specific sequences at the start of a transmission, facilitate initial alignment by offering a burst of transitions to quickly acquire lock before the data payload begins. Line codes that limit maximum run lengths further support recovery by ensuring periodic transitions, minimizing the risk of prolonged phase uncertainty.

Self-Synchronizing Features

Self-synchronizing line codes enable the recovery of bit boundaries directly from transitions embedded in the data signal itself, eliminating the need for prolonged sequences or separate clock references to prevent bit slips. In such codes, the encoding scheme ensures sufficient signal changes—arising from data-dependent or guaranteed transitions—that allow the receiver's timing circuits to align with the transmitter's bit clock after a short acquisition period. This intrinsic timing information is crucial for maintaining in asynchronous or burst-mode transmissions, where external aids may be impractical. A key characteristic of these codes is the enforcement of transitions at regular intervals, often every few bits, to provide reliable cues for clock extraction. For instance, features a transition in the middle of each bit period for , with a transition at the start of the bit period indicating a binary 0 and its absence indicating a binary 1, ensuring at least one change per bit and facilitating rapid self-alignment. These features offer significant advantages, particularly in bursty traffic scenarios common to packet-switched networks, by minimizing preamble overhead and enabling quick resynchronization with just a handful of bits. However, codes exhibiting low transition probabilities—such as (NRZ) formats during extended runs of identical symbols—may still necessitate auxiliary hardware, like phase-locked loops, to avoid prolonged lock times. Limitations arise in low-activity patterns, where sparse transitions increase vulnerability to timing . Synchronization loss can be detected by observing the absence of transitions exceeding the code's maximum run-length limit, which signals potential bit slip and prompts a resynchronization attempt. In run-length limited designs, this threshold—often capped at 3 to 5 bits—serves as a direct indicator, allowing the system to revert to a or reinitialize timing extraction without widespread . Such monitoring integrates seamlessly with the code's structure, enhancing robustness in noisy channels.

Categories of Line Codes

Binary and Bipolar Codes

Binary line codes represent using two voltage levels, typically for transmission, while bipolar variants employ three levels to enhance certain properties. (NRZ) codes maintain a constant voltage level throughout each bit period, making them simple to implement but prone to certain limitations. NRZ-level (NRZ-L) encoding assigns a positive voltage to binary 0 and a negative voltage to binary 1, or vice versa, without returning to zero between bits. This scheme supports high rates due to its straightforward structure but introduces a significant DC component, especially in long sequences of identical bits, which can cause baseline wander in AC-coupled systems. Additionally, is challenging because extended runs of 0s or 1s produce no transitions, complicating at the receiver. NRZ-inverted (NRZ-I) addresses some issues by defining a transition at the start of each bit period for binary 1, while binary 0 causes no change from the previous level. This results in better transition for with frequent 1s, reducing the risk of prolonged no-transition periods compared to NRZ-L, though it still suffers from DC imbalance and sensitivity to errors in the initial state. Return-to-zero (RZ) codes mitigate some NRZ drawbacks by using a pulse width of half the bit period, returning the signal to zero midway through each bit. For binary 1, a pulse (positive or negative) occupies the first half, followed by zero in the second half; binary 0 remains at zero throughout. This design aids synchronization through regular mid-bit transitions and reduces DC content by ensuring the signal returns to baseline, but it requires twice the bandwidth of NRZ due to the higher transition rate. RZ is particularly advantageous in environments needing clear pulse separation, though its complexity increases implementation costs. Bipolar codes extend binary signaling by alternating polarities for marks (1s), using three levels: positive, negative, and zero. Alternate mark inversion (AMI) encodes binary 0 as zero voltage and binary 1 as alternating positive and negative pulses, adhering to polarity rules that prevent consecutive marks of the same polarity. This eliminates the DC component inherent in NRZ, as the average voltage over time approaches zero, and provides good synchronization during sequences rich in 1s due to frequent transitions. However, long runs of 0s cause no transitions, leading to potential loss of timing and reduced ones density, which can degrade performance in digital hierarchies like T1 lines. To address the zeros problem in AMI, bipolar with 8-zero substitution (B8ZS) substitutes any sequence of eight consecutive 0s with a specific pattern: 000+-0-+, where + and - are bipolar violations (two consecutive pulses of the same polarity). This insertion maintains the required ones density for reliable transmission and allows error detection via the intentional violations, which do not occur in normal AMI encoding. B8ZS is standardized for T1/DS1 interfaces, ensuring compatibility while preserving bandwidth efficiency. The following table compares key properties of representative binary and bipolar codes:
CodeBandwidth RequirementDC BalanceSynchronization Capability
NRZ-LLow (bit rate)PoorPoor (no transitions in runs)
NRZ-ILow (bit rate)ModerateModerate (transitions on 1s)
RZHigh (2x )GoodGood (mid-bit transitions)
AMILow ()ExcellentGood for 1s, poor for 0 runs

Multilevel and Block Codes

Multilevel line codes utilize more than two signaling levels to encode data, thereby increasing the information density per symbol while minimizing bandwidth requirements and . A prominent example is MLT-3 (Multi-Level Transmit-3), employed in 100BASE-TX Ethernet as defined in IEEE 802.3u. This scheme operates with four states cycling through voltage levels 0, +1, 0, -1, effectively using three voltage levels: +1, 0, -1. It builds upon NRZI (Non-Return-to-Zero Inverted) encoding by mapping transitions: a binary '1' in the NRZI signal causes the output level to advance to the next state in the cycle (0 → +1 → 0 → -1 → 0), while a '0' maintains the current level. This cycling reduces the maximum transition to one-fourth of the , halving the effective compared to NRZI alone (from 62.5 MHz to 31.25 MHz for 125 MBaud operation), which aids in and lowers emissions. Block codes, often denoted as mB/nB, group m bits of data into n-bit codewords, where n > m, to impose constraints that enhance transmission reliability. The coding rate is given by R=mnR = \frac{m}{n}, representing the efficiency of data throughput relative to the transmitted symbols; for instance, common schemes yield R = 0.8. These codes select codewords from an expanded symbol space to ensure DC balance (equal numbers of 1s and 0s over time), sufficient transitions for synchronization, and avoidance of long run lengths of identical bits. Additionally, they provide inherent error detection by designating certain codewords as invalid or reserved for control signals, allowing receivers to flag transmission errors without dedicated parity bits. By mapping data blocks to these constrained symbols, block codes achieve higher spectral efficiency than binary schemes, supporting denser data rates over limited bandwidth media. The 4B/5B code exemplifies this approach in (100 Mbps) variants like 100BASE-FX, where groups of 4 bits are encoded into 5-bit symbols, incurring a 25% overhead (R = 4/5 = 0.8). Each 4-bit maps to one of 16 symbols chosen to guarantee at least two transitions per symbol and limit consecutive zeros to three, facilitating clock extraction; control symbols like (11111) or J/K for frame delimiting further aid synchronization. This encoding, combined with NRZI, ensures robust performance over fiber or twisted-pair. In (1000BASE-X), the 8B/10B code extends this principle, encoding 8-bit bytes into 10-bit characters (R = 8/10 = 0.8, 25% overhead) while maintaining running disparity for DC balance—codewords are selected such that the disparity (1s minus 0s) is either +2 or -2, alternating to keep the baseline near zero. It supports 256 symbols plus 12 control characters (e.g., K28.5 for alignment), with mandatory transitions in special symbols for bit-level recovery; invalid sequences detect single- and some multi-bit errors. may be applied in certain implementations to further randomize patterns and reduce peaks. For higher speeds, the 64B/66B code in 10GBASE-R Ethernet (IEEE 802.3ae) processes 64-bit blocks into 66-bit transmission units (R = 64/66 ≈ 0.9699, ~3% overhead), balancing efficiency with reliability. A 2-bit sync header (01 for data blocks, 10 for control) precedes the scrambled 64-bit , enabling frame delineation and ; the self-synchronizing , based on a with polynomial x58+x39+1x^{58} + x^{39} + 1, whitens the data to minimize low-frequency content and aid . Control blocks embed up to eight ordered sets (e.g., /S/ for start, /T/ for terminate), supporting detection via header mismatches or invalid block types, while the low overhead allows 10 Gb/s data over a 10.3125 Gb/s line rate. This design prioritizes higher density and reduced complexity compared to cascading multiple 8B/10B stages.

Optical-Specific Codes

Optical line codes for fiber optic transmission are designed to mitigate challenges unique to light propagation, such as intensity modulation via on-off keying (OOK), where binary data is encoded by varying the optical power between "on" and "off" states, but this approach induces frequency chirp in directly modulated lasers, leading to spectral broadening that worsens with fiber length. Chirp reduction is critical, often achieved through external electro-optic modulators that separate intensity modulation from laser frequency shifts, thereby preserving signal integrity over distance. Additionally, dispersion effects—primarily chromatic dispersion, which causes pulse broadening due to wavelength-dependent group velocities, and polarization mode dispersion, which splits pulses based on polarization states—degrade signal quality in high-bit-rate systems, necessitating line codes that minimize these impairments. Non-return-to-zero on-off keying (NRZ-OOK) serves as the standard line code for short-haul optical links due to its simplicity in implementation using direct modulation or Mach-Zehnder modulators, requiring minimal bandwidth as the signal remains high or low throughout each bit period. However, NRZ-OOK exhibits sensitivity to timing jitter, as prolonged "on" or "off" states reduce distinct pulse edges, complicating and amplifying errors from accumulated or dispersion-induced distortions in receiver timing circuits. Return-to-zero (RZ) formats address these limitations in long-haul applications by employing a 50% duty cycle, where each "1" bit pulse occupies half the bit period before returning to zero, enhancing clock recovery through sharper transitions that facilitate synchronization even after extensive amplification and dispersion. Variants like carrier-suppressed RZ (CSRZ) further optimize performance by suppressing the optical carrier via dual-drive modulation, introducing a π phase shift between adjacent pulses to enable phase-based encoding, which improves tolerance to nonlinear effects while maintaining the RZ benefits for clock extraction. Advanced formats such as optical duobinary coding achieve spectral compression by correlating adjacent bits through a simple delay-and-add filter, effectively halving the required bandwidth compared to NRZ (from approximately R/2 Hz to R/4 Hz for bit rate R) and allowing higher data rates over bandwidth-limited fibers. In duobinary systems, eye diagram analysis is essential for assessing optical (OSNR), as the three-level (corresponding to 00, 01/10, 11 bit pairs) reveals margins, with wider eye openings indicating better OSNR tolerance and reduced bit error rates. These codes are standardized in ITU-T Recommendation G.957 for SONET/SDH optical interfaces, which specifies binary NRZ as the baseline line coding for all system interfaces, scrambled per G.707 to ensure DC balance and spectral properties suitable for optical transmission up to STM-64/OC-192 rates.

Advanced Topics and Applications

Error Control Integration

Line codes incorporate basic error detection mechanisms to identify transmission anomalies without relying on higher-layer protocols. In bipolar formats such as alternate mark inversion (AMI), error detection leverages the rule that consecutive marks (logical 1s) must alternate in polarity; a violation of this alternation, known as a bipolar violation, indicates a bit error, as every single-bit error disrupts the expected polarity sequence. Similarly, in run-length limited (RLL) codes, invalid transitions that exceed the maximum or minimum run length of zeros (or ones) between transitions serve as detectable violations, allowing the receiver to flag potential errors in the constrained sequence. Beyond standalone detection, line codes often integrate with (FEC) schemes, functioning as outer codes that complement inner FEC layers like Reed-Solomon codes for enhanced reliability. In concatenated systems, the line code processes the output of the inner FEC, where violations in the line code signal decoding issues in the preceding layer; for instance, Reed-Solomon serves as the outer code to correct burst errors after the line code detects and marks anomalies. A practical example is the 8B/10B code, where running disparity errors—deviations from the balanced ±2 or 0 disparity—trigger flags that inform the FEC decoder to initiate correction, thereby improving overall coding gain without additional overhead. Certain line code designs exhibit self-correcting properties that mitigate specific error types, such as polarity inversions. Differential encoding achieves polarity-independent detection by representing data through transitions rather than absolute levels, ensuring that an inverted signal polarity does not alter the decoded output, as the receiver tracks changes relative to the previous state. This approach enhances (BER) performance; for example, bipolar signaling yields an approximate 3 dB gain in over unipolar schemes for equivalent error probabilities, due to the doubled between symbols (±A versus 0/A). Despite these features, line codes offer only rudimentary error handling, primarily detecting and hinting at burst errors through violations rather than performing deep correction, which is deferred to higher-layer FEC or protocols for comprehensive recovery.

Performance in Transmission Media

In electrical transmission media, such as twisted-pair cables, the Alternate Mark Inversion (AMI) line code is commonly employed in T1 lines operating at 1.544 Mbps, where it transmits pulses over unshielded twisted-pair wiring to minimize crosstalk and electromagnetic interference while maintaining signal integrity over distances up to 6,000 feet. AMI's bipolar signaling helps reduce DC components, but it can suffer from baseline wander in long sequences of zeros, impacting performance in noisy environments typical of twisted-pair channels. To mitigate inter-symbol interference (ISI) caused by the limited bandwidth of twisted-pair (typically 1-4 MHz for voice-grade lines), partial response signaling introduces controlled ISI at the transmitter, allowing the receiver to use simpler equalization techniques like duobinary decoding, which improves bandwidth efficiency without excessive noise enhancement. Coaxial cables, offering higher bandwidth (up to several GHz depending on type, such as RG-6 supporting 1 GHz), are used for digital transmission in systems like early cable modems or HDSL, where line codes such as AMI or pseudoternary formats are applied to extend reach beyond twisted-pair limits while contending with rates of about 67 dB/km at 100 MHz. These codes must balance spectral occupancy with the cable's (typically 75 Ω) to avoid reflections and signal distortion, though bandwidth constraints still necessitate to prevent excessive ISI over longer runs (e.g., 500-1000 meters at multi-Mbps rates). In optical media, (RZ) and (NRZ) line codes exhibit differing responses to dispersion and ; NRZ generally outperforms RZ in long-haul links due to its narrower spectral width, which reduces chromatic dispersion effects (e.g., broadening of ~1 ps/nm/km in standard single-mode ), leading to lower bit error rates (BER) under losses of 0.2 dB/km at 1550 nm. RZ codes, with their return-to-zero s, provide better but suffer higher sensitivity to nonlinearity and dispersion, increasing power penalties by 2-3 dB compared to NRZ in dispersion-compensated systems. Power budget calculations for optical links incorporate receiver sensitivity, which for NRZ-coded systems at 10 Gb/s can reach -18 to -24 dBm (depending on PIN or APD detectors), ensuring a minimum margin of 6-10 dB after accounting for loss and connector penalties. For wireless adaptations, particularly short-range RF systems like operating in the 2.4 GHz ISM band, NRZ serves as the line code before Gaussian (GFSK) modulation, enabling data rates up to 1 Mbps over distances of 10-100 meters while keeping the signal simple and DC-balanced. However, multipath and Doppler shifts in RF channels introduce ISI, necessitating equalization at the receiver—such as minimum mean-square (MMSE) linear equalizers—to compensate for channel distortions and maintain low BER (e.g., <10^{-6}) without excessive complexity in power-constrained devices. Key performance metrics across media include power spectral density (PSD) comparisons; for instance, Manchester coding yields a PSD shaped like sinc²(fT) with a null at DC and broader main lobe (extending to 1.5/T, where T is bit duration), making it suitable for AC-coupled channels but requiring twice the bandwidth of NRZ's rectangular PSD, which concentrates energy from DC to 0.5/T for efficient electrical transmission. This spectral difference influences media choice, as NRZ's low-frequency content aids twisted-pair and efficiency, while Manchester's null supports optical and AC coupling.

Modern Implementations and Evolutions

In the evolution of Ethernet standards, line codes have progressed from simpler schemes in early implementations to more sophisticated integrated with (FEC) to support higher data rates and reliability. The 10GBASE-R physical coding sublayer (PCS) introduced the 64B/66B , which encodes 64 bits of data into 66 bits for transmission using (NRZ) signaling, providing DC balance, , and low overhead of approximately 3.125% while enabling 10.3125 Gbaud operation across various media. This scheme was extended in post-2010 standards, such as IEEE 802.3ba for 40G and 100G Ethernet, where 100GBASE-R employs 64B/66B across 10 lanes of NRZ at 10.3125 Gbaud each, achieving 100 Gbit/s aggregate with integrated Reed-Solomon FEC (RS(528,514)) to enhance performance in noisy environments. Further advancements in IEEE 802.3bs (2017) for 200G and 400G Ethernet incorporate Reed-Solomon RS(544,514) FEC alongside 64B/66B in some configurations, particularly for and applications, reducing error rates and supporting denser integration in data centers. In telecommunications infrastructure, the Optical Transport Network (OTN) defined by ITU-T G.709 utilizes advanced block coding derivatives to multiplex and transport high-capacity signals efficiently. OTN frames incorporate 64B/66B-like block codes transcoded into 512B/513B structures for mapping Fibre Channel or Ethernet payloads, ensuring synchronization and error detection across optical domains with an overhead of about 6.7% while supporting rates up to 100 Gbit/s per lambda in OTU4 configurations. In 5G New Radio (NR), polar codes serve as the channel coding scheme for control channels per 3GPP TS 38.212, influencing the physical layer design by enabling low-latency encoding that integrates with line-level modulation like π/2-BPSK, thereby optimizing baseband-to-line transitions for enhanced spectral efficiency in mmWave and sub-6 GHz bands. Recent advancements in line codes emphasize multilevel signaling to boost capacity in . The adoption of with 4 levels (PAM-4) in 400G Ethernet , standardized in IEEE 802.3bs from 2018, encodes two bits per symbol using four amplitude levels, enabling 53.125 Gbps per at 26.5625 Gbaud over four parallel (e.g., in 400GBASE-DR4) with RS-FEC, achieving up to 10 km reach on single-mode fiber (e.g., in 400GBASE-LR8 with eight ) while maintaining power efficiency. Probabilistic shaping techniques further refine this by distributing symbol probabilities according to the Gaussian , as demonstrated in probabilistically shaped PAM-4 systems, which approach the Shannon limit with gains of 1-2 dB in over uniform constellations, particularly in long-haul coherent . Looking toward future trends, coherent detection in optical transceivers mitigates impairments like chromatic dispersion digitally, thereby reducing the reliance on heavy line code overhead for equalization and allowing simpler NRZ or PAM-4 schemes to operate closer to raw capacity limits; IEEE 802.3df, approved in , standardizes 800G Ethernet with higher-order PAM4 (up to 112 Gbaud per lane) and advanced FEC for and metro applications. Emerging quantum-safe adaptations for secure line communications, as of 2025, integrate such as lattice-based schemes into OTN and Ethernet framing to protect against quantum attacks on encryption, with standards from ETSI and NIST enabling hybrid classical-quantum over lines without altering core line coding structures.

References

  1. https://web.stanford.edu/class/ee179/lectures/old_notes/notes14.pdf
  2. https://www.utdallas.edu/~torlak/courses/ee4367/lectures/CodingI.pdf
  3. https://web.stanford.edu/class/ee179/lectures/notes14.pdf
  4. https://www.scs.stanford.edu/10au-cs144/notes/l8.pdf
  5. http://www.spec.gmu.edu/~pparis/classes/notes_500/07-Line-Codes.pdf
  6. https://barry.ece.gatech.edu/digital/supp/19spectrum.pdf
  7. https://eh.net/encyclopedia/history-of-the-u-s-telegraph-industry/
  8. https://insight.ieeeusa.org/articles/your-engineering-heritage-pulse-code-modulation-it-all-started-75-years-ago-with-alec-reeves/
  9. https://www.itu.int/rec/dologin_pub.asp?lang=e&id=T-REC-G.703-199810-S!!PDF-E&type=items
  10. https://www.siue.edu/~yadwang/ECE375_Lec8.pdf
  11. https://sierrahardwaredesign.com/basic-networking/running-disparity-rd/
  12. https://www.ti.com/lit/pdf/scaa062
  13. https://imapsource.org/api/v1/articles/57229-line-coding-methods-for-high-speed-serial-links.pdf
  14. https://ieeexplore.ieee.org/document/5390392
  15. https://grouper.ieee.org/groups/802/17/documents/presentations/may2001/gfp.pdf
  16. https://www.geeksforgeeks.org/digital-logic/difference-between-unipolar-polar-and-bipolar-line-coding-schemes/
  17. https://www.tutorialspoint.com/digital_communication/digital_communication_line_codes.htm
  18. https://ronny.cswp.cs.technion.ac.il/wp-content/uploads/sites/54/2016/05/chapters1-9.pdf
  19. https://cmrr-star.ucsd.edu/static/pubs/psrll.pdf
  20. https://www.tek.com/en/documents/primer/clock-recovery-primer-part-1
  21. https://web.stanford.edu/class/archive/ee/ee371/ee371.1066/lectures/Old/Older/lect_15_1up.pdf
  22. https://www.sciencedirect.com/topics/engineering/clock-recovery
  23. https://web.engr.oregonstate.edu/~anandt/papers/shu_jssc_2015.pdf
  24. https://www.eecis.udel.edu/~vsaxena/courses/ece504/Handouts/Razavi1996_PLL_IEEExplore.pdf
  25. https://www.ieee802.org/3/bs/public/adhoc/logic/feb16_17/ghiasi_01_0217_logic.pdf
  26. https://blog.teledynelecroy.com/2021/11/what-is-differential-manchester-encoding.html
  27. https://www.cs.nmt.edu/~cs353/Lectures/Lecture_04_Digital_and_Analog_Transmission_Ch04.pdf
  28. https://www.analog.com/media/en/technical-documentation/application-notes/ee-269.pdf
  29. https://www.iol.unh.edu/sites/default/files/knowledgebase/ge/pcs.pdf
  30. https://www.ieee802.org/3/z/public/presentations/mar1996/RT8B10B.pdf
  31. https://www.iol.unh.edu/sites/default/files/knowledgebase/10gec/10GbE_Cl49.pdf
  32. https://www.sciencedirect.com/topics/physics-and-astronomy/optical-communication
  33. https://orbit.dtu.dk/files/5589919/Tokle-PhD-SentToPrint2.pdf
  34. https://www.intechopen.com/chapters/1192710
  35. https://www.synopsys.com/photonic-solutions/product-applications/advanced-modulation-formats/optsim-csrz-modulation.html
  36. https://ieeexplore.ieee.org/document/4149749
  37. https://optiwave.com/wp-content/uploads/2014/04/DuobinaryModulationForOpticalSystems.pdf
  38. https://opg.optica.org/fulltext.cfm?uri=oe-16-24-19600
  39. https://ieeexplore.ieee.org/document/965974
  40. https://ntrs.nasa.gov/api/citations/19900019023/downloads/19900019023.pdf
  41. https://www.ieee802.org/3/efm/public/sep01/ivry_1_0901.pdf
  42. https://people.ece.ubc.ca/~edc/3525.jan2014/lectures/lec7.pdf
  43. https://www.academia.edu/38214602/Line_coding
  44. https://www.tek.com/en/documents/primer/t1-network-technology-essentials-successful-field-service-technicians
  45. https://www.analog.com/media/en/technical-documentation/data-sheets/ds26521.pdf
  46. https://www2.eecs.berkeley.edu/Pubs/TechRpts/1986/ERL-86-79.pdf
  47. https://cioffi-group.stanford.edu/doc/book/chap3.pdf
  48. https://ieeexplore.ieee.org/document/1094786
  49. https://www.caledoniancable.com/English/product/Coaxial_Cables/RGType_75Ohm/RG%206QS.htm
  50. https://broadbandlibrary.com/the-untapped-capacity-of-coaxial-cable/
  51. https://scholarworks.calstate.edu/downloads/ks65hh09n
  52. https://www.researchgate.net/publication/335306755_Performance_Analysis_of_Dispersion_Compensation_Fiber_on_NRZ_and_RZ_Modulation_with_Difference_Power_Transmission
  53. https://www.fiberoptics4sale.com/blogs/wave-optics/optical-receiver-sensitivity
  54. https://www.diva-portal.org/smash/get/diva2:21778/FULLTEXT01.pdf
  55. https://wirelesspi.com/a-classification-of-equalization-techniques/
  56. https://ieeexplore.ieee.org/iel7/8919/10196078/10144806.pdf
  57. https://people.ece.ubc.ca/~edc/3525.fall2023/lab4.pdf
  58. https://www.ieee802.org/3/bn/public/mar13/hajduczenia_3bn_04_0313.pdf
  59. https://www.ieee802.org/3/df/public/22_02/wang_3df_01_220215.pdf
  60. https://www.all-electronics.de/files/2025/10/15/417-2081250-otn-tutorial-053751.pdf
  61. https://www.mathworks.com/help/5g/gs/polar-coding.html
  62. https://blogs.cisco.com/sp/pam4-for-400g-optical-interfaces-and-beyond-part-1
  63. https://www.ieee802.org/3/bs/baseline_3bs_0715.pdf
  64. https://www.ieee802.org/3/df/
  65. https://www.etsi.org/events/2450-etsi-iqc-quantum-safe-cryptography-conference-2025
Add your contribution
Related Hubs
User Avatar
No comments yet.