Hubbry Logo
Pulse-code modulationPulse-code modulationMain
Open search
Pulse-code modulation
Community hub
Pulse-code modulation
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Pulse-code modulation
Pulse-code modulation
Pulse-code modulation
View on Wikipedia
from Wikipedia

Pulse-code modulation
Filename extension
.L16, .WAV, .AIFF, .AU, .PCM[1]
Internet media type
audio/L16, audio/L8,[2] audio/L20, audio/L24[3][4]
Type code"AIFF" for L16,[1] none[3]
Magic numberVaries
Type of formatUncompressed audio
Contained byAudio CD, AES3, WAV, AIFF, AU, M2TS, VOB, and many others
Open format?Yes
Free format?Yes[5]
Passband modulation
Analog modulation
Digital modulation
Hierarchical modulation
Spread spectrum
See also

Pulse-code modulation (PCM) is a method used to digitally represent analog signals. It is the standard form of digital audio in computers, compact discs, digital telephony and other digital audio applications. In a PCM stream, the amplitude of the analog signal is sampled at uniform intervals, and each sample is quantized to the nearest value within a range of digital steps. Shannon, Oliver, and Pierce were inducted into the National Inventors Hall of Fame for their PCM patent granted in 1952.[6][7][8]

Linear pulse-code modulation (LPCM) is a specific type of PCM in which the quantization levels are linearly uniform.[5] This is in contrast to PCM encodings in which quantization levels vary as a function of amplitude (as with the A-law algorithm or the μ-law algorithm). Though PCM is a more general term, it is often used to describe data encoded as LPCM.

A PCM stream has two basic properties that determine the stream's fidelity to the original analog signal: the sampling rate, which is the number of times per second that samples are taken; and the bit depth, which determines the number of possible digital values that can be used to represent each sample.

History

[edit]

Early electrical communications started to sample signals in order to multiplex samples from multiple telegraphy sources and to convey them over a single telegraph cable. The American inventor Moses G. Farmer conceived telegraph time-division multiplexing (TDM) as early as 1853. Electrical engineer W. M. Miner, in 1903, used an electro-mechanical commutator for time-division multiplexing multiple telegraph signals; he also applied this technology to telephony. He obtained intelligible speech from channels sampled at a rate above 3500–4300 Hz; lower rates proved unsatisfactory.

In 1920, the Bartlane cable picture transmission system used telegraph signaling of characters punched in paper tape to send samples of images quantized to 5 levels.[9] In 1926, Paul M. Rainey of Western Electric patented a facsimile machine that transmitted its signal using 5-bit PCM, encoded by an opto-mechanical analog-to-digital converter.[10] The machine did not go into production.[11]

British engineer Alec Reeves, unaware of previous work, conceived the use of PCM for voice communication in 1937 while working for International Telephone and Telegraph in France. He described the theory and its advantages, but no practical application resulted. Reeves filed for a French patent in 1938, and his US patent was granted in 1943.[12] By this time Reeves had started working at the Telecommunications Research Establishment.[11]

The first transmission of speech by digital techniques, the SIGSALY encryption equipment, conveyed high-level Allied communications during World War II. In 1949, for the Canadian Navy's DATAR system, Ferranti Canada built a working PCM radio system that was able to transmit digitized radar data over long distances.[13]

PCM in the late 1940s and early 1950s used a cathode-ray coding tube with a plate electrode having encoding perforations.[14] As in an oscilloscope, the beam was swept horizontally at the sample rate while the vertical deflection was controlled by the input analog signal, causing the beam to pass through higher or lower portions of the perforated plate. The plate collected or passed the beam, producing current variations in binary code, one bit at a time. Rather than natural binary, the grid of Goodall's later tube was perforated to produce a glitch-free Gray code and produced all bits simultaneously by using a fan beam instead of a scanning beam.[15]

In the United States, the National Inventors Hall of Fame has honored Bernard M. Oliver[16] and Claude Shannon[17] as the inventors of PCM,[18] as described in "Communication System Employing Pulse Code Modulation", U.S. patent 2,801,281 filed in 1946 and 1952, granted in 1956. Another patent by the same title was filed by John R. Pierce in 1945, and issued in 1948: U.S. patent 2,437,707. The three of them published "The Philosophy of PCM" in 1948.[19]

The T-carrier system, introduced in 1961, uses two twisted-pair transmission lines to carry 24 PCM telephone calls sampled at 8 kHz and 8-bit resolution. This development improved capacity and call quality compared to the previous frequency-division multiplexing schemes.

In 1973, adaptive differential pulse-code modulation (ADPCM) was developed, by P. Cummiskey, Nikil Jayant and James L. Flanagan.[20]

Digital audio recordings

[edit]
Main articles: Digital audio and Digital recording

In 1967, the first PCM recorder was developed by NHK's research facilities in Japan.[21] The 30 kHz 12-bit device used a compander (similar to DBX Noise Reduction) to extend the dynamic range, and stored the signals on a video tape recorder. In 1969, NHK expanded the system's capabilities to 2-channel stereo and 32 kHz 13-bit resolution. In January 1971, using NHK's PCM recording system, engineers at Denon recorded the first commercial digital recordings.[note 1][21]

In 1972, Denon unveiled the first 8-channel digital recorder, the DN-023R, which used a 4-head open reel broadcast video tape recorder to record in 47.25 kHz, 13-bit PCM audio.[note 2] In 1977, Denon developed the portable PCM recording system, the DN-034R. Like the DN-023R, it recorded 8 channels at 47.25 kHz, but it used 14-bits "with emphasis, making it equivalent to 15.5 bits."[21]

In 1979, the first digital pop album, Bop till You Drop, was recorded. It was recorded in 50 kHz, 16-bit linear PCM using a 3M digital tape recorder.[22]

The compact disc (CD) brought PCM to consumer audio applications with its introduction in 1982. The CD uses a 44,100 Hz sampling frequency and 16-bit resolution and stores up to 80 minutes of stereo audio per disc.

Digital telephony

[edit]
Main article: Digital telephony

The rapid development and wide adoption of PCM digital telephony was enabled by metal–oxide–semiconductor (MOS) switched capacitor (SC) circuit technology, developed in the early 1970s.[23] This led to the development of PCM codec-filter chips in the late 1970s.[23][24] The silicon-gate CMOS (complementary MOS) PCM codec-filter chip, developed by David A. Hodges and W.C. Black in 1980,[23] has since been the industry standard for digital telephony.[23][24] By the 1990s, telecommunication networks such as the public switched telephone network (PSTN) had been largely digitized with very-large-scale integration (VLSI) CMOS PCM codec-filters, widely used in electronic switching systems for telephone exchanges, user-end modems and a wide range of digital transmission applications such as the integrated services digital network (ISDN), cordless telephones and cell phones.[24]

Implementations

[edit]

PCM is the method of encoding typically used for uncompressed digital audio.[note 3]

  • The 4ESS switch introduced time-division switching into the US telephone system in 1976, based on medium scale integrated circuit technology.[25]
  • LPCM is used for the lossless encoding of audio data in the compact disc Red Book standard (informally also known as Audio CD), introduced in 1982.
  • AES3 (specified in 1985, upon which S/PDIF is based) is a particular format using LPCM.
  • LaserDiscs with digital sound have an LPCM track on the digital channel.
  • On PCs, PCM and LPCM often refer to the format used in WAV (defined in 1991) and AIFF audio container formats (defined in 1988). LPCM data may also be stored in other formats such as AU, raw audio format (header-less file) and various multimedia container formats.
  • LPCM has been defined as a part of the DVD (since 1995) and Blu-ray (since 2006) standards.[26][27][28] It is also defined as a part of various digital video and audio storage formats (e.g. DV since 1995,[29] AVCHD since 2006[30]).
  • LPCM is used by HDMI (defined in 2002), a single-cable digital audio/video connector interface for transmitting uncompressed digital data.
  • RF64 container format (defined in 2007) uses LPCM and also allows non-PCM bitstream storage: various compression formats contained in the RF64 file as data bursts (Dolby E, Dolby AC3, DTS, MPEG-1/MPEG-2 Audio) can be "disguised" as PCM linear.[31]

Modulation

[edit]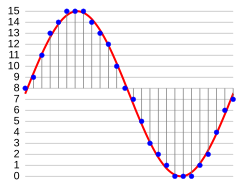
Sampling and quantization of a signal (red) for 4-bit LPCM over a time domain at specific frequency

In the diagram, a sine wave (red curve) is sampled and quantized for PCM. The sine wave is sampled at regular intervals, shown as vertical lines. For each sample, one of the available values (on the y-axis) is chosen. The PCM process is commonly implemented on a single integrated circuit called an analog-to-digital converter (ADC). This produces a fully discrete representation of the input signal (blue points) that can be easily encoded as digital data for storage or manipulation. Several PCM streams could also be multiplexed into a larger aggregate data stream, generally for transmission of multiple streams over a single physical link. One technique is called time-division multiplexing (TDM) and is widely used, notably in the modern public telephone system.

Demodulation

[edit]

The electronics involved in producing an accurate analog signal from the discrete data are similar to those used for generating the digital signal. These devices are digital-to-analog converters (DACs). They produce a voltage or current (depending on type) that represents the value presented on their digital inputs. This output would then generally be filtered and amplified for use.

To recover the original signal from the sampled data, a demodulator can apply the procedure of modulation in reverse. After each sampling period, the demodulator reads the next value and transitions the output signal to the new value. As a result of these transitions, the signal retains a significant amount of high-frequency energy due to imaging effects. To remove these undesirable frequencies, the demodulator passes the signal through a reconstruction filter that suppresses energy outside the expected frequency range (greater than the Nyquist frequency ).[note 4]

Standard sampling precision and rates

[edit]

Common sample depths for LPCM are 8, 16, 20 or 24 bits per sample.[1][2][3][32]

LPCM encodes a single sound channel. Support for multichannel audio depends on file format and relies on synchronization of multiple LPCM streams.[5][33] While two channels (stereo) is the most common format, systems can support up to 8 audio channels (7.1 surround)[2][3] or more.

Common sampling frequencies are 48 kHz as used with DVD format videos, or 44.1 kHz as used in CDs. Sampling frequencies of 96 kHz or 192 kHz can be used on some equipment, but the benefits have been debated.[34]

Limitations

[edit]

The Nyquist–Shannon sampling theorem shows PCM devices can operate without introducing distortions within their designed frequency bands if they provide a sampling frequency at least twice that of the highest frequency contained in the input signal. For example, in telephony, the usable voice frequency band ranges from approximately 300 to 3400 Hz.[35] For effective reconstruction of the voice signal, telephony applications therefore typically use an 8000 Hz sampling frequency which is more than twice the highest usable voice frequency.

Regardless, there are potential sources of impairment implicit in any PCM system:

  • Choosing a discrete value that is near but not exactly at the analog signal level for each sample leads to quantization error. When dithering is used to compensate for this, it introduces additional noise.[note 5]
  • Between samples no measurement of the signal is made; the sampling theorem guarantees non-ambiguous representation and recovery of the signal only if it has no energy at frequency fs/2 or higher (one half the sampling frequency, known as the Nyquist frequency); higher frequencies will not be correctly represented or recovered and add aliasing distortion to the signal below the Nyquist frequency.
  • As samples are dependent on time, an accurate clock is required for accurate reproduction. If either the encoding or decoding clock is not stable, these imperfections will directly affect the output quality of the device.[note 6]

Processing and coding

[edit]

Some forms of PCM combine signal processing with coding. Older versions of these systems applied the processing in the analog domain as part of the analog-to-digital process; newer implementations do so in the digital domain. These simple techniques have been largely rendered obsolete by modern transform-based audio compression techniques, such as modified discrete cosine transform (MDCT) coding.

  • Linear PCM (LPCM) is PCM with linear quantization.[5]
  • Differential PCM (DPCM) encodes the PCM values as differences between the current and the predicted value. An algorithm predicts the next sample based on the previous samples, and the encoder stores only the difference between this prediction and the actual value. If the prediction is reasonable, fewer bits can be used to represent the same information. For audio, this type of encoding reduces the number of bits required per sample by about 25% compared to PCM.
  • Adaptive differential pulse-code modulation (ADPCM) is a variant of DPCM that varies the size of the quantization step, to allow further reduction of the required bandwidth for a given signal-to-noise ratio.
  • Delta modulation is a form of DPCM that uses one bit per sample to indicate whether the signal is increasing or decreasing compared to the previous sample.

In telephony, a standard audio signal for a single phone call is encoded as 8,000 samples per second, of 8 bits each, giving a 64 kbit/s digital signal known as DS0. The default signal compression encoding on a DS0 is either μ-law (mu-law) PCM (North America and Japan) or A-law PCM (Europe and most of the rest of the world). These are logarithmic compression systems where a 12- or 13-bit linear PCM sample number is mapped into an 8-bit value. This system is described by international standard G.711.

Where circuit costs are high and loss of voice quality is acceptable, it sometimes makes sense to compress the voice signal even further. An ADPCM algorithm is used to map a series of 8-bit μ-law or A-law PCM samples into a series of 4-bit ADPCM samples. In this way, the capacity of the line is doubled. The technique is detailed in the G.726 standard.

Audio coding formats and audio codecs have been developed to achieve further compression. Some of these techniques have been standardized and patented. Advanced compression techniques, such as modified discrete cosine transform (MDCT) and linear predictive coding (LPC), are now widely used in mobile phones, voice over IP (VoIP) and streaming media.

Encoding for serial transmission

[edit]
Main article: Line code
See also: T-carrier and E-carrier

PCM can be either return-to-zero (RZ) or non-return-to-zero (NRZ). For a NRZ system to be synchronized using in-band information, there must not be long sequences of identical symbols, such as ones or zeroes. For binary PCM systems, the density of 1-symbols is called ones-density.[36]

Ones-density is often controlled using precoding techniques such as run-length limited encoding, where the PCM code is expanded into a slightly longer code with a guaranteed bound on ones-density before modulation into the channel. In other cases, extra framing bits are added into the stream, which guarantees at least occasional symbol transitions.

Another technique used to control ones-density is the use of a scrambler on the data, which will tend to turn the data stream into a stream that looks pseudo-random, but where the data can be recovered exactly by a complementary descrambler. In this case, long runs of zeroes or ones are still possible on the output but are considered unlikely enough to allow reliable synchronization.

In other cases, the long term DC value of the modulated signal is important, as building up a DC bias will tend to move communications circuits out of their operating range. In this case, special measures are taken to keep a count of the cumulative DC bias and to modify the codes if necessary to make the DC bias always tend back to zero.

Many of these codes are bipolar codes, where the pulses can be positive, negative or absent. In the typical alternate mark inversion code, non-zero pulses alternate between being positive and negative. These rules may be violated to generate special symbols used for framing or other special purposes.

Nomenclature

[edit]

The word pulse in the term pulse-code modulation refers to the pulses to be found in the transmission line. This perhaps is a natural consequence of this technique having evolved alongside two analog methods, pulse-width modulation and pulse-position modulation, in which the information to be encoded is represented by discrete signal pulses of varying width or position, respectively.[citation needed] In this respect, PCM bears little resemblance to these other forms of signal encoding, except that all can be used in time-division multiplexing, and the numbers of the PCM codes are represented as electrical pulses.

See also

[edit]

Explanatory notes

[edit]

References

[edit]

Further reading

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Pulse-code modulation

View on Grokipedia
from Grokipedia
Pulse-code modulation (PCM) is a method used to digitally represent analog signals, in which the amplitude of the signal is sampled at uniform time intervals, quantized into a finite set of discrete levels, and then encoded into a series of binary codes representing the quantized values. This process transforms continuous analog waveforms into a discrete digital format suitable for transmission, storage, and processing in digital systems. PCM serves as the foundational technique for digital audio representation in applications such as compact discs, computers, and telephony. Invented in 1937 by British engineer Alec H. Reeves while working at International Telephone and Telegraph (ITT) Laboratories in , PCM was initially conceived as a way to transmit multiple voice channels securely over noisy analog lines during by converting them into digital pulses resistant to interference. Reeves patented the technique in 1938 (French patent 852,183), and it was first described in a 1939 publication, marking it as a pioneering step toward digital communications. Although overlooked initially due to the dominance of analog technologies, Bell Laboratories developed practical implementations in the , constructing the first working PCM system for experimental in 1943. The core steps of PCM involve three main stages: sampling, where the analog signal's is measured at a rate at least twice the highest frequency component (per the Nyquist-Shannon sampling theorem to avoid ); quantization, which maps each sample to the nearest level in a predefined set of discrete values, introducing minimal distortion; and encoding, where these quantized levels are converted into words, typically using a fixed number of bits per sample (e.g., 8 bits for 256 levels). The fidelity of PCM depends on the sampling rate, quantization levels, and bit depth; for instance, standard audio uses 44.1 kHz sampling and 16-bit encoding for high-quality reproduction. PCM's significance lies in its robustness against noise and errors compared to analog methods, enabling in digital systems, and it underpins modern telecommunications, including the systems introduced by in 1962 for commercial long-distance telephony. Its adoption revolutionized data transmission, paving the way for the digital revolution in audio, video, and communications, with variants like linear PCM remaining uncompressed standards in production.

Fundamentals

Sampling

Sampling is the initial step in pulse-code modulation (PCM), where a continuous analog signal is transformed into a sequence of discrete-time samples by measuring its amplitude at regular intervals. This process creates a pulse-amplitude modulated (PAM) signal, consisting of narrow pulses whose amplitudes correspond to the instantaneous values of the original waveform at each sampling instant. Uniform sampling ensures that the time between samples, known as the sampling period TsT_s, is constant, with Ts=1fsT_s = \frac{1}{f_s}, where fsf_s is the sampling frequency. The Nyquist-Shannon sampling theorem provides the theoretical foundation for this process, stating that a band-limited continuous-time signal can be perfectly reconstructed from its samples if the sampling frequency fsf_s is greater than or equal to twice the highest frequency component fmax⁡f_{\max} in the signal, i.e., fs≥2fmax⁡f_s \geq 2 f_{\max}. This requirement, often called the , prevents , a distortion where higher frequencies masquerade as lower ones in the sampled signal. The theorem was first articulated by in 1928 regarding telegraph transmission limits and formalized by in 1949 for communication systems. To ensure compliance with the Nyquist-Shannon theorem, an —a —is essential before sampling; it attenuates components above fs/2f_s / 2, band-limiting the signal to avoid artifacts. This filter limits the signal's bandwidth to the , preserving the integrity of the sampled representation. In audio applications, sampling converts continuous acoustic waveforms into discrete PAM samples; for instance, human hearing extends to about 20 kHz, so compact discs use a sampling of 44.1 kHz—more than twice this bandwidth—to capture high-fidelity sound without . These PAM samples form the basis for subsequent PCM stages, such as quantization.

Quantization

Quantization in pulse-code modulation (PCM) involves discretizing the of each sampled signal value from a continuous range to one of a of discrete levels, approximating the original with a digital representation. In uniform quantization, the full range from Vmin⁡V_{\min} to Vmax⁡V_{\max} is divided into 2n2^n equally spaced levels, where nn is the number of bits per sample, resulting in a fixed step size Δ=Vmax⁡−Vmin⁡2n\Delta = \frac{V_{\max} - V_{\min}}{2^n}. This process maps each sample to the nearest quantization level, introducing an inherent approximation that forms the basis of fidelity in PCM. The difference between the original sample value and its quantized counterpart is known as the quantization error, which manifests as in the reconstructed signal. For a uniform quantizer assuming the error is uniformly distributed over −Δ/2-\Delta/2 to Δ/2\Delta/2, the mean squared error is Δ2/12\Delta^2/12. For sinusoidal input signals spanning the full , the (SQNR) is given by SQNR=6.02n+1.76 dB\mathrm{SQNR} = 6.02n + 1.76 \, \mathrm{dB}, providing a theoretical measure of quantization performance that improves approximately 6 dB per additional bit. This formula highlights the trade-off between bit depth and level, with higher nn reducing error but increasing bandwidth requirements. Uniform quantizers are categorized into mid-riser and mid-tread types based on the placement of the level relative to the decision thresholds. In a mid-riser quantizer, the input falls midway between two output levels (e.g., between -1 and +1), resulting in no output code and potential DC offset, often using sign-magnitude representation. Conversely, a mid-tread quantizer positions the at the center of a quantization interval, including a output level for input and typically employing coding, which rounds small signals to and avoids offset. These designs influence error characteristics, with mid-tread often preferred for signals crossing frequently, such as audio. Quantization errors in PCM arise primarily from two sources: granular noise and overload noise. Granular noise refers to the small-scale distortions within the quantizer's , akin to the uniform error distribution in each step, which dominates for signals fitting within the levels. Overload noise occurs when the input exceeds the maximum representable level, causing clipping and large distortions, mitigated by ensuring the signal stays within Vmin⁡V_{\min} to Vmax⁡V_{\max} or using headroom in practice. While basic PCM relies on uniform quantization for , non-uniform quantization extends this by effectively varying step sizes through —compressing the signal before uniform quantization and expanding it afterward—to allocate finer levels to smaller amplitudes, reducing overall impairment for signals with wide dynamic ranges like speech. This approach maintains the simplicity of uniform coding while improving SQNR for low-level signals without altering the core PCM .

Binary Encoding

In the binary encoding stage of pulse-code modulation (PCM), the discrete amplitude levels resulting from quantization are mapped to fixed-length binary codes, forming the pulse codes that represent the original signal for digital transmission or storage. Each quantized level is assigned a unique binary word, typically consisting of nn bits where the number of levels N=2nN = 2^n, allowing representation of NN distinct values. Common encoding schemes include natural binary coding, where levels are assigned sequential binary numbers (e.g., level 0 as 0000, level 1 as 0001), and Gray coding, which ensures that adjacent levels differ by only one bit to reduce error propagation in noisy channels (e.g., level 0 as 0000, level 1 as 0001, level 2 as 0011). The bit rate RbR_b of the resulting PCM signal is determined by the product of the number of bits per sample nn and the sampling frequency fsf_s, given by Rb=n⋅fsR_b = n \cdot f_s where RbR_b is in bits per second. For instance, in telephony applications using 8 bits per sample and an 8 kHz sampling rate, this yields a bit rate of 64 kbps. In multi-channel PCM systems, such as those in digital telephony, binary-encoded samples from multiple channels are organized into time-division multiplexed (TDM) to enable efficient transmission. Each frame typically includes one binary word from each channel plus additional synchronization bits for frame alignment and timing recovery at the receiver. For example, the T1 carrier system 24 channels using 8-bit PCM words per channel, resulting in a 193-bit frame (24 × 8 + 1 framing bit) transmitted at 8,000 per second. As an illustrative example, consider a 16-level quantizer (N=16N = 16, n=4n = 4) encoding levels from 0 to 15. In natural binary coding, the assignments are straightforward increments, while Gray coding adjusts for single-bit transitions:
LevelNatural BinaryGray Code
000000000
100010001
200100011
300110010
.........
1411101001
1511111000

History

Invention and Early Developments

Pulse-code modulation (PCM) was invented in 1937 by British engineer Alec H. Reeves while working at in , . Reeves conceived PCM as a digital alternative to analog transmission methods to mitigate cumulative noise in long-distance circuits, where traditional analog signals degraded progressively over repeated amplification stages. By sampling the analog , quantizing the levels, and encoding them as binary pulses, PCM enabled error-free regeneration of the signal at intermediate points, preserving quality over extended distances. Reeves filed a for the technique in in 1938 (French Patent 852,183, granted 1938), with equivalent filings leading to British Patent 535,860 in 1939 and U.S. Patent 2,272,070 in 1942. At the time, technology limited practical implementation, and the invention received little immediate attention, though it marked a pivotal conceptual advance in signal representation. This innovation built on prior analog pulse modulation schemes, such as (PAM) and (PWM), which modulated pulse characteristics continuously but remained susceptible to noise interference during transmission. PCM's fully discrete binary encoding eliminated this vulnerability by converting the signal into a robust digital format amenable to logical regeneration, laying the groundwork for noise-immune communication. In 1948, Claude E. Shannon's foundational paper, "," provided rigorous theoretical underpinnings for PCM and digital systems broadly. Published in the Technical Journal, it defined limits for reliable transmission amid noise and validated PCM's sampling and quantization processes through information-theoretic principles, including the notion that band-limited signals could be faithfully represented digitally without loss. Bell Laboratories advanced early PCM experimentation from 1938 to 1943, developing prototypes for systems that integrated PCM with techniques to compress and digitize speech. These efforts culminated in the system, the first practical use of PCM for transmission, operational from 1943 for transatlantic military communications during . integrated PCM with a 12-channel to analyze speech into 10 frequency bands, pitch, and voicing; these parameters were sampled at 50 Hz and quantized using 6-level companded PCM, enabling intelligible encrypted noisy channels. Post-World War II, declassified aspects of and related work spurred military adoption of PCM in enhanced secure links and data transmission, driving innovations in digital military through the 1950s.

Adoption in Digital Audio

The adoption of pulse-code modulation (PCM) in consumer audio began in the late with Sony's introduction of the PCM-1 processor in 1977, the world's first commercially available recorder designed for home use. This device encoded analog audio signals into PCM format at 44.056 kHz sampling rate and 16-bit depth, allowing users to record and playback stereo audio onto video cassette recorders without the and distortion inherent in analog systems. Priced at around $2,000, the PCM-1 marked a pivotal shift toward accessible , enabling audiophiles to capture broadcasts or live performances with unprecedented fidelity. This momentum culminated in the development of the (CD) standard in 1980 through a collaboration between and , which specified 16-bit PCM encoding at a 44.1 kHz sampling rate for two-channel stereo audio. The 44.1 kHz rate was selected to accommodate the full audible frequency range up to 20 kHz while fitting 74 minutes of playback on a 12 cm disc, balancing quality and capacity through careful error correction and modulation techniques. Released commercially in 1982, the CD revolutionized audio distribution by providing durable, high-fidelity playback free from wear-related degradation, quickly becoming the dominant format for music albums and establishing PCM as the foundation of storage. By the 1980s and 1990s, PCM integrated deeply into digital audio workstations (DAWs), transforming music production from analog tape-based workflows to computer-driven environments. Early DAWs like Soundstream's 1977 system and Digidesign's (introduced in 1991) relied on PCM for multi-track recording, allowing engineers to layer dozens of audio tracks with precise editing capabilities. Formats such as Apple's (AIFF), developed in 1988 for uncompressed PCM on Macintosh systems, and Microsoft's Waveform Audio File Format (), released in 1991, standardized PCM data storage, facilitating seamless exchange and processing across platforms. The impact of PCM on music production was profound, particularly in enabling multi-track recording without the generational loss associated with analog duplication, where each copy introduced noise and frequency roll-off. Digital PCM tracks could be copied, edited, and mixed indefinitely while preserving original signal integrity, empowering producers to experiment with complex arrangements—such as orchestral overdubs or electronic layering—without quality degradation. This non-destructive nature accelerated the shift to all-digital studios by the mid-1990s, democratizing professional-grade production and influencing genres from pop to hip-hop.

Integration in Telephony

The integration of pulse-code modulation (PCM) into telephony began with the Bell System's deployment of the T1 carrier system in 1962, which represented the first commercial digital transmission of voice signals over distance. This system employed 8-bit PCM encoding at an 8 kHz sampling rate to digitize 24 independent voice channels, allowing for their combination via time-division multiplexing (TDM) on a single pair of twisted copper wires. The T1's introduction addressed longstanding issues with analog transmission, such as signal degradation over long distances, by converting voice to a robust digital format that could be regenerated without accumulating noise. Central to this integration was the establishment of the PCM hierarchy, where the fundamental DS0 signal defines a single 64 kbit/s voice channel derived from PCM sampling and quantization. Higher levels, such as DS1, multiplex 24 DS0 channels into a 1.544 Mbit/s stream using TDM framing, enabling efficient aggregation for trunk lines in the . This hierarchical structure supported scalable digital transport, replacing in analog systems with a more bandwidth-efficient and noise-resistant approach. To ensure global interoperability, the Telecommunication Standardization Sector () adopted Recommendation in 1972, specifying PCM for voice frequencies with two algorithms: μ-law for North American and Japanese systems, and A-law for international use. These logarithmic methods enhanced the of 8-bit quantization for human speech, allocating more levels to quieter signals while maintaining toll-quality audio at 64 kbit/s per channel. became the foundational for digital telephony, influencing subsequent network designs worldwide. The widespread adoption of PCM facilitated a profound shift in infrastructure during the 1970s and 1980s, transitioning from analog frequency-division multiplexed lines to digital switching centers and long-haul transmission systems. This evolution dramatically reduced noise and distortion in transcontinental calls, as digital repeaters could regenerate PCM signals bit-for-bit, preventing the cumulative errors inherent in analog amplification over thousands of miles. By the late , PCM underpinned the core of global voice networks, enabling clearer and more reliable .

PCM Process

Modulation

Pulse-code modulation (PCM) represents the process of converting an into a digital pulse train through a series of integrated steps: sampling, quantization, and binary encoding. This modulation technique begins with an analog input signal, which is first passed through a to prevent , followed by sampling to produce a modulated (PAM) signal. The PAM signal consists of discrete samples taken at regular intervals, typically using a sample-and-hold circuit to maintain each sample value constant during the holding period. These samples are then quantized into a finite set of discrete levels, and finally encoded into words to form a serial stream of pulses representing the original signal in digital form. The step-by-step pipeline of PCM modulation proceeds as follows: the analog input x(t)x(t) is sampled at a rate satisfying the Nyquist criterion to yield discrete-time samples xnx_n, forming a PAM waveform where each corresponds to the instantaneous signal value at sampling instants. Next, quantization maps these continuous samples to the nearest levels from a predefined set of 2b2^b levels (for bb-bit quantization), introducing a controlled . The quantized values are then converted to binary codes via an encoder, producing a parallel binary output that is multiplexed into a serial stream for transmission. This serial stream consists of fixed-width pulses whose presence or absence encodes the binary '1's and '0's, resulting in a robust digital representation suitable for noisy channels. Sample-and-hold circuits are to the sampling stage, ensuring accurate capture of the analog voltage during quantization and encoding. A typical block diagram of a PCM modulator illustrates this pipeline with key components: an input , a sampler incorporating a sample-and-hold circuit to generate PAM pulses, a quantizer to discretize s, a binary encoder to produce words, and a serial to form the output train. The sampler switches between sampling the input (acquiring the voltage) and holding it steady, feeding stable levels to the quantizer, which outputs indices corresponding to bins. The encoder translates these indices into binary sequences, often 8 bits per sample, serialized into a unipolar or bipolar stream. To optimize the and reduce quantization noise for signals like speech with varying amplitudes, techniques such as μ-law and A-law are applied before quantization. compresses the during modulation (compression) and expands it during , allocating more quantization levels to smaller signals for better . The μ-law , standardized for North American systems with μ = 255, is given by: F(x)=\sgn(x)ln⁡(1+μ∣x∣)ln⁡(1+μ),∣x∣≤1F(x) = \sgn(x) \frac{\ln(1 + \mu |x|)}{\ln(1 + \mu)}, \quad |x| \leq 1 This logarithmic compression approximates the human ear's sensitivity, providing finer resolution at low amplitudes. Similarly, the A-law, used in European systems with A ≈ 87.6, employs a piecewise function: F(x)={\sgn(x)A∣x∣1+ln⁡A,∣x∣≤1A\sgn(x)1+ln⁡(A∣x∣)1+ln⁡A,1A<∣x∣≤1F(x) = \begin{cases} \sgn(x) \frac{A |x|}{1 + \ln A}, & |x| \leq \frac{1}{A} \\ \sgn(x) \frac{1 + \ln (A |x|)}{1 + \ln A}, & \frac{1}{A} < |x| \leq 1 \end{cases} Both techniques effectively extend the usable to about 48 dB for 8-bit PCM, prioritizing perceptual quality over linear accuracy. As a form of digital pulse modulation, PCM differs fundamentally from analog variants like (PPM), where the position of pulses varies continuously with the signal amplitude within fixed-width frames. In contrast, PCM encodes the signal as discrete binary pulse sequences, enabling error detection, noise immunity, and compatibility with digital systems, though at the cost of higher bandwidth requirements.

Demodulation

The demodulation of (PCM) reverses the modulation process to reconstruct the original from the received digital bit stream. This involves receiving the serial , synchronizing it, converting it back to quantized levels, and applying filtering to recover a smooth continuous . The fidelity of the reconstructed signal depends on accurate timing recovery and proper filtering to mitigate distortions introduced during transmission and conversion. The PCM demodulator begins with bit stream reception and regeneration, where the incoming serial data—potentially degraded by or —is regenerated using or equalizers to restore clean pulses. Critical to this stage is error handling through bit synchronization and , which extract the timing information embedded in data transitions to align bits correctly and prevent slips or errors that could misalign code words. circuits, such as phase-locked loops, lock onto the data's embedded clock by detecting transitions, ensuring the receiver operates at the same as the transmitter; failure to achieve this can lead to bit errors exceeding 10^{-6} in practical systems. Following regeneration, the serial bit stream undergoes serial-to-parallel conversion, grouping bits into multi-bit words corresponding to the original sample resolution (e.g., 8 bits per sample). These words are then decoded to represent the quantized levels, effectively mapping the binary codes back to discrete voltage steps that approximate the sampled signal values. Digital-to-analog conversion (DAC) follows, where the decoded levels are transformed into an analog staircase waveform using sample-and-hold circuits that maintain each quantized value constant until the next sample arrives, providing a approximation of the signal. In theory, ideal reconstruction employs sinc interpolation to interpolate between samples smoothly, but practical DACs rely on the subsequent filtering stage to approximate this. The hold operation introduces a sinc-shaped droop, which is compensated in to preserve up to the . Finally, low-pass filtering reconstructs the continuous by smoothing the staircase output and removing high-frequency components, including spectral images (replicas of the signal shifted by multiples of the sampling ) that arise from the sampling process. The filter's is typically set near half the sampling rate to pass the original signal bandwidth while attenuating images above it, ensuring minimal or ; poor can introduce phase shifts or ringing, degrading signal by up to several dB in peak signal-to-noise ratio. Effective filter implementation, such as using designs, balances sharpness and computational efficiency for real-time applications.

Standards and Applications

Sampling Precision and Rates

In pulse-code modulation (PCM) systems for audio, common standards balance computational efficiency with perceptual quality. For telephony applications, the ITU-T G.711 standard employs an 8-bit depth and 8 kHz sampling rate to capture voice frequencies up to approximately 4 kHz, resulting in a 64 kbit/s bit rate suitable for narrowband communication. This rate originated in early digital telephony to accommodate limited channel capacity while preserving intelligible speech. The format, defined by the IEC 60908 standard, uses a 16-bit depth and 44.1 kHz sampling rate for audio, providing a of about 96 dB and capturing frequencies up to 20 kHz to meet human auditory limits. extends beyond this, typically employing a 24-bit depth and 96 kHz sampling rate to achieve greater fidelity, with a exceeding 144 dB and reduced artifacts for professional and applications. The choice of sampling precision and rates involves trade-offs between bandwidth requirements and audio fidelity. Higher bit depths enhance dynamic range and reduce perceptible distortion, while elevated sampling rates improve frequency response and enable gentler anti-aliasing filters; however, they increase data throughput, demanding more storage and transmission capacity. Oversampling, where the initial rate exceeds the final output (e.g., 4x or 8x), benefits PCM by spreading spectral artifacts over a wider band before decimation, easing filter design and improving overall signal integrity without proportionally inflating final bandwidth. In video and data applications, PCM adapts to component signals; for instance, the SMPTE 259M standard for (SDI) uses a 10-bit depth and 13.5 MHz sampling rate for in standard-definition formats, supporting 4:2:2 color sampling at 270 Mbit/s to maintain video quality over links. By 2025, professional audio workflows have evolved toward 32-bit floating-point PCM, often at 48 kHz or higher rates, to provide virtually unlimited headroom (over 1500 dB dynamic range) and prevent clipping during mixing and processing, as adopted in digital audio workstations and field recorders.

Key Implementations

In , Pulse Code Modulation (PCM) forms the backbone of digital voice transmission in standards like T1 and E1 lines. T1 lines, standardized for , employ PCM to multiplex 24 voice channels, each sampled at 8 kHz and quantized to 8 bits using μ-law , achieving a total of 1.544 Mbps for carrier-grade voice transport. E1 lines, prevalent in and internationally, similarly utilize PCM with A-law to support 30 voice channels plus signaling, delivering 2.048 Mbps for reliable digital . In modern VoIP systems, the codec implements PCM directly, encoding voice at 64 kbps with either μ-law or A-law variants to ensure toll-quality networks, as defined in Recommendation G.711. For digital audio applications, PCM serves as the uncompressed standard for high-fidelity storage and playback. (CD) players rely on 16-bit linear PCM sampled at 44.1 kHz for stereo audio, providing a dynamic range of approximately 96 dB as specified in the Red Book audio standard developed by and . MP3 encoding begins with PCM input, where the raw —typically 16-bit at 44.1 kHz—is perceptually analyzed and compressed, but the pre-compression PCM stage preserves the original signal integrity before lossy transformation per the MPEG-1 Audio Layer III specification. Streaming services such as Tidal and deliver lossless audio tracks in PCM-based formats like , maintaining bit-perfect reproduction of the source material at resolutions up to 24-bit/192 kHz for audiophile-grade playback. In data transmission, PCM enables the digitization and framing of signals for robust network delivery. Ethernet-based systems incorporate PCM through protocols like Telemetry over Internet Protocol (TMoIP), which encapsulates PCM streams into Ethernet packets for real-time transfer of multiplexed data, supporting applications in industrial monitoring with frame-aligned packing at rates up to 10 Mbps. Satellite communications extensively use PCM for and payload data, where analog signals are converted to serial PCM bitstreams and modulated onto carriers for transmission over transponders, as demonstrated in (TDMA) experiments achieving error-free data rates of 64 kbps per channel. Emerging implementations leverage PCM in next-generation wireless technologies as of 2025. In networks, adaptive variants like differential PCM (ADPCM) are integrated into architectures for high-fidelity indoor radio access, compressing radio signals for efficient fronthaul transmission over legacy multimode fiber in distributed antenna systems.

Advanced Techniques

Signal Processing

Once the has been encoded into a PCM through sampling and quantization, various techniques can be applied to manipulate, enhance, or protect the resulting digital representation. These post-encoding operations treat the PCM data as a discrete-time sequence, enabling efficient computation in digital domains such as audio production, , and storage systems. Digital filtering and equalization are fundamental processes applied directly to PCM bitstreams to shape the of the signal. Low-pass, high-pass, or band-pass filters remove unwanted noise or emphasize specific spectral components, often implemented using (FIR) or (IIR) structures that operate sample-by-sample on the quantized values. For instance, adaptive equalization adjusts the amplitude of frequency bands to compensate for channel distortions in transmission, ensuring faithful reproduction of the original audio characteristics. In audio mixing applications, automatic equalization leverages semantic descriptors to derive parametric settings, improving tonal balance across tracks. These techniques are computationally efficient on PCM data due to its uniform bit depth and sampling rate, allowing real-time processing in hardware like digital signal processors (DSPs). Effects such as reverb can also be applied to PCM bitstreams to simulate acoustic environments, convolving the signal with impulse responses derived from room simulations or measured spaces. Digital reverb algorithms, including Schroeder's early methods using and all-pass filters, process the PCM samples to add spatial depth without altering the core encoding structure. This manipulation enhances immersion in applications like music production, where the PCM stream serves as the input to engines that output a modified at the same rate. Modern implementations integrate these effects in software like workstations, preserving the integrity of the PCM format while enabling creative alterations. Multi-rate processing techniques, including decimation and interpolation, allow modification of the PCM sampling rate to adapt the signal for different bandwidth requirements or storage constraints. Decimation reduces the sampling rate by integer factors through low-pass filtering followed by downsampling, preventing aliasing while compressing data for lower-rate systems like telephony. Conversely, interpolation upsamples the PCM bitstream by zero-insertion and subsequent low-pass filtering to expand the rate, useful in converting legacy audio to high-resolution formats. These operations are efficient in PCM contexts, as they operate on the fixed-point or floating-point representations without requantization. Multistage designs cascade multiple decimation or interpolation stages to achieve non-integer rate changes, optimizing computational load in digital audio resampling. Error correction coding integrates with PCM frames to mitigate transmission or storage errors, embedding redundancy into the bitstream for robustness. Reed-Solomon codes, operating over Galois fields, add parity symbols to blocks of PCM samples, enabling detection and correction of burst errors common in optical media. In the Compact Disc (CD) standard, cross-interleaved Reed-Solomon coding protects 16-bit PCM audio frames, correcting up to 3,500 consecutive erroneous bits per sector through de-interleaving and decoding. This approach ensures high fidelity in playback, with the corrected PCM stream seamlessly reconstructing the original signal. Similar techniques appear in digital audio broadcasting, where convolutional interleaving enhances error resilience without impacting the base PCM structure. Recent advancements in AI-based leverage neural networks to enhance low-rate PCM audio, predicting high-frequency details absent in the original encoding. Generative adversarial networks (GANs), such as NU-GAN, train on paired low- and high-resolution datasets to upsample audio from 22 kHz to 44.1 kHz, demonstrating improved perceptual quality through ABX preference tests where generated audio is only slightly distinguishable from originals. These models process PCM bitstreams as input sequences, outputting samples that reduce artifacts in speech or enhancement, bridging gaps in traditional interpolation methods. Applications include real-time in mobile devices and archival upgrades, where infers plausible waveforms from quantized data.

Coding and Compression

Coding and compression techniques in pulse-code modulation (PCM) aim to minimize the data volume required for representing quantized samples while preserving signal fidelity, building upon the binary encoding of PCM samples as the foundational representation. These methods exploit redundancies in audio or signal data, such as correlations between consecutive samples or statistical patterns in bit sequences, to achieve efficient storage and transmission without fundamentally altering the PCM framework. Differential pulse-code modulation (DPCM) enhances PCM by encoding the differences between consecutive samples rather than absolute values, leveraging the predictability of signals like speech or audio where successive samples often exhibit high . In DPCM, a predictor estimates the current sample based on prior ones, and only the —typically smaller in magnitude—is quantized and transmitted, reducing the required bit depth per sample and thus the overall bitrate. This approach can achieve compression ratios of 2:1 or better for correlated signals, with performance depending on the predictor's accuracy, often implemented as a . Seminal work on DPCM for and speech signals demonstrated its in lowering transmission rates while maintaining perceptual quality. Adaptive differential pulse-code modulation (ADPCM) extends DPCM by dynamically adjusting the quantization step size based on the signal's characteristics, such as variations, to optimize bitrate allocation and minimize . In applications, ADPCM operates at bitrates from 16 to 40 kbit/s, enabling toll-quality bandwidth-limited channels by adapting to short-term signal statistics. The (ITU) standardized ADPCM in , which specifies embedded coding for flexible rates and has been widely adopted in digital communication systems for its balance of compression and robustness to errors. Similarly, G.727 provides multi-bit embedded ADPCM for integrated services digital network (ISDN) voice coding. Lossless compression methods applied to PCM streams, such as the Free Lossless Audio Codec (FLAC), achieve data reduction through reversible techniques without altering the original quantized samples, ensuring bit-identical reconstruction. FLAC employs , rice coding for residuals, and frame-based organization to compress PCM audio by 30-70% on average, depending on the signal's , making it suitable for archival storage and high-fidelity playback. Developed by the , FLAC supports sample rates up to 655 kHz and bit depths to 32 bits, with its specification formalized in RFC 9639 for applications. In contrast, lossy compression formats like , derived from PCM via perceptual coding, discard inaudible components to attain higher ratios—often 10:1 or more—while introducing controlled artifacts. , standardized in ISO/IEC 11172-3, processes PCM inputs through psychoacoustic modeling and (MDCT) to prioritize audible frequencies, enabling widespread use in streaming and portable media despite irreversible data loss. Entropy coding further refines PCM compression by assigning shorter codes to frequent bit patterns or symbols in the quantized data stream, approaching the theoretical entropy limit. Huffman coding, a variable-length prefix code, is commonly applied post-quantization in audio systems to encode PCM residuals or transform coefficients, yielding additional 10-20% bitrate savings in codecs like those for digital audio broadcasting. Arithmetic coding offers superior efficiency over Huffman by representing entire sequences as fractional numbers within a [0,1) range, achieving compression closer to the source entropy, particularly for PCM data with skewed symbol probabilities; it has been integrated into advanced audio coders for its adaptability to adaptive models. Recent advancements in neural network-based PCM compression, tailored for 2025 streaming applications, leverage models like and generative adversarial networks (GANs) to learn compact latent representations of PCM audio streams, enabling near-lossless or ultra-low bitrate encoding. For instance, AI-driven deep models achieve near-lossless compression ratios up to 30:1 for PCM audio using layered encoding. Hybrid neural codecs, such as LSPnet, operate at 1.2 kbit/s for high-fidelity speech while maintaining end-to-end differentiability for streaming integration. Similarly, RVQGAN-based methods for multichannel PCM, such as higher-order , enable low-bitrate compression (e.g., 16 kbps per channel) for immersive 16-channel audio while preserving quality. These techniques, presented at conferences like Interspeech 2025, outperform traditional methods in perceptual quality metrics for dynamic content.

Serial Transmission Encoding

In pulse-code modulation (PCM), serial transmission encoding involves converting parallel PCM code words into a continuous bit stream suitable for reliable propagation over communication channels, ensuring minimal distortion and synchronization between transmitter and receiver. This process typically begins with multiplexing multiple PCM channels using (TDM), where samples from each channel are sequentially interleaved to form frames. Each frame includes dedicated framing bits to delineate boundaries and maintain alignment, preventing data misalignment during transmission. For instance, in standard systems, 24 or 32 channels are multiplexed, resulting in bit rates such as 1.544 Mbps for T1 or 2.048 Mbps for E1 hierarchies. To mitigate issues like DC component accumulation in the transmitted signal, which can saturate transformers or amplifiers in long-haul links, various line coding schemes are applied to the serial bit stream. (NRZ) encoding represents binary 1 as a positive voltage and 0 as zero or negative, offering simplicity but risking in long sequences of identical bits. Alternate mark inversion (AMI), commonly used in early PCM systems like T1 lines, encodes binary 1s as alternating positive and negative pulses while 0s remain at zero, effectively balancing the signal to eliminate DC offset and aiding error detection through violation checks. encoding, an alternative biphase scheme, ensures a mid-bit transition for every symbol—high-to-low for 0 and low-to-high for 1—providing inherent clock information and self-synchronization but at the cost of doubled bandwidth compared to NRZ. These schemes are specified in Recommendation G.703 for hierarchical digital interfaces, ensuring compatibility in PCM-based networks. Framing and are critical in TDM-PCM to identify the start of each frame and interleave channels without overlap. or framing bits, often a fixed pattern like 101 or alternating 1s and 0s, are inserted periodically to provide timing references, allowing the receiver to align its clock and demultiplex channels accurately. In the G.704 frame structure for 2.048 Mb/s PCM, 32 time slots accommodate 30 voice channels plus 2 signaling slots, with an additional framing bit per frame to achieve , forming superframes for enhanced alignment across multiple frames. Channel interleaving arranges bits from successive samples in a round-robin fashion, optimizing bandwidth usage while the framing overhead—typically 1 bit per 256 bits—ensures robust recovery even under bit errors. Scrambling further enhances serial transmission by randomizing the bit stream to guarantee frequent transitions, which are essential for at the receiver via phase-locked loops or data-edge detection. Without scrambling, pathological sequences of all 0s or 1s could lead to loss of timing . In synchronous digital systems building on PCM hierarchies, frame-synchronous using a like x^7 + x^6 + 1 is applied before transmission, with descrambling at the receiver to restore the original data; this approach, defined in G.783 for SDH equipment, ensures a balanced and sufficient edge density for reliable clock extraction. In fiber-optic implementations, PCM serial streams are converted to optical pulses using modulators, enabling high-speed, low-loss transmission over silica fibers. Line codes like NRZ or (RZ) are adapted for optical domains to minimize and dispersion, supporting bit rates up to gigabits per second in systems like /SDH, which extend PCM hierarchies. For example, a PCM current differential relaying system over fiber optics achieves secure, high-fidelity transmission for protection signaling, as demonstrated in utility applications. For wireless PCM transmission in networks, serial encoding supports fronthaul links where digitized signals—often PCM-encoded IQ samples—are serialized for optical or transport to remote radio units. In 3GPP-defined fronthaul, adaptive differential PCM variants reduce quantization bits while maintaining fidelity, enabling efficient TDM over with rates exceeding 25 Gbps to handle massive demands.

Limitations

Quantization Effects

In pulse-code modulation (PCM) systems, quantization introduces two primary sources of : granular noise and overload . Granular occurs when the input signal amplitude lies within the quantizer's , resulting from the or to the nearest quantization level; for a uniform quantizer with step size Δ, the error e is bounded by |e| ≤ Δ/2 and assumes a uniform f_e(e) = 1/Δ for -Δ/2 ≤ e ≤ Δ/2, approximating additive under high-resolution conditions. Overload arises when the input signal exceeds the quantizer's maximum or minimum levels, causing clipping with unbounded errors whose mirrors the tails of the input signal's distribution, such as Gaussian for typical audio signals, leading to nonlinear clipping artifacts. These sources degrade signal , with granular dominating at low signal levels and overload at high amplitudes. To mitigate quantization-induced distortion, dithering techniques add a controlled low-amplitude signal to the input before quantization, randomizing the and decorrelating it from the signal. This linearizes the overall quantizer , suppressing harmonic components and limit cycles while converting deterministic quantization errors into benign random ; for instance, subtractive dither, where the dither is removed post-quantization, ensures the remains uncorrelated, though non-subtractive variants are common in audio for simplicity. Dithering is particularly effective in reducing audible artifacts like or in low-level signals, with optimal dither amplitude typically matching the quantization step size. Quantization effects directly limit the of PCM systems, defined as the of maximum signal power to the , yielding approximately 6.02n dB for an n-bit uniform quantizer assuming a full-scale input. (THD) arises from nonlinear quantization errors, manifesting as spurious harmonics that increase with signal amplitude and correlate with granular patterns; dithering reduces THD by randomizing these errors, often lowering it below -90 dB in well-designed systems. The signal-to-quantization (SQNR) quantifies this , serving as a key metric for evaluating quantization . In modern (HDR) audio, high-bit-depth PCM formats, such as 24-bit or 32-bit, minimize quantization effects by extending the to over 144 dB, rendering inaudible even in quiet passages and supporting extended headroom for transient peaks without overload. This enables HDR workflows in production, where quantization is negligible compared to other sources like self-noise, preserving perceptual transparency across wide amplitude spans.

Bandwidth and Practical Constraints

In pulse-code modulation (PCM) systems, the transmission bandwidth for signaling is determined by the and . For binary PCM using (NRZ) encoding, the minimum required bandwidth BB is given by B=nfs2B = \frac{n f_s}{2}, where nn is the number of bits per sample and fsf_s is the sampling frequency; this arises because the of the serial bit stream is half the for rectangular pulses, ensuring the signal fits within the channel without excessive . Higher-order pulse shapes, such as raised-cosine filters, increase this to B=(1+α)nfs2B = \frac{(1 + \alpha) n f_s}{2} with factor α\alpha, but the limit remains tied to the Nyquist criterion for the Rb=nfsR_b = n f_s. Power consumption in analog-to-digital converters (ADCs) and digital-to-analog converters (DACs) used for and reconstruction scales nonlinearly with sampling rate and bit resolution, often following a figure-of-merit like power efficiency in fJ/conversion-step, which degrades at higher fsf_s due to increased switching activity and overhead. In multi-channel PCM systems, such as those in or audio arrays, issues emerge as total power grows roughly linearly with channel count, but shared clocking and can mitigate this; however, for dense deployments exceeding 64 channels, thermal management and voltage scaling become critical to avoid exceeding 1-10 mW per channel limits in implementations. For instance, successive-approximation-register ADCs in PCM setups consume power proportional to n×fsn \times f_s, limiting deployment in battery-constrained or high-density environments without advanced low-power techniques like dynamic element matching. Practical constraints in PCM implementation include clock jitter and aperture uncertainty, which introduce timing errors during sampling. Clock jitter, the random variation in sampling instant, generates noise equivalent to en=A⋅2πf⋅σje_n = A \cdot 2\pi f \cdot \sigma_j (where AA is signal , ff is input , and σj\sigma_j is jitter standard deviation), degrading signal-to-noise ratio (SNR) at high frequencies and requiring jitter below 1 ps rms for audio-grade PCM at 20 kHz. Aperture uncertainty, synonymous with sampling jitter in track-and-hold circuits, arises from switch non-idealities and amplifier slew rates, amplifying errors in wideband signals; mitigation involves low-jitter phase-locked loops, but residual uncertainty limits effective resolution to 10-12 bits in high-speed systems sampling above 1 GHz. From a 2025 perspective, high-rate PCM in data centers—used for processing vast volumes in AI-driven audio analysis or —exacerbates environmental impacts by contributing to elevated energy demands; data centers overall consumed 4% of U.S. in 2024, with projections doubling by 2030 due to compute-intensive tasks like high-fsf_s , leading to increased carbon emissions unless offset by renewable integration. Standard sampling rates, such as 48 kHz in , directly scale these bandwidth and power needs in aggregated systems.

Terminology

Core Definitions

Pulse-code modulation (PCM) is a digital representation technique for analog signals that involves three primary steps: sampling the continuous-time signal at discrete intervals, quantizing each sample to one of a of levels, and encoding the quantized values into a binary pulse code for transmission or storage. This process converts the analog waveform into a series of binary digits, enabling robust digital handling while preserving the essential of the original signal. According to the Nyquist-Shannon sampling theorem, the sampling rate must exceed twice the signal's maximum frequency to allow faithful reconstruction without . PCM differs fundamentally from , which approximates the signal by encoding only the incremental change (difference) between consecutive samples using a single bit per sample, rather than the full value. Similarly, sigma-delta modulation extends this differential approach through and noise shaping, integrating feedback to push quantization noise outside the signal band, achieving higher effective resolution at the cost of increased sampling rates, unlike PCM's direct multi-bit encoding of absolute levels. Key terms in PCM include "pulse code," which denotes the binary sequence of pulses representing the encoded quantized samples, forming the core of the digital signal. Companding refers to the combined compression and expansion process applied to the signal's dynamic range before and after quantization, respectively, to optimize bit allocation by emphasizing lower-amplitude signals and thereby reducing overall quantization error. Oversampling describes the practice of sampling at a frequency substantially higher than the Nyquist rate, which facilitates anti-aliasing filtering and can improve signal fidelity when paired with decimation. The term "linear PCM" specifically indicates uncompressed PCM with uniform quantization, where amplitude levels are spaced equally, ensuring consistent resolution across the full dynamic range but requiring more bits for low-noise performance in signals with wide amplitude variations. In contrast, compressed variants of PCM incorporate non-linear quantization through companding laws, such as μ-law (common in North America) or A-law (used in Europe), which allocate finer steps to smaller signals and coarser steps to larger ones, enhancing the signal-to-quantization-noise ratio for applications like telephony while maintaining the same number of bits per sample.

Notation and Symbols

In descriptions of pulse-code modulation (PCM), the continuous-time analog input signal is conventionally denoted by x(t)x(t), where tt is the time variable. The discrete-time quantized samples derived from this signal after sampling and quantization are typically represented as xqx_q, with kk indexing the sample number. The sampling , which determines the rate of signal sampling according to the Nyquist criterion, is symbolized as fsf_s. The number of bits used for quantization, influencing the resolution and , is denoted by nn, yielding 2n2^n possible quantization levels. The quantization error, representing the difference between the original signal value and its quantized approximation at any point, is expressed as eq=x−xqe_q = x - x_q. This notation is standard in PCM analyses to quantify distortion introduced by the quantization process. Diagrammatic conventions in PCM literature commonly employ block diagrams to illustrate system components. The modulator block diagram features sequential blocks labeled as "low-pass filter" (input: x(t)x(t)), "sampler" (output: sampled pulses), "quantizer" (output: xqx_q), and "binary encoder" (output: bit stream). The demodulator mirrors this with "decoder," "digital-to-analog converter," and "low-pass filter" (output: reconstructed x^(t)\hat{x}(t)), with arrows indicating signal flow and labels for key parameters like fsf_s and nn. Notations exhibit variations across standards to accommodate application-specific requirements. In the ITU-T G.711 recommendation for voice frequency PCM, fs=8000f_s = 8000 Hz and n=8n = 8 are standardized, with companding functions denoted as A-law, with A=87.6A = 87.6, defined piecewise as F(x)=\sgn(x)1+ln⁡(A∣x∣)1+ln⁡AF(x) = \sgn(x) \frac{1 + \ln(A |x|)}{1 + \ln A} for 0≤∣x∣<1/A0 \leq |x| < 1/A, and F(x)=\sgn(x)A∣x∣1+ln⁡AF(x) = \sgn(x) \frac{A |x|}{1 + \ln A} for 1/A≤∣x∣≤11/A \leq |x| \leq 1; or μ-law, where μ=255\mu = 255 and F(x)=\sgn(x)ln⁡(1+μ∣x∣)ln⁡(1+μ)F(x) = \sgn(x) \frac{\ln(1 + \mu |x|)}{\ln(1 + \mu)} for 0≤∣x∣≤10 \leq |x| \leq 1. Conversely, the AES3 standard for professional digital audio interfaces uses flexible notations, with fsf_s ranging from 32 kHz to 192 kHz (e.g., fs=44.1f_s = 44.1 kHz for compact disc audio) and nn from 16 to 24 bits, emphasizing linear PCM without companding and subframe preambles (Z, Y, X) for synchronization.

References

  1. https://www.loc.gov/preservation/digital/formats/fdd/fdd000011.shtml
  2. https://www.oit.va.gov/services/trm/StandardPage.aspx?tid=5339
  3. https://ethw.org/Pulse_Code_Modulation
  4. https://www.analog.com/media/en/training-seminars/design-handbooks/data-conversion-handbook/chapter1.pdf
  5. https://www.allaboutcircuits.com/news/how-alec-reeves-revolutionized-telecom-pulse-code-modulation/
  6. https://digital-library.theiet.org/doi/pdf/10.1049/piee.1979.0269
  7. https://ocw.mit.edu/courses/mas-632-conversational-computer-systems-fall-2008/2f14b7dfe31a3ef6fcb8d686065e134a_schmandt_ch3.pdf
  8. https://www.loc.gov/preservation/digital/formats/fdd/fdd000016.shtml
  9. https://ethw.org/Bell_Utilizes_PCM_Multiplexing
  10. https://www.acsce.edu.in/acsce/wp-content/uploads/2020/03/ADC-module-3-final.pdf
  11. https://bayes.wustl.edu/Manual/CertainTopicsInTelegraphTransmissionTheory.pdf
  12. https://webusers.imj-prg.fr/~antoine.chambert-loir/enseignement/2020-21/shannon/shannon1949.pdf
  13. https://www.digikey.com/en/articles/the-basics-of-anti-aliasing-low-pass-filters
  14. https://vtda.org/pubs/BSTJ/vol26-1947/articles/bstj26-3-395.pdf
  15. https://www.cis.rit.edu/class/simg712-90/notes/14-Quantization.pdf
  16. https://sites.pitt.edu/~dtipper/PM.pdf
  17. https://jcsites.juniata.edu/faculty/rhodes/dap/Chapter5.pdf
  18. http://class.ece.iastate.edu/djchen/ee509/2018/IEEE1241-2011.pdf
  19. https://www.eecis.udel.edu/~arce/files/Courses/StatSP/Slides_Set_2.pdf
  20. https://ecse.rpi.edu/courses/CStudio/RTA_lab/Lab_text_references/Carlson_Ch12.pdf
  21. https://www.ece.ucf.edu/wp-content/uploads/2019/09/EEL4515_LabManual.pdf
  22. http://jontalle.web.engr.illinois.edu/uploads/537.F18/Papers/Smith-muLaw.57.pdf
  23. https://www.sciencedirect.com/science/article/pii/B9780123735805500387
  24. https://weiyaolin.github.io/comm/comm_files/comm_ch04_ADC_en.pdf
  25. https://www.albedotelecom.com/src/lib/WP-E1-T1-PDH.pdf
  26. https://www.electrical4u.com/binary-to-gray-code-converter-and-grey-to-binary-code-converter/
  27. https://www.aes-media.org/historical/html/recording.technology.history/digital.html
  28. https://patents.google.com/patent/US2272070A/en
  29. http://ieeexplore.ieee.org/document/4668716/
  30. https://people.math.harvard.edu/~ctm/home/text/others/shannon/entropy/entropy.pdf
  31. https://www.nsa.gov/portals/75/documents/about/cryptologic-heritage/historical-figures-publications/publications/wwii/sigsaly.pdf
  32. https://www.aes-media.org/historical/html/recording.technology.history/sigsaly.html
  33. https://www.sony.co.jp/en/Products/proaudio/en/story/story02.html
  34. https://www.vintagedigital.com.au/sony-pcm-1/
  35. https://www.philips.com/c-dam/corporate/research/technologies/cd/The-Emergence-of-the-Compact-Disc_v2.pdf
  36. https://www.dutchaudioclassics.nl/The-six-meetings-Philips-Sony-1979-1980-The-Start-of-Digital-Audio/
  37. https://hub.yamaha.com/proaudio/pa-history/the-history-of-the-daw/
  38. https://www.loc.gov/preservation/digital/formats/fdd/fdd000002.shtml
  39. https://audiophilereview.com/cd-dac-digital/some-of-the-whys-and-hows-of-apples-aiff-music-files/
  40. https://vintageking.com/blog/history-of-digital-recording/
  41. https://www.allelcoelec.com/blog/PCM-vs.Dolby-Digital-The-Ultimate-Guide-to-High-Fidelity-and-Surround-Sound-Audio-Technologies.html
  42. https://ui.adsabs.harvard.edu/abs/1965BSTJ...44.1405F/abstract
  43. https://www.rfcafe.com/references/ai/electronics-technology-principles/t1-transmission-system-1-bell-telephone-laboratories-ai.htm
  44. https://www.historyofinformation.com/detail.php?id=3364
  45. https://zytrax.com/tech/data_rates.htm
  46. https://www.rd.usda.gov/files/UTP_Bulletins_1751H-403.pdf
  47. https://www.t1rex.com/ds1t1.html
  48. https://www.itu.int/ITU-T/recommendations/rec.aspx?rec=7410
  49. https://www.loc.gov/preservation/digital/formats/fdd/fdd000038.shtml
  50. https://www.sciencedirect.com/topics/engineering/pulse-code-modulation
  51. https://www.cisco.com/c/en/us/support/docs/voice/h323/8123-waveform-coding.html
  52. https://www.scribd.com/doc/123999732/PCM-Tutorial-4
  53. https://www.utdallas.edu/~kjp/EE4250/lab7.pdf
  54. https://www.elprocus.com/pulse-code-modulation-and-demodulation/
  55. https://www.utdallas.edu/~mtacca/courses/EE3150/Spring-2012/Exp6.pdf
  56. https://www.allaboutcircuits.com/technical-articles/companding-logarithmic-laws-implementation-and-consequences/
  57. https://www.ti.com/lit/an/spra163a/spra163a.pdf
  58. https://circuitglobe.com/difference-between-pam-pwm-and-ppm.html
  59. https://www.tutorialspoint.com/digital_communication/digital_communication_pulse_code_modulation.htm
  60. https://www.tek.com/en/documents/primer/clock-recovery-primer-part-1
  61. https://www.analog.com/en/resources/technical-articles/equalizing-techniques-flatten-dac-frequency-response.html
  62. https://eng.libretexts.org/Bookshelves/Electrical_Engineering/Signal_Processing_and_Modeling/Signals_and_Systems_(Baraniuk_et_al.)/10:_Sampling_and_Reconstruction/10.04:_Perfect_Reconstruction
  63. https://aes2.org/audio-topics/high-resolution-audio-2/
  64. https://www.thebroadcastbridge.com/content/entry/16951/practical-sdi-and-ip-part-1
  65. https://www.sounddevices.com/32-bit-float-files-explained/
  66. https://www.analog.com/en/resources/technical-articles/selecting-a-t1e1j1-singlechip-transceiver.html
  67. https://www.dpstele.com/e1/index.php
  68. https://www.travsonic.com/red-book-cd-format/
  69. http://www.mp3-tech.org/programmer/docs/mp3_theory.pdf
  70. https://www.sonarworks.com/blog/glossary/pcm-audio
  71. https://gdpspace.com/wp-content/uploads/Telemetry-over-Internet-Protocaol-TMoIP.pdf
  72. https://ieeexplore.ieee.org/document/1090622
  73. https://opg.optica.org/oe/fulltext.cfm?uri=oe-29-2-1945
  74. https://www.eecs.qmul.ac.uk/~josh/documents/2012/WangReiss-AES1322012-DecimationFilters.pdf
  75. https://arxiv.org/pdf/2403.08099
  76. https://arxiv.org/pdf/2202.08898
  77. https://ccrma.stanford.edu/courses/192b/Digital_Audio_Systems.pdf
  78. https://arxiv.org/pdf/1807.08636
  79. https://users.ece.utexas.edu/~bevans/courses/rtdsp/lectures/10_Data_Conversion/AP_Understanding_PDM_Digital_Audio.pdf
  80. https://audiopub.co.kr/wp-content/uploads/2020/08/Cross-Interleave-Reed-Solomon-Codes-and-Compact-Disc.pdf
  81. https://www.researchgate.net/publication/265634360_Reed-Solomon_codes_and_the_compact_disc
  82. https://arxiv.org/abs/2010.11362
  83. https://kuleshov.github.io/audio-super-res/
  84. https://onlinelibrary.wiley.com/doi/abs/10.1002/j.1538-7305.1966.tb01052.x
  85. https://ieeexplore.ieee.org/document/1090059
  86. https://www.itu.int/rec/T-REC-G.726/e
  87. https://www.itu.int/rec/T-REC-G.727
  88. https://xiph.org/flac/faq.html
  89. https://datatracker.ietf.org/doc/rfc9639/
  90. https://www.ciitresearch.org/dl/index.php/pdcs/article/view/PDCS092010004
  91. https://www.researchgate.net/publication/395910353_AI-Driven_Near-Lossless_Audio_Compression_Modeling_via_Autoencoders
  92. https://www.isca-archive.org/interspeech_2025/zhang25l_interspeech.pdf
  93. https://www.researchgate.net/publication/396329408_Compression_of_Scene-Based_Higher_Order_Ambisonics_with_Multichannel_RVQGAN
  94. https://www.itu.int/rec/T-REC-G.703/en
  95. https://www.itu.int/rec/T-REC-G.783/en
  96. https://ieeexplore.ieee.org/document/4112364
  97. https://www.researchgate.net/publication/387412310_Digital_Mobile_Fronthaul_Based_on_Adaptive_Differential_Pulse_Code_Modulation
  98. https://www.siue.edu/~yadwang/ECE375_Lec6.pdf
  99. https://www.mdpi.com/2079-9268/8/2/12
  100. https://trace.tennessee.edu/cgi/viewcontent.cgi?referer=&httpsredir=1&article=1106&context=utk_graddiss
  101. https://www.researchgate.net/publication/224218075_Analysis_of_Power_Consumption_and_Linearity_in_Capacitive_Digital-to-Analog_Converters_Used_in_Successive_Approximation_ADCs
  102. https://www.analog.com/media/en/technical-documentation/application-notes/an-756.pdf
  103. https://www.researchgate.net/publication/239576616_Aperture_Time_Aperture_Jitter_Aperture_Delay_Time-_Removing_the_Confusion
  104. https://www.pewresearch.org/short-reads/2025/10/24/what-we-know-about-energy-use-at-us-data-centers-amid-the-ai-boom/
  105. https://www.digitizationguidelines.gov/term.php?term=pulsecodemodulation
  106. http://www2.egr.uh.edu/~glover/applets/Sampling/Sampling.html
  107. https://www.digitizationguidelines.gov/term.php?term=linearpulsecodemodulation
  108. https://www2.eecs.berkeley.edu/Pubs/TechRpts/1976/ERL-m-587.pdf
  109. https://daskalakispiros.com/files/Ebooks/digital-communication-proakis-salehi-5th-edition.pdf
  110. https://srinix.org/lecture_notes/SEM6/CE%28MOD-3%29.pdf
  111. https://www.itu.int/rec/T-REC-G.711/
  112. https://picture.iczhiku.com/resource/eetop/WHKDelrzgeFUkvMc.pdf
Add your contribution
Related Hubs
User Avatar
No comments yet.