Hubbry Logo
Triple-alpha processTriple-alpha processMain
Open search
Triple-alpha process
Community hub
Triple-alpha process
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Triple-alpha process
Triple-alpha process
Triple-alpha process
View on Wikipedia
from Wikipedia
Overview of the triple-alpha process

The triple-alpha process is a set of nuclear fusion reactions by which three helium-4 nuclei (alpha particles) are transformed into carbon.[1][2]

In stars

[edit]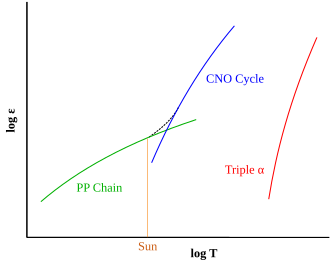
Comparison of the energy output (ε) of proton–proton (PP), CNO and Triple-α fusion processes at different temperatures (T). The dashed line shows the combined energy generation of the PP and CNO processes within a star.

Helium accumulates in the cores of stars as a result of the proton–proton chain reaction and the carbon–nitrogen–oxygen cycle.

Nuclear fusion reactions of two helium-4 nuclei produces beryllium-8, which is highly unstable, and decays back into smaller nuclei with a half-life of 8.19×10−17 s, unless within that time a third alpha particle fuses with the beryllium-8 nucleus[3] to produce an excited resonance state of carbon-12,[4] called the Hoyle state. This nearly always decays back into three alpha particles, but once in about 2421.3 times, it releases energy and changes into the stable base form of carbon-12.[5] When a star runs out of hydrogen to fuse in its core, it begins to contract and heat up. If the central temperature rises to 108 K,[6] six times hotter than the Sun's core, alpha particles can fuse fast enough to get past the beryllium-8 barrier and produce significant amounts of stable carbon-12.

4
2He + 4
2He → 8
4Be 		 (−0.0918 MeV)
8
4Be + 4
2He → 12
6C + 2γ 		 (+7.367 MeV)

The net energy release of the process is 7.275 MeV.

As a side effect of the process, some carbon nuclei fuse with additional helium to produce a stable isotope of oxygen and energy:

12
6C + 4
2He → 16
8O + γ (+7.162 MeV)

Nuclear fusion reactions of helium with hydrogen produces lithium-5, which also is highly unstable, and decays back into smaller nuclei with a half-life of 3.7×10−22 s.

Fusing with additional helium nuclei can create heavier elements in a chain of stellar nucleosynthesis known as the alpha process, but these reactions are only significant at higher temperatures and pressures than in cores undergoing the triple-alpha process. This creates a situation in which stellar nucleosynthesis produces large amounts of carbon and oxygen, but only a small fraction of those elements are converted into neon and heavier elements. Oxygen and carbon are the main "ash" of helium-4 burning.

In neutron stars

[edit]

Material that accretes from a companion star onto the surface of a neutron star may begin this helium-burning process in a local region. The burning wave is estimated to travel at 50 to 500 km/s, traversing the surface in around one second. Within this second, the neutron star rapidly rotates, moving the brighter burning region in and out of view. This intensity modulation allows the rotational frequency to be measured, sometimes up to 300 Hz.

Some neutron stars have been measured with such an intensity modulation at 600 Hz. A suggested origin is neutron stars which rotate at 300 Hz, but have two burning regions. The second burning region is theorized to form almost immediately after the first, exactly on the opposite side of the neutron star, due to the convergence of gravitational wave from the initial thermonuclear ignition.[7]

Primordial carbon

[edit]
Main article: Big Bang nucleosynthesis

The triple-alpha process is ineffective at the pressures and temperatures early in the Big Bang. One consequence of this is that no significant amount of carbon was produced in the Big Bang.

Resonances

[edit]

Ordinarily, the probability of the triple-alpha process is extremely small. However, the beryllium-8 ground state has almost exactly the energy of two alpha particles. In the second step, 8Be + 4He has almost exactly the energy of an excited state of 12C. This resonance greatly increases the probability that an incoming alpha particle will combine with beryllium-8 to form carbon. The existence of this resonance was predicted by Fred Hoyle before its observation, based on the physical necessity for it to exist, in order for carbon to be formed in stars. The prediction and then discovery of this energy resonance and process supported Hoyle's hypothesis of stellar nucleosynthesis, which posited that all chemical elements had originally been formed from hydrogen, the true primordial substance. The anthropic principle has been cited to explain the fact that nuclear resonances are sensitively arranged to create large amounts of carbon and oxygen in the universe.[8][9]

Reaction rate and stellar evolution

[edit]

The triple-alpha steps are strongly dependent on the temperature and density of the stellar material. The power released by the reaction is approximately proportional to the temperature to the 40th power, and the density squared.[10] In contrast, the proton–proton chain reaction produces energy at a rate proportional to the fourth power of temperature, the CNO cycle at about the 17th power of the temperature, and both are linearly proportional to the density. This strong temperature dependence has consequences for the late stage of stellar evolution, the red-giant stage.

For lower mass stars on the red-giant branch, the helium accumulating in the core is prevented from further collapse only by electron degeneracy pressure. The entire degenerate core is at the same temperature and pressure, so when its density becomes high enough, fusion via the triple-alpha process rate starts throughout the core. The core is unable to expand in response to the increased energy production until the pressure is high enough to lift the degeneracy. As a consequence, the temperature increases, causing an increased reaction rate in a positive feedback cycle that becomes a runaway reaction. This process, known as the helium flash, lasts a matter of seconds but burns 60–80% of the helium in the core. During the core flash, the star's energy production can reach approximately 1011 solar luminosities which is comparable to the luminosity of a whole galaxy,[11] although no effects will be immediately observed at the surface, as the whole energy is used up to lift the core from the degenerate to normal, gaseous state. Since the core is no longer degenerate, hydrostatic equilibrium is once more established and the star begins to "burn" helium at its core and hydrogen in a spherical layer above the core. The star enters a steady helium-burning phase which lasts about 10% of the time it spent on the main sequence (the Sun is expected to burn helium at its core for about a billion years after the helium flash).[12]

In higher mass stars, which evolve along the asymptotic giant branch, carbon and oxygen accumulate in the core as helium is burned, while hydrogen burning shifts to further-out layers, resulting in an intermediate helium shell. However, the boundaries of these shells do not shift outward at the same rate due to differing critical temperatures and temperature sensitivities for hydrogen and helium burning. When the temperature at the inner boundary of the helium shell is no longer high enough to sustain helium burning, the core contracts and heats up, while the hydrogen shell (and thus the star's radius) expand outward. Core contraction and shell expansion continue until the core becomes hot enough to reignite the surrounding helium. This process continues cyclically – with a period on the order of 1000 years – and stars undergoing this process have periodically variable luminosity. These stars also lose material from their outer layers in a stellar wind driven by radiation pressure, which ultimately becomes a superwind as the star enters the planetary nebula phase.[13]

Discovery

[edit]

The triple-alpha process is highly dependent on carbon-12 and beryllium-8 having resonances with slightly more energy than helium-4. Based on known resonances, by 1952 it seemed impossible for ordinary stars to produce carbon as well as any heavier element.[14] Nuclear physicist William Alfred Fowler had noted the beryllium-8 resonance, and Edwin Salpeter had calculated the reaction rate for 8Be, 12C, and 16O nucleosynthesis taking this resonance into account.[15][16] However, Salpeter calculated that red giants burned helium at temperatures of 2·108 K or higher, whereas other recent work hypothesized temperatures as low as 1.1·108 K for the core of a red giant.

Salpeter's paper mentioned in passing the effects that unknown resonances in carbon-12 would have on his calculations, but the author never followed up on them. It was instead astrophysicist Fred Hoyle who, in 1953, used the abundance of carbon-12 in the universe as evidence for the existence of a carbon-12 resonance. The only way Hoyle could find that would produce an abundance of both carbon and oxygen was through a triple-alpha process with a carbon-12 resonance near 7.68 MeV, which would also eliminate the discrepancy in Salpeter's calculations.[14]

Hoyle went to Fowler's lab at Caltech and said that there had to be a resonance of 7.68 MeV in the carbon-12 nucleus. (There had been reports of an excited state at about 7.5 MeV.[14]) Fred Hoyle's audacity in doing this is remarkable, and initially, the nuclear physicists in the lab were skeptical. Finally, a junior physicist, Ward Whaling, fresh from Rice University, who was looking for a project decided to look for the resonance. Fowler permitted Whaling to use an old Van de Graaff generator that was not being used. Hoyle was back in Cambridge when Fowler's lab discovered a carbon-12 resonance near 7.65 MeV a few months later, validating his prediction. The nuclear physicists put Hoyle as first author on a paper delivered by Whaling at the summer meeting of the American Physical Society. A long and fruitful collaboration between Hoyle and Fowler soon followed, with Fowler even coming to Cambridge.[17]

The final reaction product lies in a 0+ state (spin 0 and positive parity). Since the Hoyle state was predicted to be either a 0+ or a 2+ state, electron–positron pairs or gamma rays were expected to be seen. However, when experiments were carried out, the gamma emission reaction channel was not observed, and this meant the state must be a 0+ state. This state completely suppresses single gamma emission, since single gamma emission must carry away at least 1 unit of angular momentum. Pair production from an excited 0+ state is possible because their combined spins (0) can couple to a reaction that has a change in angular momentum of 0.[18]

Improbability and fine-tuning

[edit]
Main article: Fine-tuned universe

Carbon is a necessary component of all known life. 12C, a stable isotope of carbon, is abundantly produced in stars due to three factors:

  1. The decay lifetime of a 8Be nucleus is four orders of magnitude larger than the time for two 4He nuclei (alpha particles) to scatter.[19]
  2. An excited state of the 12C nucleus exists a little (0.3193 MeV) above the energy level of 8Be + 4He. This is necessary because the ground state of 12C is 7.3367 MeV below the energy of 8Be + 4He; a 8Be nucleus and a 4He nucleus cannot reasonably fuse directly into a ground-state 12C nucleus. However, 8Be and 4He use the kinetic energy of their collision to fuse into the excited 12C (kinetic energy supplies the additional 0.3193 MeV necessary to reach the excited state), which can then transition to its stable ground state. According to one calculation, the energy level of this excited state must be between about 7.3 MeV and 7.9 MeV to produce sufficient carbon for life to exist, and must be further "fine-tuned" to between 7.596 MeV and 7.716 MeV in order to produce the abundant level of 12C observed in nature.[20] The Hoyle state has been measured to be about 7.65 MeV above the ground state of 12C.[21]
  3. In the reaction 12C + 4He → 16O, there is an excited state of oxygen which, if it were slightly higher, would provide a resonance and speed up the reaction. In that case, insufficient carbon would exist in nature; almost all of it would have converted to oxygen.[19]

Some scholars argue the 7.656 MeV Hoyle resonance, in particular, is unlikely to be the product of mere chance. Fred Hoyle argued in 1982 that the Hoyle resonance was evidence of a "superintellect";[14] Leonard Susskind in The Cosmic Landscape rejects Hoyle's intelligent design argument.[22] Instead, some scientists believe that different universes, portions of a vast "multiverse", have different fundamental constants:[23] according to this controversial fine-tuning hypothesis, life can only evolve in the minority of universes where the fundamental constants happen to be fine-tuned to support the existence of life. Other scientists reject the hypothesis of the multiverse on account of the lack of independent evidence.[24]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Triple-alpha process

View on Grokipedia
from Grokipedia
The triple-alpha process is a sequence of nuclear fusion reactions in which three helium-4 nuclei, also known as alpha particles, combine to produce a nucleus, releasing in the form of gamma radiation. This process occurs primarily in the cores of low- to intermediate-mass stars during their helium-burning phase, after the exhaustion of fuel, when central temperatures surpass approximately 100 million . First theoretically outlined by Edwin Salpeter in 1952 as a mechanism for generation in helium-rich stellar interiors, the process is essential for , enabling the formation of carbon—the fourth most abundant element in the —and serving as a precursor to the synthesis of heavier elements like oxygen and in more advanced stages. The reaction proceeds in two main steps: first, two alpha particles fuse to form an unstable nucleus, which has a very short lifetime of about 10⁻¹⁶ seconds; second, this captures a third to form , with the overall reaction being endothermic in the initial step but exothermic overall, yielding a net energy release of 7.275 MeV. The efficiency of this process hinges on a critical in the nucleus at 7.65 MeV above its —known as the Hoyle state—predicted by astrophysicist in 1953 to explain the observed cosmic abundance of carbon, and subsequently confirmed experimentally. Without this resonance, the reaction rate would be insufficient to account for carbon production in stars, highlighting the process's sensitivity to nuclear structure and its implications for the chemical evolution of the universe. In low-mass stars, the triple-alpha process contributes to the , a rapid ignition event that stabilizes the star's core against collapse.

Fundamentals

Definition

The triple-alpha process is a three-body nuclear fusion reaction in which three helium-4 nuclei (alpha particles) combine to form a single carbon-12 nucleus, releasing energy in the form of gamma radiation. This process represents a key pathway in stellar nucleosynthesis, enabling the transformation of helium ash from prior hydrogen fusion stages into more complex elements. In astrophysics, the triple-alpha process holds fundamental significance as the dominant mechanism responsible for synthesizing nearly all carbon in the universe, which is essential for the formation of heavier elements and the chemical evolution of cosmic structures. Carbon produced via this reaction serves as a building block for subsequent alpha-capture sequences that generate oxygen and other isotopes. The net balance of the reaction is given by 3 \, ^4\mathrm{He} \rightarrow ^{12}\mathrm{C} + 7.274 \, \mathrm{MeV}, where the Q-value reflects the mass difference converted to , powering stellar interiors during helium exhaustion. This process activates during the helium burning phase of , typically in the cores of low- to intermediate-mass stars after core hydrogen depletion, providing a sustained source that alters the star's structure and .

Reaction Mechanism

The triple-alpha process proceeds through two sequential alpha-particle capture reactions, approximating what is fundamentally a three-body interaction due to the transient nature of the intermediate nucleus. In the first step, two nuclei fuse to form in its : 4He+4He→8Be,^4\mathrm{He} + ^4\mathrm{He} \to ^8\mathrm{Be}, releasing a Q-value of -91.84 keV, indicating an just above the energy threshold for stability. The resulting ^8Be nucleus is highly unstable, with a of approximately 8.2 \times 10^{-17} seconds, primarily decaying back into two alpha particles via the strong interaction. The second step requires the rapid capture of a third ^4He nucleus by ^8Be before its decay: 8Be+4He→12C∗,^8\mathrm{Be} + ^4\mathrm{He} \to ^{12}\mathrm{C}^*, where ^{12}C^* denotes the excited Hoyle state, with a Q-value of 7.367 MeV relative to the initial reactants. The brevity of the ^8Be lifetime—far shorter than the timescale for a direct three-body collision—necessitates modeling the overall process as these two two-body reactions, though quantum mechanical treatments account for the intermediate's virtual existence. At the relevant stellar temperatures of around 10^8 , the high repulsion between positively charged alpha particles presents a significant barrier to fusion, approximately 5-10 MeV in height. Quantum tunneling through this barrier enables the reactions to occur at these relatively low energies (corresponding to velocities), with the tunneling probability exponentially sensitive to and enhancing the effective .

Astrophysical Settings

In Stellar Interiors

The triple-alpha process plays a central role in the evolution of low- to intermediate-mass stars (approximately 0.8 to 8 solar masses) during their ascent along the and subsequent phases, where it ignites after the exhaustion of in the , leading to fusion in a predominantly helium-rich environment. In these stars, the process first manifests as the in degenerate cores of lower-mass objects (below about 2 solar masses), where rapid ignition occurs at the center, followed by stable core burning on the . For higher-mass stars, non-degenerate core burning proceeds more gradually without a flash. This burning phase sustains the star's for millions of years, stabilizing the core against further contraction. The physical conditions required for the triple-alpha process in these stellar interiors are temperatures around 10810^8 and densities on the order of 10510^5 g/cm³, with the core composition dominated by (mass fraction Y≈0.98Y \approx 0.98) accumulated from prior fusion. These conditions arise as the inert core contracts post-hydrogen exhaustion, heating via release until the reaction threshold is met; the high density enhances collision rates among alpha particles despite the . In (AGB) stars, the process contributes substantially to energy generation through episodic shell burning around the carbon-oxygen core, triggered after shell exhaustion during thermal pulses that drive mass loss and mixing. As the primary source of carbon-12 in such stars, the triple-alpha process produces "primary" carbon whose abundance is independent of initial , directly from . The resulting can capture additional alpha particles to form , yielding core C/O mass ratios typically between 0.25 and 0.5 at the end of central helium burning, depending on and ; these ratios are lower in more massive stars due to enhanced alpha captures. In AGB phases, convective mixing events like the third transport this carbon to the surface, elevating atmospheric C/O ratios and classifying some stars as carbon stars when C/O exceeds 1.

In Neutron Stars

In the crusts of neutron stars, particularly in accreting systems, the triple-alpha process can proceed through pycnonuclear fusion at densities on the order of 10810^8 to 101010^{10} g/cm³, where quantum zero-point oscillations enable tunneling between alpha particles despite low temperatures, rendering the reaction largely independent of thermal activation. This non-thermal pathway contrasts with the temperature-driven process in stellar interiors, as pycnonuclear rates rely on the dense packing of nuclei in a degenerate gas, with calculated rates for alpha-particle plasmas showing values significantly lower than stellar estimates but sufficient to influence local evolution under compression. Such reactions occur in the outer crust, where helium-rich matter from accretion may accumulate before deeper processing. These pycnonuclear events play a key role in the thermal evolution and compositional structure of crusts by releasing through carbon formation, contributing to deep crustal heating that counters core cooling and maintains observable surface temperatures in quiescent phases of accreting systems. In accreting , the from triple-alpha pycnonuclear fusion, alongside electron captures, deposits at depths corresponding to the deep crust, altering impurity profiles and lattice properties that affect emission and luminosity during cooling. This process helps determine the layered composition, with carbon production potentially seeding further alpha captures that build heavier nuclei in the inner crust, influencing overall crustal rigidity and evolution. During neutron star mergers, the triple-alpha process experiences enhancement via neutron upscattering, where free s in the neutron-rich excite the Hoyle state in 12^{12}C, providing an alternative decay channel that boosts the effective rate by up to a factor of 46 at neutron densities of 10610^6 g/cm³ and temperatures around 7 GK. This neutron-catalyzed mechanism, distinct from pure pycnonuclear or paths, becomes relevant in the dynamic, low-electron-fraction conditions of merger remnants, potentially accelerating carbon production in the r-process environment and impacting nucleosynthetic yields. Unlike stellar settings, the merger enhancement arises from inelastic rather than equilibrium , highlighting the role of neutron bath density in modifying reaction kinetics under extreme compactness.

Nuclear Aspects

Key Resonances

The triple-alpha process relies on specific nuclear resonances in (¹²C) that enhance the efficiency of fusion under stellar conditions. The Hoyle state, an excited 0⁺ level at 7.65 MeV above the ¹²C , acts as the primary resonant state for the second alpha capture step, where ⁸Be + ⁴He forms the compound ¹²C nucleus at this excitation energy, facilitating subsequent de-excitation to the stable . This state's narrow total width of approximately 8.5 eV is crucial, as it prolongs the lifetime of the , increasing the likelihood of radiative decay over dissociation back into alpha particles and thereby boosting the overall reaction efficiency by orders of magnitude compared to non-resonant processes. While the ¹²C (0⁺ at 0 MeV) and higher 0⁺ excited states (e.g., at ~9.6 MeV and ~10.8 MeV) also contribute to potential capture channels, the Hoyle state's energy—positioned just 0.38 MeV above the three-alpha breakup threshold—makes it uniquely effective for the low densities and temperatures in helium-burning stars. The Hoyle state was experimentally confirmed using particle accelerators, with key observations from proton bombardment of ¹¹B targets at the Caltech Kellogg Radiation Laboratory in 1957, revealing the at 7.65 MeV excitation through gamma-ray in the ¹¹B(p,γ)¹²C reaction, and assigning spin-parity J^π = 0⁺ based on angular distribution and selection rules. Subsequent experiments at facilities like the tandem accelerators at TUNL and HIγS have refined these properties, confirming the to 7.654 MeV and width to 8.5 ± 0.1 eV via and inelastic excitation studies. Quantum mechanically, the resonance enhances the reaction cross-section through the formation of a quasi-bound compound state, where the incoming ⁸Be + ⁴He system tunnels into the of ¹²C at the Hoyle energy, leading to a sharp peak in the capture probability when the relative matches the resonance condition; this Breit-Wigner-like enhancement arises from the overlap of the incoming with the resonant eigenstate, far exceeding the non-resonant tail contributions.

Reaction Rates

The for the triple-alpha process, which governs the production of from three nuclei, is expressed as λ = ρ² ⟨σv⟩ / m_He, where ρ is the mass density, ⟨σv⟩ is the velocity-averaged cross-section for the effective two-step sequential capture (accounting for the unstable ⁸Be intermediate), and m_He is the mass of a nucleus. This formulation arises from treating the process as equilibrium formation of ⁸Be followed by alpha capture, making the overall rate proportional to ρ² rather than ρ³ for a direct interaction. The rate exhibits a strong dependence, peaking around 10⁸ in typical helium-burning environments, where thermal energies align with the key resonances involved. The triple-alpha rate is highly sensitive to the parameters of the ⁸Be (particularly its energy and width near 92 keV above the two-alpha threshold) and the Hoyle state in ¹²C (the 0⁺ at 7.654 MeV, which enhances the capture probability). Small variations in these energies—on the order of a few keV—can alter the rate by factors of 10³ or more due to the narrow resonant nature of the reactions, emphasizing the fine-tuning required for efficient carbon production. This sensitivity underscores the process's role in , where deviations could significantly impact helium exhaustion times. Recent experimental efforts have refined the rate by addressing previously overestimated corrections, such as upscattering effects on the Hoyle state decay. Measurements in using a time projection chamber at the Edwards Accelerator Laboratory revealed that -induced enhancement of the triple-alpha rate is suppressed near threshold, reducing the predicted boost to less than 50 at 7 GK for densities of 10⁶ g cm⁻³—far below prior Hauser-Feshbach estimates exceeding 100—and limiting the impact to order unity at lower temperatures, thereby tightening overall rate uncertainties to around 10-20%. A measurement refined the radiative width of the Hoyle state to 3.75(40) × 10^{-3} eV, consistent with prior values but reducing associated uncertainties in rate calculations. These results resolve discrepancies in high-density environments and align with stellar models without invoking large adjustments. Computational methods, particularly R-matrix theory, are essential for extrapolating laboratory data on alpha capture and to the low stellar energies (E < 1 MeV) inaccessible to direct experiments. R-matrix fits parameterize the ⁸Be(α,γ)¹²C and related reactions by matching interior nuclear wave functions to exterior scattering, incorporating interference effects and subthreshold states to yield analytic rate expressions valid across temperatures from 0.01 to 10 GK; recent analyses (2025) incorporating these interferences have significantly increased the quoted uncertainty in the rate at peak temperatures, with interference effects contributing approximately 75% to the total uncertainty, highlighting ongoing theoretical challenges.

Historical Context

Theoretical Prediction

The liquid drop model of the atomic nucleus, initially proposed by in 1928 to explain alpha decay through quantum tunneling and further developed by in 1935 into a semi-empirical mass formula, laid foundational groundwork for understanding nuclear stability and binding energies relevant to fusion processes in stars. In the 1930s, these models informed early speculations on helium burning as a potential energy source in stellar interiors after hydrogen exhaustion, though detailed mechanisms remained elusive due to limited knowledge of nuclear cross-sections. By the 1940s, theoretical stellar evolution models, building on work by and others, indicated that post-main-sequence stars, particularly , required efficient helium-to-carbon fusion to sustain energy production and match observed luminosities and abundances. A key challenge in pre-1950s nuclear astrophysics was the apparent improbability of the three-body alpha-alpha-alpha reaction, as direct three-body collisions in stellar plasmas are exceedingly rare, occurring at rates far too low to account for the observed cosmic abundance of carbon without intermediate resonances to enhance the process. This issue was highlighted in early calculations, which showed that helium burning via such a mechanism would be inefficient unless stabilized by short-lived intermediate states like beryllium-8, yet the instability of these intermediates further suppressed yields. Stellar models thus predicted a "helium burning problem," where insufficient carbon production would halt further nucleosynthesis and contradict empirical evidence from spectroscopy. The breakthrough came in 1952 when Edwin Salpeter formalized the sequential triple-alpha process, proposing that two alpha particles first form an unstable beryllium-8 nucleus, which then captures a third alpha to produce carbon-12, estimating reaction rates sufficient for helium burning in evolved stars. Building on this, Fred Hoyle in 1953 predicted that to match the observed interstellar carbon abundance—essential for subsequent element synthesis—the reaction rate required enhancement via a specific excited state in carbon-12 at approximately 7.65 MeV above the ground state, a resonance that would dramatically boost the capture probability without direct experimental evidence at the time. This prediction stemmed from integrating nuclear theory with big-bang nucleosynthesis limits and stellar evolution needs, emphasizing carbon's role as a catalyst and product in advanced burning stages.

Discovery and Experiments

The Hoyle state, crucial for the triple-alpha process, was first experimentally observed in 1953 at the California Institute of Technology (Caltech) by D. N. F. Dunbar, R. E. Pixley, W. A. Wenzel, and W. Whaling using the ^{14}N(d,α)^{12}C reaction, revealing a resonance at 7.65 MeV in carbon-12. This discovery provided initial evidence for an excited state in carbon-12 that could facilitate helium fusion, though its spin and parity remained unconfirmed at the time. In 1957, C. W. Cook, W. A. Fowler, C. C. Lauritsen, and T. Lauritsen at Caltech further investigated the state using the beta decay of boron-12, establishing its J^π = 0^+ nature and suitability for enhancing the triple-alpha reaction rate, thereby confirming Hoyle's theoretical prediction. During the 1960s and 1970s, a series of beam experiments refined the nuclear parameters essential to the triple-alpha process, including the lifetime of the beryllium-8 ground state and cross-sections for alpha-alpha interactions. For instance, alpha-alpha elastic scattering measurements at facilities like the provided precise determinations of the beryllium-8 resonance width (approximately 5.6 eV), corresponding to a lifetime of about 10^{-16} seconds, which governs the intermediate step in the sequential capture. These studies, often using tandem accelerators, also quantified alpha capture cross-sections on beryllium-8 analogs, reducing uncertainties in the overall reaction rate by factors of several percent and validating the process's efficiency in stellar environments. Modern experimental efforts have shifted to underground laboratories to minimize cosmic-ray backgrounds, enabling measurements at the ultra-low energies relevant to astrophysics. The Laboratory Underground for Nuclear Astrophysics (LUNA) in Italy's Gran Sasso National Laboratory has conducted indirect studies of helium-burning reactions, including precise determinations of the Hoyle state's gamma-decay branching ratio (about 0.4%) through proton capture on boron-11, which informs the triple-alpha rate without direct three-body observation. Similarly, the Jinping Underground Nuclear Astrophysics (JUNA) facility in China, operational since the early 2020s, employs a high-current accelerator to pursue direct measurements of reaction cross-sections at stellar temperatures (around 0.1 GK), targeting refinements to the beryllium-8 lifetime and Hoyle state parameters with unprecedented precision. Recent advances include 2022 investigations into neutron-enhanced triple-alpha rates, using neutron inelastic scattering on to populate the Hoyle state and assess modifications in dense stellar media. These studies, combining experimental data from neutron beam facilities with ab initio simulations and indirect techniques like transfer reactions, indicate that neutron upscattering could alter the effective rate by up to 10-20% in neutron-rich environments, though confirmation requires further validation. More recent work in 2023 has used ab initio methods to explore the emergent geometry of the Hoyle state, providing insights into its cluster structure, while 2024 experiments with charged particle spectroscopy have clarified the radiative decay branching, further refining rate uncertainties.

Implications

Stellar Nucleosynthesis

The triple-alpha process serves as the primary mechanism for synthesizing carbon-12 in the helium-burning cores of stars, providing the seed nucleus that initiates further nucleosynthetic chains through successive alpha-particle captures. Following the formation of 12^{12}C, the reaction 12^{12}C + ^4He→16He \to ^{16}O + \gammaproducesoxygen−16,whichthenundergoesadditionalcaptures:produces oxygen-16, which then undergoes additional captures:^{16}O+4O + ^4He \to ^{20}Ne+γNe + \gamma to form neon-20, and 20^{20}Ne + ^4He→24He \to ^{24}Mg + \gamma$ to yield magnesium-24. These alpha-ladder reactions, occurring under the high temperatures and densities of helium exhaustion phases, build up the bulk of elements up to silicon in massive stars, contributing significantly to the even-even isotopic abundances observed in stellar ejecta. In massive (M > 8 M_\sun), the triple-alpha process and subsequent alpha captures during core helium burning produce substantial quantities of carbon and oxygen, which are later processed and expelled in core-collapse supernovae, enriching the with these elements. Low- to intermediate-mass (1-8 M_\sun) on the () experience pulses in their helium shells, where the triple-alpha process generates carbon that is mixed to the surface via third dredge-up episodes, leading to carbon-rich envelopes and the formation of carbon . These AGB winds and planetary nebulae release processed material, playing a key role in the galactic enrichment of carbon, with models indicating that AGB contribute approximately one third of the interstellar carbon in solar neighborhoods. The reaction rate of the triple-alpha process exerts a strong influence on , as even modest variations—such as a 1% change—can alter helium-burning lifetimes by several percent and final core masses by up to 0.01 M_\sun in low-mass , thereby affecting the onset of subsequent burning stages and the star's fate. Stellar models demonstrate that higher rates accelerate evolution, shortening the phase and influencing the efficiency of mass loss, while lower rates prolong helium burning and enhance the production of certain isotopes. In AGB stars, the carbon produced via the triple-alpha process indirectly activates the by facilitating s in the helium-intershell regions during thermal pulses. Partial mixing after hydrogen-shell burning creates 13^{13}C pockets, which serve as the primary through the reaction 13^{13}C(\alpha, n)^{16}O,whilehighertemperaturesactivatethesecondaryO, while higher temperatures activate the secondary ^{22}Ne(α,n)25Ne(\alpha, n)^{25}Mg source involving neon from prior alpha captures; these neutrons drive slow neutron captures on iron-peak seeds, synthesizing up to half of the heavy elements beyond iron observed in the galaxy.

Fine-Tuning and Improbability

The efficiency of the triple-alpha process hinges on the precise alignment of nuclear parameters, particularly the existence of the Hoyle state in , without which the would drop by a factor of approximately 10^{7}, making stellar carbon production virtually impossible and precluding the abundance of carbon necessary for . This extreme sensitivity underscores the improbability of the process occurring at rates sufficient for in red giants. Calculations show that the absence of this would suppress the formation of carbon to levels incompatible with observed cosmic abundances. Further fine-tuning is evident in the energy levels of carbon-12, where shifts on the order of 0.2 MeV or more in the Hoyle state would disrupt the resonance overlap, reducing carbon yields by orders of magnitude and altering the carbon-to-oxygen ratio essential for planetary habitability. The strength of the strong nuclear force also plays a critical role; a variation of just 0.4% to 0.5% in the nucleon-nucleon interaction strength can shift these energy levels sufficiently to either overproduce oxygen or underproduce carbon, inhibiting the balanced synthesis required for complex chemistry. Such precision in fundamental parameters amplifies the process's delicacy. These features have fueled discussions within the framework, as articulated by and , who connected the tuned nuclear resonances to the universe's capacity to support observers through efficient carbon production in stars. Carter's weak posits that observed constants must permit life, with the triple-alpha process serving as a prime illustration of how slight deviations would render the inhospitable. However, critiques, including those from , argue that Fred Hoyle's original prediction of the Hoyle state was a straightforward astrophysical inference rather than an anthropic retrofitting, while theories in contemporary cosmology counter apparent fine-tuning by proposing that our universe is one of many with varying parameters, selected via .

Primordial Carbon

(BBN), which occurred approximately 10 seconds to 20 minutes after the at temperatures around 10910^9 K, primarily produces , , , , and trace amounts of lithium-7, but fails to synthesize significant quantities of carbon-12. The high photon-to-baryon ratio, η≈6×10−10\eta \approx 6 \times 10^{-10}, results in a vast excess of energetic photons relative to baryons, leading to the rapid of any nascent heavier nuclei formed during this epoch. This photodisintegration equilibrium prevents the accumulation of elements beyond , as the intense radiation field promptly breaks apart unstable intermediates. Helium burning in the BBN environment halts at 4^4He due to the absence of stable nuclei at mass numbers 5 and 8, which would be necessary stepping stones to 12^{12}C via sequential alpha captures. At the prevailing temperatures of roughly 10910^9 , the reaction rates for such captures are insufficient to overcome the , and the brief duration of the phase—coupled with the expanding, low-density conditions—further suppresses any potential buildup of heavier species. Theoretical calculations incorporating these constraints confirm that no stable intermediates can form effectively, rendering carbon production negligible under primordial conditions. Early theoretical models, such as those developed by Salpeter in the , demonstrated that the cosmological yield of carbon from BBN is extraordinarily low, on the order of less than 10−1010^{-10} relative to abundance, due to the dilute density and high of the early compared to stellar interiors. More recent detailed network calculations extending BBN to include CNO elements confirm that the primordial carbon-to-hydrogen ratio is on the order of 10−1510^{-15} or less, underscoring the inefficiency of the process. As a result, all observed cosmic carbon originates exclusively from via the triple-alpha process, a fact corroborated by the carbon abundances in metal-poor stars, which preserve signatures of the first generations of massive stars without primordial contamination.

References

  1. https://adsabs.harvard.edu/full/1952ApJ...115..326S
  2. http://hyperphysics.phy-astr.gsu.edu/hbase/Astro/helfus.html
  3. https://astronomy.swin.edu.au/cosmos/t/Triple+Alpha+Process
  4. https://iopscience.iop.org/article/10.1088/0004-637X/741/1/61
  5. https://ui.adsabs.harvard.edu/abs/1992ApJ...397..579S/abstract
  6. https://www.aanda.org/articles/aa/full_html/2011/06/aa15954-10/aa15954-10.html
  7. https://www.frontiersin.org/journals/physics/articles/10.3389/fphy.2022.942726/full
  8. https://www.nature.com/articles/s41467-022-29848-7
  9. https://www.sciencedirect.com/science/article/abs/pii/S0146641014000453
  10. https://link.aps.org/doi/10.1103/PhysRevLett.109.252501
  11. https://www.sciencedirect.com/science/article/pii/S037026932400738X
  12. https://link.springer.com/article/10.1140/epja/s10050-020-00093-0
  13. https://www.sciencedirect.com/science/article/pii/S0370269324006415
  14. https://www.sciencedirect.com/science/article/pii/S037026932500382X
  15. https://ui.adsabs.harvard.edu/abs/1952ApJ...115..326S/abstract
  16. https://link.aps.org/doi/10.1103/PhysRev.92.649
  17. https://link.aps.org/doi/10.1103/PhysRev.107.508
  18. https://www.nature.com/articles/s41467-023-38391-y
  19. https://www.nature.com/articles/s41598-024-68415-6
  20. https://iopscience.iop.org/article/10.3847/1538-4357/ad0a89
  21. https://ned.ipac.caltech.edu/level5/March15/Karakas/Karakas5.html
  22. https://arxiv.org/abs/1107.4984
  23. https://iopscience.iop.org/article/10.1088/0004-637X/718/1/357
  24. https://link.aps.org/doi/10.1103/RevModPhys.83
  25. https://www.aanda.org/articles/aa/full_html/2022/01/aa39318-20/aa39318-20.html
  26. https://philsci-archive.pitt.edu/5332/1/3alphaphil.pdf
  27. https://arxiv.org/pdf/astro-ph/9908247
  28. https://arxiv.org/pdf/nucl-th/0010052
  29. https://pdg.lbl.gov/2023/reviews/rpp2023-rev-bbang-nucleosynthesis.pdf
  30. https://www.aanda.org/articles/aa/full_html/2010/07/aa13315-09/aa13315-09.html
Add your contribution
Related Hubs
User Avatar
No comments yet.