Spherical astronomy

Spherical astronomyMain

Community hub

Spherical astronomy

8 pages, 0 posts

0 subscribers

Recent from talks

Be the first to start a discussion here.

Recent from talks

Be the first to start a discussion here.

Contribute something

About hubMembersContent overviewUpdatesRules

Main reference articles

Spherical astronomy

View on Wikipedia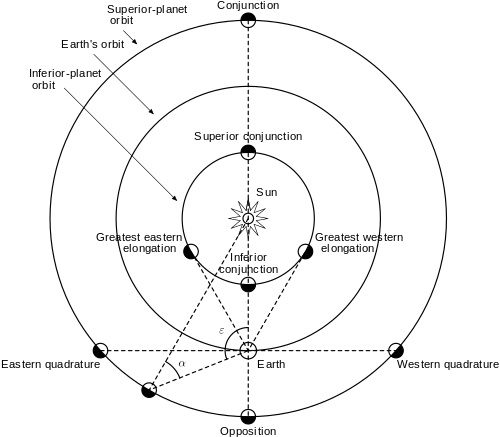

from Wikipedia

Spherical astronomy, or positional astronomy, is a branch of observational astronomy used to locate astronomical objects on the celestial sphere, as seen at a particular date, time, and location on Earth. It relies on the mathematical methods of spherical trigonometry and the measurements of astrometry.

This is the oldest branch of astronomy and dates back to antiquity. Observations of celestial objects have been, and continue to be, important for religious and astrological purposes, as well as for timekeeping and navigation. The science of actually measuring positions of celestial objects in the sky is known as astrometry.

The primary elements of spherical astronomy are celestial coordinate systems and time. The coordinates of objects on the sky are listed using the equatorial coordinate system, which is based on the projection of Earth's equator onto the celestial sphere. The position of an object in this system is given in terms of right ascension (α) and declination (δ). The latitude and local time can then be used to derive the position of the object in the horizontal coordinate system, consisting of the altitude and azimuth.

The coordinates of celestial objects such as stars and galaxies are tabulated in a star catalog, which gives the position for a particular year. However, the combined effects of axial precession and nutation will cause the coordinates to change slightly over time. The effects of these changes in Earth's motion are compensated by the periodic publication of revised catalogs.

To determine the position of the Sun and planets, an astronomical ephemeris (a table of values that gives the positions of astronomical objects in the sky at a given time) is used, which can then be converted into suitable real-world coordinates.

The unaided human eye can perceive about 6,000 stars, of which about half are below the horizon at any one time. On modern star charts, the celestial sphere is divided into 88 constellations. Every star lies within a constellation. Constellations are useful for navigation. Polaris lies nearly due north to an observer in the Northern Hemisphere. This pole star is always at a position nearly directly above the North Pole.

Positional phenomena

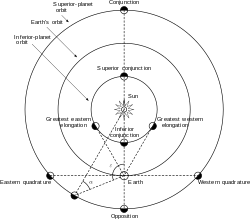
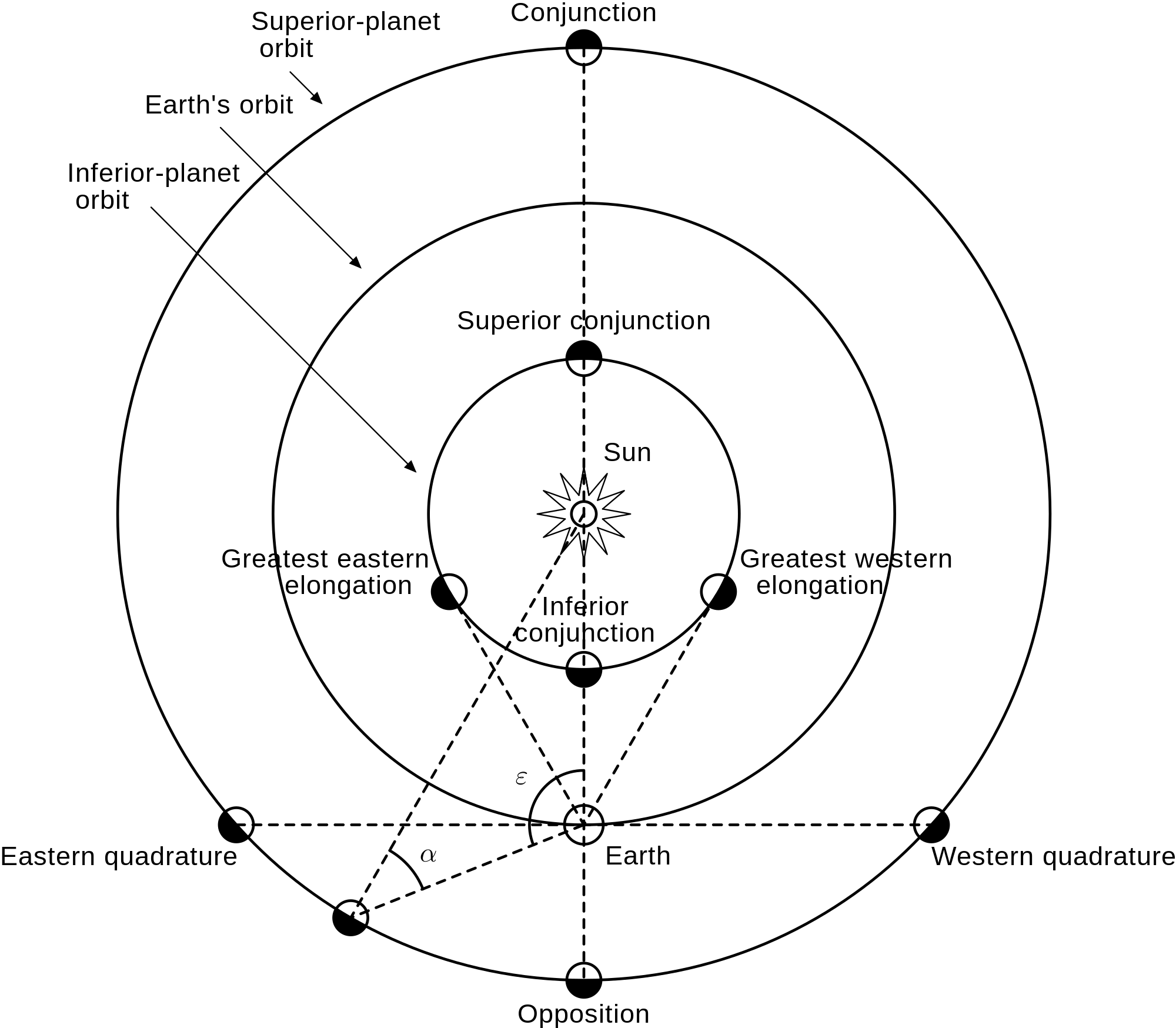
[edit]

Planets which are in conjunction form a line which passes through the center of the Solar System.
The ecliptic is the plane which contains the orbit of a planet, usually in reference to Earth.
Elongation refers to the angle formed by a planet, with respect to the system's center and a viewing point.
- A quadrature occurs when the position of a body (moon or planet) is such that its elongation is 90° or 270°; i.e. the body-earth-sun angle is 90°
Superior planets have a larger orbit than Earth's, while the inferior planets (Mercury and Venus) orbit the Sun inside Earth's orbit.
A transit may occur when an inferior planet passes through a point of conjunction.

Ancient structures associated with positional astronomy include

[edit]

References

[edit]

Robin M. Green, Spherical Astronomy, 1985, Cambridge University Press, ISBN 0-521-31779-7
William M. Smart, edited by Robin M. Green, Textbook on Spherical Astronomy, 1977, Cambridge University Press, ISBN 0-521-29180-1. (This classic text has been re-issued)

External links

[edit]

Software

NOVAS is an integrated package of subroutines for the computation of a wide variety of common astrometric quantities and transformations, in Fortran and C, from the U.S. Naval Observatory.
jNOVAS is a java wrapper for library developed and distributed by The United States Naval Meteorology and Oceanography Command (NMOC) with included JPL planetary and lunar ephemeris DE421 binary file published by the Jet Propulsion Laboratory.

Course notes and tutorials

Astronomy

Astronomy by

Manner	Amateur Observational Sidewalk Space telescope
Celestial subject	Galactic / Extragalactic Local system Solar
EM methods	Radio Submillimetre Infrared (Far-infrared) Visible-light (optical) Ultraviolet X-ray History Gamma-ray
Other methods	Neutrino Cosmic rays Gravitational radiation High-energy Radar Spherical Multi-messenger
Culture	Australian Aboriginal Babylonian Chinese Egyptian Greek Hebrew Indian Inuit Maya Medieval Islamic Persian Serbian folk Tibetan

Optical
telescopes

Revisions and contributors Edit on Wikipedia Read on Wikipedia

View on Grokipedia

from Grokipedia

Spherical astronomy, also known as positional astronomy, is the branch of astronomy that studies the positions, motions, and apparent paths of celestial objects as projected onto an imaginary celestial sphere surrounding Earth, employing principles of spherical geometry and trigonometry to determine their locations independent of distance.^[1]^[2] At its core, the celestial sphere serves as a fundamental construct: an infinite-radius sphere centered on the observer, where stars and other objects appear fixed relative to one another, facilitating the simplification of their diurnal and annual motions despite vast actual distances.^[3]^[2] Key elements include the celestial poles (projections of Earth's rotational axis), the celestial equator (90° from the poles), and the vernal equinox (the point where the ecliptic intersects the equator, marking the zero for right ascension).^[3]^[1] Central to spherical astronomy are various coordinate systems for precisely locating objects, such as the equatorial system using right ascension (measured eastward from the vernal equinox in hours, where 1 hour equals 15°) and declination (angular distance north or south of the celestial equator, ranging from -90° to +90°), which provides a fixed, observer-independent framework.^[3]^[2] Other systems include the horizontal (altitude and azimuth, local to the observer), ecliptic (based on Earth's orbital plane, tilted 23.4° to the equator), and galactic coordinates (aligned with the Milky Way's plane).^[1]^[2] Transformations between these systems rely on spherical trigonometry, where triangles on the sphere have angle sums exceeding 180° due to curvature.^[1] The field also addresses dynamic effects influencing positions, including precession (a slow wobble of Earth's axis at about 50.3 arcseconds per year, completing a cycle every ~26,000 years and shifting the vernal equinox), nutation (smaller periodic oscillations up to ~17 arcseconds), aberration (apparent displacement due to Earth's velocity and light's finite speed, up to 20.5 arcseconds), and parallax (annual shift for nearby stars due to Earth's orbit, up to 1 arcsecond for objects at 1 parsec).^[1]^[2] Atmospheric refraction further alters observed altitudes by bending light rays.^[1] Time measurement is integral, distinguishing sidereal time (based on Earth's rotation relative to distant stars, with a sidereal day of 23 hours 56 minutes 4 seconds) from solar time (tied to the Sun, yielding a mean solar day of 24 hours), enabling calculations of hour angles and Julian dates for precise epoch referencing in star catalogs.^[3]^[2] These concepts underpin applications in astrometry, navigation, celestial mechanics (including Kepler's laws for orbital predictions), and modern surveys like those using the International Celestial Reference System.^[1]^[2]

Fundamentals of the Celestial Sphere

The Celestial Sphere Concept

The celestial sphere is an imaginary sphere of infinite radius centered on the observer on Earth, serving as a projection surface for all celestial bodies regardless of their actual distances from the planet.^[3] This model treats stars and other distant objects as fixed points embedded on the sphere's inner surface, effectively ignoring their vast separations to simplify positional astronomy.^[4] By conceptualizing the sky as this uniform dome, observers can map and predict the apparent positions of celestial objects as if they lie on a single, expansive vault.^[5] The concept emerged as an innovation in ancient Greek astronomy, where it provided a geometric framework for understanding the heavens, and was formalized by Claudius Ptolemy in his Almagest around 150 AD.^[6]^[7] Ptolemy's treatise integrated observations from earlier Greek and Babylonian astronomers, using the celestial sphere to describe the motions of stars, planets, and the Sun within a geocentric system.^[8] In this model, the apparent daily rotation of the celestial sphere results from Earth's rotation on its axis, creating the illusion of stars rising in the east and setting in the west, while the stellar background remains fixed relative to distant cosmic reference points.^[9] The sphere completes a full 360-degree rotation in approximately 23 hours and 56 minutes of solar time, defining the length of a sidereal day.^[10] This distinction highlights how the celestial sphere abstracts Earth's motion to focus on observer-relative phenomena.

Spherical Geometry in Astronomy

Spherical geometry provides the foundational framework for understanding celestial observations by modeling the sky as the surface of a sphere, where distances and directions are measured along curved paths rather than straight lines. On this celestial sphere, great circles represent the shortest paths between any two points and are formed by the intersection of the sphere with planes passing through its center; examples include the celestial equator and the observer's meridian, which serve as primary reference lines for locating celestial objects.^[11] Small circles, in contrast, arise from intersections with planes not passing through the center and appear as parallel bands, such as those offset from the equator; poles are defined as the endpoints of an axis perpendicular to a great circle's plane, with the north and south celestial poles marking the projections of Earth's rotational axis. The zenith denotes the point directly overhead on the celestial sphere, while the nadir is its antipodal point directly below the observer, both aligned with the local vertical.^[3]^[12] Angular measurements in spherical geometry are expressed as arc lengths along great circles, typically in degrees, where a full great circle spans 360 degrees; this differs fundamentally from planar geometry, as all great circles intersect, precluding the existence of parallel lines that neither converge nor diverge. These arcs relate to solid angles, which quantify the apparent size of celestial objects as the area projected onto the unit sphere, measured in steradians or square degrees to assess coverage of the sky. For instance, the entire celestial sphere subtends a solid angle of 4π steradians, equivalent to 41,253 square degrees, enabling astronomers to evaluate field-of-view extents without linear approximations.^[13]^[14] A key application illustrates these principles: the celestial equator is the great circle resulting from projecting Earth's equatorial plane onto the celestial sphere, dividing the sky into northern and southern hemispheres and intersecting the local horizon at the east and west points for observers at any latitude. This projection ensures that the celestial equator appears tilted relative to the horizon, with its orientation varying by the observer's position on Earth. Fundamentally, all observers perceive the same infinite celestial sphere encompassing all stars and distant objects, but their local reference frames—such as the zenith and horizon—shift according to latitude, altering the visible portion and angular relations without changing the sphere's intrinsic geometry.^[15]^[5]^[3] In spherical polygons, such as triangles formed by great circle arcs, the sum of interior angles exceeds 180 degrees by an amount known as the spherical excess, which is proportional to the enclosed area and reflects the sphere's positive curvature; this excess, measured in degrees or radians, distinguishes spherical figures from their planar counterparts and underpins area calculations on the celestial sphere. These geometric properties extend briefly to applications like declination circles, which form small circles parallel to the celestial equator for gridding positions.^[12]^[13]

Celestial Coordinate Systems

Equatorial Coordinate System

The equatorial coordinate system is a fundamental framework in spherical astronomy for specifying the positions of celestial objects relative to the celestial sphere, projecting Earth's equatorial plane onto this imaginary sphere centered at the observer. It uses two primary coordinates: right ascension (RA) and declination (Dec), analogous to longitude and latitude on Earth but oriented toward the fixed stars. This system provides a stable, Earth-centered reference that remains consistent across different observation times and locations, making it ideal for cataloging and tracking stars, galaxies, and other distant objects. Right ascension measures the angular distance eastward along the celestial equator from the vernal equinox—the point where the ecliptic intersects the celestial equator in the spring—to the object's hour circle, expressed in hours, minutes, and seconds of time (ranging from 0^h to 24^h, where 24^h equals 360°). Declination, in contrast, quantifies the angular distance north or south of the celestial equator to the object, measured in degrees, arcminutes, and arcseconds (from -90° at the south celestial pole to +90° at the north celestial pole). These coordinates define a unique position for any point on the celestial sphere, with the vernal equinox serving as the zero point for RA due to its alignment with the direction of Earth's orbit around the Sun. The modern equatorial system is formalized under the International Celestial Reference System (ICRS), a quasi-inertial frame defined by extragalactic radio sources for high-precision astrometry, ensuring long-term stability. Its origins trace back to the ancient Greek astronomer Hipparchus, who in his star catalog around 127 BC introduced a similar system using the vernal equinox and celestial equator to plot stellar positions, laying the groundwork for systematic celestial mapping. For stars, RA and Dec values are effectively fixed over human timescales (neglecting minor proper motion), enabling consistent referencing across epochs and facilitating the creation of enduring star catalogs like the Hipparcos Catalogue. However, the system requires periodic adjustments due to the precession of the equinoxes, a slow wobble in Earth's rotational axis caused by gravitational torques from the Sun and Moon, which shifts the vernal equinox position by approximately 50.3 arcseconds per year along the ecliptic. To account for this, coordinates are specified for a standard epoch, with J2000.0 (January 1, 2000, at 12:00 Terrestrial Time) serving as the current international reference epoch for most astronomical catalogs and observations. These epoch corrections ensure that positions remain accurate for epoch-specific applications, such as space mission planning or long-term monitoring.

Horizon Coordinate System

The horizon coordinate system, also known as the alt-azimuth system, is an observer-centered framework used in spherical astronomy to specify the position of celestial objects relative to the local horizon and zenith.^[16] In this system, a celestial body's position is defined by two angular coordinates: altitude, which measures the vertical height above the horizon ranging from -90° at the nadir (directly below the observer) to +90° at the zenith (directly overhead), and azimuth, which measures the horizontal direction along the horizon from true north, ranging from 0° to 360° clockwise.^[17] These coordinates provide a practical way to describe the apparent location of stars, planets, and other objects as seen from a specific point on Earth, changing continuously due to the planet's rotation.^[18] The zenith serves as the reference point at 90° altitude, lying directly above the observer along the local vertical, while the horizon forms the fundamental plane at 0° altitude, dividing the visible sky from the ground.^[19] The local meridian, an imaginary great circle passing through the zenith and nadir, intersects the horizon at the north and south points, with azimuth values of 0° (north) and 180° (south) along this line.^[20] Positions in the horizon system depend on the observer's latitude and longitude, as well as the local sidereal time, making it inherently local and time-variable; for instance, at the equator (latitude 0°), the north and south celestial poles lie on the horizon, rendering no stars circumpolar and allowing the entire celestial sphere to rise and set daily.^[21] This coordinate system has been essential for naked-eye astronomical observations since ancient times, particularly in Babylonian astronomy around 1000 BC, where angular measurements in units like the cubit (equivalent to about 2.5° in the sky) were used to record altitudes and azimuths of celestial events such as planetary positions and lunar crescents.^[22] Babylonian astronomers employed these local measurements to track diurnal motions and predict visibility, laying foundational practices for positional astronomy without telescopic aids.^[23] At higher latitudes, the horizon system highlights phenomena like circumpolar stars, which remain perpetually above the horizon and never set due to their proximity to the celestial pole relative to the observer's latitude; for example, at the North Pole (90°N latitude), Polaris (the North Star) and surrounding stars in Ursa Minor circle the zenith without dipping below the horizon.^[24] These stars trace daily paths parallel to the horizon, always visible and serving as reliable navigational aids in polar regions.^[25] Transformation between the horizon system and the equatorial coordinate system can be achieved via spherical trigonometry, accounting for the observer's location and time.^[18]

Ecliptic and Galactic Systems

The ecliptic coordinate system is a spherical coordinate framework used in astronomy to specify positions on the celestial sphere relative to the ecliptic plane, which is the apparent path of the Sun's annual motion as projected from Earth's orbit around the Sun. This plane intersects the celestial sphere along a great circle known as the ecliptic, inclined at approximately 23.44° to the celestial equator due to Earth's axial tilt. In this system, positions are defined by two angular coordinates: ecliptic longitude (λ), measured eastward along the ecliptic from the vernal equinox (the point where the ecliptic crosses the celestial equator from south to north), and ecliptic latitude (β), measured northward or southward from the ecliptic plane, ranging from -90° to +90°. The vernal equinox serves as the zero point for longitude, aligning with the direction of Earth's orbit at the March equinox, and the system is particularly suited for describing the motions of solar system bodies like planets and the Moon, which cluster near the ecliptic.^[26]^[27] The ecliptic system's origins trace back to ancient astronomy, where it facilitated predictions of planetary positions and eclipses, but its modern formalization aligns with the International Astronomical Union's (IAU) definitions within the International Celestial Reference System (ICRS). Variants include the mean ecliptic (accounting for precession over long timescales) and the true ecliptic (incorporating nutation for short-term effects), enabling precise transformations to other systems like equatorial coordinates via rotation matrices. In spherical astronomy, this system is essential for analyzing orbital dynamics and heliocentric phenomena, as it naturally aligns with the geometry of Earth's revolution, reducing computational complexity in ephemeris calculations compared to equatorial or horizon-based frames. For instance, the positions of the zodiac constellations are traditionally referenced to the ecliptic, highlighting its role in historical and observational practices.^[28]^[3] The galactic coordinate system, in contrast, orients the celestial sphere with respect to the plane of the Milky Way galaxy, providing a framework for studying galactic structure and stellar distributions beyond the solar system. Defined by the IAU in 1958 and refined in subsequent resolutions, it uses galactic longitude (l), measured eastward from the galactic center along the galactic equator (the great circle where the galactic plane intersects the celestial sphere), and galactic latitude (b), the angular distance north or south of this plane, both in degrees. The zero point for longitude is the direction toward the galactic center in Sagittarius, at approximately right ascension 17h45m and declination -29° in equatorial coordinates (J2000.0 epoch), while the north galactic pole is positioned at declination +27.13° and right ascension 12h51.4m. This system was established using radio observations of neutral hydrogen (HI) emissions to define the galactic plane accurately, marking a shift from earlier ad hoc definitions based on visible star counts.^[29]^[30] In spherical astronomy, the galactic system excels for mapping extragalactic objects and analyzing the Milky Way's rotation and spiral arms, as it minimizes distortions from the solar system's position within the galaxy. The IAU's 1958 definition tied it to the B1950.0 equatorial epoch using the FK4 catalog, but updates in 1984 and alignments with the J2000.0 FK5 system, and later the ICRS, ensure compatibility with modern astrometry from missions like Gaia. Key parameters include a position angle of 123° between the galactic and equatorial planes, facilitating coordinate transformations essential for multi-wavelength surveys. This system's adoption revolutionized galactic dynamics studies, enabling quantitative models of the galaxy's mass distribution and kinematics without the biases of solar-centric views.^[31]^[29]

Time Measurement and Celestial Motion

Sidereal and Solar Time

In spherical astronomy, time measurement relies on the apparent motion of celestial bodies against the background of the celestial sphere, with sidereal and solar time serving as fundamental scales for tracking positions in coordinate systems. Sidereal time measures intervals relative to the fixed stars, reflecting Earth's rotation period with respect to the distant stellar background and the vernal equinox. One sidereal day, the time for Earth to complete one rotation relative to the vernal equinox, lasts 23 hours, 56 minutes, and 4.091 seconds of mean solar time.^[32] This shorter duration compared to the solar day arises because Earth's orbital motion around the Sun causes the stars to appear to advance eastward by about 1 degree each day, requiring an additional 4 minutes of rotation to realign the vernal equinox with the local meridian.^[10] Solar time, in contrast, is based on the Sun's apparent position, aligning with daily human experience and civil calendars. The mean solar day averages 24 hours, accounting for Earth's orbital motion that lengthens the interval between successive solar noons by approximately 4 minutes relative to the sidereal period. Apparent solar time tracks the true Sun's position, which varies due to Earth's elliptical orbit and axial tilt, while mean solar time uses a fictional "mean Sun" moving uniformly along the celestial equator to provide consistent 24-hour days. The difference between apparent and mean solar time, known as the equation of time, reaches up to 16 minutes throughout the year, requiring corrections for precise astronomical or navigational use.^[33]^[34] Local sidereal time (LST) at an observer's location is defined as the hour angle of the vernal equinox, equivalent to the right ascension of celestial objects currently crossing the local meridian. LST enables astronomers to determine which stars or objects are at zenith or culminate at a given moment, serving as the temporal framework for equatorial coordinates by linking right ascension directly to the observer's sky. For instance, if LST equals 12 hours, objects with right ascension of 12 hours lie on the meridian.^[35]^[36] The distinction between sidereal and solar scales extends to longer periods, rooted in Earth's orbital dynamics. A sidereal year, the time for Earth to orbit the Sun relative to the fixed stars, spans 365.256 days, while the tropical year—marking the interval between vernal equinoxes and driving seasonal cycles—is shorter at 365.242 days due to the precession of Earth's axis, which shifts the equinox westward by about 50 arcseconds annually.^[37] This orbital progression underlies the daily discrepancy in time scales and ensures that sidereal time advances by roughly 4 minutes per solar day, facilitating the tracking of diurnal motion across the celestial sphere. Historically, the standardization of Greenwich Mean Sidereal Time (GMST) in the 19th century supported coordinated observations at major observatories, as the Royal Observatory at Greenwich began distributing precise sidereal time signals via telegraph to align telescopes and ephemerides worldwide. This development coincided with the broader adoption of uniform time standards for astronomy and navigation, enhancing accuracy in positional measurements.^[38]

Diurnal Motion of Celestial Bodies

The diurnal motion of celestial bodies refers to the apparent daily rotation of the stars and other objects across the sky, resulting from Earth's rotation on its axis at an angular speed of approximately 15° per hour.^[39] This rotation causes all celestial objects to appear to rise in the east and set in the west, following paths parallel to the celestial equator.^[40] The uniformity of this angular speed means that every star and solar system body seems to traverse the sky at the same rate, regardless of its distance from Earth, though the actual trajectory of each path depends on the observer's latitude and the object's position.^[41] Stars trace circular paths known as diurnal circles, centered on the celestial poles, with the size and inclination of these circles determined by the star's declination—the angular distance north or south of the celestial equator. Objects on the celestial equator follow great circles that rise due east and set due west, while those with higher declinations describe smaller, more tilted arcs; stars near the poles, such as Polaris in the northern hemisphere, trace tight circles around the north celestial pole without rising or setting for observers at mid-latitudes.^[42] At the equator, these paths are perpendicular to the horizon, becoming increasingly parallel to it as latitude increases, and appearing vertical at the poles where the celestial equator aligns with the horizon.^[40] While fixed stars exhibit pure diurnal motion, the Sun, Moon, and planets display a superimposed eastward drift relative to the stellar background due to their orbital motions around the Sun or Earth. The Sun advances about 1° per day along the ecliptic, completing a full circuit against the stars in one year, whereas the Moon shifts roughly 13° eastward daily and planets vary in their rates, occasionally showing retrograde (westward) motion during opposition.^[43]^[44] This differential motion is coordinated with sidereal time measurements to predict precise positions.^[45] Observers can visualize diurnal motion through long-exposure photography, where stars produce characteristic trails—concentric arcs around the celestial poles—revealing the rotational paths over hours or nights.^[46]

Positional Astronomy Phenomena

Rising, Setting, and Twilight

In spherical astronomy, the rising and setting of celestial bodies occur when their apparent altitude reaches 0° relative to the observer's horizon, marking the transition between visibility and invisibility due to Earth's rotation. These events depend on the observer's latitude, the body's declination on the celestial sphere, and the local sidereal time (LST), which determines the body's position along its diurnal path. For instance, at the equinoxes, when the Sun's declination is 0°, it rises due east and sets due west regardless of latitude, as the celestial equator aligns with the horizon's east-west line.^[24]^[3] Atmospheric refraction complicates these observations by bending light rays from celestial bodies toward the observer, making objects near the horizon appear higher than their true geometric position—typically by about 0.5° (or 30 arcminutes) at the horizon itself. This effect raises the apparent altitude, causing bodies to become visible slightly earlier at rising and remain visible longer at setting; for the Sun, it advances sunrise and delays sunset by approximately 2 minutes compared to a refraction-free calculation.^[47]^[48] Twilight refers to the transitional periods of partial illumination following sunset or preceding sunrise, defined by the Sun's geometric position below the horizon in the horizon coordinate system. Civil twilight spans from when the Sun's center is 0° to 6° below the horizon, providing enough light for ordinary outdoor activities without artificial illumination. Nautical twilight extends from 6° to 12° below the horizon, allowing identification of the horizon for navigation while brighter stars become visible. Astronomical twilight covers 12° to 18° below the horizon, during which the sky transitions to full darkness suitable for most astronomical observations, as the Sun's influence on scattered light diminishes significantly. These definitions, standardized for computational purposes, account for refraction and are used globally by observatories.^[49]^[50] At high latitudes, rising and setting phenomena exhibit extremes due to the inclination of Earth's axis. Above the Arctic Circle (approximately 66.5°N), the midnight sun occurs during summer solstice periods, where the Sun remains continuously above the horizon for 24 hours or more, never setting; conversely, polar night brings continuous darkness in winter. These polar day and night cycles arise because the celestial pole's elevation exceeds 23.5° (Earth's axial tilt), preventing the Sun from crossing the horizon.^[51]^[52] Historically, observations of solar rising and setting positions served as key markers for ancient calendars, enabling the tracking of seasonal changes. For example, ancient inhabitants of the Basin of Mexico aligned structures to monitor sunrise azimuths against the eastern horizon, achieving an accurate 365-day solar calendar that synchronized agricultural cycles with solstices and equinoxes. Similarly, Egyptian astronomers noted the annual shifts in the Sun's rising point along the horizon to define their civil year and predict Nile floods.^[53]^[54]

Culminations and Transits

In spherical astronomy, culmination refers to the passage of a celestial body across an observer's local meridian, the great circle passing through the zenith and the north and south points on the horizon.^[55] This event occurs twice daily for most bodies due to Earth's rotation, marking the moments of maximum and minimum altitude relative to the horizon. Transit specifically denotes the instant when the body's center crosses the meridian, distinguishing it from the broader culmination which encompasses the positional peak.^[56] Upper culmination happens when the body crosses the meridian above the celestial pole, achieving its highest altitude and optimal visibility for observation.^[57] Conversely, lower culmination occurs below the pole, at the lowest altitude, often near the northern horizon for northern observers. The altitude

h

at upper culmination for a body with declination

\delta

observed at latitude

\phi

is given by

h = 90^\circ - \phi + \delta,

assuming the upper limb; this relation arises from the geometry of the celestial equator and meridian.^[58] Transits serve critical applications in timekeeping and positioning. The timing of a star's meridian transit equals its right ascension in sidereal time, enabling precise synchronization of clocks at observatories by comparing observed transits to ephemerides.^[59] Historically, such observations defined local mean time, with upper transits of the mean Sun marking noon along the prime meridian. In modern observatories, meridian transits facilitate accurate telescope alignment and astrometric measurements. The lunar distance method, prominent from the 18th century, leveraged the Moon's rapid motion relative to stars during transits to determine longitude without chronometers, as refined by Nevil Maskelyne and tested during the 1761 transit of Venus expedition.^[60] A seminal historical application of culmination appears in Eratosthenes' circa 240 BCE measurement of Earth's circumference. At noon— the Sun's upper culmination— on the summer solstice, no shadow fell in a well at Syene (modern Aswan), indicating the Sun's zenith position, while in Alexandria, about 800 kilometers north, a vertical gnomon cast a shadow at an angle of approximately 7.2 degrees. Assuming parallel solar rays, Eratosthenes equated this angle to the central arc between the sites, yielding an Earth circumference of roughly 39,375 kilometers (using Egyptian stadia), remarkably close to the modern value of 40,075 kilometers.^[61] The prediction of culminations relies on local sidereal time, where a body's hour angle reaches zero at meridian crossing, allowing schedules for observations.^[35]

Historical Development

Ancient Positional Astronomy

Ancient positional astronomy emerged in Mesopotamia around 2000 BC, where Babylonian astronomers conducted systematic observations from elevated temple platforms known as ziggurats to track celestial bodies and predict planetary motions.^[62] These efforts relied on a sexagesimal (base-60) system for measuring angles, which divided the circle into 360 degrees and remains foundational to modern right ascension and declination coordinates.^[63]^[64] In ancient Greece, Hipparchus advanced these practices around 130 BC by compiling the first comprehensive star catalog, documenting approximately 850 stars with their positions and brightnesses relative to the ecliptic.^[65] He also discovered the precession of the equinoxes, estimating its rate at about 1° per century through comparisons of ancient and contemporary observations.^[65] Building on this, Ptolemy's Almagest (circa 150 AD) synthesized a geocentric model incorporating analogs to latitude and longitude for stellar and planetary positions, using ecliptic coordinates to describe celestial motions with mathematical precision.^[66] These Greek developments profoundly influenced later equatorial and ecliptic coordinate systems. Meanwhile, in China, Zhang Heng constructed a water-powered armillary sphere in 125 AD, a mechanical model of the celestial sphere that facilitated precise measurements of star positions and planetary paths by simulating equatorial and ecliptic rings.^[67] In India, Aryabhata's Aryabhatiya (499 AD) introduced models for planetary motion along the ecliptic, calculating positions using sine-based approximations and recognizing Earth's rotation as contributing to apparent celestial movement.^[68] Early methods for determining positions included the gnomon, a vertical rod whose shadow length varied with solar altitude to measure latitude and seasonal changes, employed across Egyptian, Babylonian, and Chinese traditions.^[69] For nocturnal observations, the Egyptian merkhet—a plumb-line device aligned with circumpolar stars—enabled accurate timing of stellar transits across the meridian, achieving alignments within a degree.^[70]^[71]

Prehistoric and Ancient Observational Structures

Prehistoric and ancient observational structures represent some of the earliest known human-built sites intentionally aligned with celestial events, primarily to track solstices, equinoxes, and lunar cycles for calendrical and agricultural purposes. These megalithic monuments, constructed from large stones or earthworks, demonstrate an empirical understanding of spherical astronomy through precise orientations toward horizon points of rising and setting celestial bodies. Alignments in such sites often achieved accuracies within 1° of true astronomical positions, reflecting sophisticated observational techniques without written records.^[72] One of the oldest examples is the Nabta Playa stone circle in southern Egypt, dating to approximately 4800 BC during the Neolithic period. This site features a linear arrangement of megaliths aligned with the summer solstice sunrise and a cattle-burial complex oriented toward cardinal directions, suggesting its use in marking seasonal monsoons critical for pastoral nomadism and early agriculture. Excavations revealed over 30 stone structures, including a "calendar circle" with stones positioned to track solstices, predating other known astronomical sites by millennia.^[73] In Europe, the Goseck circle in Germany, constructed around 4900 BC, consists of concentric ditches and palisades forming a henge-like enclosure with gates aligned to the winter solstice sunrise and sunset. This Neolithic structure, one of the earliest solar observatories, allowed observers to note the sun's position through narrow openings, likely for ritual and seasonal timing in farming communities. The site's design emphasizes the shortest day of the year, with arcs separated by 97.5° to capture solstitial extremes.^[74] Stonehenge in England, built in phases from about 3000 BC, exemplifies British megalithic astronomy with its central Heel Stone aligned to the summer solstice sunrise, visible from the monument's axis. The surrounding Aubrey Holes, a ring of 56 chalk pits from an earlier phase around 3100 BC, may have held timber posts used to sight lunar risings and settings, tracking the 18.6-year lunar standstill cycle essential for long-term calendars. These features supported agricultural planning by predicting seasonal changes.^[75]^[76] Later examples include the Mayan pyramid of El Castillo at Chichen Itza in Mexico, completed around 900 AD, where the structure's balustrades create a shadow illusion of a descending serpent during the spring and autumn equinoxes. This equinox alignment, combined with the pyramid's orientation to solar and Venus cycles, served ceremonial and calendrical functions in a society reliant on maize agriculture. The precision of the shadow effect highlights advanced horizon-based observations.^[77] Interpretations of these structures fall within archaeoastronomy, a field that examines potential celestial intents through alignments and statistics, though debates persist over intentionality versus coincidence. Alexander Thom's 1960s hypothesis of a standardized "megalithic yard" unit (approximately 0.829 meters) used in site geometries, including lunar alignments at sites like Stonehenge, suggested a unified prehistoric measuring system but has faced criticism for statistical biases in data selection. Despite controversies, such structures underscore early applications of positional astronomy for societal needs.^[78]

Mathematical Foundations

Spherical Trigonometry Principles

Spherical triangles are formed by the intersections of three great circles on the surface of a sphere, where the sides of the triangle correspond to arcs of these great circles and are measured in angular units up to 180°.^[79] Unlike planar triangles, the sum of the interior angles in a spherical triangle exceeds 180°, reflecting the curvature of the sphere.^[79] These triangles provide the foundational framework for computations involving positions and paths on the celestial sphere, such as determining angular distances between celestial bodies. The core identities of spherical trigonometry include the spherical law of cosines for sides and angles. For a spherical triangle with sides

a

b

c

(in angular measure) and opposite angles

A

B

C

, the cosine rule for sides is given by

\cos c = \cos a \cos b + \sin a \sin b \cos C

while the rule for angles is

\cos C = -\cos A \cos B + \sin A \sin B \cos c.

^[79] These formulas, derived from the geometry of the sphere, enable the solution of triangles when sufficient elements are known, analogous to planar trigonometry but accounting for spherical excess.^[80] A key application in positional computations is the pole formula, which relates equatorial coordinates to horizontal ones in the astronomical triangle. Specifically, the declination

\delta

of a celestial body can be found from the observer's latitude

\phi

, the altitude

h

, and the azimuth

A

using

\sin \delta = \sin \phi \sin h + \cos \phi \cos h \cos A.

^[81] This identity stems directly from applying the spherical law of cosines to the triangle formed by the celestial pole, zenith, and the body's position. Girard's theorem quantifies the geometric consequence of sphericity by linking the area of a spherical triangle to its angular excess. For a sphere of radius

R

, the area

K

K = R^2 (A + B + C - \pi)

, where angles are in radians; on the unit sphere (

R = 1

), the area equals the excess in steradians.^[79] This result highlights how spherical triangles enclose finite areas proportional to their angular deviation from planarity. The principles of spherical trigonometry were first systematically developed by Menelaus of Alexandria in his treatise Sphaerica around 100 CE, where he established theorems for spherical triangles including analogs to Euclidean propositions.^[82] In the 15th century, Regiomontanus (Johann Müller) advanced the field by reorganizing and systematizing both planar and spherical trigonometry in works like De triangulis omnimodis, making it more accessible for astronomical applications.^[83]

Position and Distance Calculations

In spherical astronomy, coordinate conversions between the equatorial and horizon systems are essential for determining the observable position of celestial bodies from a specific location on Earth. The local hour angle

H

, defined as the difference between the local sidereal time and the right ascension

\alpha

of the body (converted to degrees by multiplying hours by 15), serves as a key parameter in these transformations. The altitude

a

above the horizon is computed using the formula

\sin a = \sin \delta \sin \phi + \cos \delta \cos \phi \cos H,

where

\delta

is the declination and

\phi

is the observer's latitude; this equation derives from the spherical law of cosines applied to the astronomical triangle formed by the zenith, north celestial pole, and the body.^[84] A practical example of such conversions involves finding the azimuth

A

(the horizontal angle from north) when the altitude and declination are known. Using the same astronomical triangle, the azimuth is given by

\cos A = \frac{\sin \delta - \sin \phi \sin a}{\cos \phi \cos a},

with the quadrant determined by the sign of

\sin A = -\frac{\cos \delta \sin H}{\cos a}

; this allows observers to align telescopes or compute bearings without direct measurement of

H

.^[84] The angular distance

d

between two celestial points, such as stars with coordinates

(\alpha_1, \delta_1)

and

(\alpha_2, \delta_2)

, is calculated via the spherical law of cosines for sides:

\cos d = \sin \delta_1 \sin \delta_2 + \cos \delta_1 \cos \delta_2 \cos(\alpha_1 - \alpha_2),

yielding the great-circle separation on the celestial sphere, which is crucial for identifying close pairs or resolving ambiguities in astrometry.^[85] Corrections for stellar positions include annual parallax, arising from Earth's orbital motion, which shifts nearby stars by up to about 1 arcsecond against background stars at the parsec distance (where parallax

\pi = 1''

); for instance, Proxima Centauri's parallax is approximately 0.768 arcseconds (as of 2023).^[86]^[87] Proper motion, the apparent annual shift due to transverse velocity, is measured in milliarcseconds per year but reaches 10.35''/year for Barnard's Star, the fastest known, requiring adjustments in long-term catalogs.^[88] For navigation and broader positional computations on the sphere, the great-circle distance employs the haversine formula for numerical stability, especially over short arcs:

d = 2R \arcsin\left(\sqrt{\sin^2\left(\frac{\Delta\delta}{2}\right) + \cos\delta_1 \cos\delta_2 \sin^2\left(\frac{\Delta\alpha}{2}\right)}\right),

d=2Rarcsin(sin2(2Δδ)+cosδ1cosδ2sin2(2Δα)

), where $R$ is the sphere's radius (Earth's mean radius of 6371 km for terrestrial applications) and $\Delta\delta, \Delta\alpha$ are differences in declination and right ascension; this variant minimizes errors in iterative solutions compared to direct cosine inversions.^[89]

Modern Applications

Spherical astronomy underpins celestial navigation, a technique that uses observations of celestial bodies to determine position on Earth's surface. Navigators employ instruments like the sextant to measure the altitude of stars or other objects above the horizon, enabling latitude calculation. For instance, the altitude of Polaris directly corresponds to the observer's latitude in the Northern Hemisphere, as the star's position near the celestial north pole makes its elevation angle equal to the geographic latitude. Longitude determination historically relied on comparing local time of a celestial event, such as a star's transit across the meridian, with Greenwich Mean Time obtained from a precise marine chronometer, allowing computation of the east-west position via the Earth's rotation.^[90]^[91]^[92]^[93] Celestial navigation reached its zenith in the 19th century for maritime exploration but declined sharply with the advent of GPS in the late 20th century. Nonetheless, it remains a critical backup method in aviation and military operations, where GPS vulnerabilities like jamming pose risks. With clear skies and skilled observation, modern celestial fixes achieve positional accuracy better than 1 nautical mile, sufficient for safe navigation in emergencies. A notable historical application occurred during Captain James Cook's 1769 expedition to observe the transit of Venus from Tahiti, where chronometer-based timing of the event helped establish the site's longitude with unprecedented precision for the era, aiding broader Pacific mapping efforts.^[94]^[95]^[96]^[97] In astrometry, spherical astronomy facilitates precise measurement of stellar positions, distances, and motions using telescopic observations projected onto the celestial sphere. Ground-based telescopes long served this purpose, but space missions have revolutionized accuracy by avoiding atmospheric distortion. The European Space Agency's Hipparcos satellite, operational from 1989 to 1993, cataloged positions, parallaxes, and proper motions for 117,955 stars with a precision of about 0.001 arcseconds for brighter objects, marking a 200-fold improvement over prior ground-based efforts.^[98]^[99] The successor Gaia mission, launched in 2013, with science operations concluding in January 2025, extends this to billions of stars, producing the most comprehensive stellar catalog to date. By 2022's Data Release 3, Gaia had measured positions and proper motions for nearly 1.8 billion stars with microarcsecond (about 10^{-6} arcseconds) precision, enabling detailed mapping of the Milky Way's structure, dynamics, and evolution through parallax-derived distances and annual proper motion vectors. These datasets support studies of galactic kinematics, where proper motions reveal stellar velocities relative to the solar system. Following the conclusion of science operations in January 2025, the mission's data processing continues, with Data Release 4 scheduled for 2026, expected to refine astrometric parameters for over 2 billion sources.^[100]^[101]^[102]

Computational Tools in Spherical Astronomy

Computational tools in spherical astronomy encompass a range of software applications and algorithms designed to simulate, visualize, and analyze celestial positions on the spherical sky, enabling precise handling of coordinate transformations and orbital predictions in modern observational workflows. Open-source planetarium software like Stellarium provides realistic 3D renderings of the night sky, incorporating more than 220 million stars from the Gaia DR3 catalog and deep-sky objects to facilitate interactive exploration of spherical coordinates from any Earth location.^[103] Mobile applications such as SkySafari extend this capability to handheld devices, offering telescope control and space simulation features with extensive databases of solar system objects for on-the-go astrometric planning.^[104] For professional image analysis, tools like SAOImage DS9 support visualization of astronomical data in FITS format, allowing users to overlay spherical grids and perform region-based measurements critical for astrometric calibration.^[105] Algorithms for handling dynamic aspects of the celestial sphere rely on numerical methods to account for Earth's motion, such as precession and nutation, which alter apparent positions over time. The IAU 2000A model employs series expansions and numerical integration to compute these effects with microarcsecond precision, forming the basis for transforming coordinates between reference frames.^[106] Ephemeris systems like JPL Horizons generate high-accuracy positional data for solar system bodies by integrating orbital equations, providing spherical coordinates (right ascension and declination) tailored to specific observers or epochs.^[107] Virtual reality tools such as Celestia enable immersive 3D navigation of the celestial sphere, rendering stars, planets, and galaxies to visualize spherical geometry and relative positions in real time.^[108] Artificial intelligence now enhances anomaly detection in astrometric datasets, as demonstrated in analyses of Gaia mission data where deep learning identifies outliers in positional measurements with over 99% accuracy, aiding the discovery of unusual celestial motions.^[109] In large-scale surveys like the Legacy Survey of Space and Time (LSST) at the Vera C. Rubin Observatory, which achieved first light in June 2025 and began full operations later that year, machine learning techniques improve data processing by modeling observational uncertainties, thereby reducing systematic errors in photometric and astrometric reductions to enhance overall survey precision.^[110]^[111] Integration of these tools is facilitated through APIs and libraries that support real-time coordinate conversions essential for spherical astronomy applications. For instance, the PyEphem Python library computes high-precision positions of celestial bodies, including transformations between equatorial, ecliptic, and horizon systems, making it a staple for scripting automated analyses.

History

Media collections

Spherical astronomy

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Spherical astronomy

Positional phenomena

Ancient structures associated with positional astronomy include

See also

References

External links