Recent from talks
Nothing was collected or created yet.
Affine transformation
View on Wikipedia
In Euclidean geometry, an affine transformation or affinity (from the Latin, affinis, "connected with") is a geometric transformation that preserves lines and parallelism, but not necessarily Euclidean distances and angles.
More generally, an affine transformation is an automorphism of an affine space (Euclidean spaces are specific affine spaces), that is, a function which maps an affine space onto itself while preserving both the dimension of any affine subspaces (meaning that it sends points to points, lines to lines, planes to planes, and so on) and the ratios of the lengths of parallel line segments. Consequently, sets of parallel affine subspaces remain parallel after an affine transformation. An affine transformation does not necessarily preserve angles between lines or distances between points, though it does preserve ratios of distances between points lying on a straight line.
If X is the point set of an affine space, then every affine transformation on X can be represented as the composition of a linear transformation on X and a translation of X. Unlike a purely linear transformation, an affine transformation need not preserve the origin of the affine space. Thus, every linear transformation is affine, but not every affine transformation is linear.
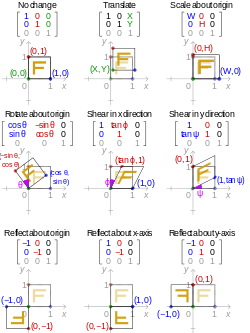
Examples of affine transformations include translation, scaling, homothety, similarity, reflection, rotation, hyperbolic rotation, shear mapping, and compositions of them in any combination and sequence.
Viewing an affine space as the complement of a hyperplane at infinity of a projective space, the affine transformations are the projective transformations of that projective space that leave the hyperplane at infinity invariant, restricted to the complement of that hyperplane.
A generalization of an affine transformation is an affine map[1] (or affine homomorphism or affine mapping) between two (potentially different) affine spaces over the same field k. Let (X, V, k) and (Z, W, k) be two affine spaces with X and Z the point sets and V and W the respective associated vector spaces over the field k. A map f : X → Z is an affine map if there exists a linear map mf : V → W such that mf (x − y) = f (x) − f (y) for all x, y in X.[2]
Definition
[edit]Let X be an affine space over a field k, and V be its associated vector space. An affine transformation is a bijection f from X onto itself that is an affine map; this means that a linear map g from V to V is well defined by the equation here, as usual, the subtraction of two points denotes the free vector from the second point to the first one, and "well-defined" means that implies that
If the dimension of X is at least two, a semiaffine transformation f of X is a bijection from X onto itself satisfying:[3]
- For every d-dimensional affine subspace S of X, then f (S) is also a d-dimensional affine subspace of X.
- If S and T are parallel affine subspaces of X, then f (S) and f (T) are parallel.
These two conditions are satisfied by affine transformations, and express what is precisely meant by the expression that "f preserves parallelism".
These conditions are not independent as the second follows from the first.[4] Furthermore, if the field k has at least three elements, the first condition can be simplified to: f is a collineation, that is, it maps lines to lines.[5]
Structure
[edit]By the definition of an affine space, V acts on X, so that, for every pair in X × V there is associated a point y in X. We can denote this action by . Here we use the convention that are two interchangeable notations for an element of V. By fixing a point c in X one can define a function mc : X → V by mc(x) = cx→. For any c, this function is one-to-one, and so, has an inverse function mc−1 : V → X given by . These functions can be used to turn X into a vector space (with respect to the point c) by defining:[6]
- and
This vector space has origin c and formally needs to be distinguished from the affine space X, but common practice is to denote it by the same symbol and mention that it is a vector space after an origin has been specified. This identification permits points to be viewed as vectors and vice versa.
For any linear transformation λ of V, we can define the function L(c, λ) : X → X by
Then L(c, λ) is an affine transformation of X which leaves the point c fixed.[7] It is a linear transformation of X, viewed as a vector space with origin c.
Let σ be any affine transformation of X. Pick a point c in X and consider the translation of X by the vector , denoted by Tw. Translations are affine transformations and the composition of affine transformations is an affine transformation. For this choice of c, there exists a unique linear transformation λ of V such that[8] That is, an arbitrary affine transformation of X is the composition of a linear transformation of X (viewed as a vector space) and a translation of X.
This representation of affine transformations is often taken as the definition of an affine transformation (with the choice of origin being implicit).[9][10][11]
Representation
[edit]As shown above, an affine map is the composition of two functions: a translation and a linear map. Ordinary vector algebra uses matrix multiplication to represent linear maps, and vector addition to represent translations. Formally, in the finite-dimensional case, if the linear map is represented as a multiplication by an invertible matrix and the translation as the addition of a vector , an affine map acting on a vector can be represented as
Augmented matrix
[edit]Using an augmented matrix and an augmented vector, it is possible to represent both the translation and the linear map using a single matrix multiplication. The technique requires that all vectors be augmented with a "1" at the end, and all matrices be augmented with an extra row of zeros at the bottom, an extra column—the translation vector—to the right, and a "1" in the lower right corner. If is a matrix,
is equivalent to the following
The above-mentioned augmented matrix is called an affine transformation matrix. In the general case, when the last row vector is not restricted to be , the matrix becomes a projective transformation matrix (as it can also be used to perform projective transformations).
This representation exhibits the set of all invertible affine transformations as the semidirect product of and . This is a group under the operation of composition of functions, called the affine group.
Ordinary matrix-vector multiplication always maps the origin to the origin, and could therefore never represent a translation, in which the origin must necessarily be mapped to some other point. By appending the additional coordinate "1" to every vector, one essentially considers the space to be mapped as a subset of a space with an additional dimension. In that space, the original space occupies the subset in which the additional coordinate is 1. Thus the origin of the original space can be found at . A translation within the original space by means of a linear transformation of the higher-dimensional space is then possible (specifically, a shear transformation). The coordinates in the higher-dimensional space are an example of homogeneous coordinates. If the original space is Euclidean, the higher dimensional space is a real projective space.
The advantage of using homogeneous coordinates is that one can combine any number of affine transformations into one by multiplying the respective matrices. This property is used extensively in computer graphics, computer vision and robotics.
Example augmented matrix
[edit]Suppose you have three points that define a non-degenerate triangle in a plane, or four points that define a non-degenerate tetrahedron in 3-dimensional space, or generally n + 1 points x1, ..., xn+1 that define a non-degenerate simplex in n-dimensional space. Suppose you have corresponding destination points y1, ..., yn+1, where these new points can lie in a space with any number of dimensions. (Furthermore, the new points need not form a non-degenerate simplex, nor even be distinct from each other.) The unique augmented matrix M that achieves the affine transformation for every i is
Properties
[edit]
Properties preserved
[edit]An affine transformation preserves:
- collinearity between points: three or more points which lie on the same line (called collinear points) continue to be collinear after the transformation.
- parallelism: two or more lines which are parallel, continue to be parallel after the transformation.
- convexity of sets: a convex set continues to be convex after the transformation. Moreover, the extreme points of the original set are mapped to the extreme points of the transformed set.[12]
- ratios of lengths of parallel line segments: for distinct parallel segments defined by points and , and , the ratio of and is the same as that of and .
- barycenters of weighted collections of points.
Groups
[edit]As an affine transformation is invertible, the square matrix appearing in its matrix representation is invertible. The matrix representation of the inverse transformation is thus
The invertible affine transformations (of an affine space onto itself) form the affine group, which has the general linear group of degree as subgroup and is itself a subgroup of the general linear group of degree .
The similarity transformations form the subgroup where is a scalar times an orthogonal matrix. For example, if the affine transformation acts on the plane and if the determinant of is 1 or −1 then the transformation is an equiareal mapping. Such transformations form a subgroup called the equi-affine group.[13] A transformation that is both equi-affine and a similarity is an isometry of the plane taken with Euclidean distance.
Each of these groups has a subgroup of orientation-preserving or positive affine transformations: those where the determinant of is positive. In the last case this is in 3D the group of rigid transformations (proper rotations and pure translations).
If there is a fixed point, we can take that as the origin, and the affine transformation reduces to a linear transformation. This may make it easier to classify and understand the transformation. For example, describing a transformation as a rotation by a certain angle with respect to a certain axis may give a clearer idea of the overall behavior of the transformation than describing it as a combination of a translation and a rotation. However, this depends on application and context.
Affine maps
[edit]An affine map between two affine spaces is a map on the points that acts linearly on the vectors (that is, the vectors between points of the space). In symbols, determines a linear transformation such that, for any pair of points :
or
We can interpret this definition in a few other ways, as follows.
If an origin is chosen, and denotes its image , then this means that for any vector :
If an origin is also chosen, this can be decomposed as an affine transformation that sends , namely
followed by the translation by a vector .
The conclusion is that, intuitively, consists of a translation and a linear map.
Alternative definition
[edit]Given two affine spaces and , over the same field, a function is an affine map if and only if for every family of weighted points in such that we have[14] In other words, preserves barycenters.
Example
[edit]Let be the three-dimensional Euclidean space, a plane, and both be equipped with a Cartesian coordinate system. If is a parallel projection or, more generally, is generated by an axonometry, then is affine and surjective. Hence it can be represented by with a matrix of rank 2 and a column vector In case this is treated in more detail in the section Coordinate calculation at Axonometry.
History
[edit]The word "affine" as a mathematical term is defined in connection with tangents to curves in Euler's 1748 Introductio in analysin infinitorum.[15] Felix Klein attributes the term "affine transformation" to Möbius and Gauss.[10]
Image transformation
[edit]In their applications to digital image processing, the affine transformations are analogous to printing on a sheet of rubber and stretching the sheet's edges parallel to the plane. This transform relocates pixels requiring intensity interpolation to approximate the value of moved pixels, bicubic interpolation is the standard for image transformations in image processing applications. Affine transformations scale, rotate, translate, mirror and shear images as shown in the following examples:[16]
| Transformation name | Affine matrix | Example |
|---|---|---|
| Identity (transform to original image) | 
| |
| Translation | 
| |
| Reflection | 
| |
| Scale | 
| |
| Rotate |  where θ = π/6 =30° | |
| Shear | 
|
The affine transforms are applicable to the registration process where two or more images are aligned (registered). An example of image registration is the generation of panoramic images that are the product of multiple images stitched together.
Affine warping
[edit]The affine transform preserves parallel lines. However, the stretching and shearing transformations warp shapes, as the following example shows:

|

|
This is an example of image warping. However, the affine transformations do not facilitate projection onto a curved surface or radial distortions.
In the plane
[edit]
Every affine transformations in a Euclidean plane is the composition of a translation and an affine transformation that fixes a point; the latter may be
- a homothety,
- rotations around the fixed point,
- a scaling, with possibly negative scaling factors, in two directions (not necessarily perpendicular); this includes reflections,
- a shear mapping
- a squeeze mapping.
Given two non-degenerate triangles ABC and A′B′C′ in a Euclidean plane, there is a unique affine transformation T that maps A to A′, B to B′ and C to C′. Each of ABC and A′B′C′ defines an affine coordinate system and a barycentric coordinate system. Given a point P, the point T(P) is the point that has the same coordinates on the second system as the coordinates of P on the first system.
Affine transformations do not respect lengths or angles; they multiply areas by the constant factor
- area of A′B′C′ / area of ABC.
A given T may either be direct (respect orientation), or indirect (reverse orientation), and this may be determined by comparing the orientations of the triangles.
Examples
[edit]Over the real numbers
[edit]The functions with and in and , are precisely the affine transformations of the real line.
In plane geometry
[edit]
In , the transformation shown at left is accomplished using the map given by:
Transforming the three corner points of the original triangle (in red) gives three new points which form the new triangle (in blue). This transformation skews and translates the original triangle.
In fact, all triangles are related to one another by affine transformations. This is also true for all parallelograms, but not for all quadrilaterals.
See also
[edit]- Anamorphosis – artistic applications of affine transformations
- Affine geometry
- 3D projection
- Homography
- Flat (geometry)
- Bent function
- Multilinear polynomial
Notes
[edit]- ^ Berger 1987, p. 38.
- ^ Samuel 1988, p. 11.
- ^ Snapper & Troyer 1989, p. 65.
- ^ Snapper & Troyer 1989, p. 66.
- ^ Snapper & Troyer 1989, p. 69.
- ^ Snapper & Troyer 1989, p. 59.
- ^ Snapper & Troyer 1989, p. 76,87.
- ^ Snapper & Troyer 1989, p. 86.
- ^ Wan 1993, pp. 19–20.
- ^ a b Klein 1948, p. 70.
- ^ Brannan, Esplen & Gray 1999, p. 53.
- ^ Reinhard Schultz. "Affine transformations and convexity" (PDF). Retrieved 27 February 2017.
- ^ Oswald Veblen (1918) Projective Geometry, volume 2, pp. 105–7.
- ^ Schneider, Philip K.; Eberly, David H. (2003). Geometric Tools for Computer Graphics. Morgan Kaufmann. p. 98. ISBN 978-1-55860-594-7.
- ^ Euler, Leonhard (1748). Introductio in analysin infinitorum (in Latin). Vol. II. Book II, sect. XVIII, art. 442
- ^ Gonzalez, Rafael (2008). 'Digital Image Processing, 3rd'. Pearson Hall. ISBN 9780131687288.
References
[edit]- Berger, Marcel (1987), Geometry I, Berlin: Springer, ISBN 3-540-11658-3
- Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1999), Geometry, Cambridge University Press, ISBN 978-0-521-59787-6
- Nomizu, Katsumi; Sasaki, S. (1994), Affine Differential Geometry (New ed.), Cambridge University Press, ISBN 978-0-521-44177-3
- Klein, Felix (1948) [1939], Elementary Mathematics from an Advanced Standpoint: Geometry, Dover
- Samuel, Pierre (1988), Projective Geometry, Springer-Verlag, ISBN 0-387-96752-4
- Sharpe, R. W. (1997). Differential Geometry: Cartan's Generalization of Klein's Erlangen Program. New York: Springer. ISBN 0-387-94732-9.
- Snapper, Ernst; Troyer, Robert J. (1989) [1971], Metric Affine Geometry, Dover, ISBN 978-0-486-66108-7
- Wan, Zhe-xian (1993), Geometry of Classical Groups over Finite Fields, Chartwell-Bratt, ISBN 0-86238-326-9
External links
[edit] Media related to Affine transformation at Wikimedia Commons
Media related to Affine transformation at Wikimedia Commons- "Affine transformation", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Geometric Operations: Affine Transform, R. Fisher, S. Perkins, A. Walker and E. Wolfart.
- Weisstein, Eric W. "Affine Transformation". MathWorld.
- Affine Transform by Bernard Vuilleumier, Wolfram Demonstrations Project.
- Affine Transformation with MATLAB



















![{\displaystyle {\begin{bmatrix}\mathbf {y} \\1\end{bmatrix}}=\left[{\begin{array}{ccc|c}&A&&\mathbf {b} \\0&\cdots &0&1\end{array}}\right]{\begin{bmatrix}\mathbf {x} \\1\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b09421e40cbc57b25a3c80bec8e9af3de6411bc7)

![{\displaystyle \left[{\begin{array}{ccc|c}0&\cdots &0&1\end{array}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88adf2c935d77058a03eab5193223733d4892449)













![{\displaystyle \left[{\begin{array}{ccc|c}&A^{-1}&&-A^{-1}{\vec {b}}\ \\0&\ldots &0&1\end{array}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5d016fcc241e75cc9da0e54e1e87d397331f0a96)








































