Hubbry Logo
Cross-polytopeCross-polytopeMain
Open search
Cross-polytope
Community hub
Cross-polytope
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Cross-polytope
Cross-polytope
Cross-polytope
View on Wikipedia
from Wikipedia
Cross-polytopes of dimension 2 to 5
A 2-dimensional cross-polytope A 3-dimensional cross-polytope
2 dimensions
square 		3 dimensions
octahedron
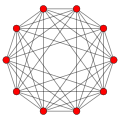
A 4-dimensional cross-polytope A 5-dimensional cross-polytope
4 dimensions
16-cell 		5 dimensions
5-orthoplex

In geometry, a cross-polytope,[1] hyperoctahedron, orthoplex,[2] staurotope,[3] or cocube is a regular, convex polytope that exists in n-dimensional Euclidean space. A 2-dimensional cross-polytope is a square, a 3-dimensional cross-polytope is a regular octahedron, and a 4-dimensional cross-polytope is a 16-cell. Its facets are simplexes of the previous dimension, while the cross-polytope's vertex figure is another cross-polytope from the previous dimension.

The vertices of a cross-polytope can be chosen as the unit vectors pointing along each co-ordinate axis – i.e. all the permutations of (±1, 0, 0, ..., 0). The cross-polytope is the convex hull of its vertices. The n-dimensional cross-polytope can also be defined as the closed unit ball (or, according to some authors, its boundary) in the ℓ1-norm on Rn, those points x = (x1, x2..., xn) satisfying

An n-orthoplex can be constructed as a bipyramid with an (n−1)-orthoplex base.

The cross-polytope is the dual polytope of the hypercube. The vertex-edge graph of an n-dimensional cross-polytope is the Turán graph T(2n, n) (also known as a cocktail party graph [4]).

Low-dimensional examples

[edit]

In 1 dimension the cross-polytope is a line segment, which can be chosen as the interval [−1, +1].

In 2 dimensions the cross-polytope is a square. If the vertices are chosen as {(±1, 0), (0, ±1)}, the square's sides are at right angles to the axes; in this orientation a square is often called a diamond.

In 3 dimensions the cross-polytope is a regular octahedron—one of the five convex regular polyhedra known as the Platonic solids.

The 4-dimensional cross-polytope also goes by the name hexadecachoron or 16-cell. It is one of the six convex regular 4-polytopes. These 4-polytopes were first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century. The vertices of the 4-dimensional hypercube, or tesseract, can be divided into two sets of eight, the convex hull of each set forming a cross-polytope. Moreover, the polytope known as the 24-cell can be constructed by symmetrically arranging three cross-polytopes.[5]

n dimensions

[edit]

The cross-polytope family is one of three regular polytope families, labeled by Coxeter as βn, the other two being the hypercube family, labeled as γn, and the simplex family, labeled as αn. A fourth family, the infinite tessellations of hypercubes, he labeled as δn.[6]

The n-dimensional cross-polytope has 2n vertices, and 2n facets ((n − 1)-dimensional components) all of which are (n − 1)-simplices. The vertex figures are all (n − 1)-cross-polytopes. The Schläfli symbol of the cross-polytope is {3,3,...,3,4}.

The dihedral angle of the n-dimensional cross-polytope is . This gives: δ2 = arccos(0/2) = 90°, δ3 = arccos(−1/3) = 109.47°, δ4 = arccos(−2/4) = 120°, δ5 = arccos(−3/5) = 126.87°, ... δ∞ = arccos(−1) = 180°.

The hypervolume of the n-dimensional cross-polytope is

For each pair of non-opposite vertices, there is an edge joining them. More generally, each set of k + 1 orthogonal vertices corresponds to a distinct k-dimensional component which contains them. The number of k-dimensional components (vertices, edges, faces, ..., facets) in an n-dimensional cross-polytope is thus given by (see binomial coefficient):

[7]

The extended f-vector for an n-orthoplex can be computed by (1,2)n, like the coefficients of polynomial products. For example a 16-cell is (1,2)4 = (1,4,4)2 = (1,8,24,32,16).

There are many possible orthographic projections that can show the cross-polytopes as 2-dimensional graphs. Petrie polygon projections map the points into a regular 2n-gon or lower order regular polygons. A second projection takes the 2(n−1)-gon petrie polygon of the lower dimension, seen as a bipyramid, projected down the axis, with 2 vertices mapped into the center.

Cross-polytope elements
n βn
k11 		Name(s)
Graph 		Graph
2n-gon 		Schläfli Coxeter-Dynkin
diagrams 		Vertices Edges Faces Cells 4-faces 5-faces 6-faces
0 β0 Point
0-orthoplex 		. ( )
1            
1 β1 Line segment
1-orthoplex 		{ }
2 1          
2 β2
−111 		Square
2-orthoplex
Bicross 		{4}
2{ } = { }+{ }
4 4 1        
3 β3
011 		Octahedron
3-orthoplex
Tricross 		{3,4}
{31,1}
3{ }

6 12 8 1      
4 β4
111 		16-cell
4-orthoplex
Tetracross 		{3,3,4}
{3,31,1}
4{ }

8 24 32 16 1    
5 β5
211 		5-orthoplex
Pentacross 		{33,4}
{3,3,31,1}
5{ }

10 40 80 80 32 1  
6 β6
311 		6-orthoplex
Hexacross 		{34,4}
{33,31,1}
6{ }

12 60 160 240 192 64 1
...
n βn
(n−3)11 		n-orthoplex
n-cross 		{3n − 2,4}
{3n − 3,31,1}
n{} 		...
...
... 		2n 0-faces, ... k-faces ..., 2n (n−1)-faces

The vertices of an axis-aligned cross polytope are all at equal distance from each other in the Manhattan distance (L1 norm). Kusner's conjecture states that this set of 2d points is the largest possible equidistant set for this distance.[8]

Generalized orthoplex

[edit]

Regular complex polytopes can be defined in complex Hilbert space called generalized orthoplexes (or cross polytopes), βp
n = 2{3}2{3}...2{4}p, or ... Real solutions exist with p = 2, i.e. β2
n = βn = 2{3}2{3}...2{4}2 = {3,3,..,4}. For p > 2, they exist in . A p-generalized n-orthoplex has pn vertices. Generalized orthoplexes have regular simplexes (real) as facets.[9] Generalized orthoplexes make complete multipartite graphs, βp
2 make Kp,p for complete bipartite graph, βp
3 make Kp,p,p for complete tripartite graphs βp
n creates Kpn or Turán graphs . An orthogonal projection can be defined that maps all the vertices equally-spaced on a circle, with all pairs of vertices connected, except multiples of n. The regular polygon perimeter in these orthogonal projections is called a petrie polygon.

Generalized orthoplexes
p = 2 p = 3 p = 4 p = 5 p = 6 p = 7 p = 8

2{4}2 = {4} =
K2,2
2{4}3 =
K3,3
2{4}4 =
K4,4
2{4}5 =
K5,5
2{4}6 =
K6,6
2{4}7 =
K7,7
2{4}8 =
K8,8

2{3}2{4}2 = {3,4} =
K2,2,2
2{3}2{4}3 =
K3,3,3
2{3}2{4}4 =
K4,4,4
2{3}2{4}5 =
K5,5,5
2{3}2{4}6 =
K6,6,6
2{3}2{4}7 =
K7,7,7
2{3}2{4}8 =
K8,8,8

2{3}2{3}2
{3,3,4} =
K2,2,2,2
2{3}2{3}2{4}3

K3,3,3,3
2{3}2{3}2{4}4

K4,4,4,4
2{3}2{3}2{4}5

K5,5,5,5
2{3}2{3}2{4}6

K6,6,6,6
2{3}2{3}2{4}7

K7,7,7,7
2{3}2{3}2{4}8

K8,8,8,8

2{3}2{3}2{3}2{4}2
{3,3,3,4} =
K2,2,2,2,2
2{3}2{3}2{3}2{4}3

K3,3,3,3,3
2{3}2{3}2{3}2{4}4

K4,4,4,4,4
2{3}2{3}2{3}2{4}5

K5,5,5,5,5
2{3}2{3}2{3}2{4}6

K6,6,6,6,6
2{3}2{3}2{3}2{4}7

K7,7,7,7,7
2{3}2{3}2{3}2{4}8

K8,8,8,8,8

2{3}2{3}2{3}2{3}2{4}2
{3,3,3,3,4} =
K2,2,2,2,2,2
2{3}2{3}2{3}2{3}2{4}3

K3,3,3,3,3,3
2{3}2{3}2{3}2{3}2{4}4

K4,4,4,4,4,4
2{3}2{3}2{3}2{3}2{4}5

K5,5,5,5,5,5
2{3}2{3}2{3}2{3}2{4}6

K6,6,6,6,6,6
2{3}2{3}2{3}2{3}2{4}7

K7,7,7,7,7,7
2{3}2{3}2{3}2{3}2{4}8

K8,8,8,8,8,8
[edit]

Cross-polytopes can be combined with their dual cubes to form compound polytopes:

  • In two dimensions, we obtain the octagrammic star figure {⁠8/2⁠},
  • In three dimensions we obtain the compound of cube and octahedron,
  • In four dimensions we obtain the compound of tesseract and 16-cell.

See also

[edit]

Citations

[edit]
  1. ^ Coxeter 1973, pp. 121–122, §7.21. illustration Fig 7-2B.
  2. ^ Conway, J. H.; Sloane, N. J. A. (1991). "The Cell Structures of Certain Lattices". In Hilton, P.; Hirzebruch, F.; Remmert, R. (eds.). Miscellanea Mathematica. Berlin: Springer. pp. 89–90. doi:10.1007/978-3-642-76709-8_5. ISBN 978-3-642-76711-1.
  3. ^ McMullen, Peter (2020). Geometric Regular Polytopes. Cambridge University Press. p. 92. ISBN 978-1-108-48958-4.
  4. ^ Weisstein, Eric W. "Cocktail Party Graph". MathWorld.
  5. ^ Bengtsson, Ingemar; Życzkowski, Karol (2017). Geometry of Quantum States: An Introduction to Quantum Entanglement (2nd ed.). Cambridge University Press. p. 162. ISBN 978-1-107-02625-4.
  6. ^ Coxeter 1973, pp. 120–124, §7.2.
  7. ^ Coxeter 1973, p. 121, §7.2.2..
  8. ^ Guy, Richard K. (1983), "An olla-podrida of open problems, often oddly posed", American Mathematical Monthly, 90 (3): 196–200, doi:10.2307/2975549, JSTOR 2975549.
  9. ^ Coxeter, Regular Complex Polytopes, p. 108

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Cross-polytope

View on Grokipedia
from Grokipedia
A cross-polytope, also known as an orthoplex, hyperoctahedron, or cocube, is a regular in n-dimensional defined as the of the 2n points formed by all permutations of the coordinates (±1, 0, ..., 0). It generalizes the to higher dimensions and is one of the three regular convex polytopes that exist in every dimension n ≥ 3 (the others being the n- and the n-). The cross-polytope has 2n vertices, 2n facets (each an (n-1)-simplex), and its skeleton is the complete multipartite graph K2,2,...,2 (n parts), which is isomorphic to the cocktail party graph. Its Schläfli symbol is {3,3,...,3,4} with (n-2) threes, reflecting its regular structure where all edges are equal and faces are equilateral triangles up to the facets. Notably, the cross-polytope is the dual polytope of the n-dimensional hypercube, meaning their vertices correspond to the hypercube's facets and vice versa, and this duality extends to their symmetry groups, both belonging to the hyperoctahedral group of order 2n n!. In low dimensions, the cross-polytope takes familiar forms: in 1D, it is a ; in 2D, a square with vertices at (±1,0) and (0,±1); in 3D, the regular octahedron with 6 vertices and 8 triangular faces; and in 4D, the (or hexadecachoron) with 8 vertices, 32 triangular faces, and 16 tetrahedral cells. The volume of an n-dimensional cross-polytope with edge length s is given by (2n / n!) * (s / √2)n, derived by decomposing it into n! hyperpyramids from the center. These polytopes appear in , optimization (as the unit ball in the ℓ1 norm), and symmetry studies, with applications in and combinatorial designs.

Definition and Construction

Geometric Definition

The nn-dimensional cross-polytope, also known as the orthoplex or hyperoctahedron, is defined as the of the $2npointsconsistingofthe[standardbasis](/page/Standardbasis)vectorspoints consisting of the [standard basis](/page/Standard_basis) vectorse_iandtheirnegativesand their negatives-e_iforfori=1,\dots,ninin\mathbb{R}^n.Thisconstructionplacesallverticesatunitdistancefromtheoriginalongthecoordinateaxes,formingacentrallysymmetricfigurethatisthe. This construction places all vertices at unit distance from the origin along the coordinate axes, forming a centrally symmetric figure that is the L_1$-ball of radius 1. As a , the cross-polytope exhibits the highest degree of among convex polytopes in nn dimensions, with all facets being regular simplices and vertex figures being regular (n−1)(n-1)-dimensional cross-polytopes. Its is {3,3,…,3,4}\{3,3,\dots,3,4\}, consisting of n−2n-2 entries of 3 followed by a 4 (for n≥2n \geq 2). This symbol encodes the recursive structure where each ridge is surrounded by four facets, distinguishing it from other regular polytopes like the or . The name "cross-polytope" derives from the star-like or cross-shaped appearance in low dimensions, where the vertices align along perpendicular axes intersecting at the center, evoking a generalized . It plays a foundational role as the simplest uniform polytope dual to the nn-dimensional , meaning their faces and vertices correspond in a polarity that preserves the regular .

Vertex Coordinates

The vertices of the nn-dimensional cross-polytope are given by the $2npointspoints\pm \mathbf{e}_i \in \mathbb{R}^nforfori = 1, \dots, n,where, where \mathbf{e}_idenotesthedenotes thei-th [standard basis](/page/Standard_basis) vector with a $1 in the ii-th coordinate and $0elsewhere.[](https://mathworld.wolfram.com/CrossPolytope.html)Thesepointshavecoordinatesfeaturingexactlyoneelsewhere.[](https://mathworld.wolfram.com/CrossPolytope.html) These points have coordinates featuring exactly one\pm 1andzerosinallotherpositions,andthecross−polytopeisthe[convexhull](/page/Convexhull)ofthisvertexset.[](https://mathworld.wolfram.com/CrossPolytope.html)Inthisstandardembedding,eachvertexliesatanand zeros in all other positions, and the cross-polytope is the [convex hull](/page/Convex_hull) of this vertex set.[](https://mathworld.wolfram.com/CrossPolytope.html) In this standard embedding, each vertex lies at an\ell_2-distance of $1 from the origin, yielding a circumradius of $1$. An equivalent representation arises as the unit ball under the ℓ1\ell_1-norm: {x∈Rn:∑i=1n∣xi∣≤1}.\{ x \in \mathbb{R}^n : \sum_{i=1}^n |x_i| \leq 1 \}. This formulation confirms the same $2nverticesvertices\pm \mathbf{e}_i$, as these points saturate the norm bound while all other points in the set satisfy it strictly. The facets of the cross-polytope, which are (n−1)(n-1)-dimensional simplices, are defined by the supporting half-spaces ∑i=1nϵixi≤1,\sum_{i=1}^n \epsilon_i x_i \leq 1, where each ϵ=(ϵ1,…,ϵn)\epsilon = (\epsilon_1, \dots, \epsilon_n) is a choice of signs with ϵi∈{±1}\epsilon_i \in \{ \pm 1 \}, producing 2n2^n such inequalities in total. These hyperplanes touch the polytope at its facets, with the normal vectors ϵ\epsilon corresponding to the vertices of the dual hypercube (up to scaling). Alternative scalings of the cross-polytope are common for specific applications, such as normalizing to unit inradius (the distance from the origin to a facet) or unit edge length; for instance, scaling the standard vertex coordinates by 1/n1/\sqrt{n}
Add your contribution
Related Hubs
User Avatar
No comments yet.