Hubbry Logo
Phase (matter)Phase (matter)Main
Open search
Phase (matter)
Community hub
Phase (matter)
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Phase (matter)
Phase (matter)
Phase (matter)
View on Wikipedia
from Wikipedia
Part of a series on
Chemistry
Key components
Branches
Research

In the physical sciences, a phase is a region of material that is chemically uniform, physically distinct, and (often) mechanically separable. In a system consisting of ice and water in a glass jar, the ice cubes are one phase, the water is a second phase, and the humid air is a third phase over the ice and water. The glass of the jar is a different material, in its own separate phase. (See state of matter § Glass.)

More precisely, a phase is a region of space (a thermodynamic system), throughout which all physical properties of a material are essentially uniform.[1][2]: 86 [3]: 3  Examples of physical properties include density, index of refraction, magnetization and chemical composition.

The term phase is sometimes used as a synonym for state of matter, but there can be several immiscible phases of the same state of matter (as where oil and water separate into distinct phases, both in the liquid state).

A small piece of rapidly melting argon ice shows the transition from solid to liquid.

Types of phases

[edit]
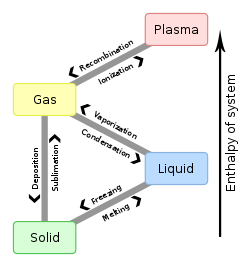
Iron-carbon phase diagram, showing the conditions necessary to form different phases

Distinct phases may be described as different states of matter such as gas, liquid, solid, plasma or Bose–Einstein condensate. Useful mesophases between solid and liquid form other states of matter.

Distinct phases may also exist within a given state of matter. As shown in the diagram for iron alloys, several phases exist for both the solid and liquid states. Phases may also be differentiated based on solubility as in polar (hydrophilic) or non-polar (hydrophobic). A mixture of water (a polar liquid) and oil (a non-polar liquid) will spontaneously separate into two phases. Water has a very low solubility (is insoluble) in oil, and oil has a low solubility in water. Solubility is the maximum amount of a solute that can dissolve in a solvent before the solute ceases to dissolve and remains in a separate phase. A mixture can separate into more than two liquid phases and the concept of phase separation extends to solids, i.e., solids can form solid solutions or crystallize into distinct crystal phases. Metal pairs that are mutually soluble can form alloys, whereas metal pairs that are mutually insoluble cannot.

As many as eight immiscible liquid phases have been observed.[a] Mutually immiscible liquid phases are formed from water (aqueous phase), hydrophobic organic solvents, perfluorocarbons (fluorous phase), silicones, several different metals, and also from molten phosphorus. Not all organic solvents are completely miscible, e.g. a mixture of ethylene glycol and toluene may separate into two distinct organic phases.[b]

Phases do not need to macroscopically separate spontaneously. Emulsions and colloids are examples of immiscible phase pair combinations that do not physically separate.

Phase equilibrium

[edit]

Left to equilibration, many compositions will form a uniform single phase, but depending on the temperature and pressure even a single substance may separate into two or more distinct phases. Within each phase, the properties are uniform but between the two phases properties differ.

Water in a closed jar with an air space over it forms a two-phase system. Most of the water is in the liquid phase, where it is held by the mutual attraction of water molecules. Even at equilibrium molecules are constantly in motion and, once in a while, a molecule in the liquid phase gains enough kinetic energy to break away from the liquid phase and enter the gas phase. Likewise, every once in a while a vapor molecule collides with the liquid surface and condenses into the liquid. At equilibrium, evaporation and condensation processes exactly balance and there is no net change in the volume of either phase.

At room temperature and pressure, the water jar reaches equilibrium when the air over the water has a humidity of about 3%. This percentage increases as the temperature goes up. At 100 °C and atmospheric pressure, equilibrium is not reached until the air is 100% water. If the liquid is heated a little over 100 °C, the transition from liquid to gas will occur not only at the surface but throughout the liquid volume: the water boils.

Number of phases

[edit]
See also: Multiphasic liquid
A typical phase diagram for a single-component material, exhibiting solid, liquid and gaseous phases. The solid green line shows the usual shape of the liquid–solid phase line. The dotted green line shows the anomalous behavior of water when the pressure increases. The triple point and the critical point are shown as red dots.

For a given composition, only certain phases are possible at a given temperature and pressure. The number and type of phases that will form is hard to predict and is usually determined by experiment. The results of such experiments can be plotted in phase diagrams.

The phase diagram shown here is for a single component system. In this simple system, phases that are possible, depend only on pressure and temperature. The markings show points where two or more phases can co-exist in equilibrium. At temperatures and pressures away from the markings, there will be only one phase at equilibrium.

In the diagram, the blue line marking the boundary between liquid and gas does not continue indefinitely, but terminates at a point called the critical point. As the temperature and pressure approach the critical point, the properties of the liquid and gas become progressively more similar. At the critical point, the liquid and gas become indistinguishable. Above the critical point, there are no longer separate liquid and gas phases: there is only a generic fluid phase referred to as a supercritical fluid. In water, the critical point occurs at around 647 K (374 °C or 705 °F) and 22.064 MPa.

An unusual feature of the water phase diagram is that the solid–liquid phase line (illustrated by the dotted green line) has a negative slope. For most substances, the slope is positive as exemplified by the dark green line. This unusual feature of water is related to ice having a lower density than liquid water. Increasing the pressure drives the water into the higher density phase, which causes melting.

Another interesting though not unusual feature of the phase diagram is the point where the solid–liquid phase line meets the liquid–gas phase line. The intersection is referred to as the triple point. At the triple point, all three phases can coexist.

Experimentally, phase lines are relatively easy to map due to the interdependence of temperature and pressure that develops when multiple phases form. Gibbs' phase rule suggests that different phases are completely determined by these variables. Consider a test apparatus consisting of a closed and well-insulated cylinder equipped with a piston. By controlling the temperature and the pressure, the system can be brought to any point on the phase diagram. From a point in the solid stability region (left side of the diagram), increasing the temperature of the system would bring it into the region where a liquid or a gas is the equilibrium phase (depending on the pressure). If the piston is slowly lowered, the system will trace a curve of increasing temperature and pressure within the gas region of the phase diagram. At the point where gas begins to condense to liquid, the direction of the temperature and pressure curve will abruptly change to trace along the phase line until all of the water has condensed.

Interfacial phenomena

[edit]
Further information: Surface science

Between two phases in equilibrium there is a narrow region where the properties are not that of either phase. Although this region may be very thin, it can have significant and easily observable effects, such as causing a liquid to exhibit surface tension. In mixtures, some components may preferentially move toward the interface. In terms of modeling, describing, or understanding the behavior of a particular system, it may be efficacious to treat the interfacial region as a separate phase.

Crystal phases

[edit]

A single material may have several distinct solid states capable of forming separate phases. Water is a well-known example of such a material. For example, water ice is ordinarily found in the hexagonal form ice Ih, but can also exist as the cubic ice Ic, the rhombohedral ice II, and many other forms. Polymorphism is the ability of a solid to exist in more than one crystal form. For pure chemical elements, polymorphism is known as allotropy. For example, diamond, graphite, and fullerenes are different allotropes of carbon.

Phase transitions

[edit]
Main article: Phase transition

When a substance undergoes a phase transition (changes from one state of matter to another) it usually either takes up or releases energy. For example, when water evaporates, the increase in kinetic energy as the evaporating molecules escape the attractive forces of the liquid is reflected in a decrease in temperature. The energy required to induce the phase transition is taken from the internal thermal energy of the water, which cools the liquid to a lower temperature; hence evaporation is useful for cooling. See Enthalpy of vaporization. The reverse process, condensation, releases heat. The heat energy, or enthalpy, associated with a solid to liquid transition is the enthalpy of fusion and that associated with a solid to gas transition is the enthalpy of sublimation.

Phases out of equilibrium

[edit]

While phases of matter are traditionally defined for systems in thermal equilibrium, work on quantum many-body localized (MBL) systems has provided a framework for defining phases out of equilibrium. MBL phases never reach thermal equilibrium, and can allow for new forms of order disallowed in equilibrium via a phenomenon known as localization protected quantum order. The transitions between different MBL phases and between MBL and thermalizing phases are novel dynamical phase transitions whose properties are active areas of research.[citation needed]

Notes

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Phase (matter)

View on Grokipedia
from Grokipedia
In physics and chemistry, a phase of refers to one of the distinct physical forms that substances can take, characterized by the arrangement, motion, and interactions of their constituent particles, which are influenced primarily by and . The most fundamental phases are , , gas, and plasma, with each displaying unique properties such as , , and response to external forces; for instance, maintain a fixed and due to strong intermolecular forces, while gases expand to fill their owing to weak particle interactions. Solids consist of particles arranged in a highly ordered, often crystalline structure, resulting in high (e.g., at 0.9167 g/cm³), rigidity, and near-incompressibility, as the molecules vibrate in fixed positions without significant displacement. Liquids feature particles that are close together but mobile enough to flow and conform to a 's bottom surface, maintaining a definite (e.g., at 0.9997 g/cm³) while being nearly incompressible, with intermolecular forces intermediate between those in solids and gases. Gases, in contrast, have particles that are widely spaced and move independently at high speeds, leading to low (e.g., at 0.0006 g/cm³), high , and the ability to completely fill any . Plasma, often considered the fourth fundamental phase, arises when sufficient —typically from extreme —ionizes a gas, stripping electrons from atoms to create a of positively charged ions, free electrons, and neutral particles, which collectively exhibit collective electrical conductivity and responsiveness to electromagnetic fields; this state is prevalent in natural phenomena like stars, , and the aurora, comprising over 99% of the visible . Matter transitions between phases through processes such as (solid to liquid), (liquid to gas), (gas to plasma), and their reverses, which occur at specific temperatures and pressures defined by phase diagrams and require exchanges like . Beyond these core phases, exotic states exist under extreme conditions, including Bose-Einstein condensates at near-absolute zero temperatures, where particles behave as a single quantum wave, and supercritical fluids above critical points, but these are less common in everyday contexts. Understanding phases is essential in fields ranging from to , as it governs the behavior of substances in technological applications like semiconductors, systems, and production.

Fundamental Concepts

Definition and Characteristics

In , a phase of is defined as a physically distinct, homogeneous portion that is mechanically separable and exhibits uniform physical properties throughout its extent. This uniformity ensures that properties such as density and remain constant within the phase, distinguishing it from surrounding regions. Common examples include the , , and gaseous forms of a substance, where each represents a separate phase coexisting under specific conditions. Key characteristics of a phase include its consistent composition and , which give rise to invariant intensive properties across the entire region, and its demarcation by well-defined interfaces that separate it from other phases. For instance, in a containing and at 0°C, the constitutes a phase with a fixed crystalline and of approximately 0.917 g/cm³, while the surrounding forms a distinct phase with a of 1 g/cm³, bounded by the ice-water interface. These interfaces arise due to abrupt changes in properties at phase boundaries, maintaining the homogeneity within each phase. The concept of phases in matter originated in 19th-century thermodynamics, with foundational contributions from in his 1876 memoir "On the Equilibrium of Heterogeneous Substances," where he formalized the treatment of multiphase systems. Gibbs' work established phases as essential components in analyzing among heterogeneous substances. Mathematically, a phase is represented as a in space where intensive variables—such as TT, pressure PP, and μ\mu—remain constant throughout, reflecting the phase's homogeneity and equilibrium conditions. This constancy of intensive variables ensures that the phase behaves as a single, uniform entity, with properties analytically varying only across phase boundaries.

Distinction from States of Matter

In thermodynamics, states of matter refer to the broad, macroscopic categories describing the physical form of a substance based on the arrangement and motion of its particles, such as , , gas, or plasma. These states characterize the overall behavior of matter under varying conditions of and , with solids featuring rigid structures, liquids having definite volume but fluidity, gases exhibiting high compressibility, and plasmas involving ionized particles. In contrast, a phase denotes a specific, homogeneous within a where all intensive properties—like , , , and composition—remain uniform and continuous throughout, separated from other regions by distinct interfaces. This distinction arises because phases emphasize spatial and compositional uniformity in a , potentially encompassing multiple states or portions thereof, whereas states focus on qualitative behavioral classifications. A key difference is that multiple distinct phases can coexist within the same , particularly when substances do not mix homogeneously. For instance, and are both in the state but form two separate phases due to their immiscibility, creating an interface where one layer floats atop the other without blending, as oil molecules are nonpolar and repel the polar water molecules./Equilibria/Physical_Equilibria/Immiscible_Liquids_and_Steam_Distillation) This separation persists under standard conditions because the intermolecular forces prevent across the boundary, resulting in two homogeneous liquid regions with differing densities and compositions./Equilibria/Physical_Equilibria/Immiscible_Liquids_and_Steam_Distillation) Conversely, a single system can exhibit phases spanning different states, as seen at the of , where solid , , and coexist in equilibrium at precisely 0.01°C and 611.657 Pa; here, the three phases represent distinct states (solid, liquid, gas) but share the same while maintaining separate homogeneous regions. The conceptual separation between phases and states evolved in the late 19th and early 20th centuries through foundational thermodynamic work. formalized the phase concept in 1876 by defining it as a uniform portion of a separable by mechanical means, building on earlier observations of critical points by in 1869, where and gas distinctions vanish. In early 20th-century literature, "phase" was occasionally used interchangeably with "" to describe basic forms like or , reflecting less precise terminology before the recognition of immiscible mixtures and complex equilibria became standard. Modern , however, maintains a clear distinction to account for multi-component s and non-analytic transitions between homogeneous regions, as emphasized in Gibbs' derivations.

Classification of Phases

Classical Phases

The classical phases of matter refer to the fundamental states observed under everyday conditions, characterized primarily by the arrangement, motion, and intermolecular forces of particles such as atoms or molecules. These phases—solid, liquid, gas, and plasma—exhibit distinct macroscopic properties arising from microscopic behaviors, with transitions between them occurring at specific temperatures and pressures, such as or points. In the solid phase, matter possesses a fixed shape and volume due to strong intermolecular forces that hold particles in a tightly packed, often ordered lattice structure, limiting their motion to vibrations around fixed positions. Most solids are crystalline, with particles arranged in a repeating , though amorphous solids, such as , lack long-range order and exhibit more disordered particle arrangements while still maintaining rigidity. A classic example is , the solid form of below its of 0°C at standard , where water molecules form a . The liquid phase features a fixed but no fixed shape, as particles are close together with relatively strong intermolecular forces that allow them to slide past one another, resulting in disordered arrangement and fluid flow. This dense but mobile molecular motion enables liquids to conform to the shape of their container while maintaining cohesion. For , this phase exists between 0°C and 100°C at , where molecules move freely yet remain in close proximity. In the gaseous phase, matter lacks both fixed shape and volume, with particles widely separated and exhibiting weak intermolecular forces, leading to random, high-speed motion that allows expansion to fill any available . The low and lack of regular arrangement distinguish gases from denser phases. , or above 100°C at standard pressure, exemplifies this, as molecules collide frequently but travel large distances between interactions. The plasma phase, often considered the fourth classical phase, consists of ionized gas where atoms are stripped of electrons, producing a of free electrons and ions that renders the medium highly conductive and responsive to electromagnetic fields. A key property is Debye shielding, in which mobile charges rearrange to screen internal over a characteristic distance called the , maintaining quasi-neutrality despite the presence of charged particles. Plasmas form at extremely high temperatures or energies, as in stars like the Sun, where and exist predominantly in this ionized state. These phases transition via processes like (solid to ) or ( to gas), driven by changes in that overcome intermolecular forces, with boundaries roughly defined by critical temperatures such as water's 0°C and 100°C points.

Exotic and Quantum Phases

Exotic phases of emerge under extreme conditions, such as ultralow temperatures, high energies, or specialized quantum interactions, where quantum mechanical effects dominate and classical descriptions fail. These phases often exhibit collective behaviors not seen in everyday , liquids, gases, or plasmas, including macroscopic quantum coherence and topological protection. Unlike classical phases, they challenge traditional notions of equilibrium and , revealing new forms of order in quantum many-body systems. A Bose-Einstein condensate (BEC) is a quantum phase formed when a dilute gas of bosons is cooled to temperatures near , causing a significant fraction of particles to occupy the lowest , leading to wave-like interference and . This phase was first achieved experimentally in 1995 using rubidium-87 atoms by Eric Cornell and at , with Wolfgang soon confirming it in sodium-23, earning the 2001 . In a BEC, manifests as frictionless flow and quantized vortices, enabling applications in precision measurements and quantum simulation. The represents an analogous quantum phase for fermions, which obey the and cannot all occupy the same state like bosons. Predicted theoretically in the early , it was first observed in 2003 by Deborah Jin's group at using atoms tuned near a Feshbach to form Cooper pairs in a superfluid state. This phase bridges fermionic in neutron stars and high-temperature superconductors, exhibiting pairing without a energy gap in the simplest models. Quark-gluon plasma (QGP) is a high-temperature, high-density phase where quarks and gluons are deconfined from hadrons, behaving as a nearly with minimal . This state, thought to have filled the microseconds after the , was first evidenced in heavy-ion collisions at CERN's in 2000 and confirmed at the (RHIC) in 2005, with the (LHC) providing further insights in the 2010s through lead-lead collisions reaching temperatures over 4 trillion Kelvin. At the LHC, QGP studies reveal collective flow patterns and jet quenching, informing . Topological phases of matter are characterized by global properties invariant under continuous deformations, hosting robust edge or protected against defects, unlike symmetry-broken phases. The integer , discovered in 1980 by Klaus von Klitzing in heterostructures under strong magnetic fields at millikelvin temperatures, exemplifies this with quantized Hall conductance in plateaus, earning the 1985 . Subsequent developments, such as fractional quantum Hall states in 1982, revealed anyonic excitations, while topological insulators—bulk insulating with conducting surfaces—emerged in the , enabling dissipationless quantum transport. Supercritical fluids constitute a phase beyond the critical point, where and exceed those allowing phase coexistence, resulting in a homogeneous without a distinct liquid-gas meniscus or . In this regime, properties like and vary continuously, enabling solvent-like behavior for applications in extraction and reactions; for example, above 31°C and 73 diffuses like a gas while dissolving like a . This phase lacks the equilibrium criteria typical of classical transitions, as no is involved. Time crystals represent a recent quantum phase breaking spontaneously, exhibiting periodic motion in time without external energy input, analogous to spatial crystals. Proposed by in 2012 as a nonequilibrium Floquet system, they were first observed experimentally in 2017 using nitrogen-vacancy centers in by the Lukin group (Choi et al.) and in trapped ions by the Monroe group, showing subharmonic responses to periodic drives. By 2025, realizations in superconducting qubits and ultracold atoms have advanced understanding of out-of-equilibrium quantum order, with potential for . In 2025, ongoing research has uncovered additional exotic quantum states, including a quantum liquid crystal realized using Google's superconducting quantum processor and the first spin-triplet excitonic insulator created by a UC Irvine team, further expanding the classification of quantum phases of matter.

Phase Equilibrium

Criteria for Equilibrium

In phase equilibrium, multiple phases of a substance coexist stably without any net change in their amounts or properties over time, requiring specific thermodynamic conditions to prevent spontaneous processes such as heat flow, volume changes, or between phases. Thermal equilibrium is achieved when the is uniform across all coexisting phases, ensuring no net occurs between them due to temperature gradients. This condition arises from the , which defines as the property equalized in systems in . Mechanical equilibrium demands that the pressure is the same in all phases, resulting in no acting at the interfaces and preventing any tendency for one phase to expand or contract at the expense of another. In systems without external fields or significant surface tension effects, this equality of pressure maintains the mechanical stability of the phase boundaries. Chemical equilibrium requires that the chemical potential of each component, denoted as μi\mu_i, is identical across all phases, given by μi(α)=μi(β)=⋯\mu_i^{(\alpha)} = \mu_i^{(\beta)} = \cdots for phases α,β,…\alpha, \beta, \ldots, which eliminates any driving force for diffusion or phase conversion. For multicomponent systems, the chemical potential of component ii in a phase is the partial molar Gibbs free energy, μi=(∂G∂ni)T,P,nj\mu_i = \left( \frac{\partial G}{\partial n_i} \right)_{T,P,n_j}, and its equality ensures no net mass transfer. These criteria collectively determine the conditions under which phases are in stable coexistence, as quantified by the Gibbs , F=C−P+2F = C - P + 2, where FF represents the (variables like and that can be independently varied), CC the number of components, and PP the number of phases; the full derivation of this rule follows in subsequent discussions. A classic example is the equilibrium between liquid and its vapor at 100°C and 1 atm , where the , , and of are equal in both phases, allowing to occur without net change in the system unless external conditions are altered. The foundational formulation of these equilibrium criteria and the associated was developed by J. Willard Gibbs in his 1876 paper "On the Equilibrium of Heterogeneous Substances," which established the thermodynamic framework for heterogeneous s.

Gibbs Phase Rule

The Gibbs phase rule provides a quantitative relation for the number of in a multiphase at . It is stated as F=C−P+2F = C - P + 2, where FF is the number of (independent intensive variables that can be varied without changing the number of phases), CC is the number of independent chemical components, and PP is the number of phases present. This form accounts for and pressure as the two fundamental intensive variables in systems without additional constraints. The derivation arises from the conditions for phase equilibrium, where the chemical potential μi\mu_i of each component ii must be equal across all phases: μi(α)=μi(β)=⋯\mu_i^{(\alpha)} = \mu_i^{(\beta)} = \cdots for phases α,β,…\alpha, \beta, \ldots. The in each phase satisfies the Gibbs-Duhem relation, dμi=−si dT+vi dPd\mu_i = -s_i \, dT + v_i \, dP, where sis_i and viv_i are the partial molar entropy and volume of component ii, ensuring consistency at constant and . To determine FF, consider the total intensive variables: TT, PP, and C−1C-1 independent composition variables (e.g., mole fractions) per phase, yielding 2+P(C−1)2 + P(C-1) variables. Equilibrium imposes C(P−1)C(P-1) constraints from the equality of chemical potentials for each component across PP phases. Subtracting these gives F=2+P(C−1)−C(P−1)=C−P+2F = 2 + P(C-1) - C(P-1) = C - P + 2. This formulation was originally developed by J. Willard Gibbs in his foundational work on heterogeneous equilibria. Variants of the rule apply under specific conditions. For condensed systems where pressure is fixed (e.g., isobaric phase diagrams neglecting vapor phases), the rule simplifies to F=C−P+1F = C - P + 1, as one degree of freedom is eliminated. In like azeotropes, where compositions are constrained to be identical across phases, the effective number of components reduces, further lowering FF. Applications of the rule predict the dimensionality of phase equilibria in diagrams. For a unary system (C=1C = 1) at the triple point, where solid, liquid, and vapor phases coexist (P=3P = 3), F=1−3+2=0F = 1 - 3 + 2 = 0, making the point invariant—neither TT nor PP can vary without altering the phases, as seen in water's triple point at 0.01°C and 611.7 Pa. In a binary eutectic system (C=2C = 2) at constant pressure, the eutectic point involves three phases (liquid plus two solids, P=3P = 3), yielding F=2−3+1=0F = 2 - 3 + 1 = 0, an invariant point where temperature and overall composition fix the system, such as in the lead-tin alloy at 183°C. The rule has limitations, assuming thermal, mechanical, and in closed, non-reactive systems without external fields like electric or magnetic influences. It does not apply to systems with reactions that alter component counts or to metastable states where kinetics prevent equilibrium.

Phase Transitions

Types of Transitions

Phase transitions are classified primarily according to the Ehrenfest scheme, which categorizes them based on the order of the thermodynamic derivatives that exhibit discontinuities at the transition point. Introduced by in 1933, this classification distinguishes transitions by the nature of singularities in the , such as the . First-order phase transitions are characterized by discontinuities in the first derivatives of the , including and , which manifest as absorption or release and a abrupt change in . These transitions involve a coexistence of two phases separated by a two-phase region, with the transition line described by the Clapeyron equation relating , , , and change. A representative example is the freezing of , where and phases coexist at 0°C and 1 atm, accompanied by a volume expansion and release of . In contrast, second-order phase transitions, also known as continuous transitions, feature continuous first derivatives but discontinuities in second derivatives, such as specific heat, , and , with no involved. These transitions occur without phase coexistence and often involve , as elaborated in Lev Landau's 1937 theory, which introduces an order parameter to describe the gradual onset of order in the system. An example is the ferromagnetic-to-paramagnetic transition in materials like iron at the , where vanishes continuously but specific heat shows a jump; another is the approach to the critical point in the liquid-gas transition, marked by due to density fluctuations. Higher-order phase transitions, extending the Ehrenfest classification beyond second order, involve discontinuities only in derivatives of order three or higher, making them exceedingly rare in practice and often theoretical. The lambda transition in at approximately 2.17 K exemplifies a second-order transition with higher-order characteristics in its specific heat anomaly, though strictly classified as second-order; true higher-order examples remain elusive in classical systems but appear in some quantum models. Martensitic transitions represent a distinct mechanism, being diffusionless and driven by shear deformation in , where atoms move cooperatively over short distances without long-range . These are typically but occur rapidly via displacive mechanisms, producing a twinned microstructure; a key example is the austenite-to-martensite transformation in upon rapid cooling, enhancing hardness without compositional change. The Ehrenfest classification provides a thermodynamic foundation but has limitations for critical phenomena, where modern approaches like better capture symmetry and order parameter dynamics, bridging classical and quantum transitions.

Thermodynamics of Transitions

Phase transitions are governed by fundamental thermodynamic principles that describe the balance between , , and free energy changes during the shift between phases. The , defined as G=H−TSG = H - TS, where HH is , TT is , and SS is , serves as the key potential for determining phase stability at constant and . At the equilibrium transition point between two phases, the change in is zero (ΔG=0\Delta G = 0), indicating that the two phases coexist with equal chemical potentials. During a phase transition, a is absorbed or released to account for the required to reorganize molecular structures without a temperature change. For instance, the latent heat of fusion for melting is 334 J/g, representing the needed to transition from to liquid at 0°C. This latent heat, often denoted as ΔH\Delta H, quantifies the change and is positive for endothermic transitions like or . The Clausius-Clapeyron relates the slope of the phase boundary in a pressure-temperature to the thermodynamic properties of the transition: dPdT=ΔHTΔV\frac{dP}{dT} = \frac{\Delta H}{T \Delta V} where ΔV\Delta V is the volume change across the transition. This , derived from the equality of chemical potentials in coexisting phases, predicts how transition temperatures vary with ; for example, it explains the slight decrease in water's under increased . In first-order phase transitions, arises due to kinetic barriers, leading to (where a liquid persists below its freezing point) or (where a liquid exceeds its without vaporizing). This phenomenon occurs because of the new phase requires overcoming an barrier, resulting in metastable states that deviate from equilibrium conditions. Near the critical point of a second-order transition, such as the liquid-gas critical point, emerge, characterized by a diverging correlation length that describes the spatial extent of fluctuations in density or order parameters. These phenomena exhibit universality, where systems in the same universality class—determined by dimensionality, symmetry, and range of interactions—share identical critical exponents, independent of microscopic details. The of state, given by (P+aVm2)(Vm−b)=RT\left( P + \frac{a}{V_m^2} \right) (V_m - b) = RT where VmV_m is the , aa accounts for attractive forces, and bb for molecular volume, provides a mean-field model for the liquid-gas . It predicts a transition below the critical temperature, with a coexistence region resolved via the Maxwell construction to ensure equal areas under the pressure-volume isotherm, capturing the van der Waals loops as metastable extensions.

Structural Aspects

Crystal Phases

Crystalline solids are characterized by a high degree of long-range atomic order, where atoms, ions, or molecules are arranged in a repeating three-dimensional lattice. This periodic structure gives rise to distinct physical properties such as and sharp melting points. The possible lattice types are described by the 14 Bravais lattices, which represent the unique ways to fill space with identical points under in seven crystal systems: triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic. When these lattices are combined with the 32 crystallographic point groups and additional symmetry operations like screw axes and glide planes, they yield the 230 space groups that fully classify all known three-dimensional crystal symmetries. A key feature of crystalline solids is polymorphism, the ability of a single chemical substance to crystallize in multiple distinct lattice structures, often resulting in varied properties like density, hardness, or reactivity. For instance, carbon exhibits polymorphism as diamond, which has a rigid three-dimensional tetrahedral network leading to exceptional hardness, and graphite, featuring stacked layers of hexagonal rings that enable lubricity and electrical conductivity. Similarly, elemental phosphorus displays allotropes—polymorphic forms specific to elements—including white phosphorus, a highly reactive molecular solid composed of P4 tetrahedra, and red phosphorus, a more stable, amorphous polymeric network with extended P-P bonds. These structural differences arise from variations in bonding and packing efficiency under different synthesis conditions. Liquid crystals introduce partial order as mesophases between fully crystalline solids and isotropic liquids, exhibiting long-range orientational order but short-range positional order. In the nematic phase, rod-like molecules align parallel along a director axis while maintaining fluid-like positional disorder, allowing flow like a liquid. The smectic phases build on this with additional layering: in smectic A, molecules are perpendicular to the layers with positional order within planes, whereas smectic C features tilted molecules relative to the layer normal, enhancing properties like in certain materials. These phases are temperature-dependent and common in applications such as displays due to their responsiveness to . Pressure-induced polymorphism is exemplified by water's ice phases, where more than 20 known polymorphs exist depending on thermodynamic conditions as of 2025. Ice Ih, the hexagonal form prevalent in and glaciers at , transitions under compression to denser structures like ice II, a rhombohedral lattice stable approximately between 0.2 and 2.1 GPa and temperatures from 190 to 253 , which features more compact hydrogen-bonded networks. Recent discoveries, such as Ice XXI in 2025, highlight ongoing research into high-pressure ices under extreme conditions. These polymorphs influence phenomena such as planetary interiors and . The internal structure of crystals is elucidated through X-ray diffraction (XRD), a technique that probes atomic arrangements by analyzing scattering patterns. Diffraction peaks arise from constructive interference of reflected from lattice planes, as described by : nλ=2dsin⁡θn\lambda = 2d \sin\theta where nn is a positive denoting the reflection order, λ\lambda is the , dd is the spacing between planes, and θ\theta is the angle of incidence. This relationship allows determination of lattice parameters and assignment from measured diffraction angles.

Interfacial Phenomena

Interfacial phenomena occur at the boundaries between distinct phases of , where properties differ significantly from those in the bulk phases due to the imbalance of intermolecular forces. These interfaces are typically sharp, on the order of molecular dimensions, and exhibit a surface free energy, denoted as γ and measured in joules per square meter (J/), which represents the excess free energy per unit area required to create the interface. This surface free energy arises from the asymmetry in bonding at the boundary, leading to a tendency to minimize the interfacial area. Surface tension, a manifestation of this surface free energy in fluid phases, acts tangentially to the interface and drives the system toward configurations of minimal area, such as spherical droplets. For a curved liquid-vapor interface, the pressure difference across the boundary is given by the Young-Laplace : ΔP=γ(1R1+1R2)\Delta P = \gamma \left( \frac{1}{R_1} + \frac{1}{R_2} \right) where R1R_1 and R2R_2 are the principal radii of , and ΔP\Delta P is the jump from the concave to the convex side. This explains the higher internal in small droplets or bubbles, influencing phenomena like droplet stability and coalescence. Adsorption refers to the preferential accumulation of molecules or ions at the interface compared to the bulk phases, which can alter the surface free energy. The Gibbs adsorption isotherm quantifies this effect, relating the surface excess concentration Γ\Gamma (moles per unit area) to changes in with solute concentration: Γ=−1RTdγdln⁡C\Gamma = -\frac{1}{RT} \frac{d\gamma}{d \ln C} where RR is the , TT is , and CC is the bulk concentration. Surfactants, for instance, adsorb at liquid-air or liquid-liquid interfaces, reducing γ\gamma and stabilizing dispersions. Wetting describes how a spreads on a solid surface, governed by the balance of interfacial tensions at the three-phase contact line. The equilibrium θ\theta is determined by Young's equation: γSV=γSL+γLVcos⁡θ\gamma_{SV} = \gamma_{SL} + \gamma_{LV} \cos \theta where γSV\gamma_{SV}, γSL\gamma_{SL}, and γLV\gamma_{LV} are the solid-vapor, solid-liquid, and liquid-vapor interfacial tensions, respectively. A θ<90∘\theta < 90^\circ indicates (spreading), while θ>90∘\theta > 90^\circ indicates non-wetting (beading). This balance influences applications like coatings and . Representative examples illustrate these principles. Soap bubbles feature two interfaces (inner and outer soap film-air boundaries), resulting in a pressure difference of ΔP=4γ/r\Delta P = 4\gamma / r for a bubble of radius rr, which maintains the spherical shape against internal pressure. Emulsions, such as oil-in-water mixtures, rely on reduced interfacial tension from adsorbed to prevent droplet coalescence and achieve long-term stability. Capillarity, or , arises from the interplay of and at a solid-liquid-vapor interface in narrow tubes. For a in a cylindrical tube of rr, the height hh of rise is given by: h=2γcos⁡θρgrh = \frac{2\gamma \cos \theta}{\rho g r} where ρ\rho is the density and gg is . This phenomenon drives fluid transport in porous media and biological systems, such as plant xylem.

Non-Equilibrium Behavior

Phases Out of Equilibrium

Non-equilibrium phases in matter arise when kinetic barriers prevent systems from reaching , allowing transient states to persist under conditions where a more stable phase should form. These phases are governed by the rates of atomic or molecular rearrangements rather than minimizing free energy, leading to structures that are temporarily stable due to slow or high activation energies. For instance, supersaturated solutions maintain excess solute beyond the equilibrium limit because of the precipitate phase is kinetically hindered. A key mechanism sustaining non-equilibrium phases is , the initial formation of a new phase embryo within the parent phase, which faces an barrier due to interfacial tension. In , the free energy change for forming a spherical nucleus of radius rr is given by ΔG=−43πr3ΔGv+4πr2γ\Delta G = -\frac{4}{3}\pi r^3 \Delta G_v + 4\pi r^2 \gamma, where ΔGv\Delta G_v is the bulk free energy difference driving the transformation and γ\gamma is the interfacial energy. The critical nucleus size corresponds to the maximum ΔG∗=16πγ33(ΔGv)2\Delta G^* = \frac{16\pi \gamma^3}{3 (\Delta G_v)^2}, beyond which growth becomes favorable; this barrier ΔG∗\Delta G^* determines the nucleation rate via J∝exp⁡(−ΔG∗/kT)J \propto \exp(-\Delta G^* / kT). In contrast, occurs in unstable regions of the where the free energy is concave, leading to spontaneous without a barrier. Small compositional fluctuations amplify via uphill , driven by the negative of the free energy with respect to composition, resulting in interconnected domains that coarsen over time. This process is described by the Cahn-Hilliard , ∂c∂t=∇⋅(M∇μ)\frac{\partial c}{\partial t} = \nabla \cdot (M \nabla \mu), where cc is concentration, MM is mobility, and μ\mu is the . Representative examples of non-equilibrium phases include amorphous metals, formed by rapid cooling of molten alloys at rates exceeding 10610^6 K/s to suppress kinetics. Pioneering work on Pd-Si alloys demonstrated that such locks the liquid structure into a glassy state, far from the equilibrium crystalline phase. Similarly, colloidal glasses emerge in dense suspensions of particles with short-range attractions, where caging effects and kinetic arrest prevent equilibration into ordered or fluid states, yielding jammed, non-ergodic structures. These phases eventually approach equilibrium through relaxation processes dominated by , with characteristic times scaling as τ∼L2/D\tau \sim L^2 / D, where LL is a length scale (e.g., domain size) and DD is the diffusion coefficient. In non-equilibrium systems, such relaxation can span seconds to years, depending on and composition, as diffusive fluxes gradually reduce stored .

Metastable Phases

Metastable phases represent local minima in the free energy landscape of a , where the phase possesses a higher free energy than the globally equilibrium phase but remains persistent due to kinetic constraints. These states are thermodynamically unstable yet can endure for extended periods under ambient conditions, as the is trapped in a configuration that is only marginally perturbed by . A classic example is diamond, which exists as a metastable phase relative to graphite at standard temperature and pressure; despite graphite's lower free energy, the transformation is inhibited by substantial kinetic barriers, allowing diamonds to persist indefinitely in jewelry and natural deposits. Another prominent case involves supercooled liquids that avoid upon rapid cooling, forming amorphous —metastable solids with structural disorder akin to the state but higher than the crystalline counterpart. These , such as silica in window panes, maintain rigidity over human timescales despite their inherent instability. The longevity of metastable phases stems from high kinetic barriers that impede the transition to the equilibrium state, often requiring overcoming activation energies on the order of electronvolts per atom for atomic reconfiguration or . For instance, in carbon systems, the rearrangement from diamond's tetrahedral network to graphite's layered structure demands breaking strong covalent bonds, resulting in activation energies exceeding 1 eV, which thermal energies at room temperature rarely surmount. High-pressure techniques, such as those employing diamond anvil cells, enable the synthesis and recovery of metastable phases by compressing materials to gigapascal levels, where novel structures form that revert slowly or not at all upon decompression. In these experiments, nanocrystals of semiconductors like can be trapped in high-pressure rock-salt phases under ambient conditions, demonstrating how extreme pressures create kinetic traps with activation barriers over 1.3 eV per particle. In , metastable phases are harnessed to engineer alloys with exceptional mechanical properties, such as high strength coupled with , by exploiting transformation-induced plasticity during deformation. For example, composed of iron, , , and in dual-phase configurations achieve yield strengths above 1 GPa while maintaining elongations over 50%, outperforming traditional metals through controlled that delays phase transitions until high strains. Recent advancements in computational materials discovery, particularly using (DFT), have enabled predictions of novel metastable phases by mapping free energy landscapes and identifying kinetically accessible structures far from equilibrium. As of June 2025, schemes integrated with graph neural networks trained on DFT data from thousands of materials have identified new high-pressure phase transformations in various systems. These tools also guide selective synthesis of metastable polymorphs in solid-state reactions, quantifying reaction energies to favor desired high-energy phases over competitors.

References

  1. https://chem.libretexts.org/Courses/Bellarmine_University/BU%3A_Chem_104_(Christianson)/Phase_1%3A_The_Phases_of_Matter/1%3A_Gases/1.1%3A_The_Phases_of_Matter
  2. https://pressbooks.online.ucf.edu/chemistryfundamentals/chapter/phases-and-classification-of-matter/
  3. https://www.chem.purdue.edu/gchelp/liquids/character.html
  4. https://www.engineeringtoolbox.com/saturated-steam-properties-d_457.html
  5. https://www.pppl.gov/about/about-plasmas-and-fusion
  6. https://www.energy.gov/science/doe-explainsplasma
  7. https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node61.html
  8. https://courses.ems.psu.edu/png520/m14_p3.html
  9. https://engineering.purdue.edu/~wassgren/teaching/ME20000/NotesAndReading/Lec07_Reading_Wassgren.pdf
  10. https://scholar.harvard.edu/files/schwartz/files/9-phases.pdf
  11. https://archive.org/download/Onequilibriumhe00Gibb/Onequilibriumhe00Gibb.pdf
  12. https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node11.html
  13. https://www.gps.caltech.edu/~asimow/glossary.html
  14. https://schwartz.scholars.harvard.edu/sites/g/files/omnuum7046/files/schwartz/files/9-phases_0.pdf
  15. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_General_Chemistry_(Petrucci_et_al.)/12%3A_Intermolecular_Forces%3A_Liquids_And_Solids/12.4%3A_Phase_Diagrams
  16. https://www.grc.nasa.gov/www/k-12/airplane/state.html
  17. https://farside.ph.utexas.edu/teaching/plasma/lectures1/node7.html
  18. https://www.psfc.mit.edu/resources/fusion-101/what-is-plasma/
  19. https://www.nature.com/collections/fdbjbijfea
  20. https://www.nobelprize.org/uploads/2018/06/advanced-physicsprize2001.pdf
  21. https://www.science.org/content/article/fermi-condensate-created
  22. https://www.nature.com/articles/news040126-12
  23. https://cds.cern.ch/record/2698979/files/10.1140_epjst_e2019-900263-x.pdf
  24. https://link.aps.org/doi/10.1103/RevModPhys.89.041004
  25. https://www.nature.com/articles/ncomms3331
  26. https://pubs.acs.org/doi/10.1021/acsomega.1c00474
  27. https://physics.aps.org/articles/v10/5
  28. https://www.science.org/doi/10.1126/science.abo3382
  29. https://www.sciencedaily.com/releases/2025/09/250912195119.htm
  30. https://modernsciences.org/new-quantum-matter-uc-irvine-august-2025/
  31. https://www.thermopedia.com/content/1020/
  32. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/DeVoes_Thermodynamics_and_Chemistry/08%253A_Phase_Transitions_and_Equilibria_of_Pure_Substances/8.01%253A_Phase_Equilibria
  33. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%253A_Principles_of_Modern_Chemistry_%28Oxtoby_et_al.%29/Unit_3%253A_The_States_of_Matter/10%253A_Solids_Liquids_and_Phase_Transitions/10.4%253A_Phase_Equilibrium
  34. https://serc.carleton.edu/research_education/equilibria/phaserule.html
  35. https://ocw.mit.edu/courses/3-00-thermodynamics-of-materials-fall-2002/df5d18e388b3d9e8d2ff6158cf35776c_lecture_26_oneside.PDF
  36. https://archive.org/details/Onequilibriumhe00GibbA
  37. https://arxiv.org/pdf/1612.03062
  38. http://archive.ujp.bitp.kiev.ua/files/journals/53/si/53SI08p.pdf
  39. https://www.doitpoms.ac.uk/tlplib/superelasticity/martensitic_crystallography.php
  40. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_General_Chemistry_(Petrucci_et_al.)/18%3A_Chemical_Thermodynamics/18.03%3A_The_Gibbs_Free_Energy
  41. https://pressbooks.online.ucf.edu/phy2053bc/chapter/phase-change-and-latent-heat/
  42. https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node64.html
  43. https://courses.physics.illinois.edu/phys466/fa2016/lnotes/PhaseTransitions.pdf
  44. https://www.physics.utah.edu/~wu/phys7310-16/notes/Phase_Transt-2.pdf
  45. https://geo.libretexts.org/Bookshelves/Geology/Mineralogy_%28Perkins_et_al.%29/11%253A_Crystallography/11.06%253A_Space_Groups
  46. https://www.chemistry.mcmaster.ca/~xman/cccw18/files/Crystal_Systems_and_Space_Groups_coloured.pdf
  47. https://byustudies.byu.edu/article/polymorphism-and-high-pressure
  48. https://byjus.com/chemistry/polymorphism/
  49. https://chem.libretexts.org/Bookshelves/Inorganic_Chemistry/Supplemental_Modules_and_Websites_%28Inorganic_Chemistry%29/Descriptive_Chemistry/Elements_Organized_by_Block/2_p-Block_Elements/Group_15%253A_The_Nitrogen_Family/Z015_Chemistry_of_Phosphorous
  50. https://chem.libretexts.org/Bookshelves/General_Chemistry/Book%253A_General_Chemistry%253A_Principles_Patterns_and_Applications_%28Averill%29/11%253A_Fluids/11.08%253A_Liquid_Crystals
  51. https://www.sciencedirect.com/topics/chemistry/smectic-phase
  52. https://www.researchgate.net/publication/232371182_Thermodynamics_of_high-pressure_ice_polymorphs_Ice_II
  53. https://www.sci.news/othersciences/physicalchemistry/ice-xxi-14285.html
  54. https://discovery.ucl.ac.uk/id/eprint/100076/1/14058.pdf
  55. https://serc.carleton.edu/research_education/geochemsheets/BraggsLaw.html
  56. https://chem.libretexts.org/Bookshelves/Analytical_Chemistry/Supplemental_Modules_%28Analytical_Chemistry%29/Analytical_Sciences_Digital_Library/Courseware/Introduction_to_X-ray_Diffraction_%28XRD%29/03_Basic_Theory/02_Diffraction__and_Braggs_Law
  57. https://ocw.mit.edu/courses/18-357-interfacial-phenomena-fall-2010/04759cfc15c79928ca9f72a18b3864dd_MIT18_357F10_lec_all.pdf
  58. https://farside.ph.utexas.edu/teaching/336L/Fluidhtml/node41.html
  59. https://web.mit.edu/nnf/education/wettability/wetting.html
  60. https://farside.ph.utexas.edu/teaching/336L/Fluidhtml/node42.html
  61. https://math.mit.edu/sites/bush/wp-content/uploads/2018/02/18.357-LecNotes-2010.pdf
  62. https://farside.ph.utexas.edu/teaching/336L/Fluidhtml/node45.html
  63. https://pmc.ncbi.nlm.nih.gov/articles/PMC6362205/
  64. https://pubs.aip.org/aip/jcp/article-pdf/28/2/258/11106115/258_1_online.pdf
  65. https://pubs.aip.org/aip/jap/article/36/7/2267/165280/Amorphous-Phase-in-Palladium-Silicon-Alloys
  66. https://www.pnas.org/doi/10.1073/pnas.0902294106
  67. https://link.springer.com/article/10.1134/S0036024417080350
  68. https://perssongroup.lbl.gov/papers/sun-2016-metastability.pdf
  69. https://www.wtamu.edu/~cbaird/sq/2013/12/17/why-do-diamonds-last-forever/
  70. https://pmc.ncbi.nlm.nih.gov/articles/PMC5754753/
  71. https://www.science.org/doi/10.1126/science.abq7684
  72. https://www.science.org/doi/10.1126/sciadv.abo7333
  73. https://www.nature.com/articles/s41524-025-01682-7
Add your contribution
Related Hubs
User Avatar
No comments yet.