Versine

The versine^{[3][4][5][6][7]} or versed sine^{[8][9][10][11][12]} is a trigonometric function already appearing in some of the earliest trigonometric tables. It is symbolized in formulas using the abbreviations versin, sinver,^[13][14] vers, or siv.^[15][16] In Latin, it is known as the sinus versus (flipped sine), versinus, versus, or sagitta (arrow).^[17]

Expressed in terms of common trigonometric functions sine, cosine, and tangent, the versine is equal to $${\displaystyle \operatorname {versin} \theta =1-\cos \theta =2\sin ^{2}{\frac {\theta }{2}}=\sin \theta \,\tan {\frac {\theta }{2}}}$$

There are several related functions corresponding to the versine:

• The versed cosine,^{[18][nb 1]} or vercosine, abbreviated vercosin, vercos, or vcs
• The coversed sine or coversine^[19] (in Latin, cosinus versus or coversinus), abbreviated coversin, covers,^[20][21][22] cosiv, or cvs^[23]

Special tables were also made of half of the versed sine, because of its particular use in the haversine formula used historically in navigation.

• The haversed sine^[24] or haversine (Latin semiversus),^[25][26] abbreviated haversin, semiversin, semiversinus, havers, hav,^[27][28] hvs,^{[nb 2]} sem, or hv.^[29] It is defined as

$${\displaystyle {\text{hav}}\ \theta =\sin ^{2}\left({\frac {\theta }{2}}\right)={\frac {1-\cos \theta }{2}}}$$

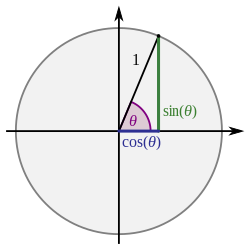
The ordinary sine function (see note on etymology) was sometimes historically called the sinus rectus ("straight sine"), to contrast it with the versed sine (sinus versus).^[31] The meaning of these terms is apparent if one looks at the functions in the original context for their definition, a unit circle:

For a vertical chord AB of the unit circle, the sine of the angle θ (representing half of the subtended angle Δ) is the distance AC (half of the chord). On the other hand, the versed sine of θ is the distance CD from the center of the chord to the center of the arc. Thus, the sum of cos(θ) (equal to the length of line OC) and versin(θ) (equal to the length of line CD) is the radius OD (with length 1). Illustrated this way, the sine is vertical (rectus, literally "straight") while the versine is horizontal (versus, literally "turned against, out-of-place"); both are distances from C to the circle.

This figure also illustrates the reason why the versine was sometimes called the sagitta, Latin for arrow.^[17][30] If the arc ADB of the double-angle Δ = 2θ is viewed as a "bow" and the chord AB as its "string", then the versine CD is clearly the "arrow shaft".

In further keeping with the interpretation of the sine as "vertical" and the versed sine as "horizontal", sagitta is also an obsolete synonym for the abscissa (the horizontal axis of a graph).^[30]

In 1821, Cauchy used the terms sinus versus (siv) for the versine and cosinus versus (cosiv) for the coversine.^{[15][16][nb 1]}

As θ goes to zero, versin(θ) is the difference between two nearly equal quantities, so a user of a trigonometric table for the cosine alone would need a very high accuracy to obtain the versine in order to avoid catastrophic cancellation, making separate tables for the latter convenient.^[12] Even with a calculator or computer, round-off errors make it advisable to use the sin² formula for small θ.

Another historical advantage of the versine is that it is always non-negative, so its logarithm is defined everywhere except for the single angle (θ = 0, 2π, …) where it is zero—thus, one could use logarithmic tables for multiplications in formulas involving versines.

In fact, the earliest surviving table of sine (half-chord) values (as opposed to the chords tabulated by Ptolemy and other Greek authors), calculated from the Surya Siddhantha of India dated back to the 3rd century BC, was a table of values for the sine and versed sine (in 3.75° increments from 0 to 90°).^[31]

The versine appears as an intermediate step in the application of the half-angle formula sin²(⁠θ/2⁠) = ⁠1/2⁠versin(θ), derived by Ptolemy, that was used to construct such tables.

The haversine, in particular, was important in navigation because it appears in the haversine formula, which is used to reasonably accurately compute distances on an astronomic spheroid (see issues with the Earth's radius vs. sphere) given angular positions (e.g., longitude and latitude). One could also use sin²(⁠θ/2⁠) directly, but having a table of the haversine removed the need to compute squares and square roots.^[12]

An early utilization by José de Mendoza y Ríos of what later would be called haversines is documented in 1801.^[14][32]

The first known English equivalent to a table of haversines was published by James Andrew in 1805, under the name "Squares of Natural Semi-Chords".^[33][34][17]

In 1835, the term haversine (notated naturally as hav. or base-10 logarithmically as log. haversine or log. havers.) was coined^[35] by James Inman^[14][36][37] in the third edition of his work Navigation and Nautical Astronomy: For the Use of British Seamen to simplify the calculation of distances between two points on the surface of the Earth using spherical trigonometry for applications in navigation.^[3][35] Inman also used the terms nat. versine and nat. vers. for versines.^[3]

Other high-regarded tables of haversines were those of Richard Farley in 1856^[33][38] and John Caulfield Hannyngton in 1876.^[33][39]

The haversine continues to be used in navigation and has found new applications in recent decades, as in Bruce D. Stark's method for clearing lunar distances utilizing Gaussian logarithms since 1995^[40][41] or in a more compact method for sight reduction since 2014.^[29]

While the usage of the versine, coversine and haversine as well as their inverse functions can be traced back centuries, the names for the other five cofunctions appear to be of much younger origin.

One period (0 < θ < 2π) of a versine or, more commonly, a haversine waveform is also commonly used in signal processing and control theory as the shape of a pulse or a window function (including Hann, Hann–Poisson and Tukey windows), because it smoothly (continuous in value and slope) "turns on" from zero to one (for haversine) and back to zero.^{[nb 2]} In these applications, it is named Hann function or raised-cosine filter.

${\displaystyle {\textrm {versin}}(\theta ):=2\sin ^{2}\!\left({\frac {\theta }{2}}\right)=1-\cos(\theta )\,}$[4]
${\displaystyle {\textrm {coversin}}(\theta ):={\textrm {versin}}\!\left({\frac {\pi }{2}}-\theta \right)=1-\sin(\theta )\,}$[4]
${\displaystyle {\textrm {vercosin}}(\theta ):=2\cos ^{2}\!\left({\frac {\theta }{2}}\right)=1+\cos(\theta )\,}$[18]
${\displaystyle {\textrm {haversin}}(\theta ):={\frac {{\textrm {versin}}(\theta )}{2}}=\sin ^{2}\!\left({\frac {\theta }{2}}\right)={\frac {1-\cos(\theta )}{2}}\,}$[4]

The functions are circular rotations of each other.

${\displaystyle {\begin{aligned}\mathrm {versin} (\theta )&=\mathrm {coversin} \left(\theta +{\frac {\pi }{2}}\right)=\mathrm {vercosin} \left(\theta +\pi \right)\end{aligned}}}$

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {versin} (x)=\sin {x}}$[42]	${\displaystyle \int \mathrm {versin} (x)\,\mathrm {d} x=x-\sin {x}+C}$[4][42]
${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {vercosin} (x)=-\sin {x}}$	${\displaystyle \int \mathrm {vercosin} (x)\,\mathrm {d} x=x+\sin {x}+C}$
${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {coversin} (x)=-\cos {x}}$[19]	${\displaystyle \int \mathrm {coversin} (x)\,\mathrm {d} x=x+\cos {x}+C}$[19]
${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} x}}\mathrm {haversin} (x)={\frac {\sin {x}}{2}}}$[24]	${\displaystyle \int \mathrm {haversin} (x)\,\mathrm {d} x={\frac {x-\sin {x}}{2}}+C}$[24]

Inverse functions like arcversine (arcversin, arcvers,^[8] avers,^[43][44] aver), arcvercosine (arcvercosin, arcvercos, avercos, avcs), arccoversine (arccoversin, arccovers,^[8] acovers,^[43][44] acvs), arccovercosine (arccovercosin, arccovercos, acovercos, acvc), archaversine (archaversin, archav, haversin⁻¹,^[45] invhav,^[46][47][48] ahav,^[43][44] ahvs, ahv, hav^−1[49][50]), archavercosine (archavercosin, archavercos, ahvc), archacoversine (archacoversin, ahcv) or archacovercosine (archacovercosin, archacovercos, ahcc) exist as well:

${\displaystyle \operatorname {arcversin} (y)=\arccos \left(1-y\right)\,}$[43][44]

${\displaystyle \operatorname {arcvercos} (y)=\arccos \left(y-1\right)\,}$

${\displaystyle \operatorname {arccoversin} (y)=\arcsin \left(1-y\right)\,}$[43][44]

${\displaystyle \operatorname {arccovercos} (y)=\arcsin \left(y-1\right)\,}$

${\displaystyle \operatorname {archaversin} (y)=2\arcsin \left({\sqrt {y}}\right)=\arccos \left(1-2y\right)\,}$[43][44][45][46][47][49][50]

${\displaystyle \operatorname {archavercos} (y)=2\arccos \left({\sqrt {y}}\right)=\arccos \left(2y-1\right)}$

${\displaystyle \operatorname {archacoversin} (y)=\arcsin \left(1-2y\right)\,}$

${\displaystyle \operatorname {archacovercos} (y)=\arcsin \left(2y-1\right)\,}$

These functions can be extended into the complex plane.^[42][19][24]

Maclaurin series:^[24]

${\displaystyle {\begin{aligned}\operatorname {versin} (z)&=\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}z^{2k}}{(2k)!}}\\\operatorname {haversin} (z)&=\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}z^{2k}}{2(2k)!}}\end{aligned}}}$

${\displaystyle \lim _{\theta \to 0}{\frac {\operatorname {versin} (\theta )}{\theta }}=0}$^[8]

${\displaystyle {\begin{aligned}{\frac {\operatorname {versin} (\theta )+\operatorname {coversin} (\theta )}{\operatorname {versin} (\theta )-\operatorname {coversin} (\theta )}}-{\frac {\operatorname {exsec} (\theta )+\operatorname {excsc} (\theta )}{\operatorname {exsec} (\theta )-\operatorname {excsc} (\theta )}}&={\frac {2\operatorname {versin} (\theta )\operatorname {coversin} (\theta )}{\operatorname {versin} (\theta )-\operatorname {coversin} (\theta )}}\\[3pt][\operatorname {versin} (\theta )+\operatorname {exsec} (\theta )]\,[\operatorname {coversin} (\theta )+\operatorname {excsc} (\theta )]&=\sin(\theta )\cos(\theta )\end{aligned}}}$^[8]

When the versine v is small in comparison to the radius r, it may be approximated from the half-chord length L (the distance AC shown above) by the formula^[51] $${\displaystyle v\approx {\frac {L^{2}}{2r}}.}$$

Alternatively, if the versine is small and the versine, radius, and half-chord length are known, they may be used to estimate the arc length s (AD in the figure above) by the formula $${\displaystyle s\approx L+{\frac {v^{2}}{r}}}$$ This formula was known to the Chinese mathematician Shen Kuo, and a more accurate formula also involving the sagitta was developed two centuries later by Guo Shoujing.^[52]

A more accurate approximation used in engineering^[53] is $${\displaystyle v\approx {\frac {s^{\frac {3}{2}}L^{\frac {1}{2}}}{8r}}}$$

The term versine is also sometimes used to describe deviations from straightness in an arbitrary planar curve, of which the above circle is a special case. Given a chord between two points in a curve, the perpendicular distance v from the chord to the curve (usually at the chord midpoint) is called a versine measurement. For a straight line, the versine of any chord is zero, so this measurement characterizes the straightness of the curve. In the limit as the chord length L goes to zero, the ratio ⁠8v/L²⁠ goes to the instantaneous curvature. This usage is especially common in rail transport, where it describes measurements of the straightness of the rail tracks^[54] and it is the basis of the Hallade method for rail surveying.

The term sagitta (often abbreviated sag) is used similarly in optics, for describing the surfaces of lenses and mirrors.

• Trigonometric identities
• Exsecant and excosecant
• Versiera (Witch of Agnesi)
• Exponential minus 1
• Natural logarithm plus 1