Recent from talks
Nothing was collected or created yet.
Abelian group
View on WikipediaIn mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commutative. With addition as an operation, the integers and the real numbers form abelian groups, and the concept of an abelian group may be viewed as a generalization of these examples. Abelian groups are named after the Norwegian mathematician Niels Henrik Abel.[1]
The concept of an abelian group underlies many fundamental algebraic structures, such as fields, rings, vector spaces, and algebras. The theory of abelian groups is generally simpler than that of their non-abelian counterparts, and finite abelian groups are very well understood and fully classified.
| Algebraic structure → Group theory Group theory |
|---|
 |
Definition
[edit]An abelian group is a set , together with an operation ・ , that combines any two elements and of to form another element of denoted . The symbol ・ is a general placeholder for a concretely given operation. To qualify as an abelian group, the set and operation, , must satisfy four requirements known as the abelian group axioms (some authors include in the axioms some properties that belong to the definition of an operation: namely that the operation is defined for any ordered pair of elements of A, that the result is well-defined, and that the result belongs to A):
- Associativity
- For all , , and in , the equation holds.
- Identity element
- There exists an element in , such that for all elements in , the equation holds.
- Inverse element
- For each in there exists an element in such that , where is the identity element.
- Commutativity
- For all , in , .
A group in which the group operation is not commutative is called a "non-abelian group" or "non-commutative group".[2]
Facts
[edit]Notation
[edit]There are two main notational conventions for abelian groups – additive and multiplicative.
| Convention | Operation | Identity | Powers | Inverse |
|---|---|---|---|---|
| Addition | 0 | |||
| Multiplication | or | 1 |
Generally, the multiplicative notation is the usual notation for groups, while the additive notation is the usual notation for modules and rings. The additive notation may also be used to emphasize that a particular group is abelian, whenever both abelian and non-abelian groups are considered, with some notable exceptions being near-rings and partially ordered groups, where an operation is written additively even when non-abelian.[3][4]
Multiplication table
[edit]To verify that a finite group is abelian, a table (matrix) – known as a Cayley table – can be constructed in a similar fashion to a multiplication table.[5] If the group is under the operation , the -th entry of this table contains the product .
The group is abelian if and only if this table is symmetric about the main diagonal. This is true since the group is abelian iff for all , which is iff the entry of the table equals the entry for all , i.e. the table is symmetric about the main diagonal.
Examples
[edit]- For the integers and the operation addition , denoted , the operation + combines any two integers to form a third integer, addition is associative, zero is the additive identity, every integer has an additive inverse, , and the addition operation is commutative since for any two integers and .
- Every cyclic group is abelian, because if , are in , then . Thus the integers, , form an abelian group under addition, as do the integers modulo , .
- Every ring is an abelian group with respect to its addition operation. In a commutative ring the invertible elements, or units, form an abelian multiplicative group. In particular, the real numbers are an abelian group under addition, and the nonzero real numbers are an abelian group under multiplication.
- Every subgroup of an abelian group is normal, so each subgroup gives rise to a quotient group. Subgroups, quotients, and direct sums of abelian groups are again abelian. The finite simple abelian groups are exactly the cyclic groups of prime order.[6]
- The concepts of abelian group and -module agree. More specifically, every -module is an abelian group with its operation of addition, and every abelian group is a module over the ring of integers in a unique way.
In general, matrices, even invertible matrices, do not form an abelian group under multiplication because matrix multiplication is generally not commutative. However, some groups of matrices are abelian groups under matrix multiplication – one example is the group of rotation matrices.
Historical remarks
[edit]Camille Jordan named abelian groups after the Norwegian mathematician Niels Henrik Abel, who had found that the commutativity of the group of a polynomial implies that the roots of the polynomial can be calculated by using radicals.[7][8]
Properties
[edit]If is a natural number and is an element of an abelian group written additively, then can be defined as ( summands) and . In this way, becomes a module over the ring of integers. In fact, the modules over can be identified with the abelian groups.[9]
Theorems about abelian groups (i.e. modules over the principal ideal domain ) can often be generalized to theorems about modules over an arbitrary principal ideal domain. A typical example is the classification of finitely generated abelian groups which is a specialization of the structure theorem for finitely generated modules over a principal ideal domain. In the case of finitely generated abelian groups, this theorem guarantees that an abelian group splits as a direct sum of a torsion group and a free abelian group. The former may be written as a direct sum of finitely many groups of the form for prime, and the latter is a direct sum of finitely many copies of .
If are two group homomorphisms between abelian groups, then their sum , defined by , is again a homomorphism. (This is not true if is a non-abelian group.) The set of all group homomorphisms from to is therefore an abelian group in its own right.
Somewhat akin to the dimension of vector spaces, every abelian group has a rank. It is defined as the maximal cardinality of a set of linearly independent (over the integers) elements of the group.[10] Finite abelian groups and torsion groups have rank zero, and every abelian group of rank zero is a torsion group. The integers and the rational numbers have rank one, as well as every nonzero additive subgroup of the rationals. On the other hand, the multiplicative group of the nonzero rationals has an infinite rank, as it is a free abelian group with the set of the prime numbers as a basis (this results from the fundamental theorem of arithmetic).
The center of a group is the set of elements that commute with every element of . A group is abelian if and only if it is equal to its center . The center of a group is always a characteristic abelian subgroup of . If the quotient group of a group by its center is cyclic then is abelian.[11]
Finite abelian groups
[edit]Cyclic groups of integers modulo , , were among the first examples of groups. It turns out that an arbitrary finite abelian group is isomorphic to a direct sum of finite cyclic groups of prime power order, and these orders are uniquely determined, forming a complete system of invariants. The automorphism group of a finite abelian group can be described directly in terms of these invariants. The theory had been first developed in the 1879 paper of Georg Frobenius and Ludwig Stickelberger and later was both simplified and generalized to finitely generated modules over a principal ideal domain, forming an important chapter of linear algebra.
Any group of prime order is isomorphic to a cyclic group and therefore abelian. Any group whose order is a square of a prime number is also abelian.[12] In fact, for every prime number there are (up to isomorphism) exactly two groups of order , namely and .
Classification
[edit]The fundamental theorem of finite abelian groups states that every finite abelian group can be expressed as the direct sum of cyclic subgroups of prime-power order; it is also known as the basis theorem for finite abelian groups. Moreover, automorphism groups of cyclic groups are examples of abelian groups.[13] This is generalized by the fundamental theorem of finitely generated abelian groups, with finite groups being the special case when G has zero rank; this in turn admits numerous further generalizations.
The classification was proven by Leopold Kronecker in 1870, though it was not stated in modern group-theoretic terms until later, and was preceded by a similar classification of quadratic forms by Carl Friedrich Gauss in 1801; see history for details.
The cyclic group of order is isomorphic to the direct sum of and if and only if and are coprime. It follows that any finite abelian group is isomorphic to a direct sum of the form
in either of the following canonical ways:
- the numbers are powers of (not necessarily distinct) primes,
- or divides , which divides , and so on up to .
For example, can be expressed as the direct sum of two cyclic subgroups of order 3 and 5: . The same can be said for any abelian group of order 15, leading to the remarkable conclusion that all abelian groups of order 15 are isomorphic.
For another example, every abelian group of order 8 is isomorphic to either (the integers 0 to 7 under addition modulo 8), (the odd integers 1 to 15 under multiplication modulo 16), or .
See also list of small groups for finite abelian groups of order 30 or less.
Automorphisms
[edit]One can apply the fundamental theorem to count (and sometimes determine) the automorphisms of a given finite abelian group . To do this, one uses the fact that if splits as a direct sum of subgroups of coprime order, then
Given this, the fundamental theorem shows that to compute the automorphism group of it suffices to compute the automorphism groups of the Sylow -subgroups separately (that is, all direct sums of cyclic subgroups, each with order a power of ). Fix a prime and suppose the exponents of the cyclic factors of the Sylow -subgroup are arranged in increasing order:
for some . One needs to find the automorphisms of
One special case is when , so that there is only one cyclic prime-power factor in the Sylow -subgroup . In this case the theory of automorphisms of a finite cyclic group can be used. Another special case is when is arbitrary but for . Here, one is considering to be of the form
so elements of this subgroup can be viewed as comprising a vector space of dimension over the finite field of elements . The automorphisms of this subgroup are therefore given by the invertible linear transformations, so
where is the appropriate general linear group. This is easily shown to have order
In the most general case, where the and are arbitrary, the automorphism group is more difficult to determine. It is known, however, that if one defines
and
then one has in particular , , and
One can check that this yields the orders in the previous examples as special cases (see Hillar & Rhea).
Finitely generated abelian groups
[edit]An abelian group A is finitely generated if it contains a finite set of elements (called generators) such that every element of the group is a linear combination with integer coefficients of elements of G.
Let L be a free abelian group with basis There is a unique group homomorphism such that
This homomorphism is surjective, and its kernel is finitely generated (since integers form a Noetherian ring). Consider the matrix M with integer entries, such that the entries of its jth column are the coefficients of the jth generator of the kernel. Then, the abelian group is isomorphic to the cokernel of linear map defined by M. Conversely every integer matrix defines a finitely generated abelian group.
It follows that the study of finitely generated abelian groups is totally equivalent with the study of integer matrices. In particular, changing the generating set of A is equivalent with multiplying M on the left by a unimodular matrix (that is, an invertible integer matrix whose inverse is also an integer matrix). Changing the generating set of the kernel of M is equivalent with multiplying M on the right by a unimodular matrix.
The Smith normal form of M is a matrix
where U and V are unimodular, and S is a matrix such that all non-diagonal entries are zero, the non-zero diagonal entries are the first ones, and is a divisor of for i > j. The existence and the shape of the Smith normal form proves that the finitely generated abelian group A is the direct sum
where r is the number of zero rows at the bottom of S (and also the rank of the group). This is the fundamental theorem of finitely generated abelian groups.
The existence of algorithms for Smith normal form shows that the fundamental theorem of finitely generated abelian groups is not only a theorem of abstract existence, but provides a way for computing expression of finitely generated abelian groups as direct sums.[14]
Infinite abelian groups
[edit]The simplest infinite abelian group is the infinite cyclic group . Any finitely generated abelian group is isomorphic to the direct sum of copies of and a finite abelian group, which in turn is decomposable into a direct sum of finitely many cyclic groups of prime power orders. Even though the decomposition is not unique, the number , called the rank of , and the prime powers giving the orders of finite cyclic summands are uniquely determined.
By contrast, classification of general infinitely generated abelian groups is far from complete. Divisible groups, i.e. abelian groups in which the equation admits a solution for any natural number and element of , constitute one important class of infinite abelian groups that can be completely characterized. Every divisible group is isomorphic to a direct sum, with summands isomorphic to and Prüfer groups for various prime numbers , and the cardinality of the set of summands of each type is uniquely determined.[15] Moreover, if a divisible group is a subgroup of an abelian group then admits a direct complement: a subgroup of such that . Thus divisible groups are injective modules in the category of abelian groups, and conversely, every injective abelian group is divisible (Baer's criterion). An abelian group without non-zero divisible subgroups is called reduced.
Two important special classes of infinite abelian groups with diametrically opposite properties are torsion groups and torsion-free groups, exemplified by the groups (periodic) and (torsion-free).
Torsion groups
[edit]An abelian group is called periodic or torsion, if every element has finite order. A direct sum of finite cyclic groups is periodic. Although the converse statement is not true in general, some special cases are known. The first and second Prüfer theorems state that if is a periodic group, and it either has a bounded exponent, i.e., for some natural number , or is countable and the -heights of the elements of are finite for each , then is isomorphic to a direct sum of finite cyclic groups.[16] The cardinality of the set of direct summands isomorphic to in such a decomposition is an invariant of .[17] These theorems were later subsumed in the Kulikov criterion. In a different direction, Helmut Ulm found an extension of the second Prüfer theorem to countable abelian -groups with elements of infinite height: those groups are completely classified by means of their Ulm invariants.[18]
Torsion-free and mixed groups
[edit]An abelian group is called torsion-free if every non-zero element has infinite order. Several classes of torsion-free abelian groups have been studied extensively:
- Free abelian groups, i.e. arbitrary direct sums of
- Cotorsion and algebraically compact torsion-free groups such as the -adic integers
- Slender groups[19]
An abelian group that is neither periodic nor torsion-free is called mixed. If is an abelian group and is its torsion subgroup, then the factor group is torsion-free. However, in general the torsion subgroup is not a direct summand of , so is not isomorphic to . Thus the theory of mixed groups involves more than simply combining the results about periodic and torsion-free groups. The additive group of integers is torsion-free -module.[20]
Invariants and classification
[edit]One of the most basic invariants of an infinite abelian group is its rank: the cardinality of the maximal linearly independent subset of . Abelian groups of rank 0 are precisely the periodic groups, while torsion-free abelian groups of rank 1 are necessarily subgroups of and can be completely described. More generally, a torsion-free abelian group of finite rank is a subgroup of . On the other hand, the group of -adic integers is a torsion-free abelian group of infinite -rank and the groups with different are non-isomorphic, so this invariant does not even fully capture properties of some familiar groups.
The classification theorems for finitely generated, divisible, countable periodic, and rank 1 torsion-free abelian groups explained above were all obtained before 1950 and form a foundation of the classification of more general infinite abelian groups. Important technical tools used in classification of infinite abelian groups are pure and basic subgroups. Introduction of various invariants of torsion-free abelian groups has been one avenue of further progress. See the books by Irving Kaplansky, László Fuchs, Phillip Griffith, and David Arnold, as well as the proceedings of the conferences on Abelian Group Theory published in Lecture Notes in Mathematics for more recent findings.
Additive groups of rings
[edit]The additive group of a ring is an abelian group, but not all abelian groups are additive groups of rings (with nontrivial multiplication). Some important topics in this area of study are:
- Tensor product
- A.L.S. Corner's results on countable torsion-free groups
- Shelah's work to remove cardinality restrictions
- Burnside ring
Relation to other mathematical topics
[edit]Many large abelian groups possess a natural topology, which turns them into topological groups.
The collection of all abelian groups, together with the homomorphisms between them, forms the category , the prototype of an abelian category.
Wanda Szmielew (1955) proved that the first-order theory of abelian groups, unlike its non-abelian counterpart, is decidable. Most algebraic structures other than Boolean algebras are undecidable.
There are still many areas of current research:
- Amongst torsion-free abelian groups of finite rank, only the finitely generated case and the rank 1 case are well understood;
- There are many unsolved problems in the theory of infinite-rank torsion-free abelian groups;
- While countable torsion abelian groups are well understood through simple presentations and Ulm invariants, the case of countable mixed groups is much less mature.
- Many mild extensions of the first-order theory of abelian groups are known to be undecidable.
- Finite abelian groups remain a topic of research in computational group theory.
Moreover, abelian groups of infinite order lead, quite surprisingly, to deep questions about the set theory commonly assumed to underlie all of mathematics. Take the Whitehead problem: are all Whitehead groups of infinite order also free abelian groups? In the 1970s, Saharon Shelah proved that the Whitehead problem is:
- Undecidable in ZFC (Zermelo–Fraenkel axioms), the conventional axiomatic set theory from which nearly all of present-day mathematics can be derived. The Whitehead problem is also the first question in ordinary mathematics proved undecidable in ZFC;
- Undecidable even if ZFC is augmented by taking the generalized continuum hypothesis as an axiom;
- Positively answered if ZFC is augmented with the axiom of constructibility (see statements true in L).
A note on typography
[edit]Among mathematical adjectives derived from the proper name of a mathematician, the word "abelian" is rare in that it is usually spelled with a lowercase a, rather than an uppercase A, the lack of capitalization being a tacit acknowledgment not only of the degree to which Abel's name has been institutionalized but also of how ubiquitous in modern mathematics are the concepts introduced by him.[21]
See also
[edit]| Algebraic structures |
|---|
- Commutator subgroup – Smallest normal subgroup by which the quotient is commutative
- Abelianization – Quotienting a group by its commutator subgroup
- Dihedral group of order 6 – Non-commutative group with 6 elements, the smallest non-abelian group
- Elementary abelian group – Commutative group in which all nonzero elements have the same order
- Grothendieck group – Abelian group extending a commutative monoid
- Pontryagin duality – Duality for locally compact abelian groups
Notes
[edit]- ^ Jacobson (2009), p. 41.
- ^ Ramík, J., Pairwise Comparisons Method: Theory and Applications in Decision Making (Cham: Springer Nature Switzerland, 2020), p. 11.
- ^ Auslander, M., & Buchsbaum, D., Groups, Rings, Modules (Mineola, NY: Dover Publications, 1974), pp. 28–29.
- ^ Stanojkovski, M., Intense Automorphisms of Finite Groups (Providence, RI: American Mathematical Society, 2021) pp. 9–14.
- ^ Isaev, A. P., & Rubakov, V. A., Theory of Groups and Symmetries: Finite Groups, Lie Groups, and Lie Algebras (Singapore: World Scientific, 2018), p. 10.
- ^ Rose 2012, p. 32.
- ^ Cox, D. A., Galois Theory (Hoboken, NJ: John Wiley & Sons, 2004), pp. 144–145.
- ^ Kepner, J., & H. Jananthan, Mathematics of Big Data (Cambridge, MA: MIT Press, 2018), pp. 157–158.
- ^ Eklof, Paul C., & Göbel, Rüdiger, eds., Abelian Groups and Modules: International Conference in Dublin, August 10–14, 1998 (Basel: Springer Basel AG, 1999), pp. 94–97.
- ^ Dixon, M. R., Kurdachenko, L. A., & Subbotin, I. Y., Linear Groups: The Accent on Infinite Dimensionality (Milton Park, Abingdon-on-Thames & Oxfordshire: Taylor & Francis, 2020), pp. 49–50.
- ^ Rose 2012, p. 48.
- ^ Rose 2012, p. 79.
- ^ Kurzweil, H., & Stellmacher, B., The Theory of Finite Groups: An Introduction (New York, Berlin, Heidelberg: Springer Verlag, 2004), pp. 43–54.
- ^ Finkelstein, L., & Kantor, W. M., eds., Groups and Computation II: Workshop on Groups and Computation, June 7–10, 1995 (Providence: AMS, 1997), pp. 26–27.
- ^ For example, .
- ^ Countability assumption in the second Prüfer theorem cannot be removed: the torsion subgroup of the direct product of the cyclic groups for all natural is not a direct sum of cyclic groups.
- ^ Faith, C. C., Rings and Things and a Fine Array of Twentieth Century Associative Algebra (Providence: AMS, 2004), p. 6.
- ^ Gao, S., Invariant Descriptive Set Theory (Boca Raton, FL: CRC Press, 2008), p. 317.
- ^ Albrecht, U., "Products of Slender Abelian Groups", in Göbel, R., & Walker, E., eds., Abelian Group Theory: Proceedings of the Third Conference Held on Abelian Group Theory at Oberwolfach, August 11-17, 1985 (New York: Gordon & Breach, 1987), pp. 259–274.
- ^ Lal, R., Algebra 2: Linear Algebra, Galois Theory, Representation Theory, Group Extensions and Schur Multiplier (Berlin, Heidelberg: Springer, 2017), p. 206.
- ^ "Abel Prize Awarded: The Mathematicians' Nobel". Archived from the original on 31 December 2012. Retrieved 3 July 2016.
References
[edit]- Cox, David (2004). Galois Theory. Wiley-Interscience. ISBN 9781118031339. MR 2119052.
- Fuchs, László (1970). Infinite Abelian Groups. Pure and Applied Mathematics. Vol. 36-I. Academic Press. MR 0255673.
- Fuchs, László (1973). Infinite Abelian Groups. Pure and Applied Mathematics. Vol. 36-II. Academic Press. MR 0349869.
- Griffith, Phillip A. (1970). Infinite Abelian group theory. Chicago Lectures in Mathematics. University of Chicago Press. ISBN 0-226-30870-7.
- Herstein, I. N. (1975). Topics in Algebra (2nd ed.). John Wiley & Sons. ISBN 0-471-02371-X.
- Hillar, Christopher; Rhea, Darren (2007). "Automorphisms of finite abelian groups" (PDF). American Mathematical Monthly. 114 (10): 917–923. arXiv:math/0605185. Bibcode:2006math......5185H. doi:10.1080/00029890.2007.11920485. JSTOR 27642365. S2CID 1038507. Archived from the original (PDF) on 2006-06-29. Retrieved 2023-12-27.
- Jacobson, Nathan (2009). Basic Algebra I (2nd ed.). Dover Publications. ISBN 978-0-486-47189-1.
- Rose, John S. (2012). A Course on Group Theory. Dover Publications. ISBN 978-0-486-68194-8. Unabridged and unaltered republication of a work first published by the Cambridge University Press, Cambridge, England, in 1978.
- Szmielew, W. M. (1955). "Elementary Properties of Abelian Groups" (PDF). Fundamenta Mathematicae. 41 (2): 203–271. doi:10.4064/fm-41-2-203-271. MR 0072131. Zbl 0248.02049.
- Robinson, Abraham; Zakon, Elias (1960). "Elementary Properties of Ordered Abelian Groups" (PDF). Transactions of the American Mathematical Society. 96 (2): 222–236. doi:10.2307/1993461. JSTOR 1993461. Archived (PDF) from the original on 2022-10-09.
External links
[edit]- "Abelian group". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
Abelian group
View on GrokipediaDefinition and Fundamentals
Definition
In abstract algebra, an Abelian group is a group whose operation satisfies the commutativity property, meaning that the order of elements does not affect the result of the operation.[9] Formally, given a group equipped with a binary operation , the group is Abelian if for all , .[10] This condition augments the standard group axioms—closure, associativity, identity element, and invertibility—with the additional requirement of commutativity, distinguishing Abelian groups from general groups where the operation may not commute.[11] The commutativity axiom simplifies the structure of these groups, facilitating their classification and application in broader algebraic contexts such as number theory and topology.[12] For contrast, consider the general linear group for , which consists of invertible matrices over the real numbers under matrix multiplication; this group is non-Abelian because matrix multiplication is not commutative in general (e.g., distinct Pauli matrices fail to commute). Thus, Abelian groups represent a fundamental subclass where symmetry in the operation enables more tractable theoretical developments.[13]Basic Notation
In the study of Abelian groups, two primary notations are employed to denote the group operation, reflecting the commutative nature of the structure. The additive notation represents an Abelian group as , where the binary operation is addition, emphasizing the module-like properties over the integers.[14] In this convention, the identity element is denoted by , and the inverse of an element is written as , satisfying .[15] Conversely, the multiplicative notation denotes the group as , with the operation often written as multiplication or juxtaposition for ; here, the identity is (or sometimes ), and the inverse of is , such that .[16] Additive notation is preferentially used for Abelian groups to highlight their additive structure, while multiplicative notation appears in contexts like general groups or specific examples such as the nonzero rationals under multiplication.[17] The group of integers under addition, denoted , serves as the prototypical infinite cyclic Abelian group and is fundamental in the theory.[18] In additive notation, with the operation , identity , and inverses for . This group generates many others through quotients and extensions, underscoring its central role.[19] Finite cyclic Abelian groups of order are commonly notated as (or ) in additive form, consisting of residue classes modulo with componentwise addition. Here, the generator is the class of , and elements are for , with the relation . This notation aligns with the ring of integers modulo but focuses on the additive group structure.[20] For combining Abelian groups, the direct product is denoted in multiplicative notation, but for additive Abelian groups, the direct sum is standard, with the operation defined componentwise: .[21] This distinguishes the infinite case, where direct sums restrict to finitely supported tuples, from direct products that allow arbitrary tuples, though for finite groups they coincide. The symbol reinforces the additive convention and is extended to finite direct sums .[22]Illustrative Examples
Finite Abelian Groups
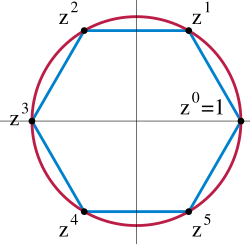
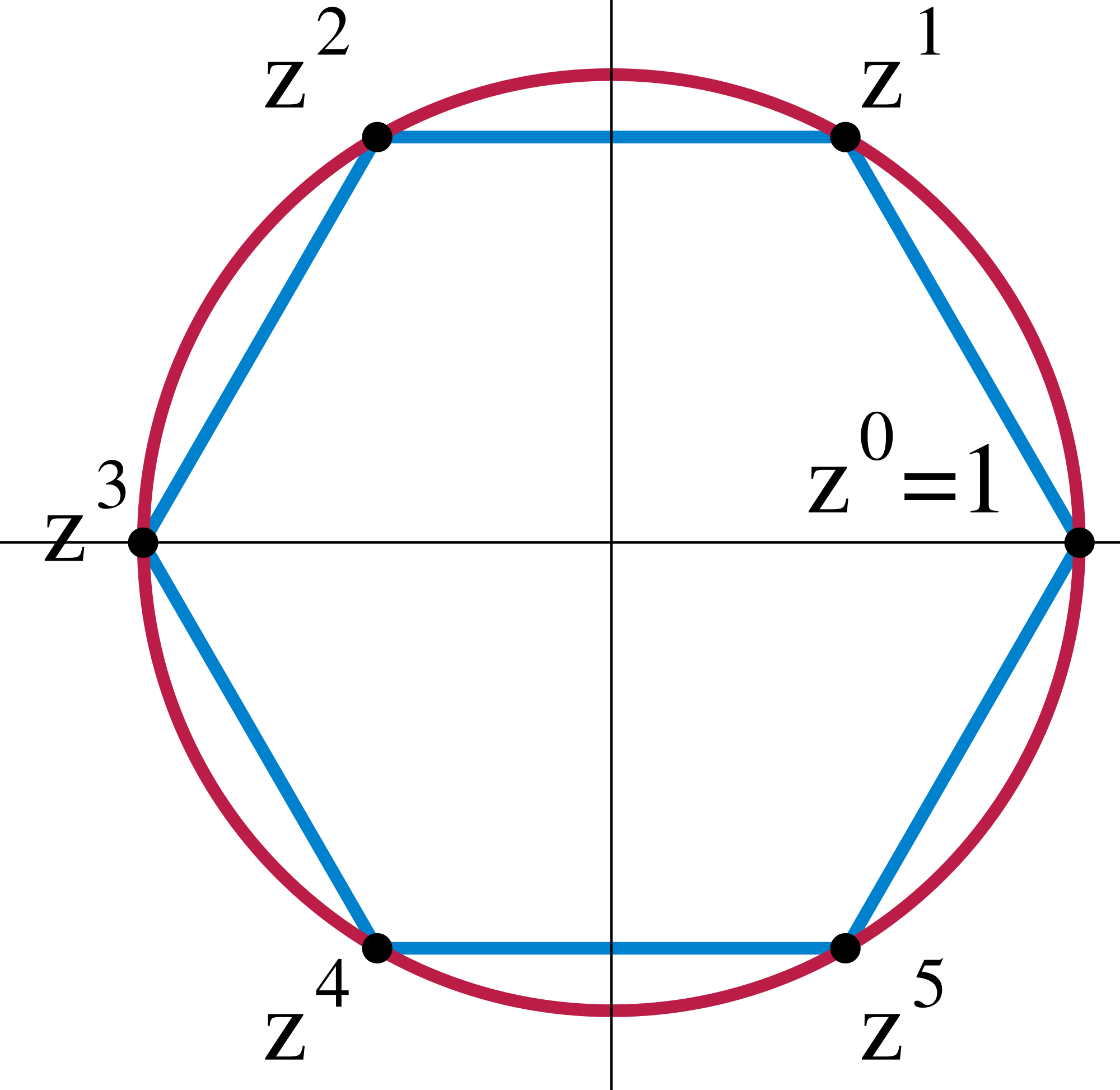
Finite Abelian groups provide essential examples that demonstrate the structure and operations within commutative group theory. One fundamental class consists of cyclic groups of finite order, denoted , which are generated by a single element under addition modulo . For instance, the group has elements with the operation of addition modulo 3, where , , and .[23] Similarly, comprises elements under addition modulo 4, yielding , , , and so forth up to .[23] These cyclic groups arise naturally as the rotation subgroups of regular polygons. The rotation group of a regular -gon is isomorphic to , consisting of rotations by multiples of radians around the center, which commute due to the cyclic nature of the symmetries.[24] For example, the rotations of an equilateral triangle form , while those of a square form .[24] Direct products of cyclic groups yield additional finite Abelian groups, where the operation is componentwise addition. Consider , with elements as ordered pairs where and , and addition modulo 2 in the first component and modulo 4 in the second; this group has order 8 and is non-cyclic since no single element generates all pairs (the maximum order of any element is 4). A prominent example is the Klein four-group , isomorphic to , which has elements under componentwise addition modulo 2; every non-identity element has order 2, distinguishing it from cyclic groups of the same order.[25] The group's operation table is as follows:| + | (0,0) | (1,0) | (0,1) | (1,1) |
|---|---|---|---|---|
| (0,0) | (0,0) | (1,0) | (0,1) | (1,1) |
| (1,0) | (1,0) | (0,0) | (1,1) | (0,1) |
| (0,1) | (0,1) | (1,1) | (0,0) | (1,0) |
| (1,1) | (1,1) | (0,1) | (1,0) | (0,0) |