Hubbry Logo
Structural formulaStructural formulaMain
Open search
Structural formula
Community hub
Structural formula
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Structural formula
Structural formula
Structural formula
View on Wikipedia
from Wikipedia
Skeletal structural formula of Vitamin B12. Many organic molecules are too complicated to be specified by a molecular formula.

The structural formula of a chemical compound is a graphic representation of the molecular structure (determined by structural chemistry methods), showing how the atoms are connected to one another.[1] The chemical bonding within the molecule is also shown, either explicitly or implicitly. Unlike other chemical formula types,[a] which have a limited number of symbols and are capable of only limited descriptive power, structural formulas provide a more complete geometric representation of the molecular structure. For example, many chemical compounds exist in different isomeric forms, which have different enantiomeric structures but the same molecular formula. There are multiple types of ways to draw these structural formulas such as: Lewis structures, condensed formulas, skeletal formulas, Newman projections, Cyclohexane conformations, Haworth projections, and Fischer projections.[3]

Several systematic chemical naming formats, as in chemical databases, are used that are equivalent to, and as powerful as, geometric structures. These chemical nomenclature systems include SMILES, InChI and CML. These systematic chemical names can be converted to structural formulas and vice versa, but chemists nearly always describe a chemical reaction or synthesis using structural formulas rather than chemical names, because the structural formulas allow the chemist to visualize the molecules and the structural changes that occur in them during chemical reactions. ChemSketch and ChemDraw are popular downloads/websites that allow users to draw reactions and structural formulas, typically in the Lewis Structure style.

Structures in structural formulas

[edit]

Bonds

[edit]

Bonds are often shown as a line that connects one atom to another. One line indicates a single bond. Two lines indicate a double bond, and three lines indicate a triple bond. In some structures the atoms in between each bond are specified and shown. However, in some structures, the carbon molecules are not written out specifically. Instead, these carbons are indicated by a corner that forms when two lines connect. Additionally, Hydrogen atoms are implied and not usually drawn out. These can be inferred based on how many other atoms the carbon is attached to. For example, if Carbon A is attached to one other Carbon B, Carbon A will have three hydrogens in order to fill its octet.[4]

This shows the bonds in relation to the electrons being shared.
This shows how bonds are depicted to connect to other atoms in the various structural formulas used.

Electrons

[edit]
Charges on atoms and their formation

Electrons are usually shown as colored-in circles. One circle indicates one electron. Two circles indicate a pair of electrons. Typically, a pair of electrons will also indicate a negative charge. By using the colored circles, the number of electrons in the valence shell of each respective atom is indicated, providing further descriptive information regarding the reactive capacity of that atom in the molecule.[4]

Charges

[edit]

Oftentimes, atoms will have a positive or negative charge as their octet may not be complete. If the atom is missing a pair of electrons or has a proton, it will have a positive charge. If the atom has electrons that are not bonded to another atom, there will be a negative charge. In structural formulas, the positive charge is indicated by ⊕, and the negative charge is indicated by ⊖ .[4]

This image shows the wedges in the structural formula and how they indicate the stereochemistry of the compound.

Stereochemistry (Skeletal formula)

[edit]
Skeletal formula of strychnine. A solid wedged bond seen for example at the nitrogen (N) at top indicates a bond pointing above-the-plane, while a dashed wedged bond seen for example at the hydrogen (H) at bottom indicates a below-the-plane bond.

Chirality in skeletal formulas is indicated by the Natta projection method. Stereochemistry is used to show the relative spatial arrangement of atoms in a molecule. Wedges are used to show this, and there are two types: dashed and filled. A filled wedge indicates that the atom is in the front of the molecule; it is pointing above the plane of the paper towards the front. A dashed wedge indicates that the atom is behind the molecule; it is pointing below the plane of the paper. When a straight, un-dashed line is used, the atom is in the plane of the paper. This spatial arrangement provides an idea of the molecule in a 3-dimensional space and there are constraints as to how the spatial arrangements can be arranged.[4]

Unspecified stereochemistry

[edit]
Fructose, with a bond at the hydroxyl (OH) group upper left of image with unknown or unspecified stereochemistry

Wavy single bonds represent unknown or unspecified stereochemistry or a mixture of isomers. For example, the adjacent diagram shows the fructose molecule with a wavy bond to the HOCH2− group at the left. In this case the two possible ring structures are in chemical equilibrium with each other and also with the open-chain structure. The ring automatically opens and closes, sometimes closing with one stereochemistry and sometimes with the other.[citation needed]

Skeletal formulas can depict cis and trans isomers of alkenes. Wavy single bonds are the standard way to represent unknown or unspecified stereochemistry or a mixture of isomers (as with tetrahedral stereocenters). A crossed double-bond has been used sometimes, but is no longer considered an acceptable style for general use.[5]

Alkene stereochemistry

Lewis structures

[edit]
Representation of molecules by the Lewis structure
Main article: Lewis structure

Lewis structures (or "Lewis dot structures") are flat graphical formulas that show atom connectivity and lone pair or unpaired electrons, but not three-dimensional structure. This notation is mostly used for small molecules. Each line represents the two electrons of a single bond. Two or three parallel lines between pairs of atoms represent double or triple bonds, respectively. Alternatively, pairs of dots may be used to represent bonding pairs. In addition, all non-bonded electrons (paired or unpaired) and any formal charges on atoms are indicated. Through the use of Lewis structures, the placement of electrons, whether it is in a bond or in lone pairs, will allow for the identification of the formal charges of the atoms in the molecule to understand the stability and determine the most likely molecule (based on molecular geometry difference) that would be formed in a reaction. Lewis structures do give some thought to the geometry of the molecule as oftentimes, the bonds are drawn at certain angles to represent the molecule in real life. Lewis structure is best used to calculate formal charges or how atoms bond to each other as both electrons and bonds are shown. Lewis structures give an idea of the molecular and electronic geometry which varies based on the presence of bonds and lone pairs and through this one could determine the bond angles and hybridization as well.

Condensed formulas

[edit]

In early organic-chemistry publications, where use of graphics was strongly limited, a typographic system arose to describe organic structures in a line of text. Although this system tends to be problematic in application to cyclic compounds, it remains a convenient way to represent simple structures:

CH3CH2OH (ethanol)

Parentheses are used to indicate multiple identical groups, indicating attachment to the nearest non-hydrogen atom on the left when appearing within a formula, or to the atom on the right when appearing at the start of a formula:

(CH3)2CHOH or CH(CH3)2OH (2-propanol)

In all cases, all atoms are shown, including hydrogen atoms. It is also helpful to show the carbonyls where the C=O is implied through the O being placed in the parentheses. For example:

CH3C(O)CH3 (acetone)

Therefore, it is important to look to the left of the atom in the parentheses to make sure what atom it is attached to. This is helpful when converting from condensed formula to another form of structural formula such as skeletal formula or Lewis structures. There are different ways to show the various functional groups in the condensed formulas such as aldehyde as CHO, carboxylic acids as CO2H or COOH, esters as CO2R or COOR. However, the use of condensed formulas does not give an immediate idea of the molecular geometry of the compound or the number of bonds between the carbons, it needs to be recognized based on the number of atoms attached to the carbons and if there are any charges on the carbon.[6]

Skeletal formulas

[edit]
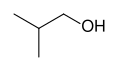
Main article: Skeletal formula

Skeletal formulas are the standard notation for more complex organic molecules. In this type of diagram, first used by the organic chemist Friedrich August Kekulé von Stradonitz,[7] the carbon atoms are implied to be located at the vertices (corners) and ends of line segments rather than being indicated with the atomic symbol C. Hydrogen atoms attached to carbon atoms are not indicated: each carbon atom is understood to be associated with enough hydrogen atoms to give the carbon atom four bonds. The presence of a positive or negative charge at a carbon atom takes the place of one of the implied hydrogen atoms. Hydrogen atoms attached to atoms other than carbon must be written explicitly. An additional feature of skeletal formulas is that by adding certain structures the stereochemistry, that is the three-dimensional structure, of the compound can be determined. Often times, the skeletal formula can indicate stereochemistry through the use of wedges instead of lines. Solid wedges represent bonds pointing above the plane of the paper, whereas dashed wedges represent bonds pointing below the plane.

Perspective drawings

[edit]

Newman projection and sawhorse projection

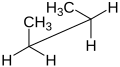
[edit]

The Newman projection and the sawhorse projection are used to depict specific conformers or to distinguish vicinal stereochemistry. In both cases, two specific carbon atoms and their connecting bond are the center of attention. The only difference is a slightly different perspective: the Newman projection looking straight down the bond of interest, the sawhorse projection looking at the same bond but from a somewhat oblique vantage point. In the Newman projection, a circle is used to represent a plane perpendicular to the bond, distinguishing the substituents on the front carbon from the substituents on the back carbon. In the sawhorse projection, the front carbon is usually on the left and is always slightly lower. Sometimes, an arrow is used to indicate the front carbon. The sawhorse projection is very similar to a skeletal formula, and it can even use wedges instead of lines to indicate the stereochemistry of the molecule. The sawhorse projection is set apart from the skeletal formulas because the sawhorse projection is not a very good indicator of molecule geometry and molecular arrangement. Both a Newman and Sawhorse Projection can be used to create a Fischer Projection.[citation needed]

  • Newman projection of butane
    Newman projection of butane
  • Sawhorse projection of butane
    Sawhorse projection of butane

Cyclohexane conformations

[edit]

Certain conformations of cyclohexane and other small-ring compounds can be shown using a standard convention. For example, the standard chair conformation of cyclohexane involves a perspective view from slightly above the average plane of the carbon atoms and indicates clearly which groups are axial (pointing vertically up or down) and which are equatorial (almost horizontal, slightly slanted up or down). Bonds in front may or may not be highlighted with stronger lines or wedges. The conformations progress as follows: chair to half-chair to twist-boat to boat to twist-boat to half-chair to chair. The cyclohexane conformations may also be used to show the potential energy present at each stage as shown in the diagram. The chair conformations (A) have the lowest energy, whereas the half-chair conformations (D) have the highest energy. There is a peak/local maximum at the boat conformation (C), and there are valleys/local minimums at the twist-boat conformations (B). In addition, cyclohexane conformations can be used to indicate if the molecule has any 1,3 diaxial-interactions which are steric interactions between axial substituents on the 1,3, and 5 carbons.[8]

Chair conformation of beta-D-Glucose
The cyclohexane conformations in relation to the potential energy at each conformation

Haworth projection

[edit]

The Haworth projection is used for cyclic sugars. Axial and equatorial positions are not distinguished; instead, substituents are positioned directly above or below the ring atom to which they are connected. Hydrogen substituents are typically omitted.

However, an important thing to keep in mind while reading an Haworth projection is that the ring structures are not flat. Therefore, Haworth does not provide 3-D shape. Sir Norman Haworth, was a British Chemist, who won a Nobel Prize for his work on Carbohydrates and discovering the structure of Vitamin C. During his discovery, he also deducted different structural formulas which are now referred to as Haworth Projections. In a Haworth Projection a pyranose sugar is depicted as a hexagon and a furanose sugar is depicted as a pentagon. Usually an oxygen is placed at the upper right corner in pyranose and in the upper center in a furanose sugar. The thinner bonds at the top of the ring refer to the bonds as being farther away and the thicker bonds at the bottom of the ring refer to the end of the ring that is closer to the viewer.[9]

Fischer and Haworth projection of Glucopyranose
Haworth projection of beta-D-Glucose

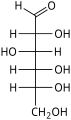
Fischer projection

[edit]

The Fischer projection is mostly used for linear monosaccharides. At any given carbon center, vertical bond lines are equivalent to stereochemical hashed markings, directed away from the observer, while horizontal lines are equivalent to wedges, pointing toward the observer. The projection is unrealistic, as a saccharide would never adopt this multiply eclipsed conformation. Nonetheless, the Fischer projection is a simple way of depicting multiple sequential stereocenters that does not require or imply any knowledge of actual conformation. A Fischer projection will restrict a 3-D molecule to 2-D, and therefore, there are limitations to changing the configuration of the chiral centers. Fischer projections are used to determine the R and S configuration on a chiral carbon and it is done using the Cahn Ingold Prelog rules. It is a convenient way to represent and distinguish between enantiomers and diastereomers.[9]

  • Fischer projection of D-Glucose
    Fischer projection of D-Glucose

Limitations

[edit]

A structural formula is a simplified model that cannot represent certain aspects of chemical structures. For example, formalized bonding may not be applicable to dynamic systems such as delocalized bonds. Aromaticity is such a case and relies on convention to represent the bonding. Different styles of structural formulas may represent aromaticity in different ways, leading to different depictions of the same chemical compound. Another example is formal double bonds where the electron density is spread outside the formal bond, leading to partial double bond character and slow inter-conversion at room temperature. For all dynamic effects, temperature will affect the inter-conversion rates and may change how the structure should be represented. There is no explicit temperature associated with a structural formula, although many assume that it would be standard temperature.[citation needed]

See also

[edit]

Notes

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Structural formula

View on Grokipedia
from Grokipedia
A structural formula is a diagrammatic representation in chemistry that illustrates the arrangement of atoms within a and the chemical bonds connecting them, providing a visual depiction of molecular connectivity. Unlike a molecular formula, which simply lists the types and numbers of atoms (e.g., C₂H₆O for ethanol), or an empirical formula, which gives the simplest whole-number ratio of atoms (e.g., CH₃O), a structural formula explicitly shows how atoms are linked, enabling distinction between isomers like ethanol (CH₃CH₂OH) and dimethyl ether (CH₃OCH₃). Structural formulas exist in several formats to balance detail and clarity, particularly in . Expanded structural formulas display every atom and bond individually, such as H–O–H for , highlighting all covalent connections. Condensed structural formulas simplify this by grouping atoms and omitting some bonds, as in CH₃CH₂OH for , while skeletal or line-angle formulas—common for complex organic molecules—represent carbon atoms implicitly at line intersections or ends, with hydrogens assumed to fill valences, focusing on the carbon and functional groups. Lewis structures, another variant, additionally include lone pairs, multiple bonds (single, double, triple), and formal charges to convey electron distribution, as seen in (CH₄) with four single bonds. These representations are fundamental in chemistry, especially , where a molecular alone cannot uniquely identify a compound due to possible structural isomers differing in atom connectivity and thus in and reactivity. Structural formulas embody the theoretical core of the discipline by serving as both descriptive notations and predictive models for molecular behavior, facilitating the design of syntheses, analysis of reaction mechanisms, and comprehension of . For instance, they reveal how double bonds or rings influence counts in stable carbon-based compounds, underscoring their role in advancing chemical understanding and applications.

Fundamentals of Structural Formulas

Definition and Purpose

A structural formula is a diagrammatic representation that depicts the arrangement of atoms within a , explicitly showing the connections between atoms via chemical bonds, in contrast to a molecular formula, which only specifies the types and numbers of atoms present without indicating their linkages. For instance, the molecular formula C₆H₆ represents but does not reveal its cyclic structure, whereas a structural formula illustrates the hexagonal ring of carbon atoms with alternating double bonds. This distinction is crucial because molecular formulas alone cannot differentiate between compounds with the same atomic composition but different connectivities, such as the various isomers of C₄H₁₀O. The concept of structural formulas originated in the , pioneered by chemists seeking to explain the valence and connectivity in organic molecules. Friedrich played a pivotal role in 1858 by proposing that carbon atoms could form chains, establishing tetravalency as a key principle, and in 1865, he introduced the cyclic structural formula for , depicting it as a ring of six carbon atoms to account for its stability and reactivity. This innovation marked a shift from empirical observations to visual models of molecular architecture, enabling chemists to represent bonding patterns systematically. Structural formulas serve to elucidate isomerism by highlighting variations in atomic connectivity, which lead to distinct molecular behaviors despite identical molecular formulas; for example, they distinguish n-butane from , both C₄H₁₀, by showing linear versus branched chains. They also facilitate the depiction of reaction mechanisms, allowing chemists to trace bond breaking and forming in stepwise processes, as seen in illustrations of nucleophilic substitutions where explicit bond arrangements clarify intermediate structures. Furthermore, by revealing patterns, structural formulas help predict physical influenced by molecular , such as points differing between straight-chain and branched alkanes due to variations in intermolecular forces.

Representation of Bonds

In structural formulas, covalent bonds are visually represented by lines connecting atomic symbols, with the type of bond indicated by the number and style of lines used. A , involving the sharing of one pair of s between two atoms, is depicted as a single solid straight line; for instance, the C-H bonds in are shown this way. Double bonds, which share two pairs, are represented by two parallel solid lines, as seen in the C=O bond of (H₂C=O). Triple bonds, sharing three pairs, use three parallel lines, such as in the N≡N bond of nitrogen gas. Non-covalent interactions, like hydrogen bonds or van der Waals forces, are conventionally shown with dashed lines to distinguish them from covalent linkages, emphasizing their weaker nature without implying electron sharing. These representations adhere to fundamental valence rules, ensuring that atoms achieve stable electron configurations as per the for elements in the second period of the periodic table, where eight valence electrons are typically sought. In depictions, this means carbon, for example, forms four bonds to complete its octet, as illustrated in (CH₄), where the central carbon connects to four s via single bonds, each satisfying its duet rule with one bond. Similar conventions apply to other atoms: oxygen often forms two bonds and has two s (implied in basic structural formulas), while forms three bonds and one . Violations of the occur in certain cases, such as with elements beyond the second period, but standard organic structural formulas prioritize octet compliance for main-group elements unless exceptions like compounds (e.g., BF₃ with six electrons around ) are specified. For aromatic compounds, bond representation departs from simple alternating single and double bonds to convey delocalization. In (C₆H₆), the classic Kekulé structure uses three alternating double bonds in a hexagonal ring to suggest , but a more accurate notation employs a inscribed within the hexagon to symbolize the uniform, delocalized π-electron across all six C-C bonds, each of equal (approximately 1.39 ). This circle convention highlights the stability of the aromatic system without implying localized double bonds. Although two-dimensional structural formulas do not explicitly depict angles, they implicitly convey standard molecular geometries based on hybridization and valence electron pairs. For sp³-hybridized carbons with four single bonds, a tetrahedral with bond angles of about 109.5° is assumed, as in the carbon framework of alkanes; deviations, such as in cyclopropane's strained 60° angles, are noted separately but not shown in basic line drawings. This implicit geometry aids in understanding reactivity and shape without requiring three-dimensional projections.

Representation of Electrons and Charges

In structural formulas, non-bonding electrons, known as lone pairs, are represented by pairs of dots placed adjacent to the atom to which they belong, illustrating the complete configuration without overlapping with bond representations. For example, in the (H₂O), the oxygen atom is depicted with two lone pairs as four dots (two pairs) positioned above and below the atom, alongside its two single bonds to atoms. This notation emphasizes the fulfillment for second-period elements, where lone pairs contribute to the atom's stability. Formal charges on atoms within a structural formula are indicated by superscript numbers placed next to the atom, such as +1 or -1, to denote deviations from neutrality due to distribution in bonds and lone pairs. The is calculated using the formula: Formal charge=(valence electrons)−(non-bonding electrons)−12(bonding electrons)\text{Formal charge} = (\text{valence electrons}) - (\text{non-bonding electrons}) - \frac{1}{2} (\text{bonding electrons}) For instance, in a like the methyl cation (CH₃⁺), the central carbon bears a +1 formal charge as a superscript, reflecting its six valence electrons (three from bonds and none non-bonding) compared to its group 4A valence of four. This convention helps identify reactive sites and validate resonance structures in molecules. Unpaired electrons, characteristic of radicals, are shown as a single dot adjacent to the atom or group, distinguishing them from paired lone pairs or shared bonding electrons. In the methyl radical (CH₃•), the dot follows the formula to signify the carbon's , highlighting its high reactivity and odd-electron nature. This simple dot notation is essential for depicting involved in chain reactions and ./01%3A_Structure_and_Bonding/1.04%3A_Lewis_Structures_Continued) For polyatomic ions, the entire structural formula is enclosed in square brackets, with the net ionic charge indicated as a superscript outside the brackets to convey the overall electron imbalance distributed across the . The sulfate ion, for example, is represented as [O₃S(=O)₂]²⁻ (or in dot notation with lone pairs), where the 2- charge outside the brackets accounts for the two extra electrons beyond neutral sulfur and oxygen valences. This bracketing ensures clarity in ionic compounds and distinguishes the ion from neutral molecules.

Planar Structural Representations

Lewis Structures

Lewis structures, also known as Lewis dot diagrams or electron-dot structures, represent the arrangement of valence electrons in atoms, ions, and molecules, illustrating covalent bonds as shared electron pairs and lone pairs on atoms. Developed by in his 1916 paper "The Atom and the Molecule," these diagrams emphasize the role of valence electrons in forming stable octet configurations, where most atoms achieve eight electrons in their outer shells to mimic stability. This approach provides a visual tool for predicting , reactivity, and bonding without delving into . The construction of a Lewis structure involves a step-by-step process to ensure accurate electron distribution:
  1. Calculate the total number of valence electrons by summing the valence electrons from all atoms in the formula, adding electrons for negative charges or subtracting for positive charges.
  2. Sketch the skeletal framework by arranging atoms, placing the central atom (typically the least electronegative, excluding ) and connecting others with single bonds represented as lines or pairs of dots.
  3. Distribute the remaining valence electrons as lone pairs to peripheral atoms first, aiming to complete their octets (or duets for ).
  4. Assign any leftover electrons to the central atom; if its octet is incomplete, form multiple bonds by converting lone pairs into shared double or triple bonds as needed.
For (NH3), the features as the central atom with three single bonds to atoms (each bond as a pair of shared electrons) and one on , resulting in eight electrons around and two around each . This satisfies the for while highlighting its potential as a Lewis base due to the . Certain molecules require resonance structures to depict delocalized electrons that cannot be confined to a single Lewis diagram; the actual bonding is a hybrid of these equivalent forms. In (O3), two resonance structures show a alternating between the central oxygen and each terminal oxygen, with the real exhibiting partial double-bond character in both O-O links and 1.5 . Exceptions to the arise in cases where stable structures deviate from eight valence electrons around an atom. Odd-electron molecules, like the radical (NO2), contain an , preventing all atoms from achieving octets and often resulting in reactive free radicals. Expanded octets occur in hypervalent compounds such as (SF6), where sulfur bonds to six fluorines using 12 electrons, possible for main-group elements beyond the second period, which can exceed the octet through hypervalent bonding mechanisms. Electron-deficient species, exemplified by (BF3), have with only six electrons in three bonds, making it a Lewis prone to accepting additional electron pairs. These exceptions underscore the octet rule's utility as a guideline rather than an absolute law, guiding structure prediction while accommodating diverse bonding scenarios.

Condensed Formulas

Condensed structural formulas represent the connectivity of atoms in a using a linear, text-based notation that omits explicit bond lines while grouping atoms and substituents to convey structure efficiently. This format is particularly useful in for depicting carbon chains and branches without the visual complexity of full diagrams. The notation relies on implied single bonds between adjacent atoms, with carbon atoms assumed at intersections or chains unless specified otherwise, and atoms grouped directly with their attached carbons using subscripts for multiples. Parentheses are employed to indicate branches or substituents attached to the same atom, ensuring clarity in non-linear arrangements; for example, (2-methylpropane) is written as CH₃CH(CH₃)CH₃, where the parentheses denote the branching from the second carbon. In straight-chain alkanes, repeating units are abbreviated, as in n-octane represented as CH₃(CH₂)₆CH₃, which compactly shows the six methylene groups between terminal methyls. One key advantage of condensed formulas is their compactness, making them ideal for describing long or repetitive carbon chains without drawing extensive lines, thus facilitating quick communication in chemical literature and calculations. This brevity retains essential connectivity information while reducing the space required compared to expanded structural representations. However, condensed formulas can introduce limitations in clarity, particularly with complex branching, where arises if parentheses are omitted or misinterpreted, potentially leading to confusion between isomers. Proper use of grouping symbols is essential to avoid such issues, though they do not depict three-dimensional aspects or multiple bonds as explicitly as other notations. To convert a to a condensed , remove all explicit bond lines and electron dots, then group atoms with their respective carbons, using subscripts for identical groups and parentheses for branches to preserve the skeletal arrangement. This process simplifies the visual while maintaining the molecular topology. Skeletal formulas serve as further simplifications by omitting indications entirely.

Skeletal Formulas

Skeletal formulas, also known as line-angle or bond-line notations, provide a streamlined visual representation of organic molecules by emphasizing the connectivity of the carbon framework. In this system, each vertex or terminus of a line denotes a carbon atom, while the lines themselves signify covalent bonds, with single bonds as solid lines and double bonds as paired lines or indicated explicitly. Hydrogen atoms attached to carbon are routinely omitted, as they are inferred to satisfy the four-valence requirement of carbon, thereby reducing visual complexity without sacrificing essential structural information. To reflect the tetrahedral arrangement around carbon atoms, linear chains in skeletal formulas are conventionally drawn in a zig-zag , where each segment represents a C-C bond angled to mimic bond angles near 109.5°. This approach facilitates quick recognition of chain length and branching, as intersections indicate branch points or ring closures. For cyclic structures, bonds form closed polygons, with commonly illustrated as a regular featuring three alternating double bonds to denote its , or equivalently, a enclosing a circle to symbolize uniform electron delocalization across the ring./15%3A_Benzene_and_Aromatic_Compounds/15.02%3A_The_Structure_of_Benzene) In , skeletal formulas serve as the standard for illustrating intricate molecules like steroids, which possess a characteristic tetracyclic core of three six-membered rings fused to one five-membered ring, allowing chemists to focus on placements and stereocenters amid dense connectivity. Heteroatoms, such as oxygen or , are explicitly labeled with their atomic symbols at bond junctions or ends, and electrons may be depicted as dots when clarification of reactivity or charge is required, though they are frequently implied based on standard valences. Basic skeletal formulas assume a two-dimensional planar layout, though wedge and dash notations can be incorporated briefly to denote at chiral centers.

Stereochemical and Perspective Representations

Basic Stereochemistry Notation

Basic stereochemistry notation in structural formulas provides a two-dimensional method to indicate the spatial of atoms around chiral centers and double bonds, allowing chemists to depict stereoisomers without requiring full three-dimensional models. These notations are essential for representing molecules where the arrangement of substituents affects properties such as reactivity and . Commonly applied to planar representations like skeletal formulas, they use simple line conventions to convey depth or relative positioning. For chiral centers, typically tetrahedral carbon atoms with four different substituents, wedge and dash notations specify whether a bond projects toward or away from the viewer. A solid represents a substituent coming out of the plane toward the observer, while a dashed line or hashed indicates a substituent receding behind the plane. These conventions, with the narrow end of the attached to the stereogenic , unambiguously define the in a perspective drawing. For example, in (2R,3R)-, solid wedges are used for the hydroxyl groups projecting forward. Hashed lines, consisting of parallel short dashes, are an alternative to plain dashed lines for enhanced clarity in printed media. In alkenes and other compounds with restricted rotation around s, cis-trans isomerism is denoted by the relative positioning of substituents on adjacent carbons. When the double bond is represented linearly, forward slashes (/) and backslashes () on the connecting bonds indicate whether substituents are on the same (cis) or opposite (trans) sides; for instance, in (E)-2-butene, the methyl groups are shown with opposing slashes to denote trans configuration. This slash notation is particularly useful in condensed or skeletal structural formulas to avoid ambiguity in chain depictions. For more complex cases where substituents differ, the E/Z system supersedes cis/trans, but the slash method remains a visual aid in drawings. When the at a center or is unspecified or represents a , wavy lines are employed to connect substituents, signaling an unknown or racemic configuration without implying a specific . The "rac" prefix may accompany such drawings to explicitly denote a of enantiomers. According to IUPAC guidelines, wavy bonds should be used judiciously, often with accompanying text for clarity, and are preferred over plain bonds when is intentionally ambiguous. To assign at chiral centers in these notations, the Cahn-Ingold-Prelog (CIP) priority rules are applied: substituents are ranked by (or further by attached atoms), the lowest-priority group is oriented away, and the configuration is designated (clockwise) or (counterclockwise) when viewing the remaining groups in decreasing priority. This system integrates seamlessly with wedge-dash drawings by determining the order after establishing the perspective. The CIP rules, formalized in 1966, ensure consistent across structural representations.

Fischer Projections

Fischer projections are a two-dimensional convention for depicting the three-dimensional arrangement of with multiple chiral centers, particularly useful for linear representations of biomolecules. Developed by German chemist in 1891 to elucidate the of carbohydrates, this method simplifies the visualization of tetrahedral geometries by projecting the molecule onto a plane while adhering to specific orientation rules. The standard drawing rules for Fischer projections position the main carbon chain vertically, with the most oxidized carbon (such as a ) placed at the top and the least oxidized at the bottom. Horizontal bonds are understood to project forward out of the plane of the paper toward the viewer, while vertical bonds extend backward behind the plane. This eclipsed conformation assumes all bonds are in the same plane for simplicity, though actual molecules adopt staggered arrangements; the projection prioritizes stereochemical clarity over conformational accuracy. A classic example is the of D-glucose, an aldohexose, which illustrates the D configuration through the positioning of hydroxyl groups. The open-chain form is drawn as follows, with the at the top and the CH₂OH at the bottom:

CHO | H-C-OH | HO-C-H | H-C-OH | H-C-OH | CH₂OH

CHO | H-C-OH | HO-C-H | H-C-OH | H-C-OH | CH₂OH

Here, the hydroxyl groups on carbons 2, 4, and 5 point to the right (horizontal bonds forward), while the one on carbon 3 points to the left, defining the specific stereoisomer. This arrangement corresponds to the (2R,3S,4R,5R) at the chiral centers. Interconversions of projections must preserve ; a 180° in the plane of the paper yields an equivalent representation, as it maintains the relative positions of substituents. However, a 90° or 270° inverts the configuration, effectively generating the , so such manipulations are invalid without adjustment. To assign R/S designations, one can mentally swap two horizontal substituents to reorient the lowest-priority group vertically (backward), then apply the Cahn-Ingold-Prelog priority rules while viewing the projection as a ; an odd number of swaps inverts the configuration. Fischer projections find primary applications in representing the of , where the / designation is based on the configuration at the penultimate carbon (OH on the right for D-series), and in , with natural L- showing the amino group on the left when the is at the top. These projections facilitated resolution of sugar enantiomers and remain standard in biochemical for open-chain forms.

Newman and Sawhorse Projections

Newman projections are a type of structural representation used in to visualize the three-dimensional conformation of molecules by looking straight down a specific bond, typically a carbon-carbon ./Chapter_03:_Structure_of_Alkanes/3.4:_Structure_and_Conformations_of_Alkanes/3.4.1:_Newman_Projections) This method was introduced in 1952 by Melvin S. Newman to facilitate the analysis of rotational isomers and torsional strain in alkanes. In a , the front carbon atom is represented as a dot at the center of a circle, with its three substituents depicted as lines extending outward at 120-degree angles; the rear carbon is shown as a larger circle, with its substituents as lines projecting from the circle's perimeter./Chapter_03:_Structure_of_Alkanes/3.4:_Structure_and_Conformations_of_Alkanes/3.4.1:_Newman_Projections) For (C₂H₆), the staggered conformation—where the front and rear atoms are offset by 60 degrees—represents the lowest-energy arrangement due to minimized steric repulsion, while the eclipsed conformation, with substituents aligned at 0 degrees, is a high-energy ./Chapter_03:_Structure_of_Alkanes/3.4:_Structure_and_Conformations_of_Alkanes/3.4.1:_Newman_Projections) Central to interpreting Newman projections is the concept of the , which measures the torsion between bonds on adjacent atoms and is defined as the angle between two planes formed by four atoms connected to the two central atoms in question. In these projections, dihedral angles determine the relative positions of substituents: an anti (or antiperiplanar) arrangement occurs at 180 degrees, maximizing separation; a gauche position is at 60 degrees, introducing some steric interactions; and a synperiplanar (or eclipsed) alignment at 0 degrees leads to significant torsional strain. These terms describe the conformational preferences driven by van der Waals repulsions and effects, allowing chemists to predict molecular stability without computational modeling. Sawhorse projections complement Newman projections by providing a perspective view of molecular conformations from an oblique angle, resembling the shape of a carpenter's sawhorse, with the carbon-carbon bond drawn as a zigzag line and substituents extending at tetrahedral angles. This representation emphasizes the three-dimensional torsion around the bond, making it easier to visualize dihedral angles and substituent orientations in a way that bridges two-dimensional drawings and physical models. Unlike the end-on view of Newman projections, sawhorse drawings highlight the spatial relationships in acyclic chains, aiding in the qualitative assessment of steric hindrance. A key application of these projections is in analyzing n-butane (C₄H₁₀), where rotation around the central C2-C3 bond yields distinct conformers. The anti conformation, with the terminal methyl groups at a 180-degree , is the global energy minimum due to optimal spacing that avoids steric clashes between the methyl groups./Chapters/Chapter_04:_Alkanes/3.09:_Conformations_of_Butane) In contrast, the gauche conformer at 60 degrees is slightly higher in energy by approximately 0.9 kcal/mol (3.8 kJ/mol), reflecting the partial overlap of the methyl groups, while eclipsed forms represent barriers to rotation./Chapters/Chapter_04:_Alkanes/3.09:_Conformations_of_Butane) This energy profile, observable in both Newman and sawhorse views, underscores the preference for staggered arrangements in alkanes and informs reactivity in larger hydrocarbons.

Haworth Projections

Haworth projections provide a simplified two-dimensional representation of the cyclic forms of monosaccharides, particularly (five-membered) and (six-membered) rings, by depicting the ring as a flat polygon with substituents oriented above or below the plane to convey stereochemical information. This convention, introduced by British chemist Walter Norman Haworth during his structural elucidations of carbohydrates in the late , facilitates the visualization of anomeric configurations and other chiral centers relative to the ring plane. The construction of a begins with the of the open-chain , where cyclization occurs via formation, typically involving the carbonyl at C1 and the hydroxyl at C4 or C5. The ring is drawn as a regular for forms, with the ring oxygen positioned at the upper right corner and the anomeric carbon (C1) at the rightmost vertex; for forms, a pentagon is used with similar orientation. Substituents that appear on the right side of the are placed below the ring plane (dashed lines or downward bonds), while those on the left are placed above (wedged lines or upward bonds); in D-series sugars, the CH₂OH group at C5 projects upward. This method preserves the relative while approximating the envelope-like pucker of the actual ring. A representative example is the Haworth projection of β-D-glucopyranose, the predominant cyclic form of D-glucose. The hexagon ring has the anomeric hydroxyl (at C1) oriented upward (indicating the β configuration), the hydroxyl at C2 downward, the hydroxyl at C3 upward, the hydroxyl at C4 downward, and the CH₂OH at C5 upward; all these positions correspond to equatorial orientations in the more accurate conformation. This depiction highlights the all-equatorial arrangement that contributes to the stability of β-D-glucopyranose in . The influences the at the anomeric carbon in projections, favoring the axial (downward in standard depiction) orientation of electronegative substituents like the hydroxyl group in α-anomers due to hyperconjugative stabilization involving the ring oxygen's , which overrides typical steric preferences for equatorial positions. In glucose, however, the β-anomer (equatorial, upward) predominates because of additional anomeric stabilization from solvent interactions, but the effect is pronounced in other sugars like or in glycosides where axial configurations enhance reactivity in enzymatic contexts. Despite their utility, projections have limitations in accurately conveying three-dimensional structure, as they portray the ring as fully planar rather than puckered, omitting details of bond angles and torsional strains present in real or conformations that affect stability and biological function.

, a six-membered carbon ring, adopts various conformations that are represented in structural formulas to depict its three-dimensional arrangement and energy preferences. The most stable conformation is the form, where the ring puckers such that adjacent carbon atoms alternate above and below the average plane of the ring. In this structure, the twelve C-H bonds are divided into six axial bonds, which point vertically parallel to the ring's axis of symmetry, and six equatorial bonds, which extend outward at an angle approximately 109.5 degrees from the ring plane. This arrangement minimizes both angle strain and torsional strain, making the the predominant conformation at , comprising over 99.9% of the population. Less stable conformations include the and twist-boat forms, which arise during dynamic interconversions of the ring. The conformation features four carbon atoms in a planar arrangement with the remaining two lifted out of the plane, resulting in eclipsed C-C bonds that introduce significant torsional strain, estimated at about 6.9 kcal/mol above the . Additionally, steric repulsion occurs between the "flagpole" hydrogens on the lifted carbons (positions 1 and 4), further elevating its energy to approximately 7.2 kcal/mol relative to the . The twist-boat, a slightly distorted version of the , alleviates some of this strain by twisting the ring, lowering its energy to about 5.5 kcal/mol above the while still being a local minimum. In structural representations, the conformation of is typically drawn as a zigzag with alternating up and down bonds to indicate the puckered shape, while substituents are shown using solid wedges for bonds coming out of the plane (equatorial or axial as appropriate) and dashed wedges for those receding behind the plane. For example, in , the equatorial position for the methyl group is preferred due to reduced steric interactions with axial hydrogens, stabilizing that conformer by about 1.7 kcal/mol compared to the axial form. This preference is crucial for predicting reactivity and physical properties in substituted cyclohexanes. The interconversion between chair conformations, known as a , occurs rapidly at through a involving half-chair or twist-boat intermediates, with an energy barrier of approximately 10.8 kcal/mol (45 kJ/mol). This process inverts the axial and equatorial positions but preserves the relative up/down orientation of substituents, allowing dynamic equilibration without breaking bonds. The barrier height was experimentally determined using , confirming the low that enables millions of flips per second per molecule.

Limitations and Extensions

Inherent Limitations

Structural formulas, being two-dimensional depictions, inherently struggle to convey the three-dimensional of molecules, including precise bond angles, torsional strains, and dynamic conformations that influence reactivity and . For instance, the tetrahedral around a carbon atom with 109.5° bond angles in is flattened into a planar , requiring chemists to rely on mental visualization or physical models to infer spatial relationships. This disconnect can lead to incomplete understanding of molecular behavior, as 2D representations omit volumetric aspects and electrostatic distributions that are crucial for interactions like enzyme-substrate binding. Ambiguities arise particularly in simplified forms like skeletal or condensed formulas, where hydrogen atoms are often implied rather than explicitly shown, potentially causing errors in valence counting or isomer identification for those unfamiliar with conventions. Stereochemical information, such as chirality at asymmetric centers, is likewise absent without supplementary notations like wedges or dashes, allowing multiple stereoisomers to appear identical and risking misinterpretation in synthesis or analysis. Even bond representations can be unclear; for example, a linearly aligned might ambiguously suggest cis-trans isomerism if not specified. For large and complex molecules, such as proteins or , structural formulas become overcrowded with intersecting lines and symbols, rendering them impractical for detailed scrutiny and prone to visual clutter that obscures functional groups or connectivity. This challenge is exacerbated in biomolecules, where thousands of atoms lead to unwieldy diagrams that prioritize brevity over clarity, often necessitating drastic abbreviations that sacrifice precision. Historically, early structural formulas developed in the by chemists like emphasized connectivity but ignored spatial orientations and quantum mechanical phenomena, such as electron delocalization in structures. These classical depictions treated bonds as fixed and localized, failing to account for the hybrid nature of systems like , where quantum effects demand multiple contributing forms beyond a single 2D drawing. This limitation persisted until the integration of in the 1930s, which revealed how traditional formulas oversimplified electron distribution.

Computational and 3D Extensions

Molecular modeling software extends traditional structural formulas by enabling the creation and manipulation of interactive 3D representations of molecules. Tools such as , developed by Signals, allow users to draw 2D structures and generate 3D models with depth-shading and conformational analysis, facilitating visualization of and for chemists and biologists. Similarly, Avogadro, an open-source molecular editor, supports cross-platform 3D visualization and editing, including optimization of molecular structures using force fields, making it widely used in and . These software packages address the static limitations of 2D formulas by providing rotatable, scalable views that reveal spatial arrangements not apparent in planar depictions. SMILES (Simplified Molecular Input Line Entry System) notation serves as a text-based extension for computational handling of structural formulas, allowing compact representation of molecules for input into modeling software and databases. For instance, the SMILES string "CC(O)C" denotes isopropanol, where "C" represents carbon atoms, "O" oxygen, and parentheses indicate branching. This linear format enables automated parsing and generation of 3D coordinates, bridging manual drawing with algorithmic processing in cheminformatics applications. In , visualizations derived from (DFT) calculations produce advanced 3D models that incorporate electronic structure data beyond empirical formulas. Ball-and-stick models, where atoms are depicted as spheres connected by rods representing bonds, and space-filling models, showing atomic van der Waals radii, are commonly generated from DFT outputs to illustrate optimized geometries and electron densities. Software like (VMD) facilitates these representations by loading DFT results from packages such as Gaussian, enabling interactive analysis of molecular orbitals and vibrational modes. As of 2025, AI-driven methods have further integrated structural formulas with predictive , particularly for complex biomolecules. , developed by , predicts protein structures from sequences with high accuracy, outputting 3D coordinates that align with traditional structural notations while revealing folding patterns; recent database updates synchronized with UniProt release 2025_03 have expanded coverage to over 200 million structures. This approach combines sequence-based "formulas" with computed 3D ensembles, accelerating and by providing verifiable models validated against experimental data.

References

  1. https://www.chem.fsu.edu/chemlab/chm1045/chem_formulas.html
  2. https://mccord.cm.utexas.edu/chembook/page.php?chnum=1&sect=14
  3. https://www2.chemistry.msu.edu/faculty/reusch/virttxtjml/intro3.htm
  4. https://www.utdallas.edu/~scortes/ochem/OChem1_Lecture/Class_Materials/04_lewis_res_struct.pdf
  5. https://www.journals.uchicago.edu/doi/10.1093/bjps/axp052
  6. https://openstax.org/books/chemistry-2e/pages/2-4-chemical-formulas
  7. https://www.sciencehistory.org/education/scientific-biographies/august-kekule-and-archibald-scott-couper/
  8. https://pubmed.ncbi.nlm.nih.gov/25257125/
  9. https://pressbooks-dev.oer.hawaii.edu/chemistry/chapter/reaction-mechanisms/
  10. http://www.chem.latech.edu/~deddy/Lectnote/Chapt9.html
  11. https://users.highland.edu/~jsullivan/genchem/s04_bonding_elements.html
  12. https://williams.chemistry.gatech.edu/structure/molecular_interactions/mol_int.html
  13. https://www.chem.uwec.edu/Chem150_Resources/content/elaborations/unitx/unit1-d-structural-formulas.html
  14. https://personal.utdallas.edu/~scortes/ochem/OChem1_Lecture/Class_Materials/03_coval_bonding.pdf
  15. https://www2.chemistry.msu.edu/faculty/reusch/virttxtjml/react3.htm
  16. https://projects.iq.harvard.edu/files/lifesciences1abookv1/files/chapter_01_-_atomic_structure_and_chemical_bonding_01.pdf
  17. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Chemistry_-_The_Central_Science_(Brown_et_al.)/08%3A_Basic_Concepts_of_Chemical_Bonding/8.03%3A_Lewis_Symbols_and_Structures
  18. https://pubs.acs.org/doi/10.1021/ja02261a002
  19. https://www.chem.fsu.edu/chemlab/chm1lab/molstructure/background.html
  20. https://terpconnect.umd.edu/~wbreslyn/chemistry/Lewis-Structures/lewis-structure-for-NH3.html
  21. https://chem.libretexts.org/Bookshelves/Inorganic_Chemistry/Inorganic_Chemistry_(LibreTexts)/03:_Simple_Bonding_Theory/3.01:_Lewis_Electron-Dot_Diagrams/3.1.02:_Breaking_the_octet_rule_with_higher_electron_counts_(hypervalent_atoms)
  22. http://guweb2.gonzaga.edu/faculty/cronk/CHEM101pub/Lewis_structures_II.html
  23. https://ocw.uci.edu/upload/files/51A_chapter_1_2018.pdf
  24. https://s1.lite.msu.edu/res/msu/botonl/b_online/library/newton/Chy251_253/Lectures/LewisStructures/LewisStructures.html
  25. https://faculty.fiu.edu/~kellerl/SolomonsLKChapter1%2C2-1.pdf
  26. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Organic_Chemistry_(Morsch_et_al.)/27%3A_Biomolecules_-_Lipids/27.06%3A_Steroids
  27. https://publications.iupac.org/pac/2006/pdf/7810x1897.pdf
  28. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Book%253A_Organic_Chemistry_with_a_Biological_Emphasis_v2.0_%28Soderberg%29/03%253A_Conformations_and_Stereochemistry/3.04%253A_Chirality_and_stereoisomers
  29. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Organic_Chemistry_%28Morsch_et_al.%29/07%253A_Alkenes-_Structure_and_Reactivity/7.05%253A_Cis-Trans_Isomerism_in_Alkenes
  30. https://www2.chemistry.msu.edu/faculty/reusch/virttxtjml/chapt6.htm
  31. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Supplemental_Modules_%28Organic_Chemistry%29/Chirality/Absolute_Configuration_R-S_Sequence_Rules
  32. https://www.news-medical.net/life-sciences/Fischer-and-Haworth-Projections-of-Carbohydrates.aspx
  33. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Organic_Chemistry_I_%28Liu%29/05%253A_Stereochemistry/5.05%253A_Fisher_Projection
  34. https://www.chem.ucalgary.ca/courses/350/Carey5th/Ch07/ch7-7.html
  35. https://chem.libretexts.org/Courses/University_of_Connecticut/Chem_2444%253A_%28Second_Semester_Organic_Chemistry%29_UConn/12%253A_Carbohydrates_and_Sugars/12.02%253A_Fischer_Projections
  36. https://www.masterorganicchemistry.com/2019/05/21/how-to-determine-r-and-s-configurations-on-a-fischer-projection/
  37. https://www.chemistrylearner.com/fischer-projection.html
  38. https://chem.libretexts.org/Courses/can/CHEM_232_-_Organic_Chemistry_II_%28Puenzo%29/12%253A_Biomolecules-_Amino_Acids_Peptides_and_Proteins/12.02%253A_Structures_of_Amino_Acids
  39. https://www.nasonline.org/wp-content/uploads/2024/06/newman-melvin.pdf
  40. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Organic_Chemistry_(Morsch_et_al.)/04:_Organic_Compounds_-_Cycloalkanes/3.03:_Conformational_Analysis_of_Ethane_and_Propane
  41. https://openstax.org/books/organic-chemistry/pages/3-7-conformations-of-other-alkanes
  42. https://www.nobelprize.org/prizes/chemistry/1937/haworth/facts/
  43. https://chem.libretexts.org/Courses/Brevard_College/CHE_301_Biochemistry/02%253A_Carbohydrates/2.06%253A_Cyclic_Structures_of_Monosaccharides
  44. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Organic_Chemistry_I_%28Liu%29/04%253A_Conformations_of_Alkanes_and_Cycloalkanes/4.03%253A_Conformation_Analysis_of_Cyclohexane
  45. https://www.masterorganicchemistry.com/2014/05/30/the-cyclohexane-chair-flip/
  46. https://www.masterorganicchemistry.com/2014/06/06/the-cyclohexane-chair-flip-energy-diagram/
  47. https://chem.libretexts.org/Bookshelves/General_Chemistry/CLUE%3A_Chemistry_Life_the_Universe_and_Everything/04%3A_Heterogeneous_Compounds/4.1%3A_3D_and_2D_Representations
  48. https://openoregon.pressbooks.pub/introductoryorganic/chapter/drawing-and-interpreting-organic-formulas/
  49. https://www.sciencedirect.com/science/article/abs/pii/B9780444516756500220
  50. https://www.researchgate.net/publication/240432734_A_Brief_History_of_the_Theory_of_Resonance_and_of_its_Interpretation
  51. https://revvitysignals.com/blog/evolution-chemdraw
  52. https://avogadro.cc/
  53. https://jcheminf.biomedcentral.com/articles/10.1186/1758-2946-4-17
  54. https://www.daylight.com/dayhtml/doc/theory/theory.smiles.html
  55. http://opensmiles.org/opensmiles.html
  56. https://www.ks.uiuc.edu/Training/Tutorials/vmd-qmvis/qmvis-tutorial.pdf
  57. https://www.ks.uiuc.edu/Research/vmd/
  58. https://deepmind.google/science/alphafold/
  59. https://www.nature.com/articles/s41586-021-03819-2
  60. https://www.embl.org/news/science-technology/google-deepmind-partnership-renewal/
Add your contribution
Related Hubs
User Avatar
No comments yet.