Hubbry Logo
Energy conversion efficiencyEnergy conversion efficiencyMain
Open search
Energy conversion efficiency
Community hub
Energy conversion efficiency
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Energy conversion efficiency
Energy conversion efficiency
Energy conversion efficiency
View on Wikipedia
from Wikipedia
Useful output energy is always lower than input energy.
Efficiency of power plants, world total, 2008

Energy conversion efficiency (η) is the ratio between the useful output of an energy conversion machine and the input, in energy terms. The input, as well as the useful output may be chemical, electric power, mechanical work, light (radiation), or heat. The resulting value, η (eta), ranges between 0 and 1.[1][2][3]

Overview

[edit]

Energy conversion efficiency depends on the usefulness of the output. All or part of the heat produced from burning a fuel may become rejected waste heat if, for example, work is the desired output from a thermodynamic cycle. Energy converter is an example of an energy transformation. For example, a light bulb falls into the categories energy converter. Even though the definition includes the notion of usefulness, efficiency is considered a technical or physical term. Goal or mission oriented terms include effectiveness and efficacy.

Generally, energy conversion efficiency is a dimensionless number between 0 and 1.0, or 0% to 100%. Efficiencies cannot exceed 100%, which would result in a perpetual motion machine, which is impossible.

However, other effectiveness measures that can exceed 1.0 are used for refrigerators, heat pumps and other devices that move heat rather than convert it. It is not called efficiency, but the coefficient of performance, or COP. It is a ratio of useful heating or cooling provided relative to the work (energy) required. Higher COPs equate to higher efficiency, lower energy (power) consumption and thus lower operating costs. The COP usually exceeds 1, especially in heat pumps, because instead of just converting work to heat (which, if 100% efficient, would be a COP of 1), it pumps additional heat from a heat source to where the heat is required. Most air conditioners have a COP of 2.3 to 3.5.[4]

When talking about the efficiency of heat engines and power stations the convention should be stated, i.e., HHV (a.k.a. Gross Heating Value, etc.) or LCV (a.k.a. Net Heating value), and whether gross output (at the generator terminals) or net output (at the power station fence) are being considered. The two are separate but both must be stated. Failure to do so causes endless confusion.

Related, more specific terms include

Chemical conversion efficiency

[edit]

The change of Gibbs energy of a defined chemical transformation at a particular temperature is the minimum theoretical quantity of energy required to make that change occur (if the change in Gibbs energy between reactants and products is positive) or the maximum theoretical energy that might be obtained from that change (if the change in Gibbs energy between reactants and products is negative). The energy efficiency of a process involving chemical change may be expressed relative to these theoretical minima or maxima. The difference between the change of enthalpy and the change of Gibbs energy of a chemical transformation at a particular temperature indicates the heat input required or the heat removal (cooling) required to maintain that temperature.[5]

A fuel cell may be considered to be the reverse of electrolysis. For example, an ideal fuel cell operating at a temperature of 25 °C having gaseous hydrogen and gaseous oxygen as inputs and liquid water as the output could produce a theoretical maximum amount of electrical energy of 237.129 kJ (0.06587 kWh) per gram mol (18.0154 gram) of water produced and would require 48.701 kJ (0.01353 kWh) per gram mol of water produced of heat energy to be removed from the cell to maintain that temperature.[6]

An ideal electrolysis unit operating at a temperature of 25 °C having liquid water as the input and gaseous hydrogen and gaseous oxygen as products would require a theoretical minimum input of electrical energy of 237.129 kJ (0.06587 kWh) per gram mol (18.0154 gram) of water consumed and would require 48.701 kJ (0.01353 kWh) per gram mol of water consumed of heat energy to be added to the unit to maintain that temperature.[6] It would operate at a cell voltage of 1.24 V.

For a water electrolysis unit operating at a constant temperature of 25 °C without the input of any additional heat energy, electrical energy would have to be supplied at a rate equivalent of the enthalpy (heat) of reaction or 285.830 kJ (0.07940 kWh) per gram mol of water consumed.[6] It would operate at a cell voltage of 1.48 V. The electrical energy input of this cell is 1.20 times greater than the theoretical minimum so the energy efficiency is 0.83 compared to the ideal cell. 

A water electrolysis unit operating with a higher voltage that 1.48 V and at a temperature of 25 °C would have to have heat energy removed in order to maintain a constant temperature and the energy efficiency would be less than 0.83.

The large entropy difference between liquid water and gaseous hydrogen plus gaseous oxygen accounts for the significant difference between the Gibbs energy of reaction and the enthalpy (heat) of reaction.

Fuel heating values and efficiency

[edit]

In Europe the usable energy content of a fuel is typically calculated using the lower heating value (LHV) of that fuel, the definition of which assumes that the water vapor produced during fuel combustion (oxidation) remains gaseous, and is not condensed to liquid water so the latent heat of vaporization of that water is not usable. Using the LHV, a condensing boiler can achieve a "heating efficiency" in excess of 100% (this does not violate the first law of thermodynamics as long as the LHV convention is understood, but does cause confusion). This is because the apparatus recovers part of the heat of vaporization, which is not included in the definition of the lower heating value of a fuel.[citation needed] In the U.S. and elsewhere, the higher heating value (HHV) is used, which includes the latent heat for condensing the water vapor, and thus the thermodynamic maximum of 100% efficiency cannot be exceeded.

Wall-plug efficiency, luminous efficiency, and efficacy

[edit]
The absolute irradiance of four different gases when used in a flashtube. Xenon is by far the most efficient of the gases, although krypton is more effective at a specific wavelength of light.
The sensitivity of the human eye to various wavelengths. Assuming each wavelength equals 1 watt of radiant energy, only the center wavelength is perceived as 683 candelas (1 watt of luminous energy), equaling 683 lumens. The vertical colored-lines represent the 589 (yellow) sodium line, and popular 532 nm (green), 671 nm (red), 473 nm (blue), and 405 nm (violet) laser pointers.
A Sankey diagram showing the multiple stages of energy loss between the wall plug and the light output of a fluorescent lamp. The greatest losses occur due to the Stokes shift.

In optical systems such as lighting and lasers, the energy conversion efficiency is often referred to as wall-plug efficiency. The wall-plug efficiency is the measure of output radiative-energy, in watts (joules per second), per total input electrical energy in watts. The output energy is usually measured in terms of absolute irradiance and the wall-plug efficiency is given as a percentage of the total input energy, with the inverse percentage representing the losses.

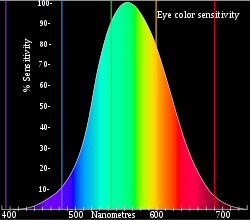
The wall-plug efficiency differs from the luminous efficiency in that wall-plug efficiency describes the direct output/input conversion of energy (the amount of work that can be performed) whereas luminous efficiency takes into account the human eye's varying sensitivity to different wavelengths (how well it can illuminate a space). Instead of using watts, the power of a light source to produce wavelengths proportional to human perception is measured in lumens. The human eye is most sensitive to wavelengths of 555 nanometers (greenish-yellow) but the sensitivity decreases dramatically to either side of this wavelength, following a Gaussian power-curve and dropping to zero sensitivity at the red and violet ends of the spectrum. Due to this the eye does not usually see all of the wavelengths emitted by a particular light-source, nor does it see all of the wavelengths within the visual spectrum equally. Yellow and green, for example, make up more than 50% of what the eye perceives as being white, even though in terms of radiant energy white-light is made from equal portions of all colors (i.e.: a 5 mW green laser appears brighter than a 5 mW red laser, yet the red laser stands-out better against a white background). Therefore, the radiant intensity of a light source may be much greater than its luminous intensity, meaning that the source emits more energy than the eye can use. Likewise, the lamp's wall-plug efficiency is usually greater than its luminous efficiency. The effectiveness of a light source to convert electrical energy into wavelengths of visible light, in proportion to the sensitivity of the human eye, is referred to as luminous efficacy, which is measured in units of lumens per watt (lm/w) of electrical input-energy.

Unlike efficacy (effectiveness), which is a unit of measurement, efficiency is a unitless number expressed as a percentage, requiring only that the input and output units be of the same type. The luminous efficiency of a light source is thus the percentage of luminous efficacy per theoretical maximum efficacy at a specific wavelength. The amount of energy carried by a photon of light is determined by its wavelength. In lumens, this energy is offset by the eye's sensitivity to the selected wavelengths. For example, a green laser pointer can have greater than 30 times the apparent brightness of a red pointer of the same power output. At 555 nm in wavelength, 1 watt of radiant energy is equivalent to 683 lumens, thus a monochromatic light source at this wavelength, with a luminous efficacy of 683 lm/w, would have a luminous efficiency of 100%. The theoretical-maximum efficacy lowers for wavelengths at either side of 555 nm. For example, low-pressure sodium lamps produce monochromatic light at 589 nm with a luminous efficacy of 200 lm/w, which is the highest of any lamp. The theoretical-maximum efficacy at that wavelength is 525 lm/w, so the lamp has a luminous efficiency of 38.1%. Because the lamp is monochromatic, the luminous efficiency nearly matches the wall-plug efficiency of < 40%.[7][8]

Calculations for luminous efficiency become more complex for lamps that produce white light or a mixture of spectral lines. Fluorescent lamps have higher wall-plug efficiencies than low-pressure sodium lamps, but only have half the luminous efficacy of ~ 100 lm/w, thus the luminous efficiency of fluorescents is lower than sodium lamps. A xenon flashtube has a typical wall-plug efficiency of 50–70%, exceeding that of most other forms of lighting. Because the flashtube emits large amounts of infrared and ultraviolet radiation, only a portion of the output energy is used by the eye. The luminous efficacy is therefore typically around 50 lm/w. However, not all applications for lighting involve the human eye nor are restricted to visible wavelengths. For laser pumping, the efficacy is not related to the human eye so it is not called "luminous" efficacy, but rather simply "efficacy" as it relates to the absorption lines of the laser medium. Krypton flashtubes are often chosen for pumping Nd:YAG lasers, even though their wall-plug efficiency is typically only ~ 40%. Krypton's spectral lines better match the absorption lines of the neodymium-doped crystal, thus the efficacy of krypton for this purpose is much higher than xenon; able to produce up to twice the laser output for the same electrical input.[9][10] All of these terms refer to the amount of energy and lumens as they exit the light source, disregarding any losses that might occur within the lighting fixture or subsequent output optics. Luminaire efficiency refers to the total lumen-output from the fixture per the lamp output.[11]

With the exception of a few light sources, such as incandescent light bulbs, most light sources have multiple stages of energy conversion between the "wall plug" (electrical input point, which may include batteries, direct wiring, or other sources) and the final light-output, with each stage producing a loss. Low-pressure sodium lamps initially convert the electrical energy using an electrical ballast, to maintain the proper current and voltage, but some energy is lost in the ballast. Similarly, fluorescent lamps also convert the electricity using a ballast (electronic efficiency). The electricity is then converted into light energy by the electrical arc (electrode efficiency and discharge efficiency). The light is then transferred to a fluorescent coating that only absorbs suitable wavelengths, with some losses of those wavelengths due to reflection off and transmission through the coating (transfer efficiency). The number of photons absorbed by the coating will not match the number then reemitted as fluorescence (quantum efficiency). Finally, due to the phenomenon of the Stokes shift, the re-emitted photons will have a longer wavelength (thus lower energy) than the absorbed photons (fluorescence efficiency). In very similar fashion, lasers also experience many stages of conversion between the wall plug and the output aperture. The terms "wall-plug efficiency" or "energy conversion efficiency" are therefore used to denote the overall efficiency of the energy-conversion device, deducting the losses from each stage, although this may exclude external components needed to operate some devices, such as coolant pumps.[12][13]

Example of energy conversion efficiency

[edit]
Conversion process Conversion type Energy efficiency
Electricity generation
Gas turbine Chemical to electrical up to 40%
Gas turbine plus steam turbine (combined cycle) Chemical to thermal+electrical (cogeneration) up to 63.08%[14] In December 2017, GE claimed >64% in its latest 826 MW 9HA.02 plant, up from 63.7%. They said this was due to advances in additive manufacturing and combustion. Their press release said that they planned to achieve 65% by the early 2020s.[15][self-published source]
Water turbine Gravitational to electrical up to 95%[16][self-published source] (practically achieved)
Wind turbine Kinetic to electrical up to 50% (HAWT in isolation,[17] up to 25–40% HAWTs in close proximity, up to 35–40% VAWT in isolation, up to 41–47% VAWT series-farm.[18] 3128 HAWTs older than 10 years in Denmark showed that half had no decrease, while the other half saw a production decrease of 1.2% per year.[19] Theoretical limit = 16/27= 59%)
Solar cell Radiative to electrical 6–40% (technology-dependent, 15–20% most often, median degradation for x-Si technologies in the 0.5–0.6%/year[20] range with the mean in the 0.8–0.9%/year range. Hetero-interface technology (HIT) and microcrystalline silicon (μc-Si) technologies, although not as plentiful, exhibit degradation around 1%/year and resemble thin-film products more closely than x-Si.[21] infinite-stack limit: 86.8% concentrated[22] 68.7% unconcentrated[23])
Fuel cell Chemical to thermal+electrical (cogeneration) The energy efficiency of a fuel cell is generally between 40 and 60%; however, if waste heat is captured in a cogeneration scheme, efficiencies of up to 85% can be obtained.[24]
World average fossil fuel electricity generation power plant as of 2008 [25] Chemical to electrical Gross output 39%, Net output 33%
Electricity storage
Lithium-ion battery Chemical to electrical/reversible 80–90%[26]
Nickel–metal hydride battery Chemical to electrical/reversible 66%[27]
Lead-acid battery Chemical to electrical/reversible 50–95%[28]
Pumped-storage hydroelectricity gravitational to electrical/reversible 70–85%[29]
Engine/motor
Combustion engine Chemical to kinetic 10–50%[30]
Electric motor Electrical to kinetic 70–99.99% (> 200 W); 50–90% (10–200 W); 30–60% (< 10 W)
Turbofan Chemical to kinetic 20–40%[31]
Natural process
Photosynthesis Radiative to chemical 0.1% (average)[32] to 2% (best);[33] up to 6% in principle[34] (see main: Photosynthetic efficiency)
Muscle Chemical to kinetic 14–27%
Appliance
Household refrigerator Electrical to thermal low-end systems ~ 20%; high-end systems ~ 40–50%
Incandescent light bulb Electrical to radiative ~ 80% wall-plug efficiency[35] 0.7–5.1% luminous efficiency[36]
Light-emitting diode (LED) Electrical to radiative 4.2–53%[37][failed verification][dubious – discuss]
Fluorescent lamp Electrical to radiative 8.0–15.6%,[36] 28%[38]
Low-pressure sodium lamp Electrical to radiative 15.0–29.0%,[36] 40.5%[38]
Metal-halide lamp Electrical to radiative 9.5–17.0%,[36] 24%[38]
Switched-mode power supply Electrical to electrical currently up to 96% practically
Electric shower Electrical to thermal 90–95% (multiply by the energy efficiency of electricity generation to compare with other water-heating systems)
Electric heater Electrical to thermal ~100% (essentially all energy is converted into heat, multiply by the energy efficiency of electricity generation to compare with other heating systems)
Others
Firearm Chemical to kinetic ~30% (.300 Hawk ammunition)
Electrolysis of water Electrical to chemical 50–70% (80–94% theoretical maximum)

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Energy conversion efficiency

View on Grokipedia
from Grokipedia
Energy conversion efficiency is a fundamental measure in and that quantifies the effectiveness with which a device or system transforms one form of into a desired useful form, typically expressed as the ratio of useful energy output to total energy input, often as a : η = (useful output / total input) × 100%. This metric applies to diverse processes, from mechanical work in engines to electrical power in generators, where "useful" output depends on the device's intended purpose—for instance, mechanical power from an or from a —while losses manifest as or other unusable forms. The concept underscores the principle of from of , ensuring that all input is either converted or dissipated, but never created or destroyed. The maximum attainable efficiency in energy conversion is constrained by thermodynamic laws, particularly the second law, which accounts for irreversibilities like friction and entropy generation that inevitably reduce output. For heat engines converting thermal energy to mechanical work, the theoretical upper limit is the Carnot efficiency, given by η_Carnot = 1 - (T_cold / T_hot), where temperatures are in absolute scale; real devices achieve far less due to practical losses. In direct conversion systems, such as photovoltaic cells that transform solar radiation into electricity, quantum and thermodynamic limits further cap performance, with the Shockley-Queisser limit setting a single-junction maximum around 33% under standard conditions. These limits highlight why no conversion process can reach 100% efficiency, guiding the design of more effective technologies across fields like power generation and renewable energy. Enhancing energy conversion efficiency is vital for , as it minimizes resource consumption, cuts operational costs, and reduces in applications ranging from transportation to production. For example, high-efficiency electric motors in industrial settings can reach 90-95% efficiency, converting nearly all electrical input to mechanical output, compared to incandescent bulbs that manage only about 5% for production. In power plants, combined-cycle gas turbines achieve up to 60% efficiency by sequentially converting fuel energy through combustion and cycles, far surpassing traditional plants at around 33%. Advances in materials and design, such as in thermoelectric devices that harvest , continue to push practical efficiencies closer to theoretical bounds, supporting global efforts to optimize energy systems amid growing demands.

Fundamentals

Definition and Principles

Energy conversion efficiency, often denoted as η, is defined as the ratio of useful output to the total input in a conversion process, typically expressed as a : η=EoutEin×100%\eta = \frac{E_{\text{out}}}{E_{\text{in}}} \times 100\%. This metric quantifies how effectively a device or transforms from one form to another, such as mechanical work from or electrical power from , while accounting only for the desired output form as "useful." The concept applies across various domains, including thermal, electrical, and chemical s, but always hinges on distinguishing useful from losses like heat or friction. The fundamental principles governing energy conversion efficiency stem from the . The first law, which embodies the , ensures that the total energy output equals the input, but it does not guarantee that all output is useful, allowing for inevitable transformations into less desirable forms. The second law introduces irreversibility through increase, prohibiting any process from achieving 100% and setting theoretical limits, such as the Carnot efficiency as the maximum for heat engines operating between two temperatures. These laws establish that while perfect conversion is impossible, efficiencies can approach optimal values under ideal conditions, guiding the design of real-world systems. Energy conversion efficiency plays a critical role in promoting by minimizing waste and optimizing resource use, thereby supporting efforts in and environmental management. Higher efficiencies reduce operational costs, lower , and enhance , positioning efficiency improvements as a cornerstone of clean energy transitions. In environmental contexts, efficient conversions decrease reliance on fossil fuels and mitigate climate impacts, aligning with global policies aimed at reducing . The concept traces its origins to Sadi Carnot's 1824 work, Réflexions sur la puissance motrice du feu, which analyzed the efficiency limits of heat engines and laid the groundwork for thermodynamic theory. Carnot's insights, initially focused on steam engines during the , evolved in the to encompass broader frameworks, influencing standards for diverse conversion technologies amid growing concerns over resource scarcity and .

Basic Efficiency Formulas

Energy conversion efficiency is fundamentally derived from the principle of conservation of energy, which states that the total energy input to a system equals the sum of the useful energy output and the energy lost to various dissipative processes. The basic formula for efficiency, denoted as η, is given by η=(EusefulEinput)×100%\eta = \left( \frac{E_{\text{useful}}}{E_{\text{input}}} \right) \times 100\% where EusefulE_{\text{useful}} is the energy delivered in the desired form (e.g., mechanical work or electrical power), and EinputE_{\text{input}} is the total energy supplied to the system, both typically measured in joules (J) according to SI conventions. This expression quantifies the fraction of input energy successfully converted, with the percentage form standardizing reporting for comparability across devices. In time-dependent systems, such as continuous processes, efficiency is often expressed in terms of power, where power PP represents the rate of energy transfer (in watts, W, or J/s). The power efficiency variant is ηp=(PoutPin)×100%\eta_p = \left( \frac{P_{\text{out}}}{P_{\text{in}}} \right) \times 100\% with PoutP_{\text{out}} as the useful power output and PinP_{\text{in}} as the input power. This formulation arises directly from the energy efficiency by dividing both numerator and denominator by time, preserving the ratio while accounting for steady-state operation. For instance, in electrical systems, input and output may be quantified in watt-hours (Wh) for integrated energy over time, convertible to joules via 1 Wh = 3600 J. Efficiency is inherently limited below 100% due to dissipative losses, which convert portions of the input into unusable forms such as or . These losses stem from irreversible processes governed by the second law of thermodynamics, increasing and preventing perfect conversion in practical systems. Common examples include frictional dissipation in mechanical components, where is transformed into , and ohmic heating in electrical conductors. To ensure consistency, efficiencies are reported using SI units for (J) and power (W), with alternative units like watt-hours or British thermal units (BTU, where 1 BTU ≈ 1055 J) converted accordingly for international standardization.

Thermal and Chemical Conversions

Heat Engine Efficiency

Heat engines convert into mechanical work through thermodynamic cycles, operating between a hot source and a cold sink. The first practical , the atmospheric engine invented by in 1712, used to create a that drove a , though it suffered from low due to repeated heating and cooling of the . significantly improved this design in 1769 by introducing a separate condenser, which prevented cylinder cooling during operation and thereby reduced fuel consumption by about 75%, marking a pivotal advancement in engine practicality. The theoretical maximum efficiency for any operating reversibly between two temperatures is given by the Carnot efficiency, derived from the second law of for a cycle consisting of two isothermal and two adiabatic processes. In this ideal reversible engine, QhQ_h is absorbed from the hot reservoir at temperature ThT_h (in ), and QcQ_c is rejected to the cold reservoir at TcT_c, with the efficiency defined as the ratio of net work output to heat input: ηCarnot=1−TcTh=1−QcQh.\eta_{Carnot} = 1 - \frac{T_c}{T_h} = 1 - \frac{Q_c}{Q_h}. This formula arises because, for reversible processes, the entropy change over the cycle must be zero, leading to QhTh=QcTc\frac{Q_h}{T_h} = \frac{Q_c}{T_c}, which directly yields the efficiency expression. Real s, however, cannot achieve this limit due to inherent irreversibilities but approximate it through specific cycles. Common real-world cycles include the Otto cycle for spark-ignition gasoline engines, the Diesel cycle for compression-ignition engines, and the Rankine cycle for steam turbines. The ideal Otto cycle efficiency depends on the compression ratio rr (the ratio of maximum to minimum volume) and the specific heat ratio γ\gamma (approximately 1.4 for air), given by ηOtto=1−1rγ−1,\eta_{Otto} = 1 - \frac{1}{r^{\gamma-1}}, which increases with higher rr but is limited in practice to avoid auto-ignition; typical gasoline engines achieve 20-30% thermal efficiency. Diesel engines, using higher compression ratios (15-25), yield 30-40% efficiency, benefiting from more complete combustion at elevated pressures. Steam power plants based on the Rankine cycle, involving boiling water to produce vapor that expands through a turbine, typically operate at 30-45% efficiency in modern setups, enhanced by superheating the steam to reduce moisture losses. Efficiency in real heat engines is reduced by irreversibilities such as mechanical in , which dissipates energy as , and losses across finite temperature differences in heat exchangers. These factors increase generation beyond the reversible case, lowering the net work output relative to the Carnot limit. Improvements can mitigate such losses; for instance, supercharging forces additional air into the cylinder to boost and allow leaner mixtures for better efficiency, while in hybrid systems captures during deceleration to recharge batteries, typically recovering 60-70% of the braking energy that would otherwise be lost as .

Chemical Fuel Efficiency

Chemical fuel efficiency refers to the effectiveness with which the stored in fuels is converted into usable through oxidation processes, primarily . This is fundamentally limited by the fuel's inherent content and the completeness of the reaction, but practical losses arise from incomplete burning and heat dissipation. Key metrics distinguish between the higher heating value (HHV), which accounts for the of in combustion products, and the lower heating value (LHV), which excludes this heat by assuming water remains as vapor. For hydrocarbon fuels like , the HHV is approximately 46.4 MJ/kg, reflecting the maximum recoverable under ideal conditions where exhaust gases are cooled to ambient temperature and water is liquefied. Combustion efficiency, denoted as ηcomb\eta_{\text{comb}}, quantifies the fraction of a fuel's theoretical energy that is actually released during burning and is calculated as ηcomb=(energy releasedtheoretical maximum from stoichiometry)×100%\eta_{\text{comb}} = \left( \frac{\text{energy released}}{\text{theoretical maximum from stoichiometry}} \right) \times 100\%. This theoretical maximum is derived from the fuel's stoichiometric reaction with oxygen, assuming complete conversion to CO2_2 and H2_2O without side products. In practice, ηcomb\eta_{\text{comb}} approaches 99% or higher in well-controlled systems but can drop below 95% due to factors such as suboptimal air-fuel ratios, which lead to incomplete combustion. The air-fuel ratio, typically around 14.7:1 by mass for gasoline under stoichiometric conditions, must be precisely managed; excess air promotes complete oxidation but increases heat losses through flue gases, while insufficient air results in unburned hydrocarbons and carbon monoxide formation. In broader systems like boilers, overall chain efficiency encompasses the entire process from storage and delivery to output, often ranging from 70% to 90% depending on fuel type, design, and operation. For or oil-fired boilers, modern units achieve 85-95% efficiency by minimizing stack losses and optimizing , though older coal-fired systems may fall to 70-80% due to ash handling and incomplete burning. This chain efficiency builds on combustion performance but subtracts losses from fuel handling, , and , highlighting the need for integrated controls to maximize usable to working fluids like or hot water. Efficiency in chemical fuel conversion is closely linked to environmental impacts, as incomplete combustion not only reduces energy yield but also elevates emissions of pollutants like carbon monoxide (CO) and nitrogen oxides (NOx). CO arises from partial oxidation of carbon under oxygen-limited conditions, while NOx forms from high-temperature reactions between nitrogen and oxygen in air. These emissions prompted regulatory responses, such as the U.S. Clean Air Act of 1970, which established national standards for ambient air quality and mandated controls on stationary and mobile sources to curb CO and NOx from combustion processes. Post-1970 advancements in combustion technology, driven by these regulations, have significantly improved both efficiency and emission profiles in fuel-burning systems.

Electrical and Optical Conversions

Electrical Power Efficiency

Electrical power efficiency refers to the effectiveness of converting from one form to another, such as (AC) to (DC), voltage level changes, or frequency adjustments, primarily through devices. These conversions are essential in applications ranging from household appliances to and electric vehicles (EVs), where minimizing losses directly impacts energy savings and system performance. Key metrics focus on the ratio of output power to input power, accounting for resistive, magnetic, and switching losses inherent in components like diodes, transistors, and inductors. Wall-plug efficiency, denoted as η_wp, measures the overall power conversion from the electrical outlet to the usable output of a device, calculated as η_wp = (P_delivered / P_wall) × 100%, where P_delivered is the power provided to the load and P_wall is the power drawn from the wall socket. This metric encompasses all losses in the power supply chain, including those from rectification, , and filtering. For typical household appliances equipped with switched-mode power supplies, η_wp ranges from approximately 80% to 95%, with modern designs certified under standards like achieving higher values at various load levels to reduce standby consumption and operational heat. Transformer efficiency, expressed as η_trans = (P_secondary / P_primary) × 100%, quantifies the power transfer from primary to secondary windings while accounting for no-load and load-dependent losses. Core losses arise from , where energy is dissipated due to reorientation in the iron core, and eddy currents, induced circulating currents opposing the ; these are collectively around 1-2% in efficient designs. Copper losses, primarily I²R resistive heating in the windings, increase with load current and can be mitigated by using low-resistance materials and optimal winding configurations. High-frequency designs, operating above 20 kHz, minimize these losses by enabling smaller cores with reduced material volume and better distribution, often achieving overall efficiencies exceeding 98% in switched-mode power supplies. The development of practical transformers began in 1885 with William Stanley's design, which featured closed iron cores and improved insulation, enabling reliable AC voltage stepping for commercial power distribution and marking a pivotal advancement in electrical systems. Subsequent innovations in , such as the (IGBT) introduced in the early 1980s, further enhanced conversion efficiency by providing high-voltage switching with low conduction losses, reducing overall system dissipation in applications like motor drives and inverters. Inverter and rectifier efficiencies are critical for bidirectional power conversions, such as DC to AC in solar inverters or AC to DC in EV chargers, where η_inv ≈ 90-98% is typical for modern silicon-based systems. Efficiency can be approximated as η = 1 - (I²R losses / P_in), with I²R representing conduction losses in switches and filters, alongside switching losses from transitions; these are minimized through soft-switching techniques and wide-bandgap materials like . In solar photovoltaic systems, high-quality inverters achieve 95-98% efficiency at peak loads, while EV rectifiers using topologies like rectifiers reach similar levels to support fast charging with minimal harmonic distortion.

Luminous and Photonic Efficiency

quantifies the efficiency with which a light source produces , defined as the ratio of (measured in lumens, lm) to electrical power input (in watts, W), yielding units of lm/W. This metric is inherently tied to the human-visible (approximately 380–780 nm), as the lumen weighting function, based on the eye's photopic sensitivity curve peaking at 555 nm, emphasizes wavelengths perceived most brightly by humans. Traditional incandescent bulbs achieve around 15 lm/W, largely due to significant losses outside the visible range, while modern light-emitting diodes (LEDs) reach 150–250 lm/W as of 2025 by more selectively emitting in the visible . In photonic-to-electrical conversion, photovoltaic (PV) efficiency measures the fraction of incident converted to electrical power, expressed as ηpv=PelectricalPincident solar×100%\eta_{pv} = \frac{P_{electrical}}{P_{incident\ solar}} \times 100\% where PelectricalP_{electrical} is the output electrical power and Pincident solarP_{incident\ solar} is the incident , typically under standard conditions of 1000 W/m². The theoretical upper bound for single-junction PV cells is the Shockley-Queisser limit, approximately 33% for an optimal bandgap of 1.34 eV, arising from fundamental thermodynamic constraints including balance and the bandgap energy EgE_g, where photons with energy below EgE_g are not absorbed and those above EgE_g lose excess energy as . This limit assumes radiative recombination as the sole loss mechanism and perfect absorption for photons exceeding EgE_g. For electrical-to-photonic conversion in LEDs, wall-plug efficiency is the ratio of output ( in watts) to input electrical power, given by η=ΦradiantPelectrical×100%\eta = \frac{\Phi_{radiant}}{P_{electrical}} \times 100\% where Φradiant\Phi_{radiant} accounts for all emitted photons, including non-visible ones. A key loss in white LEDs, which use emitters and phosphors, is the , where absorbed higher-energy photons are re-emitted at lower-energy wavelengths, dissipating about 20–30% of energy as and reducing overall . Advancements in lighting include organic LEDs (OLEDs), which achieved luminous efficacies exceeding 100 lm/W in the 2010s through improved phosphorescent emitters and exciplex hosts that enhance internal quantum efficiency. In solar applications, perovskite PV cells surpassed 25% efficiency by 2023 via strategies like anion fixation and Pb passivation to minimize defects and improve charge extraction, with certified single-junction efficiencies exceeding 26% as of 2025.

Measurement and Applications

Efficiency in Devices and Systems

In integrated devices such as heat pumps, efficiency is often quantified using the (COP), defined as the ratio of useful heating or cooling provided to the work input required, which can exceed 100% because the device transfers heat from an external source rather than converting input alone. For instance, modern heat pumps achieve COP values of 3 to 4, corresponding to 300-400% efficiency under optimal conditions, due to the incorporation of low-grade environmental heat alongside electrical work. Optimization in such devices follows international standards like , which establishes a systematic framework for systems to identify, monitor, and improve across organizational operations. As of 2025, has been updated to include enhanced AI integration for , further supporting efficiency improvements in systems. Compliance with enables continual reduction in by integrating efficiency into business processes, often yielding measurable gains in device-level . At the system level, overall energy conversion efficiency in chained processes, such as power generation, transmission, and distribution, is calculated as the product of individual stage efficiencies: ηsystem=∏ηi\eta_{\text{system}} = \prod \eta_i where ηi\eta_i represents the efficiency of each subprocess. This multiplicative approach highlights how even small losses at one stage compound across the system; for example, electric grid transmission and distribution losses typically range from 5% to 10% globally, with the U.S. averaging about 5% annually due to resistive heating and other dissipative effects. In large-scale systems, these losses underscore the need for holistic optimization to maintain high aggregate efficiency. Efficiency measurement in devices and systems relies on standardized testing protocols that distinguish between controlled laboratory conditions and variable real-world operation. The U.S. Environmental Protection Agency (EPA) economy ratings, for instance, are derived from tests simulating city and highway driving cycles, providing a benchmark that often overestimates real-world performance by 10-30% due to factors like traffic, weather, and driver behavior. testing measures vehicle power output and fuel consumption under repeatable loads, enabling precise efficiency assessments but requiring adjustments for on-road discrepancies through factors like the 5-cycle method. These protocols ensure comparability across systems while informing regulatory compliance and design improvements. Advancements in smart grids, incorporating (AI) for predictive load balancing and fault detection, have the potential to reduce system-level energy losses by up to 15% in pilot implementations, with broader applications showing 5-10% improvements as of 2025. AI algorithms analyze vast datasets from sensors to minimize transmission inefficiencies, such as by dynamically routing power flows, with pilot projects demonstrating up to 15% loss reductions in microgrids. These technologies integrate with existing standards like to scale efficiency gains across industrial and utility systems.

Practical Examples and Limitations

In power generation, combined cycle gas turbines represent a practical advancement, achieving efficiencies of approximately 60% by recovering exhaust from the gas turbine to drive a secondary , thereby maximizing energy extraction from combustion. plants, however, are constrained to around 33% efficiency due to the relatively low steam temperatures—typically below 300°C—imposed by reactor safety limits on coolant conditions, which reduce the temperature differential available for work extraction. In the transportation sector, electric vehicles exemplify high energy conversion efficiency, with overall efficiencies reaching about 90%, far surpassing the 20-30% well-to-wheel efficiency of vehicles, where much is lost as heat in the engine and exhaust. further boosts performance by recovering 60-80% of the dissipated during braking through the acting as a generator, which can contribute 10-30% to overall energy efficiency depending on driving conditions and battery state. A key limitation in all energy conversions stems from the second law of thermodynamics, which requires an increase in entropy for any real process, inherently prohibiting 100% efficiency as some energy must dissipate as unusable heat. Beyond physical constraints, economic trade-offs often limit adoption of higher-efficiency designs; for instance, in renewables like solar and wind systems, pursuing marginal efficiency gains can escalate upfront costs, influencing deployment decisions based on levelized cost of energy analyses. The 2017 illustrates these principles in electric mobility, attaining drivetrain efficiency of around 90% through optimized permanent magnet motors and inverters, which minimized losses in a compact, high-voltage architecture. Similarly, modern horizontal-axis wind turbines achieve practical efficiencies of 40-50%, limited by aerodynamic drag and mechanical losses but approaching the theoretical Betz limit of 59.3% that caps power extraction from an undisturbed wind stream.

References

  1. https://personal.ems.psu.edu/~radovic/fundamentals4.html
  2. https://www.e-education.psu.edu/egee102/node/1938
  3. https://personal.ems.psu.edu/~radovic/Chapter4.pdf
  4. https://esc.fsu.edu/documents/lectures/ECSI/Thermodynamics.pdf
  5. https://www.energy.gov/eere/solar/solar-performance-and-efficiency
  6. https://netl.doe.gov/sites/default/files/2024-08/Energy%2520Conversion%2520Engineering.pdf
  7. https://www.nap.edu/read/12621/page/315
  8. https://aether.lbl.gov/www/classes/p10/heat-engine.html
  9. https://www.iea.org/energy-system/energy-efficiency-and-demand/energy-efficiency
  10. https://www.eia.gov/energyexplained/use-of-energy/efficiency-and-conservation.php
  11. https://www.epa.gov/energy/learn-about-energy-and-its-impact-environment
  12. https://geosci.uchicago.edu/~moyer/GEOS24705/Readings/Carnot_article_1998.pdf
  13. https://www.physics.uci.edu/~silverma/units.html
  14. https://pressbooks.online.ucf.edu/phy2053bc/chapter/carnots-perfect-heat-engine-the-second-law-of-thermodynamics-restated/
  15. https://faculty.wcas.northwestern.edu/jmokyr/monster.PDF
  16. https://geosci.uchicago.edu/~moyer/GEOS24705/Notes/Lecture4Slides.pdf
  17. https://www.egr.msu.edu/~lira/supp/steam/wattbio.html
  18. https://galileo.phys.virginia.edu/classes/152.mf1i.spring02/CarnotEngine.htm
  19. https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node24.html
  20. https://www.grc.nasa.gov/www/k-12/airplane/ottoa.html
  21. https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node26.html
  22. https://www.nuclear-power.com/nuclear-engineering/thermodynamics/thermodynamic-cycles/otto-cycle-otto-engine/theory-of-otto-cycle-gasoline-engine/
  23. https://www.nuclear-power.com/nuclear-engineering/thermodynamics/thermodynamic-cycles/diesel-cycle-diesel-engine/thermal-efficiency-for-diesel-cycle/
  24. https://testbook.com/question-answer/rankine-cycle-efficiency-of-a-good-steam-power-pla--588c6c4ae9f1310a69f3b693
  25. https://dieselnet.com/tech/engine_efficiency.php
  26. https://www.energy.gov/sites/prod/files/2014/03/f8/deer11_edwards.pdf
  27. https://www.evengineeringonline.com/how-are-the-efficiency-and-benefits-of-regenerative-braking-measured-in-evs/
  28. https://www.sciencedirect.com/topics/engineering/high-heating-value
  29. https://www.cement-co2-protocol.org/en/Content/Internet_Manual/tasks/lower_and_higher_heating_values.htm
  30. https://www.engineeringtoolbox.com/fuels-higher-calorific-values-d_169.html
  31. https://www.sciencedirect.com/topics/physics-and-astronomy/combustion-efficiency
  32. https://www.sciencedirect.com/topics/earth-and-planetary-sciences/combustion-efficiency
  33. https://x-engineer.org/air-fuel-ratio/
  34. https://www.engineeringtoolbox.com/boiler-combustion-efficiency-d_271.html
  35. https://www.energy.gov/energysaver/furnaces-and-boilers
  36. https://www.sciencedirect.com/topics/engineering/boiler-efficiency
  37. https://www.engineeringtoolbox.com/boiler-efficiency-d_438.html
  38. https://www.epa.gov/sites/default/files/2020-10/documents/c02s01.pdf
  39. https://www.epa.gov/laws-regulations/summary-clean-air-act
  40. https://www.congress.gov/crs-product/RL30853
  41. https://www.monolithicpower.com/en/learning/mpscholar/ac-power/transformers/transformer-efficiency-and-losses
  42. https://www.energystar.gov/sites/default/files/powersupplysummary.pdf
  43. https://resources.altium.com/p/external-power-supply-efficiency-ratings
  44. https://eepower.com/technical-articles/transformer-losses-and-efficiency/
  45. https://edisontechcenter.org/Transformers.html
  46. https://www.ieee-pels.org/magazine/igbt-inventor-awarded-the-2024-millennium-technology-prize/
  47. https://courses.ems.psu.edu/eme812/node/738
  48. https://ratedpower.com/blog/utility-scale-pv-losses/
  49. https://www.avnet.com/americas/resources/article/designing-vienna-rectifiers-for-ev-chargers/
  50. https://www.rp-photonics.com/luminous_efficacy_and_efficiency.html
  51. https://www.engineeringtoolbox.com/luminous-efficacy-d_1932.html
  52. https://www.yujiintl.com/high-luminous-efficacy-lighting/
  53. https://www1.eere.energy.gov/buildings/publications/pdfs/ssl/led_energy_efficiency.pdf
  54. https://www.ossila.com/pages/radiative-efficiency-limit
  55. https://www.rp-photonics.com/wall_plug_efficiency.html
  56. https://www1.eere.energy.gov/buildings/publications/pdfs/ssl/report_led_november_2002a_1.pdf
  57. https://onlinelibrary.wiley.com/doi/abs/10.1002/adfm.201701314
  58. https://www.nature.com/articles/s41467-023-36229-1
  59. https://www.fluxim.com/research-blogs/perovskite-silicon-tandem-pv-record-updates
  60. https://buildingdecarb.org/why-efficiency-matters
  61. https://www.cnet.com/home/energy-and-utilities/a-heat-pump-is-more-than-100-efficient-yes-really-heres-how/
  62. https://www.iso.org/iso-50001-energy-management.html
  63. https://www.iso.org/standard/69426.html
  64. https://betterbuildingssolutioncenter.energy.gov/iso-50001/what-iso-50001
  65. https://www.e-education.psu.edu/egee102/node/1944
  66. https://www.eia.gov/tools/faqs/faq.php?id=105&t=3
  67. https://data.worldbank.org/indicator/EG.ELC.LOSS.ZS
  68. https://www.epa.gov/greenvehicles/fuel-economy-and-ev-range-testing
  69. https://advocacy.consumerreports.org/research/epa-mpg-label-analysis-2016/
  70. https://nepis.epa.gov/Exe/ZyPURL.cgi?Dockey=9100WZS0.TXT
  71. https://www.weforum.org/stories/2025/01/energy-ai-net-zero/
  72. https://www.ijesi.org/papers/Vol%2814%29i4/1404168174.pdf
  73. https://atb-archive.nrel.gov/electricity/2018/index.html?t=cg
  74. https://www.nuclear-power.com/nuclear-engineering/thermodynamics/laws-of-thermodynamics/thermal-efficiency/thermal-efficiency-of-nuclear-power-plants/
  75. https://witricity.com/media/blog/ev-vs-ice-surprising-differences
  76. https://openstax.org/books/physics/pages/12-3-second-law-of-thermodynamics-entropy
  77. https://www.epa.gov/sites/default/files/2018-07/documents/mbg_2-1_analyticframework.pdf
  78. https://www.epa.gov/greenvehicles/electric-vehicle-myths
  79. https://www.windedition.com/what-is-betz-limit-for-wind-turbine-efficiency/
Add your contribution
Related Hubs
User Avatar
No comments yet.