Hubbry Logo
General equilibrium theoryGeneral equilibrium theoryMain
Open search
General equilibrium theory
Community hub
General equilibrium theory
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
General equilibrium theory
General equilibrium theory
General equilibrium theory
View on Wikipedia
from Wikipedia
Part of a series on
Economics
Principles of Economics
Tools and methodology
Economic theory

Empirical methods

Prescriptive and policy

Branches and subfields
Applications

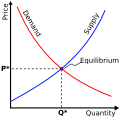
In economics, general equilibrium theory attempts to explain the behavior of supply, demand, and prices in a whole economy with several or many interacting markets, by seeking to prove that the interaction of demand and supply will result in an overall general equilibrium. General equilibrium theory contrasts with the theory of partial equilibrium, which analyzes a specific part of an economy while its other factors are held constant.[1]

General equilibrium theory both studies economies using the model of equilibrium pricing and seeks to determine in which circumstances the assumptions of general equilibrium will hold. The theory dates to the 1870s, particularly the work of French economist Léon Walras in his pioneering 1874 work Elements of Pure Economics.[2] The theory reached its modern form with the work of Lionel W. McKenzie (Walrasian theory), Kenneth Arrow and Gérard Debreu (Hicksian theory) in the 1950s.

Overview

[edit]

Broadly speaking, general equilibrium tries to give an understanding of the whole economy using a "bottom-up" approach, starting with individual markets and agents. Therefore, general equilibrium theory has traditionally been classified as part of microeconomics. The difference is not as clear as it used to be, since much of modern macroeconomics has emphasized microeconomic foundations, and has constructed general equilibrium models of macroeconomic fluctuations. General equilibrium macroeconomic models usually have a simplified structure that only incorporates a few markets, like a "goods market" and a "financial market". In contrast, general equilibrium models in the microeconomic tradition typically involve a multitude of different goods markets. They are usually complex and require computers to calculate numerical solutions.

In a market system the prices and production of all goods, including the price of money and interest, are interrelated: a change in the price of one good may affect the price of another good. Calculating the equilibrium price of just one good, in theory, requires an analysis that accounts for all of the millions of different goods that are available. It is often assumed that agents are price takers, and under that assumption two common notions of equilibrium exist: Walrasian, or competitive equilibrium, and its generalization: a price equilibrium with transfers.

Friedrich Hayek's influential essay "The Use of Knowledge in Society" (1945) articulated what scholars have since identified as a fundamental challenge to the informational assumptions underlying general equilibrium theory. Hayek argued that economic knowledge is inherently dispersed across countless individuals and often exists in tacit, context-specific forms that cannot be aggregated or centralized. This posed a problem for some models, whether Walrasian equilibrium theory or centralized economic planning, that presumes complete information or the possibility of gathering all relevant data in one place.[3][4]

Hayek proposed that market prices serve as decentralized information signals, distilling complex local knowledge about preferences, resources, and opportunities into summary statistics that coordinate economic decisions across society without requiring centralized knowledge or direction.[5][4] While predating the full Arrow-Debreu formalization (1954), Hayek's essay has been interpreted by subsequent economists both as a critique of the informational feasibility of perfect-information equilibrium models and as an explanation of how real-world market processes achieve coordination through price mechanisms despite pervasive ignorance and uncertainty. This perspective emphasizes economic processes and discovery over static equilibrium states.[3]

Walrasian equilibrium

[edit]

The first attempt in neoclassical economics to model prices for a whole economy was made by Léon Walras. Walras' Elements of Pure Economics provides a succession of models, each taking into account more aspects of a real economy (two commodities, many commodities, production, growth, money). Some think Walras was unsuccessful and that the later models in this series are inconsistent.[6][7]

In particular, Walras's model was a long-run model in which prices of capital goods are the same whether they appear as inputs or outputs and in which the same rate of profits is earned in all lines of industry. This is inconsistent with the quantities of capital goods being taken as data. But when Walras introduced capital goods in his later models, he took their quantities as given, in arbitrary ratios. (In contrast, Kenneth Arrow and Gérard Debreu continued to take the initial quantities of capital goods as given, but adopted a short run model in which the prices of capital goods vary with time and the own rate of interest varies across capital goods.)

Walras was the first to lay down a research program widely followed by 20th-century economists. In particular, the Walrasian agenda included the investigation of when equilibria are unique and stable— Walras' Lesson 7 shows neither uniqueness, nor stability, nor even existence of an equilibrium is guaranteed. Walras also proposed a dynamic process by which general equilibrium might be reached, that of the tâtonnement or groping process.

The tâtonnement process is a model for investigating stability of equilibria. Prices are announced (perhaps by an "auctioneer"), and agents state how much of each good they would like to offer (supply) or purchase (demand). No transactions and no production take place at disequilibrium prices. Instead, prices are lowered for goods with positive prices and excess supply. Prices are raised for goods with excess demand. The question for the mathematician is under what conditions such a process will terminate in equilibrium where demand equates to supply for goods with positive prices and demand does not exceed supply for goods with a price of zero. Walras was not able to provide a definitive answer to this question (see Unresolved Problems in General Equilibrium below).

Marshall and Sraffa

[edit]

In partial equilibrium analysis, the determination of the price of a good is simplified by just looking at the price of one good, and assuming that the prices of all other goods remain constant. The Marshallian theory of supply and demand is an example of partial equilibrium analysis. Partial equilibrium analysis is adequate when the first-order effects of a shift in the demand curve do not shift the supply curve. Anglo-American economists became more interested in general equilibrium in the late 1920s and 1930s after Piero Sraffa's demonstration that Marshallian economists cannot account for the forces thought to account for the upward-slope of the supply curve for a consumer good.

If an industry uses little of a factor of production, a small increase in the output of that industry will not bid the price of that factor up. To a first-order approximation, firms in the industry will experience constant costs, and the industry supply curves will not slope up. If an industry uses an appreciable amount of that factor of production, an increase in the output of that industry will exhibit increasing costs. But such a factor is likely to be used in substitutes for the industry's product, and an increased price of that factor will have effects on the supply of those substitutes. Consequently, Sraffa argued, the first-order effects of a shift in the demand curve of the original industry under these assumptions includes a shift in the supply curve of substitutes for that industry's product, and consequent shifts in the original industry's supply curve. General equilibrium is designed to investigate such interactions between markets.

Continental European economists made important advances in the 1930s.[8] Walras' arguments for the existence of general equilibrium often were based on the counting of equations and variables. Such arguments are inadequate for non-linear systems of equations and do not imply that equilibrium prices and quantities cannot be negative, a meaningless solution for his models. The replacement of certain equations by inequalities and the use of more rigorous mathematics improved general equilibrium modeling.[9]

Modern concept of general equilibrium in economics

[edit]
See also: Financial economics § State prices, Financial economics § Arbitrage-free pricing and equilibrium, and Asset pricing § General Equilibrium Asset Pricing

The modern conception of general equilibrium is provided by the Arrow–Debreu–McKenzie model, developed jointly by Kenneth Arrow, Gérard Debreu, and Lionel W. McKenzie in the 1950s.[10][11] Debreu presents this model in Theory of Value (1959) as an axiomatic model, following the style of mathematics promoted by Nicolas Bourbaki. In such an approach, the interpretation of the terms in the theory (e.g., goods, prices) are not fixed by the axioms.

Three important interpretations of the terms of the theory have been often cited. First, suppose commodities are distinguished by the location where they are delivered. Then the Arrow-Debreu model is a spatial model of, for example, international trade.

Second, suppose commodities are distinguished by when they are delivered. That is, suppose all markets equilibrate at some initial instant of time. Agents in the model purchase and sell contracts, where a contract specifies, for example, a good to be delivered and the date at which it is to be delivered. The Arrow–Debreu model of intertemporal equilibrium contains forward markets for all goods at all dates. No markets exist at any future dates.

Third, suppose contracts specify states of nature which affect whether a commodity is to be delivered: "A contract for the transfer of a commodity now specifies, in addition to its physical properties, its location and its date, an event on the occurrence of which the transfer is conditional. This new definition of a commodity allows one to obtain a theory of [risk] free from any probability concept..."[12]

These interpretations can be combined. So the complete Arrow–Debreu model can be said to apply when goods are identified by when they are to be delivered, where they are to be delivered and under what circumstances they are to be delivered, as well as their intrinsic nature. So there would be a complete set of prices for contracts such as "1 ton of Winter red wheat, delivered on 3rd of January in Minneapolis, if there is a hurricane in Florida during December". A general equilibrium model with complete markets of this sort seems to be a long way from describing the workings of real economies, however, its proponents argue that it is still useful as a simplified guide as to how real economies function.

Some of the recent work in general equilibrium has in fact explored the implications of incomplete markets, which is to say an intertemporal economy with uncertainty, where there do not exist sufficiently detailed contracts that would allow agents to fully allocate their consumption and resources through time. While it has been shown that such economies will generally still have an equilibrium, the outcome may no longer be Pareto optimal. The basic intuition for this result is that if consumers lack adequate means to transfer their wealth from one time period to another and the future is risky, there is nothing to necessarily tie any price ratio down to the relevant marginal rate of substitution, which is the standard requirement for Pareto optimality. Under some conditions the economy may still be constrained Pareto optimal, meaning that a central authority limited to the same type and number of contracts as the individual agents may not be able to improve upon the outcome, what is needed is the introduction of a full set of possible contracts. Hence, one implication of the theory of incomplete markets is that inefficiency may be a result of underdeveloped financial institutions or credit constraints faced by some members of the public. Research still continues in this area.

Properties and characterization of general equilibrium

[edit]
See also: Fundamental theorems of welfare economics

Basic questions in general equilibrium analysis are concerned with the conditions under which an equilibrium will be efficient, which efficient equilibria can be achieved, when an equilibrium is guaranteed to exist and when the equilibrium will be unique and stable.

First Fundamental Theorem of Welfare Economics

[edit]

The First Fundamental Welfare Theorem asserts that market equilibria are Pareto efficient. In other words, the allocation of goods in the equilibria is such that there is no reallocation which would leave a consumer better off without leaving another consumer worse off. In a pure exchange economy, a sufficient condition for the first welfare theorem to hold is that preferences be locally nonsatiated. The first welfare theorem also holds for economies with production regardless of the properties of the production function. Implicitly, the theorem assumes complete markets and perfect information. In an economy with externalities, for example, it is possible for equilibria to arise that are not efficient.

The first welfare theorem is informative in the sense that it points to the sources of inefficiency in markets. Under the assumptions above, any market equilibrium is tautologically efficient. Therefore, when equilibria arise that are not efficient, the market system itself is not to blame, but rather some sort of market failure.

Second Fundamental Theorem of Welfare Economics

[edit]

Even if every equilibrium is efficient, it may not be that every efficient allocation of resources can be part of an equilibrium. However, the second theorem states that every Pareto efficient allocation can be supported as an equilibrium by some set of prices. In other words, all that is required to reach a particular Pareto efficient outcome is a redistribution of initial endowments of the agents after which the market can be left alone to do its work. This suggests that the issues of efficiency and equity can be separated and need not involve a trade-off. The conditions for the second theorem are stronger than those for the first, as consumers' preferences and production sets now need to be convex (convexity roughly corresponds to the idea of diminishing marginal rates of substitution i.e. "the average of two equally good bundles is better than either of the two bundles").

Existence

[edit]

Even though every equilibrium is efficient, neither of the above two theorems say anything about the equilibrium existing in the first place. To guarantee that an equilibrium exists, it suffices that consumer preferences be strictly convex. With enough consumers, the convexity assumption can be relaxed both for existence and the second welfare theorem. Similarly, but less plausibly, convex feasible production sets suffice for existence; convexity excludes economies of scale.

Proofs of the existence of equilibrium traditionally rely on fixed-point theorems such as Brouwer fixed-point theorem for functions (or, more generally, the Kakutani fixed-point theorem for set-valued functions). See Competitive equilibrium#Existence of a competitive equilibrium. The proof was first due to Lionel McKenzie,[13] and Kenneth Arrow and Gérard Debreu.[14] In fact, the converse also holds, according to Uzawa's derivation of Brouwer's fixed point theorem from Walras's law.[15] Following Uzawa's theorem, many mathematical economists consider proving existence a deeper result than proving the two Fundamental Theorems.

Another method of proof of existence, global analysis, uses Sard's lemma and the Baire category theorem; this method was pioneered by Gérard Debreu and Stephen Smale.

Nonconvexities in large economies

[edit]
Main article: Shapley–Folkman lemma

Starr (1969) applied the Shapley–Folkman–Starr theorem to prove that even without convex preferences there exists an approximate equilibrium. The Shapley–Folkman–Starr results bound the distance from an "approximate" economic equilibrium to an equilibrium of a "convexified" economy, when the number of agents exceeds the dimension of the goods.[16] Following Starr's paper, the Shapley–Folkman–Starr results were "much exploited in the theoretical literature", according to Guesnerie,[17]: 112  who wrote the following:

some key results obtained under the convexity assumption remain (approximately) relevant in circumstances where convexity fails. For example, in economies with a large consumption side, nonconvexities in preferences do not destroy the standard results of, say Debreu's theory of value. In the same way, if indivisibilities in the production sector are small with respect to the size of the economy, [ . . . ] then standard results are affected in only a minor way.[17]: 99 

To this text, Guesnerie appended the following footnote:

The derivation of these results in general form has been one of the major achievements of postwar economic theory.[17]: 138 

In particular, the Shapley-Folkman-Starr results were incorporated in the theory of general economic equilibria[18][19][20] and in the theory of market failures[21] and of public economics.[22]

Uniqueness

[edit]
See also: Sonnenschein–Mantel–Debreu theorem

Although generally (assuming convexity) an equilibrium will exist and will be efficient, the conditions under which it will be unique are much stronger.[23] The Sonnenschein–Mantel–Debreu theorem, proven in the 1970s, states that the aggregate excess demand function inherits only certain properties of individual's demand functions, and that these (continuity, homogeneity of degree zero, Walras' law and boundary behavior when prices are near zero) are the only real restriction one can expect from an aggregate excess demand function. Any such function can represent the excess demand of an economy populated with rational utility-maximizing individuals.

There has been much research on conditions when the equilibrium will be unique, or which at least will limit the number of equilibria. One result states that under mild assumptions the number of equilibria will be finite (see regular economy) and odd (see index theorem). Furthermore, if an economy as a whole, as characterized by an aggregate excess demand function, has the revealed preference property (which is a much stronger condition than revealed preferences for a single individual) or the gross substitute property then likewise the equilibrium will be unique. All methods of establishing uniqueness can be thought of as establishing that each equilibrium has the same positive local index, in which case by the index theorem there can be but one such equilibrium.

Determinacy

[edit]

Given that equilibria may not be unique, it is of some interest to ask whether any particular equilibrium is at least locally unique. If so, then comparative statics can be applied as long as the shocks to the system are not too large. As stated above, in a regular economy equilibria will be finite, hence locally unique. One reassuring result, due to Debreu, is that "most" economies are regular.

Work by Michael Mandler (1999) has challenged this claim.[24] The Arrow–Debreu–McKenzie model is neutral between models of production functions as continuously differentiable and as formed from (linear combinations of) fixed coefficient processes. Mandler accepts that, under either model of production, the initial endowments will not be consistent with a continuum of equilibria, except for a set of Lebesgue measure zero. However, endowments change with time in the model and this evolution of endowments is determined by the decisions of agents (e.g., firms) in the model. Agents in the model have an interest in equilibria being indeterminate:

Indeterminacy, moreover, is not just a technical nuisance; it undermines the price-taking assumption of competitive models. Since arbitrary small manipulations of factor supplies can dramatically increase a factor's price, factor owners will not take prices to be parametric.[24]: 17 

When technology is modeled by (linear combinations) of fixed coefficient processes, optimizing agents will drive endowments to be such that a continuum of equilibria exist:

The endowments where indeterminacy occurs systematically arise through time and therefore cannot be dismissed; the Arrow-Debreu-McKenzie model is thus fully subject to the dilemmas of factor price theory.[24]: 19 

Some have questioned the practical applicability of the general equilibrium approach based on the possibility of non-uniqueness of equilibria.

Stability

[edit]

In a typical general equilibrium model the prices that prevail "when the dust settles" are simply those that coordinate the demands of various consumers for various goods. But this raises the question of how these prices and allocations have been arrived at, and whether any (temporary) shock to the economy will cause it to converge back to the same outcome that prevailed before the shock. This is the question of stability of the equilibrium, and it can be readily seen that it is related to the question of uniqueness. If there are multiple equilibria, then some of them will be unstable. Then, if an equilibrium is unstable and there is a shock, the economy will wind up at a different set of allocations and prices once the convergence process terminates. However, stability depends not only on the number of equilibria but also on the type of the process that guides price changes (for a specific type of price adjustment process see Walrasian auction). Consequently, some researchers have focused on plausible adjustment processes that guarantee system stability, i.e., that guarantee convergence of prices and allocations to some equilibrium. When more than one stable equilibrium exists, where one ends up will depend on where one begins. The theorems that have been mostly conclusive when related to the stability of a typical general equilibrium model are closed related to that of the most local stability.

Unresolved problems in general equilibrium

[edit]

Research building on the Arrow–Debreu–McKenzie model has revealed some problems with the model. The Sonnenschein–Mantel–Debreu results show that, essentially, any restrictions on the shape of excess demand functions are stringent. Some think this implies that the Arrow–Debreu model lacks empirical content.[25] Therefore, an unsolved problem is

  • Is Arrow–Debreu–McKenzie equilibria stable and unique?

A model organized around the tâtonnement process has been said to be a model of a centrally planned economy, not a decentralized market economy. Some research has tried to develop general equilibrium models with other processes. In particular, some economists have developed models in which agents can trade at out-of-equilibrium prices and such trades can affect the equilibria to which the economy tends. Particularly noteworthy are the Hahn process, the Edgeworth process and the Fisher process.

The data determining Arrow-Debreu equilibria include initial endowments of capital goods. If production and trade occur out of equilibrium, these endowments will be changed further complicating the picture.

In a real economy, however, trading, as well as production and consumption, goes on out of equilibrium. It follows that, in the course of convergence to equilibrium (assuming that occurs), endowments change. In turn this changes the set of equilibria. Put more succinctly, the set of equilibria is path dependent... [This path dependence] makes the calculation of equilibria corresponding to the initial state of the system essentially irrelevant. What matters is the equilibrium that the economy will reach from given initial endowments, not the equilibrium that it would have been in, given initial endowments, had prices happened to be just right. – (Franklin Fisher).[26]

The Arrow–Debreu model in which all trade occurs in futures contracts at time zero requires a very large number of markets to exist. It is equivalent under complete markets to a sequential equilibrium concept in which spot markets for goods and assets open at each date-state event (they are not equivalent under incomplete markets); market clearing then requires that the entire sequence of prices clears all markets at all times. A generalization of the sequential market arrangement is the temporary equilibrium structure, where market clearing at a point in time is conditional on expectations of future prices which need not be market clearing ones.

Although the Arrow–Debreu–McKenzie model is set out in terms of some arbitrary numéraire, the model does not encompass money. Frank Hahn, for example, has investigated whether general equilibrium models can be developed in which money enters in some essential way. One of the essential questions he introduces, often referred to as the Hahn's problem is: "Can one construct an equilibrium where money has value?" The goal is to find models in which existence of money can alter the equilibrium solutions, perhaps because the initial position of agents depends on monetary prices.

Some critics of general equilibrium modeling contend that much research in these models constitutes exercises in pure mathematics with no connection to actual economies. In a 1979 article, Nicholas Georgescu-Roegen complains: "There are endeavors that now pass for the most desirable kind of economic contributions although they are just plain mathematical exercises, not only without any economic substance but also without any mathematical value."[27] He cites as an example a paper that assumes more traders in existence than there are points in the set of real numbers.

Although modern models in general equilibrium theory demonstrate that under certain circumstances prices will indeed converge to equilibria, critics hold that the assumptions necessary for these results are extremely strong. As well as stringent restrictions on excess demand functions, the necessary assumptions include perfect rationality of individuals; complete information about all prices both now and in the future; and the conditions necessary for perfect competition. However, some results from experimental economics suggest that even in circumstances where there are few, imperfectly informed agents, the resulting prices and allocations may wind up resembling those of a perfectly competitive market (although certainly not a stable general equilibrium in all markets).[citation needed]

Frank Hahn defends general equilibrium modeling on the grounds that it provides a negative function. General equilibrium models show what the economy would have to be like for an unregulated economy to be Pareto efficient.[citation needed]

Computing general equilibrium

[edit]
Main articles: Applied general equilibrium and Computable general equilibrium

Until the 1970s general equilibrium analysis remained theoretical. With advances in computing power and the development of input–output tables, it became possible to model national economies, or even the world economy, and attempts were made to solve for general equilibrium prices and quantities empirically.

Applied general equilibrium (AGE) models were pioneered by Herbert Scarf in 1967, and offered a method for solving the Arrow–Debreu General Equilibrium system in a numerical fashion. This was first implemented by John Shoven and John Whalley (students of Scarf at Yale) in 1972 and 1973, and were a popular method up through the 1970s.[28][29] In the 1980s however, AGE models faded from popularity due to their inability to provide a precise solution and its high cost of computation.

Computable general equilibrium (CGE) models surpassed and replaced AGE models in the mid-1980s, as the CGE model was able to provide relatively quick and large computable models for a whole economy, and was the preferred method of governments and the World Bank. CGE models are heavily used today, and while 'AGE' and 'CGE' is used inter-changeably in the literature, Scarf-type AGE models have not been constructed since the mid-1980s, and the CGE literature at current is not based on Arrow-Debreu and General Equilibrium Theory as discussed in this article. CGE models, and what is today referred to as AGE models, are based on static, simultaneously solved, macro balancing equations (from the standard Keynesian macro model), giving a precise and explicitly computable result.[30]

Other schools

[edit]

General equilibrium theory is a central point of contention and influence between the neoclassical school and other schools of economic thought, and different schools have varied views on general equilibrium theory. Some, such as the Keynesian and Post-Keynesian schools, strongly reject general equilibrium theory as "misleading" and "useless". Disequilibrium macroeconomics and different non-equilibrium approaches were developed as alternatives. Other schools, such as new classical macroeconomics, developed from general equilibrium theory.

Keynesian and Post-Keynesian

[edit]

Keynesian and Post-Keynesian economists, and their underconsumptionist predecessors criticize general equilibrium theory specifically, and as part of criticisms of neoclassical economics generally. Specifically, they argue that general equilibrium theory is neither accurate nor useful, that economies are not in equilibrium, that equilibrium may be slow and painful to achieve, and that modeling by equilibrium is "misleading", and that the resulting theory is not a useful guide, particularly for understanding of economic crises.[31][32]

Let us beware of this dangerous theory of equilibrium which is supposed to be automatically established. A certain kind of equilibrium, it is true, is reestablished in the long run, but it is after a frightful amount of suffering.

— Simonde de Sismondi, New Principles of Political Economy, vol. 1, 1819, pp. 20-21.

The long run is a misleading guide to current affairs. In the long run we are all dead. Economists set themselves too easy, too useless a task if in tempestuous seasons they can only tell us that when the storm is past the ocean is flat again.

— John Maynard Keynes, A Tract on Monetary Reform, 1923, ch. 3

It is as absurd to assume that, for any long period of time, the variables in the economic organization, or any part of them, will "stay put," in perfect equilibrium, as to assume that the Atlantic Ocean can ever be without a wave.

— Irving Fisher, The Debt-Deflation Theory of Great Depressions, 1933, p. 339

Robert Clower and others have argued for a reformulation of theory toward disequilibrium analysis to incorporate how monetary exchange fundamentally alters the representation of an economy as though a barter system.[33]

New classical macroeconomics

[edit]

While general equilibrium theory and neoclassical economics generally were originally microeconomic theories, new classical macroeconomics builds a macroeconomic theory on these bases. In new classical models, the macroeconomy is assumed to be at its unique equilibrium, with full employment and potential output, and that this equilibrium is assumed to always have been achieved via price and wage adjustment (market clearing). The best-known such model is real business-cycle theory, in which business cycles are considered to be largely due to changes in the real economy, unemployment is not due to the failure of the market to achieve potential output, but due to equilibrium potential output having fallen and equilibrium unemployment having risen.

Socialist economics

[edit]

Within socialist economics, a sustained critique of general equilibrium theory (and neoclassical economics generally) is given in Anti-Equilibrium,[34] based on the experiences of János Kornai with the failures of Communist central planning, although Michael Albert and Robin Hahnel later based their Parecon model on the same theory.[35]

New structural economics

[edit]

The structural equilibrium model is a matrix-form computable general equilibrium model in new structural economics.[36] [37] This model is an extension of the John von Neumann's general equilibrium model (see Computable general equilibrium for details). Its computation can be performed using the R package GE.[38] The structural equilibrium model can be used for intertemporal equilibrium analysis, where time is treated as a label that differentiates between types of commodities and firms, meaning commodities are distinguished by when they are delivered and firms are distinguished by when they produce. The model can include factors such as taxes, money, endogenous production functions, and endogenous institutions, etc. The structural equilibrium model can include excess tax burdens, meaning that the equilibrium in the model may not be Pareto optimal. When production functions and/or economic institutions are treated as endogenous variables, the general equilibrium is referred to as structural equilibrium.

See also

[edit]

Notes

[edit]

Further reading

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

General equilibrium theory

View on Grokipedia
from Grokipedia

General equilibrium theory is a mathematical framework in economics that analyzes the simultaneous interactions of supply, demand, and prices across all markets in an economy to determine a state where no agent can improve their welfare by unilateral action, assuming perfect competition, rational agents, and complete markets. Originating with Léon Walras's Éléments d'économie politique pure in 1874, the theory posits that an economy can reach a configuration where aggregate excess demands are zero at some price vector, with agents maximizing utility subject to budget constraints.
Key developments include the Arrow-Debreu model of 1954, which extended Walrasian ideas to incorporate production, time, and uncertainty through contingent commodities, proving the existence of competitive equilibria under convexity assumptions via fixed-point theorems like Brouwer's or Kakutani's. This model supports the first fundamental theorem of welfare economics, stating that every competitive equilibrium allocation is Pareto efficient, and the second theorem, asserting that any Pareto efficient allocation can be decentralized as a competitive equilibrium with suitable initial endowments or transfers. These results provide a theoretical justification for markets as mechanisms for efficient resource allocation absent externalities or market failures.
Despite its foundational role, general equilibrium theory has notable limitations and controversies, particularly the Sonnenschein-Mantel-Debreu (SMD) theorem from the 1970s, which demonstrates that aggregate excess demand functions satisfy only weak properties—homogeneity, Walras' law, and continuity—implying virtually any such function can arise from optimizing individual behaviors, thus precluding unique equilibria or strong comparative statics predictions. This indeterminacy undermines the theory's empirical testability and predictive power, as real economies exhibit path dependence, frictions, and disequilibria not captured by static models. Empirical applications remain challenging, with validations often relying on computable general equilibrium models for policy simulations rather than direct falsification, highlighting a disconnect between the theory's mathematical rigor and observable market dynamics.

Foundations and Core Concepts

Definition and Basic Principles

General equilibrium theory is a framework in theoretical that models the as a system of interdependent markets where prices and quantities are determined simultaneously across all goods, services, and . It extends partial equilibrium by incorporating feedback effects between markets, positing that no isolated market can be in equilibrium without considering the entire economic structure. This approach originated with Léon Walras's work in Éléments d'économie politique pure (1874), which introduced the idea of mutual interdependence among markets. At its core, the theory defines a Walrasian equilibrium (or competitive equilibrium) as a configuration of prices pp and allocations xx such that: (i) each chooses a bundle maximizing subject to their derived from endowment values at those prices; (ii) each producer selects inputs and outputs to maximize profits given constraints; and (iii) markets clear, meaning equals (zero excess demand) for every . This equilibrium ensures compatibility without centralized coordination, relying on decentralized price signals. , a foundational implication, states that if all but one market clears, the last must also clear, reflecting the budget constraints' accounting identity. Basic principles hinge on idealized assumptions to guarantee equilibrium existence and properties: agents are rational price-takers in perfectly competitive markets; preferences are complete, transitive, and often convex (to avoid corner solutions); production technologies exhibit constant or increasing returns with convex input sets; endowments are fixed; and information is perfect with no externalities or public goods in the baseline model. Price formation occurs via an auctioneer-like tâtonnement process, where prices rise in excess demand and fall in , converging to equilibrium without actual trade until balance. These elements enable theorems like the first welfare theorem, linking competitive equilibria to under the stated conditions.

Walrasian Equilibrium and Tâtonnement Process

The Walrasian equilibrium, also known as competitive equilibrium, consists of a price vector and an allocation of goods such that each consumer's bundle maximizes subject to their , each producer's output maximizes profits given input prices, and equals in every market, ensuring no excess demand or supply exists. This concept, formalized by in the first edition of Éléments d'économie politique pure published in 1874, extends partial equilibrium analysis to an economy with multiple interdependent markets, where prices coordinate decentralized decisions to achieve simultaneous . Under standard assumptions like , , and continuity of excess demand functions, existence of such an equilibrium is guaranteed by fixed-point theorems, such as Brouwer's, applied to the excess demand correspondence. Central to Walras's framework is , which states that the value of aggregate excess demand is zero at any price vector, implying that if all but one market clear, the last must also clear; this reduces the number of independent equilibrium conditions to one fewer than the number of markets. In a Walrasian equilibrium, the price vector lies in the positive (prices strictly positive under free disposal), and the allocation is feasible, with total consumption not exceeding endowments plus production. These properties underpin the first welfare theorem, which holds that every Walrasian equilibrium allocation is Pareto efficient, provided assumptions like no externalities and complete markets are met. The tâtonnement process, French for "groping," describes a hypothetical adjustment mechanism proposed by Walras to illustrate how equilibrium might be reached dynamically. An imaginary auctioneer announces trial prices, eliciting excess demand signals from agents without permitting actual trades; if excess demand is positive in a market, the auctioneer raises the price proportionally, and if negative, lowers it, iterating until excess demands vanish across all markets. This process assumes gross substitutability—where an increase in one good's price raises demand for others—to ensure stability, as price adjustments then converge monotonically to equilibrium from any initial positive price vector. However, the mechanism precludes out-of-equilibrium transactions, rendering it a theoretical device rather than a realistic depiction of market dynamics, and stability fails without substitutability, as demonstrated in counterexamples where tâtonnement cycles or diverges. Walras refined the idea across editions of his work, emphasizing its role in proving equilibrium stability under competitive conditions, though later analyses, such as those by Scarf in 1960, highlighted instabilities in nonlinear economies.

Role in Neoclassical Economics

General equilibrium theory constitutes the analytical core of , providing a mathematical framework to model how prices, production, and consumption adjust simultaneously across all markets to achieve economy-wide consistency. In this paradigm, agents—households maximizing utility subject to budget constraints and firms maximizing profits—are assumed to operate under , with complete information and , leading to a Walrasian equilibrium where excess demands vanish for every good and factor. This structure underpins the neoclassical vision of markets as self-coordinating mechanisms, extending partial equilibrium analysis (as in single-market supply-demand models) to interlinked sectors, thereby resolving potential inconsistencies like derived demands or input-output feedbacks. The theory's integration into neoclassical doctrine is evident in its support for the first fundamental theorem of , which asserts that, under conditions of local non-satiation, convexity of preferences, and no externalities, a competitive equilibrium allocation is Pareto efficient—meaning no reallocation can improve one agent's welfare without harming another. Proven rigorously in the Arrow-Debreu model of , this result validates the allocative of decentralized markets without central planning, influencing policy prescriptions favoring minimal intervention to preserve price signals. The second fundamental theorem complements this by showing that any Pareto-efficient allocation can be achieved as a competitive equilibrium through appropriate lump-sum transfers, reinforcing the neoclassical emphasis on equity adjustments separate from efficiency considerations. Beyond static efficiency, general equilibrium theory frames dynamic extensions in neoclassical growth models, such as those incorporating and intertemporal optimization, while serving as a benchmark for empirical simulations in (CGE) models used by institutions like the World Bank for trade and analysis since the . However, its reliance on idealized assumptions—such as infinite divisibility of goods and absence of transaction costs—positions it as a normative ideal rather than a descriptive tool, with neoclassical economists employing it to derive testable implications on , like how tariff removals shift equilibria toward . This methodological role persists despite critiques, as it anchors the deductive rigor distinguishing neoclassical approaches from inductive or institutional alternatives.

Historical Evolution

Precursors and Early Ideas (18th-19th Centuries)

Richard Cantillon's Essai sur la Nature du Commerce en Général, circulated in manuscript around 1730 and published posthumously in 1755, introduced early notions of economy-wide interdependence through a circular flow of spending among three classes: landowners, undertakers (entrepreneurs or farmers bearing risk), and hirelings (wage laborers). Cantillon described markets for land, labor, necessities, and luxuries as interconnected, with prices and quantities adjusting via entrepreneurial to achieve a balanced state where aggregate expenditures equal aggregate receipts, prefiguring equilibrium concepts by emphasizing self-regulating market processes without central coordination. François Quesnay advanced these ideas in 1758 with the , a schematic representation of sectoral flows in the French economy divided into three classes: the productive class (farmers producing surplus agricultural goods), the proprietary class (landowners receiving net product as rent), and the sterile class (artisans and merchants providing non-reproductive services). The model traces a "zigzag" sequence of monetary advances and repayments—farmers expend on sterile goods, artisans purchase , and exports close the circuit—culminating in a reproductive equilibrium where the initial distribution of cash returns to landlords, maintaining constant output and surplus under fixed proportions and full circulation. Quesnay used the Tableau to illustrate conditions for economic balance, warning that deviations like excessive sterile spending erode the agricultural surplus essential for growth, thus highlighting causal links between sectoral imbalances and systemic decline. In the early 19th century, classical economists built on these foundations implicitly by assuming simultaneous across factors and goods in growth and distribution models. Jean-Baptiste Say's 1803 treatise articulated "," positing that total production generates equivalent demand, ensuring economy-wide equilibrium absent monetary hoarding, though critiqued later for overlooking temporary gluts. David Ricardo's 1817 modeled rent, wages, and profits interdependently under , treating relative prices as determined by labor costs across sectors in a , an approach that anticipated general interdependence without explicit tâtonnement dynamics. These works privileged empirical observations of agricultural and trade patterns but lacked mathematical simultaneity, serving as conceptual bridges to formalized general equilibrium.

Léon Walras and Vilfredo Pareto (Late 19th-Early 20th Centuries)

Léon Walras established the core framework of general equilibrium theory through his seminal work Éléments d'économie politique pure, first published in 1874, in which he modeled the economy as a network of simultaneous equations ensuring that excess demand is zero in every market at equilibrium prices. Walras demonstrated that the number of independent equations equals the number of unknowns (prices and quantities), allowing for a unique solution under his assumptions of constant returns, perfect competition, and rational agents maximizing utility subject to budget constraints. To address how equilibrium might be reached dynamically, he proposed the tâtonnement process, an iterative price adjustment mechanism simulated by a hypothetical auctioneer who raises prices in excess-demand markets and lowers them in excess-supply markets, preventing trade until balance is achieved across all sectors. This approach highlighted the interdependence of markets, departing from partial equilibrium analysis by integrating production, exchange, and consumption in a cohesive system. Vilfredo Pareto, succeeding Walras as professor of political economy at the University of Lausanne in 1893, advanced general equilibrium theory by generalizing its foundations and shifting emphasis toward observable behavior over subjective utility. In his Cours d'économie politique (1896–1897) and Manuel d'économie politique (1906), Pareto formalized equilibrium conditions using the concept of ophelimity—a measurable index of preference satisfaction replacing cardinal utility—to derive demand functions from revealed choices, thereby extending Walrasian analysis to cases without interpersonal utility comparisons. Pareto's framework confirmed that a competitive equilibrium satisfies efficiency criteria, introducing the notion that reallocations improving one agent's welfare without harming others are impossible at optimum, a condition now termed Pareto efficiency. He critiqued Walras' reliance on utility maximization by focusing on ordinal preferences and equilibrium stability through marginal adjustments, while incorporating money and production more flexibly, thus solidifying the Lausanne school's contributions to interdependence and welfare analysis in general equilibrium. Together, Walras and Pareto's iterative refinements established general equilibrium as a cornerstone of neoclassical economics, emphasizing mathematical rigor and systemic balance over isolated market dynamics.

Arrow-Debreu Formalization (1950s)

The Arrow-Debreu formalization emerged in the early 1950s as a rigorous axiomatic treatment of Walrasian general equilibrium, culminating in the 1954 paper "Existence of an Equilibrium for a Competitive Economy" by Kenneth J. Arrow and Gérard Debreu. This work integrated production, exchange, and consumption into a single model, extending prior partial proofs—such as those by Abraham Wald for separate exchange and production models—by demonstrating equilibrium existence under unified conditions. The model posits an economy with multiple consumers possessing endowments and continuous, convex preferences represented by utility functions, and firms with convex production sets characterized by constant or decreasing returns. Central to the formalization is the specification of commodities as vectors distinguished by physical attributes, location, date of delivery, and state of nature, enabling complete markets for contingent claims without explicit dynamics or sequential trading. Prices form a vector in Euclidean space corresponding to the commodity space, and equilibrium requires a non-negative price vector such that aggregate excess demand—defined as the difference between demanded and supplied quantities across all agents—is zero everywhere, satisfying Walras' law (sum of excess demands valued at equilibrium prices equals zero). Production is modeled via net output vectors feasible under technological constraints, with firms maximizing profits given prices, while consumers maximize utility subject to budget constraints incorporating endowments and shares in firm profits. Existence is established by mapping the normalized price simplex to itself via the excess demand correspondence, which is upper hemicontinuous, convex-valued, and satisfies gross substitutability or similar conditions under convexity assumptions. and Debreu invoke Kakutani's —a of Brouwer's—to guarantee a fixed point where excess demand vanishes, thus proving equilibrium attainment; this approach relaxes some of Wald's restrictions, such as requiring strictly quasi-concave . The framework assumes no free production (infeasible net outputs bounded away from origin), survival (preferences bounded below), and continuity, ensuring the model's primitives align with empirical realism in competitive settings while prioritizing mathematical consistency. This 1954 contribution marked a pivotal axiomatization, embedding time, , and spatial differentiation into a static competitive structure, and laid groundwork for subsequent extensions like Debreu's 1959 Theory of Value, which popularized the notation. Independent contemporaneous proofs, such as Lionel McKenzie's 1954 Econometrica article, reinforced the result using similar fixed-point methods, underscoring the era's convergence on amid debates over stability and . The formalization's emphasis on convexity and completeness has been critiqued for idealizing away real-world frictions like incomplete information or non-convexities, yet it remains a benchmark for analyzing decentralized .

Mathematical Framework

Key Assumptions and Primitives

The primitives of general equilibrium theory, as formalized in the Arrow-Debreu model, consist of a finite-dimensional commodity space where commodities are distinguished by their objective attributes, including physical properties, location, date of delivery, and state of nature, represented as vectors in RL\mathbb{R}^L with LL denoting the number of distinct commodities. Consumers form a finite set II, each endowed with an initial resource vector ωi∈R+L\omega_i \in \mathbb{R}^L_+ and a preference relation ≿i\succsim_i over consumption sets Xi⊆R+LX_i \subseteq \mathbb{R}^L_+, typically assumed to be complete, transitive, reflexive, continuous, convex, and satisfying local nonsatiation to ensure well-behaved demand. Producers comprise a finite set JJ, each defined by a production set Yj⊆RLY_j \subseteq \mathbb{R}^L that is closed, convex, contains the origin (possibility of inaction), satisfies free disposal (y∈Yjy \in Y_j implies y′≤y∈Yjy' \leq y \in Y_j), and often exhibits constant or increasing returns bounded by convexity assumptions for equilibrium existence. Ownership of firms is distributed among consumers via share vectors θi=(θij)j∈J\theta_i = (\theta_{ij})_{j \in J} with ∑i∈Iθij=1\sum_{i \in I} \theta_{ij} = 1 for each jj. Key assumptions underpinning the model include , under which all agents are price-takers despite finite numbers, implying infinitesimal influence on prices and no strategic behavior. Markets are complete, encompassing spot and forward transactions for all commodities across time and contingencies, with prices p∈R++Lp \in \mathbb{R}^L_{++} normalized by a numeraire good to eliminate in this framework. Agents possess about all primitives, preferences, and technologies, enabling rational maximization: consumers solve max⁡≿ixi∈Xi\max_{\succsim_i} x_i \in X_i subject to p⋅xi≤p⋅ωi+∑jθijπjp \cdot x_i \leq p \cdot \omega_i + \sum_j \theta_{ij} \pi_j, where πj\pi_j are firm profits, while firms maximize max⁡Yjp⋅yj\max_{Y_j} p \cdot y_j. No externalities affect preferences or productions, and survival conditions ensure aggregate endowments support positive consumption possibilities, preventing unattainable equilibria. Convexity of preferences and production sets is imposed to guarantee continuity and quasiconcavity of excess demand functions, facilitating existence proofs via fixed-point theorems, though these idealize away from empirical irregularities like non-convexities observed in real technologies.

Equilibrium Conditions and Excess Demand

In general equilibrium theory, a Walrasian equilibrium is defined as a price vector p∗∈R++Lp^* \in \mathbb{R}_{++}^L (normalized such that ∑pi=1\sum p_i = 1) and an allocation of consumption bundles to households and production plans to firms such that each household maximizes subject to its at p∗p^*, each firm maximizes profits at p∗p^*, and aggregate excess demand is zero across all LL markets: Z(p∗)=0Z(p^*) = 0. This condition ensures , where total demand equals total supply for every good, reflecting the interdependence of markets under and rational agents. The excess demand function Z(p)Z(p) aggregates individual behaviors into market-level imbalances, given by Z(p)=∑hDh(p)−∑fyf(p)−ωZ(p) = \sum_h D^h(p) - \sum_f y^f(p) - \omega, where Dh(p)D^h(p) is the correspondence of hh (derived from maximization), yf(p)y^f(p) is the supply from firm ff (from ), and ω\omega is the aggregate endowment. Under standard assumptions of continuous, strictly quasi-concave utilities and convex production sets, Z(p)Z(p) is well-defined, upper hemicontinuous, and satisfies key properties: homogeneity of degree zero (Z(λp)=Z(p)Z(\lambda p) = Z(p) for λ>0\lambda > 0), implying price scaling invariance; Walras' law (p⋅Z(p)=0p \cdot Z(p) = 0 for all pp, arising from agents exhausting their budgets); and boundary behavior where Zj(p)→+∞Z_j(p) \to +\infty as pj→0+p_j \to 0^+ while other prices are fixed, ensuring drives prices up. Walras' law, formalized by Léon Walras in his 1874 Éléments d'économie politique pure and later named by Oskar Lange in 1942, captures the accounting identity that unspent income in one market implies excess demand elsewhere, reducing the independent equations to L−1L-1 for equilibrium determination. Equilibrium requires solving Zj(p)=0Z_j(p) = 0 for j=1,…,L−1j = 1, \dots, L-1, with the LL-th market clearing residually; non-satisfaction in any market violates overall balance, as excess supply in one necessitates excess demand in others to preserve value consistency. These conditions underpin existence proofs via fixed-point theorems, such as Brouwer's, by mapping excess demand into a compact set where a zero exists, though they assume no gross complementarities or non-convexities that could introduce discontinuities.

Fixed-Point Theorems and Proof Techniques

The existence of a Walrasian equilibrium in general equilibrium models is established through fixed-point theorems, which guarantee a solution to systems where excess demand vanishes across all markets. These theorems address the challenge of finding price vectors p∗p^* such that aggregate demand equals aggregate supply, without assuming explicit solvability of the underlying equations. In the Arrow-Debreu framework, the proof constructs a compact convex domain, typically the price simplex Δ={p≥0∣∑pi=1}\Delta = \{ p \geq 0 \mid \sum p_i = 1 \}, and defines an excess demand correspondence Z(p)Z(p) that satisfies Walras' law (p⋅Z(p)=0p \cdot Z(p) = 0) and other properties like continuity and convexity of preferences. Brouwer's fixed-point theorem, proved in 1911, asserts that any continuous single-valued function mapping a compact, convex set in Euclidean space into itself has at least one fixed point. This result applies in simplified equilibrium models where mappings are single-valued, such as certain representative agent economies, by showing that a price adjustment function ϕ(p)=p+Z(p)∥p+Z(p)∥\phi(p) = \frac{p + Z(p)}{\|p + Z(p)\|} (normalized to the simplex) is continuous and thus admits a fixed point p∗p^* where Z(p∗)=0Z(p^*) = 0. However, standard general equilibrium settings feature set-valued mappings due to non-unique optima in consumer choice or production, necessitating extensions beyond Brouwer's theorem. Kakutani's , established in 1941, generalizes Brouwer's result to upper hemicontinuous correspondences with nonempty, convex, compact values defined on a compact, . Upper hemicontinuity ensures that for any pn→pp_n \to p, the images Z(pn)Z(p_n) remain "close" to Z(p)Z(p) in a set-theoretic sense, while convexity of values (e.g., from and production sets) preserves the theorem's applicability. In the 1954 Arrow-Debreu proof, the correspondence ψ(p)={q∈Δ∣q=p+z∥p+z∥,z∈Z(p)}\psi(p) = \{ q \in \Delta \mid q = \frac{p + z}{\|p + z\|}, z \in Z(p) \} is shown to be upper hemicontinuous with convex values, yielding a fixed point p∗∈ψ(p∗)p^* \in \psi(p^*), which implies Z(p∗)={0}Z(p^*) = \{0\} under the model's assumptions of and . This technique, independently used by McKenzie in 1954, relies on gross substitutes or boundary conditions to rule out boundary equilibria where some prices are zero. Proof techniques often involve verifying the hypotheses: continuity of excess derives from the continuity of and production functions; convexity from quasi-concavity of preferences and convexity of sets; and compactness from finite commodities and boundedness. Alternative approaches, such as Tarski's for lattices (applied in some Walrasian proofs as of 2025), offer lattice-structured equilibria but require monotonicity assumptions not always present in Arrow-Debreu settings. These methods underscore the reliance on topological properties rather than dynamical stability, highlighting that existence holds without uniqueness or adjustability.

Fundamental Properties

Existence Proofs and Non-Convexities

The existence of a competitive equilibrium in the Arrow-Debreu model was formally established by and in their 1954 Econometrica paper, which demonstrated that under specified conditions, including and production sets, an economy admits at least one price vector supporting zero excess demand across all markets. This proof relies on constructing an excess demand correspondence that is upper hemicontinuous, convex-valued, and satisfies Walras' law, then applying Kakutani's fixed-point theorem to guarantee a fixed point corresponding to equilibrium prices. Kakutani's theorem, a generalization of for set-valued mappings, ensures the existence of a price vector in the such that the associated excess demand has a zero in its image, provided the commodity space is finite-dimensional and production technologies exhibit constant or decreasing to maintain convexity. Convexity assumptions are pivotal: preferences must be representable by continuous, strictly quasi-concave functions ensuring convex upper contour sets, while firm production sets require convexity to guarantee convex correspondences. Without these, the excess mapping may fail upper or convex-valuedness, invalidating the fixed-point application and potentially precluding equilibrium . Lionel McKenzie independently reached a similar result in , emphasizing the theorem's robustness under local non-satiation and survival assumptions, which ensure positive prices and bounded . Non-convexities introduce significant challenges, as they violate the core structural assumptions of the standard proofs; for instance, non-convex preferences—such as those with satiation points or lexicographic orders—can render the correspondence non-convex, leading to discontinuities in aggregate excess demand that evade fixed-point guarantees. In production contexts, non-convex technologies like increasing (common in indivisibilities or setup costs) produce non-convex profit sets, where firms may not achieve optimal scale at competitive prices, resulting in equilibria that are approximate at best or absent in pure strategy forms. Empirical relevance arises in sectors with fixed costs, where market equilibria may fail to clear without subsidies or entry barriers, as non-convexity amplifies the scope for multiple or no Walrasian outcomes. Efforts to address non-convexities include relaxing fixed-point reliance via degree theory or homotopy methods for constructive existence, though these often yield only approximate equilibria or require additional restrictions like finite agents. Star-shaped or asymptotically convex sets have been proposed to restore existence under milder conditions, but such generalizations do not universally apply and highlight the fragility of pure competitive equilibria in realistic economies with scale economies. Consequently, non-convex models frequently exhibit sunspot-driven indeterminacy or necessitate mixed strategies, underscoring that standard general equilibrium existence hinges on idealized convexity absent in many applied settings.

Uniqueness, Determinacy, and Stability

In the Arrow-Debreu model, while of competitive equilibrium is established under standard assumptions of and production sets, is not guaranteed without further restrictions. Multiple equilibria can arise due to the flexibility of excess functions, which, as demonstrated by the Sonnenschein-Mantel-Debreu theorem, can approximate arbitrary continuous functions satisfying basic properties like Walras' law and boundary conditions, allowing for non-unique price vectors clearing all markets. Conditions sufficient for include gross substitutability, where an increase in the price of one good leads to non-decreasing for all other , ensuring that the excess mapping is contractive or satisfies properties implying a single fixed point. Additionally, in economies where endowments are nearly Pareto optimal, local holds, as shown by Balasko's results on the geometry of equilibrium manifolds. Determinacy in general equilibrium theory refers to the property that equilibria form a of isolated points on the price simplex, typically requiring regularity conditions on preferences and technologies to avoid continua of equilibria. In smooth economies with differentiable functions, the equilibrium correspondence is generically finite and locally unique, with the degree of the equilibrium mapping determining the number of solutions near generic perturbations. However, in non-regular cases or with infinite-dimensional spaces, indeterminacy can occur, as infinite-horizon models may exhibit continua of perfect foresight equilibria deviating from steady states. These properties underscore that determinacy relies on structural assumptions beyond those for mere , such as the transversality of the equilibrium manifold to the . Stability analysis focuses on dynamic processes like Walrasian tâtonnement, where prices adjust proportionally to excess demands: p˙i=zi(p)\dot{p}_i = z_i(p) for each good ii, with no occurring out of equilibrium. Under the assumption of weak gross substitutability—where cross-price effects are non-negative—the tâtonnement process is locally stable around equilibrium, as the of excess demand has a negative real part for all eigenvalues, ensuring convergence via Lyapunov criteria. Global stability requires stronger conditions, such as strict gross substitutability combined with homogeneity, though counterexamples exist even then in multi-good settings due to potential cycles in price adjustments. In production economies, stability extends if firms' supply responses reinforce substitutability, but decentralized mechanisms can introduce strategic deviations undermining Walrasian convergence. These results highlight that stability is neither generic nor assured in model, depending critically on empirical plausibility of substitutability across markets.

First and Second Welfare Theorems

The First Fundamental Theorem of Welfare Economics asserts that any competitive equilibrium allocation in a general equilibrium model is Pareto efficient, provided that agents' preferences are continuous, convex, and locally non-satiated, production technologies exhibit constant or increasing returns with convex sets, markets are complete, there are no externalities, and agents behave as price takers. This result implies that no alternative feasible allocation can improve the welfare of one agent without reducing that of another, under the specified conditions. The proof proceeds by contradiction: suppose an equilibrium allocation x∗x^* is not Pareto efficient, so there exists a feasible allocation x′x' that strictly improves for at least one agent ii while not decreasing it for others. At equilibrium prices p∗p^*, agent ii's would then permit xi′x'_i, contradicting the assumption that xi∗x_i^* maximizes ii's subject to the p∗⋅xi∗=p∗⋅ei+πip^* \cdot x_i^* = p^* \cdot e_i + \pi_i, where eie_i is the endowment and πi\pi_i is profit share. non-satiation ensures that any welfare-improving deviation would violate budget constraints at equilibrium prices, while convexity guarantees that marginal rates of substitution and transformation align with relative prices. These assumptions exclude real-world frictions like market incompleteness or monopolistic power, limiting the theorem's direct applicability but establishing a benchmark for in idealized settings. The Second Fundamental Theorem of Welfare Economics states that any Pareto efficient allocation can be achieved as a competitive equilibrium allocation through appropriate lump-sum transfers of initial endowments, assuming preferences and production sets are strictly convex, continuous, and locally non-satiated, with complete markets and no externalities. Strict convexity ensures the supporting equilibrium prices are unique up to scaling and that the allocation lies in the interior of the feasible set, allowing transfers to redistribute wealth without altering relative incentives. To establish this, for a given Pareto optimal allocation x0x^0, equilibrium prices p0p^0 are found such that xi0x_i^0 maximizes each consumer's utility subject to the budget p0⋅xi0=p0⋅ωip^0 \cdot x_i^0 = p^0 \cdot \omega_i, where ωi\omega_i are adjusted endowments satisfying aggregate feasibility ∑ωi=∑ei+y0\sum \omega_i = \sum e_i + y^0, and y0y^0 is the production plan. Firms maximize profits at p0p^0, ensuring zero aggregate profits under constant returns. The theorem underscores that efficiency and equity are separable in theory—desirable distributions can be attained via initial transfers followed by undistorted markets—but requires strong convexity to avoid corner solutions or multiple supporting prices. In the Arrow-Debreu framework, these theorems collectively demonstrate that competitive equilibria achieve efficiency without central planning, contingent on the idealized assumptions.

Empirical Dimensions

Microeconomic Tests and Consumer/Producer Behavior

Microeconomic tests of general equilibrium theory assess whether individual agent behaviors—specifically, consumers' maximization and producers' under price-taking assumptions—align with observed data, providing foundational support for Walrasian primitives. These tests typically employ methods, which derive necessary and sufficient conditions for without imposing parametric forms on preferences or technologies. For consumers, the Generalized of (GARP) tests whether a of prices and chosen bundles can be rationalized by a locally nonsatiated, continuous function; Afriat's theorem establishes that finite observations satisfy GARP if and only if such a exists. Empirical applications to household expenditure data, including food panels and consumption surveys, generally find that choices satisfy GARP or its variants, indicating broad consistency with utility maximization despite occasional violations attributable to measurement error or unobserved heterogeneity. For example, tests on U.S. consumer food panel data from the mid-20th century confirmed adherence to the Strong Axiom of Revealed Preference (SARP, a linear approximation of GARP) in aggregate patterns, though individual-level inconsistencies arose in about 10-15% of cases, often resolvable by allowing for measurement issues. More recent analyses of collective household models, incorporating intra-household bargaining, apply revealed preference characterizations to datasets like the British Family Expenditure Survey (1970-1988), revealing that while Pareto-efficient allocations hold under income pooling for couples, deviations occur with children, yet overall optimization remains supported when accounting for distribution factors. These findings affirm the microeconomic realism of consumer demand in general equilibrium setups, where agents respond to relative prices via compensated demand slopes (Slutsky terms) that are negative semidefinite. Producer behavior tests analogously verify , checking if firm netput choices (outputs minus inputs) are consistent with convex production sets and price-taking. Revealed preference for producers requires that observed choices not be dominated by alternatives affordable at prevailing prices, akin to GARP but framed via the profit function's superadditivity and monotonicity. Empirical evidence from firm-level production data supports this in competitive industries; a revealed preference analysis of U.S. firms (1993-1998) found input-output decisions fully rationalizable by , with no profitable deviations possible given estimated technologies and prices. Broader tests on market data, such as cross-firm comparisons in , confirm implications like the and negative semidefiniteness of the Allen-Uzawa elasticities of substitution, derived from minimization dual to , holding in panels from the postwar U.S. . Such tests bolster general equilibrium by validating decentralized optimization, essential for equilibrium existence via fixed-point arguments. Even in biological systems mimicking exchange, confirms Walrasian consistency: experiments on mycorrhizal fungi trading for carbon with host plants (2019 data) showed endowment-driven price adjustments (e.g., 5.16-24.78 carbon per unit) satisfying GARP and equilibrium conditions, with no opportunities. However, while these pass rationality checks, they do not preclude aggregate indeterminacies, as restrictions impose weak constraints on excess functions.

Macroeconomic Evidence and Computable Models

(CGE) models operationalize general equilibrium theory by numerically approximating economy-wide equilibria through systems of nonlinear equations solved via algorithms like nonlinear complementarity or , calibrated to empirical macroeconomic data such as (GDP), sectoral outputs, and trade flows from sources including input-output tables and matrices. These models assume and rational optimization across agents, enabling simulations of policy-induced shifts in relative prices and that propagate through intersectoral linkages to aggregate variables like and . Empirical validation of CGE models often proceeds via within-sample replication of base-year data and out-of-sample historical simulations, where model-generated paths for macroeconomic indicators are compared to observed outcomes. For example, global CGE frameworks like the Global Trade Analysis Project (GTAP) have been tested against agricultural price data from 1986–2001, demonstrating that calibrated excess demand functions can replicate observed variability in international commodity prices under trade distortions, thus supporting the models' capacity to capture equilibrium responses to shocks. Similarly, dynamic CGE variants calibrated to national accounts have forecasted disaggregated GDP components with errors lower than naive trend extrapolations in cases like post-reform sectoral growth in developing economies. In macroeconomic policy analysis, CGE models provide evidence for general equilibrium effects by quantifying spillovers from interventions, such as trade liberalization's impact on aggregate welfare. Simulations for the (NAFTA), conducted prior to its 1994 implementation, projected modest GDP gains of 0.5–2% for through efficiency improvements in , with ex-post evaluations confirming directional increases in Mexican exports and , albeit with variances attributable to unmodeled frictions like labor mobility constraints. Institutions including the World Bank have relied on such models for over 30 years to assess structural reforms, where baseline equilibria calibrated to 2020s data for low-income countries replicate observed macroeconomic recoveries post-COVID-19, including rebounds in investment-to-GDP ratios around 25–30%. These applications underscore CGE's role in tracing causal chains from micro primitives to macro aggregates, though direct econometric tests of Walrasian equilibrium conditions—such as zero aggregate excess —lack robust macro-level confirmation due to challenges.

Limitations from Aggregation and Sonnenschein-Mantel-Debreu Results

The Sonnenschein-Mantel-Debreu (SMD) results demonstrate that aggregate excess demand functions in general equilibrium models, derived from individual utility-maximizing agents with continuous, strictly convex preferences and positive endowments, satisfy only minimal restrictions: continuity, homogeneity of degree zero in prices, and Walras' law (the value of aggregate excess demand is zero at all prices). These properties alone do not impose additional structure, such as monotonicity or the weak axiom of revealed preference, on the aggregate function. Consequently, for economies with more than two goods, almost any function meeting these boundary conditions can be realized as the aggregate excess demand of some economy populated by rational agents, revealing that microeconomic rationality imposes negligible constraints on macroeconomic behavior. This lack of structure undermines the aggregation process central to general equilibrium theory, where individual demands and supplies must sum to coherent market-level functions for equilibrium analysis. Without further assumptions—like identical enabling a representative agent—the transition from micro to macro yields indeterminate outcomes, including potential multiple equilibria, non-convexities in aggregate responses, and failure of stability under tâtonnement price adjustment. For instance, aggregate excess demand need not exhibit gross substitutability, allowing upward-sloping segments that violate intuitive partial equilibrium intuitions and complicate proofs. These findings, established in the early 1970s, highlight how distributional effects and heterogeneity across agents can generate arbitrary aggregate dynamics, rendering general equilibrium predictions empirically vacuous without ad hoc restrictions. The SMD results thus expose a core limitation: general equilibrium theory excels in proving under idealized conditions but falters in delivering testable, determinate implications for real economies, particularly in macroeconomic applications or simulations that rely on aggregated behaviors. They imply that phenomena like market instability or coordination failures cannot be ruled out by appeals to individual rationality alone, challenging derivations of macro models from foundations and necessitating alternative approaches for in multi-market settings. While extensions incorporating large agent numbers or specific forms can restore some structure, the theorems underscore the fragility of aggregation, prompting critiques that general equilibrium remains more a mathematical construct than a robust empirical framework.

Criticisms and Debates

Theoretical Shortcomings and Unresolved Problems

General equilibrium theory encounters significant challenges in establishing of equilibria. Under standard assumptions of and production sets, multiple equilibria can coexist, as demonstrated in models with non-convexities or specific endowment distributions, rendering predictions indeterminate without additional restrictions. This non- arises because the fixed-point mappings, such as those from Brouwer's theorem, generally yield sets rather than single points, and local uniqueness requires stringent conditions like gross substitutability that rarely hold broadly. Stability of the equilibrium adjustment process remains unresolved, particularly for Walrasian tatonnement dynamics where prices adjust based on excess demands. While stability holds under the gross substitutes assumption, counterexamples abound in general cases, with trajectories potentially or diverging, as shown in multi-good economies without such restrictions. These issues stem from the absence of a decentralized mechanism for convergence, leaving the Walrasian as an implausible coordinating device rather than a realistic market process. The Sonnenschein-Mantel-Debreu theorem further erodes the theory's microfoundational claims by revealing that aggregate excess demand functions, derived from rational individual behaviors, satisfy only weak properties—homogeneity, Walras' law, and continuity—allowing virtually any such function consistent with these. This implies that general equilibrium imposes negligible empirical restrictions on economy-wide outcomes, challenging the aggregation from individual rationality to macroeconomic predictability. Incorporation of and financial assets poses persistent difficulties, with the treating as neutral or superfluous in static models, yet failing to resolve its essential role in facilitating trade or avoiding inefficiencies without ad hoc assumptions. Dynamic extensions struggle with time inconsistencies and , where forward-looking behaviors lead to equilibria or self-fulfilling prophecies unbound by fundamentals. Formal inconsistencies arise from the theory's reliance on incomplete axiomatic systems, where unresolved logical gaps—such as undecidability in infinite-horizon settings—undermine claims of completeness, echoing Gödelian limitations adapted to economic modeling. These theoretical voids persist despite refinements, as core proofs evade causal processes for equilibrium attainment, prioritizing over realizability.

Keynesian and Interventionist Critiques

Keynesian economists contend that general equilibrium theory (GET), with its core Walrasian assumption of through flexible prices and wages, unrealistically precludes and demand-driven fluctuations. , in The General Theory of Employment, Interest, and Money (1936), argued that classical models—precursors to formal GET—erroneously presume as the natural outcome of supply-side adjustments, whereas deficiencies, driven by volatile investment decisions and preferences, can trap economies in equilibria. This critique highlights GET's static framework, which neglects time, uncertainty, and non-neutral money, rendering it incapable of explaining historical episodes like the , where U.S. unemployment peaked at 24.9% in 1933 despite falling wages. Post-Keynesian extensions amplify this by emphasizing fundamental uncertainty and non-ergodic processes, where future outcomes lack probabilistic stationarity, undermining GET's reliance on and equilibrium convergence via tâtonnement. Robert Clower's 1965 dual-decision further posits that agents face effective demands constrained by perceived sets in disequilibrium, not the notional plans assumed in GET, leading to coordination failures absent in Walrasian auctioneer processes. Empirical support for such views draws from persistent post-recession gaps, as seen in the Eurozone's 12% average rate from 2012–2015, which rigidities and demand shortfalls exacerbated beyond supply-side explanations. Critics like (1986) add that financial instability, fueled by speculative booms, generates endogenous crises incompatible with GET's stable equilibrium paths. Interventionist critiques, often overlapping with Keynesian macro concerns, target GET's idealized conditions—perfect competition, complete information, and no externalities—as insufficient for real-world policy, necessitating active government roles to address market imperfections. (1994) argued that information asymmetries, unmodeled in standard GET, produce inefficiencies like in credit markets, justifying interventions such as countercyclical ; for instance, the 2009 U.S. American Recovery and Reinvestment Act, injecting $831 billion, correlated with GDP growth rebound from -2.5% in 2009 to 2.6% in 2010. However, these views assume interventions correct rather than distort equilibria, overlooking issues like , where U.S. federal spending rose 60% from 2000–2020 amid persistent deficits exceeding 5% of GDP annually post-2008. Proponents maintain GET's welfare theorems falter under dynamic settings with , as in Europe's post-2008 sovereign debt crisis, where bailouts totaling €500 billion stabilized banking but entrenched . Such arguments prioritize causal interventions over , though empirical tests, like applications, reveal policy ineffectiveness when agents anticipate changes, as in the 1970s under expansionary Keynesian regimes.

Market Process and Austrian Perspectives

Austrian economists, building on the work of , , and , conceptualize the market not as a static state of general equilibrium but as a dynamic market process characterized by entrepreneurial discovery, error correction, and the coordination of dispersed, through price signals. In this view, economic coordination emerges spontaneously from individual actions under uncertainty, rather than from predefined equilibrium conditions requiring or a hypothetical to clear all markets simultaneously. , a prominent Austrian theorist, emphasizes entrepreneurial alertness—the ability of individuals to recognize and act on profit opportunities arising from disequilibria—as the driving force propelling the market toward greater coordination, distinct from the optimizing behavior assumed in neoclassical models. This process-oriented approach rejects the Walrasian tâtonnement mechanism in general equilibrium theory (GET), which presumes iterative price adjustments without genuine discovery or time passage, arguing instead that real markets involve ongoing trial-and-error amid ignorance and heterogeneity. Hayek's critique of Walrasian GET centers on its failure to account for the knowledge problem: economic knowledge is fragmented, subjective, and context-specific, impossible to aggregate into the simultaneous equations of a central planner or equilibrium model. In his 1945 essay "The Use of Knowledge in Society," Hayek illustrates how prices serve as signals conveying this dispersed information, enabling decentralized decision-making that GET overlooks by assuming actors possess all relevant data . Austrians contend that GET's static equilibrium constructs—featuring perfect foresight, complete markets, and passive price-taking—abstract away from causal realities like time preferences, capital heterogeneity, and institutional evolution, rendering the theory incapable of explaining how prices form or resources allocate in a world of genuine uncertainty. Ludwig Lachmann extended this by highlighting radical uncertainty and , where expectations diverge and equilibrium may never be attained, contrasting sharply with GET's assumptions. While some economists, including Austrian sympathizers like Leland Yeager, defend aspects of GET as a useful benchmark for analyzing coordination despite its limitations, the dominant Austrian position holds that the theory's reliance on unrealistic axioms—such as auctioneer-mediated adjustments without transactions—obscures the entrepreneurial market essential for understanding real-world economic order. Empirical implications arise in critiques of policy interventions: Austrians argue that GET-inspired models underestimate disruptions to the discovery from distortions, as seen in Hayek's analysis of business cycles where artificial credit expansion misallocates resources away from sustainable coordination. This perspective prioritizes —the of exchange—as a of mutual benefit through , over GET's focus on end-state efficiency, offering a framework where market imperfections foster rather than mere deviations from optimality.

Applications and Extensions

Policy Analysis and Development Economics

Computable general equilibrium (CGE) models, derived from general equilibrium theory, serve as primary tools for by simulating economy-wide effects of interventions such as tax reforms, trade liberalization, and removals. These models numerically approximate Walrasian equilibria, incorporating multi-sector production, consumption, fiscal operations, and while enforcing constraints and . Originating in the 1970s, CGE applications extended theoretical general equilibrium frameworks to empirical data calibration, enabling quantitative predictions of welfare changes, output shifts, and distributional impacts under alternative policy scenarios. In , CGE models evaluate structural policies in low-income contexts, where market imperfections like informal sectors and dualistic labor markets are often parameterized. Early applications in the 1980s supported planning in developing economies, evolving to assess (IMF) and World Bank structural adjustment programs, including tariff reductions and . For instance, CGE simulations quantified alleviation from openness in countries like post-NAFTA, projecting GDP growth of 0.5-1% annually alongside household income variations by quintile. The World Bank has employed multisectoral CGE frameworks to analyze policy reforms in , estimating that a 10% uniform cut could boost real GDP by 2-4% over five years while increasing unskilled wage shares by 1-3%, though results hinge on Armington trade elasticities typically set at 4-8. These models inform development aid allocation and poverty impact assessments by linking policy shocks to micro-level outcomes via representative agents or stratified households. IMF applications integrate CGE with fiscal multipliers to evaluate sustainability reforms, as in dynamic models forecasting 1-2% GDP contractions from in emerging markets during the sovereign episodes. However, reliance on long-run equilibrium assumptions overlooks short-term disequilibria prevalent in developing economies, prompting hybrid extensions with partial equilibrium elements for transitional dynamics. Empirical validation draws from matrices calibrated to , ensuring consistency with observed base-year data like India's 2011-12 input-output tables showing agriculture's 18% GDP share. Despite limitations in capturing endogenous growth or financial frictions, CGE remains a benchmark for in policy design, prioritizing efficiency gains over equity unless distributional modules are activated.

Financial Markets and Incomplete Markets

In general equilibrium theory, financial markets facilitate intertemporal and state-contingent transfers of through assets like and bonds, but these typically span only a proper subspace of the full set of possible future states of nature, rendering markets . This incompleteness contrasts with the Arrow-Debreu model's complete markets, where contingent claims exist for every state, enabling full risk-sharing and Pareto-optimal allocations. In incomplete settings, agents' portfolio choices constrain consumption possibilities to the asset payoff span, often leaving idiosyncratic risks unhedgeable. Equilibrium in such economies, formalized by Radner (1972) as plans, prices, and expectations where spot and asset markets clear sequentially, faces challenges in due to discontinuities in the spanned space as asset prices vary. Hart (1975) constructed examples showing non- when short-selling is unrestricted and asset spans jump discontinuously. Duffie and Shafer (1985) resolved this generically by applying fixed-point theorems on the manifold of subspaces, proving equilibrium for finite-horizon economies with smooth preferences and endowments, assuming no . A key departure from complete markets is the generic constrained inefficiency of equilibria: even optimizing within the spanned subspace, allocations fail Pareto optimality when multiple agents and commodities exist, as transfers improving welfare for some without harming others become feasible via additional securities or taxes. Geanakoplos and Polemarchakis (1986) demonstrated this for economies with at least two agents, two commodities, and asset spans strictly between one and the full state space dimension, implying potential gains from constrained interventions like issuing new assets. In financial applications, underpin where equilibrium returns reflect covariances with aggregate endowment s projectable onto the span, rather than full marginal utilities; this yields properties and approximations like the (CAPM) under mean-variance assumptions and limited assets. Multi-period extensions over finite horizons incorporate sequential trading, where no-arbitrage enforces bounds on , but incompleteness propagates, amplifying inefficiencies in risk allocation across time and . Nominal assets introduce price-level indeterminacy, yielding continua of equilibria unless anchors like real securities are present. These frameworks link real and financial sectors, explaining phenomena like excess volatility or limited corporate leverage under s, while highlighting realism over complete-market ideals.

Dynamic and Stochastic General Equilibrium

Dynamic stochastic general equilibrium (DSGE) models extend static general equilibrium frameworks to incorporate time, uncertainty, and intertemporal optimization by representative agents, such as households maximizing over consumption and labor supply, and firms maximizing profits under production technologies subject to shocks like disturbances. These models assume , where agents form forecasts using all available information, and require that all markets clear in every period, deriving aggregate fluctuations from microeconomic foundations rather than behavioral equations. Originating in the real business cycle (RBC) paradigm introduced by Finn E. Kydland and in their 1982 paper "Time to Build and Aggregate Fluctuations," DSGE models initially emphasized real shocks—particularly technology innovations—as the primary drivers of s, with flexible prices ensuring efficient . Kydland and Prescott calibrated their RBC model to match empirical moments of U.S. data, such as the of output and hours worked, demonstrating that shock-driven responses could replicate key business cycle regularities without invoking monetary factors. Subsequent developments integrated New Keynesian elements, including nominal rigidities like sticky prices and wages, to address empirical observations of monetary non-neutrality, while retaining the core DSGE structure of dynamic optimization and stochastic processes modeled via Markov chains or autoregressive forms. Solution methods typically involve log-linearizing equations around the and applying techniques like the Blanchard-Kahn conditions for saddle-path stability, or more advanced global methods for nonlinear dynamics; shifted from to Bayesian approaches using likelihood-based inference on observables like GDP and inflation. For instance, the Smets-Wouters model for the area, estimated on quarterly data from 1985 onward, incorporates habit formation in consumption, adjustment costs in , and wage-price stickiness, achieving fits to multiple macroeconomic series via posterior mode . In applications, DSGE models facilitate counterfactual policy simulations, such as evaluating the welfare effects of monetary rules or fiscal multipliers under uncertainty, with central banks like the employing them for forecasting and ; the FRBNY DSGE model, for example, processes over 20 shocks and observables to generate impulse responses aligned with historical episodes like the 2008 recession. These frameworks underscore causal mechanisms where shocks propagate through general equilibrium interactions, such as a positive shock raising output and via substitution effects, though their reliance on identifying shock variances from covariances has sparked debates on structural versus reduced-form interpretations. Empirical validation often hinges on comparing model-generated variances and correlations to post-1945 U.S. aggregates, where RBC variants explain about 50-70% of output volatility via Solow residuals, per calibration exercises.

Recent Advances

Improvements in Testability and Uniqueness

Recent developments in have enhanced the of general equilibrium models by deriving nonparametric conditions under which observed data are consistent with equilibrium allocations, even in multi-agent settings. These advances, building on Afriat's theorem and extending to collective household models and public goods economies, allow for empirical rejection of general equilibrium without strong parametric assumptions on preferences or production. For instance, in economies with externalities or public decisions, testable implications arise from efficiency constraints on feasible sets, enabling welfare analysis from observational data. Such tests address aggregation challenges posed by the Sonnenschein-Mantel-Debreu (SMD) results, which imply that aggregate excess demand lacks structure beyond continuity and , complicating direct falsification. By focusing on differentiable approach to the equilibrium manifold or rationalization of expenditure , recent frameworks recover individual from market outcomes under generic conditions, preserving core implications like while permitting empirical scrutiny in applied contexts such as labor or equilibria. On , theoretical progress has identified sufficient conditions for a unique competitive equilibrium in otherwise flexible models, mitigating SMD-induced multiplicity. In two-good economies, aggregate 's local downward slope—ensured by heterogeneous preferences or effects—guarantees a unique, equilibrium, extending beyond classical gross substitutability assumptions. Broader advances incorporate monotonicity or network structures in multi-agent interactions, yielding and global stability in general equilibrium with production, as in quantitative models where agent heterogeneity and input-output linkages impose discipline on excess . These results hold generically for constant and homothetic production, facilitating policy counterfactuals without reliance on multiple equilibria. In financial and macroeconomic applications, or dynamic adjustments further restrict multiplicity, with recent proofs establishing under constant relative risk aversion variants or survival constraints.

Computational Methods and Big Data Integration

Computational methods have become indispensable for analyzing general equilibrium theory (GET), as analytical solutions to Walrasian equilibria prove intractable for multi-sector economies with heterogeneous agents and nonlinear interactions. (CGE) models operationalize GET by embedding microeconomic foundations into numerical frameworks calibrated to , solving systems of nonlinear equations representing and optimization conditions through iterative algorithms like fixed-point or nonlinear solvers. These models typically employ matrices to initialize parameters and simulate policy shocks, such as changes, by tracing adjustments in prices, outputs, and welfare across sectors. Software suites like GEMPACK facilitate solutions for large-scale CGE systems with thousands of variables, using Johansen's method for linear approximations or more advanced nonlinear techniques to handle dynamics. In dynamic and extensions of GET, computational approaches address time inconsistency and via methods such as value function or projection techniques on discrete grids, enabling of representative-agent growth models under shocks like fluctuations. For heterogeneous-agent models, homotopy continuation algorithms compute equilibria in by tracing paths from known solutions to target parameter sets, mitigating convergence issues in high-dimensional spaces. These techniques reveal that equilibrium relies on continuity and convexity assumptions, but numerical instability can arise from multiple equilibria or non-convexities, necessitating robustness checks like perturbation analysis. Integration of big data refines GET by leveraging micro-level datasets for parameter estimation and empirical validation, countering the Lucas critique through evidence-based calibration of agent behaviors and preferences. Lars Peter Hansen's framework emphasizes reattaching aggregate GE models to micro empirical distributions, using household survey data to inform heterogeneity in consumption and production functions, thereby improving predictive accuracy for policy counterfactuals. Machine learning augments this by approximating solutions in complex dynamic GE models; for instance, deep reinforcement learning algorithms solve heterogeneous-agent economies with millions of states, learning optimal policies that converge to epsilon-equilibria faster than traditional grid-based methods. Multi-agent reinforcement learning has been applied to microfounded dynamic stochastic GE models, enabling computation of meta-equilibria across agent types calibrated to big datasets like transaction-level trade records, though challenges persist in ensuring global optimality amid approximation errors. Such integrations highlight causal pathways from data-driven primitives to equilibrium outcomes, but require validation against out-of-sample aggregates to avoid overfitting.

Intersections with Behavioral and Evolutionary Economics

Behavioral economics challenges the foundational assumptions of general equilibrium theory (GET), particularly the postulate of hyper-rational agents with consistent, utility-maximizing preferences under full information. Empirical evidence from laboratory and field experiments documents persistent deviations, such as , reference dependence, and heuristic-driven choices, which undermine the coherence of Walrasian equilibria. Recent theoretical work integrates these insights into GET frameworks, demonstrating that behavioral biases can coexist with well-defined equilibria; for example, in one-sector growth models with or prospect-theoretic preferences, steady-state capital levels adjust predictably to environmental shocks, with biases amplifying volatility in transitional dynamics. Such extensions reveal aggregate implications: in multi-agent general equilibrium settings, heterogeneous behavioral types lead to inefficient allocations unless offset by mechanisms like commitment devices or interventions, yet the may exhibit pseudo-rationality at the macro level due to offsetting errors across agents. Linking axiomatic with behavioral primitives allows analysis of and welfare in , where biases distort equilibrium prices but do not preclude existence or uniqueness under mild convexity conditions. These models preserve GET's core structure while incorporating micro-founded deviations, supported by to on savings and consumption patterns showing over decades. Evolutionary economics intersects GET by emphasizing dynamic processes of variation, selection, and retention in economic systems, contrasting with GET's static, ahistorical equilibria that assume given preferences and technologies. Traditional GET overlooks and Schumpeterian innovation waves, treating the as closed to exogenous novelties, whereas evolutionary models portray firms and strategies as evolving populations subject to competitive selection. offers a partial synthesis, reframing market interactions as repeated games where strategies evolve via replicator dynamics toward evolutionarily stable states analogous to Nash equilibria in GET, with applications to oligopolistic pricing and entry-exit under . Emerging frameworks embed evolutionary dynamics into generalized equilibrium models, such as stochastic processes approximating long-run growth paths where selection filters inefficient routines, yielding emergent allocations that mimic without central planning. Empirical validation draws from firm-level data on survival rates and diffusion, indicating that evolutionary selection imposes discipline akin to competitive equilibria, though with greater emphasis on historical contingencies absent in standard GET. These intersections highlight GET's adaptability but underscore its limitations in capturing non-ergodic, open-ended economic change.

References

  1. http://dido.econ.yale.edu/~gean/art/1987-newpalgrave1.pdf
  2. https://www.bu.edu/eci/files/2019/06/stilldead.pdf
  3. http://dido.econ.yale.edu/~gean/art/p1274.pdf
  4. https://eml.berkeley.edu/~fechenique/lecture_notes/echenique_GE.pdf
  5. https://www.journals.uchicago.edu/doi/pdf/10.1086/261484
  6. https://sites.pitt.edu/~luca/ECON2100/2018Class/lecture_20.pdf
  7. https://faculty.sites.iastate.edu/tesfatsi/archive/tesfatsi/WalrasIntro.pdf
  8. http://www.hetwebsite.net/het/essays/stable/walrastatonnement.htm
  9. https://journals.openedition.org/oeconomia/1631
  10. https://economics.ucr.edu/papers/papers00/00-05.pdf
  11. https://d-nb.info/1192183819/34
  12. https://scispace.com/pdf/the-explanatory-role-of-general-equilibrium-theory-an-1w5i5yfmv7.pdf
  13. https://economics.mit.edu/sites/default/files/publications/Theory%252C%2520General%2520Equilibrium%252C%2520Political%2520Economy%2520and.pdf
  14. https://scholarship.law.duke.edu/cgi/viewcontent.cgi?article=5139&context=lcp
  15. https://www.econlib.org/library/Essays/JLibSt/hykCnt.html
  16. https://www.hetwebsite.net/het/essays/youth/cantsys.htm
  17. https://www.hetwebsite.net/het/essays/physioc/tableauoverview.htm
  18. https://www.iioa.org/conferences/intermediate-2008/pdf/2b2_Steenge.pdf
  19. https://www.hetwebsite.net/het/profiles/walras.htm
  20. http://digamo.free.fr/walras96.pdf
  21. https://competitionandappropriation.econ.ucla.edu/wp-content/uploads/sites/95/2020/12/WalkerOnWalras.pdf
  22. https://www.citeco.fr/10000-years-history-economics/industrial-revolutions/leon-walras-publishes-elements-deconomie-politique-pure-elements-of-pure-economics
  23. http://users.econ.umn.edu/~jchipman/DALLOZ5.pdf
  24. https://global.oup.com/academic/product/manual-of-political-economy-9780199607952
  25. https://api.pageplace.de/preview/DT0400.9780191650635_A23595287/preview-9780191650635_A23595287.pdf
  26. https://cooperative-individualism.org/pareto-vilfredo_the-new-theories-of-economics-1897-sep.pdf
  27. https://www.tandfonline.com/doi/abs/10.1080/09538259.2021.1889173
  28. https://faculty.sites.iastate.edu/tesfatsi/archive/tesfatsi/ModernEconTheory.AKirman2021.pdf
  29. https://www.jstor.org/stable/1907353
  30. https://www.econometricsociety.org/publications/econometrica/1954/07/01/existence-equilibrium-competitive-economy
  31. https://web.stanford.edu/class/msande311/arrow-debreu.pdf
  32. https://coin.wne.uw.edu.pl/mbrzezinski/teaching/HE4/BlaugFormalistRevolution.pdf
  33. https://econweb.ucsd.edu/~rstarr/ARTICLEwnotes.pdf
  34. https://hope.econ.duke.edu/sites/hope.econ.duke.edu/files/McKenzie_paper_SSRN.pdf
  35. https://ageconsearch.umn.edu/record/15587/files/wp000001.pdf
  36. https://www.nobelprize.org/uploads/2018/06/debreu-lecture.pdf
  37. https://econweb.ucsd.edu/~rstarr/webpage200B2017/SectionIIA1221.pdf
  38. https://scholar.harvard.edu/files/basilico/files/hart_notes_2013.pdf
  39. https://www.wider.unu.edu/sites/default/files/WP13.pdf
  40. https://math.uchicago.edu/~may/REU2019/REUPapers/Liu%2CZhengyang.pdf
  41. https://faculty.fiu.edu/~boydj/microii/microg02-l.pdf
  42. https://www.hetwebsite.net/het/essays/math/fixedpoint.htm
  43. https://arxiv.org/html/2503.03275v2
  44. https://www.maths.tcd.ie/~dwilkins/Courses/MAU34804/MAU34804_Resources/HistoryOfFixedPointTheoremsInGeneralEquilibriumTheory.html
  45. https://www.econometricsociety.org/uploads/Obituaries%2520Past%2520Presidents/arrow_geanakoplos.pdf
  46. https://www.hetwebsite.net/het/essays/get/existence.htm
  47. https://arxiv.org/pdf/2503.16890
  48. https://www.sciencedirect.com/science/article/pii/S0022053107001068
  49. https://www.ineteconomics.org/perspectives/blog/general-equilibrium-theory-sound-and-fury-signifying-nothing
  50. http://dido.econ.yale.edu/~djb/pub/equi-anal.pdf
  51. https://www.jstor.org/stable/1914230
  52. https://cae.economics.cornell.edu/05-16.pdf
  53. https://www.sciencedirect.com/science/article/pii/030440688290012X
  54. https://sites.pitt.edu/~luca/ECON2100/2018Class/lecture_21.pdf
  55. https://link.springer.com/article/10.1007/s001990050282
  56. https://www.sciencedirect.com/science/article/abs/pii/0022053188901317
  57. https://www.redalyc.org/pdf/221/22130201.pdf
  58. https://hal.science/hal-01764115/document
  59. https://www.sciencedirect.com/science/article/pii/S0304406896007896
  60. https://www.cigionline.org/sites/default/files/inet2012gintis_thestabilityofwalrasiangeneral.pdf
  61. http://users.econ.umn.edu/~tkehoe/papers/uniqueness.pdf
  62. https://sites.pitt.edu/~luca/ECON2100/2018Class/lecture_17.pdf
  63. https://www.alexbcunha.com/files/research/papers/paper09.pdf
  64. https://www.ias.edu/sites/default/files/sss/papers/econpaper74.pdf
  65. https://tamuz.caltech.edu/teaching/ss205b/lectures.pdf
  66. https://courses.cit.cornell.edu/econ6100/notes/LecAD20.pdf
  67. https://people.ischool.berkeley.edu/~hal/Papers/2005/revpref.pdf
  68. https://www.jstor.org/stable/1909164
  69. https://www.nowpublishers.com/article/DownloadEBook/ECO-016
  70. https://www.sciencedirect.com/science/article/abs/pii/S0167268124003871
  71. https://www.jstor.org/stable/2525321
  72. https://pmc.ncbi.nlm.nih.gov/articles/PMC8271793/
  73. https://chambers.georgetown.domains/grpt.pdf
  74. https://www.un.org/en/development/desa/policy/mdg_workshops/eclac_training_mdgs/sanchez2004_chapter7.pdf
  75. https://www.sciencedirect.com/science/article/pii/0305750X9190003Z
  76. https://www.pep-net.org/sites/pep-net.org/files/typo3doc/pdf/files_events/Valenzuela-Hertel-2004.pdf
  77. https://ideas.repec.org/h/eee/hacchp/v1y2013icp1271-1330.html
  78. https://www.pep-net.org/sites/pep-net.org/files/typo3doc/pdf/DevarajanRobinson.pdf
  79. https://blogs.worldbank.org/en/africacan/how-cge-models-influence-policy
  80. https://www.minneapolisfed.org/economic-research/conferences/~/media/files/research/events/1995_11-17/Canova_EquilibriumModels.pdf
  81. https://www.jstor.org/stable/1913184
  82. https://www.sciencedirect.com/science/article/pii/0022053174901008
  83. https://www.sciencedirect.com/science/article/pii/0304406874900329
  84. https://www.econometricsociety.org/publications/econometrica/1972/05/01/market-excess-demand-functions
  85. https://econpapers.repec.org/RePEc:eee:jetheo:v:7:y:1974:i:3:p:348-353
  86. https://link.springer.com/article/10.1007/BF01213945
  87. https://www.sciencedirect.com/science/article/pii/S0304406824000697
  88. https://www.hetecon.net/wp-content/uploads/2019/08/Ekeland2.pdf
  89. https://dspace.mit.edu/bitstream/handle/1721.1/64194/stabilityofgener00fish.pdf?sequence=1
  90. https://www.cambridge.org/core/journals/journal-of-the-history-of-economic-thought/article/what-a-difference-a-sum-makes-success-and-failure-in-the-rationalization-of-demand/A0474093FB6555BB0708D0431823E47B
  91. http://digamo.free.fr/ackerman4.pdf
  92. https://faculty.sites.iastate.edu/tesfatsi/archive/tesfatsi/ParadoxesProblemsWithEquilEcon.KDogra2024.pdf
  93. https://www.econlib.org/library/Enc/bios/Kirzner.html
  94. https://www.libertarianism.org/publications/essays/austrian-vs-neoclassical-economics-equilibrium
  95. https://www.auburn.edu/~garriro/j1scham.htm
  96. https://iea.org.uk/publications/research/how-markets-work-disequilibrium-entrepreneurship-and-discovery/
  97. https://www.libertarianism.org/publications/essays/socialist-economic-calculation
  98. http://4liberty.eu/hayek-market-mechanism-and-criticism-of-socialism/
  99. https://public.econ.duke.edu/~bjc18/docs/Wieser%2C%2520Hayek%2C%2520and%2520Equilibrium%2520Theory.pdf
  100. https://mises.org/quarterly-journal-austrian-economics/error-equilibrium-and-equilibration-austrian-price-theory
  101. https://departments.gmu.edu/rae/archives/VOL11_1-2_1999/yeager.pdf
  102. https://www.elidourado.com/p/austrian-macro-right-and-wrong
  103. https://oll.libertyfund.org/publications/liberty-matters/peter-boettke-israel-kirzner-competition-entrepreneurship
  104. https://www.sciencedirect.com/science/article/pii/S1573447105800075
  105. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=2805040
  106. https://documents.worldbank.org/en/publication/documents-reports/documentdetail/722951468181728853/cge-models-for-the-analysis-of-trade-policy-in-developing-countries
  107. https://www.elibrary.imf.org/downloadpdf/view/journals/001/2025/077/001.2025.issue-077-en.pdf
  108. https://www.tandfonline.com/doi/full/10.1080/23322039.2020.1829802
  109. https://people.bu.edu/isw/papers/cge.pdf
  110. https://dornsife.usc.edu/michael-magill/wp-content/uploads/sites/385/2023/12/Palgrave_Incomplete_Markets.pdf
  111. https://mitpress.mit.edu/9780262133241/theory-of-incomplete-markets-volume-1/
  112. http://www.dklevine.com/archive/refs41115.pdf
  113. https://www.sciencedirect.com/science/article/pii/0022053175900289
  114. https://dornsife.usc.edu/michael-magill/theory-of-incomplete-markets/
  115. https://www.sciencedirect.com/topics/social-sciences/dynamic-stochastic-general-equilibrium
  116. https://www.nber.org/papers/w24811
  117. https://www.nobelprize.org/uploads/2018/06/advanced-economicsciences2004.pdf
  118. https://www.kellogg.northwestern.edu/faculty/rebelo/htm/rbc.pdf
  119. https://faculty.wcas.northwestern.edu/lchrist/research/JEP_2017/DSGE_final.pdf
  120. https://www.nber.org/papers/w21862
  121. https://libertystreeteconomics.newyorkfed.org/2014/09/a-birds-eye-view-of-the-frbny-dsge-model/
  122. https://www.nber.org/system/files/working_papers/w12772/w12772.pdf
  123. https://www.sfu.ca/~bkrauth/econ808/808_lec5.pdf
  124. https://www.sciencedirect.com/science/article/abs/pii/S030440682400079X
  125. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4732492
  126. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=5114772
  127. https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4327883
  128. https://cs3.mit.edu/publication/13808
  129. https://wilcoxen.maxwell.insightworks.com/pages/371.html
  130. https://www.uni-augsburg.de/de/fakultaet/wiwi/prof/vwl/heer/dgebook/
  131. https://www.sciencedirect.com/science/article/pii/S0165188998000177
  132. https://link.springer.com/book/10.1007/978-3-540-76591-2
  133. https://larspeterhansen.org/wp-content/uploads/2016/11/Microdata-and-GE-Models.pdf
  134. https://arxiv.org/abs/2103.16977
  135. https://arxiv.org/abs/2201.01163
  136. https://www.elibrary.imf.org/view/journals/001/2023/040/article-A001-en.xml
  137. https://scholar.harvard.edu/files/laibson/files/laibson_8_lecture_general_equilibrium_wv.pdf
  138. https://www.econ.kyoto-u.ac.jp/~wakai/research/papers/kw-dissertation-02.pdf
  139. https://link.springer.com/book/10.1007/978-3-540-68664-4
  140. https://plato.stanford.edu/entries/game-evolutionary/
  141. https://www.sciencedirect.com/science/article/abs/pii/S0304406821000768
Add your contribution
Related Hubs
User Avatar
No comments yet.