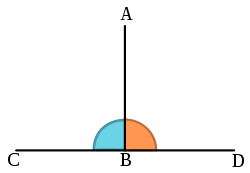Orthogonality

OrthogonalityMain

Community hub

Orthogonality

8 pages, 0 posts

0 subscribers

Recent from talks

Be the first to start a discussion here.

Recent from talks

Be the first to start a discussion here.

Contribute something

About hubMembersContent overviewUpdatesRules

Main reference articles

Orthogonality

View on Wikipedia

from Wikipedia

Not found

Revisions and contributors Edit on Wikipedia Read on Wikipedia

View on Grokipedia

from Grokipedia

Orthogonality is a fundamental geometric and algebraic concept denoting the perpendicularity of two lines, planes, or curves at their intersection point, or more abstractly, the independence between elements in a vector space or inner product space where their inner product equals zero.^[1] In Euclidean geometry, orthogonal lines form a 90-degree angle, a property central to coordinate systems and projections.^[1] This idea generalizes to higher dimensions and non-Euclidean settings, underpinning theorems in linear algebra and analysis.^[2] In linear algebra, two vectors

\mathbf{u}

and

\mathbf{v}

\mathbb{R}^n

are orthogonal if their dot product

\mathbf{u} \cdot \mathbf{v} = 0

, implying they are perpendicular when visualized in space.^[3] A set of vectors is orthogonal if every pair is orthogonal, and orthonormal if additionally each has unit length; such bases simplify computations like projections and decompositions.^[4] Orthogonal complements of subspaces partition the ambient space, with applications in solving systems of equations and least squares problems.^[5] In physics, orthogonality manifests in coordinate systems where axes are mutually perpendicular, facilitating calculations in classical mechanics and electromagnetism.^[6] In quantum mechanics, wavefunctions are orthogonal if their integral product vanishes, signifying incompatible or mutually exclusive states, a cornerstone for superposition and measurement postulates.^[7] This extends to eigenfunctions of commuting operators, ensuring non-interfering observables.^[8] Beyond mathematics and physics, orthogonality informs design principles in computer science, where it describes systems or languages allowing independent feature combinations without unintended interactions—for instance, in instruction sets or programming paradigms where modifying one aspect does not affect others.^[9] In statistics, orthogonal variables or contrasts are uncorrelated, enabling efficient experimental designs and variance decomposition.^[10] These applications highlight orthogonality's role in promoting simplicity, stability, and modularity across disciplines.^[11]

Origins and General Concept

Etymology

The term "orthogonality" originates from Ancient Greek, combining ὀρθός (orthós), meaning "straight," "right," or "upright," with γωνία (gōnía), meaning "angle," to literally denote "right-angled."^[12] This etymological root reflects the geometric notion of perpendicularity at its core. The adjective form "orthogonal" evolved through Medieval Latin orthogōnālis and orthogōnius, both signifying "right-angled," before entering Middle French as orthogonal in the sense of pertaining to right angles.^[13] In English, "orthogonal" first appeared in 1571 in a mathematical context, in Thomas Digges's "A Geometrical Practise, named Pantometria," where it described right angles.^[14] The noun "orthogonality," specifically denoting the property or state of being orthogonal, emerged later in the 19th century, with its earliest documented use in 1872 within Philosophical Transactions of the Royal Society, marking a shift toward more abstract mathematical applications.^[15] Although the concept of right angles—implicitly orthogonal—was foundational in Euclid's Elements (c. 300 BCE), where perpendicular lines were defined as those forming equal adjacent angles, the Greek term itself was absent; Euclid relied on descriptive phrases rather than the compound word.^[16] By the 19th century, mathematicians like Carl Friedrich Gauss incorporated "orthogonal" into advanced geometric frameworks, such as in his 1827 Disquisitiones generales circa superficies curvas, where he discussed orthogonal coordinate systems on curved surfaces, establishing the term's modern mathematical connotation.^[17] In the 20th century, "orthogonal" extended beyond geometry to non-spatial senses, such as unrelatedness in statistics and independence in computing, influenced by its perpendicular origin but applied to abstract structures like vector spaces and functions.

Fundamental Principles

Orthogonality serves as a foundational relation in abstract mathematical and scientific contexts, denoting a form of independence or non-interference between elements, where their interactions yield a null effect under a defined metric. This concept generalizes the geometric idea of perpendicularity, extending it to diverse structures beyond physical lines or planes, such that two elements are orthogonal if they do not influence or overlap in their contributions to a system.^[18] In essence, orthogonality embodies mutual exclusivity, ensuring that the properties or behaviors of one element remain unaltered by the presence or variation of another.^[1] A key property of orthogonality is its promotion of decomposability and simplicity within complex systems, as orthogonal elements can be analyzed or modified independently without propagating effects across the whole. This mirrors the behavior of perpendicular lines in Euclidean space, which intersect at a right angle but maintain distinct directions thereafter, providing a intuitive analogy for the abstract principle.^[19] Such independence facilitates efficient representations and computations, as seen in the construction of bases or frameworks where orthogonal components span the space without redundancy.^[18] Understanding orthogonality requires a preliminary grasp of elements like vectors within a structured space, where the space defines the framework for assessing relations such as alignment or separation. In engineering and scientific design, this principle manifests in non-interfering components—for instance, modular systems where altering one subsystem leaves others unaffected—enhancing reliability and scalability across disciplines.^[20] This broad applicability underscores orthogonality's role as a prerequisite for more specialized interpretations in various fields.^[19]

Mathematics

Geometric and Vector Orthogonality

In Euclidean geometry, two lines are orthogonal if they intersect at a right angle of 90 degrees, and this concept extends to planes that intersect such that their normal vectors are perpendicular.^[1] Orthogonality in this context captures the idea of perpendicularity, fundamental to constructing geometric figures like rectangles and cubes.^[21] For vectors in Euclidean space, two vectors

\vec{u}

and $\vec{v}$

are orthogonal if their dot product satisfies $\vec{u} \cdot \vec{v} = 0$

⋅v

=0, which geometrically means the vectors are perpendicular and form a 90-degree angle.^[22] This condition arises from the dot product formula $\vec{u} \cdot \vec{v} = \|\vec{u}\| \|\vec{v}\| \cos \theta$

⋅v

=∥u

∥∥v

∥cosθ, where $\theta = 90^\circ$ yields $\cos 90^\circ = 0$ .^[22] Orthogonal vectors exhibit key properties that simplify computations in Euclidean spaces: their dot product is zero, they are linearly independent, and for orthogonal sets, the norm of their sum squares equals the sum of their squared norms, as in the Pythagorean theorem extended to vectors: $\|\vec{u} + \vec{v}\|^2 = \|\vec{u}\|^2 + \|\vec{v}\|^2$

∥2=∥u

∥2+∥v

∥2.^[23] These properties ensure that orthogonal bases, such as the standard unit vectors in Cartesian coordinates, preserve vector lengths and angles during projections and transformations, forming the foundation for orthogonal coordinate systems like the 2D xy-plane or 3D xyz-space where axes are mutually perpendicular. Examples of geometric and vector orthogonality abound in spatial representations: in 2D, the x- and y-axes are orthogonal vectors $\hat{i}$ and $\hat{j}$ with $\hat{i} \cdot \hat{j} = 0$ ; in 3D, adding the z-axis $\hat{k}$ maintains mutual orthogonality for defining positions and directions.^[22] In crystallography, orthogonal lattice structures, such as those in cubic or orthorhombic crystals, rely on perpendicular axes to describe repeating unit cells where lattice vectors meet at 90 degrees, enabling symmetric arrangements of atoms.^[25] The historical roots of orthogonality trace to ancient geometry, where the Pythagorean theorem (circa 500 BCE) established the relationship for perpendicular lines in right triangles, later generalized to vectors.^[23] Modern vector orthogonality emerged in the late 19th century through the independent work of J. Willard Gibbs and Oliver Heaviside, who formalized vector analysis with the dot product to quantify perpendicularity in physical applications. Gibbs's lectures from 1881–1884, published posthumously, defined the scalar (dot) product for orthogonal unit vectors, solidifying orthogonality as a core tool in multidimensional geometry.

Linear Algebra and Inner Product Spaces

In linear algebra, an orthogonal basis for a finite-dimensional inner product space is a basis consisting of vectors that are pairwise orthogonal, meaning the inner product of any two distinct vectors is zero. This property simplifies computations such as finding coordinates of vectors in the basis, as the coefficients are simply the inner products divided by the squared norms of the basis vectors. An orthonormal basis extends this by requiring each vector to have unit length, so the norm of every basis vector is 1; such bases are particularly useful for preserving lengths and angles in transformations and for efficient matrix representations like the QR decomposition. The Gram-Schmidt process provides a constructive method to obtain an orthogonal or orthonormal basis from any linearly independent set of vectors in an inner product space. Given vectors

\mathbf{u}_1, \mathbf{u}_2, \dots, \mathbf{u}_n

, the algorithm proceeds iteratively: set

\mathbf{v}_1 = \mathbf{u}_1

; for

k = 2

n

, define

\mathbf{v}_k = \mathbf{u}_k - \sum_{j=1}^{k-1} \proj_{\mathbf{v}_j} \mathbf{u}_k

, where the projection subtracts the components of

\mathbf{u}_k

along the previous orthogonal vectors to ensure

\mathbf{v}_k

is orthogonal to

\{\mathbf{v}_1, \dots, \mathbf{v}_{k-1}\}

. To obtain an orthonormal basis, normalize each

\mathbf{v}_k

by dividing by its norm,

\mathbf{e}_k = \mathbf{v}_k / \|\mathbf{v}_k\|

. This process, originally formalized by Erhard Schmidt in 1907, is numerically stable for well-conditioned bases and forms the basis for algorithms in numerical linear algebra. Central to these concepts is the orthogonal projection, which decomposes a vector

\mathbf{v}

onto a subspace spanned by another vector

\mathbf{u}

(with

\mathbf{u} \neq \mathbf{0}

) as the unique vector in that direction closest to

\mathbf{v}

. The formula is

\proj_{\mathbf{u}} \mathbf{v} = \frac{\mathbf{u} \cdot \mathbf{v}}{\mathbf{u} \cdot \mathbf{u}} \mathbf{u},

where

\mathbf{u} \cdot \mathbf{v}

is the inner product; the remainder

\mathbf{v} - \proj_{\mathbf{u}} \mathbf{v}

is orthogonal to

\mathbf{u}

. For projections onto subspaces with orthogonal bases, the operation extends linearly, enabling decompositions like the least-squares approximation in overdetermined systems. Inner product spaces abstract the notion of orthogonality beyond finite-dimensional Euclidean spaces to infinite-dimensional settings, such as spaces of continuous functions, where the inner product generalizes the dot product. Two functions

f

and

g

are orthogonal if their inner product

\langle f, g \rangle = \int_a^b f(x) g(x) \, dx = 0

over the interval

[a, b]

, allowing bases of orthogonal functions to represent elements via series expansions similar to vector coordinates. A key application is the Fourier series, where the set

\{1, \cos(nx), \sin(nx) \mid n = 1, 2, \dots\}

forms an orthogonal basis for the space of square-integrable functions on

[-\pi, \pi]

under the

L^2

inner product

\langle f, g \rangle = \int_{-\pi}^{\pi} f(x) g(x) \, dx

; orthogonality follows from integral identities like

\int_{-\pi}^{\pi} \sin(mx) \cos(nx) \, dx = 0

for all positive integers

m, n

, enabling the decomposition of periodic functions into sums of these basis elements with coefficients given by inner products.

Advanced Mathematical Applications

In advanced mathematical contexts, orthogonal matrices play a central role in preserving geometric structures and facilitating numerical computations. An orthogonal matrix

Q

is a square matrix satisfying

Q^T Q = I

, where

Q^T

is the transpose and

I

is the identity matrix, ensuring that the columns (and rows) form an orthonormal basis.^[26] This property implies that orthogonal matrices preserve the Euclidean norm of vectors, as

\|Qx\| = \|x\|

for any vector

x

, making them ideal for representing rotations and reflections in Euclidean space.^[27] A key application is the QR decomposition, where any invertible matrix

A

factors as

A = QR

with

Q

orthogonal and

R

upper triangular, enabling stable solutions to linear systems and eigenvalue problems through algorithms like the QR iteration.^[28] In combinatorics, orthogonality addresses the independence of combinatorial structures, notably through orthogonal Latin squares and Hadamard matrices, which maximize informational content in designs. Two Latin squares of order

n

are orthogonal if, when superimposed, every ordered pair of symbols appears exactly once, enabling the construction of mutually orthogonal sets up to

n-1

squares for applications in experimental design theory.^[29] Hadamard matrices,

\pm 1

matrices

H

of order

n

(where

n = 1, 2

or a multiple of 4) satisfy

H^T H = nI

, achieving the maximal determinant bound of

\pm n^{n/2}

, which quantifies the highest possible "volume" spanned by their rows in the context of combinatorial optimization.^[30] These matrices are pivotal in coding theory and block designs, where their orthogonality ensures minimal interference among components.^[31] Orthogonal polynomials in number theory provide a framework for approximating functions and solving differential equations, characterized by their orthogonality with respect to a weight function over an interval. Classical examples include Legendre polynomials

P_n(x)

[-1, 1]

with weight 1, and Hermite polynomials

H_n(x)

(-\infty, \infty)

with weight

e^{-x^2}

, both forming complete orthogonal bases for

L^2

spaces.^[32] These sequences satisfy a three-term recurrence relation, such as

x P_n(x) = \frac{n+1}{2n+1} P_{n+1}(x) + \frac{n}{2n+1} P_{n-1}(x)

for Legendre polynomials, which facilitates efficient computation and reveals their role in spectral methods and quantum mechanics approximations.^[33] Recent developments since 2000 have extended orthogonality to category theory, where it defines independence between functors or morphisms, enhancing the study of accessible categories. Two morphisms

f: A \to B

and

g: C \to D

are orthogonal, denoted

f \perp g

, if for any commutative square, there exists a unique diagonal morphism making it a pullback, capturing "non-interference" in categorical compositions.^[34] In accessible categories, definable orthogonality classes—sets of objects or morphisms closed under certain operations—are shown to be small (of bounded cardinality), with the required large-cardinal assumptions depending on the Levy hierarchy complexity of the defining formulas, impacting model theory and higher-dimensional algebra.^[35] This framework unifies prior notions of independence across mathematics, with applications in homotopy theory and logic.

Physics

Optics

In optics, orthogonality describes the perpendicular relationship between light rays and wavefronts, a foundational principle in geometric optics. Light rays, defined as lines perpendicular to the surfaces of constant phase (wavefronts), propagate in the direction normal to these wavefronts in homogeneous media. This orthogonality facilitates ray tracing simulations, where rays are modeled as straight paths that bend at interfaces according to Snell's law, with angles measured relative to the surface normal—the line perpendicular to the interface. For instance, at orthogonal (normal) incidence, where the ray is perpendicular to the boundary, refraction occurs without angular deviation, as the sine of zero degrees yields no bending term in the law.^[36]^[37]^[38] Polarization further exemplifies orthogonality through the mutual perpendicularity of electric field components. Unpolarized light can be decomposed into two orthogonal linear polarizations, such as s- (senkrecht, perpendicular to the plane of incidence) and p- (parallel) components, which experience distinct reflection and transmission behaviors at interfaces. In birefringent materials, like calcite, an incident ray splits into ordinary and extraordinary rays polarized along orthogonal principal axes, each propagating with a different refractive index due to the material's anisotropic structure. Polarizing filters exploit this by transmitting vibrations aligned with their axis while absorbing the orthogonal component, enabling applications like glare reduction.^[39]^[40]^[41]^[42] In interferometry, orthogonality supports the independence of resonant modes in Fabry-Pérot cavities, enhancing spectral resolution. These cavities, formed by two parallel mirrors, sustain transverse electromagnetic (TEM) modes whose field distributions are orthogonal, meaning their overlap integrals vanish, preventing energy transfer between modes. This allows the cavity to resolve closely spaced wavelengths based on the free spectral range between orthogonal or higher-order modes, crucial for precision spectroscopy. The geometric orthogonality here echoes vector perpendicularity in defining field directions orthogonal to propagation.^[43] This application of orthogonality traces to the 17th century, when Christiaan Huygens proposed his wave principle in Traité de la Lumière (1678), positing that every point on a wavefront emits secondary spherical wavelets, with the new wavefront as their envelope and rays perpendicular to it—incorporating orthogonality to explain diffraction and propagation./University_Physics_III_-Optics_and_Modern_Physics(OpenStax)/01%3A_The_Nature_of_Light/1.07%3A_Huygenss_Principle)^[44]

Special Relativity and Hyperbolic Orthogonality

In special relativity, spacetime is modeled by Minkowski space, a four-dimensional manifold equipped with the Minkowski metric

ds^2 = -c^2 dt^2 + dx^2 + dy^2 + dz^2

, where

c

is the speed of light.^[45] This indefinite metric distinguishes it from the positive-definite Euclidean metric used in classical geometry, leading to a pseudo-Riemannian structure where the inner product of two four-vectors

u^\mu = (u^0, \mathbf{u})

and

v^\mu = (v^0, \mathbf{v})

is given by

g(u, v) = -u^0 v^0 + \mathbf{u} \cdot \mathbf{v}

.^[46] Two four-vectors are orthogonal if their Minkowski inner product vanishes,

g(u, v) = 0

; for spacelike vectors (those with positive norm), this orthogonality aligns with intuitive perpendicularity in spatial directions, but the indefinite signature allows timelike vectors (negative norm) to be orthogonal only to spacelike ones, not to other timelike vectors.^[47] Hyperbolic orthogonality arises in this framework due to the hyperbolic geometry of the timelike sector, where the set of unit timelike vectors forms a hyperboloid rather than a sphere.^[48] A timelike vector and a spacelike vector are hyperbolically orthogonal if their inner product is zero, corresponding to perpendicular worldlines in rapidity space, where rapidity

\phi

parameterizes boosts via

v = c \tanh \phi

.^[47] For instance, the worldline of a particle at rest (along the time axis) is hyperbolically orthogonal to the spatial axes, illustrating how simultaneity and causality are relative across inertial frames.^[48] Lorentz transformations, which map between inertial frames while preserving the speed of light, maintain the Minkowski metric and thus all orthogonal relations between four-vectors.^[46] These transformations form the Lorentz group, satisfying

\Lambda^T \eta \Lambda = \eta

, where

\eta = \operatorname{diag}(-1, 1, 1, 1)

is the metric tensor, ensuring that if

g(u, v) = 0

in one frame, it remains zero in another.^[46] In particle physics, orthogonal boosts exemplify this preservation: successive boosts in perpendicular directions (e.g., along x and y axes) result in a combined transformation that includes a rotation (Thomas-Wigner rotation), but the orthogonality of the boost directions is invariant under the Lorentz group.^[46] Null vectors, with zero norm (

g(u, u) = 0

), represent lightlike paths and are orthogonal to themselves; they form the boundaries of light cones, separating timelike (causal) from spacelike (acausal) intervals and defining the causal structure of spacetime.^[49] The four-vector formalism, introduced by Minkowski building on Einstein's 1905 theory, uses orthogonality in the Minkowski inner product to ensure energy-momentum conservation across frames: the total four-momentum

P^\mu = \sum p^\mu

(where

p^\mu = (E/c, \mathbf{p})

for each particle) is a timelike four-vector conserved in collisions, with its norm yielding the invariant rest mass via

P \cdot P = -M^2 c^2

.^[50]^[45] This orthogonality condition guarantees that projections (e.g., energy in one frame orthogonal to spatial momentum adjustments) align relativistically without violating invariance.^[46]

Quantum Mechanics

In quantum mechanics, the state of a physical system is described by a vector in a complex Hilbert space, where orthogonality plays a central role in defining non-overlapping possibilities. The bra-ket notation, developed by Paul Dirac in the 1930s and formalized in his 1939 monograph, provides a compact way to express the inner product between states |ψ⟩ and |φ⟩ as ⟨ψ|φ⟩.^[51] Two quantum states are orthogonal if their inner product vanishes, ⟨ψ|φ⟩ = 0, which corresponds to zero spatial or probabilistic overlap between their wavefunctions; according to the Born rule, this implies a zero probability for transitioning from one state to the other upon measurement.^[52] This property ensures that orthogonal states represent mutually exclusive outcomes, forming the foundation for probabilistic interpretations in quantum theory.^[53] A complete orthonormal basis in the Hilbert space allows any quantum state to be expanded as a linear superposition of basis vectors with complex coefficients. For instance, the position eigenstates |x⟩, satisfying ⟨x|x'⟩ = δ(x - x'), form such a basis, enabling the representation of wavefunctions ψ(x) = ⟨x|ψ⟩; similarly, momentum eigenstates |p⟩ provide another complete orthonormal set related by Fourier transform.^[54] These bases, drawn from the inner product structure of Hilbert spaces as in linear algebra, underpin the expansion of arbitrary states and the resolution of the identity operator, ∫ |x⟩⟨x| dx = I.^[55] Orthogonality here guarantees that the expansion coefficients are the projections ⟨φ|ψ⟩ onto the basis states |φ⟩, preserving unitarity and normalization.^[56] Observables, such as position or energy, are represented by self-adjoint (Hermitian) operators whose spectral decomposition features orthogonal eigenspaces for distinct eigenvalues./08%3A_The_Postulates_of_Quantum_Mechanics/8.07%3A_Postulates_3_and_4_of_Quantum_Mechanics/8.7.01%3A_Eigenfunctions_of_Operators_are_Orthogonal) This orthogonality follows from the properties of Hermitian operators, ensuring real eigenvalues and the ability to choose orthonormal eigenvectors within degenerate subspaces.^[57] If two Hermitian operators A and B commute, [A, B] = 0, they share a common orthonormal basis of simultaneous eigenstates, permitting compatible measurements without disturbance.^[58] Representative examples illustrate these principles: for a spin-1/2 particle, the spin-up |↑⟩ and spin-down |↓⟩ states along the z-axis are orthogonal, with ⟨↑|↓⟩ = 0, forming a basis for the two-dimensional Hilbert space.^[59] In quantum entanglement, the four Bell states—such as |Φ⁺⟩ = (1/√2)(|00⟩ + |11⟩)—constitute a complete orthonormal basis for the two-qubit Hilbert space, demonstrating orthogonality among maximally entangled pure states, though mixtures of such states may not preserve overall orthogonality.^[60]

Computer Science and Information Technology

Orthogonal Instruction Sets

In computer architecture, an orthogonal instruction set refers to an instruction set architecture (ISA) in which each operation is self-contained and independent, with no implicit dependencies on specific registers, modes, or states, allowing all instructions to uniformly access all registers and addressing modes without restrictions.^[61] This design ensures that instructions operate in isolation, avoiding side effects that could complicate program behavior or hardware implementation.^[61] The primary benefits of orthogonal instruction sets include simplified compiler design and optimization, as the uniformity reduces the need to handle irregular interactions between instructions, leading to fewer bugs and more predictable code generation.^[61] In contrast, non-orthogonal ISAs like those in complex instruction set computing (CISC) architectures often impose limitations, such as restricted register access for certain operations, which can increase compilation complexity and error rates. Additionally, orthogonality facilitates hardware pipelining and parallel execution by minimizing inter-instruction dependencies, enhancing overall system performance and ease of verification.^[61] Historically, the IBM System/360, introduced in the 1960s, represented an early milestone in orthogonal design by separating addressing modes from functional operations, enabling a unified ISA across a family of compatible machines and influencing subsequent architectures.^[62] This approach evolved through the reduced instruction set computing (RISC) paradigm in the 1980s, with architectures like MIPS and ARM emphasizing orthogonality through uniform register files—typically 32 general-purpose registers accessible by all instructions—and fixed-length formats to further eliminate irregularities.^[63] Modern extensions of this principle appear in graphics processing units (GPUs), such as AMD's RDNA3, where orthogonal ALU operations support efficient parallel workloads without stalling dependencies.^[64] The degree of orthogonality in an ISA is typically assessed by the extent to which all possible combinations of operations, operands, and addressing modes are supported without exclusions or special cases.^[61] For instance, highly orthogonal RISC designs like ARM's A64 achieve near-complete uniformity, with every arithmetic instruction able to use any of the 31 general-purpose registers, contrasting with less orthogonal systems where such flexibility is limited to specific subsets.^[65]

Programming and System Design

In software engineering, orthogonality refers to the design of APIs where functions operate independently, with parameters that do not produce hidden interactions or side effects, allowing changes to one component without impacting others. This principle aligns with the Unix philosophy, which advocates for small, modular tools that compose orthogonally to form complex systems, as exemplified by command-line utilities like grep and sort that process streams without assuming specific formats.^[66]^[67] Key design principles incorporating orthogonality include separation of concerns, where distinct aspects of a system—such as data management, user interface, and business logic—are isolated to minimize interdependencies. In languages like Rust, orthogonal error handling achieves this through the Result<T, E> type and Error trait, which separate error propagation from core logic without introducing exceptions or implicit control flow, enabling explicit and composable error management.^[68]^[69] Representative examples illustrate these principles in practice. In Model-View-Controller (MVC) frameworks, orthogonality is promoted by decoupling the model (data and logic), view (presentation), and controller (input handling), ensuring modifications to the user interface do not affect data processing, as seen in implementations like Ruby on Rails or Spring MVC. Orthogonal persistence in databases extends this to storage, treating persistent and transient objects uniformly regardless of type or lifetime, as in systems like Napier88, where reachability from persistent roots automatically manages data longevity without explicit save operations.^[70]^[71] Challenges arise in balancing orthogonality with performance, as highly independent components can introduce overhead from communication or indirection, potentially degrading efficiency in resource-constrained environments; for instance, excessive modularity may increase latency in real-time systems. A case study is Lisp's orthogonal syntax, which uses a minimal, homoiconic structure where code and data share the same form, enabling powerful macros and metaprogramming without syntactic exceptions, though this uniformity can complicate readability for non-Lisp programmers.^[72]^[73] In the 2020s, modern trends emphasize orthogonality in microservices architectures, where services handle distinct domains independently, scalable via containerization tools like Docker, which isolates deployments without altering underlying application logic. This approach facilitates independent scaling and updates, though it requires careful management of inter-service communication to maintain performance.^[74]^[75]

Communications and Signal Processing

Orthogonal Frequency-Division Multiplexing

Orthogonal frequency-division multiplexing (OFDM) is a digital modulation technique that divides a high-rate data stream into multiple parallel low-rate streams, each modulated onto a distinct subcarrier frequency. These subcarriers are closely spaced orthogonal sinusoids, with frequency spacing equal to the inverse of the symbol duration

T

, ensuring that the signals do not interfere with each other at the receiver despite overlapping spectra. This orthogonality eliminates inter-carrier interference (ICI), allowing efficient use of the available bandwidth. In practice, the transmitter employs an inverse fast Fourier transform (IFFT) to generate the time-domain OFDM symbol from frequency-domain data symbols, while the receiver uses a fast Fourier transform (FFT) for demodulation, making the system computationally efficient.^[76] The mathematical foundation of OFDM's orthogonality lies in the property of exponential functions over the symbol interval. Specifically, for subcarrier indices

k

and

m

, and fundamental frequency

f = 1/T

, the condition holds that

\int_0^T e^{j 2 \pi k f t} \cdot e^{-j 2 \pi m f t} \, dt = 0 \quad \text{for } k \neq m.

This integral represents the inner product of the subcarrier signals, yielding zero for distinct frequencies, which confirms their mutual orthogonality and enables perfect recovery of each subcarrier's data without crosstalk.^[76] The technique was pioneered by S. B. Weinstein and P. M. Ebert in 1971, who demonstrated that the discrete Fourier transform (DFT) could efficiently implement multicarrier modulation and demodulation for data transmission, including the addition of a guard interval to preserve orthogonality in dispersive channels.^[76] OFDM gained practical traction in the 1990s through standardization efforts, with the European Telecommunications Standards Institute (ETSI) adopting it in the Digital Audio Broadcasting (DAB) standard (EN 300 401) in 1995, marking one of the first commercial deployments for robust audio transmission over multipath environments. OFDM has become integral to modern wireless communications, underpinning standards such as IEEE 802.11a (introduced in 1999) and subsequent Wi-Fi amendments (802.11g/n/ac/ax), where it supports high data rates in the 2.4 GHz and 5 GHz bands. It is also central to 4G LTE and 5G NR cellular networks, as specified by 3GPP, enabling broadband mobile data over wide channels. A primary advantage is its inherent resistance to multipath fading: the long symbol duration per subcarrier results in frequency-selective fading that affects subcarriers individually as flat fading, simplifying equalization with one-tap frequency-domain processing per subcarrier. Despite these benefits, OFDM exhibits significant drawbacks, including a high peak-to-average power ratio (PAPR), where the composite signal's amplitude peaks can be much higher than the average, necessitating linear amplifiers that operate inefficiently and increase power consumption.^[77] To maintain orthogonality and mitigate inter-symbol interference in multipath channels while aiding synchronization, a cyclic prefix—a repeated suffix of the OFDM symbol—is prepended, typically comprising 10-25% of the symbol length, which incurs a bandwidth overhead and reduces overall spectral efficiency.^[76]^[77]

Orthogonal Codes and Modulation

Orthogonal codes are binary sequences engineered to exhibit zero cross-correlation between distinct codes, allowing multiple signals to coexist in the same frequency band with minimal interference. This property enables efficient multiple access in communication systems by decorrelating user signals at the receiver. A classic example is the Walsh-Hadamard codes, derived from Hadamard matrices of order

2^k

, which maintain perfect orthogonality when time-aligned and are widely used in downlink CDMA systems to assign unique spreading sequences to users.^[78]^[79]^[80] In orthogonal modulation techniques, signals are transmitted over mutually orthogonal dimensions to maximize spectral efficiency and reduce crosstalk. Quadrature Amplitude Modulation (QAM) exemplifies this by employing independent in-phase (I) and quadrature (Q) channels, which are phase-shifted by 90 degrees and thus orthogonal, permitting the simultaneous modulation of two data streams onto a single carrier without mutual interference. This approach doubles the data rate compared to single-channel modulation while preserving signal integrity in additive white Gaussian noise channels.^[81]^[82] Spread-spectrum systems leverage orthogonal codes to achieve robust multiple access and anti-jamming capabilities. In direct-sequence spread spectrum (DSSS), these codes spread the signal across a wider bandwidth, enhancing resistance to interference. The Global Positioning System (GPS) utilizes pseudo-random noise (PRN) codes, particularly Gold codes for the coarse/acquisition (C/A) signal, which feature low cross-correlation values approximating orthogonality among the 32 satellite codes, enabling precise signal separation and acquisition even in multipath environments.^[83]^[84]^[85] The performance benefits of orthogonal codes include significant bit error rate (BER) reduction through effective decorrelation, which suppresses multi-user interference in CDMA setups. For instance, in AWGN channels, Walsh-Hadamard codes yield lower BER compared to non-orthogonal sequences at equivalent signal-to-noise ratios, as validated by simulations showing BER improvements by orders of magnitude for multiuser scenarios. These gains approach the Shannon capacity limits for multiple-access channels, where orthogonal signaling achieves near-optimal rates by partitioning the channel into independent subchannels, bounded by

C = B \log_2(1 + \text{SNR})

per dimension, with minimal interference penalty.^[86]^[87]^[88] Advances in the 2010s and 2020s have integrated orthogonal principles with chaotic sequences for enhanced physical layer security. Chaos-based orthogonal modulation schemes, such as those embedding chaotic maps into orthogonal time-frequency spaces or NOMA frameworks, scramble signals to thwart eavesdroppers while maintaining low BER and high secrecy rates over fading channels. These methods, often applied in satellite and wireless systems, exploit the broadband nature of chaos for key generation and signal masking, outperforming traditional encryption in resource-constrained environments.^[89]^[90]^[91]

Quantitative Analysis

Statistics and Econometrics

In statistics and econometrics, orthogonality refers to the independence or uncorrelatedness between components of a model, which facilitates estimation, inference, and interpretation by ensuring that effects are separable without interference. This property is foundational in linear models, where orthogonal elements simplify computations and enhance efficiency. For instance, orthogonal designs and estimators leverage this to partition variance and avoid biases from correlated predictors or errors.^[92] Orthogonal polynomials serve as a basis for polynomial regression, particularly for modeling continuous quantitative predictors, where they ensure that higher-degree terms are uncorrelated with lower-degree ones, thus stabilizing coefficient estimates and reducing multicollinearity. Legendre polynomials, defined over the interval

[-1, 1]

with respect to the uniform weight function, are commonly used for continuous data in least squares regression, as their cross-products sum to zero, allowing sequential testing of polynomial degrees without confounding.^[93] In analysis of variance (ANOVA) for balanced experimental designs, orthogonal polynomials enable the decomposition of total variation into orthogonal components, such as linear and quadratic trends, facilitating hypothesis tests on specific patterns. This approach simplifies ordinary least squares (OLS) estimation by decorrelating the design matrix columns, improving numerical stability and interpretability.^[92]^[94] A key application in econometrics is the instrumental variables (IV) method, which addresses endogeneity in regression models by imposing an orthogonality condition between instruments

Z

and error terms

u

, formally

E[Z \cdot u] = 0

, ensuring unbiased estimation of causal effects. This condition, first formalized in the context of errors-in-variables models, allows valid instruments to correlate with endogenous regressors while remaining exogenous to the disturbance, as in two-stage least squares procedures.^[95] Orthogonal contrasts in experimental design further exemplify this, where linear combinations of group means are constructed such that their coefficients sum to zero across pairs, partitioning the sum of squares in ANOVA into independent single-degree-of-freedom tests for balanced data. Principal component analysis (PCA) extracts orthogonal factors by transforming correlated variables into uncorrelated principal components via eigenvectors of the covariance matrix, maximizing variance explanation while minimizing redundancy.^[96]^[97] These properties underpin the efficiency of OLS under classical assumptions, as articulated in the Gauss-Markov theorem, which states that if errors are uncorrelated (orthogonal) with mean zero and constant variance, OLS yields the best linear unbiased estimator (BLUE) among all linear unbiased estimators. Developed in the early 19th century, this theorem relies on the orthogonality of residuals to the regressors in the projection sense, ensuring minimal variance without requiring normality. By avoiding multicollinearity through orthogonal bases or instruments, these techniques enhance model reliability in high-dimensional settings.^[98]

Economics

In economics, orthogonality refers to the independence or uncorrelated nature of variables, shocks, or factors, which facilitates the isolation of causal effects in modeling and policy analysis. A key application is in structural vector autoregression (SVAR) models, where economic disturbances are decomposed into orthogonal shocks—uncorrelated innovations that represent underlying structural forces such as monetary policy changes or supply disruptions.^[99] These orthogonal shocks enable impulse response analysis to trace how independent disturbances, like a contractionary monetary policy shock, affect variables such as interest rates, economic activity, and bond premiums over time.^[100] By assuming orthogonality among shocks, policymakers can identify the isolated impact of fiscal or monetary interventions without confounding correlations, as seen in evaluations of U.S. monetary transmission mechanisms.^[101] In growth theory, orthogonality appears in factor models extending the Solow model, where latent variables representing technology or productivity are treated as orthogonal to observable inputs like capital accumulation and labor growth. This assumption allows empirical tests to attribute cross-country output differences to independent factors, such as investment rates, without bias from correlated technology residuals. For instance, in augmented Solow frameworks, orthogonal latent technology differences explain long-run per capita income variations, isolating their role from proximate causes like savings rates.^[102] Such decompositions enhance the model's ability to interpret both temporal growth patterns and international disparities by ensuring factors like human capital accumulation operate independently of physical capital dynamics.^[103] Examples of orthogonality include the decomposition of gross domestic product (GDP) into orthogonal components via factor models, which separate macroeconomic risks and explained variations in economic activity. In these approaches, an optimal orthogonalization isolates the contributions of variables like consumption and investment to GDP fluctuations, revealing the relative importance of domestic versus global drivers in GDP-at-risk forecasts.^[104] Similarly, in auction theory, orthogonality underpins assumptions of independent private values, where bidders' signals or valuations are uncorrelated, enabling efficient mechanism design and revenue predictions in sealed-bid formats.^[105] Policy implications arise from the orthogonality principle in fiscal-monetary interactions, where shocks from one policy are assumed independent of the other to avoid biases in impact assessments, as in the Tanzi effect of the 1980s, which highlighted inflation's erosive role on tax revenues amid delayed fiscal adjustments.^[106] This independence supports targeted interventions, such as orthogonalizing fiscal shocks to monetary policy in VAR analyses, ensuring unbiased estimates of effects like government spending on output.^[107] Recent developments in behavioral economics incorporate orthogonality for utility separation, particularly through the concept of orthogonal independence, which restricts additivity axioms to cases where alternatives are orthogonal—uncorrelated in attributes. Post-2010 studies show this property holds for spherical preferences, where indifference curves form spheres, allowing clean separation of utility components like risk attitudes from consumption bundles without violating behavioral anomalies.^[108] This framework advances utility modeling by accommodating empirical deviations from expected utility while maintaining independence in orthogonal dimensions.^[109]

Biological and Chemical Sciences

Taxonomy and Classification

In biological taxonomy, classification systems use non-overlapping, mutually exclusive categories to ensure distinct and unique evolutionary lineages for organisms, particularly within cladistic frameworks. This approach aligns with the core tenet of cladistics, where monophyletic groups (clades) form hierarchical structures without membership overlap at equivalent levels, reflecting shared derived characters (synapomorphies) that trace independent evolutionary paths from common ancestors. Such structures prevent ambiguity in classification by maintaining clear boundaries between taxa, allowing researchers to reconstruct phylogenies based on non-redundant evidence.^[110] The principles underlying classification in the Linnaean system structure taxa into hierarchical ranks with independent diagnostic criteria—meaning attributes at levels like genus and species operate without correlation or redundancy. For instance, genus-level traits often encompass broader anatomical or ecological features, while species-level distinctions focus on finer reproductive or genetic incompatibilities, enabling a nested yet non-intersecting framework where taxa at the same rank remain mutually exclusive. This independence facilitates precise identification and evolutionary inference, as emphasized in traditional taxonomic practice.^[111] Practical examples include identification guides employing matrix-based or multi-access keys, such as those utilizing sets of independent morphological characters scored separately to pinpoint taxa without sequential bias. A prominent modern application is DNA barcoding, where complementary genetic loci like the mitochondrial COI gene combined with nuclear ITS regions provide non-correlated data for species authentication, enhancing accuracy in complex floras or faunas. These methods ensure robust discrimination by leveraging traits that evolve along distinct pathways.^[112] Challenges arise from convergent evolution, where unrelated lineages develop similar traits due to analogous selective pressures, introducing homoplasy that blurs evolutionary boundaries and misleads cladistic analyses by simulating false synapomorphies. For example, wing structures in bats, birds, and insects exemplify convergence, complicating tree reconstruction if independence assumptions fail. Contemporary solutions incorporate Bayesian models, which probabilistically integrate prior knowledge of trait evolution and account for non-independence via Markov chain Monte Carlo sampling, yielding more reliable hierarchical inferences despite homoplasy.^[113]^[114] Historically, Charles Darwin's 1859 On the Origin of Species laid foundational influence by advocating classification via multiple independent traits to capture natural affinities, moving beyond artificial systems toward evolutionary independence in character assessment. This perspective evolved into cladistics, formalized by Willi Hennig in the 1960s, who rigorously defined monophyletic taxa as non-overlapping units bound by unique synapomorphies, establishing clear boundaries as a cornerstone of phylogenetic systematics.

Chemistry and Organic Synthesis

In organic synthesis, orthogonality refers to the use of protecting groups that can be selectively removed under specific conditions without impacting others, enabling precise control in multi-step reactions. This concept is fundamental to constructing complex molecules, particularly in peptide and natural product synthesis, where multiple functional groups must be manipulated independently. Orthogonal protecting groups minimize side reactions and improve overall yield by allowing sequential deprotections tailored to the reaction sequence.^[115] A landmark strategy incorporating orthogonality emerged in the 1960s with Robert Bruce Merrifield's solid-phase peptide synthesis (SPPS), which utilized the tert-butoxycarbonyl (Boc) group for temporary Nα-amino protection, removable by acid treatment, alongside benzyl-based groups for side chains that required hydrogenation for cleavage. This approach revolutionized peptide assembly by anchoring the growing chain to a resin, facilitating iterative coupling and deprotection cycles. Later advancements enhanced orthogonality; in 1972, Louis A. Carpino introduced the 9-fluorenylmethoxycarbonyl (Fmoc) group, which is base-labile and thus compatible with acid-sensitive Boc, allowing dual protection schemes in SPPS. The Fmoc/Boc pair exemplifies orthogonality, as Fmoc deprotection with piperidine leaves Boc intact, and vice versa with trifluoroacetic acid, enabling efficient synthesis of peptides up to 50 residues long with high purity.^[116]^[117]^[115] In total synthesis, orthogonal protecting groups facilitate selective functionalization of polyfunctional substrates, such as in the assembly of alkaloids or polyketides, where distinct alcohol or amine groups are unmasked stepwise to direct regioselective couplings. For instance, combinations like allyl esters (removable by palladium catalysis) with silyl ethers (fluoride-labile) allow targeted modifications in carbohydrate or terpene syntheses without global deprotection. Click chemistry further exemplifies orthogonality through modular ligation reactions; the copper-catalyzed azide-alkyne cycloaddition (CuAAC) operates selectively alongside strain-promoted azide-alkyne cycloaddition (SPAAC) or inverse electron-demand Diels-Alder (IEDDA) reactions, enabling multiple orthogonal conjugations in a single pot for dendrimer or conjugate construction. These methods achieve near-quantitative yields under mild conditions, streamlining the synthesis of architecturally complex targets.^[118]^[118] The advantages of orthogonal strategies include enhanced efficiency in multi-step sequences, as they reduce purification needs and error propagation from incomplete deprotections, often boosting overall yields by 20-50% in complex syntheses compared to non-orthogonal schemes. Recent developments in the 2010s have introduced light-orthogonal catalysis, where photoremovable protecting groups, such as nitrobenzyl or coumarin derivatives, are cleaved by specific wavelengths of light without thermal or chemical interference, complementing traditional orthogonal sets. This photolabile approach has been applied in spatiotemporal control of reactions, as reviewed in advancements enabling precise release in polymer or small-molecule synthesis.^[119]

Bioorthogonal and Supramolecular Chemistry

Bioorthogonal chemistry encompasses chemical reactions that proceed selectively within living organisms without disrupting endogenous biochemical pathways, enabling precise modifications of biomolecules such as proteins, glycans, and lipids. The concept was introduced by Carolyn R. Bertozzi in 2003 to describe transformations involving non-native functional groups that are inert to biological nucleophiles and electrophiles.^[120] A foundational example is the strain-promoted azide-alkyne cycloaddition (SPAAC), which facilitates efficient ligation between azides and strained cyclooctynes under physiological conditions, avoiding the toxicity of copper catalysts required in traditional click chemistry. This reaction, first reported by Bertozzi's group in 2004, has rates on the order of 1 M⁻¹ s⁻¹, allowing real-time imaging of cellular processes in vivo. The biocompatibility and high selectivity of SPAAC stem from the orthogonal reactivity of the azide and alkyne moieties, which do not cross-react with abundant biomolecules like thiols or amines.^[121] These bioorthogonal reactions have transformed applications in drug delivery and molecular imaging by permitting targeted conjugation of therapeutic payloads or fluorescent probes to specific cellular targets. For instance, SPAAC has been employed to label sialic acids on cell surfaces for tracking tumor glycans in live mice, demonstrating minimal off-target reactivity and enabling high-resolution visualization. The field's impact was recognized with the 2022 Nobel Prize in Chemistry, awarded to Bertozzi, Morten Meldal, and K. Barry Sharpless for pioneering click chemistry and its bioorthogonal extensions, which have accelerated advancements in targeted therapies. Kinetic orthogonality in these systems ensures that multiple reactions can coexist without interference, enhancing modularity in complex biological environments. In supramolecular chemistry, orthogonality manifests through the independent operation of distinct non-covalent interactions, such as hydrogen bonding and π-π stacking, within host-guest assemblies to construct hierarchical structures. These interactions are designed to be mutually exclusive, allowing precise control over self-assembly without competitive binding; for example, crown ether-based host-guest complexation can pair orthogonally with ureido-pyrimidinone hydrogen bonds to form dynamic polymers. Such orthogonal motifs enable the creation of responsive materials with tunable properties, including stimuli-responsive disassembly for controlled release. In metal-organic frameworks (MOFs), orthogonal ligands—featuring perpendicular binding arms—facilitate the synthesis of intricate topologies, such as twisted frameworks that enhance porosity and catalytic sites while maintaining structural integrity.^[122]^[123] The biocompatibility of these supramolecular systems arises from their reliance on weak, reversible bonds under mild aqueous conditions, mirroring biological recognition events and minimizing cytotoxicity. Applications extend to drug delivery, where orthogonal host-guest interactions encapsulate therapeutics for site-specific release, and to imaging, via self-assembling probes that aggregate selectively at disease sites. Overall, the kinetic orthogonality of these non-covalent forces—evidenced by dissociation constants differing by orders of magnitude—ensures robust, interference-free functionality in vivo, paralleling the selectivity principles of bioorthogonal covalent reactions.^[124]

Analytical and Biochemical Applications

In analytical chemistry, orthogonal methods integrate complementary separation techniques that operate on independent principles to enhance resolution and detection of complex mixtures. For instance, high-performance liquid chromatography coupled with mass spectrometry (HPLC-MS) combines chromatographic separation based on hydrophobicity or charge with mass spectrometric identification by mass-to-charge ratio, allowing for the orthogonal analysis of impurities and degradation products in pharmaceuticals.^[125] This approach is particularly valuable in medicinal chemistry for screening and purifying compounds, as the independence of the mechanisms minimizes overlap and improves overall analytical specificity.^[126] In biochemistry, orthogonality extends to techniques like two-dimensional gel electrophoresis (2D-GE), where proteins are separated in the first dimension by isoelectric focusing (based on charge) and in the second by sodium dodecyl sulfate-polyacrylamide gel electrophoresis (based on molecular weight), providing orthogonal dimensions for high-resolution proteomics.^[127] Similarly, orthogonal tags in proteomics, such as bioorthogonal noncanonical amino acid tagging (BONCAT), enable selective labeling of newly synthesized proteins without interference from endogenous processes, facilitating quantitative analysis of dynamic proteomes.^[128] These methods yield benefits including enhanced resolution of analytes, reduced false positives, and improved quantitative accuracy in identifying low-abundance species.^[129] Orthogonal enzymes play a key role in metabolic engineering by enabling non-interfering pathways that avoid competition with host metabolism, such as orthogonal fatty acid biosynthesis systems in Escherichia coli that redirect flux toward desired products like oleochemicals.^[130] Recent advances in orthogonal spectroscopy, particularly the integration of infrared (IR) and nuclear magnetic resonance (NMR) since the early 2000s, provide complementary structural insights—IR for vibrational modes identifying functional groups and NMR for atomic connectivity—boosting automated structure elucidation in complex biomolecules.^[131] Multimodal fusion models combining these spectra have achieved high accuracy in verifying molecular structures, with IR adding orthogonal vibrational data to resolve ambiguities in NMR predictions.^[132]

Other Disciplines

Art and Design

In visual arts and architecture, orthogonality refers to the use of perpendicular lines and planes to create structured compositions, often enhancing spatial depth and balance. During the Renaissance, artists employed orthogonal lines as visual rays converging toward vanishing points to simulate three-dimensional space on a two-dimensional surface, a technique pioneered in linear perspective drawing. For instance, Leonardo da Vinci utilized orthogonals to guide the viewer's eye from the edges of the canvas to a central vanishing point, achieving realistic depictions of architecture and landscapes.^[133]^[134] In modernist design principles of the early 20th century, orthogonal grids became foundational for abstract compositions, emphasizing harmony through perpendicular arrangements. The De Stijl movement, emerging in the 1910s in the Netherlands, championed these grids as a means to purify form, reducing visual elements to horizontal and vertical lines intersecting at right angles. Piet Mondrian's compositions exemplify this, featuring bold perpendicular black lines dividing colored rectangles into asymmetrical yet balanced fields, as seen in works like Composition with Red, Blue, and Yellow (1930), where orthogonality underscores universal harmony over representational content.^[135]^[136] Similarly, orthogonal symmetry appears in Islamic geometric tiles, where repeating patterns on square grids create intricate, perpendicular motifs that evoke infinite extension and spiritual order, such as the star-and-polygon designs in the Alhambra's decorations.^[137]^[138] Conceptually, orthogonality in abstract art facilitates the independence of form from narrative content, allowing perpendicular elements to stand as autonomous structures that prioritize relational dynamics over depiction. This separation enables artists to explore pure visual relationships, where lines and shapes interact without symbolic burden. The Bauhaus school in the 1920s further amplified this influence, promoting orthogonal modularity in design to foster functional, adaptable systems; Walter Gropius and László Moholy-Nagy integrated perpendicular grids into furniture and architecture, viewing them as modular building blocks for industrialized production and spatial organization.^[139]^[140]

System Reliability

Orthogonal redundancy in system reliability refers to the use of independent backup mechanisms designed to fail in uncorrelated ways, ensuring that a single fault does not propagate across all redundant components. This approach enhances fault tolerance by minimizing common-mode failures, where multiple systems succumb to the same error source. In engineering contexts, orthogonal redundancy is achieved through diverse implementation strategies, such as varying algorithms, hardware, or development processes, to promote failure independence. A seminal example is N-version programming, where multiple functionally equivalent software versions are developed independently from the same specification to tolerate design faults. The core principle is failure independence, assuming that faults in different versions occur randomly and do not coincide, thereby allowing a voting mechanism to select the correct output. This technique has been applied in safety-critical applications, including flight control software, to achieve high reliability without single points of failure. Experiments have validated the assumption of low correlated failure rates under independent development conditions, though complete orthogonality remains challenging due to shared specifications.^[141] In safety-critical design, fault orthogonality emphasizes the separation of detection, isolation, and recovery mechanisms to ensure robust error handling, particularly in aviation software where failures can have catastrophic consequences. Principles include using diverse verification techniques—such as structural coverage analysis, requirements-based testing, and formal methods—to orthogonally confirm system behavior and detect latent faults. This orthogonality reduces the risk of undetected errors escaping into deployment, aligning with guidelines that mandate independence between development and verification activities to avoid bias.^[142] Triple modular redundancy (TMR) exemplifies orthogonal checks in hardware fault tolerance, employing three identical modules with a majority voter to mask single faults, augmented by independent monitoring circuits for error detection. In aerospace guidance systems, TMR with orthogonal redundancy—such as triple-component setups using voting across independent sensors—provides one-failure fault tolerance by isolating failures through diverse signal paths. Similarly, Byzantine fault tolerance (BFT) in distributed systems uses orthogonal replicas to consensus on states despite arbitrary faults, tolerating up to one-third malicious or erroneous nodes via independent execution and agreement protocols.^[143] A key metric for evaluating orthogonal detection is the coverage factor, defined as the probability that a fault-tolerant system successfully detects and recovers from a fault before it impacts the output. This factor quantifies the effectiveness of redundancy, with values approaching 1 indicating high orthogonality in fault handling; for instance, in nuclear safety analyses, coverage factors above 0.99 are targeted for critical modules to ensure system performability.^[144] Standards like RTCA DO-178C, released in 2011, incorporate orthogonality requirements for aerospace software certification by mandating diverse and independent methods for verification at higher design assurance levels (A and B), including structural code coverage and traceability to mitigate common faults. These guidelines ensure that fault-tolerant architectures, such as those using orthogonal redundancy, meet stringent safety objectives without over-reliance on any single technique.

Neuroscience

In neuroscience, orthogonality refers to the independent encoding of information across distinct neural pathways or populations, allowing the brain to process multiple dimensions of stimuli without interference. This concept is evident in the segregation of sensory modalities, where visual, auditory, and somatosensory cortices maintain distinct neural codes to prevent cross-talk. For instance, the visual cortex (V1) processes orientation and motion independently from auditory processing in the temporal lobe, enabling parallel computation of sensory inputs. Such orthogonal representations facilitate efficient information integration while preserving modality-specific fidelity.^[145] Seminal work by David Hubel and Torsten Wiesel in the 1960s demonstrated orthogonal-like organization in the primary visual cortex through orientation-selective receptive fields. They identified simple and complex cells with elongated fields tuned to specific stimulus orientations, such as horizontal or vertical edges, which collectively span a continuum of directions (e.g., 0° to 180°). This arrangement implies functional orthogonality, as neurons with perpendicular tuning preferences (e.g., 0° and 90°) respond independently to orthogonal stimulus components, forming the basis for edge detection and feature binding in vision. Their findings, derived from cat and monkey electrophysiology, revealed columnar structures where adjacent neurons share similar orientations, further supporting modular, non-overlapping processing.^[146] Population coding exemplifies orthogonality at the ensemble level, where groups of neurons encode multidimensional stimuli through nearly independent firing patterns. In the visual system, neural populations in area V4 represent object position orthogonally from background features like depth or rotation, maintaining decoding accuracy (correlation coefficients ~0.66–0.70) across variations. This separation minimizes distortion when decoding multiple stimuli simultaneously, as orthogonal subspaces allow additive vector representations without crosstalk. Similarly, in the second somatosensory cortex (S2), sensory (e.g., texture) and contextual (e.g., category) responses occupy orthogonal neural subspaces, enabling faithful signal processing amid behavioral demands.^[147]^[148]^[145] Specific examples illustrate these principles in navigation and sensory transmission. Hippocampal place cells generate orthogonal firing patterns across environments, with uncorrelated activity maps in CA3 for different rooms (e.g., only 6% of cells active in ≥6 of 11 similar rooms), supporting high-capacity episodic memory by decorrelating representations to avoid interference. In the optic nerve, retinal ganglion cells (RGCs) transmit orthogonal signals via diverse subtypes—such as ON/OFF center-surround and direction-selective cells—each carrying independent visual features (e.g., contrast vs. motion) without overlap in their spike trains, ensuring lossless relay to the lateral geniculate nucleus.^[149]30996-2)^[150] Functional magnetic resonance imaging (fMRI) studies from the 2000s onward have confirmed orthogonality through task designs that isolate cognitive processes. By presenting orthogonal stimuli (e.g., concurrent verbal and spatial tasks), researchers observed independent activation in prefrontal and parietal modules, with minimal overlap in BOLD signals, underscoring functional independence in higher cognition. These designs reveal how brain regions process attributes like scene temperature or sound only when task-relevant, aligning with modular theories.^[151]^[152] Orthogonality underpins cognitive modularity, allowing specialized processing while enabling integration, but disruptions lead to disorders like synesthesia. In grapheme-color synesthesia, cross-activation between adjacent sensory areas (e.g., auditory and visual cortices) erodes modality boundaries, causing involuntary blending (e.g., letters evoking colors) due to hyperconnectivity or reduced inhibition. This non-orthogonality highlights the brain's reliance on segregated pathways for typical perception, with implications for understanding conditions involving sensory overflow.^[153]

Philosophy

In philosophy, orthogonality refers to conceptual independence between propositions or ideas, where one neither logically entails nor contradicts the other, allowing them to coexist without mutual implication. This notion is particularly useful in analyzing debates where apparent tensions arise from assumed dependencies rather than inherent conflicts. For instance, in discussions of free will and determinism, some philosophers argue that the two can be orthogonal: determinism describes the causal structure of the universe, while free will pertains to the agent's capacity for rational deliberation and action, without one negating the possibility of the other in compatibilist frameworks.^[154] In epistemology, orthogonality highlights the separation of knowledge domains, such as factual scientific inquiry and normative ethical evaluation. David Hume's famous is-ought distinction exemplifies this, positing that descriptive statements about what "is" (empirical facts) cannot derive prescriptive statements about what "ought" to be (moral obligations), rendering science and ethics independent realms that operate on distinct principles without one subsuming or refuting the other. This separation underscores how epistemological methods in science focus on verifiable evidence, while ethical reasoning relies on values and sentiments, avoiding direct entailment between the two.^[155] Key examples illustrate orthogonality's role in philosophical analysis. Willard Van Orman Quine's doctrine of ontological relativity, developed in the 1960s, posits that ontological commitments—what exists—are relative to the linguistic or conceptual framework adopted, with different languages or theories yielding orthogonal ontologies that neither confirm nor deny each other absolutely but stand independently relative to their background assumptions. Similarly, in modal logic, orthogonality appears in formal systems modeling geometric or relational independence, such as logics where modalities for parallelism or perpendicularity represent non-interfering possibilities, extending philosophical inquiries into necessity and possibility without hierarchical dependence. Ludwig Wittgenstein's concept of language games, introduced in the 1920s and elaborated later, further embodies this through distinct rule sets governing different forms of discourse, implying orthogonal "games" where meanings and valid moves operate independently without universal overlap or contradiction..pdf) (Note: This links to a public domain or accessible version; original publication: Blackwell, 1953.) Applications of orthogonality aid in resolving paradoxes by introducing independent assumptions that disentangle conflicting premises. For example, paradoxes arising from assumed interconnections, such as those in set theory or semantics, can be addressed by treating certain elements as orthogonal, allowing revision of one without affecting the other. In postmodern deconstructions, Jacques Derrida's approach similarly reveals how binary oppositions (e.g., presence/absence) are not inherently linked but artificially hierarchized, promoting orthogonal readings that undermine presumed entailments and open multiple interpretive independences.

Gaming

In game design, orthogonality refers to the principle of creating mechanics that operate independently of one another, minimizing unintended interactions and allowing systems to function without interference. This approach ensures that elements like combat, resource management, and exploration in role-playing games (RPGs) can evolve separately, such as when crafting mechanics remain unaffected by combat outcomes, enabling players to specialize without systemic conflicts.^[156] The benefits of orthogonal mechanics include enhanced player freedom, as individuals can pursue diverse strategies without one system dominating others, and more balanced progression, where advancements in one area do not inadvertently unbalance the overall experience. By designing qualitatively distinct elements—such as movement types that are perpendicular in function rather than incremental—developers multiply the game's strategic depth exponentially, fostering replayability and emergent gameplay.^[156]^[157] A prominent example is Dwarf Fortress, where orthogonal simulations model independent aspects of a procedurally generated world, including geology, biology, and social dynamics, allowing complex interactions to arise naturally without core systems overlapping disruptively. Similarly, roguelikes employ orthogonal procedural elements, such as item designs where beneficial artifacts carry inherent trade-offs (e.g., powerful weapons with vulnerabilities) and detrimental ones offer niche utilities, ensuring varied procedural generations maintain fairness and depth across playthroughs.^[158]^[159] The MDA (Mechanics, Dynamics, Aesthetics) framework, developed in the early 2000s, underpins this theory by separating game components into mechanics (rules and systems), dynamics (runtime behaviors), and aesthetics (emotional responses), where orthogonal mechanics contribute to richer, non-conflicting dynamics without altering intended player aesthetics.^[160] In the 2020s, orthogonality has influenced virtual reality (VR) design by emphasizing spatial independence, such as distinct locomotion systems (e.g., teleportation versus smooth movement) that do not interfere with interaction mechanics, enhancing immersion without motion sickness trade-offs. In esports, orthogonal differentiation aids balance by creating units or abilities with incomparable properties—e.g., high-damage low-mobility versus low-damage high-mobility options—allowing fair competition across skill levels while evaluating balance through restricted playtesting to isolate interactions.^[161]^[162]^[157]

Law

In legal reasoning and jurisprudence, orthogonality refers to principles, doctrines, or issues that are independent of one another, meaning they do not intersect, influence, or overlap in their application, much like perpendicular lines in geometry that neither converge nor diverge from mutual relevance. This concept promotes clarity and precision in legal analysis by isolating distinct elements, preventing confusion or redundant considerations in adjudication. For instance, during oral arguments before the U.S. Supreme Court, attorneys have employed the term to denote that one legal proposition bears no relation to another, as when Solicitor General Paul Clement described two arguments as "entirely orthogonal" to emphasize their irrelevance to the case at hand.^[163] Similarly, in doctrinal discussions, orthogonality underscores how certain factors, such as a defendant's negligence being "entirely orthogonal" to the resulting injury, negate causal links under tort law without implicating other liabilities.^[164] Orthogonal doctrines exemplify this independence through separate legal tests that operate without necessary overlap. In contract and tort law, for example, liability for breach of agreement under contract principles is assessed via distinct criteria—such as mutual assent and consideration—from tort liability for negligence, which focuses on duty, breach, causation, and damages; a contractual violation does not automatically trigger tort remedies, preserving the autonomy of each framework to avoid doctrinal bleed and ensure targeted application.^[165] This separation is prized in legal doctrine for enhancing clarity and averting wasteful redundancies, as overlapping elements can obscure judicial decision-making and lead to inconsistent outcomes.^[166] In jurisprudence, orthogonal jurisdictions further illustrate this by delineating spheres of authority, such as federal versus state powers under the U.S. Constitution, where federal supremacy in enumerated areas operates independently of state police powers, minimizing interference while allowing concurrent application in non-preempted domains. Key examples appear in constitutional law and equity. Strict scrutiny, the highest standard of judicial review for fundamental rights infringements, incorporates orthogonal factors like the government's compelling interest and the law's narrow tailoring, evaluated separately to ensure rigorous yet compartmentalized analysis without one subsuming the other.^[167] In equity, orthogonal remedies provide discretionary relief—such as injunctions or specific performance—distinct from common law damages, allowing courts to address injustices where monetary compensation is inadequate, as equity historically developed as a parallel system to supplement rather than supplant legal remedies.^[168] Landmark case law reinforces these principles; Marbury v. Madison (1803) established judicial review, asserting the judiciary's orthogonal authority to interpret the Constitution independently of legislative or executive branches, thereby preventing encroachment and upholding separation of powers. In modern contexts, debates over privacy versus national security often treat these as orthogonal interests, requiring courts to balance them without presuming inherent conflict, as seen in analyses where prior precedents on one are deemed irrelevant to the other.^[169] The implications of orthogonality in law include safeguarding against judicial overreach by confining analysis to pertinent doctrines and avoiding the spillover of extraneous considerations into decision-making. In international law, orthogonal treaties exemplify this by addressing unrelated subject matters—such as trade agreements versus human rights conventions—without mutual effect or conflict, facilitating modular compliance under the Vienna Convention framework.^[170] This conceptual independence, akin to philosophical notions of non-intersecting domains, enables efficient legal systems while preserving the integrity of specialized rules.^[171]

History

Media collections

Orthogonality

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Orthogonality

Orthogonality

Origins and General Concept

Etymology

Fundamental Principles

Mathematics

Geometric and Vector Orthogonality

Add your contribution

Related Hubs

Contribute something