Community hub
0 subscribers7 pages, 0 posts
Recent from talks
All channels
Be the first to start a discussion here.
Be the first to start a discussion here.
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Welcome to the community hub built to collect knowledge and have discussions related to 5-cube.
Nothing was collected or created yet.
5-cube
View on Wikipediafrom Wikipedia
| 5-cube penteract (pent) | ||
|---|---|---|
| Type | uniform 5-polytope | |
| Schläfli symbol | {4,3,3,3} | |
| Coxeter diagram |    
| |
| 4-faces | 10 | tesseracts |
| Cells | 40 | cubes |
| Faces | 80 | squares |
| Edges | 80 | |
| Vertices | 32 | |
| Vertex figure |  5-cell | |
| Coxeter group | B5, [4,33], order 3840 | |
| Dual | 5-orthoplex | |
| Base point | (1,1,1,1,1,1) | |
| Circumradius | sqrt(5)/2 = 1.118034 | |
| Properties | convex, isogonal regular, Hanner polytope | |
In five-dimensional geometry, a 5-cube (or penteract) is a five-dimensional hypercube with 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract 4-faces.
It is represented by Schläfli symbol {4,3,3,3} or {4,33}, constructed as 3 tesseracts, {4,3,3}, around each cubic ridge.
Related polytopes
[edit]It is a part of an infinite hypercube family. The dual of a penteract is the 5-orthoplex, of the infinite family of orthoplexes.
Applying an alternation operation, deleting alternating vertices of the 5-cube, creates another uniform 5-polytope, called a 5-demicube, which is also part of an infinite family called the demihypercubes.
The penteract can be seen as an order-3 tesseractic honeycomb on a 4-sphere. It is related to the Euclidean 4-space (order-4) tesseractic honeycomb and paracompact hyperbolic honeycomb order-5 tesseractic honeycomb.
As a configuration
[edit]This configuration matrix represents the 5-cube. The rows and columns correspond to vertices, edges, faces, cells, and 4-faces. The diagonal numbers say how many of each element occur in the whole 5-cube. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[1][2]
Cartesian coordinates
[edit]The Cartesian coordinates of the vertices of a 5-cube centered at the origin and having edge length 2 are
- (±1,±1,±1,±1,±1),
while this 5-cube's interior consists of all points (x0, x1, x2, x3, x4) with -1 < xi < 1 for all i.
Images
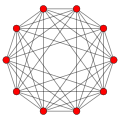
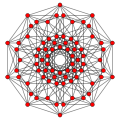
[edit]n-cube Coxeter plane projections in the Bk Coxeter groups project into k-cube graphs, with power of two vertices overlapping in the projective graphs.
| Coxeter plane | B5 | B4 / D5 | B3 / D4 / A2 |
|---|---|---|---|
| Graph | 
|
|
|
| Dihedral symmetry | [10] | [8] | [6] |
| Coxeter plane | Other | B2 | A3 |
| Graph | 
|
|
|
| Dihedral symmetry | [2] | [4] | [4] |
 Wireframe skew direction |
 B5 Coxeter plane |
 Vertex-edge graph. |
 A perspective projection 3D to 2D of stereographic projection 4D to 3D of Schlegel diagram 5D to 4D. |
 4D net of the 5-cube, perspective projected into 3D. |
Projection
[edit]The 5-cube can be projected down to 3 dimensions with a rhombic icosahedron envelope. There are 22 exterior vertices, and 10 interior vertices. The 10 interior vertices have the convex hull of a pentagonal antiprism. The 80 edges project into 40 external edges and 40 internal ones. The 40 cubes project into golden rhombohedra which can be used to dissect the rhombic icosahedron. The projection vectors are u = {1, φ, 0, -1, φ}, v = {φ, 0, 1, φ, 0}, w = {0, 1, φ, 0, -1}, where φ is the golden ratio, .
| rhombic icosahedron | 5-cube | |
|---|---|---|
| Perspective | orthogonal | |
|
|
|
It is also possible to project penteracts into three-dimensional space, similarly to projecting a cube into two-dimensional space.
 A 3D perspective projection of a penteract undergoing a simple rotation about the W1-W2 orthogonal plane
|
 A 3D perspective projection of a penteract undergoing a double rotation about the X-W1 and Z-W2 orthogonal planes
|
Symmetry
[edit]The 5-cube has Coxeter group symmetry B5, abstract structure , order 3840, containing 25 hyperplanes of reflection. The Schläfli symbol for the 5-cube, {4,3,3,3}, matches the Coxeter notation symmetry [4,3,3,3].
Prisms
[edit]All hypercubes have lower symmetry forms constructed as prisms. The 5-cube has 7 prismatic forms from the lowest 5-orthotope, { }5, and upwards as orthogonal edges are constrained to be of equal length. The vertices in a prism are equal to the product of the vertices in the elements. The edges of a prism can be partitioned into the number of edges in an element times the number of vertices in all the other elements.
| Description | Schläfli symbol | Coxeter-Dynkin diagram | Vertices | Edges | Coxeter notation Symmetry |
Order |
|---|---|---|---|---|---|---|
| 5-cube | {4,3,3,3} | |
32 | 80 | [4,3,3,3] | 3840 |
| tesseractic prism | {4,3,3}×{ } |  |
16×2 = 32 | 64 + 16 = 80 | [4,3,3,2] | 768 |
| cube-square duoprism | {4,3}×{4} | |
8×4 = 32 | 48 + 32 = 80 | [4,3,2,4] | 384 |
| cube-rectangle duoprism | {4,3}×{ }2 | |
8×22 = 32 | 48 + 2×16 = 80 | [4,3,2,2] | 192 |
| square-square duoprism prism | {4}2×{ } | |
42×2 = 32 | 2×32 + 16 = 80 | [4,2,4,2] | 128 |
| square-rectangular parallelepiped duoprism | {4}×{ }3 | |
4×23 = 32 | 32 + 3×16 = 80 | [4,2,2,2] | 64 |
| 5-orthotope | { }5 | |
25 = 32 | 5×16 = 80 | [2,2,2,2] | 32 |
Related polytopes
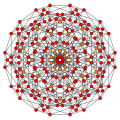
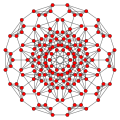
[edit]The 5-cube is 5th in a series of hypercube:
|
|
|
|
|
|
|
|
|
|
| Line segment | Square | Cube | 4-cube | 5-cube | 6-cube | 7-cube | 8-cube | 9-cube | 10-cube |
The regular skew polyhedron {4,5| 4} can be realized within the 5-cube, with its 32 vertices, 80 edges, and 40 square faces, and the other 40 square faces of the 5-cube become square holes.
This polytope is one of 31 uniform 5-polytopes generated from the regular 5-cube or 5-orthoplex.
References
[edit]- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 1973, 3rd edition, Dover, New York, p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n dimensions (n ≥ 5), ISBN 0-486-61480-8
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, wiley.com, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559–591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3–45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. (1966)
- Klitzing, Richard. "5D uniform polytopes (polytera) o3o3o3o4x - pent".
External links
[edit]- Weisstein, Eric W. "Hypercube". MathWorld.
- Olshevsky, George. "Measure polytope". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Multi-dimensional Glossary: hypercube Garrett Jones
- Maltsev, Nick E. https://www.asymptotos.com/wp-content/uploads/2023/07/Cube_5.html
5-cube
View on Grokipediafrom Grokipedia
A 5-cube, also known as a penteract, is a five-dimensional analog of the three-dimensional cube and a type of regular polytope in Euclidean space.[1] It consists of 32 vertices, 80 edges, 80 square faces, 40 cubic cells, and 10 tesseract facets, with each vertex incident to five edges and five tesseracts.[2] The structure can be defined by coordinates where each vertex is a point in with components in each dimension, ensuring all edges have unit length when appropriately scaled.[1]
As a member of the hypercube family, the 5-cube generalizes lower-dimensional cubes through recursive construction: it can be viewed as two mutually orthogonal 4-dimensional tesseracts joined at their boundaries or as the convex hull of its vertices.[1] Its Schläfli symbol is , indicating a regular polytope with square facets meeting three at a time around each edge, and so on up to the five-dimensional level.[1] The dual of the 5-cube is the five-dimensional cross-polytope, or 5-orthoplex, which has the same symmetry group but interchanges vertices and facets.[1]
Visualizing the 5-cube requires projections into lower dimensions, such as isometric views into three-dimensional space, which reveal its intricate network of interconnected lower-dimensional elements; one such projection appears in H.S.M. Coxeter's foundational work on regular polytopes.[1] In applications, 5-cubes appear in computer science for modeling high-dimensional data structures, like hypercube networks with 32 nodes for parallel computing, leveraging their high connectivity and symmetry. The 5-dimensional volume of a unit 5-cube (with edge length 1) is 1.[1]
These incidences verify the Euler characteristic of the 5-cube's boundary, which is topologically an S^4 and thus equals 2: V - E + F_2 - F_3 + F_4 = 32 - 80 + 80 - 40 + 10 = 2, where the element counts are as previously detailed.[5]
These prismatic subgroups enable uniform geometric realizations of the 5-cube where the combinatorial structure is preserved but metric anisotropies reduce the symmetry, facilitating compounds and layered constructions in higher-dimensional geometry. For instance, the tesseractic prism realizes the 5-cube with 10 tesseracts as facets under symmetry, while the cube-square duoprism uses 40 cubes as cells under . The flag count remains across all forms, as it is a combinatorial invariant, but the stabilizer subgroups vary inversely with the group orders, affecting transitivity on flags.[17]
Here, symmetric entries (e.g., 4 for edges-to-squares up and down) highlight the self-duality of the 5-cube. The off-diagonal values confirm the regularity: each row sum for rank k (excluding diagonal) equals the degree to the next rank, and column sums reflect the reverse. This matrix distinguishes the 5-cube from other 5-polytopes, such as the 5-simplex, whose incidences follow simplicial patterns (all degrees n-k=4 for up from rank k).[5]
The vertex set of 32 elements forms the hypercube graph Q_5, a bipartite graph with no complete K_{32} connectivity, but the full incidence poset extends this to a higher-dimensional geometry where elements correspond to partial coordinate fixings in {0,1}^5. This poset is isomorphic to the distributive lattice \prod_{i=1}^5 D_i, where each D_i is the diamond poset (two minimal elements covered by a maximal element, modeling fixed-0, fixed-1, and varying for each dimension). Unlike the boolean lattice B_5 (which has \binom{5}{k} elements per rank), the 5-cube's poset has \binom{5}{k} 2^{5-k} per rank k, emphasizing the dual roles of choice and fixing. This structure relates to higher incidence geometries via its chamber system, governed by the Coxeter group B_5, and to line graphs: for instance, the graph on edges (rank 1 elements) is the line graph of Q_5, with vertices adjacent if sharing a vertex, while higher ranks yield iterated line graphs capturing shared lower faces. Such relations underpin applications in combinatorial optimization and coding theory, where the 5-cube models error-correcting codes over F_2^5.[1]
Definition
Basic Description
The 5-cube is a convex regular 5-polytope that belongs to the family of hypercubes, which generalize the square and cube to higher dimensions.[1] As such, it represents the five-dimensional counterpart to the square (2-cube), cube (3-cube), and tesseract (4-cube), extending the pattern of orthogonal projections and Cartesian products into five-dimensional Euclidean space.[1] This polytope exhibits the defining properties of regularity, being convex with all facets congruent regular polytopes and all vertices equivalent under its symmetry group.[1] Consequently, it is isogonal, meaning its vertices are transitive under the symmetry operations, and isohedral, with faces that are equivalently positioned and oriented.[1] Common naming conventions for the 5-cube include "penteract," a portmanteau derived from the Greek word for five and the term tesseract, as well as "pent" as an abbreviation and "decateron," reflecting its structure with ten tesseract facets.[2] As a regular polytope, it holds a foundational position among the uniform 5-polytopes, which encompass vertex-transitive figures constructed from regular or uniform lower-dimensional elements.[2]Schläfli Symbol
The Schläfli symbol of the 5-cube is {4,3,3,3}, which recursively describes its structure as a regular 5-polytope: the symbol begins with {4} indicating square 2-faces, followed by three 3's specifying that three squares meet at each edge, three cubes {4,3} meet at each square face (forming the cubic 3-faces), and three tesseracts {4,3,3} meet at each cubic cell (forming the tesseractic 4-faces).[3] This notation, introduced by Ludwig Schläfli in the 19th century and systematized by H.S.M. Coxeter, encodes the uniformity and recursive buildup of the polytope from lower-dimensional elements, where each level's integer indicates the number of such elements incident to the previous level's feature.[1] The symbol {4,3,3,3} confirms the 5-cube's regularity, as it satisfies Schläfli's criteria for convex regular polytopes in five dimensions—specifically, the sequence produces a finite, irreducible Coxeter group with all branch numbers ≤4 and satisfying the determinant condition for positive definiteness of the Coxeter matrix—ensuring equal edge lengths, equal angles, and transitive symmetry on elements of each type.[3] Coxeter proved that such symbols for hypercubes extend indefinitely in higher dimensions without violating convexity, distinguishing them as one of three infinite families of regular polytopes beyond the Platonic solids.[1] This Schläfli symbol corresponds to the Coxeter-Dynkin diagram of type B_5, a linear chain of five nodes connected by single bonds (labeled 3, dihedral angles of \pi/3) except for a double bond (labeled 4, dihedral angle of \pi/4) between the first and second nodes, which generates the full symmetry group via reflections in five mutually perpendicular hyperplanes; the diagram's structure directly implies the hypercubic tiling's regularity in Euclidean 5-space.[4] The 5-cube can be constructed as the convex hull of its 32 vertices, equivalently realized through the Cartesian product of five line segments or as the measure polytope in five-dimensional space.[1] Alternatively, within the B_5 Coxeter group, it arises via truncation processes applied to the fundamental chamber, such as full truncation yielding the bitruncated 5-orthoplex (its dual) or rectification processes that preserve regularity from the simplex-generated family, though the hypercube itself is the "parent" form in this lineage.Combinatorial Structure
Element Counts
The 5-cube, or penteract, is a regular 5-dimensional polytope whose facial elements follow the standard enumeration for hypercubes. The number of -dimensional elements, or -faces, in an -cube is given by the formula where is the binomial coefficient.[5] For , this formula specializes as follows: there are vertices (0-faces), edges (1-faces), square faces (2-faces), cubic cells (3-faces), and tesseract cells (4-faces).[5] This combinatorial uniformity arises from the 5-cube's recursive construction, where each element corresponds to choosing varying coordinates out of 5 and fixing the positions in the remaining coordinates across 2 choices each.[5] Consequently, the incidence structure ensures that each vertex connects to 5 edges, as the hypercube graph has degree .[6] Each edge lies in 4 square faces (by selecting one additional varying direction from the remaining 4), each square face bounds 3 cubic cells (selecting one more from the remaining 3 directions), and each cubic cell is bounded by 2 tesseracts (the final choice of the last direction).[5] The complete set of facial elements is summarized in the following table:| Element Type | Number | |
|---|---|---|
| 0 | Vertices | 32 |
| 1 | Edges | 80 |
| 2 | Squares | 80 |
| 3 | Cubic cells | 40 |
| 4 | Tesseracts | 10 |
Incidence Relations
In the 5-cube, incidence relations describe the connectivity between its elements of different dimensions, specifically how lower-dimensional faces are contained within higher-dimensional ones. Each vertex (0-face) is incident to 5 edges (1-faces), each edge to 4 square faces (2-faces), each square to 3 cubic cells (3-faces), and each cubic cell to 2 tesseract cells (4-faces). More generally, in an n-dimensional hypercube such as the 5-cube (n=5), each k-face is contained in exactly (n - k) distinct (k+1)-faces. This follows from the structure of the face lattice, where a k-face is represented by a ternary string with exactly k free coordinates (marked as varying) and (n - k) fixed coordinates (set to 0 or 1); extending to a (k+1)-face requires selecting one of the (n - k) fixed coordinates to make varying, yielding precisely (n - k) such extensions. For the 5-cube, this yields the specific incidences noted above: 5 for k=0, 4 for k=1, 3 for k=2, and 2 for k=3. Conversely, each (k+1)-face in the 5-cube contains exactly 2(k+1) k-faces, as a (k+1)-face (itself a (k+1)-cube) has 2(k+1) choices for fixing one of its (k+1) varying coordinates to either 0 or 1. Thus, each square (k=1) contains 4 edges, each cube (k=2) contains 6 squares, each tesseract (k=3) contains 8 cubes, and the full 5-cube (k=4) contains 10 tesseracts. These relations hold uniformly across the 10 tesseracts that bound the 5-cube. The following table summarizes key incidence numbers for the 5-cube, focusing on the number of j-faces containing each i-face (for i < j), derived from the general hypercube formulas where the number is \binom{n-i}{j-i}.| i-face | j=1 (edges) | j=2 (squares) | j=3 (cubes) | j=4 (tesseracts) |
|---|---|---|---|---|
| vertex (0) | 5 | 10 | 10 | 5 |
| edge (1) | - | 4 | 6 | 4 |
| square (2) | - | - | 3 | 3 |
| cube (3) | - | - | - | 2 |
Geometry
Cartesian Coordinates
The 5-cube is embedded in 5-dimensional Euclidean space with its vertices at all possible combinations of coordinates , centered at the origin, yielding 32 vertices as per its combinatorial structure.[7] Adjacent vertices differ in exactly one coordinate, so the edge length is the Euclidean distance .[1] To achieve unit edge length, the coordinates are scaled by a factor of , resulting in vertices at all combinations of .[1] For this unit-edge scaling, the circumradius—the distance from the origin to any vertex—is .[1] This coordinate representation arises from the 5-cube as the Cartesian product of five identical intervals , with vertices at the product of the endpoints.[8]Metric Properties
The 5-cube, or penteract, possesses several key metric properties derived from its uniform edge length . Its 5-dimensional volume, representing the content enclosed by the polytope, is given by . For example, when , the volume is 1. This formula arises from the Cartesian product structure of the hypercube, where each dimension contributes a factor of to the measure.[9] The hypersurface area, or the total 4-dimensional content of the boundary consisting of 10 tesseract facets, is . This measure quantifies the "surface" enclosing the 5-volume and equals , reflecting two parallel 4-faces per dimension times the 4-volume of each tesseract facet. For , .[9] The 5-cube is a tangential polytope, admitting an inscribed hypersphere tangent to all facets with inradius , derived from the general relation for such polytopes .[10] This inradius remains independent of dimension for hypercubes, as the distance from the center to any facet plane is . The diameter, the maximum Euclidean distance between any two vertices, occurs between antipodal vertices differing in all five coordinates and equals .[11] This establishes the scale of the polytope's extent along its space diagonal. Additionally, the 5-cube possesses a midsphere tangent to all 80 edges at their midpoints, a property shared by regular hypercubes as tangential polytopes. The following table summarizes these measures for edge lengths and , computed using the vertex coordinates aligned with the axes from to in each dimension:Symmetry
Full Symmetry Group
The full symmetry group of the 5-cube is the hyperoctahedral group , which is isomorphic to the Weyl group of type .[12] This group has order .[13] The group is generated by the permutations of the five coordinates together with sign flips on each individual coordinate, corresponding to signed permutations of five elements.[14] As a Weyl group, it admits a presentation via the Coxeter diagram for type , which consists of five nodes arranged in a linear chain with single edges connecting the first four nodes and a double edge connecting the fourth and fifth nodes. The rotational symmetries form an index-2 subgroup of , with order .[13] The group acts transitively on the 32 vertices of the 5-cube.[15] By the orbit-stabilizer theorem, the stabilizer of any vertex therefore has order .[13][15]Prismatic Subgroups
The prismatic subgroups of the 5-cube arise from its decompositions as Cartesian products of lower-dimensional hypercubes, reflecting reduced symmetries when edge lengths are equalized within groups of coordinate directions but differ between groups. These decompositions correspond to the seven integer partitions of 5, each defining a distinct prismatic form with a direct product symmetry group consisting of the hyperoctahedral groups (Weyl groups of type ) for each part in the partition. The full symmetry group of the 5-cube is , of order , acting as signed permutations on the five coordinates.[16] The prismatic subgroups are proper subgroups preserving these product structures. For the partition (5), the form is the full 5-cube itself, with symmetry of order 3840. The partition (4,1) yields the tesseractic prism (4-cube × interval), with symmetry of order . The partition (3,2) corresponds to the cube-square duoprism (3-cube × 2-cube), with symmetry of order . The partition (3,1,1) gives a cube-rectangle duoprism (3-cube × interval × interval), with symmetry of order . The partition (2,2,1) produces a square-square duoprism prism (2-cube × 2-cube × interval), with symmetry of order . The partition (2,1,1,1) forms a square-rectangular duoprism (2-cube × interval³), with symmetry of order . Finally, the partition (1,1,1,1,1) is the 5-orthotope, with symmetry of order . The following table summarizes these seven prismatic forms, their decompositions, symmetry groups, and orders:| Partition | Prismatic Form | Decomposition | Symmetry Group | Order |
|---|---|---|---|---|
| (5) | 5-cube | 5-cube | 3840 | |
| (4,1) | Tesseractic prism | 4-cube × interval | 768 | |
| (3,2) | Cube-square duoprism | 3-cube × 2-cube | 384 | |
| (3,1,1) | Cube-rectangle duoprism | 3-cube × interval × interval | 192 | |
| (2,2,1) | Square-square duoprism prism | 2-cube × 2-cube × interval | 128 | |
| (2,1,1,1) | Square-rectangular duoprism | 2-cube × interval³ | 64 | |
| (1^5) | 5-orthotope | interval⁵ | 32 |
Representations
Configuration Model
The configuration model of the 5-cube describes its abstract combinatorial structure through the incidence relations between its elements, independent of any geometric embedding. This model captures how lower-dimensional elements are contained within higher-dimensional ones, providing a complete specification of the polytope as a partially ordered set (poset) under inclusion. The face poset of the 5-cube is ranked by dimension, with ranks corresponding to 0-faces (vertices) up to 4-faces (tesseracts), and the whole polytope as the unique 5-face. The structure is regular, meaning every k-face is combinatorially equivalent, and incidences follow a uniform pattern derived from the hypercube's construction as the Cartesian product of five line segments. These numbers arise from the general formula for incidences in an n-cube: the number of k-faces containing a fixed m-face (m < k) is \binom{n-m}{k-m}, reflecting choices of additional varying directions from the fixed ones in the m-face. For n=5, this yields the consecutive up-degrees 5 (edges per vertex), 4 (squares per edge), 3 (cubes per square), and 2 (tesseracts per cube), with the down-degrees complementing as 2 (vertices per edge), 4 (edges per square), 6 (squares per cube), 8 (cubes per tesseract), and 10 (tesseracts per 5-cube).[5] The full configuration can be represented by an incidence matrix for consecutive dimensions, where rows and columns correspond to the types of elements (0- to 4-faces), the diagonal entries are the element counts, and off-diagonal entries give the uniform incidence degrees between adjacent ranks. This matrix encodes the local structure and allows computation of global properties like the total number of flags (complete chains of faces from vertex to facet).| Element Type | Vertices (0) | Edges (1) | Squares (2) | Cubes (3) | Tesseracts (4) |
|---|---|---|---|---|---|
| Vertices (0) | 32 | 5 | - | - | - |
| Edges (1) | 2 | 80 | 4 | - | - |
| Squares (2) | - | 4 | 80 | 3 | - |
| Cubes (3) | - | - | 6 | 40 | 2 |
| Tesseracts (4) | - | - | - | 8 | 10 |