Astronomical coordinate systems

In astronomy, coordinate systems are used for specifying positions of celestial objects (satellites, planets, stars, galaxies, etc.) relative to a given reference frame, based on physical reference points available to a situated observer (e.g. the true horizon and north to an observer on Earth's surface).^[1] Coordinate systems in astronomy can specify an object's relative position in three-dimensional space or plot merely by its direction on a celestial sphere, if the object's distance is unknown or trivial.

Spherical coordinates, projected on the celestial sphere, are analogous to the geographic coordinate system used on the surface of Earth. These differ in their choice of fundamental plane, which divides the celestial sphere into two equal hemispheres along a great circle. Rectangular coordinates, in appropriate units, have the same fundamental ( $x, y$ ) plane and primary ( $x$ -axis) direction, such as an axis of rotation. Each coordinate system is named after its choice of fundamental plane.

Coordinate systems

The following table lists the common coordinate systems in use by the astronomical community. The fundamental plane divides the celestial sphere into two equal hemispheres and defines the baseline for the latitudinal coordinates, similar to the equator in the geographic coordinate system. The poles are located at ±90° from the fundamental plane. The primary direction is the starting point of the longitudinal coordinates. The origin is the zero distance point, the "center of the celestial sphere", although the definition of celestial sphere is ambiguous about the definition of its center point.

Coordinate system^[2]	Center point (origin)	Fundamental plane (0° latitude)	Poles	Coordinates		Primary direction (0° longitude)
Coordinate system^[2]	Center point (origin)	Fundamental plane (0° latitude)	Poles	Latitude	Longitude	Primary direction (0° longitude)
Horizontal (also called alt-az or el-az)	Observer	Horizon	Zenith, nadir	Altitude ( $a$ ) or elevation	Azimuth ( $A$ )	North or south point of horizon
Equatorial	Center of the Earth (geocentric), or Sun (heliocentric)	Celestial equator	Celestial poles	Declination ( $δ$ )	Right ascension ( $α$ ) or hour angle ( $h$ )	March equinox
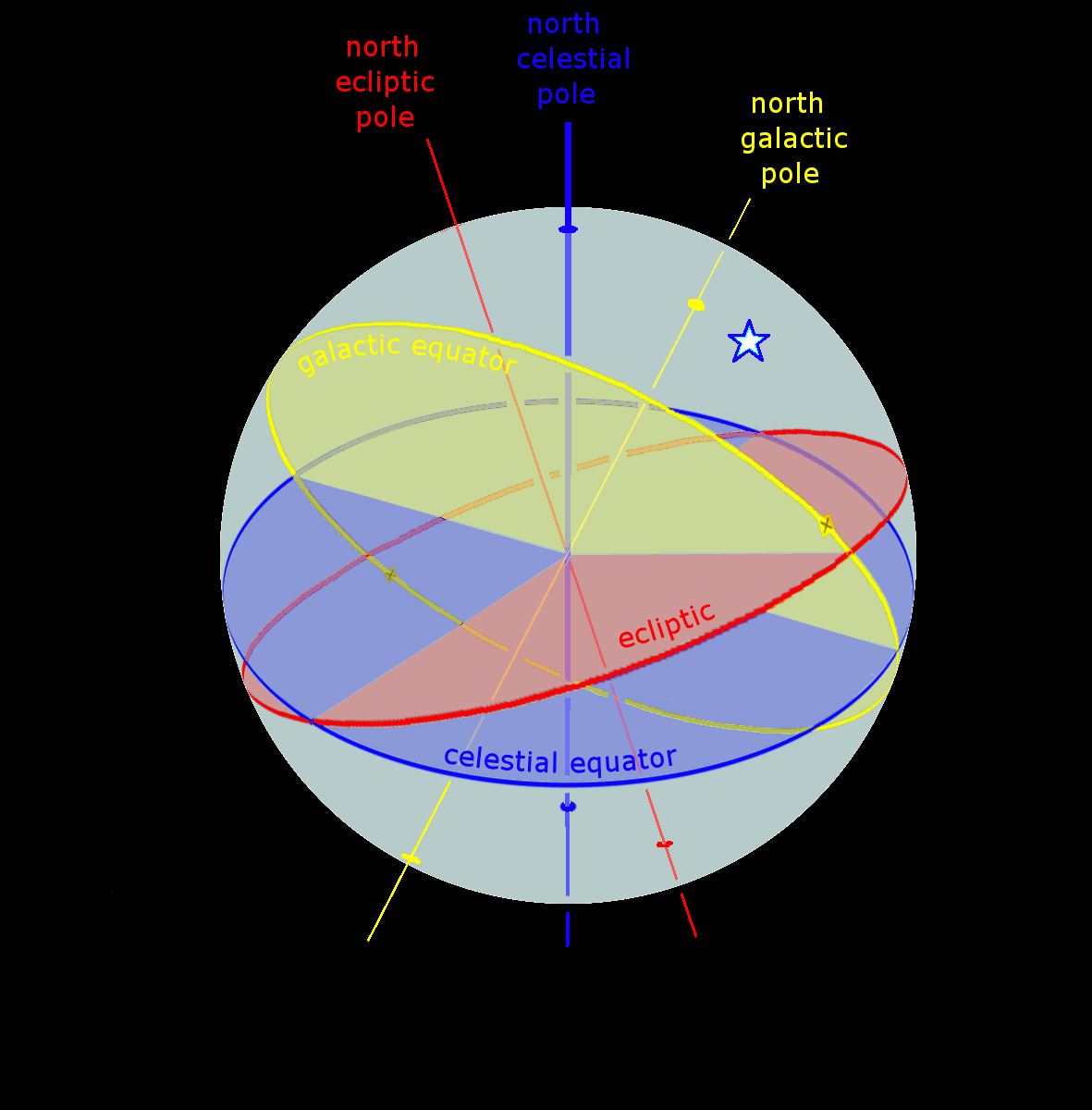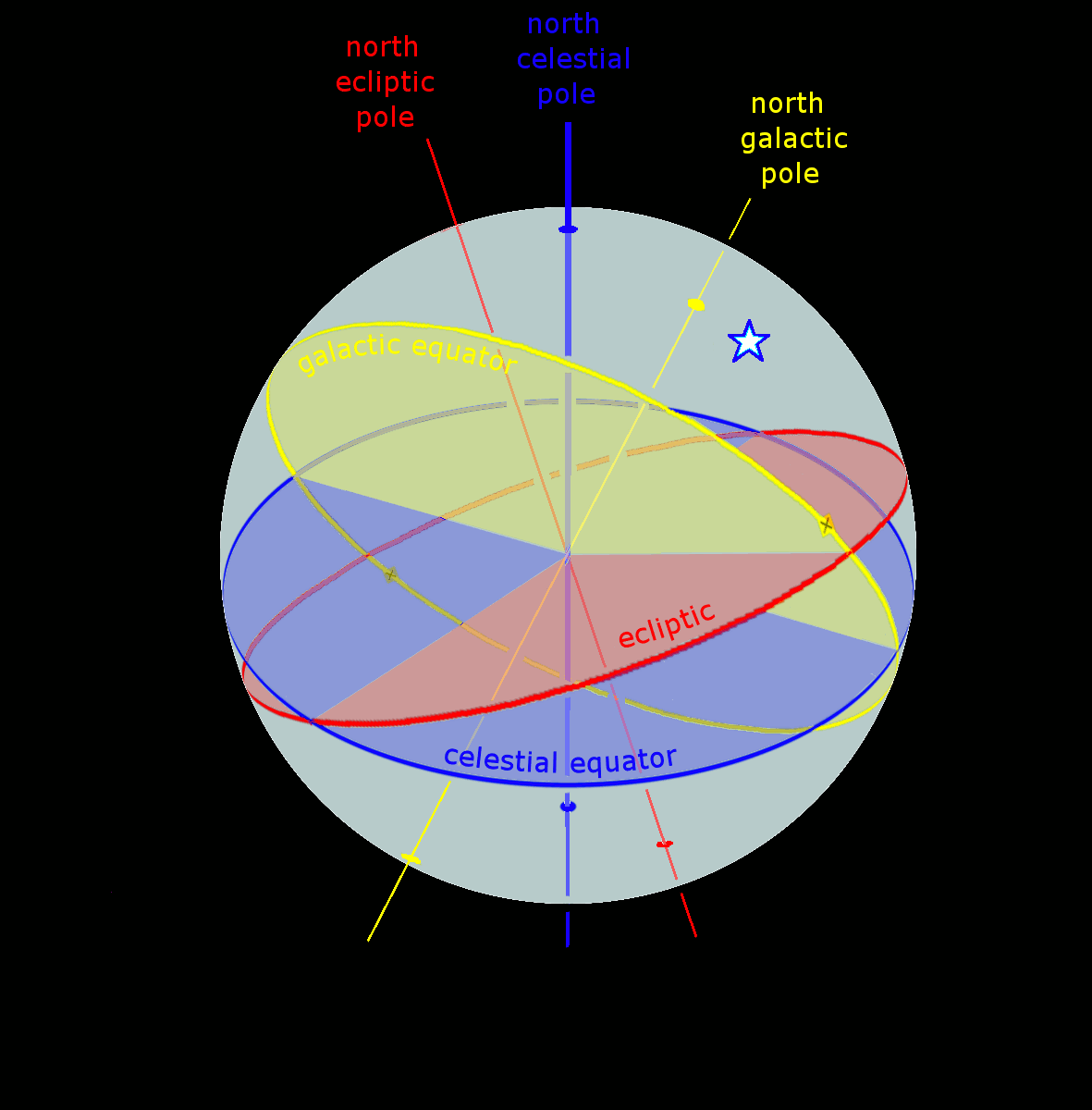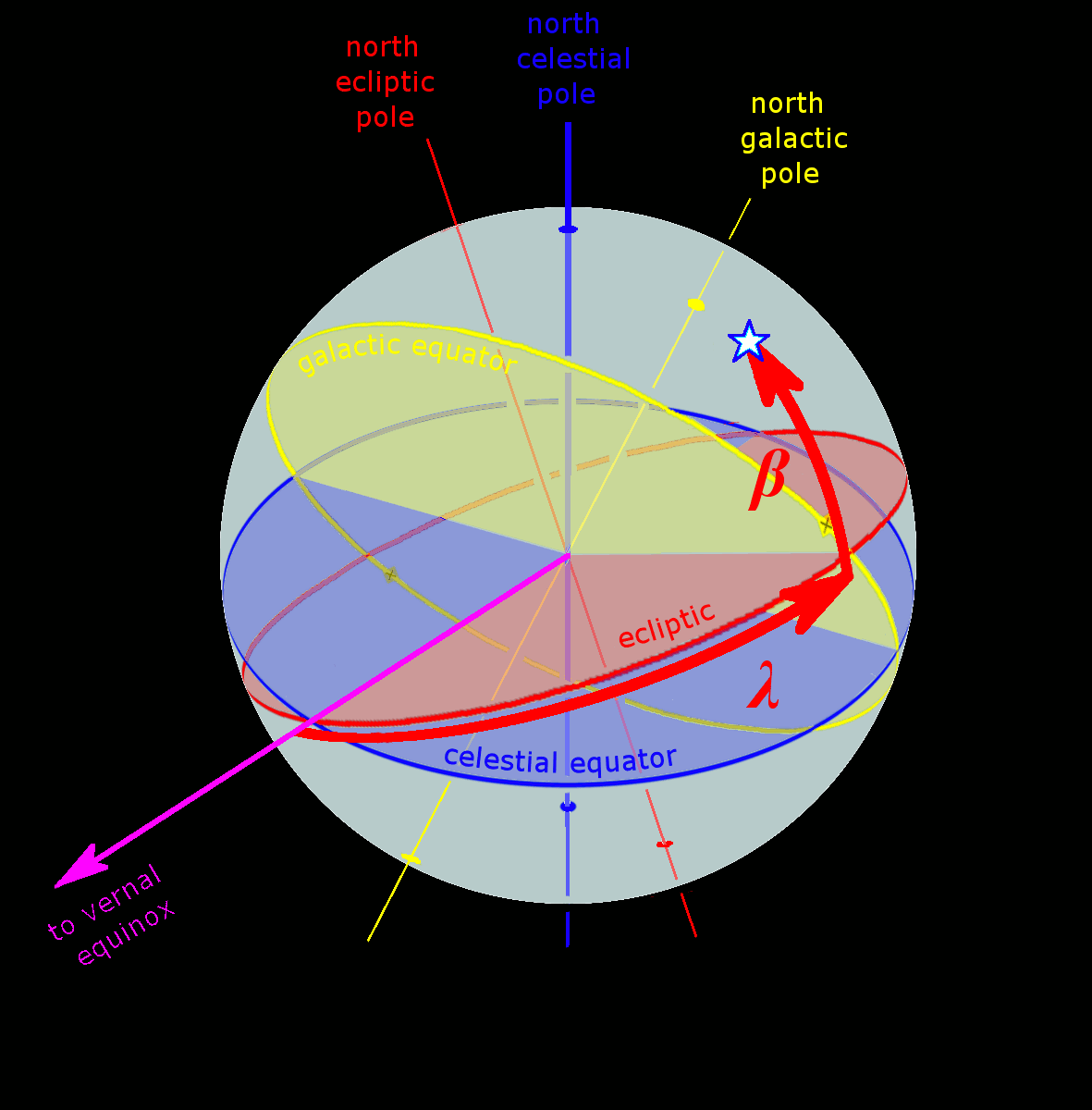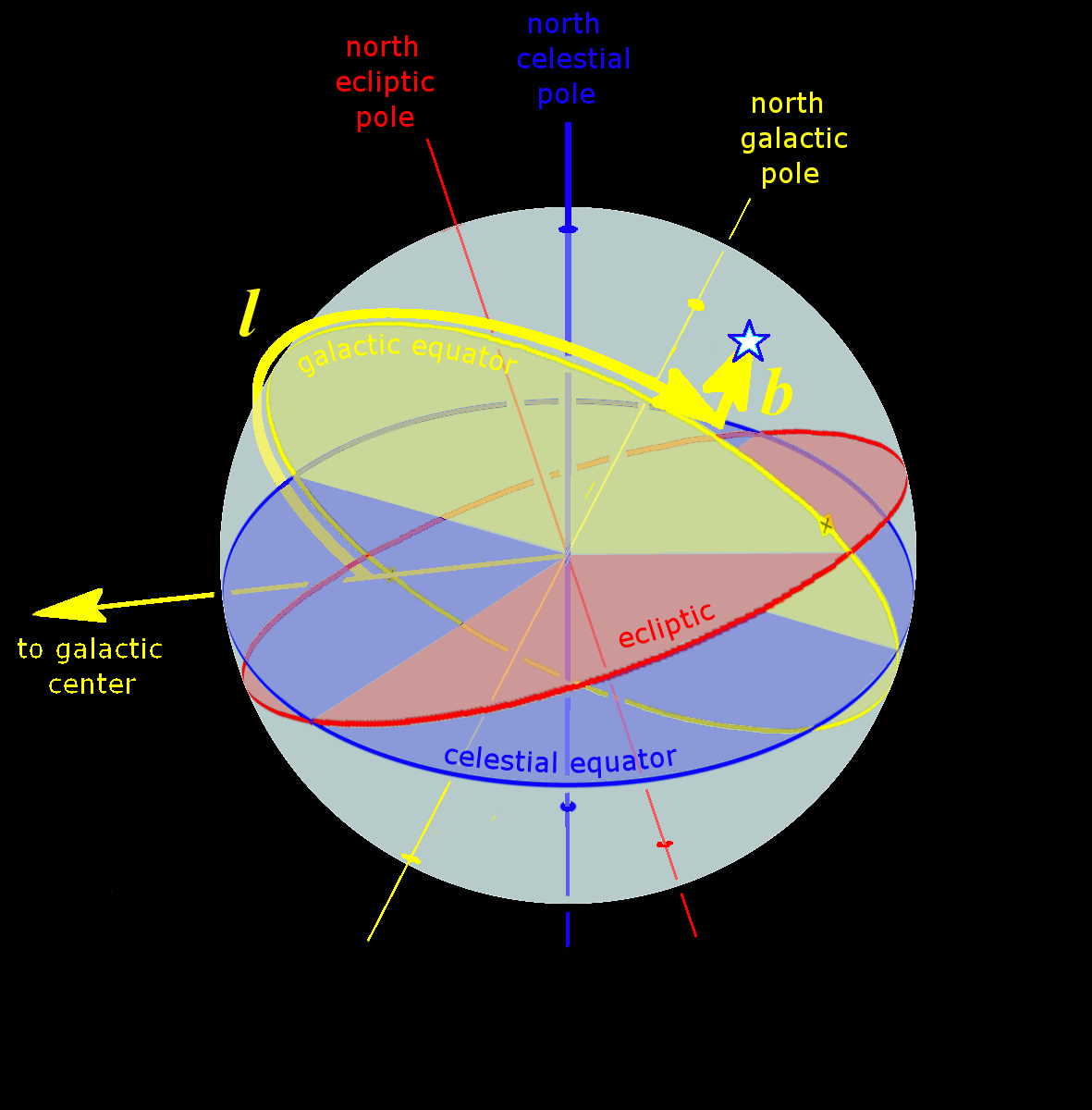
Ecliptic	Center of the Earth (geocentric), or Sun (heliocentric)	Ecliptic	Ecliptic poles	Ecliptic latitude ( $β$ )	Ecliptic longitude ( $λ$ )	March equinox
Galactic	Center of the Sun	Galactic plane	Galactic poles	Galactic latitude ( $b$ )	Galactic longitude ( $l$ )	Galactic Center
Supergalactic		Supergalactic plane	Supergalactic poles	Supergalactic latitude ( $SGB$ )	Supergalactic longitude ( $SGL$ )	Intersection of supergalactic plane and galactic plane

Horizontal system

The horizontal, or altitude-azimuth, system is based on the position of the observer on Earth, which revolves around its own axis once per sidereal day (23 hours, 56 minutes and 4.091 seconds) in relation to the star background. The positioning of a celestial object by the horizontal system varies with time, but is a useful coordinate system for locating and tracking objects for observers on Earth. It is based on the position of stars relative to an observer's ideal horizon.

Equatorial system

The equatorial coordinate system is centered at Earth's center, but fixed relative to the celestial poles and the March equinox. The coordinates are based on the location of stars relative to Earth's equator if it were projected out to an infinite distance. The equatorial describes the sky as seen from the Solar System, and modern star maps almost exclusively use equatorial coordinates.

The equatorial system is the normal coordinate system for most professional and many amateur astronomers having an equatorial mount that follows the movement of the sky during the night. Celestial objects are found by adjusting the telescope's or other instrument's scales so that they match the equatorial coordinates of the selected object to observe.

Popular choices of pole and equator are the older B1950 and the modern J2000 systems, but a pole and equator "of date" can also be used, meaning one appropriate to the date under consideration, such as when a measurement of the position of a planet or spacecraft is made. There are also subdivisions into "mean of date" coordinates, which average out or ignore nutation, and "true of date," which include nutation.

Ecliptic system

The fundamental plane is the plane of the Earth's orbit, called the ecliptic plane. There are two principal variants of the ecliptic coordinate system: geocentric ecliptic coordinates centered on the Earth and heliocentric ecliptic coordinates centered on the center of mass of the Solar System.

The geocentric ecliptic system was the principal coordinate system for ancient astronomy and is still useful for computing the apparent motions of the Sun, Moon, and planets.^[3] It was used to define the twelve astrological signs of the zodiac, for instance.

The heliocentric ecliptic system describes the planets' orbital movement around the Sun, and centers on the barycenter of the Solar System (i.e. very close to the center of the Sun). The system is primarily used for computing the positions of planets and other Solar System bodies, as well as defining their orbital elements.

Galactic system

The galactic coordinate system uses the approximate plane of the Milky Way Galaxy as its fundamental plane. The Solar System is still the center of the coordinate system, and the zero point is defined as the direction towards the Galactic Center. Galactic latitude resembles the elevation above the galactic plane and galactic longitude determines direction relative to the center of the galaxy.

Supergalactic system

The supergalactic coordinate system corresponds to a fundamental plane that contains a higher than average number of local galaxies in the sky as seen from Earth.

Converting coordinates

Conversions between the various coordinate systems are given.^[4] See the notes before using these equations.

Notation

Horizontal coordinates
- $A$ , azimuth
- $a$ , altitude
Equatorial coordinates
- $α$ , right ascension
- $δ$ , declination
- $h$ , hour angle
Ecliptic coordinates
- $λ$ , ecliptic longitude
- $β$ , ecliptic latitude
Galactic coordinates
- $l$ , galactic longitude
- $b$ , galactic latitude
Miscellaneous
- $λ o$ , observer's longitude
- $ϕ o$ , observer's latitude
- $ε$ , obliquity of the ecliptic (about 23.4°)
- $θ L$ , local sidereal time
- $θ G$ , Greenwich sidereal time

Hour angle ↔ right ascension

{\begin{aligned}h&=\theta _{\text{L}}-\alpha &&{\mbox{or}}&h&=\theta _{\text{G}}+\lambda _{\text{o}}-\alpha \\\alpha &=\theta _{\text{L}}-h&&{\mbox{or}}&\alpha &=\theta _{\text{G}}+\lambda _{\text{o}}-h\end{aligned}}

Equatorial ↔ ecliptic

The classical equations, derived from spherical trigonometry, for the longitudinal coordinate are presented to the right of a bracket; dividing the first equation by the second gives the convenient tangent equation seen on the left.^[5] The rotation matrix equivalent is given beneath each case.^[6] This division is ambiguous because tan has a period of 180° ( $π$ ) whereas cos and sin have periods of 360° (2 $π$ ).

{\begin{aligned}\tan \left(\lambda \right)&={\sin \left(\alpha \right)\cos \left(\varepsilon \right)+\tan \left(\delta \right)\sin \left(\varepsilon \right) \over \cos \left(\alpha \right)};\qquad {\begin{cases}\cos \left(\beta \right)\sin \left(\lambda \right)=\cos \left(\delta \right)\sin \left(\alpha \right)\cos \left(\varepsilon \right)+\sin \left(\delta \right)\sin \left(\varepsilon \right);\\\cos \left(\beta \right)\cos \left(\lambda \right)=\cos \left(\delta \right)\cos \left(\alpha \right).\end{cases}}\\\sin \left(\beta \right)&=\sin \left(\delta \right)\cos \left(\varepsilon \right)-\cos \left(\delta \right)\sin \left(\varepsilon \right)\sin \left(\alpha \right)\\[3pt]{\begin{bmatrix}\cos \left(\beta \right)\cos \left(\lambda \right)\\\cos \left(\beta \right)\sin \left(\lambda \right)\\\sin \left(\beta \right)\end{bmatrix}}&={\begin{bmatrix}1&0&0\\0&\cos \left(\varepsilon \right)&\sin \left(\varepsilon \right)\\0&-\sin \left(\varepsilon \right)&\cos \left(\varepsilon \right)\end{bmatrix}}{\begin{bmatrix}\cos \left(\delta \right)\cos \left(\alpha \right)\\\cos \left(\delta \right)\sin \left(\alpha \right)\\\sin \left(\delta \right)\end{bmatrix}}\\[6pt]\tan \left(\alpha \right)&={\sin \left(\lambda \right)\cos \left(\varepsilon \right)-\tan \left(\beta \right)\sin \left(\varepsilon \right) \over \cos \left(\lambda \right)};\qquad {\begin{cases}\cos \left(\delta \right)\sin \left(\alpha \right)=\cos \left(\beta \right)\sin \left(\lambda \right)\cos \left(\varepsilon \right)-\sin \left(\beta \right)\sin \left(\varepsilon \right);\\\cos \left(\delta \right)\cos \left(\alpha \right)=\cos \left(\beta \right)\cos \left(\lambda \right).\end{cases}}\\[3pt]\sin \left(\delta \right)&=\sin \left(\beta \right)\cos \left(\varepsilon \right)+\cos \left(\beta \right)\sin \left(\varepsilon \right)\sin \left(\lambda \right).\\[6pt]{\begin{bmatrix}\cos \left(\delta \right)\cos \left(\alpha \right)\\\cos \left(\delta \right)\sin \left(\alpha \right)\\\sin \left(\delta \right)\end{bmatrix}}&={\begin{bmatrix}1&0&0\\0&\cos \left(\varepsilon \right)&-\sin \left(\varepsilon \right)\\0&\sin \left(\varepsilon \right)&\cos \left(\varepsilon \right)\end{bmatrix}}{\begin{bmatrix}\cos \left(\beta \right)\cos \left(\lambda \right)\\\cos \left(\beta \right)\sin \left(\lambda \right)\\\sin \left(\beta \right)\end{bmatrix}}.\end{aligned}}

Equatorial ↔ horizontal

Azimuth ( $A$ ) is measured from the south point, turning positive to the west.^[7] Zenith distance, the angular distance along the great circle from the zenith to a celestial object, is simply the complementary angle of the altitude: $90° - a$ .^[8]

{\begin{aligned}\tan \left(A\right)&={\sin \left(h\right) \over \cos \left(h\right)\sin \left(\phi _{\text{o}}\right)-\tan \left(\delta \right)\cos \left(\phi _{\text{o}}\right)};\qquad {\begin{cases}\cos \left(a\right)\sin \left(A\right)=\cos \left(\delta \right)\sin \left(h\right);\\\cos \left(a\right)\cos \left(A\right)=\cos \left(\delta \right)\cos \left(h\right)\sin \left(\phi _{\text{o}}\right)-\sin \left(\delta \right)\cos \left(\phi _{\text{o}}\right)\end{cases}}\\[3pt]\sin \left(a\right)&=\sin \left(\phi _{\text{o}}\right)\sin \left(\delta \right)+\cos \left(\phi _{\text{o}}\right)\cos \left(\delta \right)\cos \left(h\right);\end{aligned}}

In solving the $tan(A)$ equation for $A$ , in order to avoid the ambiguity of the arctangent, use of the two-argument arctangent, denoted $atan2(x, y)$ , is recommended. The two-argument arctangent computes the arctangent of $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠y/x⁠$ , and accounts for the quadrant in which it is being computed. Thus, consistent with the convention of azimuth being measured from the south and opening positive to the west,

A=-\operatorname {atan2} (y,x)

,

where

{\begin{aligned}x&=-\sin \left(\phi _{\text{o}}\right)\cos \left(\delta \right)\cos \left(h\right)+\cos \left(\phi _{\text{o}}\right)\sin \left(\delta \right)\\y&=\cos \left(\delta \right)\sin \left(h\right)\end{aligned}}

.

If the above formula produces a negative value for $A$ , it can be rendered positive by simply adding 360°.

{\begin{aligned}{\begin{bmatrix}\cos \left(a\right)\cos \left(A\right)\\\cos \left(a\right)\sin \left(A\right)\\\sin \left(a\right)\end{bmatrix}}&={\begin{bmatrix}\sin \left(\phi _{\text{o}}\right)&0&-\cos \left(\phi _{\text{o}}\right)\\0&1&0\\\cos \left(\phi _{\text{o}}\right)&0&\sin \left(\phi _{\text{o}}\right)\end{bmatrix}}{\begin{bmatrix}\cos \left(\delta \right)\cos \left(h\right)\\\cos \left(\delta \right)\sin \left(h\right)\\\sin \left(\delta \right)\end{bmatrix}}\\&={\begin{bmatrix}\sin \left(\phi _{\text{o}}\right)&0&-\cos \left(\phi _{\text{o}}\right)\\0&1&0\\\cos \left(\phi _{\text{o}}\right)&0&\sin \left(\phi _{\text{o}}\right)\end{bmatrix}}{\begin{bmatrix}\cos \left(\theta _{L}\right)&\sin \left(\theta _{L}\right)&0\\\sin \left(\theta _{L}\right)&-\cos \left(\theta _{L}\right)&0\\0&0&1\end{bmatrix}}{\begin{bmatrix}\cos \left(\delta \right)\cos \left(\alpha \right)\\\cos \left(\delta \right)\sin \left(\alpha \right)\\\sin \left(\delta \right)\end{bmatrix}};\\[6pt]\tan \left(h\right)&={\sin \left(A\right) \over \cos \left(A\right)\sin \left(\phi _{\text{o}}\right)+\tan \left(a\right)\cos \left(\phi _{\text{o}}\right)};\qquad {\begin{cases}\cos \left(\delta \right)\sin \left(h\right)=\cos \left(a\right)\sin \left(A\right);\\\cos \left(\delta \right)\cos \left(h\right)=\sin \left(a\right)\cos \left(\phi _{\text{o}}\right)+\cos \left(a\right)\cos \left(A\right)\sin \left(\phi _{\text{o}}\right)\end{cases}}\\[3pt]\sin \left(\delta \right)&=\sin \left(\phi _{\text{o}}\right)\sin \left(a\right)-\cos \left(\phi _{\text{o}}\right)\cos \left(a\right)\cos \left(A\right);\end{aligned}}

^[a]

Again, in solving the $tan(h)$ equation for $h$ , use of the two-argument arctangent that accounts for the quadrant is recommended. Thus, again consistent with the convention of azimuth being measured from the south and opening positive to the west,

h=\operatorname {atan2} (y,x)

,

where

{\begin{aligned}x&=\sin \left(\phi _{\text{o}}\right)\cos \left(a\right)\cos \left(A\right)+\cos \left(\phi _{\text{o}}\right)\sin \left(a\right)\\y&=\cos \left(a\right)\sin \left(A\right)\\[3pt]{\begin{bmatrix}\cos \left(\delta \right)\cos \left(h\right)\\\cos \left(\delta \right)\sin \left(h\right)\\\sin \left(\delta \right)\end{bmatrix}}&={\begin{bmatrix}\sin \left(\phi _{\text{o}}\right)&0&\cos \left(\phi _{\text{o}}\right)\\0&1&0\\-\cos \left(\phi _{\text{o}}\right)&0&\sin \left(\phi _{\text{o}}\right)\end{bmatrix}}{\begin{bmatrix}\cos \left(a\right)\cos \left(A\right)\\\cos \left(a\right)\sin \left(A\right)\\\sin \left(a\right)\end{bmatrix}}\\{\begin{bmatrix}\cos \left(\delta \right)\cos \left(\alpha \right)\\\cos \left(\delta \right)\sin \left(\alpha \right)\\\sin \left(\delta \right)\end{bmatrix}}&={\begin{bmatrix}\cos \left(\theta _{L}\right)&\sin \left(\theta _{L}\right)&0\\\sin \left(\theta _{L}\right)&-\cos \left(\theta _{L}\right)&0\\0&0&1\end{bmatrix}}{\begin{bmatrix}\sin \left(\phi _{\text{o}}\right)&0&\cos \left(\phi _{\text{o}}\right)\\0&1&0\\-\cos \left(\phi _{\text{o}}\right)&0&\sin \left(\phi _{\text{o}}\right)\end{bmatrix}}{\begin{bmatrix}\cos \left(a\right)\cos \left(A\right)\\\cos \left(a\right)\sin \left(A\right)\\\sin \left(a\right)\end{bmatrix}}.\end{aligned}}

Equatorial ↔ galactic

These equations^[14] are for converting equatorial coordinates to Galactic coordinates.

{\begin{aligned}\cos \left(l_{\text{NCP}}-l\right)\cos(b)&=\sin \left(\delta \right)\cos \left(\delta _{\text{G}}\right)-\cos \left(\delta \right)\sin \left(\delta _{\text{G}}\right)\cos \left(\alpha -\alpha _{\text{G}}\right)\\\sin \left(l_{\text{NCP}}-l\right)\cos(b)&=\cos(\delta )\sin \left(\alpha -\alpha _{\text{G}}\right)\\\sin \left(b\right)&=\sin \left(\delta \right)\sin \left(\delta _{\text{G}}\right)+\cos \left(\delta \right)\cos \left(\delta _{\text{G}}\right)\cos \left(\alpha -\alpha _{\text{G}}\right)\end{aligned}}

$\alpha _{\text{G}},\delta _{\text{G}}$ are the equatorial coordinates of the North Galactic Pole and $l_{\text{NCP}}$ is the Galactic longitude of the North Celestial Pole. Referred to J2000.0 the values of these quantities are:

\alpha _{G}=192.85948^{\circ }\qquad \delta _{G}=27.12825^{\circ }\qquad l_{\text{NCP}}=122.93192^{\circ }

If the equatorial coordinates are referred to another equinox, they must be precessed to their place at J2000.0 before applying these formulae.

These equations convert to equatorial coordinates referred to B2000.0.

{\begin{aligned}\sin \left(\alpha -\alpha _{\text{G}}\right)\cos \left(\delta \right)&=\cos \left(b\right)\sin \left(l_{\text{NCP}}-l\right)\\\cos \left(\alpha -\alpha _{\text{G}}\right)\cos \left(\delta \right)&=\sin \left(b\right)\cos \left(\delta _{\text{G}}\right)-\cos \left(b\right)\sin \left(\delta _{\text{G}}\right)\cos \left(l_{\text{NCP}}-l\right)\\\sin \left(\delta \right)&=\sin \left(b\right)\sin \left(\delta _{\text{G}}\right)+\cos \left(b\right)\cos \left(\delta _{\text{G}}\right)\cos \left(l_{\text{NCP}}-l\right)\end{aligned}}

Notes on conversion

Angles in the degrees ( ° ), minutes ( ′ ), and seconds ( ″ ) of sexagesimal measure must be converted to decimal before calculations are performed. Whether they are converted to decimal degrees or radians depends upon the particular calculating machine or program. Negative angles must be carefully handled; −10° 20′ 30″ must be converted as −10° −20′ −30″.
Angles in the hours ( ^h ), minutes ( ^m ), and seconds ( ^s ) of time measure must be converted to decimal degrees or radians before calculations are performed. 1^h = 15°; 1^m = 15′; 1^s = 15″
Angles greater than 360° (2 $π$ ) or less than 0° may need to be reduced to the range 0°–360° (0–2 $π$ ) depending upon the particular calculating machine or program.
The cosine of a latitude (declination, ecliptic and Galactic latitude, and altitude) are never negative by definition, since the latitude varies between −90° and +90°.
Inverse trigonometric functions arcsine, arccosine and arctangent are quadrant-ambiguous, and results should be carefully evaluated. Use of the second arctangent function (denoted in computing as atn2(y,x) or atan2(y,x), which calculates the arctangent of $⁠ y / x ⁠$ using the sign of both arguments to determine the right quadrant) is recommended when calculating longitude/right ascension/azimuth. An equation which finds the sine, followed by the arcsin function, is recommended when calculating latitude/declination/altitude.
Azimuth ( $A$ ) is referred here to the south point of the horizon, the common astronomical reckoning. An object on the meridian to the south of the observer has $A$ = $h$ = 0° with this usage. However, n Astropy's AltAz, in the Large Binocular Telescope FITS file convention, in XEphem, in the IAU library Standards of Fundamental Astronomy and Section B of the Astronomical Almanac for example, the azimuth is East of North. In navigation and some other disciplines, azimuth is figured from the north.
The equations for altitude ( $a$ ) do not account for atmospheric refraction.
The equations for horizontal coordinates do not account for diurnal parallax, that is, the small offset in the position of a celestial object caused by the position of the observer on the Earth's surface. This effect is significant for the Moon, less so for the planets, minute for stars or more distant objects.
Observer's longitude ( $λ o$ ) here is measured positively eastward from the prime meridian, accordingly to current IAU standards.

Notes

^ Depending on the azimuth convention in use, the signs of $cos A$ and $sin A$ appear in all four different combinations. Karttunen et al.,^[9] Taff,^[10] and Roth^[11] define $A$ clockwise from the south. Lang^[12] defines it north through east, Smart^[13] north through west. Meeus (1991),^[4] p. 89: $sin δ = sin φ sin a - cos φ cos a cos A$ ; Explanatory Supplement (1961),^[5] p. 26: $sin δ = sin a sin φ + cos a cos A cos φ$ .

References

^ Kanas, Nick (2021). "Star and Solar System Maps: A History of Celestial Cartography". Research Notes of the AAS. 5 (4). American Astronomical Society: 69. Bibcode:2021RNAAS...5...69K. doi:10.3847/2515-5172/abf35c. S2CID 233522547.
^ Majewski, Steve. "Coordinate Systems". UVa Department of Astronomy. Archived from the original on 12 March 2016. Retrieved 19 March 2011.
^ Aaboe, Asger. 2001 Episodes from the Early History of Astronomy. New York: Springer-Verlag., pp. 17–19.
^ ^a ^b Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. ISBN 0-943396-35-2., chap. 12
^ ^a ^b U.S. Naval Observatory, Nautical Almanac Office; H.M. Nautical Almanac Office (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London., sec. 2A
^ U.S. Naval Observatory, Nautical Almanac Office (1992). P. Kenneth Seidelmann (ed.). Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. ISBN 0-935702-68-7., section 11.43
^ Montenbruck, Oliver; Pfleger, Thomas (2000). Astronomy on the Personal Computer. Springer-Verlag Berlin Heidelberg. ISBN 978-3-540-67221-0., pp 35-37
^ U.S. Naval Observatory, Nautical Almanac Office; U.K. Hydrographic Office, H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. p. M18. ISBN 978-0160820083.
^ Karttunen, H.; Kröger, P.; Oja, H.; Poutanen, M.; Donner, H. J. (2006). Fundamental Astronomy (5 ed.). Springer. Bibcode:2003fuas.book.....K. ISBN 978-3-540-34143-7.
^ Taff, L. G. (1981). Computational spherical astronomy. Wiley. Bibcode:1981csa..book.....T. ISBN 0-471-06257-X.
^ Roth, G. D. (23 October 1989). Handbuch für Sternenfreunde. Springer. ISBN 3-540-19436-3.
^ Lang, Kenneth R. (1978). Astrophysical Formulae. Springer. Bibcode:1978afcp.book.....L. ISBN 3-540-09064-9.
^ Smart, William Marshall (1949). Text-book on spherical astronomy. Cambridge University Press. Bibcode:1965tbsa.book.....S.
^ Poleski, Radosław (2013). "Transformation of the equatorial proper motion to the Galactic system". arXiv:1306.2945 [astro-ph.IM].

External links

NOVAS, the United States Naval Observatory's Vector Astrometry Software, an integrated package of subroutines and functions for computing various commonly needed quantities in positional astronomy.
SuperNOVAS a maintained fork of NOVAS C 3.1 with bug fixes, improvements, new features, and online documentation.
SOFA, the IAU's Standards of Fundamental Astronomy, an accessible and authoritative set of algorithms and procedures that implement standard models used in fundamental astronomy.
This article was originally based on Jason Harris' Astroinfo, which is accompanied by KStars, a KDE Desktop Planetarium for Linux/KDE.

[14] Depending on the azimuth convention in use, the signs of $cos A$ and $sin A$ appear in all four different combinations. Karttunen et al.,^[9] Taff,^[10] and Roth^[11] define $A$ clockwise from the south. Lang^[12] defines it north through east, Smart^[13] north through west. Meeus (1991),^[4] p. 89: $sin δ = sin φ sin a - cos φ cos a cos A$ ; Explanatory Supplement (1961),^[5] p. 26: $sin δ = sin a sin φ + cos a cos A cos φ$ .

[1] Kanas, Nick (2021). "Star and Solar System Maps: A History of Celestial Cartography". Research Notes of the AAS. 5 (4). American Astronomical Society: 69. Bibcode:2021RNAAS...5...69K. doi:10.3847/2515-5172/abf35c. S2CID 233522547.

[2] Majewski, Steve. "Coordinate Systems". UVa Department of Astronomy. Archived from the original on 12 March 2016. Retrieved 19 March 2011.

[3] Aaboe, Asger. 2001 Episodes from the Early History of Astronomy. New York: Springer-Verlag., pp. 17–19.

[Meeus-4] Meeus, Jean (1991). Astronomical Algorithms. Willmann-Bell, Inc., Richmond, VA. ISBN 0-943396-35-2., chap. 12

[ExplSupp-5] U.S. Naval Observatory, Nautical Almanac Office; H.M. Nautical Almanac Office (1961). Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac. H.M. Stationery Office, London., sec. 2A

[6] U.S. Naval Observatory, Nautical Almanac Office (1992). P. Kenneth Seidelmann (ed.). Explanatory Supplement to the Astronomical Almanac. University Science Books, Mill Valley, CA. ISBN 0-935702-68-7., section 11.43

[7] Montenbruck, Oliver; Pfleger, Thomas (2000). Astronomy on the Personal Computer. Springer-Verlag Berlin Heidelberg. ISBN 978-3-540-67221-0., pp 35-37

[8] U.S. Naval Observatory, Nautical Almanac Office; U.K. Hydrographic Office, H.M. Nautical Almanac Office (2008). The Astronomical Almanac for the Year 2010. U.S. Govt. Printing Office. p. M18. ISBN 978-0160820083.

[Karttunen-9] Karttunen, H.; Kröger, P.; Oja, H.; Poutanen, M.; Donner, H. J. (2006). Fundamental Astronomy (5 ed.). Springer. Bibcode:2003fuas.book.....K. ISBN 978-3-540-34143-7.

[Taff-10] Taff, L. G. (1981). Computational spherical astronomy. Wiley. Bibcode:1981csa..book.....T. ISBN 0-471-06257-X.

[Roth-11] Roth, G. D. (23 October 1989). Handbuch für Sternenfreunde. Springer. ISBN 3-540-19436-3.

[Lang-12] Lang, Kenneth R. (1978). Astrophysical Formulae. Springer. Bibcode:1978afcp.book.....L. ISBN 3-540-09064-9.

[Smart-13] Smart, William Marshall (1949). Text-book on spherical astronomy. Cambridge University Press. Bibcode:1965tbsa.book.....S.

[15] Poleski, Radosław (2013). "Transformation of the equatorial proper motion to the Galactic system". arXiv:1306.2945 [astro-ph.IM].

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[a]

[14]

[9]

[10]

[11]

[12]

[13]

History

Media collections

Astronomical coordinate systems

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Astronomical coordinate systems

Coordinate systems

Horizontal system

Equatorial system

Ecliptic system

Galactic system

Supergalactic system

Converting coordinates

Notation

Hour angle ↔ right ascension

Equatorial ↔ ecliptic

Equatorial ↔ horizontal

Equatorial ↔ galactic

Notes on conversion

See also

Notes

References

External links

Astronomical coordinate systems

Fundamentals of Astronomical Coordinates

Definition and Historical Context

Spherical Coordinate Basics

Celestial Sphere Coordinate Systems

Horizontal Coordinate System

Equatorial Coordinate System

Ecliptic Coordinate System

Extragalactic Coordinate Systems

Galactic Coordinate System

Supergalactic Coordinate System

Transformations and Conversions

Notation and General Principles

Add your contribution

Related Hubs

Contribute something