Hubbry Logo
ColorimetryColorimetryMain
Open search
Colorimetry
Community hub
Colorimetry
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Colorimetry
Colorimetry
Colorimetry
View on Wikipedia
from Wikipedia

Colorimetry is "the science and technology used to quantify and describe physically the human color perception".[1] It is similar to spectrophotometry, but is distinguished by its interest in reducing spectra to the physical correlates of color perception, most often the CIE 1931 XYZ color space tristimulus values and related quantities.[2]

History

[edit]

The Duboscq colorimeter was invented by Jules Duboscq in 1870. [3]

Instruments

[edit]

Colorimetric equipment is similar to that used in spectrophotometry. Some related equipment is also mentioned for completeness.

Two spectral reflectance curves. The object in question reflects light with shorter wavelengths while absorbing those in others, lending it a blue appearance.

Tristimulus colorimeter

[edit]
Main article: Tristimulus colorimeter

In digital imaging, colorimeters are tristimulus devices used for color calibration. Accurate color profiles ensure consistency throughout the imaging workflow, from acquisition to output.

Spectroradiometer, spectrophotometer, spectrocolorimeter

[edit]

The absolute spectral power distribution of a light source can be measured with a spectroradiometer, which works by optically collecting the light, then passing it through a monochromator before reading it in narrow bands of wavelength.

Reflected color can be measured using a spectrophotometer (also called spectroreflectometer or reflectometer), which takes measurements in the visible region (and a little beyond) of a given color sample. If the custom of taking readings at 10 nanometer increments is followed, the visible light range of 400–700 nm will yield 31 readings. These readings are typically used to draw the sample's spectral reflectance curve (how much it reflects, as a function of wavelength)—the most accurate data that can be provided regarding its characteristics.

CRT phosphors

The readings by themselves are typically not as useful as their tristimulus values, which can be converted into chromaticity co-ordinates and manipulated through color space transformations. For this purpose, a spectrocolorimeter may be used. A spectrocolorimeter is simply a spectrophotometer that can estimate tristimulus values by numerical integration (of the color matching functions' inner product with the illuminant's spectral power distribution).[6] One benefit of spectrocolorimeters over tristimulus colorimeters is that they do not have optical filters, which are subject to manufacturing variance, and have a fixed spectral transmittance curve—until they age.[7] On the other hand, tristimulus colorimeters are purpose-built, cheaper, and easier to use.[8]

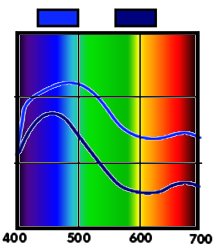
The CIE (International Commission on Illumination) recommends using measurement intervals under 5 nm, even for smooth spectra.[5] Sparser measurements fail to accurately characterize spiky emission spectra, such as that of the red phosphor of a CRT display, depicted aside.

Color temperature meter

[edit]

Photographers and cinematographers use information provided by these meters to decide what color balancing should be done to make different light sources appear to have the same color temperature. If the user enters the reference color temperature, the meter can calculate the mired difference between the measurement and the reference, enabling the user to choose a corrective color gel or photographic filter with the closest mired factor.[9]

The normals are lines of equal correlated color temperature.

Internally the meter is typically a silicon photodiode tristimulus colorimeter.[9] The correlated color temperature can be calculated from the tristimulus values by first calculating the chromaticity co-ordinates in the CIE 1960 color space, then finding the closest point on the Planckian locus.

See also

[edit]

References

[edit]

Further reading

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Colorimetry

View on Grokipedia
from Grokipedia
Colorimetry is the science and technology of measuring and specifying colors in a quantitative manner that aligns with human visual perception, replacing subjective judgments with objective numerical representations based on the properties of and the responses of the eye's photoreceptors. This field enables the prediction of when two stimuli will appear the same color to an average observer, forming the foundation for standardized color communication across industries and sciences. At its core, colorimetry relies on the principle of , the idea that human color vision can be modeled using three primary stimuli corresponding to the sensitivities of long-, medium-, and short-wavelength cones in the . Key tools include color-matching functions (CMFs), which describe the amounts of three reference primaries needed to match any spectral light, and tristimulus values (such as X, Y, Z in the CIE system), which quantify a color's position in a . These are governed by Grassmann's laws of additivity, proportionality, transitivity, and symmetry, ensuring consistent color mixing and transformation between different color spaces like CIE XYZ, CIELAB, and . Standard illuminants, such as CIE A for incandescent light or D65 for daylight, provide reference viewing conditions, while uniform color spaces facilitate the calculation of perceptual color differences using formulas like CIEDE2000. The development of colorimetry traces back to 19th-century experiments by James Clerk Maxwell on color mixture, evolving into formalized standards through the efforts of the Commission Internationale de l'Éclairage (CIE), which in 1931 adopted the CIE 1931 XYZ color space based on experimental data from Wright and Guild. Subsequent refinements, including the 1964 supplementary standard observer for larger visual fields and modifications proposed by Judd in 1951 and further refined as Judd-Vos in 1978, addressed limitations in early models, with the CIE's 2018 publication (4th edition) providing a comprehensive update incorporating modern psychophysical data. These standards have become the international benchmark for color measurement. Colorimetry finds essential applications in diverse domains, including digital imaging and display technology for accurate color reproduction on monitors and printers, industrial quality control in textiles, paints, and plastics to minimize metamerism (color shifts under different lights), and analytical chemistry for quantifying substance concentrations via colorimetric reactions in solutions like blood or water samples. In lighting design, it assesses color rendering indices to evaluate how well artificial lights mimic natural illumination, while in food science, it ensures product consistency and freshness through non-destructive color analysis. Overall, these applications underscore colorimetry's role in bridging human perception with precise scientific and technological processes.

Fundamentals of Color

Human Color Vision

Human color vision begins in the , a light-sensitive layer lining the back of the eye that converts incoming photons into neural signals. Light enters the eye through the and lens, which focus it onto the retina's photoreceptor cells: and cones. , numbering about 120 million, are highly sensitive to low light levels and mediate scotopic ( but do not contribute to color . Cones, approximately 6 million in number and concentrated in the central fovea for sharp daytime vision, are responsible for photopic (daylight) color vision and operate best under brighter conditions. There are three distinct types of cones, each containing a tuned to a primary range: L-cones (long-wavelength sensitive, peaking at approximately 564 nm in the red-yellow region), M-cones (medium-wavelength sensitive, peaking at approximately 534 nm in the green region), and S-cones (short-wavelength sensitive, peaking at approximately 420 nm in the blue-violet region). These cones are unevenly distributed, with S-cones comprising only about 5-10% of the total and absent from the fovea center, while L- and M-cones dominate there in a roughly 2:1 . The overlapping sensitivity curves of these cones allow the visual system to distinguish a wide of colors from the spanning roughly 380-780 nm. The trichromatic theory, first proposed by Thomas Young in 1801 and refined by in the 1850s, explains color perception as the result of differential activation of these three cone types. According to the Young-Helmholtz model, any color sensation arises from the combined responses of L-, M-, and S-cones to incoming light wavelengths, with the brain interpreting the relative stimulation levels to produce perceived hue, saturation, and . This theory accounts for the ability to match most colors using just three primary lights (, , ) and laid the groundwork for understanding how the eye samples the . Building on , the , introduced by Ewald Hering in , describes post-receptor processing in the visual pathway. Neural signals from cones are combined into three opponent channels: an achromatic channel contrasting black and white for luminance; a red-green chromatic channel opposing L-cone (plus some M-cone) excitation against M-cone (plus some L-cone) excitation; and a blue-yellow channel pitting S-cone excitation against combined L- and M-cone responses. This organization explains perceptual phenomena like negative afterimages, where staring at a field produces a aftereffect, and the absence of complementary hues such as reddish-green. The channels likely emerge in retinal ganglion cells and are further refined in the and . Human color vision has notable limitations, including color vision deficiencies affecting about 8% of males and 0.5% of females due to genetic variations on the . Protanopia results from absent or defective L-cones, leading to confusion between s and s with a shifted red appearance toward green; deuteranopia stems from missing M-cones, causing similar red-green impairments but with less red desaturation; and tritanopia, rarer and autosomal, arises from S-cone absence, impairing blue-yellow discrimination and often reducing overall brightness. These conditions highlight the reliance on all three types for full chromatic sensitivity. Another key limitation is metamerism, the perceptual equivalence of spectrally distinct lights or surfaces that stimulate the L-, M-, and S-cones in the same proportions. For instance, a light from one source may match a different composition under daylight but diverge under incandescent illumination, underscoring how the trichromatic system compresses infinite variations into a finite perceptual space. This phenomenon arises because the eye's three-channel encoding cannot uniquely invert power distributions. The empirical foundation for understanding color as a decomposition of white light dates to Isaac Newton's prism experiments in the 1660s. By passing sunlight through a prism, Newton observed the dispersion of white light into a continuous of colors—red, orange, yellow, green, blue, indigo, and violet—demonstrating that white is a composite rather than a fundamental hue. He further recombined these colors with a second prism to restore white light, confirming the spectral additivity and refuting earlier views of prisms merely tinting light. These findings, detailed in his 1704 , established the spectral basis for visible colors perceived by the . This physiological framework of cone responses and neural opponency directly informs tristimulus colorimetry, which approximates through three weighted integrals of data.

Spectral Properties of Light

Light, as , spans a broad of wavelengths, but the visible portion relevant to colorimetry lies approximately between 380 nm and 780 nm. Within this range, light is perceived as a continuum of colors, transitioning from violet at shorter wavelengths (around 380–450 nm) through , , orange, to at longer wavelengths (around 620–780 nm). These divisions arise from the physical properties of light waves, where determines the dominant hue observed by the under standard conditions. The key properties of light include its wavelength λ\lambda, frequency ν\nu, and associated energy. Wavelength and frequency are inversely related by the speed of light in vacuum, c=λνc = \lambda \nu, where c≈3×108c \approx 3 \times 10^8 m/s. The energy EE of a photon is given by Planck's relation E=hνE = h\nu, where hh is Planck's constant (6.62607015×10−346.62607015 \times 10^{-34} J s). Consequently, shorter wavelengths (e.g., blue light at ~450 nm) correspond to higher frequencies and thus higher photon energies compared to longer wavelengths (e.g., red light at ~650 nm), influencing photochemical and thermal effects in colorimetric applications. Blackbody radiation provides a fundamental model for thermal light emission in colorimetry, described by , which quantifies the B(λ,T)B(\lambda, T) of an ideal at temperature TT as a function of λ\lambda. This law, derived from quantum principles, predicts the distribution of radiated energy across wavelengths, peaking at a specific λmax⁡\lambda_{\max} that shifts with temperature according to : λmax⁡T=b\lambda_{\max} T = b, where b≈2.897×10−3b \approx 2.897 \times 10^{-3} m·K is Wien's displacement constant. For instance, at 3000 K (typical of incandescent sources), the peak falls in the (~966 nm), while at 6500 K (daylight-like), it aligns near the green-yellow visible region (~447 nm), establishing the scale used in illuminant definitions. In colorimetry, mixing occurs through the superposition of spectra, where combining monochromatic or sources (e.g., , , and lights) results in a resultant that determines the perceived color, as the total radiance is the sum of individual power distributions. This contrasts with subtractive mixing in pigments or dyes, which selectively absorbs portions of the incident , reducing overall and altering the transmitted or reflected . Additive principles underpin display technologies and colorimetric standards by enabling precise combinations for color reproduction. Standardized illuminants, such as CIE D65 representing average daylight, are defined by specific spectral power distributions (SPDs) across the visible range to ensure consistent colorimetric evaluations under controlled conditions. The D65 SPD, normalized at 560 nm, approximates a of 6500 K with relatively uniform energy from 400–700 nm, peaking slightly in the region to mimic outdoor . These SPDs form the basis for transforming object into tristimulus values in subsequent colorimetric computations.

Colorimetric Theory

Tristimulus Values

Tristimulus values, denoted as XX, YY, and ZZ, form the foundational representation in colorimetry for quantifying the color of a stimulus based on human vision. These values are computed from the (SPD) of the stimulus, such as the R(λ)R(\lambda) of an object or the of a filter, convolved with the spectral power distribution S(λ)S(\lambda) of the illuminant and the CIE 1931 color-matching functions xˉ(λ)\bar{x}(\lambda), yˉ(λ)\bar{y}(\lambda), and zˉ(λ)\bar{z}(\lambda). The mathematical expressions are given by: X=k∫380780R(λ)xˉ(λ)S(λ) dλX = k \int_{380}^{780} R(\lambda) \bar{x}(\lambda) S(\lambda) \, d\lambda Y=k∫380780R(λ)yˉ(λ)S(λ) dλY = k \int_{380}^{780} R(\lambda) \bar{y}(\lambda) S(\lambda) \, d\lambda Z=k∫380780R(λ)zˉ(λ)S(λ) dλZ = k \int_{380}^{780} R(\lambda) \bar{z}(\lambda) S(\lambda) \, d\lambda where the integrals span the visible spectrum (typically 380–780 nm), and kk is a normalizing constant often set to ensure Y=100Y = 100 for a perfect white reflector under the reference illuminant. The color-matching functions xˉ(λ)\bar{x}(\lambda), yˉ(λ)\bar{y}(\lambda), and zˉ(λ)\bar{z}(\lambda) were derived from experimental data collected in the late 1920s through color-matching experiments conducted independently by W. David Wright and John Guild. Wright's work involved ten observers matching spectral colors using primary lights at 700 nm (red), 546.1 nm (green), and 435.8 nm (blue), yielding trichromatic coefficients that were later transformed into the CIE framework. Guild's parallel study at the National Physical Laboratory used seven observers to determine the colorimetric purity and dominant wavelengths across the spectrum, providing complementary data that informed the standardization. These experiments revealed that all visible colors could be matched by linear combinations of three primaries, with negative values for some spectral matches indicating the need for an imaginary primary in the CIE system. The CIE 1931 standard observer functions were established by combining and mathematically transforming the Wright-Guild data at the 1931 CIE meeting, ensuring yˉ(λ)\bar{y}(\lambda) aligns with the luminosity function V(λ)V(\lambda) for photopic vision. Normalization of the tristimulus values emphasizes perceptual relevance: YY is scaled to represent luminance, directly incorporating the CIE 1924 V(λ)V(\lambda) function, which approximates the eye's sensitivity to brightness, with a maximum of 1 at 555 nm. The chromaticity coordinates, which separate color from intensity, are then derived as x=X/(X+Y+Z)x = X / (X + Y + Z), y=Y/(X+Y+Z)y = Y / (X + Y + Z), and z=1−x−yz = 1 - x - y, projecting the three-dimensional XYZ space onto a two-dimensional plane for hue and saturation analysis while preserving the sum x+y+z=1x + y + z = 1. This normalization ensures that equal-energy white has coordinates (1/3, 1/3), facilitating comparisons independent of overall brightness. A key implication of the tristimulus framework is metamerism, where distinct spectral distributions produce identical XYZXYZ values under a specific illuminant and observer, leading to visually matching colors that may differ under other conditions. For instance, two objects with different spectra can appear the same under Illuminant D65 but diverge under light due to variations in how their spectra interact with the color-matching functions. This phenomenon underscores the limitations of three-dimensional color representation, as it arises from the trichromatic nature of human vision, inspired by the three types of cells in the . The tristimulus model also embodies the linearity of color addition, as articulated in Grassmann's laws from , which state that the tristimulus values of mixed lights are the linear sum of the individual values, enabling additive mixing without interaction terms. This property allows the prediction of resulting colors from combinations of stimuli, such as in display calibration or pigment blending, provided the mixtures remain within the linear response range of the .

CIE Color Systems

The CIE 1931 XYZ color space establishes the reference framework for modern colorimetry, providing a standardized, device-independent method to quantify colors based on human visual response. Defined by the (CIE), it employs tristimulus values XX, YY, and ZZ, where YY represents and the space is designed to encompass all perceivable colors without negative values. A key visualization is the CIE 1931 diagram, which projects these values onto a two-dimensional plane using normalized coordinates x=XX+Y+Zx = \frac{X}{X+Y+Z} and y=YX+Y+Zy = \frac{Y}{X+Y+Z}. This diagram forms a characteristic horseshoe shape, with the curved spectral locus tracing pure monochromatic wavelengths from approximately 380 nm to 780 nm, and a straight line () connecting the and violet endpoints to bound the of visible colors. The CIE 15:2018 Colorimetry 4th edition updates the foundational elements, introducing cone-fundamental-based color matching functions, the CIE 2012 spectral luminous efficiency functions for 2° and 10° fields, and the CIE 2015 10° color matching functions, alongside physiologically relevant color spaces, while retaining the 1931 XYZ as the core reference. Building upon the XYZ foundation, the CIE 1976 Luv* (CIELUV) color space was developed to achieve approximate perceptual uniformity, particularly suited for applications involving additive color mixing, such as lighting and displays, under specified illuminants like CIE standard illuminant D65. It transforms XYZ tristimulus values into cylindrical coordinates: L* for lightness (ranging from 0 to 100), and u* and v* for chromaticity in opponent-color dimensions, derived from uniform chromaticity scales u' and v' to better approximate equal visual spacing. The color difference metric in this space is given by ΔEuv∗=(ΔL∗)2+(Δu∗)2+(Δv∗)2,\Delta E_{uv}^* = \sqrt{(\Delta L^*)^2 + (\Delta u^*)^2 + (\Delta v^*)^2},
Add your contribution
Related Hubs
User Avatar
No comments yet.