Hubbry Logo
Spectrum (physical sciences)Spectrum (physical sciences)Main
Open search
Spectrum (physical sciences)
Community hub
Spectrum (physical sciences)
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Spectrum (physical sciences)
Spectrum (physical sciences)
Spectrum (physical sciences)
View on Wikipedia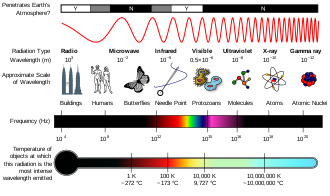
from Wikipedia
Diagram illustrating the electromagnetic spectrum

In the physical sciences, the term spectrum was introduced first into optics by Isaac Newton in the 17th century, referring to the range of colors observed when white light was dispersed through a prism.[1][2] Soon the term referred to a plot of light intensity or power as a function of frequency or wavelength, also known as a spectral density plot.

Later it expanded to apply to other waves, such as sound waves and sea waves that could also be measured as a function of frequency (e.g., noise spectrum, sea wave spectrum). It has also been expanded to more abstract "signals", whose power spectrum can be analyzed and processed. The term now applies to any signal that can be measured or decomposed along a continuous variable, such as energy in electron spectroscopy or mass-to-charge ratio in mass spectrometry. Spectrum is also used to refer to a graphical representation of the signal as a function of the dependent variable.

Etymology

[edit]
This section is an excerpt from Spectrum § Etymology.[edit]

In Latin, spectrum means "image" or "apparition", including the meaning "spectre". Spectral evidence is testimony about what was done by spectres of persons not present physically, or hearsay evidence about what ghosts or apparitions of Satan said. It was used to convict a number of persons of witchcraft at Salem, Massachusetts in the late 17th century. The word "spectrum" [Spektrum] was strictly used to designate a ghostly optical afterimage by Goethe in his Theory of Colors and Schopenhauer in On Vision and Colors.

The prefix "spectro-" is used to form words relating to spectra. For example, a spectrometer is a device used to record spectra and spectroscopy is the use of a spectrometer for chemical analysis.

Electromagnetic spectrum

[edit]
Main article: Electromagnetic spectrum
Electromagnetic emission spectrum of a fluorescent lamp

Electromagnetic spectrum refers to the full range of all frequencies of electromagnetic radiation[3] and also to the characteristic distribution of electromagnetic radiation emitted or absorbed by that particular object. Devices used to measure an electromagnetic spectrum are called spectrograph or spectrometer. The visible spectrum is the part of the electromagnetic spectrum that can be seen by the human eye. The wavelength of visible light ranges from 390 to 700 nm.[4] The absorption spectrum of a chemical element or chemical compound is the spectrum of frequencies or wavelengths of incident radiation that are absorbed by the compound due to electron transitions from a lower to a higher energy state. The emission spectrum refers to the spectrum of radiation emitted by the compound due to electron transitions from a higher to a lower energy state.

Light from many different sources contains various colors, each with its own brightness or intensity. A rainbow, or prism, sends these component colors in different directions, making them individually visible at different angles. A graph of the intensity plotted against the frequency (showing the brightness of each color) is the frequency spectrum of the light. When all the visible frequencies are present equally, the perceived color of the light is white, and the spectrum is a flat line. Therefore, flat-line spectra in general are often referred to as white, whether they represent light or another type of wave phenomenon (sound, for example, or vibration in a structure).

In radio and telecommunications, the frequency spectrum can be shared among many different broadcasters. The radio spectrum is the part of the electromagnetic spectrum corresponding to frequencies lower below 300 GHz, which corresponds to wavelengths longer than about 1 mm. The microwave spectrum corresponds to frequencies between 300 MHz (0.3 GHz) and 300 GHz and wavelengths between one meter and one millimeter.[5][6] Each broadcast radio and TV station transmits a wave on an assigned frequency range, called a channel. When many broadcasters are present, the radio spectrum consists of the sum of all the individual channels, each carrying separate information, spread across a wide frequency spectrum. Any particular radio receiver will detect a single function of amplitude (voltage) vs. time. The radio then uses a tuned circuit or tuner to select a single channel or frequency band and demodulate or decode the information from that broadcaster. If we made a graph of the strength of each channel vs. the frequency of the tuner, it would be the frequency spectrum of the antenna signal.

In astronomical spectroscopy, the strength, shape, and position of absorption and emission lines, as well as the overall spectral energy distribution of the continuum, reveal many properties of astronomical objects. Stellar classification is the categorisation of stars based on their characteristic electromagnetic spectra. The spectral flux density is used to represent the spectrum of a light-source, such as a star.

In radiometry and colorimetry (or color science more generally), the spectral power distribution (SPD) of a light source is a measure of the power contributed by each frequency or color in a light source. The light spectrum is usually measured at points (often 31) along the visible spectrum, in wavelength space instead of frequency space, which makes it not strictly a spectral density. Some spectrophotometers can measure increments as fine as one to two nanometers and even higher resolution devices with resolutions less than 0.5 nm have been reported.[7] the values are used to calculate other specifications and then plotted to show the spectral attributes of the source. This can be helpful in analyzing the color characteristics of a particular source.

Mass spectrum

[edit]
Main article: Mass spectrum
Mass spectrum of Titan's ionosphere

A plot of ion abundance as a function of mass-to-charge ratio is called a mass spectrum. It can be produced by a mass spectrometer instrument.[8] The mass spectrum can be used to determine the quantity and mass of atoms and molecules. Tandem mass spectrometry is used to determine molecular structure.

Energy spectrum

[edit]
"Energy spectrum" redirects here; not to be confused with Energy spectral density.

In physics, the energy spectrum of a particle is the number of particles or intensity of a particle beam as a function of particle energy. Examples of techniques that produce an energy spectrum are alpha-particle spectroscopy, electron energy loss spectroscopy, and mass-analyzed ion-kinetic-energy spectrometry.

Displacement

[edit]

Oscillatory displacements, including vibrations, can also be characterized spectrally.

Acoustical measurement

[edit]
Main articles: Spectrogram and Spectrum analyzer

In acoustics, a spectrogram is a visual representation of the frequency spectrum of sound as a function of time or another variable.

A source of sound can have many different frequencies mixed. A musical tone's timbre is characterized by its harmonic spectrum. Sound in our environment that we refer to as noise includes many different frequencies. When a sound signal contains a mixture of all audible frequencies, distributed equally over the audio spectrum, it is called white noise.[12]

The spectrum analyzer is an instrument which can be used to convert the sound wave of the musical note into a visual display of the constituent frequencies. This visual display is referred to as an acoustic spectrogram. Software based audio spectrum analyzers are available at low cost, providing easy access not only to industry professionals, but also to academics, students and the hobbyist. The acoustic spectrogram generated by the spectrum analyzer provides an acoustic signature of the musical note. In addition to revealing the fundamental frequency and its overtones, the spectrogram is also useful for analysis of the temporal attack, decay, sustain, and release of the musical note.

  • Approximate frequency ranges corresponding to ultrasound, with rough guide of some applications
    Approximate frequency ranges corresponding to ultrasound, with rough guide of some applications
  • Acoustic spectrogram of the words "Oh, no!" said by a young girl, showing how the discrete spectrum of the sound (bright orange lines) changes with time (the horizontal axis)
    Acoustic spectrogram of the words "Oh, no!" said by a young girl, showing how the discrete spectrum of the sound (bright orange lines) changes with time (the horizontal axis)
  • Spectrogram of dolphin vocalizations
    Spectrogram of dolphin vocalizations

Continuous versus discrete spectra

[edit]
Continuous spectrum of an incandescent lamp (mid) and discrete spectrum lines of a fluorescent lamp (bottom)

In the physical sciences, the spectrum of a physical quantity (such as energy) may be called continuous if it is non-zero over the whole spectrum domain (such as frequency or wavelength) or discrete if it attains non-zero values only in a discrete set over the independent variable, with band gaps between pairs of spectral bands or spectral lines.[13]

The classical example of a continuous spectrum, from which the name is derived, is the part of the spectrum of the light emitted by excited atoms of hydrogen that is due to free electrons becoming bound to a hydrogen ion and emitting photons, which are smoothly spread over a wide range of wavelengths, in contrast to the discrete lines due to electrons falling from some bound quantum state to a state of lower energy. As in that classical example, the term is most often used when the range of values of a physical quantity may have both a continuous and a discrete part, whether at the same time or in different situations. In quantum systems, continuous spectra (as in bremsstrahlung and thermal radiation) are usually associated with free particles, such as atoms in a gas, electrons in an electron beam, or conduction band electrons in a metal. In particular, the position and momentum of a free particle has a continuous spectrum, but when the particle is confined to a limited space its spectrum becomes discrete.

Often a continuous spectrum may be just a convenient model for a discrete spectrum whose values are too close to be distinguished, as in the phonons in a crystal.

The continuous and discrete spectra of physical systems can be modeled in functional analysis as different parts in the decomposition of the spectrum of a linear operator acting on a function space, such as the Hamiltonian operator.

The classical example of a discrete spectrum (for which the term was first used) is the characteristic set of discrete spectral lines seen in the emission spectrum and absorption spectrum of isolated atoms of a chemical element, which only absorb and emit light at particular wavelengths. The technique of spectroscopy is based on this phenomenon.

Discrete spectra are seen in many other phenomena, such as vibrating strings, microwaves in a metal cavity, sound waves in a pulsating star, and resonances in high-energy particle physics. The general phenomenon of discrete spectra in physical systems can be mathematically modeled with tools of functional analysis, specifically by the decomposition of the spectrum of a linear operator acting on a functional space.

In classical mechanics

[edit]

In classical mechanics, discrete spectra are often associated to waves and oscillations in a bounded object or domain. Mathematically they can be identified with the eigenvalues of differential operators that describe the evolution of some continuous variable (such as strain or pressure) as a function of time and/or space.

Discrete spectra are also produced by some non-linear oscillators where the relevant quantity has a non-sinusoidal waveform. Notable examples are the sound produced by the vocal cords of mammals.[14][15]: p.684  and the stridulation organs of crickets,[16] whose spectrum shows a series of strong lines at frequencies that are integer multiples (harmonics) of the oscillation frequency.

A related phenomenon is the appearance of strong harmonics when a sinusoidal signal (which has the ultimate "discrete spectrum", consisting of a single spectral line) is modified by a non-linear filter; for example, when a pure tone is played through an overloaded amplifier,[17] or when an intense monochromatic laser beam goes through a non-linear medium.[18] In the latter case, if two arbitrary sinusoidal signals with frequencies f and g are processed together, the output signal will generally have spectral lines at frequencies |mf + ng|, where m and n are any integers.

In quantum mechanics

[edit]
Main article: Decomposition of spectrum (functional analysis) § Quantum physics

In quantum mechanics, the discrete spectrum of an observable refers to the pure point spectrum of eigenvalues of the operator used to model that observable.[19][20]

Discrete spectra are usually associated with systems that are bound in some sense (mathematically, confined to a compact space).[citation needed] The position and momentum operators have continuous spectra in an infinite domain, but a discrete (quantized) spectrum in a compact domain and the same properties of spectra hold for angular momentum, Hamiltonians and other operators of quantum systems.

The quantum harmonic oscillator and the hydrogen atom are examples of physical systems in which the Hamiltonian has a discrete spectrum. In the case of the hydrogen atom the spectrum has both a continuous and a discrete part, the continuous part representing the ionization.

  • The discrete part of the emission spectrum of hydrogen
    The discrete part of the emission spectrum of hydrogen
  • Spectrum of sunlight above the atmosphere (yellow) and at sea level (red), revealing an absorption spectrum with a discrete part (such as the line due to O 2) and a continuous part (such as the bands labeled H 2O)
    Spectrum of sunlight above the atmosphere (yellow) and at sea level (red), revealing an absorption spectrum with a discrete part (such as the line due to O
    2    ) and a continuous part (such as the bands labeled H
    2    O    )
  • Spectrum of light emitted by a deuterium lamp, showing a discrete part (tall sharp peaks) and a continuous part (smoothly varying between the peaks). The smaller peaks and valleys may be due to measurement errors rather than discrete spectral lines.
    Spectrum of light emitted by a deuterium lamp, showing a discrete part (tall sharp peaks) and a continuous part (smoothly varying between the peaks). The smaller peaks and valleys may be due to measurement errors rather than discrete spectral lines.

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Spectrum (physical sciences)

View on Grokipedia
from Grokipedia
In physical sciences, a spectrum is a representation of the distribution of electromagnetic radiation—or, more broadly, other physical phenomena such as particle energies or acoustic frequencies—plotted as a function of wavelength, frequency, energy, or related parameters, often visualized as a graph or chart showing intensity variations across that range. This concept is fundamental to understanding how matter interacts with energy, as spectra reveal unique "fingerprints" of atomic and molecular structures through patterns of emission or absorption lines. The most prominent application of spectra lies in the , which encompasses all forms of electromagnetic waves from low-energy radio waves (with wavelengths up to kilometers) to high-energy gamma rays (with wavelengths shorter than atomic nuclei). This continuous range, unified by the in vacuum, enables diverse technologies and scientific inquiries, from radio communications to with X-rays. In astronomy and , analyzing stellar or cosmic spectra discloses the composition, temperature, velocity, and density of distant objects, such as stars or galaxies, by identifying elemental signatures like hydrogen's emission lines at specific wavelengths. Spectroscopy, the study and measurement of , underpins these insights by probing light-matter interactions, where excited atoms or molecules emit or absorb at discrete energies corresponding to transitions. Techniques like emission spectroscopy (measuring emitted light, e.g., from heated gases) and (measuring blocked light, e.g., through atmospheric gases) are essential in fields ranging from chemistry—for identifying pollutants or biomolecules—to , where they calibrate atomic clocks or detect exoplanets via Doppler shifts in . Beyond , spectra extend to (e.g., energy spectra of cosmic rays) and acoustics (e.g., sound frequency distributions), illustrating the topic's versatility in describing natural and engineered systems.

Fundamentals

Etymology

The term "spectrum" originates from the Latin word spectrum, meaning "image," "appearance," or "apparition," derived from the verb specere, "to look at" or "to observe." This root traces back to the Proto-Indo-European speḱ-, which also influenced the Greek verb skopein, meaning "to look at" or "to examine," highlighting a shared linguistic heritage in concepts of vision and perception. In English, the word initially entered as "spectre" or "apparition" in the late , but its scientific application began with , who first used "spectrum" in 1671 to describe the band of colors produced by dispersing white light through a prism. Newton's introduction of the term occurred in his letter to the Royal Society, published in the Philosophical Transactions, where he detailed his experiments on refraction and referred to the resulting colored band as a "colour'd Spectrum." This marked the word's adoption into , specifically within , during the , shifting its connotation from a ghostly image to a physical of dispersion. By the , as the study of expanded, the term "spectrum" transitioned to broader applications in the physical sciences through the development of , the analysis of interactions with . The integration of "spectrum" into English scientific discourse was facilitated by publications like Newton's in the Philosophical Transactions, which popularized it among scholars and paved the way for its use in describing electromagnetic phenomena, such as the continuous range of wavelengths in . This evolution reflected the term's enduring association with visual and observational aspects of physical inquiry.

Historical Development

Isaac Newton's experiments with prisms between 1666 and 1671 demonstrated that white light decomposes into a continuous band of colors, establishing the and demonstrating that white light is a heterogeneous mixture of rays with different degrees of refrangibility, in line with Newton's . In his 1672 letter to the Royal Society, Newton described how sunlight passing through a prism produced a spectrum of seven colors, which could be recombined using a second prism, proving that color arises from the refraction of different rays rather than modification of white light. In the 19th century, advanced spectral analysis by observing hundreds of dark absorption lines in the solar spectrum in 1814, using a high-precision spectroscope he invented. These lines, later named , represented a systematic mapping of solar atmospheric absorption and laid the groundwork for identifying chemical elements remotely. Building on this, and in 1859–1860 identified specific emission and absorption lines as unique signatures of elements, founding the field of through their invention of the spectroscope for chemical analysis. Their work showed that heated elements produce bright lines in emission spectra matching dark lines in absorption spectra of cooler gases, enabling the discovery of new elements like cesium and . The 20th century saw spectra drive foundational shifts in physics, beginning with Max Planck's 1900 quantum hypothesis to explain the spectrum, resolving the by proposing energy quantized in discrete packets. This interpolation formula for spectral energy density, presented to the , marked the birth of . In , Ernest Rutherford's 1911 analysis of alpha-particle off gold foil used the angular distribution of particles—effectively probing energy transfer and deflection spectra—to infer a dense , revolutionizing atomic structure understanding. The evolution continued with J.J. Thomson's development of in the 1910s, where positive trajectories in magnetic and produced mass-to-charge spectra, confirming isotopes like neon-20 and neon-22 and enabling separation. By the late 20th and early 21st centuries, spectra reached new scales; the 2012 discovery of the at the relied on ATLAS and CMS detectors reconstructing spectra from decay products, confirming the particle at 125 GeV with excess events in di-photon and four-lepton channels.

Core Concepts

Definition

In the physical sciences, a spectrum refers to the distribution of a —such as intensity, , or —as a function of an independent variable, including , , , or . This representation serves as a distribution function, illustrating how the quantity varies continuously or discretely across the specified variable, providing insight into the underlying physical processes. A key distinction exists between a spectrum and related terms: a denotes a narrow, specific range within the broader where particular features, such as absorption or emission, are prominent, whereas a continuum describes an unbroken, smooth distribution across the entire range without gaps or discrete features. The term "" encompasses both continuous and discrete forms, depending on the nature of the distribution. Understanding spectra presupposes familiarity with wave-particle duality, the fundamental concept in where physical entities, such as light or matter, exhibit both wave-like and particle-like properties, enabling the distributional patterns observed in spectral data. The notion of spectra originated with Isaac Newton's 1666 experiments dispersing white light into its components using a prism, laying the groundwork for later generalizations across physical domains.

Mathematical Representation

In physical sciences, spectra are mathematically represented through spectral density functions, which quantify the distribution of a —such as intensity, , or power—across frequencies or wavelengths. The spectral density I(ω)I(\omega) describes the intensity II as a function of ω\omega, while I(λ)I(\lambda) does so with respect to λ\lambda, providing a continuous mapping that allows integration over intervals to yield total quantities like total intensity ∫I(ω) dω\int I(\omega) \, d\omega. A fundamental tool for deriving spectral representations from time-domain signals is the Fourier transform, which decomposes waves into frequency components. The spectrum S(f)S(f) is obtained via S(f)=∫−∞∞s(t)e−i2πft dt,S(f) = \int_{-\infty}^{\infty} s(t) e^{-i 2\pi f t} \, dt, where s(t)s(t) is the time-domain signal and ff is the frequency; this transform is essential for analyzing periodic or aperiodic phenomena in wave mechanics and signal processing. For discrete spectra, such as line spectra with distinct frequencies, the representation employs Dirac delta functions to model infinitely narrow peaks. The intensity distribution is expressed as I(ω)=∑kIkδ(ω−ωk),I(\omega) = \sum_k I_k \delta(\omega - \omega_k), where IkI_k is the intensity at the discrete angular frequency ωk\omega_k, capturing the idealized sharp lines observed in atomic or molecular transitions. Normalization of spectral densities ensures physical interpretability, particularly for energy or power distributions; for instance, power spectral density is often normalized in units of watts per hertz (W/Hz), representing power per unit frequency interval to facilitate comparisons across bandwidths.

Electromagnetic Spectra

Continuous Electromagnetic Spectra

Continuous electromagnetic spectra represent smooth, unbroken distributions of radiation intensity over a range of frequencies or wavelengths, arising from thermal or accelerated charge processes without discrete features. These spectra span the entire electromagnetic domain, from radio waves with wavelengths greater than 1 meter to gamma rays with wavelengths shorter than 10−1110^{-11} meters. A canonical example is , which approximates the emission from thermally equilibrated bodies and provides a universal curve dependent solely on temperature. The blackbody spectrum is described by , derived in 1901 to resolve the —a classical prediction of infinite at short wavelengths from Rayleigh-Jeans theory. Planck introduced energy quantization in discrete units E=hνE = h\nu, where hh is Planck's constant and ν\nu is frequency, yielding the B(λ,T)B(\lambda, T) in terms of λ\lambda and TT: B(λ,T)=2hc2λ51ehc/λkT−1,B(\lambda, T) = \frac{2hc^2}{\lambda^5} \frac{1}{e^{hc / \lambda k T} - 1}, where cc is the , hh is Planck's constant, and kk is Boltzmann's constant. This formula produces characteristic curves peaking at wavelengths inversely proportional to TT (), with total energy scaling as T4T^4 (Stefan-Boltzmann law), accurately matching experimental thermal emission data and avoiding the catastrophe by suppressing high-frequency contributions at finite temperatures. Prominent sources of continuous electromagnetic spectra include incandescent solids, where dense atomic interactions enable broadband thermal emission; stars, modeled as near-blackbodies with surface temperatures from about 3000 K (cool giants) to 50,000 K (hot O-type stars), producing peaks from to ; and from relativistic electrons spiraling in magnetic fields, as observed in astrophysical jets or generated in particle accelerators, yielding power-law intensity distributions across X-rays and beyond. A cosmic exemplar is the (CMB), a relic thermal spectrum from the early universe at recombination, observed as a near-perfect blackbody with 2.725 K, spanning wavelengths around 1-2 mm.

Discrete Electromagnetic Spectra

Discrete electromagnetic spectra arise from quantized transitions in atoms and molecules, manifesting as sharp emission or absorption lines at specific wavelengths rather than a continuous distribution of . These spectra occur when electrons or molecular subsystems jump between discrete energy levels, releasing or absorbing photons of precise energies corresponding to the differences between those levels. In atomic spectra, such transitions produce characteristic line series, while in molecular spectra, they result in banded structures due to coupled rotational and vibrational modes. This quantization underpins much of and provides fingerprints for identifying elements and compounds. Atomic emission and absorption spectra exhibit discrete lines due to electron transitions between quantized energy levels in atoms. A prominent example is the Balmer series in hydrogen, observed in the visible region, where electrons transition from higher energy levels (n₂ > 2) to the n₁ = 2 level, producing lines such as Hα at 656.3 nm and Hβ at 486.1 nm. The wavelengths of these lines are described by the Rydberg formula: 1λ=R(1n12−1n22)\frac{1}{\lambda} = R \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right) where λ is the , n₁ and n₂ are positive integers with n₂ > n₁, and R is the , approximately 1.097 × 10⁷ m⁻¹ for . This generalizes Balmer's empirical relation and applies to other series like Lyman (ultraviolet, n₁ = 1) and Paschen (, n₁ = 3), enabling precise prediction of spectral positions. Absorption spectra mirror emission ones but appear as dark lines against a continuum, formed when atoms absorb photons to reach excited states. Molecular spectra in the region feature discrete rotational-vibrational bands, where transitions involve changes in both vibrational (Δv = ±1) and rotational J. For diatomic molecules, the rotational is ΔJ = ±1, leading to P-branch (ΔJ = -1) and R-branch (ΔJ = +1) lines flanking a central Q-branch (ΔJ = 0, often weak or absent). These bands appear as closely spaced lines forming envelopes, with spacing determined by the rotational constant B ≈ h/(8π²cI), where I is the . Such spectra are crucial for studying molecular structure and dynamics in gases. Applications of discrete electromagnetic spectra include the Fraunhofer lines observed in sunlight, which are absorption lines imprinted by cooler atomic gases in the Sun's atmosphere on its continuous photospheric emission. Over 500 such lines, including hydrogen's Balmer series, reveal the solar composition, dominated by hydrogen and helium. Another key application is the Zeeman effect, where spectral lines split in the presence of a magnetic field due to the interaction between the field's energy and the atom's magnetic moment, with splitting proportional to the field strength B via ΔE = μ_B g m_j B / ħ, where μ_B is the Bohr magneton. Discovered in the laboratory in 1896, its astrophysical use began in 1908 with measurements of sunspot magnetic fields up to several kilogauss, enabling remote sensing of stellar and interstellar magnetism. Mathematically, discrete lines can be represented using Dirac delta functions to model their infinitesimal width in idealized spectra.

Other Types of Spectra

Mass Spectra

In mass spectrometry, a mass spectrum represents the distribution of ions produced from a sample, plotted as ion abundance or intensity versus the (m/z), where m is the ionic mass and z is the , typically +1 for singly charged ions. This spectrum is generated by first ionizing the sample s—often through methods like electron impact or —to produce gas-phase s, which are then separated based on their m/z values using mass analyzers. Peaks in the spectrum correspond to the molecular (intact ionized ) or fragment ions resulting from bond cleavages during or subsequent collisions, providing insights into molecular structure and composition. Common mass analyzers include the , which uses oscillating radiofrequency (RF) and (DC) electric fields between four parallel rods to stabilize trajectories selectively by m/z, allowing only ions of a specific ratio to reach the detector while others are deflected. In contrast, time-of-flight (TOF) analyzers accelerate ions in an and measure their over a fixed distance, as lighter ions (lower m/z) travel faster than heavier ones under the same imparted during acceleration. These techniques enable high-resolution separation, with quadrupole systems excelling in targeted quantitative analysis and TOF providing broad-range, high-speed scanning for complex mixtures. Isotopic patterns in mass spectra arise from the natural abundance of stable , leading to clusters of peaks around the nominal ; for instance, in organic compounds rich in carbon, the ¹³C (1.1% natural abundance) produces an M+1 peak whose intensity is approximately 1.1% of the molecular (M) peak per carbon atom. This pattern is evident in molecules like (C₂H₅OH), where the molecular at m/z 46 is accompanied by an M+1 peak at m/z 47 with about 2.2% relative intensity due to two carbon atoms, and smaller contributions from ²H, ¹⁷O, and ¹⁸O create further . Such patterns aid in determining elemental composition, as the relative peak heights follow probabilistic distributions based on isotopic abundances, with approximations like %(M+1) ≈ 1.1n_C (where n_C is the number of carbons) providing quick estimates for low-molecular-weight organics. The origins of mass spectrometry trace to J.J. Thomson's experiments in 1912–1913 at the , where he analyzed "positive rays" (canal rays) from gas discharge tubes by deflecting them in crossed electric and , producing parabolic traces on photographic plates that revealed ions of different masses. In his 1913 Bakerian , Thomson identified two — one at 20 and a fainter one at 22—explaining the element's average atomic weight of 20.2 as a mixture, marking the first observation of stable isotopes via mass separation. These parabolic traces in laid the groundwork for modern analyzers, though early setups lacked the vacuum and resolution of today's instruments.

Energy Spectra

In nuclear and particle physics, energy spectra describe the distribution of energies among emitted particles or photons resulting from specific processes, providing insights into underlying interaction mechanisms and particle properties. These spectra can be continuous or exhibit peaks corresponding to discrete energy releases, and they are typically measured using detectors that resolve energy deposition events. Unlike frequency-based electromagnetic spectra, energy spectra here focus directly on kinetic or total energies of particles like electrons, neutrons, or hadrons. Beta decay spectra exemplify continuous energy distributions, where electrons (or positrons) are emitted with kinetic energies ranging from near zero up to a maximum endpoint energy Emax⁡E_{\max}, determined by the Q-value of the decay. This continuous shape arises because the energy is shared between the emitted lepton and an antineutrino (or neutrino), as described by Fermi's 1934 theory of , which applies the to calculate transition rates proportional to the density of final states. The resulting spectrum is shaped by phase space factors, interactions, and nuclear matrix elements, with the differential rate given by Fermi's integral, peaking at roughly one-third of Emax⁡E_{\max} for allowed transitions./07%3A_Radioactive_Decay_Part_II/7.02%3A_Beta_Decay) In particle accelerators, energy spectra often manifest as invariant mass distributions reconstructed from collision products, revealing resonances like the Z . Discovered in 1983 at 's in proton-antiproton collisions at s≈540\sqrt{s} \approx 540
Add your contribution
Related Hubs
User Avatar
No comments yet.