Recent from talks
Nothing was collected or created yet.
Theory of tides
View on Wikipedia
The theory of tides is the application of continuum mechanics to interpret and predict the tidal deformations of planetary and satellite bodies and their atmospheres and oceans (especially Earth's oceans) under the gravitational loading of another astronomical body or bodies (especially the Moon and Sun).
History
[edit]Classical era
[edit]The tides received relatively little attention in the civilizations around the Mediterranean Sea, as the tides there are relatively small, and the areas that experience tides do so unreliably.[1][2][3] A number of theories were advanced, however, from comparing the movements to breathing or blood flow to theories involving whirlpools or river cycles.[2] A similar "breathing earth" idea was considered by some Asian thinkers.[4] Plato reportedly believed that the tides were caused by water flowing in and out of undersea caverns.[1] Crates of Mallus attributed the tides to "the counter-movement (ἀντισπασμός) of the sea” and Apollodorus of Corcyra to "the refluxes from the Ocean".[5] An ancient Indian Purana text dated to 400-300 BC refers to the ocean rising and falling because of heat expansion from the light of the Moon.[a][6] The Yolngu people of northeastern Arnhem Land in the Northern Territory of Australia identified a link between the Moon and the tides, which they mythically attributed to the Moon filling with water and emptying out again.[7][8]
Ultimately the link between the Moon (and Sun) and the tides became known to the Greeks, although the exact date of discovery is unclear; references to it are made in sources such as Pytheas of Massilia in 325 BC and Pliny the Elder's Natural History in 77 AD. Although the schedule of the tides and the link to lunar and solar movements was known, the exact mechanism that connected them was unclear.[2] Classicists Thomas Little Heath claimed that both Pytheas and Posidonius connected the tides with the moon, "the former directly, the latter through the setting up of winds".[5] Seneca mentions in De Providentia the periodic motion of the tides controlled by the lunar sphere.[9] Eratosthenes (3rd century BC) and Posidonius (1st century BC) both produced detailed descriptions of the tides and their relationship to the phases of the Moon, Posidonius in particular making lengthy observations of the sea on the Spanish coast, although little of their work survived. The influence of the Moon on tides was mentioned in Ptolemy's Tetrabiblos as evidence of the reality of astrology.[1][10] Seleucus of Seleucia is thought to have theorized around 150 BC that tides were caused by the Moon as part of his heliocentric model.[11][12]
Aristotle, judging from discussions of his beliefs in other sources, is thought to have believed the tides were caused by winds driven by the Sun's heat, and he rejected the theory that the Moon caused the tides. An apocryphal legend claims that he committed suicide in frustration with his failure to fully understand the tides.[1] Heraclides also held "the sun sets up winds, and that these winds, when they blow, cause the high tide and, when they cease, the low tide".[5] Dicaearchus also "put the tides down to the direct action of the sun according to its position".[5] Philostratus discusses tides in Book Five of Life of Apollonius of Tyana (circa 217-238 AD); he was vaguely aware of a correlation of the tides with the phases of the Moon but attributed them to spirits moving water in and out of caverns, which he connected with the legend that spirits of the dead cannot move on at certain phases of the Moon.[b]
Medieval period
[edit]The Venerable Bede discusses the tides in The Reckoning of Time and shows that the twice-daily timing of tides is related to the Moon and that the lunar monthly cycle of spring and neap tides is also related to the Moon's position. He goes on to note that the times of tides vary along the same coast and that the water movements cause low tide at one place when there is high tide elsewhere.[13] However, he made no progress regarding the question of how exactly the Moon created the tides.[2]
Medieval rule-of-thumb methods for predicting tides were said to allow one "to know what Moon makes high water" from the Moon's movements.[14] Dante references the Moon's influence on the tides in his Divine Comedy.[15][1]
Medieval European understanding of the tides was often based on works of Muslim astronomers that became available through Latin translation starting from the 12th century.[16] Abu Ma'shar al-Balkhi, in his Introductorium in astronomiam, taught that ebb and flood tides were caused by the Moon.[16] Abu Ma'shar discussed the effects of wind and Moon's phases relative to the Sun on the tides.[16] In the 12th century, al-Bitruji contributed the notion that the tides were caused by the general circulation of the heavens.[16] Medieval Arabic astrologers frequently referenced the Moon's influence on the tides as evidence for the reality of astrology; some of their treatises on the topic influenced western Europe.[10][1] Some theorized that the influence was caused by lunar rays heating the ocean's floor.[3]
Modern era
[edit]Simon Stevin in his 1608 De spiegheling der Ebbenvloet (The Theory of Ebb and Flood) dismisses a large number of misconceptions that still existed about ebb and flood. Stevin pleads for the idea that the attraction of the Moon was responsible for the tides and writes in clear terms about ebb, flood, spring tide and neap tide, stressing that further research needed to be made.[17][18] In 1609, Johannes Kepler correctly suggested that the gravitation of the Moon causes the tides,[c] which he compared to magnetic attraction[20][2][21][22] basing his argument upon ancient observations and correlations.
In 1616, Galileo Galilei wrote Discourse on the Tides.[23] He strongly and mockingly rejects the lunar theory of the tides,[21][2] and tries to explain the tides as the result of the Earth's rotation and revolution around the Sun, believing that the oceans moved like water in a large basin: as the basin moves, so does the water.[24] But his contemporaries noticed that this made predictions that did not fit observations.[25]
René Descartes theorized that the tides (alongside the movement of planets, etc.) were caused by aetheric vortices, without reference to Kepler's theories of gravitation by mutual attraction; this was extremely influential, with numerous followers of Descartes expounding on this theory throughout the 17th century, particularly in France.[26] However, Descartes and his followers acknowledged the influence of the Moon, speculating that pressure waves from the Moon via the aether were responsible for the correlation.[3][27][4][28]

Newton, in the Principia, provides a correct explanation for the tidal force, which can be used to explain tides on a planet covered by a uniform ocean but which takes no account of the distribution of the continents or ocean bathymetry.[29]
Dynamic theory
[edit]While Newton explained the tides by describing the tide-generating forces and Daniel Bernoulli gave a description of the static reaction of the waters on Earth to the tidal potential, the dynamic theory of tides, developed by Pierre-Simon Laplace in 1775,[30] describes the ocean's real reaction to tidal forces.[31] Laplace's theory of ocean tides takes into account friction, resonance and natural periods of ocean basins. It predicts the large amphidromic systems in the world's ocean basins and explains the oceanic tides that are actually observed.[32]
The equilibrium theory—based on the gravitational gradient from the Sun and Moon but ignoring the Earth's rotation, the effects of continents, and other important effects—could not explain the real ocean tides.[33] Since measurements have confirmed the dynamic theory, many things have possible explanations now, like how the tides interact with deep sea ridges, and chains of seamounts give rise to deep eddies that transport nutrients from the deep to the surface.[34] The equilibrium tide theory calculates the height of the tide wave of less than half a meter, while the dynamic theory explains why tides are up to 15 meters.[35]
Satellite observations confirm the accuracy of the dynamic theory, and the tides worldwide are now measured to within a few centimeters.[36][37] Measurements from the CHAMP satellite closely match the models based on the TOPEX data.[38][39][40] Accurate models of tides worldwide are essential for research since the variations due to tides must be removed from measurements when calculating gravity and changes in sea levels.[41]
Laplace's tidal equations
[edit]In 1776, Laplace formulated a single set of linear partial differential equations for tidal flow described as a barotropic two-dimensional sheet flow. Coriolis effects are introduced as well as lateral forcing by gravity. Laplace obtained these equations by simplifying the fluid dynamics equations, but they can also be derived from energy integrals via Lagrange's equation.
For a fluid sheet of average thickness D, the vertical tidal elevation ζ, as well as the horizontal velocity components u and v (in the latitude φ and longitude λ directions, respectively) satisfy Laplace's tidal equations:[42]
where Ω is the angular frequency of the planet's rotation, g is the planet's gravitational acceleration at the mean ocean surface, a is the planetary radius, and U is the external gravitational tidal-forcing potential.
William Thomson (Lord Kelvin) rewrote Laplace's momentum terms using the curl to find an equation for vorticity. Under certain conditions this can be further rewritten as a conservation of vorticity.
Tidal analysis and prediction
[edit]Harmonic analysis
[edit]
Laplace's improvements in theory were substantial, but they still left prediction in an approximate state. This position changed in the 1860s when the local circumstances of tidal phenomena were more fully brought into account by Lord Kelvin's application of Fourier analysis to the tidal motions as harmonic analysis. Thomson's work in this field was further developed and extended by George Darwin, applying the lunar theory current in his time. Darwin's symbols for the tidal harmonic constituents are still used, for example: M: moon/lunar; S: sun/solar; K: moon-sun/lunisolar.
Darwin's harmonic developments of the tide-generating forces were later improved when A.T. Doodson, applying the lunar theory of E.W. Brown,[43] developed the tide-generating potential (TGP) in harmonic form, distinguishing 388 tidal frequencies.[44] Doodson's work was carried out and published in 1921.[45] Doodson devised a practical system for specifying the different harmonic components of the tide-generating potential, the Doodson numbers, a system still in use.
Since the mid-twentieth century further analysis has generated many more terms than Doodson's 388. About 62 constituents are of sufficient size to be considered for possible use in marine tide prediction, but sometimes many fewer can predict tides to useful accuracy. The calculations of tide predictions using the harmonic constituents are laborious, and from the 1870s to about the 1960s they were carried out using a mechanical tide-predicting machine, a special-purpose form of analog computer. More recently digital computers, using the method of matrix inversion, are used to determine the tidal harmonic constituents directly from tide gauge records.[46]
Tidal constituents
[edit]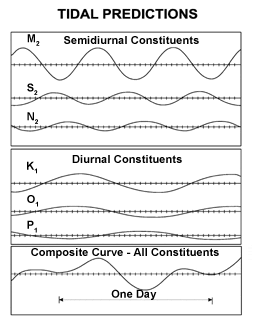
Tidal constituents combine to give an endlessly varying aggregate because of their different and incommensurable frequencies: the effect is visualized in an animation of the American Mathematical Society illustrating the way in which the components used to be mechanically combined in the tide-predicting machine. Amplitudes (half of peak-to-peak amplitude) of tidal constituents are given below for six example locations: Eastport, Maine (ME),[47] Biloxi, Mississippi (MS), San Juan, Puerto Rico (PR), Kodiak, Alaska (AK), San Francisco, California (CA), and Hilo, Hawaii (HI).
Semi-diurnal
[edit]| Species | Darwin symbol |
Period (h) |
Speed (°/h) |
Doodson coefficients | Doodson number |
Amplitude at example location (cm) | NOAA order | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n1 (L) | n2 (m) | n3 (y) | n4 (mp) | ME | MS | PR | AK | CA | HI | ||||||
| Principal lunar semidiurnal | M2 | 12.4206012 | 28.9841042 | 2 | 255.555 | 268.7 | 3.9 | 15.9 | 97.3 | 58.0 | 23.0 | 1 | |||
| Principal solar semidiurnal | S2 | 12 | 30 | 2 | 2 | −2 | 273.555 | 42.0 | 3.3 | 2.1 | 32.5 | 13.7 | 9.2 | 2 | |
| Larger lunar elliptic semidiurnal | N2 | 12.65834751 | 28.4397295 | 2 | −1 | 1 | 245.655 | 54.3 | 1.1 | 3.7 | 20.1 | 12.3 | 4.4 | 3 | |
| Larger lunar evectional | ν2 | 12.62600509 | 28.5125831 | 2 | −1 | 2 | −1 | 247.455 | 12.6 | 0.2 | 0.8 | 3.9 | 2.6 | 0.9 | 11 |
| Variational | μ2 | 12.8717576 | 27.9682084 | 2 | −2 | 2 | 237.555 | 2.0 | 0.1 | 0.5 | 2.2 | 0.7 | 0.8 | 13 | |
| Lunar elliptical semidiurnal second-order | 2N2 | 12.90537297 | 27.8953548 | 2 | −2 | 2 | 235.755 | 6.5 | 0.1 | 0.5 | 2.4 | 1.4 | 0.6 | 14 | |
| Smaller lunar evectional | λ2 | 12.22177348 | 29.4556253 | 2 | 1 | −2 | 1 | 263.655 | 5.3 | 0.1 | 0.7 | 0.6 | 0.2 | 16 | |
| Larger solar elliptic | T2 | 12.01644934 | 29.9589333 | 2 | 2 | −3 | 272.555 | 3.7 | 0.2 | 0.1 | 1.9 | 0.9 | 0.6 | 27 | |
| Smaller solar elliptic | R2 | 11.98359564 | 30.0410667 | 2 | 2 | −1 | 274.555 | 0.9 | 0.2 | 0.1 | 0.1 | 28 | |||
| Shallow water semidiurnal | 2SM2 | 11.60695157 | 31.0158958 | 2 | 4 | −4 | 291.555 | 0.5 | 31 | ||||||
| Smaller lunar elliptic semidiurnal | L2 | 12.19162085 | 29.5284789 | 2 | 1 | −1 | 265.455 | 13.5 | 0.1 | 0.5 | 2.4 | 1.6 | 0.5 | 33 | |
| Lunisolar semidiurnal | K2 | 11.96723606 | 30.0821373 | 2 | 2 | 275.555 | 11.6 | 0.9 | 0.6 | 9.0 | 4.0 | 2.8 | 35 | ||
Diurnal
[edit]| Species | Darwin symbol |
Period (h) |
Speed (°/h) |
Doodson coefficients | Doodson number |
Amplitude at example location (cm) | NOAA order | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n1 (L) | n2 (m) | n3 (y) | n4 (mp) | ME | MS | PR | AK | CA | HI | ||||||
| Lunisolar diurnal | K1 | 23.93447213 | 15.0410686 | 1 | 1 | 165.555 | 15.6 | 16.2 | 9.0 | 39.8 | 36.8 | 16.7 | 4 | ||
| Lunar diurnal | O1 | 25.81933871 | 13.9430356 | 1 | −1 | 145.555 | 11.9 | 16.9 | 7.7 | 25.9 | 23.0 | 9.2 | 6 | ||
| Lunar diurnal | OO1 | 22.30608083 | 16.1391017 | 1 | 3 | 185.555 | 0.5 | 0.7 | 0.4 | 1.2 | 1.1 | 0.7 | 15 | ||
| Solar diurnal | S1 | 24 | 15 | 1 | 1 | −1 | 164.555 | 1.0 | 0.5 | 1.2 | 0.7 | 0.3 | 17 | ||
| Smaller lunar elliptic diurnal | M1 | 24.84120241 | 14.4920521 | 1 | 155.555 | 0.6 | 1.2 | 0.5 | 1.4 | 1.1 | 0.5 | 18 | |||
| Smaller lunar elliptic diurnal | J1 | 23.09848146 | 15.5854433 | 1 | 2 | −1 | 175.455 | 0.9 | 1.3 | 0.6 | 2.3 | 1.9 | 1.1 | 19 | |
| Larger lunar evectional diurnal | ρ | 26.72305326 | 13.4715145 | 1 | −2 | 2 | −1 | 137.455 | 0.3 | 0.6 | 0.3 | 0.9 | 0.9 | 0.3 | 25 |
| Larger lunar elliptic diurnal | Q1 | 26.868350 | 13.3986609 | 1 | −2 | 1 | 135.655 | 2.0 | 3.3 | 1.4 | 4.7 | 4.0 | 1.6 | 26 | |
| Larger elliptic diurnal | 2Q1 | 28.00621204 | 12.8542862 | 1 | −3 | 2 | 125.755 | 0.3 | 0.4 | 0.2 | 0.7 | 0.4 | 0.2 | 29 | |
| Solar diurnal | P1 | 24.06588766 | 14.9589314 | 1 | 1 | −2 | 163.555 | 5.2 | 5.4 | 2.9 | 12.6 | 11.6 | 5.1 | 30 | |
Long period
[edit]| Species | Darwin symbol |
Period (h) (days) |
Speed (°/h) |
Doodson coefficients | Doodson number |
Amplitude at example location (cm) | NOAA order | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n1 (L) | n2 (m) | n3 (y) | n4 (mp) | ME | MS | PR | AK | CA | HI | ||||||
| Lunar monthly | Mm | 661.3111655 27.554631896 |
0.5443747 | 0 | 1 | −1 | 65.455 | 0.7 | 1.9 | 20 | |||||
| Solar semiannual | Ssa | 4383.076325 182.628180208 |
0.0821373 | 0 | 2 | 57.555 | 1.6 | 2.1 | 1.5 | 3.9 | 21 | ||||
| Solar annual | Sa | 8766.15265 365.256360417 |
0.0410686 | 0 | 1 | 56.555 | 5.5 | 7.8 | 3.8 | 4.3 | 22 | ||||
| Lunisolar synodic fortnightly | MSf | 354.3670666 14.765294442 |
1.0158958 | 0 | 2 | −2 | 73.555 | 1.5 | 23 | ||||||
| Lunisolar fortnightly | Mf | 327.8599387 13.660830779 |
1.0980331 | 0 | 2 | 75.555 | 1.4 | 2.0 | 0.7 | 24 | |||||
Short period
[edit]| Species | Darwin symbol |
Period (h) |
Speed (°/h) |
Doodson coefficients | Doodson number |
Amplitude at example location (cm) | NOAA order | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n1 (L) | n2 (m) | n3 (y) | n4 (mp) | ME | MS | PR | AK | CA | HI | ||||||
| Shallow water overtides of principal lunar | M4 | 6.210300601 | 57.9682084 | 4 | 455.555 | 6.0 | 0.6 | 0.9 | 2.3 | 5 | |||||
| Shallow water overtides of principal lunar | M6 | 4.140200401 | 86.9523127 | 6 | 655.555 | 5.1 | 0.1 | 1.0 | 7 | ||||||
| Shallow water terdiurnal | MK3 | 8.177140247 | 44.0251729 | 3 | 1 | 365.555 | 0.5 | 1.9 | 8 | ||||||
| Shallow water overtides of principal solar | S4 | 6 | 60 | 4 | 4 | −4 | 491.555 | 0.1 | 9 | ||||||
| Shallow water quarter diurnal | MN4 | 6.269173724 | 57.4238337 | 4 | −1 | 1 | 445.655 | 2.3 | 0.3 | 0.9 | 10 | ||||
| Shallow water overtides of principal solar | S6 | 4 | 90 | 6 | 6 | −6 | * | 0.1 | 12 | ||||||
| Lunar terdiurnal | M3 | 8.280400802 | 43.4761563 | 3 | 355.555 | 0.5 | 32 | ||||||||
| Shallow water terdiurnal | 2MK3 | 8.38630265 | 42.9271398 | 3 | −1 | 345.555 | 0.5 | 0.5 | 1.4 | 34 | |||||
| Shallow water eighth diurnal | M8 | 3.105150301 | 115.9364166 | 8 | 855.555 | 0.5 | 0.1 | 36 | |||||||
| Shallow water quarter diurnal | MS4 | 6.103339275 | 58.9841042 | 4 | 2 | −2 | 473.555 | 1.8 | 0.6 | 1.0 | 37 | ||||
Doodson numbers
[edit]In order to specify the different harmonic components of the tide-generating potential, Doodson devised a practical system which is still in use, involving what are called the Doodson numbers based on the six Doodson arguments or Doodson variables. The number of different tidal frequency components is large, but each corresponds to a specific linear combination of six frequencies using small-integer multiples, positive or negative. In principle, these basic angular arguments can be specified in numerous ways; Doodson's choice of his six "Doodson arguments" has been widely used in tidal work. In terms of these Doodson arguments, each tidal frequency can then be specified as a sum made up of a small integer multiple of each of the six arguments. The resulting six small integer multipliers effectively encode the frequency of the tidal argument concerned, and these are the Doodson numbers: in practice all except the first are usually biased upwards by +5 to avoid negative numbers in the notation. (In the case that the biased multiple exceeds 9, the system adopts X for 10, and E for 11.)[48]
The Doodson arguments are specified in the following way, in order of decreasing frequency:[48]
- is mean Lunar time, the Greenwich hour angle of the mean Moon plus 12 hours.
- is the mean longitude of the Moon.
- is the mean longitude of the Sun.
- is the longitude of the Moon's mean perigee.
- is the negative of the longitude of the Moon's mean ascending node on the ecliptic.
- or is the longitude of the Sun's mean perigee.
In these expressions, the symbols , , and refer to an alternative set of fundamental angular arguments (usually preferred for use in modern lunar theory), in which:-
- is the mean anomaly of the Moon (distance from its perigee).
- is the mean anomaly of the Sun (distance from its perigee).
- is the Moon's mean argument of latitude (distance from its node).
- is the Moon's mean elongation (distance from the sun).
It is possible to define several auxiliary variables on the basis of combinations of these.
In terms of this system, each tidal constituent frequency can be identified by its Doodson numbers. The strongest tidal constituent "M2" has a frequency of 2 cycles per lunar day, its Doodson numbers are usually written 255.555, meaning that its frequency is composed of twice the first Doodson argument, and zero times all of the others. The second strongest tidal constituent "S2" is influenced by the sun, and its Doodson numbers are 273.555, meaning that its frequency is composed of twice the first Doodson argument, +2 times the second, -2 times the third, and zero times each of the other three.[49] This aggregates to the angular equivalent of mean solar time +12 hours. These two strongest component frequencies have simple arguments for which the Doodson system might appear needlessly complex, but each of the hundreds of other component frequencies can be briefly specified in a similar way, showing in the aggregate the usefulness of the encoding.
See also
[edit]Notes
[edit]- ^ In all the oceans the water remains at all times the same in quantity, and never, increases or diminishes; but like the water in a caldron, which, in consequence of its combination with heat, expands, so the waters of the ocean swell with the increase of the moon. The waters, although really neither more nor less, dilate or contract as the moon increases or wanes in the light and dark fortnights. - The Vishnu Purana book II ch. IV
- ^ Now I myself have seen among the Celts the ocean tides just as they are described. After making various conjectures about why so vast a bulk of waters recedes and advances, I have come to the conclusion that Apollonius discerned the real truth. For in one of his letters to the Indians he says that the ocean is driven by submarine influences or spirits out of several chasms which the earth afford both underneath and around it, to advance outwards, and to recede again, whenever the influence or spirit, like the breath of our bodies, gives way and recedes. And this theory is confirmed by the course run by diseases in Gadeira, for at the time of high water the souls of the dying do not quit the bodies, and this would hardly happen, he says, unless the influence or spirit I have spoken of was also advancing towards the land. They also tell you of certain phenomena of the ocean in connection with the phases of the moon, according as it is born and reaches fullness and wanes. These phenomena I verified, for the ocean exactly keeps pace with the size of the moon, decreasing and increasing with her. - Philostratus, The Life of Apollonius of Tyana, V
- ^ "Orbis virtutis tractoriæ, quæ est in Luna, porrigitur utque ad Terras, & prolectat aquas sub Zonam Torridam, … Celeriter vero Luna verticem transvolante, cum aquæ tam celeriter sequi non possint, fluxus quidem fit Oceani sub Torrida in Occidentem, … " ("The sphere of the lifting power, which is [centered] in the moon, is extended as far as to the earth and attracts the waters under the torrid zone, … However the moon flies swiftly across the zenith; because the waters cannot follow so quickly, the tide of the ocean under the torrid [zone] is indeed made to the west, …")[19]
References
[edit]- ^ a b c d e f Tabarroni, G. (1989). "The tides and Newton". Memorie della Società Astronomia Italiana. 60: 770–777. Bibcode:1989MmSAI..60..769T. Retrieved 27 December 2020.
- ^ a b c d e f Marmer, H. A. (March 1922). "The Problems of the Tide". The Scientific Monthly. 14 (3): 209–222. Bibcode:1922SciMo..14..209M.
- ^ a b c Pugh, David T. (28 December 1987). Tides, Surges and Mean Sea-Level (PDF). JOHN WILEY & SONS. pp. 2–4. ISBN 047191505X. Retrieved 27 December 2020.
- ^ a b "Understanding Tides—From Ancient Beliefs toPresent-day Solutions to the Laplace Equations" (PDF). Vol. 33, no. 2. SIAM News.
- ^ a b c d Heath, Thomas Little (1913). Aristarchus of Samos, the ancient Copernicus. Gerstein - University of Toronto. Oxford: Clarendon Press. pp. 306–307.
- ^ Cartwright, David Edgar (1999). Tides: A Scientific History. Cambridge University Press. p. 6. ISBN 9780521797467. Retrieved 28 December 2020.
- ^ "Moon". Australian Indigenous Astronomy. Retrieved 8 October 2020.
- ^ ""Bridging the Gap" through Australian Cultural Astronomy". Archaeoastronomy & Ethnoastronomy – Building Bridges Between Cultures: 282–290. 2011.
- ^ Seneca, De Providentia, 1.4
- ^ a b Cartwright, David E. (2001). "On the Origins of Knowledge of the Sea Tides from Antiquity to the Thirteenth Century". Earth Sciences History. 20 (2): 105–126. Bibcode:2001ESHis..20..105C. doi:10.17704/eshi.20.2.m23118527q395675. JSTOR 24138749. Retrieved 27 December 2020.
- ^ Lucio Russo, Flussi e riflussi, Feltrinelli, Milano, 2003, ISBN 88-07-10349-4.
- ^ Van der Waerden, B. L. (1987). "The Heliocentric System in Greek, Persian and Hindu Astronomy". Annals of the New York Academy of Sciences. 500 (1): 525–545. Bibcode:1987NYASA.500..525V. doi:10.1111/j.1749-6632.1987.tb37224.x. S2CID 222087224.
- ^ Bede (2004). The Reckoning of Time. Translated by Faith Wallis. Liverpool University Press. pp. 64–65. ISBN 978-0-85323-693-1.
- ^ HUGHES, PAUL. "A STUDY IN THE DEVELOPMENT OF PRIMITIVE AND MODERN TIDE TABLES" (PDF). PhD Thesis, Liverpool John Moores University. Retrieved 27 December 2020.
- ^ "Princeton Dante Project: Main Poem Browser (2.0)". dante.princeton.edu.
- ^ a b c d Marina Tolmacheva (2014). Glick, Thomas F. (ed.). Geography, Chorography. Routledge. p. 188. ISBN 978-1135459321.
- ^ Simon Stevin – Flanders Marine Institute (pdf, in Dutch)
- ^ Palmerino, The Reception of the Galilean Science of Motion in Seventeenth-Century Europe, pp. 200 op books.google.nl
- ^ Johannes Kepler, Astronomia nova … (1609), p. 5 of the Introductio in hoc opus (Introduction to this work). From page 5:
- ^ Johannes Kepler, Astronomia nova ... (1609), p. 5 of the Introductio in hoc opus
- ^ a b Popova, Maria (27 December 2019). "How Kepler Invented Science Fiction ... While Revolutionizing Our Understanding of the Universe". Brain Pickings. Retrieved 27 December 2020.
- ^ Eugene, Hecht (2019). "Kepler and the origins of the theory of gravity". American Journal of Physics. 87 (3): 176–185. Bibcode:2019AmJPh..87..176H. doi:10.1119/1.5089751. S2CID 126889093.
- ^ Rice University: Galileo's Theory of the Tides, by Rossella Gigli, retrieved 10 March 2010
- ^ Tyson, Peter (29 October 2002). "Galileo's Big Mistake". NOVA. PBS. Retrieved 19 February 2014.
- ^ Naylor, Ron (2007). "Galileo's Tidal Theory". Isis. 98 (1): 1–22. Bibcode:2007Isis...98....1N. doi:10.1086/512829. PMID 17539198. S2CID 46174715.
- ^ Aiton, E.J. (1955). "Descartes's theory of the tides". Annals of Science. 11 (4): 337–348. doi:10.1080/00033795500200335.
- ^ "Voltaire, Letter XIV". Archived from the original on 13 April 2021. Retrieved 28 December 2020.
- ^ Cartwright, David Edgar (1999). Tides: A Scientific History. Cambridge University Press. p. 31. ISBN 9780521797467. Retrieved 28 December 2020.
- ^ "Static Tides – the equilibrium Theory". Archived from the original on 10 April 2014. Retrieved 14 April 2014.
- ^ "Short notes on the Dynamical theory of Laplace". 20 November 2011. Archived from the original on 2 April 2015. Retrieved 31 March 2015.
- ^ "Tide Dynamics" (PDF). faculty.washington.edu.
- ^ Ahn, Kyung-Jin (September 2009). "An Astronomer's View on the Current College-Level Textbook Descriptions of Tides" (PDF). Journal of the Korean Earth Science Society. 30 (5): 671–681. doi:10.5467/JKESS.2009.30.5.671.
- ^ Bryden, I.G. (2003). "Tidal Power Systems", in Meyers, R.A. (ed.) Encyclopedia of Physical Science and Technology. Aberdeen: Academic Press, p. 753. doi:10.1016/b0-12-227410-5/00778-x
- ^ Floor Anthoni. "Tides". Seafriends.org.nz. Retrieved 2 June 2012.
- ^ "The Cause & Nature of Tides".
- ^ "Scientific Visualization Studio TOPEX/Poseidon images". Svs.gsfc.nasa.gov. Retrieved 2 June 2012.
- ^ "TOPEX/Poseidon Western Hemisphere: Tide Height Model : NASA/Goddard Space Flight Center Scientific Visualization Studio : Free Download & Streaming : Internet Archive". 15 June 2000.
- ^ "TOPEX data used to model actual tides for 15 days from the year 2000". 15 June 2000. Archived from the original on 18 September 2015. Retrieved 14 September 2015.
- ^ "Ocean Temperatures". Archived from the original on 2 March 2014.
- ^ "OSU Tidal Data Inversion". Volkov.oce.orst.edu. Archived from the original on 22 October 2012. Retrieved 2 June 2012.
- ^ "Dynamic and residual ocean tide analysis for improved GRACE de-aliasing (DAROTA)". Archived from the original on 2 April 2015.
- ^ "The Laplace Tidal Equations and Atmospheric Tides" (PDF).
- ^ Cartwright, David Edgar (1999). Tides: A Scientific History. Cambridge University Press. pp. 163–164. ISBN 9780521797467.
- ^ S Casotto, F Biscani, "A fully analytical approach to the harmonic development of the tide-generating potential accounting for precession, nutation, and perturbations due to figure and planetary terms", AAS Division on Dynamical Astronomy, April 2004, vol.36(2), 67.
- ^ A T Doodson (1921), "The Harmonic Development of the Tide-Generating Potential", Proceedings of the Royal Society of London. Series A, Vol. 100, No. 704 (1 December 1921), pp. 305–329.
- ^ Boon, John D. (2010). Secrets of the Tide. Philadelphia, PA: Woodhead Publishing Limited. pp. 159–165. ISBN 978-1-904275-17-6.
- ^ NOAA. "Eastport, ME Tidal Constituents". NOAA. Retrieved 22 May 2012.
- ^ a b Melchior, P. (1971). "Precession-nutations and tidal potential". Celestial Mechanics. 4 (2): 190–212. Bibcode:1971CeMec...4..190M. doi:10.1007/BF01228823. S2CID 126219362. and T D Moyer (2003) already cited.
- ^ See for example Melchior (1971), already cited, at p.191.
External links
[edit]- Contributions of satellite laser ranging to the studies of earth tides Archived 28 July 2013 at the Wayback Machine
- Dynamic Theory of Tides
- Tidal Observations
- Publications from NOAA's Center for Operational Oceanographic Products and Services
Theory of tides
View on GrokipediaThese tides manifest as two high waters and two low waters per lunar day (approximately 24 hours and 50 minutes), with the Moon's gravitational pull dominating due to its proximity to Earth—despite the Sun's greater mass, the Moon's tide-generating force is about twice as strong because tidal forces vary inversely with the cube of the distance to the attracting body.[2]
The foundational explanation emerged in 1687 when Isaac Newton, in his Philosophiæ Naturalis Principia Mathematica, applied his law of universal gravitation to tides, describing them as the response of ocean waters to these celestial attractions, including the centrifugal force from Earth's rotation that contributes to the far-side bulge.[3]
Newton's equilibrium theory assumes a frictionless, global ocean that instantly adjusts to form a static, ellipsoidal shape aligned with the Earth-Moon axis, predicting basic tidal cycles such as semidiurnal tides (twice daily) and variations like spring tides (higher highs and lower lows during full and new moons when Sun, Moon, and Earth align) and neap tides (weaker tides during quarter moons).[4]
However, this idealized model overlooks Earth's rotation, continental barriers, ocean depth variations, and frictional delays, leading to inaccuracies in predicting actual tidal amplitudes and timings observed in coastal regions.[3]
In the late 18th century, Pierre-Simon Laplace advanced the field with the dynamic theory of tides, incorporating hydrodynamic equations to account for wave propagation, Coriolis effects from Earth's rotation, basin geometries, and friction, which better explain real-world complexities like amphidromic systems (rotating tidal patterns around fixed points) and the generation of over 400 harmonic tidal constituents.[3]
Subsequent refinements by scientists such as George Darwin and Arthur Doodson in the 19th and 20th centuries, along with modern integrations of satellite altimetry and numerical modeling, have enabled precise global tide predictions essential for navigation, coastal engineering, and environmental management.[3]




![{\displaystyle {\begin{aligned}{\frac {\partial \zeta }{\partial t}}&+{\frac {1}{a\cos(\varphi )}}\left[{\frac {\partial }{\partial \lambda }}(uD)+{\frac {\partial }{\partial \varphi }}\left(vD\cos(\varphi )\right)\right]=0,\\[2ex]{\frac {\partial u}{\partial t}}&-v\,2\Omega \sin(\varphi )+{\frac {1}{a\cos(\varphi )}}{\frac {\partial }{\partial \lambda }}\left(g\zeta +U\right)=0,\quad {\text{and}}\\[2ex]{\frac {\partial v}{\partial t}}&+u\,2\Omega \sin(\varphi )+{\frac {1}{a}}{\frac {\partial }{\partial \varphi }}\left(g\zeta +U\right)=0,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93fa08ee6fd9993a354e58f22257c7847c90666d)












