Hubbry Logo
FerromagnetismFerromagnetismMain
Open search
Ferromagnetism
Community hub
Ferromagnetism
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Ferromagnetism
Ferromagnetism
Ferromagnetism
View on Wikipedia
from Wikipedia
Look up ferromagnetism in Wiktionary, the free dictionary.
A magnet made of alnico, a ferromagnetic iron alloy, with its keeper
Condensed matter physics
States of matter
Phase phenomena
Electronic phases
Electronic phenomena
Magnetic phases
Quasiparticles
Soft matter
Scientists
Paramagnetism, ferromagnetism, and spin waves

Ferromagnetism is a property of certain materials (such as iron) that results in a significant, observable magnetic permeability, and in many cases, a significant magnetic coercivity, allowing the material to form a permanent magnet. Ferromagnetic materials are noticeably attracted to a magnet, which is a consequence of their substantial magnetic permeability.

Magnetic permeability describes the induced magnetization of a material due to the presence of an external magnetic field. For example, this temporary magnetization inside a steel plate accounts for the plate's attraction to a magnet. Whether or not that steel plate then acquires permanent magnetization depends on both the strength of the applied field and on the coercivity of that particular piece of steel (which varies with the steel's chemical composition and any heat treatment it may have undergone).

In physics, multiple types of material magnetism have been distinguished. Ferromagnetism (along with the similar effect ferrimagnetism) is the strongest type and is responsible for the common phenomenon of everyday magnetism.[1] A common example of a permanent magnet is a refrigerator magnet.[2] Substances respond weakly to magnetic fields by three other types of magnetism—paramagnetism, diamagnetism, and antiferromagnetism—but the forces are usually so weak that they can be detected only by lab instruments.

Permanent magnets (materials that can be magnetized by an external magnetic field and remain magnetized after the external field is removed) are either ferromagnetic or ferrimagnetic, as are the materials that are strongly attracted to them. Relatively few materials are ferromagnetic; the common ones are the metals iron, cobalt, nickel and most of their alloys, and certain rare-earth metals.

Ferromagnetism is widely used in industrial applications and modern technology, in electromagnetic and electromechanical devices such as electromagnets, electric motors, generators, transformers, magnetic storage (including tape recorders and hard disks), and nondestructive testing of ferrous materials.

Ferromagnetic materials can be divided into magnetically "soft" materials (like annealed iron) having low coercivity, which do not tend to stay magnetized, and magnetically "hard" materials having high coercivity, which do. Permanent magnets are made from hard ferromagnetic materials (such as alnico) and ferrimagnetic materials (such as ferrite) that are subjected to special processing in a strong magnetic field during manufacturing to align their internal microcrystalline structure, making them difficult to demagnetize. To demagnetize a saturated magnet, a magnetic field must be applied. The threshold at which demagnetization occurs depends on the coercivity of the material. The overall strength of a magnet is measured by its magnetic moment or, alternatively, its total magnetic flux. The local strength of magnetism in a material is measured by its magnetization.

Terms

[edit]
Ferromagnetic material: all the molecular magnetic dipoles are pointed in the same direction
Ferrimagnetic material: some of the dipoles point in the opposite direction, but their smaller contribution is overcome by the others

Historically, the term ferromagnetism was used for any material that could exhibit spontaneous magnetization: a net magnetic moment in the absence of an external magnetic field; that is, any material that could become a magnet. This definition is still in common use.[3]

In a landmark paper in 1948, Louis Néel showed that two levels of magnetic alignment result in this behavior. One is ferromagnetism in the strict sense, where all the magnetic moments are aligned. The other is ferrimagnetism, where some magnetic moments point in the opposite direction but have a smaller contribution, so spontaneous magnetization is present.[4][5]: 28–29 

In the special case where the opposing moments balance completely, the alignment is known as antiferromagnetism; antiferromagnets do not have a spontaneous magnetization.

Materials

[edit]
See also: Category:Ferromagnetic materials
Curie temperatures for some crystalline ferromagnetic and ferrimagnetic materials[6][7]
Material Curie
temp. (K)
Co 1388
Fe 1043
Fe2O3[a] 948
NiOFe2O3[a] 858
CuOFe2O3[a] 728
MgOFe2O3[a] 713
MnBi 630
Ni 627
Nd2Fe14 B 593
MnSb 587
MnOFe2O3[a] 573
Y3Fe5O12[a] 560
CrO2 386
MnAs 318
Gd 292
Tb 219
Dy 88
EuO 69
  1. ^ a b c d e f Ferrimagnetic material

Ferromagnetism is an unusual property that occurs in only a few substances. The common ones are the transition metals iron, nickel, and cobalt, as well as their alloys and alloys of rare-earth metals. It is a property not just of the chemical make-up of a material, but of its crystalline structure and microstructure. Ferromagnetism results from these materials having many unpaired electrons in their d-block (in the case of iron and its relatives) or f-block (in the case of the rare-earth metals), a result of Hund's rule of maximum multiplicity. There are ferromagnetic metal alloys whose constituents are not themselves ferromagnetic, called Heusler alloys, named after Fritz Heusler. Conversely, there are non-magnetic alloys, such as types of stainless steel, composed almost exclusively of ferromagnetic metals.

Amorphous (non-crystalline) ferromagnetic metallic alloys can be made by very rapid quenching (cooling) of an alloy. These have the advantage that their properties are nearly isotropic (not aligned along a crystal axis); this results in low coercivity, low hysteresis loss, high permeability, and high electrical resistivity. One such typical material is a transition metal-metalloid alloy, made from about 80% transition metal (usually Fe, Co, or Ni) and a metalloid component (B, C, Si, P, or Al) that lowers the melting point.

A relatively new class of exceptionally strong ferromagnetic materials are the rare-earth magnets. They contain lanthanide elements that are known for their ability to carry large magnetic moments in well-localized f-orbitals.

The table lists a selection of ferromagnetic and ferrimagnetic compounds, along with their Curie temperature (TC), above which they cease to exhibit spontaneous magnetization.

Unusual materials

[edit]

Most ferromagnetic materials are metals, since the conducting electrons are often responsible for mediating the ferromagnetic interactions. It is therefore a challenge to develop ferromagnetic insulators, especially multiferroic materials, which are both ferromagnetic and ferroelectric.[8]

A number of actinide compounds are ferromagnets at room temperature or exhibit ferromagnetism upon cooling. PuP is a paramagnet with cubic symmetry at room temperature, but which undergoes a structural transition into a tetragonal state with ferromagnetic order when cooled below its TC = 125 K. In its ferromagnetic state, PuP's easy axis is in the ⟨100⟩ direction.[9]

In NpFe2 the easy axis is ⟨111⟩.[10] Above TC ≈ 500 K, NpFe2 is also paramagnetic and cubic. Cooling below the Curie temperature produces a rhombohedral distortion wherein the rhombohedral angle changes from 60° (cubic phase) to 60.53°. An alternate description of this distortion is to consider the length c along the unique trigonal axis (after the distortion has begun) and a as the distance in the plane perpendicular to c. In the cubic phase this reduces to c/a = 1.00. Below the Curie temperature, the lattice acquires a distortion

which is the largest strain in any actinide compound.[11] NpNi2 undergoes a similar lattice distortion below TC = 32 K, with a strain of (43 ± 5) × 10−4.[11] NpCo2 is a ferrimagnet below 15 K.

In 2009, a team of MIT physicists demonstrated that a lithium gas cooled to less than one kelvin can exhibit ferromagnetism.[12] The team cooled fermionic lithium-6 to less than 150 nK (150 billionths of one kelvin) using infrared laser cooling. This demonstration is the first time that ferromagnetism has been demonstrated in a gas.

In rare circumstances, ferromagnetism can be observed in compounds consisting of only s-block and p-block elements, such as rubidium sesquioxide.[13]

In 2018, a team of University of Minnesota physicists demonstrated that body-centered tetragonal ruthenium exhibits ferromagnetism at room temperature.[14]

Electrically induced ferromagnetism

[edit]

Recent research has shown evidence that ferromagnetism can be induced in some materials by an electric current or voltage. Antiferromagnetic LaMnO3 and SrCoO have been switched to be ferromagnetic by a current. In July 2020, scientists reported inducing ferromagnetism in the abundant diamagnetic material iron pyrite ("fool's gold") by an applied voltage.[15][16] In these experiments, the ferromagnetism was limited to a thin surface layer.

Explanation

[edit]

The Bohr–Van Leeuwen theorem, discovered in the 1910s, showed that classical physics theories are unable to account for any form of material magnetism, including ferromagnetism; the explanation rather depends on the quantum mechanical description of atoms. Each of an atom's electrons has a magnetic moment according to its spin state, as described by quantum mechanics. The Pauli exclusion principle, also a consequence of quantum mechanics, restricts the occupancy of electrons' spin states in atomic orbitals, generally causing the magnetic moments from an atom's electrons to largely or completely cancel.[17] An atom will have a net magnetic moment when that cancellation is incomplete.

Origin of atomic magnetism

[edit]

One of the fundamental properties of an electron (besides that it carries charge) is that it has a magnetic dipole moment, i.e., it behaves like a tiny magnet, producing a magnetic field. This dipole moment comes from a more fundamental property of the electron: its quantum mechanical spin. Due to its quantum nature, the spin of the electron can be in one of only two states, with the magnetic field either pointing "up" or "down" (for any choice of up and down). Electron spin in atoms is the main source of ferromagnetism, although there is also a contribution from the orbital angular momentum of the electron about the nucleus. When these magnetic dipoles in a piece of matter are aligned (point in the same direction), their individually tiny magnetic fields add together to create a much larger macroscopic field.

However, materials made of atoms with filled electron shells have a total dipole moment of zero: because the electrons all exist in pairs with opposite spin, every electron's magnetic moment is cancelled by the opposite moment of the second electron in the pair. Only atoms with partially filled shells (i.e., unpaired spins) can have a net magnetic moment, so ferromagnetism occurs only in materials with partially filled shells. Because of Hund's rules, the first few electrons in an otherwise unoccupied shell tend to have the same spin, thereby increasing the total dipole moment.

These unpaired dipoles (often called simply "spins", even though they also generally include orbital angular momentum) tend to align in parallel to an external magnetic field – leading to a macroscopic effect called paramagnetism. In ferromagnetism, however, the magnetic interaction between neighboring atoms' magnetic dipoles is strong enough that they align with each other regardless of any applied field, resulting in the spontaneous magnetization of so-called domains. This results in the large observed magnetic permeability of ferromagnetics, and the ability of magnetically hard materials to form permanent magnets.

Exchange interaction

[edit]
Main article: Exchange interaction

When two nearby atoms have unpaired electrons, whether the electron spins are parallel or antiparallel affects whether the electrons can share the same orbit as a result of the quantum mechanical effect called the exchange interaction. This in turn affects the electron location and the Coulomb (electrostatic) interaction and thus the energy difference between these states.

The exchange interaction is related to the Pauli exclusion principle, which says that two electrons with the same spin cannot also be in the same spatial state (orbital). This is a consequence of the spin–statistics theorem and that electrons are fermions. Therefore, under certain conditions, when the orbitals of the unpaired outer valence electrons from adjacent atoms overlap, the distributions of their electric charge in space are farther apart when the electrons have parallel spins than when they have opposite spins. This reduces the electrostatic energy of the electrons when their spins are parallel compared to their energy when the spins are antiparallel, so the parallel-spin state is more stable. This difference in energy is called the exchange energy. In simple terms, the outer electrons of adjacent atoms, which repel each other, can move further apart by aligning their spins in parallel, so the spins of these electrons tend to line up.

This energy difference can be orders of magnitude larger than the energy differences associated with the magnetic dipole–dipole interaction due to dipole orientation,[18] which tends to align the dipoles antiparallel. In certain doped semiconductor oxides, RKKY interactions have been shown to bring about periodic longer-range magnetic interactions, a phenomenon of significance in the study of spintronic materials.[19]

The materials in which the exchange interaction is much stronger than the competing dipole–dipole interaction are frequently called magnetic materials. For instance, in iron (Fe) the exchange force is about 1,000 times stronger than the dipole interaction. Therefore, below the Curie temperature, virtually all of the dipoles in a ferromagnetic material will be aligned. In addition to ferromagnetism, the exchange interaction is also responsible for the other types of spontaneous ordering of atomic magnetic moments occurring in magnetic solids: antiferromagnetism and ferrimagnetism. There are different exchange interaction mechanisms which create the magnetism in different ferromagnetic,[20] ferrimagnetic, and antiferromagnetic substances—these mechanisms include direct exchange, RKKY exchange, double exchange, and superexchange.

Magnetic anisotropy

[edit]
Main article: Magnetic anisotropy

Although the exchange interaction keeps spins aligned, it does not align them in a particular direction. Without magnetic anisotropy, the spins in a magnet randomly change direction in response to thermal fluctuations, and the magnet is superparamagnetic. There are several kinds of magnetic anisotropy, the most common of which is magnetocrystalline anisotropy. This is a dependence of the energy on the direction of magnetization relative to the crystallographic lattice. Another common source of anisotropy, inverse magnetostriction, is induced by internal strains. Single-domain magnets also can have a shape anisotropy due to the magnetostatic effects of the particle shape. As the temperature of a magnet increases, the anisotropy tends to decrease, and there is often a blocking temperature at which a transition to superparamagnetism occurs.[21]

Magnetic domains

[edit]
Electromagnetic dynamic magnetic domain motion of grain-oriented electrical silicon steel
Kerr micrograph of a metal surface showing magnetic domains, with red and green stripes denoting opposite magnetization directions
Main article: Magnetic domain

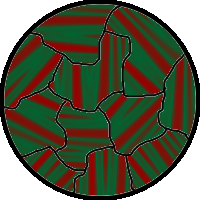
The spontaneous alignment of magnetic dipoles in ferromagnetic materials would seem to suggest that every piece of ferromagnetic material should have a strong magnetic field, since all the spins are aligned; yet iron and other ferromagnets are often found in an "unmagnetized" state. This is because a bulk piece of ferromagnetic material is divided into tiny regions called magnetic domains[22] (also known as Weiss domains). Within each domain, the spins are aligned, but if the bulk material is in its lowest energy configuration (i.e. "unmagnetized"), the spins of separate domains point in different directions and their magnetic fields cancel out, so the bulk material has no net large-scale magnetic field.

Ferromagnetic materials spontaneously divide into magnetic domains because the exchange interaction is a short-range force, so over long distances of many atoms, the tendency of the magnetic dipoles to reduce their energy by orienting in opposite directions wins out. If all the dipoles in a piece of ferromagnetic material are aligned parallel, it creates a large magnetic field extending into the space around it. This contains a lot of magnetostatic energy. The material can reduce this energy by splitting into many domains pointing in different directions, so the magnetic field is confined to small local fields in the material, reducing the volume of the field. The domains are separated by thin domain walls a number of molecules thick, in which the direction of magnetization of the dipoles rotates smoothly from one domain's direction to the other.

Magnetized materials

[edit]
Moving domain walls in a grain of silicon steel caused by an increasing external magnetic field in the "downward" direction, observed in a Kerr microscope. White areas are domains with magnetization directed up, dark areas are domains with magnetization directed down.

Thus, a piece of iron in its lowest energy state ("unmagnetized") generally has little or no net magnetic field. However, the magnetic domains in a material are not fixed in place; they are simply regions where the spins of the electrons have aligned spontaneously due to their magnetic fields, and thus can be altered by an external magnetic field. If a strong-enough external magnetic field is applied to the material, the domain walls will move via a process in which the spins of the electrons in atoms near the wall in one domain turn under the influence of the external field to face in the same direction as the electrons in the other domain, thus reorienting the domains so more of the dipoles are aligned with the external field. The domains will remain aligned when the external field is removed, and sum to create a magnetic field of their own extending into the space around the material, thus creating a "permanent" magnet. The domains do not go back to their original minimum energy configuration when the field is removed because the domain walls tend to become 'pinned' or 'snagged' on defects in the crystal lattice, preserving their parallel orientation. This is shown by the Barkhausen effect: as the magnetizing field is changed, the material's magnetization changes in thousands of tiny discontinuous jumps as domain walls suddenly "snap" past defects.

This magnetization as a function of an external field is described by a hysteresis curve. Although this state of aligned domains found in a piece of magnetized ferromagnetic material is not a minimal-energy configuration, it is metastable, and can persist for long periods, as shown by samples of magnetite from the sea floor which have maintained their magnetization for millions of years.

Heating and then cooling (annealing) a magnetized material, subjecting it to vibration by hammering it, or applying a rapidly oscillating magnetic field from a degaussing coil tends to release the domain walls from their pinned state, and the domain boundaries tend to move back to a lower energy configuration with less external magnetic field, thus demagnetizing the material.

Commercial magnets are made of "hard" ferromagnetic or ferrimagnetic materials with very large magnetic anisotropy such as alnico and ferrites, which have a very strong tendency for the magnetization to be pointed along one axis of the crystal, the "easy axis". During manufacture the materials are subjected to various metallurgical processes in a powerful magnetic field, which aligns the crystal grains so their "easy" axes of magnetization all point in the same direction. Thus, the magnetization, and the resulting magnetic field, is "built in" to the crystal structure of the material, making it very difficult to demagnetize.

Curie temperature

[edit]
Main article: Curie temperature

As the temperature of a material increases, thermal motion, or entropy, competes with the ferromagnetic tendency for dipoles to align. When the temperature rises beyond a certain point, called the Curie temperature, there is a second-order phase transition and the system can no longer maintain a spontaneous magnetization, so its ability to be magnetized or attracted to a magnet disappears, although it still responds paramagnetically to an external field. Below that temperature, there is a spontaneous symmetry breaking and magnetic moments become aligned with their neighbors. The Curie temperature itself is a critical point, where the magnetic susceptibility is theoretically infinite and, although there is no net magnetization, domain-like spin correlations fluctuate at all length scales.

The study of ferromagnetic phase transitions, especially via the simplified Ising spin model, had an important impact on the development of statistical physics. There, it was first clearly shown that mean field theory approaches failed to predict the correct behavior at the critical point (which was found to fall under a universality class that includes many other systems, such as liquid-gas transitions), and had to be replaced by renormalization group theory.[citation needed]

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Ferromagnetism

View on Grokipedia
from Grokipedia
Ferromagnetism is a fundamental property of certain materials, such as iron, nickel, , and some rare-earth elements like and , in which the atomic magnetic moments align spontaneously to produce a strong, net magnetization even in the absence of an external . This alignment results from quantum mechanical exchange interactions that couple the spins of unpaired electrons, primarily in the d-orbitals of transition metals, leading to permanent and strong attraction or repulsion to other magnets. Key characteristics include high , the formation of microscopic magnetic domains to minimize magnetostatic energy, and a critical known as the Curie point above which the material loses its ferromagnetic order and becomes paramagnetic. The phenomenon is explained by the parallel orientation of electron spins within atomic lattices, creating tiny magnetic dipoles that interact cooperatively over large scales, unlike weaker paramagnetic or diamagnetic effects in other materials. In ferromagnetic materials, this cooperative alignment persists below the —1043 K for iron, 1388 K for , and 627 K for —due to the dominance of exchange over thermal disorder. Magnetic domains, regions where spins are uniformly aligned, form to reduce overall , and their boundaries (domain walls) can move under applied fields, enabling reversal and . Ferromagnetism enables diverse applications, from permanent magnets in electric motors and devices to transformers and magnetic sensors, owing to properties like saturation magnetization, (resistance to demagnetization), and (shape change under ). Alloys such as neodymium-iron-boron (NdFeB) exhibit enhanced ferromagnetism for high-performance uses, while the effect's theoretical foundations, including mean-field approximations by and Weiss, underpin modern understandings in .

Introduction

Definition and Key Properties

Ferromagnetism is a fundamental magnetic property observed in certain materials, characterized by the spontaneous alignment of atomic magnetic moments, resulting in a net without the need for an external . This phenomenon occurs below a critical known as the (TCT_C), above which the material transitions to a paramagnetic state and loses its . The ability to retain this magnetization after the removal of an external field distinguishes ferromagnets as permanent magnets. Key properties of ferromagnetic materials include their high , denoted as χ\chi, which is positive (χ>0\chi > 0) and typically orders of magnitude larger than in paramagnetic materials, leading to strong attraction to external fields. Another hallmark is the in the curve, where the lags behind changes in the applied field, enabling and the creation of stable magnetic states. This arises from the alignment of atomic magnetic moments within microscopic regions called domains, which collectively produce the macroscopic permanent . In contrast to , where atomic moments align temporarily with an external field but randomize upon its removal (yielding small positive χ\chi), and , which induces a weak opposing (χ<0\chi < 0), ferromagnetism involves cooperative, persistent alignment. Antiferromagnetism features antiparallel alignment of moments with no net magnetization, while ferrimagnetism shows partial cancellation leading to a reduced net moment, both lacking the full spontaneous magnetization of ferromagnets. Everyday manifestations include refrigerator magnets that adhere to metallic surfaces and compass needles that align with Earth's magnetic field due to their ferromagnetic cores.

Historical Background

The phenomenon of ferromagnetism has roots in ancient observations of natural magnets. Around 600 BCE, the Greek philosopher Thales of Miletus noted that lodestone, a naturally occurring form of magnetite (Fe₃O₄), could attract iron fragments, marking one of the earliest recorded descriptions of magnetic attraction. Similarly, ancient Chinese texts from the same era describe the use of lodestone for divination and early navigational compasses, demonstrating practical awareness of its directional properties. Systematic study began in the Renaissance with William Gilbert's seminal 1600 treatise De Magnete, Magneticisque Corporibus, et de Magno Magnete Tellure, which distinguished magnetism from electricity and proposed that itself acts as a giant magnet, explaining compass behavior through experimental investigations of lodestone and iron. In the late 19th century, Pierre Curie advanced understanding in 1895 by discovering that ferromagnetic materials lose their strong magnetic properties above a critical temperature, transitioning to paramagnetic behavior, a finding derived from precise measurements of magnetic susceptibility under varying temperatures. Building on this, Pierre Weiss proposed in 1907 the molecular field theory, positing that atomic magnetic moments in ferromagnets align due to an internal "molecular field" from neighboring atoms, which also introduced the concept of magnetic domains to explain saturation and hysteresis. The 20th century brought quantum mechanical explanations, with Werner Heisenberg's 1928 theory attributing ferromagnetism to quantum exchange interactions between electron spins, where the Pauli exclusion principle favors parallel alignments in certain electron configurations, resolving the classical puzzle of spontaneous magnetization. This laid the groundwork for further developments in the 1930s, including Felix Bloch's calculations of spin-wave excitations (magnons) describing low-temperature magnetization reductions and Edmund Stoner's band theory linking ferromagnetism to electron density of states at the Fermi level in metals. Post-1950s experimental confirmations solidified these ideas, as advanced microscopy techniques directly visualized magnetic domain walls and structures, validating Weiss's domain hypothesis through observations of stripe and closure domains. More recently, the 2017 discovery of intrinsic ferromagnetism in monolayer CrI₃, a van der Waals material, extended these concepts to two dimensions, revealing layer-dependent Curie temperatures up to 45 K via magneto-optical Kerr effect measurements. Subsequent research has identified additional 2D ferromagnets with higher Curie temperatures approaching room temperature, such as CrGaS₃ (theoretically 520–814 K) and ferromagnetic semiconductors achieving 530 K experimentally as of 2025. Studies of ferromagnetism profoundly influenced 19th-century technology, particularly through integrations with electromagnetism that enabled practical electric motors; Michael Faraday's 1821 demonstration of continuous rotation via electromagnetic torque, building on Oersted's 1820 linkage of current and magnetism, paved the way for devices like the 1830s prototypes by Joseph Henry and Thomas Davenport.

Ferromagnetic Materials

Traditional Materials

Traditional ferromagnetic materials primarily consist of elemental metals, alloys, and certain oxide compounds that exhibit strong, spontaneous magnetization below their respective Curie temperatures. These materials form the foundation of magnetic technologies due to their well-characterized properties and ease of production. Among the elemental ferromagnets, iron (Fe), nickel (Ni), and cobalt (Co) are the most prominent. Iron has a Curie temperature of 1043 K and a saturation magnetization of 2.15 T, making it suitable for applications requiring high magnetic flux density. Nickel exhibits a lower Curie temperature of 627 K and saturation magnetization of 0.64 T, while cobalt displays the highest Curie temperature at 1388 K with a saturation magnetization of 1.79 T. These elements generally possess low coercivities, typically below 0.1 kA/m for pure bulk forms, which facilitates easy magnetization but limits their use in permanent magnets without alloying. Alloys such as permalloys (typically 80% Ni-20% Fe) enhance soft magnetic properties with relative permeabilities exceeding 100,000 and saturation magnetizations around 0.8 T, alongside very low coercivities of about 0.008 kA/m. Their Curie temperature is approximately 853 K. Alnico alloys (Al-Ni-Co, e.g., Alnico 5 with ~8% Al, 14% Ni, 24% Co, balance Fe) are cast permanent magnets with Curie temperatures of 810–860°C (1083–1133 K), saturation magnetizations near 1.25 T, and coercivities of 50–720 Oe (4–57 kA/m), offering high temperature stability for demanding environments. Compounds like magnetite (Fe₃O₄), a naturally occurring mineral, demonstrate ferromagnetic behavior with a Curie temperature of 853 K (580°C) and saturation magnetization of approximately 0.60 T, though it technically exhibits ferrimagnetism due to antiparallel sublattice alignments. Its low coercivity and abundance make it historically significant in geological magnetism studies. Neodymium-iron-boron (Nd₂Fe₁₄B) represents a high-performance permanent magnet compound with a Curie temperature of 585 K (312°C), saturation magnetization of 1.60 T, and high coercivities up to 1500 kA/m, enabling compact, strong magnets. These materials are prepared through smelting of ores in blast furnaces for elements like iron and subsequent alloying via melting in induction furnaces under controlled atmospheres to achieve desired compositions. Common applications include permalloys and iron-based alloys in transformer cores for efficient energy transfer, alnico and Nd₂Fe₁₄B in electric motors for torque generation, and Nd₂Fe₁₄B in hard disk drives for data storage.
MaterialCurie Temperature (K)Saturation Magnetization (T)Coercivity (kA/m)
Iron (Fe)10432.15~0.08
Nickel (Ni)6270.64~0.02–1.8
Cobalt (Co)13881.79~0.06–5.7
Permalloy (80Ni-20Fe)8530.80~0.008
Alnico 51083–11331.254–57
Magnetite (Fe₃O₄)8530.60Low (<1)
Nd₂Fe₁₄B5851.60Up to 1500
Data compiled from referenced sources above.

Exotic and Recent Developments

Rare-earth elements, such as gadolinium, exhibit exceptional ferromagnetic properties due to their high atomic magnetic moments arising from unpaired 4f electrons. Gadolinium possesses the largest atomic magnetic moment among lanthanides, with a saturation moment of approximately 7.63 μ_B per atom in pure single-crystal form, enabling strong ferromagnetic ordering below its Curie temperature of 293 K. Heusler alloys represent another class of unusual ferromagnetic materials, particularly noted for their half-metallic ferromagnetism, where conduction electrons are fully spin-polarized, leading to 100% spin polarization at the Fermi level. Quaternary Heusler compounds like CoFeMnSi demonstrate this behavior with integer total magnetic moments per formula unit, high Curie temperatures exceeding 600 K, and potential for spintronic applications due to their structural compatibility with semiconductors. Dilute magnetic semiconductors (DMS) achieve ferromagnetism through electrical doping of non-magnetic hosts with magnetic ions, enabling carrier-mediated exchange interactions. In gallium arsenide doped with manganese (Ga,Mn)As, manganese substitution induces ferromagnetism with Curie temperatures up to around 200 K in optimized films, though recent nanoparticle integrations have pushed effective room-temperature operation by enhancing magnetization stability. This doping strategy transforms the semiconductor into a ferromagnetic state, with hole-mediated coupling between Mn spins facilitating long-range order, as evidenced in epitaxial (Ga,Mn)As layers grown by molecular beam epitaxy. Two-dimensional van der Waals ferromagnets have revolutionized low-dimensional magnetism by confining ferromagnetic order to atomic layers. Chromium digermanium ditelluride (Cr₂Ge₂Te₆) was identified as an intrinsic ferromagnet in 2017, with layer-dependent Curie temperatures up to 66 K and out-of-plane anisotropy, enabling the isolation of monolayer magnets via mechanical exfoliation. This material's weak interlayer coupling allows stacking into heterostructures for spintronic devices, where spin-orbit torques can switch magnetization with low current densities, on the order of 10⁶ A/cm². Recent advances from 2023 to 2025 have expanded ferromagnetism into unconventional regimes. Strain engineering has induced ferromagnetism in traditionally antiferromagnetic materials, such as in bulk vanadium disulfide (VS₂) interlayers, where in-plane tensile strain triggers anisotropic ferromagnetic ordering below 40 K via modulation of superexchange pathways. In 2025, observations of p-wave magnetism in altermagnetic systems, such as nickel iodide (NiI₂) crystals and calcium ruthenate (Ca₃Ru₂O₇), where spin-orbit coupling mixes d- and p-wave components to yield unconventional band splittings, emerged. Earth-abundant nitrides like manganese nitride (Mn₄N) have seen synthesis breakthroughs, with epitaxial thin films achieving perpendicular magnetization and Curie temperatures above 500 K through reactive sputtering, offering sustainable alternatives to rare-earth magnets for energy applications. Despite these innovations, exotic ferromagnets face significant challenges in practical deployment. Achieving stable room-temperature operation remains elusive for many 2D and dilute systems, where thermal fluctuations disrupt long-range order, necessitating strain or gating to elevate . Scalability for quantum devices is hindered by defects in heterostructures and sensitivity to environmental noise, limiting coherence times in spin-based below milliseconds at ambient conditions.

Fundamental Mechanisms

Origin of Atomic Magnetism

The magnetic moments responsible for atomic magnetism in ferromagnetic materials originate primarily from the electrons within atoms, specifically their spin and orbital angular momenta. The spin magnetic moment of an electron is given by μs=−gμBS/ℏ\boldsymbol{\mu}_s = -g \mu_B \mathbf{S} / \hbar, where g≈2g \approx 2 is the electron g-factor, μB\mu_B is the , S\mathbf{S} is the spin angular momentum, and ℏ\hbar is the reduced Planck's constant. The orbital magnetic moment arises from the electron's orbital motion and is expressed as μl=−μBL/ℏ\boldsymbol{\mu}_l = -\mu_B \mathbf{L} / \hbar, with L\mathbf{L} as the orbital angular momentum. In most ferromagnetic atoms, the spin contribution dominates due to the near-unity g-factor for spin, while the orbital moment is often partially quenched in solid-state environments. The Pauli exclusion principle and Hund's rules govern the configuration of electrons in atomic shells, leading to net magnetic moments in certain elements. Hund's first rule maximizes the total spin SS by aligning unpaired electrons with parallel spins in degenerate orbitals, minimizing electron-electron repulsion. This is particularly relevant for partially filled d- or f-shells in transition and rare-earth metals, where the Pauli principle prevents more than two electrons per orbital (with opposite spins). Hund's second rule further maximizes the orbital angular momentum LL for the given spin multiplicity. As a result, atoms with unpaired electrons in these shells exhibit significant atomic magnetic moments, forming the basis for ferromagnetism. A representative example is the iron (Fe) atom, which in its ground state has an electron configuration of [Ar] 3d⁶ 4s², resulting in four unpaired electrons in the 3d shell according to Hund's rules. This yields a total atomic magnetic moment of approximately 4 μB\mu_B, primarily from the spin contribution (with S=2S = 2). Only specific elements in the display net atomic moments conducive to ferromagnetism at room temperature, namely , , , and . These elements feature partially filled 3d or 4f shells with sufficient unpaired electrons (e.g., 4 in Fe, 3 in Co, 2 in Ni, 7 in Gd) to produce moments of 2–4 μB\mu_B per atom, while other transition metals like or have moments that cancel or are too weak due to more balanced filling or antiferromagnetic tendencies. Elements beyond these, such as with a filled 3d shell, exhibit no net moment. In metallic ferromagnets, atomic moments transition to band magnetism, where electrons are itinerant rather than fully localized. Localized moments persist in rare-earth metals like Gd due to strong intra-atomic correlations in 4f shells, whereas in 3d transition metals like Fe, Co, and Ni, electrons form delocalized bands with partial itinerancy. The Stoner criterion determines the onset of itinerant ferromagnetism: I⋅[DOS](/page/Densityofstates)(EF)>1I \cdot \mathrm{[DOS](/page/Density_of_states)}(E_F) > 1, where II is the exchange integral and [DOS](/page/Densityofstates)(EF)\mathrm{[DOS](/page/Density_of_states)}(E_F) is the at the ; a high [DOS](/page/Densityofstates)(EF)\mathrm{[DOS](/page/Density_of_states)}(E_F) enables band splitting into majority and minority spin bands, yielding net . This atomic-scale magnetism sets the stage for interatomic exchange interactions that align moments collectively.

Exchange Interaction

The exchange interaction is the primary quantum mechanical mechanism responsible for the parallel alignment of atomic magnetic moments in ferromagnetic materials, arising from the quantum overlap of wavefunctions rather than classical dipole-dipole forces. This interaction, first theoretically described by in 1928, stabilizes the ferromagnetic order by favoring low-energy configurations where neighboring spins are aligned. The Heisenberg model provides a foundational description of this interaction, expressed through the Hamiltonian H=−J∑⟨i,j⟩Si⋅Sj,H = -J \sum_{\langle i,j \rangle} \mathbf{S}_i \cdot \mathbf{S}_j, where J>0J > 0 indicates ferromagnetic , Si\mathbf{S}_i and Sj\mathbf{S}_j are the spin operators at sites ii and jj, and the sum is over nearest-neighbor pairs. In this model, the direct exchange arises from the , where the symmetric spatial wavefunction for parallel reduces the repulsion between electrons, lowering the system's energy. For ferromagnetic metals, this direct exchange dominates short-range interactions between localized moments. In itinerant metallic ferromagnets like transition metals, the is primarily described by the Stoner mechanism of band splitting, while in systems with localized moments and conduction electrons, such as some rare-earth compounds, the indirect Ruderman-Kittel-Kasuya-Yosida ( can mediate coupling, leading to oscillatory exchange that can be ferromagnetic at short distances. In insulating ferromagnets, occurs through virtual hopping of electrons between magnetic ions via intervening non-magnetic anions, resulting in effective ferromagnetic coupling when orbital overlaps favor parallel alignments. The energy scale of the typically ranges from 10 to 100 meV per bond in common ferromagnets, such as approximately 22–25 meV for nearest-neighbor iron atoms in body-centered cubic iron, which greatly exceeds the kBT≈25k_B T \approx 25 meV at (300 K), thereby enabling stable spin alignment. This strong coupling distinguishes ferromagnetism from weaker paramagnetic behavior. A mean-field approximation, introduced by Pierre Weiss in 1907, simplifies the treatment by replacing the interactions of a given spin with an effective molecular field λM\lambda M, where MM is the average and λ\lambda is proportional to the exchange constant. This leads to the Weiss equation for the M=Nμ(coth⁡x−1x),x=μBeffkBT,Beff=B+λM,M = N \mu \left( \coth x - \frac{1}{x} \right), \quad x = \frac{\mu B_\mathrm{eff}}{k_B T}, \quad B_\mathrm{eff} = B + \lambda M, where NN is the number of magnetic atoms, μ\mu is the atomic , BB is the external field, kBk_B is Boltzmann's constant, and TT is ; this approximation captures the collective alignment driven by exchange. The sign of the exchange parameter JJ determines the magnetic order: positive JJ in the Heisenberg model promotes parallel spin alignment characteristic of ferromagnetism, whereas negative JJ favors antiparallel alignment in antiferromagnets.

Magnetic Anisotropy

describes the dependence of the on the direction of in ferromagnetic materials, arising from interactions that favor certain orientations relative to the or sample geometry. This directional preference is quantified by the anisotropy energy, which for uniaxial systems takes the form Eanis=Ksin⁡2θE_{\text{anis}} = K \sin^2 \theta, where KK is the anisotropy constant and θ\theta is the angle between the magnetization vector and the easy axis. In cubic crystals, the expression is more complex, involving higher-order terms such as Eanis=K1(α12α22+α22α32+α32α12)+K2α12α22α32E_{\text{anis}} = K_1 ( \alpha_1^2 \alpha_2^2 + \alpha_2^2 \alpha_3^2 + \alpha_3^2 \alpha_1^2 ) + K_2 \alpha_1^2 \alpha_2^2 \alpha_3^2, where αi\alpha_i are direction cosines, reflecting the symmetry of the lattice. While the provides a baseline isotropic alignment of spins, introduces these directional variations, influencing the overall stability of the ferromagnetic state. The origins of magnetic anisotropy are primarily magnetocrystalline, shape, and magnetoelastic. Magnetocrystalline anisotropy stems from spin-orbit coupling, which links the spin magnetic moments to the orbital moments and thereby to the crystal lattice directions, making certain orientations energetically favorable due to the relativistic interaction within the atomic electrons. Shape anisotropy arises from demagnetization fields, which generate stray opposing the ; elongated or thin geometries minimize this magnetostatic energy by preferring alignment along the long axis, as described by the demagnetization tensor. Magnetoelastic anisotropy results from the coupling between and lattice strain, where mechanical stress alters the crystal field and thus the spin-orbit interaction, leading to strain-dependent energy preferences. In the total magnetization energy, anisotropy contributes alongside other terms: the exchange energy promotes uniform spin alignment, the Zeeman energy −M⋅B-\mathbf{M} \cdot \mathbf{B} (where M\mathbf{M} is and B\mathbf{B} is the applied field) aligns moments with the field, and the energy enforces directional biases. This interplay defines easy and hard axes; for example, hexagonal close-packed exhibits strong uniaxial with K1≈4×105K_1 \approx 4 \times 10^5 J/m³ along the c-axis, making magnetization along this direction the lowest- state and perpendicular directions hard axes. Such effects are crucial for applications, as high anisotropy enhances resistance to demagnetization, contributing to in permanent magnets by increasing the energy barrier for spin reversal. Anisotropy constants are typically measured via torque magnetometry, in which a sample is rotated in a uniform magnetic field, and the resulting torque τ=M×B\mathbf{\tau} = \mathbf{M} \times \mathbf{B} is detected using a torsion balance or cantilever; the angular dependence of the torque reveals the energy landscape and allows extraction of KK values through Fourier analysis. This technique is particularly effective for single crystals, providing insights into how anisotropy governs macroscopic magnetic behavior without requiring domain-level details.

Domain Structure and Magnetization

Magnetic Domains

In ferromagnetic materials, magnetic domains are microscopic regions where the atomic magnetic moments are aligned parallel to each other, resulting in uniform within each domain. These domains, first postulated by Pierre Weiss in 1907 to explain the high of ferromagnets despite their atomic-scale moments, typically range from 10 to 100 μm in lateral size, though this varies with material and geometry. The boundaries between adjacent domains, known as domain walls, are thin transition regions approximately 100 nm thick, where the direction rotates gradually to connect the uniform orientations of neighboring domains. The formation of magnetic domains in bulk ferromagnets serves to minimize the total by balancing competing contributions: the exchange energy, which favors parallel alignment of moments over large volumes; the energy, which prefers specific crystallographic directions; and the demagnetization energy, which arises from stray at free surfaces and penalizes large-scale uniform . In the absence of an external field, the equilibrium domain structure emerges as a compromise that reduces the overall magnetostatic energy compared to a single-domain state, with domain sizes scaling as the of the ratio of exchange stiffness to demagnetization factors in simple models. Domain walls themselves carry energy due to the incomplete alignment within the transition region, quantified by the wall energy density σ, given by the σ = ∫ [A (dθ/dx)² + K sin²θ] dx, where A is the exchange stiffness constant, K is the constant, θ is the angle of relative to the easy axis, and the integration is across the wall thickness. This expression, derived from micromagnetic theory, shows that narrower walls increase exchange energy but reduce contributions, leading to an optimal wall width on the order of √(A/K). Two primary types of domain walls occur in ferromagnets: 180° walls, which reverse the magnetization direction between domains to close lines and minimize stray fields; and 90° walls, which redirect magnetization between easy axes, often appearing at domain branching points. In bulk materials, 180° walls typically adopt a Bloch configuration, where the magnetization rotates out of the wall plane to avoid magnetostatic costs, whereas Néel walls, with in-plane , dominate in thin films to reduce edge effects. Magnetic domains and their walls are observed using techniques that reveal surface magnetization patterns, such as Bitter pattern microscopy, which employs colloidal magnetic particles attracted to stray fields at domain boundaries, and the magneto-optical , which detects changes in reflected light polarization due to surface . These methods, developed in the early , confirm domain structures and wall motions in real time. In soft ferromagnets like pure iron, large domains and low wall energies enable easy wall motion under small fields, yielding high permeability and low , whereas hard ferromagnets like alloys feature smaller domains, pinned walls, and higher wall energies due to defects or compositions, resulting in stable for permanent magnet applications.

Magnetization Processes

In ferromagnets, magnetization processes describe the dynamic response of magnetic domains to an applied external , leading to overall material . These processes primarily involve the motion of domain walls and the of atomic magnetic moments within domains, enabling the material to achieve net while minimizing magnetostatic . motion is a key mechanism in the initial stages of magnetization. When a weak external field is applied, domain walls—boundaries separating regions of aligned moments—undergo reversible bowing or displacement, allowing favorable domains to expand slightly without permanent structural changes. As the field strengthens, irreversible wall motion occurs, where walls unpin from defects and jump abruptly, causing larger domain growth and contributing to the non-linear magnetization curve. At higher fields, rotation of magnetic moments within domains becomes dominant, aligning moments more closely with the field direction beyond easy axes. This rotation complements wall motion, particularly in materials with strong , and drives the approach to saturation. The collective effect of these processes manifests in the loop, a closed curve plotting magnetic induction BB against applied field HH. Starting from a demagnetized state, the initial follows an upward curve to saturation MsM_s, where nearly all moments align with the field. Upon field reversal, MrM_r persists as residual without external field, while HcH_c represents the reverse field needed to reduce net to zero. The loop's area quantifies energy loss per cycle due to irreversible processes like wall pinning and moment reorientation. The initial magnetization curve, from zero field to saturation, highlights the transition between mechanisms: low-field increases arise mainly from reversible and irreversible domain wall motion, while high-field portions involve primarily moment rotation as walls cease significant movement. During magnetization, the Barkhausen effect produces detectable noise from discrete jumps in magnetization, originating from sudden unpinning and motion of domain walls over obstacles like impurities or grain boundaries. These jumps, audible as clicks in early experiments, reflect the discontinuous nature of irreversible wall motion. Coercivity HcH_c is influenced by microstructural factors such as grain size and impurities, which act as pinning sites for domain walls. Smaller grains increase HcH_c by providing more pinning centers, whereas larger grains and fewer impurities reduce HcH_c, as in soft magnets like electrical steels used in transformers for efficient flux changes with minimal energy loss.

Curie Temperature

The , denoted TcT_c, is the critical temperature at which a ferromagnetic material undergoes a from a spontaneously magnetized state to a paramagnetic one, where agitation disrupts the alignment of atomic magnetic moments and vanishes. This transition marks the point where the can no sustain long-range magnetic order against . In the mean-field approximation developed by Pierre Weiss, the Curie temperature is derived from the balance between exchange energy and , yielding the Tc=2zJS(S+1)3kB,T_c = \frac{2 z J S(S+1)}{3 k_B}, where zz is the number of nearest-neighbor atoms, JJ is the exchange integral, SS is the spin angular momentum quantum number, and kBk_B is Boltzmann's constant. This treats the local field as an average over neighboring spins but overestimates TcT_c in real materials due to neglected spin fluctuations and correlations, leading to systematic deviations observed experimentally. Near TcT_c, the MM exhibits critical behavior described by the power law M∼(Tc−T)βM \sim (T_c - T)^\beta, where the β≈0.36\beta \approx 0.36 for three-dimensional Heisenberg ferromagnets, contrasting with the mean-field prediction of β=0.5\beta = 0.5 and highlighting the role of in low dimensions. The is experimentally determined from the divergence in or the lambda-shaped anomaly in specific heat, which signal the onset of the . Modifications like doping can elevate TcT_c by strengthening the , as seen in tailored alloys. For example, as of 2025, (Ga,Fe)Sb ferromagnetic semiconductors have achieved record-high TcT_c values of 470–530 K through optimized growth techniques. Above TcT_c, the material exhibits paramagnetic behavior with no net magnetization in zero field, limiting applications requiring stable ferromagnetism. For instance, bulk iron has Tc=1043T_c = 1043 K, enabling high-temperature operation, whereas early two-dimensional ferromagnets like CrI₃ have Tc≈45T_c \approx 45 K, but recent developments in materials such as epitaxial Fe₃GaTe₂ films exhibit Tc≈360T_c \approx 360 K (as of 2025), enabling progress toward room-temperature devices.

References

  1. http://hyperphysics.phy-astr.gsu.edu/hbase/Solids/ferro.html
  2. https://satheeneet.iitk.ac.in/article/physics/physics-ferromagnetism/
  3. https://cse.umn.edu/irm/2-classes-magnetic-materials
  4. http://hyperphysics.phy-astr.gsu.edu/hbase/Tables/Curie.html
  5. https://www.feynmanlectures.caltech.edu/II_36.html
  6. https://ps.uci.edu/~cyu/p115A/LectureNotes/Lecture17/html_version/lecture17.html
  7. https://courses.physics.illinois.edu/phys525/sp2024/units/magnetic2.pdf
  8. https://courses.physics.illinois.edu/phys401/sp2020/lectures/lecture12.pdf
  9. https://www.geo.arizona.edu/Paleomag/chap02.pdf
  10. http://physics.bu.edu/~duffy/semester2/d16_ferromagnetism.html
  11. https://hep.physics.illinois.edu/home/serrede/P435/Lecture_Notes/Magnetism.pdf
  12. https://www.chm.uri.edu/weuler/chm501/lectures/lecture16.html
  13. https://www6.slac.stanford.edu/news/2017-01-11-sketching-out-magnetism-electricity
  14. https://maglabweb.magnet.fsu.edu/magnet-academy/history-of-electricity-magnetism/museum/lodestone-600-bc/
  15. https://pwg.gsfc.nasa.gov/Electric/-E14-history.htm
  16. https://www.lancaster.ac.uk/fass/projects/gilbert/works/demagnete.htm
  17. https://history.aip.org/exhibits/curie/pierre.htm
  18. https://hal.science/hal-02888378v1/document
  19. http://www.neo-classical-physics.info/uploads/3/4/3/6/34363841/heisenberg_-_on_the_theory_of_ferromagnetism.pdf
  20. https://link.aps.org/doi/10.1103/RevModPhys.17.27
  21. https://www.imim.pl/files/archiwum/Vol3_2023/38.pdf
  22. https://www.nature.com/articles/nature22391
  23. https://pubs.aip.org/aip/jap/article/135/7/073903/3265797/Two-dimensional-monolayer-CrGaS3-A-ferromagnetic
  24. https://phys.org/news/2025-05-high-curie-temperature-ferromagnetic-semiconductor.html
  25. https://nationalmaglab.org/magnet-academy/history-of-electricity-magnetism/pioneers/michael-faraday/
  26. https://www.sciencedirect.com/topics/materials-science/ferromagnetic-material
  27. https://royalsocietypublishing.org/doi/10.1098/rspa.1971.0044
  28. https://physics.stackexchange.com/questions/470095/coercivity-of-pure-iron
  29. https://www.espimetals.com/index.php/technical-data/175-Permalloy%252080
  30. https://egusphere.copernicus.org/preprints/2023/egusphere-2023-2191/egusphere-2023-2191.pdf
  31. https://www.sciencedirect.com/topics/chemistry/alnico
  32. https://www.arnoldmagnetics.com/wp-content/uploads/2017/10/Cast-Alnico-Permanent-Magnet-Brochure-101117-1.pdf
  33. https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2012GC004440
  34. https://www.arnoldmagnetics.com/wp-content/uploads/2017/10/Catalog-151021.pdf
  35. https://www.okonrecycling.com/magnet-recycling-and-applications/magnet-technology/magnets-made/
  36. https://www.eclipsemagnetics.com/resources/guides/a-quick-guide-to-magnets-magnetic-metals-and-non-magnetic-metals/
  37. https://texasgateway.org/resource/203-motors-generators-and-transformers
  38. https://pubs.aip.org/aip/acp/article/29/1/329/639224/Magnetic-moments-of-ferromagnetic-gadolinium
  39. https://www.nature.com/articles/s41598-017-01782-5
  40. https://iopscience.iop.org/article/10.1088/1361-6528/ad8e6d
  41. https://link.aps.org/doi/10.1103/PhysRevLett.100.047206
  42. https://ieeexplore.ieee.org/document/8083602
  43. https://onlinelibrary.wiley.com/doi/abs/10.1002/adma.201906021
  44. https://pubs.rsc.org/en/content/articlelanding/2023/cc/d3cc01662e
  45. https://news.mit.edu/2025/physicists-observe-new-form-magnetism-0605
  46. https://www.nature.com/articles/s41535-025-00814-y
  47. https://www.semanticscholar.org/paper/Progress-in-ferrimagnetic-Mn4N-films-and-its-for-Zhang-Mi/e49b85bc6be31b7fc2551de888e9150f193486e9
  48. https://www.cell.com/cell-reports-physical-science/pdf/S2666-3864%2824%2900670-2.pdf
  49. https://www.sciencedirect.com/science/article/pii/S2666386424006702
  50. https://www.grandinetti.org/teaching/physical/resources/LectureCh20.pdf
  51. https://academic.oup.com/book/27903/chapter/203887626
  52. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Physical_Chemistry_%28LibreTexts%29/08%253A_Multielectron_Atoms/8.10%253A_Hund%27s_Rules_Determine_the_Term_Symbols_of_the_Ground_Electronic_States
  53. https://www.researchgate.net/publication/252235275_Magnetization_of_iron_clusters_from_first-principles_calculations
  54. https://www2.physics.siu.edu/~dmazumdar/575_Magnetism/Week7/Stoner_model_Magnetism_CMP.pdf
  55. https://www.feynmanlectures.caltech.edu/II_37.html
  56. https://link.aps.org/doi/10.1103/PhysRev.79.350
  57. https://www.ias.ac.in/public/Volumes/reso/009/08/0057-0066.pdf
  58. https://journals.aps.org/prb/abstract/10.1103/PhysRevB.63.054418
  59. https://www.sciencedirect.com/topics/physics-and-astronomy/magnetic-anisotropy
  60. https://refubium.fu-berlin.de/bitstream/handle/fub188/6991/02_chapter2.pdf?sequence=3&isAllowed=y
  61. https://www.sciencedirect.com/topics/engineering/magnetocrystalline-anisotropy
  62. https://cse.umn.edu/irm/3-magnetic-anisotropy
  63. https://www.sciencedirect.com/science/article/pii/S030488531200858X
  64. https://www.sciencedirect.com/science/article/pii/0304885384902488
  65. https://pubs.aip.org/aip/jap/article/120/1/013903/142875/Torque-magnetometry-of-perpendicular-anisotropy
  66. https://www.sciencedirect.com/science/article/abs/pii/S0010854517302515
  67. https://www.sciencedirect.com/topics/engineering/magnetic-domain
  68. https://www.sciencedirect.com/topics/materials-science/domain-wall
  69. https://link.aps.org/doi/10.1103/PhysRev.70.965
  70. https://pubs.aip.org/aip/jap/article/36/3/1068/695759/Kerr-Effect-and-Bitter-Pattern-Measurements-of
  71. https://www.sciencedirect.com/science/article/abs/pii/S1044580397001290
  72. https://www.sciencedirect.com/science/article/abs/pii/S092583882301561X
  73. https://chem.libretexts.org/Bookshelves/Inorganic_Chemistry/Introduction_to_Inorganic_Chemistry_%28Wikibook%29/06%253A_Metals_and_Alloys-_Structure_Bonding_Electronic_and_Magnetic_Properties/6.09%253A_Hard_and_Soft_Magnets
  74. https://iopscience.iop.org/article/10.1088/1361-6463/ad0568
  75. https://www.tandfonline.com/doi/abs/10.1080/10408437608243549
  76. https://arxiv.org/pdf/1603.08239
  77. https://www.nature.com/articles/s41586-022-04935-3
  78. http://sites.science.oregonstate.edu/~giebultt/COURSES/ph674/mfa4.pdf
  79. https://magnetism.eu/esm/2011/notes/neda-notes.pdf
  80. https://link.aps.org/doi/10.1103/PhysRevB.65.144520
  81. https://epjtechniquesandinstrumentation.springeropen.com/articles/10.1140/epjti/s40485-017-0040-y
  82. https://pubs.aip.org/aip/apl/article/126/16/162407/3345196/Very-high-Curie-temperature-470-530-K-in-Ga-Fe-Sb
  83. https://www.nature.com/articles/s41598-019-50000-x
  84. https://pubs.acs.org/doi/10.1021/acsnano.5c07732
Add your contribution
Related Hubs
User Avatar
No comments yet.