Recent from talks
Nothing was collected or created yet.
Sequence
View on Wikipedia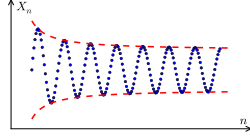
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called elements, or terms). The number of elements (possibly infinite) is called the length of the sequence. Unlike a set, the same elements can appear multiple times at different positions in a sequence, and unlike a set, the order does matter. Formally, a sequence can be defined as a function from natural numbers (the positions of elements in the sequence) to the elements at each position. The notion of a sequence can be generalized to an indexed family, defined as a function from an arbitrary index set.
For example, (M, A, R, Y) is a sequence of letters with the letter "M" first and "Y" last. This sequence differs from (A, R, M, Y). Also, the sequence (1, 1, 2, 3, 5, 8), which contains the number 1 at two different positions, is a valid sequence. Sequences can be finite, as in these examples, or infinite, such as the sequence of all even positive integers (2, 4, 6, ...).
The position of an element in a sequence is its rank or index; it is the natural number for which the element is the image. The first element has index 0 or 1, depending on the context or a specific convention. In mathematical analysis, a sequence is often denoted by letters in the form of , and , where the subscript n refers to the nth element of the sequence; for example, the nth element of the Fibonacci sequence is generally denoted as .
In computing and computer science, finite sequences are usually called strings, words or lists, with the specific technical term chosen depending on the type of object the sequence enumerates and the different ways to represent the sequence in computer memory. Infinite sequences are called streams.
The empty sequence ( ) is included in most notions of sequence. It may be excluded depending on the context.
Examples and notation
[edit]A sequence can be thought of as a list of elements with a particular order.[1][2] Sequences are useful in a number of mathematical disciplines for studying functions, spaces, and other mathematical structures using the convergence properties of sequences. In particular, sequences are the basis for series, which are important in differential equations and analysis. Sequences are also of interest in their own right, and can be studied as patterns or puzzles, such as in the study of prime numbers.
There are a number of ways to denote a sequence, some of which are more useful for specific types of sequences. One way to specify a sequence is to list all its elements. For example, the first four odd numbers form the sequence (1, 3, 5, 7). This notation is used for infinite sequences as well. For instance, the infinite sequence of positive odd integers is written as (1, 3, 5, 7, ...). Because notating sequences with ellipsis leads to ambiguity, listing is most useful for customary infinite sequences which can be easily recognized from their first few elements. Other ways of denoting a sequence are discussed after the examples.
Examples
[edit]
The prime numbers are the natural numbers greater than 1 that have no divisors but 1 and themselves. Taking these in their natural order gives the sequence (2, 3, 5, 7, 11, 13, 17, ...). The prime numbers are widely used in mathematics, particularly in number theory where many results related to them exist.
The Fibonacci numbers comprise the integer sequence in which each element is the sum of the previous two elements. The first two elements are either 0 and 1 or 1 and 1 so that the sequence is (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...).[1]
Other examples of sequences include those made up of rational numbers, real numbers and complex numbers. The sequence (.9, .99, .999, .9999, ...), for instance, approaches the number 1. In fact, every real number can be written as the limit of a sequence of rational numbers (e.g. via its decimal expansion, also see completeness of the real numbers). As another example, π is the limit of the sequence (3, 3.1, 3.14, 3.141, 3.1415, ...), which is increasing. A related sequence is the sequence of decimal digits of π, that is, (3, 1, 4, 1, 5, 9, ...). Unlike the preceding sequence, this sequence does not have any pattern that is easily discernible by inspection.
Other examples are sequences of functions, whose elements are functions instead of numbers.
The On-Line Encyclopedia of Integer Sequences comprises a large list of examples of integer sequences.[3]
Indexing
[edit]Other notations can be useful for sequences whose pattern cannot be easily guessed or for sequences that do not have a pattern such as the digits of π. One such notation is to write down a general formula for computing the nth term as a function of n, enclose it in parentheses, and include a subscript indicating the set of values that n can take. For example, in this notation the sequence of even numbers could be written as . The sequence of squares could be written as . The variable n is called an index, and the set of values that it can take is called the index set.
It is often useful to combine this notation with the technique of treating the elements of a sequence as individual variables. This yields expressions like , which denotes a sequence whose nth element is given by the variable . For example:
One can consider multiple sequences at the same time by using different variables; e.g. could be a different sequence than . One can even consider a sequence of sequences: denotes a sequence whose mth term is the sequence .
An alternative to writing the domain of a sequence in the subscript is to indicate the range of values that the index can take by listing its highest and lowest legal values. For example, the notation denotes the ten-term sequence of squares . The limits and are allowed, but they do not represent valid values for the index, only the supremum or infimum of such values, respectively. For example, the sequence is the same as the sequence , and does not contain an additional term "at infinity". The sequence is a bi-infinite sequence, and can also be written as .
In cases where the set of indexing numbers is understood, the subscripts and superscripts are often left off. That is, one simply writes for an arbitrary sequence. Often, the index k is understood to run from 1 to ∞. However, sequences are frequently indexed starting from zero, as in
In some cases, the elements of the sequence are related naturally to a sequence of integers whose pattern can be easily inferred. In these cases, the index set may be implied by a listing of the first few abstract elements. For instance, the sequence of squares of odd numbers could be denoted in any of the following ways.
Moreover, the subscripts and superscripts could have been left off in the third, fourth, and fifth notations, if the indexing set was understood to be the natural numbers. In the second and third bullets, there is a well-defined sequence , but it is not the same as the sequence denoted by the expression.
Defining a sequence by recursion
[edit]Sequences whose elements are related to the previous elements in a straightforward way are often defined using recursion. This is in contrast to the definition of sequences of elements as functions of their positions.
To define a sequence by recursion, one needs a rule, called recurrence relation to construct each element in terms of the ones before it. In addition, enough initial elements must be provided so that all subsequent elements of the sequence can be computed by successive applications of the recurrence relation.
The Fibonacci sequence is a simple classical example, defined by the recurrence relation
with initial terms and . From this, a simple computation shows that the first ten terms of this sequence are 0, 1, 1, 2, 3, 5, 8, 13, 21, and 34.
A complicated example of a sequence defined by a recurrence relation is Recamán's sequence,[4] defined by the recurrence relation
with initial term
A linear recurrence with constant coefficients is a recurrence relation of the form
where are constants. There is a general method for expressing the general term of such a sequence as a function of n; see Linear recurrence. In the case of the Fibonacci sequence, one has and the resulting function of n is given by Binet's formula.
A holonomic sequence is a sequence defined by a recurrence relation of the form
where are polynomials in n. For most holonomic sequences, there is no explicit formula for expressing as a function of n. Nevertheless, holonomic sequences play an important role in various areas of mathematics. For example, many special functions have a Taylor series whose sequence of coefficients is holonomic. The use of the recurrence relation allows a fast computation of values of such special functions.
Not all sequences can be specified by a recurrence relation. An example is the sequence of prime numbers in their natural order (2, 3, 5, 7, 11, 13, 17, ...).
Formal definition and basic properties
[edit]There are many different notions of sequences in mathematics, some of which (e.g., exact sequence) are not covered by the definitions and notations introduced below.
Definition
[edit]In this article, a sequence is formally defined as a function whose domain is an interval of integers. This definition covers several different uses of the word "sequence", including one-sided infinite sequences, bi-infinite sequences, and finite sequences (see below for definitions of these kinds of sequences). However, many authors use a narrower definition by requiring the domain of a sequence to be the set of natural numbers. This narrower definition has the disadvantage that it rules out finite sequences and bi-infinite sequences, both of which are usually called sequences in standard mathematical practice. Another disadvantage is that, if one removes the first terms of a sequence, one needs reindexing the remainder terms for fitting this definition. In some contexts, to shorten exposition, the codomain of the sequence is fixed by context, for example by requiring it to be the set of real numbers,[5] the set of complex numbers,[6] or a topological space.[7]
Although sequences are a type of function, they are usually distinguished notationally from functions in that the input is written as a subscript rather than in parentheses, that is, an rather than a(n). There are terminological differences as well: the value of a sequence at the lowest input (often 1) is called the "first element" of the sequence, the value at the second smallest input (often 2) is called the "second element", etc. Also, while a function abstracted from its input is usually denoted by a single letter, e.g. f, a sequence abstracted from its input is usually written by a notation such as , or just as Here A is the domain, or index set, of the sequence.
Sequences and their limits (see below) are important concepts for studying topological spaces. An important generalization of sequences is the concept of nets. A net is a function from a (possibly uncountable) directed set to a topological space. The notational conventions for sequences normally apply to nets as well.
Finite and infinite
[edit]The length of a sequence is defined as the number of terms in the sequence.
A sequence of a finite length is a finite sequence. A finite sequence of length n is also called an n-tuple. Finite sequences include the empty sequence, denoted ( ), that has no elements.
Normally, the term infinite sequence refers to a sequence that is infinite in one direction, and finite in the other; such a sequence has a first element, but no final element, and are called singly infinite sequence or a one-sided infinite sequence when disambiguation is needed. In contrast, a sequence that is infinite in both directions—i.e. that has neither a first nor a final element—is called a bi-infinite sequence, two-way infinite sequence, or doubly infinite sequence. A function from the set of all integers, into a set, for example the sequence of all even integers ( ..., −4, −2, 0, 2, 4, 6, 8, ... ), is bi-infinite. This sequence could be denoted .
Increasing and decreasing
[edit]A sequence is said to be monotonically increasing if each term is greater than or equal to the one before it. For example, the sequence is monotonically increasing if and only if for all If each consecutive term is strictly greater than (>) the previous term then the sequence is called strictly monotonically increasing. A sequence is monotonically decreasing if each consecutive term is less than or equal to the previous one, and is strictly monotonically decreasing if each is strictly less than the previous. If a sequence is either increasing or decreasing it is called a monotone sequence. This is a special case of the more general notion of a monotonic function.
The terms nondecreasing and nonincreasing are often used in place of increasing and decreasing in order to avoid any possible confusion with strictly increasing and strictly decreasing, respectively.
Bounded
[edit]If the sequence of real numbers (an) is such that all the terms are less than some real number M, then the sequence is said to be bounded from above. In other words, this means that there exists M such that for all n, an ≤ M. Any such M is called an upper bound. Likewise, if, for some real m, an ≥ m for all n greater than some N, then the sequence is bounded from below and any such m is called a lower bound. If a sequence is both bounded from above and bounded from below, then the sequence is said to be bounded.
Subsequences
[edit]A subsequence of a given sequence is a sequence formed from the given sequence by deleting some of the elements without disturbing the relative positions of the remaining elements. For instance, the sequence of positive even integers (2, 4, 6, ...) is a subsequence of the positive integers (1, 2, 3, ...). The positions of some elements change when other elements are deleted. However, the relative positions are preserved.
Formally, a subsequence of the sequence is any sequence of the form , where is a strictly increasing sequence of positive integers.
Other types of sequences
[edit]Some other types of sequences that are easy to define include:
- An integer sequence is a sequence whose terms are integers.
- A polynomial sequence is a sequence whose terms are polynomials.
- A positive integer sequence is sometimes called multiplicative, if anm = an am for all pairs n, m such that n and m are coprime.[8] In other instances, sequences are often called multiplicative, if an = na1 for all n. Moreover, a multiplicative Fibonacci sequence[9] satisfies the recursion relation an = an−1 an−2.
- A binary sequence is a sequence whose terms have one of two discrete values, e.g. base 2 values (0,1,1,0, ...), a series of coin tosses (Heads/Tails) H,T,H,H,T, ..., the answers to a set of True or False questions (T, F, T, T, ...), and so on.
Limits and convergence
[edit]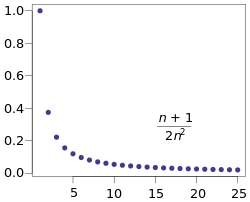
An important property of a sequence is convergence. If a sequence converges, it converges to a particular value known as the limit. If a sequence converges to some limit, then it is convergent. A sequence that does not converge is divergent.
Informally, a sequence has a limit if the elements of the sequence become closer and closer to some value (called the limit of the sequence), and they become and remain arbitrarily close to , meaning that given a real number greater than zero, all but a finite number of the elements of the sequence have a distance from less than .
For example, the sequence shown to the right converges to the value 0. On the other hand, the sequences (which begins 1, 8, 27, ...) and (which begins −1, 1, −1, 1, ...) are both divergent.
If a sequence converges, then the value it converges to is unique. This value is called the limit of the sequence. The limit of a convergent sequence is normally denoted . If is a divergent sequence, then the expression is meaningless.
Formal definition of convergence
[edit]A sequence of real numbers converges to a real number if, for all , there exists a natural number such that for all we have[5]
If is a sequence of complex numbers rather than a sequence of real numbers, this last formula can still be used to define convergence, with the provision that denotes the complex modulus, i.e. . If is a sequence of points in a metric space, then the formula can be used to define convergence, if the expression is replaced by the expression , which denotes the distance between and .
Applications and important results
[edit]If and are convergent sequences, then the following limits exist, and can be computed as follows:[5][10]
- for all real numbers
- , provided that
- for all and
Moreover:
- If for all greater than some , then .[a]
- (Squeeze theorem)
If is a sequence such that for all and ,
then is convergent, and . - If a sequence is bounded and monotonic then it is convergent.
- A sequence is convergent if and only if all of its subsequences are convergent.
Cauchy sequences
[edit]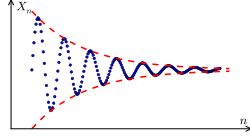
A Cauchy sequence is a sequence whose terms become arbitrarily close together as n gets very large. The notion of a Cauchy sequence is important in the study of sequences in metric spaces, and, in particular, in real analysis. One particularly important result in real analysis is Cauchy characterization of convergence for sequences:
- A sequence of real numbers is convergent (in the reals) if and only if it is Cauchy.
In contrast, there are Cauchy sequences of rational numbers that are not convergent in the rationals, e.g. the sequence defined by and is Cauchy, but has no rational limit (cf. Cauchy sequence § Non-example: rational numbers). More generally, any sequence of rational numbers that converges to an irrational number is Cauchy, but not convergent when interpreted as a sequence in the set of rational numbers.
Metric spaces that satisfy the Cauchy characterization of convergence for sequences are called complete metric spaces and are particularly nice for analysis.
Infinite limits
[edit]In calculus, it is common to define notation for sequences which do not converge in the sense discussed above, but which instead become and remain arbitrarily large, or become and remain arbitrarily negative. If becomes arbitrarily large as , we write
In this case we say that the sequence diverges, or that it converges to infinity. An example of such a sequence is an = n.
If becomes arbitrarily negative (i.e. negative and large in magnitude) as , we write
and say that the sequence diverges or converges to negative infinity.
Series
[edit]A series is, informally speaking, the sum of the terms of a sequence. That is, it is an expression of the form or , where is a sequence of real or complex numbers. The partial sums of a series are the expressions resulting from replacing the infinity symbol with a finite number, i.e. the Nth partial sum of the series is the number
The partial sums themselves form a sequence , which is called the sequence of partial sums of the series . If the sequence of partial sums converges, then we say that the series is convergent, and the limit is called the value of the series. The same notation is used to denote a series and its value, i.e. we write .
Use in other fields of mathematics
[edit]Topology
[edit]Sequences play an important role in topology, especially in the study of metric spaces. For instance:
- A metric space is compact exactly when it is sequentially compact.
- A function from a metric space to another metric space is continuous exactly when it takes convergent sequences to convergent sequences.
- A metric space is a connected space if and only if, whenever the space is partitioned into two sets, one of the two sets contains a sequence converging to a point in the other set.
- A topological space is separable exactly when there is a dense sequence of points.
Sequences can be generalized to nets or filters. These generalizations allow one to extend some of the above theorems to spaces without metrics.
Product topology
[edit]The topological product of a sequence of topological spaces is the cartesian product of those spaces, equipped with a natural topology called the product topology.
More formally, given a sequence of spaces , the product space
is defined as the set of all sequences such that for each i, is an element of . The canonical projections are the maps pi : X → Xi defined by the equation . Then the product topology on X is defined to be the coarsest topology (i.e. the topology with the fewest open sets) for which all the projections pi are continuous. The product topology is sometimes called the Tychonoff topology.
Analysis
[edit]When discussing sequences in analysis, one will generally consider sequences of the form
which is to say, infinite sequences of elements indexed by natural numbers.
A sequence may start with an index different from 1 or 0. For example, the sequence defined by xn = 1/log(n) would be defined only for n ≥ 2. When talking about such infinite sequences, it is usually sufficient (and does not change much for most considerations) to assume that the members of the sequence are defined at least for all indices large enough, that is, greater than some given N.
The most elementary type of sequences are numerical ones, that is, sequences of real or complex numbers. This type can be generalized to sequences of elements of some vector space. In analysis, the vector spaces considered are often function spaces. Even more generally, one can study sequences with elements in some topological space.
Sequence spaces
[edit]A sequence space is a vector space whose elements are infinite sequences of real or complex numbers. Equivalently, it is a function space whose elements are functions from the natural numbers to the field K, where K is either the field of real numbers or the field of complex numbers. The set of all such functions is naturally identified with the set of all possible infinite sequences with elements in K, and can be turned into a vector space under the operations of pointwise addition of functions and pointwise scalar multiplication. All sequence spaces are linear subspaces of this space. Sequence spaces are typically equipped with a norm, or at least the structure of a topological vector space.
The most important sequences spaces in analysis are the ℓp spaces, consisting of the p-power summable sequences, with the p-norm. These are special cases of Lp spaces for the counting measure on the set of natural numbers. Other important classes of sequences like convergent sequences or null sequences form sequence spaces, respectively denoted c and c0, with the sup norm. Any sequence space can also be equipped with the topology of pointwise convergence, under which it becomes a special kind of Fréchet space called an FK-space.
Linear algebra
[edit]Sequences over a field may also be viewed as vectors in a vector space. Specifically, the set of F-valued sequences (where F is a field) is a function space (in fact, a product space) of F-valued functions over the set of natural numbers.
Abstract algebra
[edit]Abstract algebra employs several types of sequences, including sequences of mathematical objects such as groups or rings.
Free monoid
[edit]If A is a set, the free monoid over A (denoted A*, also called Kleene star of A) is a monoid containing all the finite sequences (or strings) of zero or more elements of A, with the binary operation of concatenation. The free semigroup A+ is the subsemigroup of A* containing all elements except the empty sequence.
Exact sequences
[edit]In the context of group theory, a sequence
of groups and group homomorphisms is called exact, if the image (or range) of each homomorphism is equal to the kernel of the next:
The sequence of groups and homomorphisms may be either finite or infinite.
A similar definition can be made for certain other algebraic structures. For example, one could have an exact sequence of vector spaces and linear maps, or of modules and module homomorphisms.
Spectral sequences
[edit]In homological algebra and algebraic topology, a spectral sequence is a means of computing homology groups by taking successive approximations. Spectral sequences are a generalization of exact sequences, and since their introduction by Jean Leray (1946), they have become an important research tool, particularly in homotopy theory.
Set theory
[edit]An ordinal-indexed sequence is a generalization of a sequence. If α is a limit ordinal and X is a set, an α-indexed sequence of elements of X is a function from α to X. In this terminology an ω-indexed sequence is an ordinary sequence.
Computing
[edit]In computer science, finite sequences are called lists. Potentially infinite sequences are called streams. Finite sequences of characters or digits are called strings.
Streams
[edit]Infinite sequences of digits (or characters) drawn from a finite alphabet are of particular interest in theoretical computer science. They are often referred to simply as sequences or streams, as opposed to finite strings. Infinite binary sequences, for instance, are infinite sequences of bits (characters drawn from the alphabet {0, 1}). The set C = {0, 1}∞ of all infinite binary sequences is sometimes called the Cantor space.
An infinite binary sequence can represent a formal language (a set of strings) by setting the n th bit of the sequence to 1 if and only if the n th string (in shortlex order) is in the language. This representation is useful in the diagonalization method for proofs.[11]
See also
[edit]- Operations
- Examples
- Discrete-time signal
- Farey sequence
- Fibonacci sequence
- Look-and-say sequence
- Thue–Morse sequence
- List of integer sequences
- Types
- ±1-sequence
- Arithmetic progression
- Automatic sequence
- Cauchy sequence
- Constant-recursive sequence
- Geometric progression
- Harmonic progression
- Holonomic sequence
- Regular sequence
- Pseudorandom binary sequence
- Random sequence
- Related concepts
- List (computing)
- Net (topology) (a generalization of sequences)
- Ordinal-indexed sequence
- Recursion (computer science)
- Set (mathematics)
- Tuple
- Permutation
Notes
[edit]- ^ If the inequalities are replaced by strict inequalities then this is false: There are sequences such that for all , but .
References
[edit]- ^ a b "Sequences". www.mathsisfun.com. Archived from the original on 2020-08-12. Retrieved 2020-08-17.
- ^ Weisstein, Eric W. "Sequence". mathworld.wolfram.com. Archived from the original on 2020-07-25. Retrieved 2020-08-17.
- ^ Index to OEIS Archived 2022-10-18 at the Wayback Machine, On-Line Encyclopedia of Integer Sequences, 2020-12-03
- ^ Sloane, N. J. A. (ed.). "Sequence A005132 (Recamán's sequence)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 26 January 2018.
- ^ a b c Gaughan, Edward (2009). "1.1 Sequences and Convergence". Introduction to Analysis. AMS (2009). ISBN 978-0-8218-4787-9.
- ^ Edward B. Saff & Arthur David Snider (2003). "Chapter 2.1". Fundamentals of Complex Analysis. Prentice Hall. ISBN 978-01-390-7874-3. Archived from the original on 2023-03-23. Retrieved 2015-11-15.
- ^ James R. Munkres (2000). "Chapters 1&2". Topology. Prentice Hall, Incorporated. ISBN 978-01-318-1629-9. Archived from the original on 2023-03-23. Retrieved 2015-11-15.
- ^ Lando, Sergei K. (2003-10-21). "7.4 Multiplicative sequences". Lectures on generating functions. AMS. ISBN 978-0-8218-3481-7.
- ^ Falcon, Sergio (2003). "Fibonacci's multiplicative sequence". International Journal of Mathematical Education in Science and Technology. 34 (2): 310–315. Bibcode:2003IJMES..34..310F. doi:10.1080/0020739031000158362. S2CID 121280842.
- ^ Dawikins, Paul. "Series and Sequences". Paul's Online Math Notes/Calc II (notes). Archived from the original on 30 November 2012. Retrieved 18 December 2012.
- ^ Oflazer, Kemal. "FORMAL LANGUAGES, AUTOMATA AND COMPUTATION: DECIDABILITY" (PDF). cmu.edu. Carnegie-Mellon University. Archived (PDF) from the original on 29 May 2015. Retrieved 24 April 2015.










































































































