Polygonal number

In mathematics, a polygonal number is a number that counts dots arranged in the shape of a regular polygon.^[1]^: 2-3 These are one type of 2-dimensional figurate numbers.

Polygonal numbers were first studied during the 6th century BC by the Ancient Greeks, who investigated and discussed properties of oblong, triangular, and square numbers.^[1]^: 1

Definition and examples

The number 10 for example, can be arranged as a triangle (see triangular number):

But 10 cannot be arranged as a square. The number 9, on the other hand, can be (see square number):

Some numbers, like 36, can be arranged both as a square and as a triangle (see square triangular number):

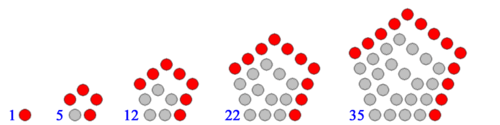
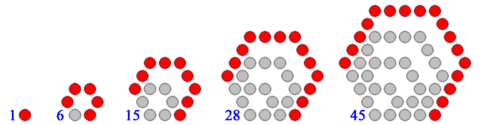
By convention, 1 is the first polygonal number for any number of sides. The rule for enlarging the polygon to the next size is to extend two adjacent arms by one point and to then add the required extra sides between those points. In the following diagrams, each extra layer is shown as in red.

Triangular numbers

The triangular number sequence is the representation of the numbers in the form of equilateral triangle arranged in a series or sequence. These numbers are in a sequence of 1, 3, 6, 10, 15, 21, 28, 36, 45, and so on.

Square numbers

Polygons with higher numbers of sides, such as pentagons and hexagons, can also be constructed according to this rule, although the dots will no longer form a perfectly regular lattice like above.

Pentagonal numbers

Hexagonal numbers

Formula

If $s$ is the number of sides in a polygon, the formula for the $n$ th $s$ -gonal number $P (s, n)$ is

P(s,n)={\frac {(s-2)n^{2}-(s-4)n}{2}}

The $n$ th $s$ -gonal number is also related to the triangular numbers $T n$ as follows:^[2]

P(s,n)=(s-2)T_{n-1}+n=(s-3)T_{n-1}+T_{n}\,.

Thus:

{\begin{aligned}P(s,n+1)-P(s,n)&=(s-2)n+1\,,\\P(s+1,n)-P(s,n)&=T_{n-1}={\frac {n(n-1)}{2}}\,,\\P(s+k,n)-P(s,n)&=kT_{n-1}=k{\frac {n(n-1)}{2}}\,.\end{aligned}}

For a given $s$ -gonal number $P (s, n) = x$ , one can find $n$ by

n={\frac {{\sqrt {8(s-2)x+{(s-4)}^{2}}}+(s-4)}{2(s-2)}}

and one can find $s$ by

s=2+{\frac {2}{n}}\cdot {\frac {x-n}{n-1}}

.

Every hexagonal number is also a triangular number

Proof without words that hexagonal numbers are odd-sided triangular numbers

Applying the formula above:

P(s,n)=(s-2)T_{n-1}+n

to the case of 6 sides gives:

P(6,n)=4T_{n-1}+n

but since:

T_{n-1}={\frac {n(n-1)}{2}}

it follows that:

P(6,n)={\frac {4n(n-1)}{2}}+n={\frac {2n(2n-1)}{2}}=T_{2n-1}

This shows that the $n$ th hexagonal number $P (6, n)$ is also the $(2 n - 1)$ th triangular number $T 2 n -1$ . We can find every hexagonal number by simply taking the odd-numbered triangular numbers:^[2]

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, ...

Table of values

The first six values in the column "sum of reciprocals", for triangular to octagonal numbers, come from a published solution to the general problem, which also gives a general formula for any number of sides, in terms of the digamma function.^[3]

$s$	Name	Formula	$n$											Sum of reciprocals^[3]^[4]	OEIS number
$s$	Name	Formula	1	2	3	4	5	6	7	8	9	10	11	Sum of reciprocals^[3]^[4]	OEIS number
2	Natural (line segment)	$.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠1/2⁠(0n2 + 2n) = n$	1	2	3	4	5	6	7	8	9	10	11	∞ (diverges)	A000027
3	Triangular	$⁠ 1 / 2 ⁠ (n 2 + n)$	1	3	6	10	15	21	28	36	45	55	66	2^[3]	A000217
4	Square	$⁠ 1 / 2 ⁠ (2 n 2 - 0 n) = n 2$	1	4	9	16	25	36	49	64	81	100	121	⁠ $π$ ²/6⁠^[3]^[α]	A000290
5	Pentagonal	$⁠ 1 / 2 ⁠ (3 n 2 - n)$	1	5	12	22	35	51	70	92	117	145	176	$3 ln 3 - ⁠ π \sqrt 3 / 3 ⁠$ ^[3]	A000326
6	Hexagonal	$⁠ 1 / 2 ⁠ (4 n 2 - 2 n) = 2 n 2 - n$	1	6	15	28	45	66	91	120	153	190	231	$2 ln 2$ ^[3]	A000384
7	Heptagonal	$⁠ 1 / 2 ⁠ (5 n 2 - 3 n)$	1	7	18	34	55	81	112	148	189	235	286	${\begin{matrix}{\tfrac {2}{3}}\ln 5\\+{\tfrac {{1}+{\sqrt {5}}}{3}}\ln {\tfrac {\sqrt {10-2{\sqrt {5}}}}{2}}\\+{\tfrac {{1}-{\sqrt {5}}}{3}}\ln {\tfrac {\sqrt {10+2{\sqrt {5}}}}{2}}\\+{\tfrac {\pi {\sqrt {25-10{\sqrt {5}}}}}{15}}\end{matrix}}$ ^[3]	A000566
8	Octagonal	$⁠ 1 / 2 ⁠ (6 n 2 - 4 n) = 3 n 2 - 2 n$	1	8	21	40	65	96	133	176	225	280	341	$⁠ 3 / 4 ⁠ ln 3 + ⁠ π \sqrt 3 / 12 ⁠$ ^[3]	A000567
9	Nonagonal	$⁠ 1 / 2 ⁠ (7 n 2 - 5 n)$	1	9	24	46	75	111	154	204	261	325	396		A001106
10	Decagonal	$⁠ 1 / 2 ⁠ (8 n 2 - 6 n) = 4 n 2 - 3 n$	1	10	27	52	85	126	175	232	297	370	451	$ln 2 + ⁠ π / 6 ⁠$	A001107
11	Hendecagonal	$⁠ 1 / 2 ⁠ (9 n 2 - 7 n)$	1	11	30	58	95	141	196	260	333	415	506		A051682
12	Dodecagonal	$⁠ 1 / 2 ⁠ (10 n 2 - 8 n)$	1	12	33	64	105	156	217	288	369	460	561		A051624
13	Tridecagonal	$⁠ 1 / 2 ⁠ (11 n 2 - 9 n)$	1	13	36	70	115	171	238	316	405	505	616		A051865
14	Tetradecagonal	$⁠ 1 / 2 ⁠ (12 n 2 - 10 n)$	1	14	39	76	125	186	259	344	441	550	671	$⁠ 2 / 5 ⁠ ln 2 + ⁠ 3 / 10 ⁠ ln 3 + ⁠ π \sqrt 3 / 10 ⁠$	A051866
15	Pentadecagonal	$⁠ 1 / 2 ⁠ (13 n 2 - 11 n)$	1	15	42	82	135	201	280	372	477	595	726		A051867
16	Hexadecagonal	$⁠ 1 / 2 ⁠ (14 n 2 - 12 n)$	1	16	45	88	145	216	301	400	513	640	781		A051868
17	Heptadecagonal	$⁠ 1 / 2 ⁠ (15 n 2 - 13 n)$	1	17	48	94	155	231	322	428	549	685	836		A051869
18	Octadecagonal	$⁠ 1 / 2 ⁠ (16 n 2 - 14 n)$	1	18	51	100	165	246	343	456	585	730	891	$⁠ 4 / 7 ⁠ ln 2 - ⁠ \sqrt 2 / 14 ⁠ ln (3 - 2 \sqrt 2)$ $+ ⁠ π (1 + \sqrt 2) / 14 ⁠$	A051870
19	Enneadecagonal	$⁠ 1 / 2 ⁠ (17 n 2 - 15 n)$	1	19	54	106	175	261	364	484	621	775	946		A051871
20	Icosagonal	$⁠ 1 / 2 ⁠ (18 n 2 - 16 n)$	1	20	57	112	185	276	385	512	657	820	1001		A051872
21	Icosihenagonal	$⁠ 1 / 2 ⁠ (19 n 2 - 17 n)$	1	21	60	118	195	291	406	540	693	865	1056		A051873
22	Icosidigonal	$⁠ 1 / 2 ⁠ (20 n 2 - 18 n)$	1	22	63	124	205	306	427	568	729	910	1111		A051874
23	Icositrigonal	$⁠ 1 / 2 ⁠ (21 n 2 - 19 n)$	1	23	66	130	215	321	448	596	765	955	1166		A051875
24	Icositetragonal	$⁠ 1 / 2 ⁠ (22 n 2 - 20 n)$	1	24	69	136	225	336	469	624	801	1000	1221		A051876
s = 25		$⁠ 1 / 2 ⁠ (23 n 2 - 21 n)$	1	25	72	142	235	351	490	652	837	1045	1276

The On-Line Encyclopedia of Integer Sequences eschews terms using Greek prefixes (e.g., "octagonal") in favor of terms using numerals (i.e., "8-gonal").

A property of this table can be expressed by the following identity (see A086270):

2\,P(s,n)=P(s+k,n)+P(s-k,n),

with

k=0,1,2,3,...,s-3.

Combinations

Some numbers, such as 36 which is both square and triangular, fall into two polygonal sets. The problem of determining, given two such sets, all numbers that belong to both can be solved by reducing the problem to Pell's equation. The simplest example of this is the sequence of square triangular numbers.

The following table summarizes the set of $s$ -gonal $t$ -gonal numbers for small values of $s$ and $t$ .

$s$	$t$	Sequence	OEIS number
4	3	1, 36, 1225, 41616, 1413721, 48024900, 1631432881, 55420693056, 1882672131025, 63955431761796, 2172602007770041, 73804512832419600, 2507180834294496361, 85170343853180456676, 2893284510173841030625, 98286503002057414584576, 3338847817559778254844961, ...	A001110
5	3	1, 210, 40755, 7906276, 1533776805, 297544793910, 57722156241751, 11197800766105800, 2172315626468283465, …	A014979
5	4	1, 9801, 94109401, 903638458801, 8676736387298001, 83314021887196947001, 799981229484128697805801, ...	A036353
6	3	All hexagonal numbers are also triangular.	A000384
6	4	1, 1225, 1413721, 1631432881, 1882672131025, 2172602007770041, 2507180834294496361, 2893284510173841030625, 3338847817559778254844961, 3853027488179473932250054441, ...	A046177
6	5	1, 40755, 1533776805, …	A046180
7	3	1, 55, 121771, 5720653, 12625478965, 593128762435, 1309034909945503, 61496776341083161, 135723357520344181225, 6376108764003055554511, 14072069153115290487843091, …	A046194
7	4	1, 81, 5929, 2307361, 168662169, 12328771225, 4797839017609, 350709705290025, 25635978392186449, 9976444135331412025, …	A036354
7	5	1, 4347, 16701685, 64167869935, …	A048900
7	6	1, 121771, 12625478965, …	A048903
8	3	1, 21, 11781, 203841, …	A046183
8	4	1, 225, 43681, 8473921, 1643897025, 318907548961, 61866420601441, 12001766689130625, 2328280871270739841, 451674487259834398561, 87622522247536602581025, 16998317641534841066320321, …	A036428
8	5	1, 176, 1575425, 234631320, …	A046189
8	6	1, 11781, 113123361, …	A046192
8	7	1, 297045, 69010153345, …	A048906
9	3	1, 325, 82621, 20985481, …	A048909
9	4	1, 9, 1089, 8281, 978121, 7436529, 878351769, 6677994961, 788758910641, 5996832038649, 708304623404049, 5385148492712041, 636056763057925561, ...	A036411
9	5	1, 651, 180868051, …	A048915
9	6	1, 325, 5330229625, …	A048918
9	7	1, 26884, 542041975, …	A048921
9	8	1, 631125, 286703855361, …	A048924

In some cases, such as $s = 10$ and $t = 4$ , there are no numbers in both sets other than 1.^{[citation needed]}

The problem of finding numbers that belong to three polygonal sets is more difficult. Katayama^[5] proved that if three different integers $s$ , $t$ , and $u$ are all at least 3 and not equal to 6, then only finitely many numbers are simultaneously $s$ -gonal, $t$ -gonal, and $u$ -gonal.

Katayama, Furuya, and Nishioka^[6] proved that if the integer $s$ is such that $s=5$ or $7\leq s\leq 12$ , then the only $s$ -gonal square triangular number is 1. For example, that paper gave the following proof for the case where $s=5$ .^[7] Suppose that $P(3,n)=P(4,p)=P(5,q)$ for some positive integers $n$ , $p$ , and $q$ . A calculation shows that the point $(x,y)$ defined by $(x,y)=(48p^{2}+3,24p(2n+1)(6q-1))$ is on the curve $Y^{2}=X^{3}-X^{2}-9X+9$ . That fact forces $(x,y)=(51,360)$ (as an elliptic curve database^[8] confirms), so $p=1$ and the result follows.

The number 1225 is hecatonicositetragonal ( $s = 124$ ), hexacontagonal ( $s = 60$ ), icosienneagonal ( $s = 29$ ), hexagonal, square, and triangular.

Notes

^ See Basel problem.

References

^ ^a ^b Tattersall, James J. (2005). Elementary Number Theory in Nine Chapters (2nd ed.). New York: Cambridge University Press. ISBN 978-0-511-75634-4.
^ ^a ^b Conway, John H.; Guy, Richard (2012-12-06). The Book of Numbers. Springer Science & Business Media. pp. 38–41. ISBN 978-1-4612-4072-3.
^ ^a ^b ^c ^d ^e ^f ^g ^h "Sums of Reciprocals of Polygonal Numbers and a Theorem of Gauss" (PDF). Archived from the original (PDF) on 2011-06-15. Retrieved 2010-06-13.
^ "Beyond the Basel Problem: Sums of Reciprocals of Figurate Numbers" (PDF). Archived from the original (PDF) on 2013-05-29. Retrieved 2010-05-13.
^ Katayama, S. (2021). "On Polygonal Square Triangular Numbers II" (PDF). J. Math. Tokushima Univ. 55: 1–10.
^ Katayama, S.; Furuya, N.; Nishioka, Y. (2020). "On Polygonal Square Triangular Numbers" (PDF). J. Math. Tokushima Univ. 54: 1–12.
^ Ibid., p. 4.
^ The LMFDB Collaboration (2025). "Elliptic curve with LMFDB label 192.a2 (Cremona label 192a2)". The L-functions and modular forms database. Retrieved July 12, 2025.

Bibliography

The Penguin Dictionary of Curious and Interesting Numbers, David Wells (Penguin Books, 1997) [ISBN 0-14-026149-4].
Polygonal number at PlanetMath.
Weisstein, Eric W. "Polygonal Numbers". MathWorld.
F. Tapson (1999). The Oxford Mathematics Study Dictionary (2nd ed.). Oxford University Press. pp. 88–89. ISBN 0-19-914-567-9.

External links

[5] See Basel problem.

[tattersall2005-1] Tattersall, James J. (2005). Elementary Number Theory in Nine Chapters (2nd ed.). New York: Cambridge University Press. ISBN 978-0-511-75634-4.

[:0-2] Conway, John H.; Guy, Richard (2012-12-06). The Book of Numbers. Springer Science & Business Media. pp. 38–41. ISBN 978-1-4612-4072-3.

[siam_07-003s-3] ^ ^a ^b ^c ^d ^e ^f ^g ^h "Sums of Reciprocals of Polygonal Numbers and a Theorem of Gauss" (PDF). Archived from the original (PDF) on 2011-06-15. Retrieved 2010-06-13.

[4] "Beyond the Basel Problem: Sums of Reciprocals of Figurate Numbers" (PDF). Archived from the original (PDF) on 2013-05-29. Retrieved 2010-05-13.

[6] Katayama, S. (2021). "On Polygonal Square Triangular Numbers II" (PDF). J. Math. Tokushima Univ. 55: 1–10.

[7] Katayama, S.; Furuya, N.; Nishioka, Y. (2020). "On Polygonal Square Triangular Numbers" (PDF). J. Math. Tokushima Univ. 54: 1–12.

[8] Ibid., p. 4.

[9] The LMFDB Collaboration (2025). "Elliptic curve with LMFDB label 192.a2 (Cremona label 192a2)". The L-functions and modular forms database. Retrieved July 12, 2025.

[1]

[2]

[3]

[4]

[α]

[5]

[6]

[7]

[8]

Authority control databases
National	United States Israel
Other	Yale LUX

History

Polygonal number

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Polygonal number

Definition and examples

Triangular numbers

Square numbers

Pentagonal numbers

Hexagonal numbers

Formula

Every hexagonal number is also a triangular number

Table of values

Combinations

See also

Notes

References

Bibliography

External links

Polygonal number

Definition and Basic Concepts

General Definition

Visual and Geometric Interpretation

Specific Examples

Triangular Numbers

Square Numbers

Pentagonal and Hexagonal Numbers

Mathematical Formulas

General Formula

Derivation of the Formula

Key Properties and Identities

Interrelations Among Polygonal Numbers

Add your contribution

Related Hubs

Contribute something