Recent from talks
Nothing was collected or created yet.
Polynomial
View on WikipediaIn mathematics, a polynomial is a mathematical expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication and exponentiation to nonnegative integer powers, and has a finite number of terms.[1][2][3][4][5] An example of a polynomial of a single indeterminate is . An example with three indeterminates is .
Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; and they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry.
Etymology
[edit]The word polynomial joins two diverse roots: the Greek poly, meaning "many", and the Latin nomen, or "name". It was derived from the term binomial by replacing the Latin root bi- with the Greek poly-. That is, it means a sum of many terms (many monomials). The word polynomial was first used in the 17th century.[6]
Notation and terminology
[edit]
The occurring in a polynomial is commonly called a variable or an indeterminate. When the polynomial is considered as an expression, is a fixed symbol which does not have any value (its value is "indeterminate"). However, when one considers the function defined by the polynomial, then represents the argument of the function, and is therefore called a "variable". Many authors use these two words interchangeably.
A polynomial in the indeterminate is commonly denoted either as or as . Formally, the name of the polynomial is , not , but the use of the functional notation dates from a time when the distinction between a polynomial and the associated function was unclear. Moreover, the functional notation is often useful for specifying, in a single phrase, a polynomial and its indeterminate. For example, "let be a polynomial" is a shorthand for "let be a polynomial in the indeterminate ". On the other hand, when it is not necessary to emphasize the name of the indeterminate, many formulas are much simpler and easier to read if the name(s) of the indeterminate(s) do not appear at each occurrence of the polynomial.
The ambiguity of having two notations for a single mathematical object may be formally resolved by considering the general meaning of the functional notation for polynomials. If denotes a number, a variable, another polynomial, or, more generally, any expression, then denotes, by convention, the result of substituting for in . Thus, the polynomial defines the function which is the polynomial function associated to . Frequently, when using this notation, one supposes that is a number. However, one may use it over any domain where addition and multiplication are defined (that is, any ring). In particular, if is a polynomial then is also a polynomial.
More specifically, when is the indeterminate , then the image of by this function is the polynomial itself (substituting for does not change anything). In other words, which justifies formally the existence of two notations for the same polynomial.
Definition
[edit]A polynomial expression is an expression that can be built from constants and symbols called variables or indeterminates by means of addition, multiplication and exponentiation to a non-negative integer power. The constants are generally numbers, but may be any expression that do not involve the indeterminates, and represent mathematical objects that can be added and multiplied. Two polynomial expressions are considered as defining the same polynomial if they may be transformed, one to the other, by applying the usual properties of commutativity, associativity and distributivity of addition and multiplication. For example and are two polynomial expressions that represent the same polynomial; so, one has the equality .
A polynomial in a single indeterminate x can always be written (or rewritten) in the form where are constants that are called the coefficients of the polynomial, and is the indeterminate.[7] The word "indeterminate" means that represents no particular value, although any value may be substituted for it. The mapping that associates the result of this substitution to the substituted value is a function, called a polynomial function.
This can be expressed more concisely by using summation notation: That is, a polynomial can either be zero or can be written as the sum of a finite number of non-zero terms. Each term consists of the product of a number – called the coefficient of the term[a] – and a finite number of indeterminates, raised to non-negative integer powers.
Classification
[edit]The exponent on an indeterminate in a term is called the degree of that indeterminate in that term; the degree of the term is the sum of the degrees of the indeterminates in that term, and the degree of a polynomial is the largest degree of any term with nonzero coefficient.[8] Because , the degree of an indeterminate without a written exponent is one.
A term with no indeterminates and a polynomial with no indeterminates are called, respectively, a constant term and a constant polynomial.[b] The degree of a constant term and of a nonzero constant polynomial is . The degree of the zero polynomial (which has no terms at all) is generally treated as not defined (but see below).[9]
For example: is a term. The coefficient is , the indeterminates are and , the degree of is two, while the degree of is one. The degree of the entire term is the sum of the degrees of each indeterminate in it, so in this example the degree is .
Forming a sum of several terms produces a polynomial. For example, the following is a polynomial: It consists of three terms: the first is degree two, the second is degree one, and the third is degree zero.
Polynomials of small degree have been given specific names. A polynomial of degree zero is a constant polynomial, or simply a constant. Polynomials of degree one, two or three are respectively linear polynomials, quadratic polynomials and cubic polynomials.[8] For higher degrees, the specific names are not commonly used, although quartic polynomial (for degree four) and quintic polynomial (for degree five) are sometimes used. The names for the degrees may be applied to the polynomial or to its terms. For example, the term in is a linear term in a quadratic polynomial.
The polynomial , which may be considered to have no terms at all, is called the zero polynomial. Unlike other constant polynomials, its degree is not zero. Rather, the degree of the zero polynomial is either left explicitly undefined, or defined as negative (either −1 or ).[10] The zero polynomial is also unique in that it is the only polynomial in one indeterminate that has an infinite number of roots. The graph of the zero polynomial, , is the -axis.
In the case of polynomials in more than one indeterminate, a polynomial is called homogeneous of degree if all of its non-zero terms have degree . The zero polynomial is homogeneous, and, as a homogeneous polynomial, its degree is undefined.[c] For example, is homogeneous of degree . For more details, see homogeneous polynomials.
The commutative law of addition can be used to rearrange terms into any preferred order. In polynomials with one indeterminate, the terms are usually ordered according to degree, either in "descending powers of ", with the term of largest degree first, or in "ascending powers of ". The polynomial is written in descending powers of . The first term has coefficient , indeterminate , and exponent . In the second term, the coefficient is . The third term is a constant. Because the degree of a non-zero polynomial is the largest degree of any one term, this polynomial has degree two.[11]
Two terms with the same indeterminates raised to the same powers are called "similar terms" or "like terms", and they can be combined, using the distributive law, into a single term whose coefficient is the sum of the coefficients of the terms that were combined. It may happen that this makes the coefficient .[12]
Polynomials can be classified by the number of terms with nonzero coefficients, so that a one-term polynomial is called a monomial,[d] a two-term polynomial is called a binomial, and a three-term polynomial is called a trinomial. A polynomial with two or more terms is also called a multinomial.[13][14]
A real polynomial is a polynomial with real coefficients. When it is used to define a function, the domain is not so restricted. However, a real polynomial function is a function from the reals to the reals that is defined by a real polynomial. Similarly, an integer polynomial is a polynomial with integer coefficients, and a complex polynomial is a polynomial with complex coefficients.
A polynomial in one indeterminate is called a univariate polynomial, a polynomial in more than one indeterminate is called a multivariate polynomial.[15] A polynomial with two indeterminates is called a bivariate polynomial.[7] These notions refer more to the kind of polynomials one is generally working with than to individual polynomials; for instance, when working with univariate polynomials, one does not exclude constant polynomials (which may result from the subtraction of non-constant polynomials), although strictly speaking, constant polynomials do not contain any indeterminates at all. It is possible to further classify multivariate polynomials as bivariate, trivariate, and so on, according to the maximum number of indeterminates allowed. Again, so that the set of objects under consideration be closed under subtraction, a study of trivariate polynomials usually allows bivariate polynomials, and so on. It is also common to say simply "polynomials in , and ", listing the indeterminates allowed.
Operations
[edit]Addition and subtraction
[edit]Polynomials can be added using the associative law of addition (grouping all their terms together into a single sum), possibly followed by reordering (using the commutative law) and combining of like terms.[12][16] For example, if and then the sum can be reordered and regrouped as and then simplified to When polynomials are added together, the result is another polynomial.[17]
Subtraction of polynomials is similar.
Multiplication
[edit]Polynomials can also be multiplied. To expand the product of two polynomials into a sum of terms, the distributive law is repeatedly applied, which results in each term of one polynomial being multiplied by every term of the other.[12] For example, if then Carrying out the multiplication in each term produces Combining similar terms yields which can be simplified to As in the example, the product of polynomials is always a polynomial.[17][9]
Composition
[edit]Given a polynomial of a single variable and another polynomial of any number of variables, the composition is obtained by substituting each copy of the variable of the first polynomial by the second polynomial.[9] For example, if and then A composition may be expanded to a sum of terms using the rules for multiplication and division of polynomials. The composition of two polynomials is another polynomial.[18]
Division
[edit]The division of one polynomial by another is not typically a polynomial. Instead, such ratios are a more general family of objects, called rational fractions, rational expressions, or rational functions, depending on context.[19] This is analogous to the fact that the ratio of two integers is a rational number, not necessarily an integer.[20][21] For example, the fraction is not a polynomial, and it cannot be written as a finite sum of powers of the variable .
For polynomials in one variable, there is a notion of Euclidean division of polynomials, generalizing the Euclidean division of integers.[e] This notion of the division results in two polynomials, a quotient and a remainder , such that and , where is the degree of . The quotient and remainder may be computed by any of several algorithms, including polynomial long division and synthetic division.[22]
When the denominator is monic and linear, that is, for some constant , then the polynomial remainder theorem asserts that the remainder of the division of by is the evaluation .[21] In this case, the quotient may be computed by Ruffini's rule, a special case of synthetic division.[23]
Factoring
[edit]All polynomials with coefficients in a unique factorization domain (for example, the integers or a field) also have a factored form in which the polynomial is written as a product of irreducible polynomials and a constant. This factored form is unique up to the order of the factors and their multiplication by an invertible constant. In the case of the field of complex numbers, the irreducible factors are linear. Over the real numbers, they have the degree either one or two. Over the integers and the rational numbers the irreducible factors may have any degree.[24] For example, the factored form of is over the integers and the reals, and over the complex numbers.
The computation of the factored form, called factorization is, in general, too difficult to be done by hand-written computation. However, efficient polynomial factorization algorithms are available in most computer algebra systems.
Calculus
[edit]Calculating derivatives and integrals of polynomials is particularly simple, compared to other kinds of functions. The derivative of the polynomial with respect to is the polynomial Similarly, the general antiderivative (or indefinite integral) of is where is an arbitrary constant. For example, antiderivatives of have the form .
For polynomials whose coefficients come from more abstract settings (for example, if the coefficients are integers modulo some prime number , or elements of an arbitrary ring), the formula for the derivative can still be interpreted formally, with the coefficient understood to mean the sum of copies of . For example, over the integers modulo , the derivative of the polynomial is the polynomial .[25]
Polynomial functions
[edit]A polynomial function is a function that can be defined by evaluating a polynomial. More precisely, a function of one argument from a given domain is a polynomial function if there exists a polynomial that evaluates to for all x in the domain of (here, is a non-negative integer and are constant coefficients).[26] Generally, unless otherwise specified, polynomial functions have complex coefficients, arguments, and values. In particular, a polynomial, restricted to have real coefficients, defines a function from the complex numbers to the complex numbers. If the domain of this function is also restricted to the reals, the resulting function is a real function that maps reals to reals.
For example, the function , defined by is a polynomial function of one variable. Polynomial functions of several variables are similarly defined, using polynomials in more than one indeterminate, as in According to the definition of polynomial functions, there may be expressions that obviously are not polynomials but nevertheless define polynomial functions. An example is the expression which takes the same values as the polynomial on the interval , and thus both expressions define the same polynomial function on this interval.
Every polynomial function is continuous, smooth, and entire.
The evaluation of a polynomial is the computation of the corresponding polynomial function; that is, the evaluation consists of substituting a numerical value to each indeterminate and carrying out the indicated multiplications and additions.
For polynomials in one indeterminate, the evaluation is usually more efficient (lower number of arithmetic operations to perform) using Horner's method, which consists of rewriting the polynomial as
Graphs
[edit]-
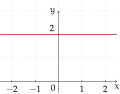
Polynomial of degree 0:
f(x) = 2 -
Polynomial of degree 1:
f(x) = 2x + 1 -
Polynomial of degree 2:
f(x) = x2 − x − 2
= (x + 1)(x − 2) -
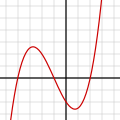
Polynomial of degree 3:
f(x) = x3/4 + 3x2/4 − 3x/2 − 2
= 1/4 (x + 4)(x + 1)(x − 2) -
Polynomial of degree 4:
f(x) = 1/14 (x + 4)(x + 1)(x − 1)(x − 3)
+ 0.5 -
Polynomial of degree 5:
f(x) = 1/20 (x + 4)(x + 2)(x + 1)(x − 1)
(x − 3) + 2 -
Polynomial of degree 6:
f(x) = 1/100 (x6 − 2x 5 − 26x4 + 28x3
+ 145x2 − 26x − 80) -
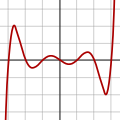
Polynomial of degree 7:
f(x) = (x − 3)(x − 2)(x − 1)(x)(x + 1)(x + 2)
(x + 3)
A polynomial function in one real variable can be represented by a graph.
-
The graph of the zero polynomial
f(x) = 0is the x-axis.
-
The graph of a degree 0 polynomial
f(x) = a0, where a0 ≠ 0,is a horizontal line with y-intercept a0
-
The graph of a degree 1 polynomial (or linear function)
f(x) = a0 + a1x, where a1 ≠ 0,is an oblique line with y-intercept a0 and slope a1.
-
The graph of a degree 2 polynomial
f(x) = a0 + a1x + a2x2, where a2 ≠ 0is a parabola.
-
The graph of a degree 3 polynomial
f(x) = a0 + a1x + a2x2 + a3x3, where a3 ≠ 0is a cubic curve.
-
The graph of any polynomial with degree 2 or greater
f(x) = a0 + a1x + a2x2 + ⋯ + anxn, where an ≠ 0 and n ≥ 2is a continuous non-linear curve.
A non-constant polynomial function tends to infinity when the variable increases indefinitely (in absolute value). If the degree is higher than one, the graph does not have any asymptote. It has two parabolic branches with vertical direction (one branch for positive x and one for negative x).
Polynomial graphs are analyzed in calculus using intercepts, slopes, concavity, and end behavior.
Equations
[edit]A polynomial equation, also called an algebraic equation, is an equation of the form[27] For example, is a polynomial equation.
When considering equations, the indeterminates (variables) of polynomials are also called unknowns, and the solutions are the possible values of the unknowns for which the equality is true (in general more than one solution may exist). A polynomial equation stands in contrast to a polynomial identity like , where both expressions represent the same polynomial in different forms, and as a consequence any evaluation of both members gives a valid equality.
In elementary algebra, methods such as the quadratic formula are taught for solving all first degree and second degree polynomial equations in one variable. There are also formulas for the cubic and quartic equations. For higher degrees, the Abel–Ruffini theorem asserts that there can not exist a general formula in radicals. However, root-finding algorithms may be used to find numerical approximations of the roots of a polynomial expression of any degree.
The number of solutions of a polynomial equation with real coefficients may not exceed the degree, and equals the degree when the complex solutions are counted with their multiplicity. This fact is called the fundamental theorem of algebra.
Solving equations
[edit]A root of a nonzero univariate polynomial P is a value a of x such that P(a) = 0. In other words, a root of P is a solution of the polynomial equation P(x) = 0 or a zero of the polynomial function defined by P. In the case of the zero polynomial, every number is a zero of the corresponding function, and the concept of root is rarely considered.
A number a is a root of a polynomial P if and only if the linear polynomial x − a divides P, that is if there is another polynomial Q such that P = (x − a) Q. It may happen that a power (greater than 1) of x − a divides P; in this case, a is a multiple root of P, and otherwise a is a simple root of P. If P is a nonzero polynomial, there is a highest power m such that (x − a)m divides P, which is called the multiplicity of a as a root of P. The number of roots of a nonzero polynomial P, counted with their respective multiplicities, cannot exceed the degree of P,[28] and equals this degree if all complex roots are considered (this is a consequence of the fundamental theorem of algebra). The coefficients of a polynomial and its roots are related by Vieta's formulas.
Some polynomials, such as x2 + 1, do not have any roots among the real numbers. If, however, the set of accepted solutions is expanded to the complex numbers, every non-constant polynomial has at least one root; this is the fundamental theorem of algebra. By successively dividing out factors x − a, one sees that any polynomial with complex coefficients can be written as a constant (its leading coefficient) times a product of such polynomial factors of degree 1; as a consequence, the number of (complex) roots counted with their multiplicities is exactly equal to the degree of the polynomial.
There may be several meanings of "solving an equation". One may want to express the solutions as explicit numbers; for example, the unique solution of 2x − 1 = 0 is 1/2. This is, in general, impossible for equations of degree greater than one, and, since the ancient times, mathematicians have searched to express the solutions as algebraic expressions; for example, the golden ratio (1+√5)/2 is the unique positive solution of x2 − x − 1 = 0 In the ancient times, they succeeded only for degrees one and two. For quadratic equations, the quadratic formula provides such expressions of the solutions. Since the 16th century, similar formulas (using cube roots in addition to square roots), although much more complicated, are known for equations of degree three and four (see cubic equation and quartic equation). But formulas for degree 5 and higher eluded researchers for several centuries. In 1824, Niels Henrik Abel proved the striking result that there are equations of degree 5 whose solutions cannot be expressed by a (finite) formula, involving only arithmetic operations and radicals (see Abel–Ruffini theorem). In 1830, Évariste Galois proved that most equations of degree higher than four cannot be solved by radicals, and showed that for each equation, one may decide whether it is solvable by radicals, and, if it is, solve it. This result marked the start of Galois theory and group theory, two important branches of modern algebra. Galois himself noted that the computations implied by his method were impracticable. Nevertheless, formulas for solvable equations of degrees 5 and 6 have been published (see quintic function and sextic equation).
When there is no algebraic expression for the roots, and when such an algebraic expression exists but is too complicated to be useful, the unique way of solving it is to compute numerical approximations of the solutions.[29] There are many methods for that; some are restricted to polynomials and others may apply to any continuous function. The most efficient algorithms allow solving easily (on a computer) polynomial equations of degree higher than 1,000 (see Root-finding algorithm).
For polynomials with more than one indeterminate, the combinations of values for the variables for which the polynomial function takes the value zero are generally called zeros instead of "roots". The study of the sets of zeros of polynomials is the object of algebraic geometry. For a set of polynomial equations with several unknowns, there are algorithms to decide whether they have a finite number of complex solutions, and, if this number is finite, for computing the solutions. See System of polynomial equations.
The special case where all the polynomials are of degree one is called a system of linear equations, for which another range of different solution methods exist, including the classical Gaussian elimination.
A polynomial equation for which one is interested only in the solutions which are integers is called a Diophantine equation. Solving Diophantine equations is generally a very hard task. It has been proved that there cannot be any general algorithm for solving them, or even for deciding whether the set of solutions is empty (see Hilbert's tenth problem). Some of the most famous problems that have been solved during the last fifty years are related to Diophantine equations, such as Fermat's Last Theorem.
Polynomial expressions
[edit]Polynomials where indeterminates are substituted for some other mathematical objects are often considered, and sometimes have a special name.
Trigonometric polynomials
[edit]A trigonometric polynomial is a finite linear combination of functions sin(nx) and cos(nx) with n taking on the values of one or more natural numbers.[30] The coefficients may be taken as real numbers, for real-valued functions.
If sin(nx) and cos(nx) are expanded in terms of sin(x) and cos(x), a trigonometric polynomial becomes a polynomial in the two variables sin(x) and cos(x) (using the multiple-angle formulae). Conversely, every polynomial in sin(x) and cos(x) may be converted, with Product-to-sum identities, into a linear combination of functions sin(nx) and cos(nx). This equivalence explains why linear combinations are called polynomials.
For complex coefficients, there is no difference between such a function and a finite Fourier series.
Trigonometric polynomials are widely used, for example in trigonometric interpolation applied to the interpolation of periodic functions. They are also used in the discrete Fourier transform.
Matrix polynomials
[edit]A matrix polynomial is a polynomial with square matrices as variables.[31] Given an ordinary, scalar-valued polynomial this polynomial evaluated at a matrix A is where I is the identity matrix.[32]
A matrix polynomial equation is an equality between two matrix polynomials, which holds for the specific matrices in question. A matrix polynomial identity is a matrix polynomial equation which holds for all matrices A in a specified matrix ring Mn(R).
Exponential polynomials
[edit]A bivariate polynomial where the second variable is substituted for an exponential function applied to the first variable, for example P(x, ex), may be called an exponential polynomial.
Related concepts
[edit]Rational functions
[edit]A rational fraction is the quotient (algebraic fraction) of two polynomials. Any algebraic expression that can be rewritten as a rational fraction is a rational function.
While polynomial functions are defined for all values of the variables, a rational function is defined only for the values of the variables for which the denominator is not zero.
The rational fractions include the Laurent polynomials, but do not limit denominators to powers of an indeterminate.
Laurent polynomials
[edit]Laurent polynomials are like polynomials, but allow negative powers of the variable(s) to occur.
Power series
[edit]Formal power series are like polynomials, but allow infinitely many non-zero terms to occur, so that they do not have finite degree. Unlike polynomials they cannot in general be explicitly and fully written down (just like irrational numbers cannot), but the rules for manipulating their terms are the same as for polynomials. Non-formal power series also generalize polynomials, but the multiplication of two power series may not converge.
Polynomial ring
[edit]A polynomial f over a commutative ring R is a polynomial all of whose coefficients belong to R. It is straightforward to verify that the polynomials in a given set of indeterminates over R form a commutative ring, called the polynomial ring in these indeterminates, denoted in the univariate case and in the multivariate case.
One has So, most of the theory of the multivariate case can be reduced to an iterated univariate case.
The map from R to R[x] sending r to itself considered as a constant polynomial is an injective ring homomorphism, by which R is viewed as a subring of R[x]. In particular, R[x] is an algebra over R.
One can think of the ring R[x] as arising from R by adding one new element x to R, and extending in a minimal way to a ring in which x satisfies no other relations than the obligatory ones, plus commutation with all elements of R (that is xr = rx). To do this, one must add all powers of x and their linear combinations as well.
Formation of the polynomial ring, together with forming factor rings by factoring out ideals, are important tools for constructing new rings out of known ones. For instance, the ring (in fact field) of complex numbers, which can be constructed from the polynomial ring R[x] over the real numbers by factoring out the ideal of multiples of the polynomial x2 + 1. Another example is the construction of finite fields, which proceeds similarly, starting out with the field of integers modulo some prime number as the coefficient ring R (see modular arithmetic).
If R is commutative, then one can associate with every polynomial P in R[x] a polynomial function f with domain and range equal to R. (More generally, one can take domain and range to be any same unital associative algebra over R.) One obtains the value f(r) by substitution of the value r for the symbol x in P. One reason to distinguish between polynomials and polynomial functions is that, over some rings, different polynomials may give rise to the same polynomial function (see Fermat's little theorem for an example where R is the integers modulo p). This is not the case when R is the real or complex numbers, whence the two concepts are not always distinguished in analysis. An even more important reason to distinguish between polynomials and polynomial functions is that many operations on polynomials (like Euclidean division) require looking at what a polynomial is composed of as an expression rather than evaluating it at some constant value for x.
Divisibility
[edit]If R is an integral domain and f and g are polynomials in R[x], it is said that f divides g or f is a divisor of g if there exists a polynomial q in R[x] such that f q = g. If then a is a root of f if and only divides f. In this case, the quotient can be computed using the polynomial long division.[33][34]
If F is a field and f and g are polynomials in F[x] with g ≠ 0, then there exist unique polynomials q and r in F[x] with and such that the degree of r is smaller than the degree of g (using the convention that the polynomial 0 has a negative degree). The polynomials q and r are uniquely determined by f and g. This is called Euclidean division, division with remainder or polynomial long division and shows that the ring F[x] is a Euclidean domain.
Analogously, prime polynomials (more correctly, irreducible polynomials) can be defined as non-zero polynomials which cannot be factorized into the product of two non-constant polynomials. In the case of coefficients in a ring, "non-constant" must be replaced by "non-constant or non-unit" (both definitions agree in the case of coefficients in a field). Any polynomial may be decomposed into the product of an invertible constant by a product of irreducible polynomials. If the coefficients belong to a field or a unique factorization domain this decomposition is unique up to the order of the factors and the multiplication of any non-unit factor by a unit (and division of the unit factor by the same unit). When the coefficients belong to integers, rational numbers or a finite field, there are algorithms to test irreducibility and to compute the factorization into irreducible polynomials (see Factorization of polynomials). These algorithms are not practicable for hand-written computation, but are available in any computer algebra system. Eisenstein's criterion can also be used in some cases to determine irreducibility.
Applications
[edit]Positional notation
[edit]In modern positional numbers systems, such as the decimal system, the digits and their positions in the representation of an integer, for example, 45, are a shorthand notation for a polynomial in the radix or base, in this case, 4 × 101 + 5 × 100. As another example, in radix 5, a string of digits such as 132 denotes the (decimal) number 1 × 52 + 3 × 51 + 2 × 50 = 42. This representation is unique. Let b be a positive integer greater than 1. Then every positive integer a can be expressed uniquely in the form
where m is a nonnegative integer and the r's are integers such that
0 < rm < b and 0 ≤ ri < b for i = 0, 1, . . . , m − 1.[35]
Interpolation and approximation
[edit]The simple structure of polynomial functions makes them quite useful in analyzing general functions using polynomial approximations. An important example in calculus is Taylor's theorem, which roughly states that every differentiable function locally looks like a polynomial function, and the Stone–Weierstrass theorem, which states that every continuous function defined on a compact interval of the real axis can be approximated on the whole interval as closely as desired by a polynomial function. Practical methods of approximation include polynomial interpolation and the use of splines.[36]
Other applications
[edit]Polynomials are frequently used to encode information about some other object. The characteristic polynomial of a matrix or linear operator contains information about the operator's eigenvalues. The minimal polynomial of an algebraic element records the simplest algebraic relation satisfied by that element. The chromatic polynomial of a graph counts the number of proper colourings of that graph.
The term "polynomial", as an adjective, can also be used for quantities or functions that can be written in polynomial form. For example, in computational complexity theory the phrase polynomial time means that the time it takes to complete an algorithm is bounded by a polynomial function of some variable, such as the size of the input.
History
[edit]Determining the roots of polynomials, or "solving algebraic equations", is among the oldest problems in mathematics. However, the elegant and practical notation we use today only developed beginning in the 15th century. Before that, equations were written out in words. For example, an algebra problem from the Chinese Arithmetic in Nine Sections, c. 200 BCE, begins "Three sheafs of good crop, two sheafs of mediocre crop, and one sheaf of bad crop are sold for 29 dou." We would write 3x + 2y + z = 29.
History of the notation
[edit]The earliest known use of the equal sign is in Robert Recorde's The Whetstone of Witte, 1557. The signs + for addition, − for subtraction, and the use of a letter for an unknown appear in Michael Stifel's Arithemetica integra, 1544. René Descartes, in La géometrie, 1637, introduced the concept of the graph of a polynomial equation. He popularized the use of letters from the beginning of the alphabet to denote constants and letters from the end of the alphabet to denote variables, as can be seen above, in the general formula for a polynomial in one variable, where the as denote constants and x denotes a variable. Descartes introduced the use of superscripts to denote exponents as well.[37]
See also
[edit]Notes
[edit]- ^ Beauregard & Fraleigh (1973, p. 153)
- ^ Burden & Faires (1993, p. 96)
- ^ Fraleigh (1976, p. 245)
- ^ McCoy (1968, p. 190)
- ^ Moise (1967, p. 82)
- ^ See "polynomial" and "binomial", Compact Oxford English Dictionary
- ^ a b Weisstein, Eric W. "Polynomial". mathworld.wolfram.com. Retrieved 2020-08-28.
- ^ a b "Polynomials | Brilliant Math & Science Wiki". brilliant.org. Retrieved 2020-08-28.
- ^ a b c Barbeau 2003, pp. 1–2
- ^ Weisstein, Eric W. "Zero Polynomial". MathWorld.
- ^ Edwards 1995, p. 78
- ^ a b c Edwards, Harold M. (1995). Linear Algebra. Springer. p. 47. ISBN 978-0-8176-3731-6.
- ^ Weisstein, Eric W. "Multinomial". mathworld.wolfram.com. Retrieved 2025-08-26.
- ^ Clapham, Christopher; Nicholson, James (2009). The Concise Oxford Dictionary of Mathematics (4th ed.). United States: Oxford University Press. p. 303. ISBN 9780199235940.
- ^ Weisstein, Eric W. "Multivariate Polynomial". mathworld.wolfram.com. Retrieved 2025-08-26.
- ^ Salomon, David (2006). Coding for Data and Computer Communications. Springer. p. 459. ISBN 978-0-387-23804-3.
- ^ a b Introduction to Algebra. Yale University Press. 1965. p. 621.
Any two such polynomials can be added, subtracted, or multiplied. Furthermore, the result in each case is another polynomial
- ^ Kriete, Hartje (1998-05-20). Progress in Holomorphic Dynamics. CRC Press. p. 159. ISBN 978-0-582-32388-9.
This class of endomorphisms is closed under composition,
- ^ Marecek, Lynn; Mathis, Andrea Honeycutt (6 May 2020). Intermediate Algebra 2e. OpenStax. §7.1.
- ^ Haylock, Derek; Cockburn, Anne D. (2008-10-14). Understanding Mathematics for Young Children: A Guide for Foundation Stage and Lower Primary Teachers. SAGE. p. 49. ISBN 978-1-4462-0497-9.
We find that the set of integers is not closed under this operation of division.
- ^ a b Marecek & Mathis 2020, §5.4]
- ^ Selby, Peter H.; Slavin, Steve (1991). Practical Algebra: A Self-Teaching Guide (2nd ed.). Wiley. ISBN 978-0-471-53012-1.
- ^ Weisstein, Eric W. "Ruffini's Rule". mathworld.wolfram.com. Retrieved 2020-07-25.
- ^ Barbeau 2003, pp. 80–2
- ^ Barbeau 2003, pp. 64–5
- ^ Varberg, Purcell & Rigdon 2007, p. 38.
- ^ Proskuryakov, I.V. (1994). "Algebraic equation". In Hazewinkel, Michiel (ed.). Encyclopaedia of Mathematics. Vol. 1. Springer. ISBN 978-1-55608-010-4.
- ^ Leung, Kam-tim; et al. (1992). Polynomials and Equations. Hong Kong University Press. p. 134. ISBN 9789622092716.
- ^ McNamee, J.M. (2007). Numerical Methods for Roots of Polynomials, Part 1. Elsevier. ISBN 978-0-08-048947-6.
- ^ Powell, Michael J. D. (1981). Approximation Theory and Methods. Cambridge University Press. ISBN 978-0-521-29514-7.
- ^ Gohberg, Israel; Lancaster, Peter; Rodman, Leiba (2009) [1982]. Matrix Polynomials. Classics in Applied Mathematics. Vol. 58. Lancaster, PA: Society for Industrial and Applied Mathematics. ISBN 978-0-89871-681-8. Zbl 1170.15300.
- ^ Horn & Johnson 1990, p. 36.
- ^ Irving, Ronald S. (2004). Integers, Polynomials, and Rings: A Course in Algebra. Springer. p. 129. ISBN 978-0-387-20172-6.
- ^ Jackson, Terrence H. (1995). From Polynomials to Sums of Squares. CRC Press. p. 143. ISBN 978-0-7503-0329-3.
- ^ McCoy 1968, p. 75
- ^ de Villiers, Johann (2012). Mathematics of Approximation. Springer. ISBN 9789491216503.
- ^ Eves, Howard (1990). An Introduction to the History of Mathematics (6th ed.). Saunders. ISBN 0-03-029558-0.
- ^ The coefficient of a term may be any number from a specified set. If that set is the set of real numbers, we speak of "polynomials over the reals". Other common kinds of polynomials are polynomials with integer coefficients, polynomials with complex coefficients, and polynomials with coefficients that are integers modulo some prime number .
- ^ This terminology dates from the time when the distinction was not clear between a polynomial and the function that it defines: a constant term and a constant polynomial define constant functions.[citation needed]
- ^ In fact, as a homogeneous function, it is homogeneous of every degree.[citation needed]
- ^ Some authors use "monomial" to mean "monic monomial". See Knapp, Anthony W. (2007). Advanced Algebra: Along with a Companion Volume Basic Algebra. Springer. p. 457. ISBN 978-0-8176-4522-9.
- ^ This paragraph assumes that the polynomials have coefficients in a field.
References
[edit]- Barbeau, E.J. (2003). Polynomials. Springer. ISBN 978-0-387-40627-5.
- Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Company, ISBN 0-395-14017-X
- Bronstein, Manuel; et al., eds. (2006). Solving Polynomial Equations: Foundations, Algorithms, and Applications. Springer. ISBN 978-3-540-27357-8.
- Burden, Richard L.; Faires, J. Douglas (1993), Numerical Analysis (5th ed.), Boston: Prindle, Weber and Schmidt, ISBN 0-534-93219-3
- Cahen, Paul-Jean; Chabert, Jean-Luc (1997). Integer-Valued Polynomials. American Mathematical Society. ISBN 978-0-8218-0388-2.
- Fraleigh, John B. (1976), A First Course In Abstract Algebra (2nd ed.), Reading: Addison-Wesley, ISBN 0-201-01984-1
- Horn, Roger A.; Johnson, Charles R. (1990). Matrix Analysis. Cambridge University Press. ISBN 978-0-521-38632-6..
- Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, vol. 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR 1878556. This classical book covers most of the content of this article.
- Leung, Kam-tim; et al. (1992). Polynomials and Equations. Hong Kong University Press. ISBN 9789622092716.
- Mayr, K. (1937). "Über die Auflösung algebraischer Gleichungssysteme durch hypergeometrische Funktionen". Monatshefte für Mathematik und Physik. 45: 280–313. doi:10.1007/BF01707992. S2CID 197662587.
- McCoy, Neal H. (1968), Introduction To Modern Algebra, Revised Edition, Boston: Allyn and Bacon, LCCN 68015225
- Moise, Edwin E. (1967), Calculus: Complete, Reading: Addison-Wesley
- Prasolov, Victor V. (2005). Polynomials. Springer. ISBN 978-3-642-04012-2.
- Sethuraman, B.A. (1997). "Polynomials". Rings, Fields, and Vector Spaces: An Introduction to Abstract Algebra Via Geometric Constructibility. Springer. ISBN 978-0-387-94848-5.
- Toth, Gabor (2021). "Polynomial Expressions". Elements of Mathematics. Undergraduate Texts in Mathematics. pp. 263–318. doi:10.1007/978-3-030-75051-0_6. ISBN 978-3-030-75050-3.
- Umemura, H. (2012) [1984]. "Resolution of algebraic equations by theta constants". In Mumford, David (ed.). Tata Lectures on Theta II: Jacobian theta functions and differential equations. Springer. pp. 261–. ISBN 978-0-8176-4578-6.
- Varberg, Dale E.; Purcell, Edwin J.; Rigdon, Steven E. (2007). Calculus (9th ed.). Pearson Prentice Hall. ISBN 978-0131469686.
- von Lindemann, F. (1884). "Ueber die Auflösung der algebraischen Gleichungen durch transcendente Functionen". Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen. 1884: 245–8.
- von Lindemann, F. (1892). "Ueber die Auflösung der algebraischen Gleichungen durch transcendente Functionen. II". Nachrichten von der Königl. Gesellschaft der Wissenschaften und der Georg-Augusts-Universität zu Göttingen. 1892: 245–8.
External links
[edit]- Markushevich, A.I. (2001) [1994], "Polynomial", Encyclopedia of Mathematics, EMS Press
- "Euler's Investigations on the Roots of Equations". Archived from the original on September 24, 2012.




















































































![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)





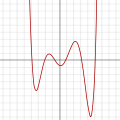





![{\displaystyle R[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ce54622cb380383ab3a42441b056626ea0d2440)
![{\displaystyle R[x_{1},\ldots ,x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58c388e003e234e12fb55533e35a211c8cf295e5)
![{\displaystyle R[x_{1},\ldots ,x_{n}]=\left(R[x_{1},\ldots ,x_{n-1}]\right)[x_{n}].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba0bbfe1bccac6aa10e3a7daba9b95381c6f05bd)



