Hubbry Logo
Semiperfect numberSemiperfect numberMain
Open search
Semiperfect number
Community hub
Semiperfect number
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Semiperfect number
Semiperfect number
Semiperfect number
View on Wikipedia
from Wikipedia

In number theory, a semiperfect number or pseudoperfect number is a natural number n equal to the sum of all or some of its proper divisors. A semiperfect number equal to the sum of all its proper divisors is a perfect number.

Key Information

The first few semiperfect numbers are: 6, 12, 18, 20, 24, 28, 30, 36, 40, ... (sequence A005835 in the OEIS)

Properties

[edit]
  • Every multiple of a semiperfect number is semiperfect.[1] A semiperfect number not divisible by any smaller semiperfect number is called primitive.
  • Every number of the form 2mp for a natural number m and an odd prime number p such that p < 2m+1 is also semiperfect.
    • In particular, every number of the form 2m(2m+1 − 1) is semiperfect, and is indeed perfect if 2m+1 − 1 is a Mersenne prime.
  • The smallest odd semiperfect number is 945.
  • A semiperfect number is necessarily either perfect or abundant. An abundant number that is not semiperfect is called a weird number.
  • Except for 2, all primary pseudoperfect numbers are semiperfect.
  • Every practical number that is not a power of two is semiperfect.
  • The natural density of the set of semiperfect numbers exists.[2]

Primitive semiperfect numbers

[edit]

A primitive semiperfect number (also called a primitive pseudoperfect number, irreducible semiperfect number or irreducible pseudoperfect number) is a semiperfect number that has no semiperfect proper divisor.[2]

The first few primitive semiperfect numbers are 6, 20, 28, 88, 104, 272, 304, 350, ... (sequence A006036 in the OEIS)

There are infinitely many such numbers. All numbers of the form 2mp, with p a prime between 2m and 2m+1, are primitive semiperfect, but not all primitive semiperfect numbers follow this form; for example, 770.[1][2] There are infinitely many odd primitive semiperfect numbers, the smallest being 945. There are infinitely many primitive semiperfect numbers that are not harmonic divisor numbers.[1]

Every semiperfect number is a multiple of a primitive semiperfect number.

See also

[edit]

Notes

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Semiperfect number

View on Grokipedia
from Grokipedia
A semiperfect number, also known as a pseudoperfect number, is a positive integer that can be expressed as the sum of some or all of its proper divisors (the positive divisors excluding the number itself). The smallest semiperfect number is 6, which is also the smallest perfect number since it equals the sum of all its proper divisors (1 + 2 + 3 = 6); subsequent examples include 12 (6 + 4 + 2 = 12), 18 (9 + 6 + 3 = 18), 20 (10 + 5 + 4 + 1 = 20), 24, 28, 30, 36, and 40. The term "pseudoperfect" was introduced by W. Sierpiński in 1965, while "semiperfect" was coined by E. Zachariou and G. Zachariou in 1972 to emphasize the partial sum aspect. Semiperfect numbers encompass all perfect numbers as a but extend to abundant numbers where a proper of divisors sums to the number, excluding deficient numbers and primes; notably, they include all multiples of 6 and all multiples of any semiperfect number. The first odd semiperfect number is 945, and the proportion of semiperfect numbers up to xx has a lower density bound of approximately 0.23790. Abundant numbers that are not semiperfect are termed , with 70 as the smallest example. These numbers relate to subset sum problems in and have been studied in connection with functions and harmonic numbers.

Definition and Examples

Definition

A , also known as a pseudoperfect number, is a that is equal to the sum of some of its proper divisors (or all of them, in the case of ).

Basic Examples

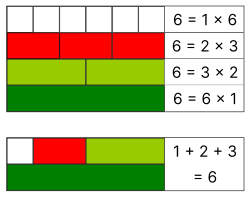
Semiperfect numbers include both , where all proper divisors sum to the number, and other cases where only a proper subset does so. The smallest semiperfect number is 6, a whose proper divisors are 1, 2, and 3, summing to 66. The next few even semiperfect numbers are 12, 18, 20, 24, 28, and 30. For 12, one subset of proper divisors is {1, 2, 3, 6}, summing to 12; another is {2, 4, 6}. For 18, the subset {3, 6, 9} sums to 18. For 20, the subset {1, 4, 5, 10} sums to 20, though other subsets also exist. The number 28 is perfect, with proper divisors 1, 2, 4, 7, and 14 summing to 28. For 30, a subset such as {5, 10, 15} sums to 30. Unlike even semiperfect numbers, which appear early in the natural numbers, odd semiperfect numbers are rarer. The smallest odd semiperfect number is 945. Its proper divisors are 1, 3, 5, 7, 9, 15, 21, 27, 35, 45, 63, 105, 135, 189, and 315, summing to 975. One subset summing to 945 is {1, 5, 7, 9, 15, 21, 35, 45, 63, 105, 135, 189, 315}. The sequence of semiperfect numbers is given by OEIS A005835.

Mathematical Properties

General Properties

A semiperfect number greater than 1 is either perfect or abundant, as the sum of all its proper divisors exceeds the number (for abundant) or equals it (for perfect), allowing subsets to sum precisely to the number, whereas deficient numbers have total proper divisor sum less than the number itself, precluding such a subset. The collection of semiperfect numbers is closed under : if nn is semiperfect, then so is any positive multiple knkn for k≥1k \geq 1. This holds because if a SS of the proper divisors of nn sums to nn, then the scaled subset {k⋅d∣d∈S}\{k \cdot d \mid d \in S\} consists of proper divisors of knkn (each k⋅d<knk \cdot d < kn since d<nd < n) and sums to knkn. Certain forms guarantee semiperfectness; for instance, every integer of the form 2mp2^m p, where m≥1m \geq 1 and pp is an odd with 2m<p<2m+12^m < p < 2^{m+1}, is semiperfect. In such cases, the divisor set—powers of 2 up to 2m2^m and their multiples by pp up to 2m−1p2^{m-1} p—permits a subset summing to 2mp2^m p, leveraging the binary structure of the powers of 2 and the size of pp. The semiperfect numbers possess a natural that exists and is positive. Every practical number except powers of 2 is semiperfect, as practical numbers enable every integer from 1 to their abundance σ(n)−n\sigma(n) - n to be written as a sum of distinct proper divisors, and non-powers-of-2 practical numbers are abundant with σ(n)−n>n\sigma(n) - n > n, thus allowing a sum to nn itself.

Relation to Abundant and Perfect Numbers

Semiperfect numbers occupy a specific position in the hierarchy of numbers classified by their divisor sums. A perfect number is one where the sum of its proper divisors equals the number itself, denoted as σ(n)−n=n\sigma(n) - n = n, or equivalently σ(n)=2n\sigma(n) = 2n, where σ(n)\sigma(n) is the sum of all divisors of nn. Semiperfect numbers include all perfect numbers and extend to certain abundant numbers, where an abundant number satisfies σ(n)−n>n\sigma(n) - n > n (or σ(n)>2n\sigma(n) > 2n), but with the additional property that some subset of its distinct proper divisors sums exactly to nn. This subset sum condition distinguishes semiperfect numbers from the broader class of abundant numbers, positioning them as a bridge between perfect numbers and those abundant numbers lacking such a subset, known as weird numbers. Weird numbers are defined precisely as abundant numbers that are not semiperfect, meaning no combination of their distinct proper divisors sums to the number itself. The smallest weird number is 70, and all known weird numbers are even, with no odd weird numbers identified despite extensive computational searches up to 102110^{21}. This contrast highlights the rarity and elusiveness of weird numbers within the abundant category, as semiperfect numbers encompass the majority of abundant instances where subset sums are feasible. Within the subclass of primitive abundant numbers—those abundant numbers whose proper divisors are all deficient—further partitioning occurs: such numbers are either primitive semiperfect (with no proper pseudoperfect divisors) or . The set of weird numbers has positive asymptotic , implying their infinite prevalence, though they form a proper subset of abundant numbers excluding the semiperfect ones. This taxonomic relation underscores the nuanced structure of abundance, where semiperfect numbers provide a measurable criterion for "balance" amid excess divisor sums.

Primitive Semiperfect Numbers

Definition

A primitive semiperfect number is a semiperfect number—defined as a equal to the sum of some of its proper divisors—such that none of its proper divisors is semiperfect. Equivalently, a primitive semiperfect number is not divisible by any other semiperfect number besides 1. Every semiperfect number is a multiple of some primitive semiperfect number. All known even perfect numbers, which are themselves semiperfect, are primitive semiperfect numbers.

Properties and Examples

Primitive semiperfect numbers exhibit several notable properties. There are infinitely many such numbers, as demonstrated by constructions of the form 2m⋅p2^m \cdot p, where pp is a prime chosen such that the number is semiperfect but no proper divisor is. Additionally, there are infinitely many odd primitive semiperfect numbers. The smallest primitive semiperfect numbers are 6, 20, 28, 88, 104, 272, 304, and 350 (sequence A006036 in the OEIS). The smallest odd primitive semiperfect number is 945. Most even primitive semiperfect numbers take the form 2m⋅p2^m \cdot p with pp an odd prime, but exceptions exist, such as 770 = 2⋅5⋅7⋅112 \cdot 5 \cdot 7 \cdot 11, which has four distinct prime factors.

History and Computation

Historical Development

The concept of semiperfect numbers originates as a generalization of perfect numbers, whose study dates to . Euclid described perfect numbers around 300 BCE in Book VII of his Elements as positive integers equal to the sum of their proper , establishing a foundational framework in for exploring divisor sums. This early work on perfect numbers provided the conceptual roots for later extensions, including those involving subsets of divisors, though such ideas remained informal for centuries. The formalization of semiperfect numbers occurred in the mid-20th century amid broader investigations into abundant numbers, where the sum of all proper divisors exceeds the number itself, naturally leading to questions about subsets that sum precisely to the number. Early mentions of these subset sum properties appeared in studies of abundant and deficient numbers, highlighting their role in bridging perfect and abundant classifications. The term "pseudoperfect number" was coined by Wacław Sierpiński in 1965 in his paper "Sur les nombres pseudoparfaits," published in Matematički Vesnik. This introduced a precise terminology for numbers expressible as the sum of some of their proper divisors, building directly on the tradition. In 1972, Andreas Zachariou and Eleni Zachariou proposed the alternative term "semiperfect number" in their paper "Perfect, semiperfect and Ore numbers," published in the Bulletin of the Mathematical Society. Their work further contextualized semiperfect numbers alongside related concepts like Ore's harmonic numbers. The recognition of the primitive subclass—semiperfect numbers none of whose proper divisors are semiperfect—emerged in the and through key contributions in the literature on subset sums. Notably, S. J. Benkoski and defined and analyzed primitive pseudoperfect numbers in their 1974 paper "On weird and pseudoperfect numbers," published in Mathematics of Computation, proving properties such as the convergence of the sum of their reciprocals. This marked a significant advancement in understanding the structure and distribution of semiperfect numbers.

Known Numbers and Searches

(OEIS) catalogs semiperfect numbers in sequence A005835 and primitive semiperfect numbers in A006036. Sequence A005835 includes over 10,000 terms, with all even semiperfect numbers enumerated up to at least 10^6, where they comprise the even abundant numbers excluding the rare even weird numbers. For primitive semiperfect numbers, A006036 lists 73 terms up to 4970, including both even and odd examples, with computational methods confirming all such numbers up to 5000. Odd semiperfect numbers are sparser and computationally more challenging to identify due to the scarcity of odd abundant numbers, but all known odd abundant numbers below 10^6 (1996 in total) are semiperfect. The smallest odd semiperfect number is 945, followed by others such as 1575 and 2205. Extensive searches have identified all odd semiperfect numbers up to 10^21, equating to all odd abundant numbers in this range, as no odd numbers have been discovered. These efforts rely on sieving techniques to first identify abundant candidates before verifying semiperfect status, with no additional odd semiperfect numbers reported beyond established lists as of 2022. Primitive odd semiperfect numbers, starting with 945, are also included in these enumerations, with A006036 noting their alignment with odd primitive abundant numbers up to known bounds. Determining whether a number is semiperfect involves solving the over its proper divisors to check if any subset sums exactly to the number, a task that is NP-complete in general due to the exponential possibilities in subset selection. However, for practical computation with numbers up to 10^21, dynamic programming algorithms are feasible, achieving efficiency in O(d(n) * n) time where d(n) is the number of divisors (typically small, under 100 for such n), by building a tracking achievable sums from the divisors. These methods enable exhaustive searches, though scaling to higher bounds requires optimized sieves to prune non-abundant candidates early. Open questions include the precise of semiperfect numbers, which exists and equals the of abundant numbers minus that of numbers, estimated positively but with refinements to weird number post-2000 showing semiperfects comprise most abundants. proved the existence of infinitely many odd primitive semiperfect numbers, resolving one infinitude question, though the overall distribution and potential gaps in large odd examples remain unexplored. No significant post-2020 discoveries of new odd semiperfect or primitive variants have emerged, with ongoing searches focusing on confirming the absence of odd numbers to solidify these classifications.
Add your contribution
Related Hubs
User Avatar
No comments yet.