Recent from talks
Nothing was collected or created yet.
Second
View on Wikipedia
| second | |
|---|---|
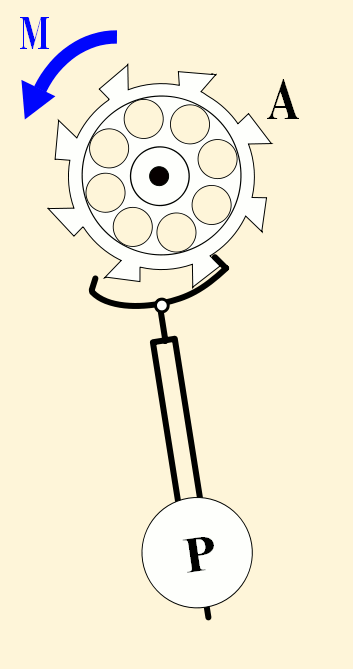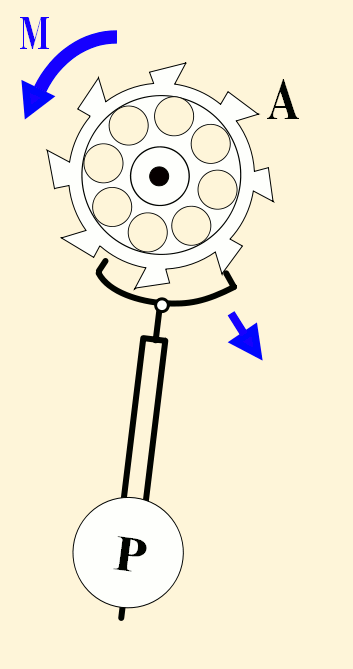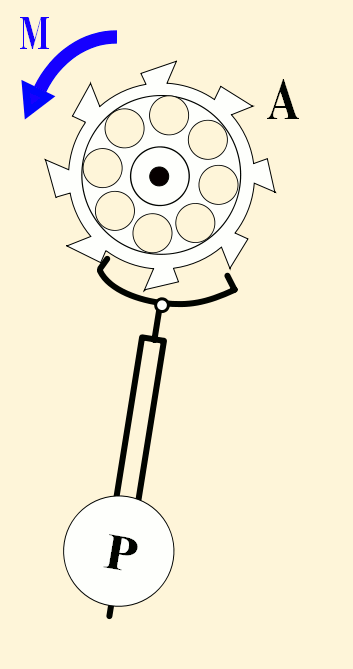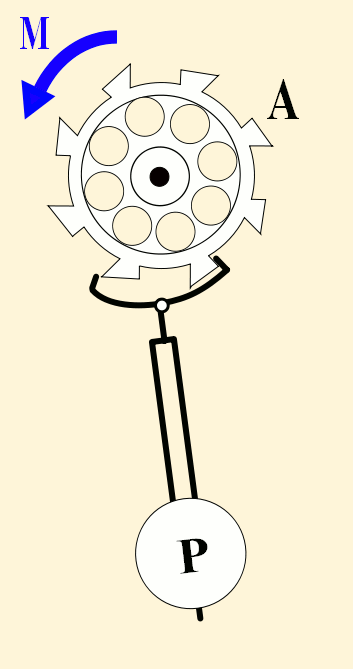
 A pendulum-governed escapement of a clock, ticking every second | |
| General information | |
| Unit system | SI |
| Unit of | time |
| Symbol | s |
The second (symbol: s) is a unit of time derived from the division of the day first into 24 hours, then to 60 minutes, and lastly to 60 seconds each, for a total of 24 × 60 × 60 = 86,400 seconds per day. The current and formal definition in the International System of Units (SI) is more precise:
The second [...] is defined by taking the fixed numerical value of the caesium frequency, ΔνCs, the unperturbed ground-state hyperfine transition frequency of the caesium 133 atom, to be 9192631770 when expressed in the unit Hz, which is equal to s−1.[1]
This current definition was adopted in 1967 when it became feasible to define the second based on fundamental properties of nature with caesium clocks.[2] As the speed of Earth's rotation varies and is slowing ever so slightly, a leap second is added at irregular intervals to civil time[nb 1] to keep clocks in sync with Earth's rotation.
The definition that is based on 1⁄86400 of a rotation of the earth is still used by the Universal Time 1 (UT1) system.
Etymology
[edit]"Minute" comes from the Latin pars minuta prima, meaning "first small part" i.e. first division of the hour – dividing into sixty, and "second" comes from the pars minuta secunda, "second small part", dividing again into sixty.[3]
Uses
[edit]Analog clocks and watches often have sixty tick marks on their faces, representing seconds (and minutes), and a "second hand" to mark the passage of time in seconds. Digital clocks and watches often have a two-digit seconds counter.
SI prefixes are frequently combined with the word second to denote subdivisions of the second: milliseconds (thousandths), microseconds (millionths), nanoseconds (billionths), and sometimes smaller units of a second. Multiples of seconds are usually counted in hours and minutes. Though SI prefixes may also be used to form multiples of the second such as kiloseconds (thousands of seconds), such units are rarely used in practice. An everyday experience with small fractions of a second is a 1-gigahertz microprocessor that has a cycle time of 1 nanosecond. Camera shutter speeds are often expressed in fractions of a second, such as 1⁄30 second or 1⁄1000 second.
Sexagesimal divisions of the day from a calendar based on astronomical observation have existed since the third millennium BC, though they were not seconds as we know them today.[4] Small divisions of time could not be measured back then, so such divisions were mathematically derived. The first timekeepers that could count seconds accurately were pendulum clocks invented in the 17th century. Starting in the 1950s, atomic clocks became better timekeepers than Earth's rotation, and they continue to set the standard today.
Clocks and solar time
[edit]A mechanical clock, which does not depend on measuring the relative rotational position of the Earth, keeps uniform time called mean time, within whatever accuracy is intrinsic to it. That means that every second, minute and every other division of time counted by the clock has the same duration as any other identical division of time. A sundial, which measures the relative position of the Sun in the sky called apparent time, does not keep uniform time. The time kept by a sundial varies by time of year, meaning that seconds, minutes and every other division of time is a different duration at different times of the year. The time of day measured with mean time versus apparent time may differ by as much as 15 minutes, but a single day differs from the next by only a small amount; 15 minutes is a cumulative difference over a part of the year. The effect is due chiefly to the obliqueness of Earth's axis with respect to its orbit around the Sun.
The difference between apparent solar time and mean time was recognized by astronomers since antiquity, but prior to the invention of accurate mechanical clocks in the mid-17th century, sundials were the only reliable timepieces, and apparent solar time was the only generally accepted standard.
Events and units of time in seconds
[edit]Fractions of a second are usually denoted in decimal notation, for example 2.01 seconds, or two and one hundredth seconds. Multiples of seconds are usually expressed as minutes and seconds, or hours, minutes and seconds of clock time, separated by colons, such as 11:23:24, or 45:23 (the latter notation can give rise to ambiguity, because the same notation is used to denote hours and minutes). It rarely makes sense to express longer periods of time like hours or days in seconds, because they are awkwardly large numbers. For the metric unit of second, there are decimal prefixes representing 10−30 to 1030 seconds.
Some common units of time in seconds are: a minute is 60 seconds; an hour is 3,600 seconds; a day is 86,400 seconds; a week is 604,800 seconds; a year (other than leap years) is 31,536,000 seconds; and a (Gregorian) century averages 3,155,695,200 seconds; with all of the above excluding any possible leap seconds. In astronomy, a Julian year is precisely 31,557,600 seconds.
Some common events in seconds are: a stone falls about 4.9 meters from rest in one second; a pendulum of length about one meter has a swing of one second, so pendulum clocks have pendulums about a meter long; the fastest human sprinters run 10 meters in a second; an ocean wave in deep water travels about 23 meters in one second; sound travels about 343 meters in one second in air; light takes 1.3 seconds to reach Earth from the surface of the Moon, a distance of 384,400 kilometers.
Other units incorporating seconds
[edit]A second is directly part of other units, such as frequency measured in hertz (inverse seconds or s−1), speed in meters per second, and acceleration in meters per second squared. The metric system unit becquerel, a measure of radioactive decay, is measured in inverse seconds and higher powers of second are involved in derivatives of acceleration such as jerk. Though many derivative units for everyday things are reported in terms of larger units of time, not seconds, they are ultimately defined in terms of the SI second; this includes time expressed in hours and minutes, velocity of a car in kilometers per hour or miles per hour, kilowatt hours of electricity usage, and speed of a turntable in rotations per minute.
Moreover, most other SI base units are defined by their relationship to the second: the meter is defined by setting the speed of light (in vacuum) to be 299 792 458 m/s, exactly; definitions of the SI base units kilogram, ampere, kelvin, and candela also depend on the second. The only base unit whose definition does not depend on the second is the mole, and only two of the 22 named derived units, radian and steradian, do not depend on the second either.
Timekeeping standards
[edit]A set of atomic clocks throughout the world keeps time by consensus: the clocks "vote" on the correct time, and all voting clocks are steered to agree with the consensus, which is called International Atomic Time (TAI). TAI "ticks" atomic seconds.[5]: 207–218
Civil time is defined to agree with the rotation of the Earth. The international standard for timekeeping is Coordinated Universal Time (UTC). This time scale "ticks" the same atomic seconds as TAI, but inserts or omits leap seconds as necessary to correct for variations in the rate of rotation of the Earth.[5]: 16–17, 207
A time scale in which the seconds are not exactly equal to atomic seconds is UT1, a form of universal time. UT1 is defined by the rotation of the Earth with respect to the Sun, and does not contain any leap seconds.[5]: 68, 232 UT1 always differs from UTC by less than a second.
Optical lattice clock
[edit]While they are not yet part of any timekeeping standard, optical lattice clocks with frequencies in the visible light spectrum now exist and are the most accurate timekeepers of all. A strontium clock with frequency 430 THz, in the red range of visible light, during the 2010s held the accuracy record: it gains or loses less than a second in 15 billion years, which is longer than the estimated age of the universe. Such a clock can measure a change in its elevation of as little as 2 cm by the change in its rate due to gravitational time dilation.[6]
History of definition
[edit]There have only ever been three definitions of the second: as a fraction of the day, as a fraction of an extrapolated year, and as the microwave frequency of a caesium atomic clock, which have each realized a sexagesimal division of the day from ancient astronomical calendars.
Sexagesimal divisions of calendar time and day
[edit]Civilizations in the classic period and earlier created divisions of the calendar as well as arcs using a sexagesimal system of counting, so at that time the second was a sexagesimal subdivision of the day (ancient second = day/60×60), not of the hour like the modern second (= hour/60×60).[citation needed] Sundials and water clocks were among the earliest timekeeping devices, and units of time were measured in degrees of arc. Conceptual units of time smaller than realisable on sundials were also used.
There are references to "second" as part of a lunar month in the writings of natural philosophers of the Middle Ages, which were mathematical subdivisions that could not be measured mechanically.[nb 2][nb 3]
Fraction of solar day
[edit]The earliest mechanical clocks, which appeared starting in the 14th century, had displays that divided the hour into halves, thirds, quarters and sometimes even 12 parts, but never by 60. In fact, the hour was not commonly divided in 60 minutes as it was not uniform in duration. It was not practical for timekeepers to consider minutes until the first mechanical clocks that displayed minutes appeared near the end of the 16th century. Mechanical clocks kept the mean time, as opposed to the apparent time displayed by sundials. By that time, sexagesimal divisions of time were well established in Europe.[nb 4]
The earliest clocks to display seconds appeared during the last half of the 16th century. The second became accurately measurable with the development of mechanical clocks. The earliest spring-driven timepiece with a second hand that marked seconds is an unsigned clock depicting Orpheus in the Fremersdorf collection, dated between 1560 and 1570.[9]: 417–418 [10] During the third quarter of the 16th century, Taqi al-Din built a clock with marks every 1⁄5 minute.[11] In 1579, Jost Bürgi built a clock for William of Hesse that marked seconds.[9]: 105 In 1581, Tycho Brahe redesigned clocks that had displayed only minutes at his observatory so they also displayed seconds, even though those seconds were not accurate. In 1587, Tycho complained that his four clocks disagreed by plus or minus four seconds.[9]: 104
In 1656, Dutch scientist Christiaan Huygens invented the first pendulum clock. It had a pendulum length of just under a meter, giving it a swing of one second, and an escapement that ticked every second. It was the first clock that could accurately keep time in seconds. By the 1730s, 80 years later, John Harrison's maritime chronometers could keep time accurate to within one second in 100 days.
In 1832, Gauss proposed using the second as the base unit of time in his millimeter–milligram–second system of units. The British Association for the Advancement of Science (BAAS) in 1862 stated that "All men of science are agreed to use the second of mean solar time as the unit of time."[12] BAAS formally proposed the CGS system in 1874, although this system was gradually replaced over the next 70 years by MKS units. Both the CGS and MKS systems used the same second as their base unit of time. MKS was adopted internationally during the 1940s, defining the second as 1⁄86,400 of a mean solar day.
Fraction of an ephemeris year
[edit]Sometime in the late 1940s, quartz crystal oscillator clocks with an operating frequency of ~100 kHz advanced to keep time with accuracy better than 1 part in 108 over an operating period of a day. It became apparent that a consensus of such clocks kept better time than the rotation of the Earth. Metrologists also knew that Earth's orbit around the Sun (a year) was much more stable than Earth's rotation. This led to proposals as early as 1950 to define the second as a fraction of a year.
The Earth's motion was described in Newcomb's Tables of the Sun (1895), which provided a formula for estimating the motion of the Sun relative to the epoch 1900 based on astronomical observations made between 1750 and 1892.[13] This resulted in adoption of an ephemeris time scale expressed in units of the sidereal year at that epoch by the IAU in 1952.[14] This extrapolated timescale brings the observed positions of the celestial bodies into accord with Newtonian dynamical theories of their motion.[13] In 1955, the tropical year, considered more fundamental than the sidereal year, was chosen by the IAU as the unit of time. The tropical year in the definition was not measured but calculated from a formula describing a mean tropical year that decreased linearly over time.
In 1956, the second was redefined in terms of a year relative to that epoch. The second was thus defined as "the fraction 1⁄31,556,925.9747 of the tropical year for 1900 January 0 at 12 hours ephemeris time".[13] This definition was adopted as part of the International System of Units in 1960.[15]
Atomic definition
[edit]Even the best mechanical, electric motorized and quartz crystal-based clocks develop discrepancies from environmental conditions; far better for timekeeping is the natural and exact "vibration" in an energized atom. The frequency of vibration (i.e., radiation) is very specific depending on the type of atom and how it is excited.[16] Since 1967, the second has been defined as exactly "the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom". This length of a second was selected to correspond exactly to the length of the ephemeris second previously defined. Atomic clocks use such a frequency to measure seconds by counting cycles per second at that frequency. Radiation of this kind is one of the most stable and reproducible phenomena of nature. The current generation of atomic clocks is accurate to within one second in a few hundred million years. Since 1967, atomic clocks based on atoms other than caesium-133 have been developed with increased precision by a factor of 100. Therefore a new definition of the second is planned.[17]
Atomic clocks now set the length of a second and the time standard for the world.[5]: 231–232
Table
[edit]| Decisions of the CIPM | Resolution of the CGPM | Information |
|---|---|---|
| That according to the decisions of the 8th General Assembly of the International Astronomical Union (Rome, 1952), the second of ephemeris time (ET) is the fraction
of the tropical year for 1900 January 0 at 12 h ET. |
The second is the fraction of the tropical year for 1900 January 0 at 12 hours ephemeris time. | 1956 CIPM
11th CGPM 1960 Resolution 9 |
| The standard to be employed is the transition between the hyperfine levels F=4, M=0 and F=3, M=0 of the ground state of the caesium 133 atom, unperturbed by external fields, and that the frequency of this transition is assigned the value 9192631770 hertz. | The second is the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium 133 atom | 13th CGPM Resolution 1
CIPM 1967 |
| This definition implies that the caesium atom is at rest and unperturbed. In consequence, in its practical realization, measurements must be corrected for velocity of the atoms with respect to the clock reference frame, for magnetic and electric fields including ambient black-body radiation, for spin-exchange effects and for other possible perturbations. | At its 1997 meeting, the CIPM affirmed that: This definition refers to a caesium atom at rest at a temperature of 0 K. This note was intended to make it clear that the definition of the SI second is based on a Cs atom unperturbed by black-body radiation, that is, in an environment whose temperature is 0 K, and that the frequencies of primary frequency standards should therefore be corrected for the shift due to ambient radiation, as stated at the meeting of the CCTF in 1999. | footnote added by the 14th meeting of the Consultative Committee for Time and Frequency in 1999
the footnote was added at the 86th (1997) meeting of the CIPM GCPM 1998 7th Edition SI Brochure |
| The definition of a unit refers to an idealized situation that can be reached in the practical realization with some uncertainty only. In this spirit, the definition of the second has to be understood as referring to atoms free of any perturbation, at rest and in the absence of electric and magnetic fields.
A future re-definition of the second would be justified if these idealized conditions can be achieved much easier than with the current definition. The definition of the second should be understood as the definition of the unit of proper time: it applies in a small spatial domain that shares the motion of the caesium atom used to realize the definition. In a laboratory sufficiently small to allow the effects of the non-uniformity of the gravitational field to be neglected when compared to the uncertainties of the realization of the second, the proper second is obtained after application of the special relativistic correction for the velocity of the atom in the laboratory. It is wrong to correct for the local gravitational field. |
The second, symbol s, is the SI unit of time. It is defined by taking the fixed numerical value of the caesium frequency, ΔνCs, the unperturbed ground-state hyperfine transition frequency of the caesium 133 atom, to be 9 192 631 770 when expressed in the unit Hz, which is equal to s−1.
The reference to an unperturbed atom is intended to make it clear that the definition of the SI second is based on an isolated caesium atom that is unperturbed by any external field, such as ambient black-body radiation. The second, so defined, is the unit of proper time in the sense of the general theory of relativity. To allow the provision of a coordinated time scale, the signals of different primary clocks in different locations are combined, which have to be corrected for relativistic caesium frequency shifts (see section 2.3.6). The CIPM has adopted various secondary representations of the second, based on a selected number of spectral lines of atoms, ions or molecules. The unperturbed frequencies of these lines can be determined with a relative uncertainty not lower than that of the realization of the second based on the 133Cs hyperfine transition frequency, but some can be reproduced with superior stability. |
Current Definition resolved in 2018 effective after the 26th GCPM approved the redefinition May 20, 2019.
SI Brochure 9 |
Future redefinition
[edit]In 2022, the best realisation of the second is done with caesium primary standard clocks such as IT-CsF2, NIST-F2, NPL-CsF2, PTB-CSF2, SU–CsFO2 or SYRTE-FO2. These clocks work by laser-cooling a cloud of Cs atoms to a microkelvin in a magneto-optic trap. These cold atoms are then launched vertically by laser light. The atoms then undergo Ramsey excitation in a microwave cavity. The fraction of excited atoms is then detected by laser beams. These clocks have 5×10−16 systematic uncertainty, which is equivalent to 50 picoseconds per day. A system of several fountains worldwide contribute to International Atomic Time. These caesium clocks also underpin optical frequency measurements.
Optical clocks are based on forbidden optical transitions in ions or atoms. They have frequencies around 1015 Hz, with a natural linewidth of typically 1 Hz, so the Q-factor is about 1015, or even higher. They have better stabilities than microwave clocks, which means that they can facilitate evaluation of lower uncertainties. They also have better time resolution, which means the clock "ticks" faster.[18] Optical clocks use either a single ion, or an optical lattice with 104–106 atoms.
Rydberg constant
[edit]A definition based on the Rydberg constant would involve fixing the value to a certain value: . The Rydberg constant describes the energy levels in a hydrogen atom with the nonrelativistic approximation .
The only viable way to fix the Rydberg constant involves trapping and cooling hydrogen. This is difficult because it is very light and the atoms move very fast, causing Doppler shifts. The radiation needed to cool the hydrogen – 121.5 nm – is also difficult. Another hurdle involves improving the uncertainty in QED calculations, specifically the Lamb shift in the 1s-2s transition of the hydrogen atom.[19]
Requirements
[edit]A redefinition must include improved optical clock reliability. TAI must be contributed to by optical clocks before the BIPM affirms a redefinition. A consistent method of sending signals must be developed before the second is redefined, such as fiber-optics.[19]
SI multiples
[edit]SI prefixes are commonly used for times shorter than one second, but rarely for multiples of a second. Instead, certain non-SI units are permitted for use with SI: minutes, hours, days, and in astronomy Julian years.[20]
| Submultiples | Multiples | ||||||
|---|---|---|---|---|---|---|---|
| Value | SI symbol | Name | Value | SI symbol | Name | Equivalent to | |
| 10−1 s | ds | decisecond | 101 s | das | decasecond | 10 seconds | |
| 10−2 s | cs | centisecond | 102 s | hs | hectosecond | 1 minute, 40 seconds | |
| 10−3 s | ms | millisecond | 103 s | ks | kilosecond | 16 minutes, 40 seconds | |
| 10−6 s | μs | microsecond | 106 s | Ms | megasecond | 1 week, 4 days, 13 hours, 46 minutes, 40 seconds | |
| 10−9 s | ns | nanosecond | 109 s | Gs | gigasecond | 31.7 years | |
| 10−12 s | ps | picosecond | 1012 s | Ts | terasecond | 31,700 years | |
| 10−15 s | fs | femtosecond | 1015 s | Ps | petasecond | 31.7 million years | |
| 10−18 s | as | attosecond | 1018 s | Es | exasecond | 31.7 billion years | |
| 10−21 s | zs | zeptosecond | 1021 s | Zs | zettasecond | 31.7 trillion years | |
| 10−24 s | ys | yoctosecond | 1024 s | Ys | yottasecond | 31.7 quadrillion years | |
| 10−27 s | rs | rontosecond | 1027 s | Rs | ronnasecond | 31.7 quintillion years | |
| 10−30 s | qs | quectosecond | 1030 s | Qs | quettasecond | 31.7 sextillion years | |
See also
[edit]Notes
[edit]- ^ Civil time is set, directly or indirectly, to Coordinated Universal Time, which includes leap seconds. Other time scales are used in scientific and technical fields that do not contain leap seconds.
- ^ In 1000, the Persian scholar al-Biruni, writing in Arabic, used the term second, and defined the division of time between new moons of certain specific weeks as a number of days, hours, minutes, seconds, thirds, and fourths after noon Sunday.[7]
- ^ In 1267, the medieval English scientist Roger Bacon, writing in Latin, defined the division of time between full moons as a number of hours, minutes, seconds, thirds, and fourths (horae, minuta, secunda, tertia, and quarta) after noon on specified calendar dates.[8]
- ^ It may be noted that 60 is the smallest multiple of the first 6 counting numbers. So a clock with 60 divisions would have a mark for thirds, fourths, fifths, sixths and twelfths (the hours); whatever units the clock would likely keep time in, would have marks.
References
[edit]- ^ "SI Brochure (2019)" (PDF). SI Brochure. BIPM. p. 130. Archived (PDF) from the original on May 23, 2019. Retrieved May 23, 2019.
- ^ Gill, Patrick (October 28, 2011). "When should we change the definition of the second?". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 369 (1953): 4109–4130. Bibcode:2011RSPTA.369.4109G. doi:10.1098/rsta.2011.0237. PMID 21930568. S2CID 6896025.
- ^ "second | Etymology of second by etymonline". www.etymonline.com. Retrieved October 4, 2024.
- ^ "mathematics – Ancient mathematical sources". Encyclopedia Britannica. Retrieved September 20, 2021.
- ^ a b c d McCarthy, Dennis D.; Seidelmann, P. Kenneth (2009). Time: From Earth Rotation to Atomic Physics. Weinheim: Wiley.
- ^ Vincent, James (April 22, 2015). "The most accurate clock ever built only loses one second every 15 billion years". TheVerge. Archived from the original on January 27, 2018. Retrieved January 26, 2018.
- ^ Al-Biruni (1879) [1000]. The chronology of ancient nations. Translated by Sachau, C. Edward. pp. 147–149. Archived from the original on September 16, 2019. Retrieved February 23, 2016.
- ^ Bacon, Roger (2000) [1267]. The Opus Majus of Roger Bacon. translated by Robert Belle Burke. University of Pennsylvania Press. table facing page 231. ISBN 1-85506-856-7.
- ^ a b c Landes, David S. (1983). Revolution in Time. Cambridge, Massachusetts: Harvard University Press. ISBN 0-674-76802-7.
- ^ Willsberger, Johann (1975). Clocks & watches. New York: Dial Press. ISBN 0-8037-4475-7. full page color photo: 4th caption page, 3rd photo thereafter (neither pages nor photos are numbered).
- ^ Selin, Helaine (July 31, 1997). Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures. Springer Science & Business Media. p. 934. ISBN 0-7923-4066-3. Archived from the original on November 20, 2016. Retrieved February 23, 2016.
- ^ Jenkin, Henry Charles Fleeming, ed. (1873). Reports of the committee on electrical standards. British Association for the Advancement of Science. p. 90. Archived from the original on November 20, 2016. Retrieved February 23, 2016.
- ^ a b c "Leap Seconds". Precise Time Department, United States Naval Observatory. Retrieved May 13, 2025.
- ^
Nautical Almanac Offices of the United Kingdom and the United States of America (1961), Explanatory Supplement to the Astronomical Ephemeris and the American Ephemeris and Nautical Almanac, p. 9,
... defined ephemeris time ... [was] adopted by the International Astronomical Union in Sept. 1952.
- ^ "SI Brochure (2006)" (PDF). SI Brochure 8th Edition. BIPM. p. 112. Archived (PDF) from the original on May 3, 2019. Retrieved May 23, 2019.
- ^ McCarthy, Dennis D.; Seidelmann, P. Kenneth (2009). "Definition and Role of a Second". Time: From Earth Rotation to Atomic Physics. Weinheim: Wiley.
- ^ Draft resolutions of the 27. General Conference on Weights and Measures in November 2022, Section E, p. 25
- ^ National Physical Laboratory (2011). "When should we change the definition of the second?". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 369 (1953): 4109–4130. Bibcode:2011RSPTA.369.4109G. doi:10.1098/rsta.2011.0237. PMID 21930568. S2CID 6896025.
- ^ a b Gill, Patrick (October 28, 2011). "When should we change the definition of the second?". Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. 369 (1953): 4109–4130. Bibcode:2011RSPTA.369.4109G. doi:10.1098/rsta.2011.0237. PMID 21930568. S2CID 6896025.
- ^ International Astronomical Union. "Recommendations Concerning Units". Archived from the original on February 16, 2007. Retrieved February 18, 2007. Reprinted from the "IAU Style Manual" by G.A. Wilkinson, Comm. 5, in IAU Transactions XXB (1987).
External links
[edit]- National Physical Laboratory: Trapped ion optical frequency standards
- High-accuracy strontium ion optical clock; National Physical Laboratory (2005)
- National Research Council of Canada: Optical frequency standard based on a single trapped ion
- NIST: Definition of the second; notice the cesium atom must be in its ground state at 0 K
- Official BIPM definition of the second
- The leap second: its history and possible future
- What is a Cesium atom clock?
- SLAC: Scales of Time – Our universe from 1018 to 10−18 seconds
Second
View on GrokipediaDefinition and Etymology
Etymology
The term "second" for the unit of time originates from the Medieval Latin secunda, a shortening of pars minuta secunda, meaning "second small part," which distinguished it from the pars minuta prima or "first small part," referring to the minute as the initial subdivision of the hour.[7] This nomenclature arose in the context of medieval astronomical and mathematical calculations, where time and angular measurements were divided hierarchically into increasingly finer portions.[7] In medieval European timekeeping, the second emerged as the smallest practical division of the hour, building on the sexagesimal (base-60) system that subdivided the minute into 60 parts.[8] This usage first appeared in written records around the late 14th century, primarily in scientific treatises on astronomy and geometry, where precise divisions were essential for computations.[7] The sexagesimal framework underpinning the second traces back to the ancient Babylonians, whose base-60 numeral system influenced Greek astronomers like Ptolemy and was later adopted across Europe for time and angle measurements.[9] This legacy ensured the second's integration into the standardized divisions of the hour and minute that persisted through the Middle Ages.[9]Current SI Definition
The second, symbol s, is the SI base unit of time. It is defined by taking the fixed numerical value of the caesium frequency Δν_Cs, the unperturbed ground-state hyperfine transition frequency of the caesium-133 atom, to be 9 192 631 770 when expressed in the unit Hz, which is equal to s⁻¹.[10] This definition corresponds to the duration of 9 192 631 770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom at rest relative to the observer and at a thermodynamic temperature of 0 K.[2] This atomic definition was established by Resolution 1 of the 13th General Conference on Weights and Measures (CGPM) in 1967, replacing earlier ephemeris-based definitions to achieve greater precision and universality. It was revised by Resolution 1 of the 26th CGPM in 2018, effective from 20 May 2019, to explicitly fix the numerical value of Δν_Cs at exactly 9 192 631 770 Hz as part of the broader redefinition of SI units using fundamental constants. The hyperfine transition in question occurs between the two hyperfine sublevels (F=3 and F=4) of the ground electronic state (6s ^2S_{1/2}) of the caesium-133 atom, producing microwave radiation at approximately 9.192 GHz.[10] Caesium-133 was selected for this definition due to the exceptional stability and reproducibility of its hyperfine transition frequency, which provides a highly accurate, invariant standard independent of environmental variations and suitable for precise metrological realizations in atomic clocks.[2]Uses and Applications
In Timekeeping and Daily Life
In mechanical clocks, the second is marked by the escapement mechanism, which regulates the release of energy from a wound spring or weight, typically advancing the second hand once per oscillation of the balance wheel or pendulum, accumulating into larger units like minutes and hours. Quartz clocks, introduced in the mid-20th century, generate seconds through a crystal oscillator vibrating at 32,768 Hz, divided electronically to produce one pulse per second that drives the timekeeping display. Digital clocks similarly derive seconds from quartz-based electronic circuits, displaying them numerically as the fundamental unit that builds to 86,400 seconds in a mean solar day.[11][12] In sports timing, the second serves as the base unit for measuring performance in events like Olympic track races, where official times are recorded to the nearest hundredth of a second using photo-finish cameras and electronic sensors to determine winners with high precision. Transportation systems, such as GPS, rely on sub-second timing synchronization between satellites and receivers, achieving accuracies better than 100 nanoseconds to enable precise location calculations essential for navigation.[13][14] The second hand on analog watches provides a visual representation of passing time, first appearing in the late 16th century and becoming a common feature on timepieces in the 18th century, serving as a cultural symbol of punctuality and the relentless progression of moments in daily life.[15][16] Human reaction times to visual stimuli average 0.2 to 0.3 seconds, influencing perceptions of time in activities like driving or gaming, where delays beyond this range can affect responsiveness.[17]In Science and Technology
In physics, the second is a fundamental base unit in the International System of Units (SI), serving as the denominator for derived units such as frequency, where the hertz (Hz) is defined as one cycle per second.[18] This makes the second essential for quantifying oscillatory phenomena, like electromagnetic waves or mechanical vibrations. For instance, the frequency of visible light ranges from about 4 × 10^14 Hz to 7.5 × 10^14 Hz, illustrating how the inverse second captures rapid periodic events at the atomic and subatomic scales./02%3A_Comparing_Model_and_Experiment/2.02%3A_Units_and_dimensions) The second also underpins units of speed and acceleration; speed is expressed in meters per second (m/s), while acceleration uses meters per second squared (m/s²).[18] A representative example is the speed of sound in dry air at 20°C, which is approximately 343 m/s, demonstrating the second's role in wave propagation and fluid dynamics calculations./Book%3A_University_Physics_I_-Mechanics_Sound_Oscillations_and_Waves(OpenStax)/17%3A_Sound/17.03%3A_Speed_of_Sound) In kinematics, acceleration due to gravity near Earth's surface is about 9.8 m/s², highlighting the unit's application in describing changes in velocity over time./02%3A_Comparing_Model_and_Experiment/2.02%3A_Units_and_dimensions) In computing, the second measures processor performance through clock cycles, with modern central processing units (CPUs) operating at gigahertz (GHz) frequencies—billions of cycles per second—to execute instructions efficiently.[19] For example, a 3 GHz CPU performs 3 × 10^9 cycles per second, enabling rapid data processing in applications from simulations to real-time graphics rendering.[20] Data transfer rates in networks and storage systems are similarly quantified in bits per second (bps), where high-speed Ethernet can reach 100 Gbps, or 10^11 bits per second, to handle large-scale information flow.[21] Astronomy employs the second for precise timing of celestial phenomena, such as the rotation periods of pulsars—rapidly spinning neutron stars that emit beams detectable as pulses, some occurring hundreds of times per second.[22] The Crab Pulsar, for instance, rotates 30 times per second, with its pulse timing providing a natural clock for verifying atomic time standards over vast distances.[23] Additionally, the second defines convenient distance units like the light-second, the distance light travels in vacuum in one second, approximately 299,792 kilometers, which scales to larger measures such as light-years for interstellar navigation and event timing.[24]Relation to Broader Time Measurements
Clocks and Solar Time
Apparent solar time, as measured by sundials, reflects the actual position of the Sun in the sky and varies throughout the year due to the Earth's elliptical orbit and axial tilt, resulting in differences from mean solar time known as the equation of time, which can reach up to ±16 minutes.[25][26] Mean solar time, in contrast, assumes a uniform rate of solar motion and forms the basis for civil timekeeping, where each second is a consistent fraction of the average solar day, ensuring clocks maintain steady intervals independent of daily solar variations.[27] Early mechanical clocks regulated their seconds through escapement mechanisms that controlled the release of energy from a weight or spring, with pendulum clocks providing precise timing by leveraging gravitational oscillation. In 1656, Christiaan Huygens developed the first practical pendulum clock, featuring a seconds pendulum with a period of 2 seconds—meaning each swing took 1 second—to drive the escapement and mark uniform seconds, dramatically improving accuracy to within seconds per day compared to prior designs.[28][29] These escapements, often anchor-style, ticked at each pendulum swing, dividing the day into equal seconds aligned with mean solar time. Modern quartz clocks achieve even greater precision by using a piezoelectric quartz crystal that oscillates at a resonant frequency when electrified, typically 32,768 Hz in wristwatches and similar devices, which is divided down through binary counters to produce 1 Hz pulses for second increments.[30][31] This frequency, a power of 2 (2^15), allows efficient digital division to generate exact 1-second intervals, making quartz mechanisms standard in contemporary timepieces for their stability and low deviation from mean solar seconds.Larger Units and Events Measured in Seconds
The second serves as the foundational unit for larger time measurements in the International System of Units (SI). By definition, there are 60 seconds in a minute. A standard day consists of 24 hours, equating to exactly 86,400 seconds. The average length of a Gregorian year is 365.2425 days, or approximately 31,556,952 seconds.[32] On human scales, durations measured in seconds illustrate everyday and lifetime experiences. For instance, the time required for light to travel from the Sun to Earth, covering approximately 149.6 million kilometers at the speed of light, is about 499 seconds, or roughly 8 minutes and 19 seconds. An average human lifespan, based on a global life expectancy of around 73 years, corresponds to approximately 2.3 billion seconds, though estimates often round to 2.4 billion seconds when considering slight variations in annual length and regional differences.[33][34] At cosmic scales, the second quantifies vast epochs. The current estimated age of the universe, derived from measurements of the cosmic microwave background by the Planck mission, is about 13.8 billion years, equivalent to roughly seconds. This immense duration underscores the second's role in expressing the timeline of cosmic evolution from the Big Bang onward.[35]Timekeeping Standards
Atomic Time Standards
Atomic time standards form the basis for realizing the SI second, with caesium fountain clocks serving as the primary frequency standards. These clocks measure the frequency of the microwave transition between two hyperfine energy levels in the ground state of the caesium-133 atom, as defined by the International System of Units. The most advanced caesium fountain clocks achieve fractional frequency uncertainties as low as 1 × 10^{-16}, corresponding to an accuracy where the clock would lose or gain no more than 1 second over approximately 300 million years.[36] The operation of a caesium fountain clock involves laser cooling caesium atoms to temperatures near absolute zero, typically around 1 microkelvin, to reduce thermal motion and enable precise measurement. The cooled atoms are then launched upward in a vacuum chamber, forming a "fountain" trajectory, during which they pass through a microwave cavity twice—once ascending and once descending. This allows a Ramsey interrogation sequence, where two separated microwave pulses interact with the atoms to determine the precise frequency of the 9,192,631,770 Hz hyperfine transition with minimal perturbation.[36] The extended flight time of about 1 second enhances the interrogation precision compared to earlier atomic beam clocks.[37] International comparisons of these primary standards are coordinated by the BIPM Time Department, which collects calibration data from caesium fountain clocks at national metrology institutes worldwide to ensure consistency in the realization of the SI second. Over 450 atomic clocks, including hydrogen masers for short-term stability and caesium fountains for long-term accuracy, contribute to the stability of International Atomic Time (TAI), but the accuracy is anchored by a subset of about a dozen high-precision caesium fountains through regular key comparisons like CCTF-K001.UTC. These comparisons use techniques such as GPS carrier-phase measurements and two-way satellite time and frequency transfer to synchronize and evaluate clock performances globally.[38][39]Coordinated Universal Time
Coordinated Universal Time (UTC) serves as the international reference time scale, maintained by the International Bureau of Weights and Measures (BIPM) in collaboration with the International Earth Rotation and Reference Systems Service (IERS). It combines International Atomic Time (TAI), a continuous scale defined by the weighted average of highly stable atomic clocks worldwide, with adjustments to align it to Universal Time UT1, which tracks Earth's irregular rotation relative to distant stars. As of November 2025, TAI leads UTC by 37 seconds, with UTC differing from TAI by an integer number of seconds, ensuring that the offset between UTC and UT1 remains within ±0.9 seconds.[40] To maintain this alignment, leap seconds—positive adjustments of one second—are inserted into UTC as needed, typically at the end of June or December following 23:59:59 UTC, creating a 23:59:60 interim. As of November 2025, since the introduction of leap seconds in 1972, 27 have been added to UTC, with the most recent on December 31, 2016; no further insertions have occurred due to Earth's rotation slowing less rapidly than anticipated.[41] In 2022, the General Conference on Weights and Measures adopted Resolution 4, directing the development of a plan to discontinue leap seconds by 2035, allowing |UT1 - UTC| to drift up to ±0.9 seconds without adjustment until at least 2135, to simplify global timekeeping systems.[42] UTC underpins critical applications requiring precise synchronization, including the Global Positioning System (GPS), where satellite signals broadcast UTC to enable accurate positioning and timing for navigation worldwide. In telecommunications, UTC ensures coordinated operations across networks, such as in mobile and internet protocols, preventing disruptions from timing mismatches. Legally, UTC forms the basis for civil time zones globally, with countries offsetting their standard times from it to regulate daily activities, broadcasting, and international agreements.Historical Development
Ancient and Sexagesimal Systems
The ancient Babylonians adopted the sexagesimal (base-60) numeral system, inherited from the Sumerians around the third millennium BCE, for astronomical and timekeeping purposes by approximately 2000 BCE. This system facilitated the division of the 24-hour day—itself derived from earlier Egyptian practices of splitting daylight and nighttime into 12 parts each—into 60 minutes per hour and 60 seconds per minute, enabling more accurate tracking of celestial movements and seasonal cycles.[43] Medieval astronomers built upon this foundation, refining sexagesimal divisions for enhanced precision in time measurement. In the 2nd century CE, Claudius Ptolemy detailed in his Almagest the subdivision of hours into 60 "first small parts" (minutes) and further into 60 "second small parts" (seconds), primarily for angular calculations in astronomy but directly applicable to temporal intervals due to the linkage between time and celestial arcs. By the 11th century, the scholar Abu Rayhan al-Biruni advanced these methods through his work on astrolabes, instruments that allowed observers to measure stellar altitudes and derive local time with accuracy approaching the second, as his designs achieved angular resolutions of up to 10 arcminutes, equivalent to roughly 40 seconds of time.[43][44] In medieval Europe, the practical adoption of these divisions occurred through monastic water clocks, which emerged in the 11th to 13th centuries to enforce the rhythm of canonical prayers by segmenting the day into unequal seasonal hours. These clepsydrae, often elaborate devices with floats and gears powered by regulated water flow, marked subdivisions into minutes for liturgical timing, while astronomical tables incorporated seconds for finer computational adjustments, bridging ancient theoretical systems with emerging mechanical timekeeping.[45]Astronomical Definitions
In the 19th century, astronomers established the mean solar second as precisely 1/86,400 of a mean solar day, a definition that formalized the division of the day into 24 hours of 60 minutes each, with each minute comprising 60 seconds.[12] This unit, rooted in the apparent motion of the Sun across the sky, provided a practical standard for timekeeping but was inherently variable due to irregularities in Earth's rotation.[46] By the mid-20th century, the limitations of relying on Earth's daily rotation became evident, prompting a shift toward a more stable astronomical reference. In 1956, the International Committee on Weights and Measures redefined the second as the ephemeris second, equivalent to 1/31,556,925.9747 of the tropical year for 1900 January 0 at 12 hours ephemeris time.[47] The tropical year, defined as the time interval between successive vernal equinoxes, offered a longer-term orbital benchmark less affected by short-term rotational fluctuations, with the specific fraction calculated from precise ephemeris observations of celestial bodies.[48] However, even this orbital-based definition faced challenges from secular changes in Earth's dynamics. Observations revealed that tidal friction from the Moon and Sun causes Earth's rotation to slow gradually, lengthening the mean solar day by approximately 1.7 milliseconds per century, which complicates the consistency of pre-atomic time standards and necessitates ongoing astronomical corrections.[49] This variability underscored the need for definitions tied to invariant natural phenomena, while the 86,400-fold division of the day traced back briefly to ancient Babylonian sexagesimal systems that influenced modern subdivisions.[50]Transition to Atomic Standard
The development of atomic clocks in the mid-20th century marked a pivotal shift from astronomical to atomic time standards, driven by the need for greater stability and reproducibility. In 1955, Louis Essen and Jack Parry at the National Physical Laboratory (NPL) in the United Kingdom constructed the first operational cesium-beam atomic clock, which measured the hyperfine transition frequency of cesium-133 atoms at approximately 9.192 GHz, achieving stability far superior to existing quartz or astronomical methods.[51] This innovation built on earlier work by Isidor Rabi and others on molecular beam resonance, providing a foundation for redefining the unit of time independent of Earth's irregular rotation.[52] By 1967, international consensus recognized atomic time's advantages, leading the 13th General Conference on Weights and Measures (CGPM) to formally adopt the atomic definition of the second. The second was defined as the duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the cesium-133 atom, unperturbed by external fields, at rest, and at a temperature of 0 K.[53] The primary rationale was atomic time's invariance, unaffected by astronomical variability such as tidal friction or geophysical changes that cause fluctuations in solar or ephemeris time. Specifically, Earth's rotation is irregular, slowing down due to tidal friction at an average rate of about 1.7 milliseconds per century in the length of the day, with short-term variations of milliseconds per year, making it unsuitable for high-precision timekeeping.[49] Atomic clocks, such as those based on cesium-133, provide the stable and accurate time essential for scientific experiments requiring sub-nanosecond precision and technologies like the Global Positioning System (GPS), which demand synchronization better than 10 nanoseconds.[49][2] To maintain continuity, the definition was calibrated so the atomic second matched the ephemeris second—previously defined as 1/31,556,925.9747 of the tropical year 1900—to within 1 part in .[2] This transition profoundly impacted practical timekeeping and technology. It enabled the precise calibration of quartz crystal oscillators, culminating in the 1969 launch of the Seiko Quartz Astron, the world's first quartz wristwatch, which achieved accuracy within 5 seconds per month by referencing atomic standards.[54] In the 1970s, atomic time became essential for the Global Positioning System (GPS), where cesium and rubidium clocks on satellites ensure the nanosecond-level synchronization required for trilateration-based positioning accurate to meters.[51]Historical Summary Table
| Era | Definition | Precision/Notes | Key Date/Event |
|---|---|---|---|
| Ancient Sexagesimal | The second as the 1/60th division of a minute in the base-60 (sexagesimal) system, yielding 86,400 seconds in a day.[55] | Approximate; limited by observational tools like sundials and water clocks, with daily errors of minutes to hours.[3] | c. 2000 BC, developed in Babylonian astronomy.[55] |
| Mean Solar | 1/86,400 of the mean solar day (average length of a day based on Earth's rotation relative to the Sun).[2] | Variable due to irregularities in Earth's rotation, including a gradual slowing of about 1.7 milliseconds per century; accuracy limited to roughly 1 part in 10^8 over short periods.[2] | Late 19th century standardization, e.g., 1884 International Meridian Conference establishing Greenwich as prime meridian.[56] |
| Ephemeris | The fraction 1/31,556,925.9747 of the tropical year for 1900 January 0 at 12 hours ephemeris time.[57] | More stable than mean solar time, with precision around 1 part in 10^8 based on astronomical ephemerides; independent of daily rotation variations.[3] | Adopted in 1956 by the International Committee for Weights and Measures (CIPM); ratified by the 11th General Conference on Weights and Measures (CGPM) in 1960.[58] |
| Atomic | The duration of 9,192,631,770 periods of the radiation corresponding to the transition between the two hyperfine levels of the ground state of the caesium-133 atom at rest at 0 K.[53] | Initial precision of about 1 part in 10^13, representing a gain of approximately 5 orders of magnitude in accuracy over the ephemeris second; enabled highly reproducible timekeeping.[3][59] | Adopted in 1967 by the 13th CGPM.[53] |
Future Redefinition
Motivations and Technical Requirements
The current definition of the second, based on the caesium-133 hyperfine transition, achieves a relative frequency uncertainty of approximately 10^{-16} in state-of-the-art realizations, limiting further advancements in precision timekeeping and metrology.[60] This precision falls short of the 10^{-18} level required to align the second with the accuracy of other SI base units, such as the metre, which benefits from a definition tied to the invariant speed of light, thereby hindering interdisciplinary applications in fundamental physics, geodesy, and telecommunications.[61] The primary motivation for redefinition stems from the need to enhance the second's stability and accuracy to support scientific progress, including tests of general relativity and improved global navigation systems, as the caesium standard's limitations increasingly constrain technological innovation.[62] The Consultative Committee for Time and Frequency (CCTF), under the International Bureau of Weights and Measures (BIPM), has outlined specific technical requirements for any new definition to ensure it surpasses the current standard while preserving compatibility.[63] These include linking the second to a fixed numerical value of an invariant physical constant, such as the Rydberg constant, to provide an unalterable foundation akin to other SI redefinitions.[64] The new standard must be globally realizable with relative uncertainties below 10^{-17} in primary standards operated by national metrology institutes, enabling widespread adoption without disrupting existing time scales like Coordinated Universal Time (UTC).[65] Additionally, continuity must be maintained by ensuring the new definition reproduces the current second to within 10^{-16} or better, avoiding any abrupt shifts in international timekeeping infrastructure.[62] Discussions on redefining the second have intensified since the 2010s, driven by advancements in atomic frequency standards that outpace caesium technology.[60] The CCTF roadmap targets a potential adoption by 2030, contingent on achieving sufficient portability, stability, and intercomparison accuracy among candidate standards at the 10^{-18} level.[61] This timeline aligns with quadrennial meetings of the General Conference on Weights and Measures (CGPM), with a draft proposal anticipated for review in 2026 if technical criteria are met.[62]Optical Clocks and Rydberg Constant
Optical clocks represent advanced atomic timekeeping devices that utilize electronic transitions in the optical frequency domain, offering significantly higher precision than the current caesium-based standard. These clocks probe narrow linewidth transitions in trapped ions or neutral atoms, enabling fractional frequency uncertainties on the order of 10^{-18}, which corresponds to an accuracy of about 1 second over 15 billion years.[60] For instance, ion-based optical clocks using the ^1S_0 to ^3P_0 transition in ^{27}Al^+ achieve systematic uncertainties as low as 5.5 \times 10^{-19}, while neutral atom systems like the ^{87}Sr clock operate at a transition frequency of approximately 429 THz with uncertainties around 8 \times 10^{-19}.[66] Such performance surpasses the limitations of caesium microwave clocks, which are constrained to around 10^{-16} accuracy due to environmental sensitivities.[61] A key feature of optical lattice clocks, particularly those using neutral atoms like strontium or ytterbium, is the use of optical lattices to trap and interrogate ensembles of atoms simultaneously. In this design, counter-propagating laser beams tuned to a "magic wavelength" (typically near 813 nm for strontium) form a one-dimensional standing wave, creating a periodic potential that confines thousands to millions of laser-cooled atoms in individual sites.[67] This lattice minimizes differential light shifts between the clock states, allowing coherent interrogation of the transition with a probe laser at the clock frequency, thereby enhancing stability and reducing decoherence from atomic collisions.[68] The standing wave structure effectively arrays the atoms in a crystal-like formation, enabling superradiant effects in larger ensembles for even better short-term stability.[69] Linking optical clocks to fundamental constants offers a pathway for redefining the second in a manner independent of specific atomic species, potentially fixing the Rydberg constant R_\infty to eliminate measurement uncertainties. The Rydberg frequency is defined as \nu_{Ry} = c R\infty, where c is the exact speed of light and R\infty \approx 1.097 \times 10^7 , \mathrm{m}^{-1} is the infinite-mass Rydberg constant, yielding \nu_{Ry} \approx 3.29 \times 10^{15} , \mathrm{Hz}.[62] This frequency can be realized through calculable transitions, such as the 1S-2S line in hydrogen, which optical clocks can measure with high precision to tie the second to quantum electrodynamics predictions.[70] A potential redefinition could thus express the second as 1 / (k \nu_{Ry}), where k is a fixed integer multiple chosen to align with practical time scales, ensuring the new standard maintains continuity with UTC while anchoring time to a universal constant with relative uncertainty below 10^{-12}.[71] This approach leverages the superior accuracy of optical clocks to refine R_\infty's value, currently known to 1.9 parts in 10^{12}, and supports applications in fundamental physics tests.[62]Recent Advances in 2025
In June 2025, an international collaboration established the largest coordinated network of optical clocks to date, simultaneously comparing ten such clocks across six countries including Finland, France, Germany, Italy, the United Kingdom, and Japan.[72] This effort utilized optical fiber links for regional connections in Europe and short-range fibers for local comparisons, supplemented by satellite links for global synchronization, achieving frequency ratio measurements with uncertainties as low as 4.4 × 10^{-18} between specific clocks like indium and ytterbium ions.[73] These sub-10^{-18} uncertainties represent a significant improvement over previous satellite-only methods, demonstrating the feasibility of a stable global optical time scale essential for verifying clock consistency ahead of potential SI redefinition.[72] Building on this, intercontinental comparisons in July 2025 extended the network's reach, linking clocks across Europe and Asia with transcontinental fiber and satellite infrastructure to confirm optical stability at levels between 10^{-16} and 10^{-18}.[74] For instance, offsets such as a 4 × 10^{-16} discrepancy in an Italian ytterbium clock were identified and resolved, ensuring agreement across the network and highlighting the robustness of these systems against propagation errors.[75] This milestone paves the way for a 2030 redefinition of the second by establishing the precision needed for an international optical standard to replace the cesium-based definition.[74] Earlier in January 2025, proposals advanced the development of optical ion clocks using thorium nuclei, with theoretical models for a Th^{5+} ion clock projecting relative uncertainties below 10^{-19} due to its closed-shell structure minimizing shifts from black-body radiation and external fields. These thorium-based designs, building on the low-energy nuclear isomer transition in thorium-229, support Rydberg constant-linked frequency standards by offering immunity to environmental perturbations that affect electronic transitions in conventional optical clocks. Such record projected accuracies underscore thorium's potential to enable a more stable redefinition of the second, with black-body radiation shifts calculated at just 4.3 × 10^{-24} at 300 K. In October 2025, the CCTF meeting highlighted ongoing progress toward redefining the second, including evaluations of optical frequency standards through international and regional comparison campaigns to assess candidate transitions and uncertainty budgets. No formal decision was made, but the discussions emphasized advances in optical clocks as key to achieving the necessary consensus for a potential redefinition by the end of the decade, around 2030.[76] Also in October 2025, research on the thorium-229 nuclear clock transition demonstrated its sensitivity to the fine-structure constant, enabling investigations into its stability with unprecedented precision. This breakthrough, published on October 15, 2025, supports the viability of nuclear clocks for probing fundamental physics and advancing toward a redefinition of the second independent of atomic electronic transitions.[77] Further work on October 27, 2025, confirmed that thorium nuclear clocks can detect variations in fundamental constants with accuracy 6,000 times greater than existing methods, reinforcing their role in future time standards.[78]Derived Units and Multiples
Units Incorporating Seconds
Derived SI units incorporating the second typically express rates, velocities, or powers where the second appears in the dimensional formula, often in inverse form to denote quantities per unit time. These units combine the second with other base units like the metre or kilogram, enabling the measurement of dynamic phenomena in physics and engineering. The International System of Units (SI) defines these coherently to ensure consistency across scientific applications.[79] The hertz (Hz) is the SI derived unit of frequency, defined as the number of cycles or events occurring per second, with the dimensional formula . It quantifies periodic phenomena, such as vibrations or oscillations. For example, alternating current (AC) mains electricity in North America operates at a standard frequency of 60 Hz.[79][80] The metre per second (m/s) serves as the coherent SI unit for speed or velocity, expressed dimensionally as . This unit measures the rate of change of position with respect to time. A representative application is the escape velocity from Earth's surface, which is approximately 11.2 km/s, the minimum speed required for an object to overcome Earth's gravitational pull without further propulsion.[79][81] Other derived units highlight the inverse role of the second in angular and energetic contexts. Angular frequency, or angular velocity, uses the radian per second (rad/s), with the dimensionless radian combined as , to describe rotational rates. Similarly, the watt (W), the SI unit of power, incorporates the second as , representing energy transfer per unit time, such as one joule per second. These units underscore the second's foundational role in quantifying time-dependent processes.[79]SI Prefixes for Seconds
The SI prefixes provide a systematic way to express multiples and submultiples of the second (s), the base unit of time in the International System of Units (SI), allowing for concise notation of time intervals ranging from ultrafast processes to extended durations. These prefixes, standardized by the General Conference on Weights and Measures and maintained by the International Bureau of Weights and Measures (BIPM), follow decimal powers of ten and apply uniformly across SI units. While all 24 prefixes (from quecto- to quetta-) are permissible for the second, practical usage is selective, favoring submultiples for short timescales in physics, chemistry, and engineering, and limited multiples for scientific measurements where traditional units like minutes or days are insufficient.[82] Submultiples of the second are prevalent in fields requiring high temporal resolution. The millisecond (ms = s) measures events on the order of human physiological responses, such as reaction times. The microsecond (µs = s) is standard in electronics for signal processing and radar timing. The nanosecond (ns = s) appears in telecommunications and particle physics for light travel distances in small media. The picosecond (ps = s) supports applications in laser spectroscopy and semiconductor characterization. The femtosecond (fs = s) enables the study of molecular dynamics in chemistry and ultrafast processes in laser-matter interactions, as demonstrated in early femtochemistry experiments using precisely timed pulses to observe atomic rearrangements. The attosecond (as = s) facilitates probing electron motion in atoms and molecules, central to attosecond physics for resolving quantum-scale phenomena in intense laser fields.[82][83][84] For multiples, adoption is more restrained due to the sexagesimal conventions in everyday timekeeping, but they find utility in specialized contexts. The kilosecond (ks = s ≈ 16.7 minutes) occasionally denotes short operational intervals in engineering and computing simulations. The megasecond (Ms = s ≈ 11.6 days) measures extended observation periods in astronomy, such as the cumulative exposure time in X-ray telescope surveys of galactic centers. Larger multiples like the gigasecond (Gs = s ≈ 31.7 years) emerge rarely in cosmological modeling, while prefixes such as deca- (das = 10 s) and hecto- (hs = s ≈ 1.67 minutes) lack common application for time, overshadowed by conventional units.[82][85]| Prefix | Symbol | Factor | Approximate Duration | Example Usage Context |
|---|---|---|---|---|
| Milli- | m | 1 ms | Physiological timings, audio processing | |
| Micro- | µ | 1 µs | Digital signal timing, computing clocks | |
| Nano- | n | 1 ns | Microwave propagation, collider events | |
| Pico- | p | 1 ps | Optical spectroscopy, charge carrier dynamics | |
| Femto- | f | 1 fs | Femtochemistry, laser filamentation | |
| Atto- | a | 1 as | Electron dynamics in attosecond pulses | |
| Kilo- | k | 1 ks ≈ 16.7 min | Simulation runtimes, short missions | |
| Mega- | M | 1 Ms ≈ 11.6 days | Astronomical exposure times |