Recent from talks
Nothing was collected or created yet.
S wave
View on Wikipedia| Part of a series on |
| Earthquakes |
|---|
 |
In seismology and other areas involving elastic waves, S waves, secondary waves, or shear waves (sometimes called elastic S waves) are a type of elastic wave and are one of the two main types of elastic body waves, so named because they move through the body of an object, unlike surface waves.[1]
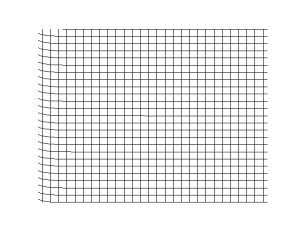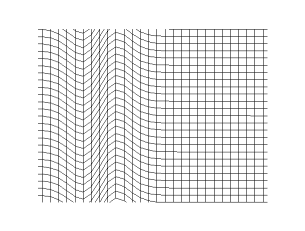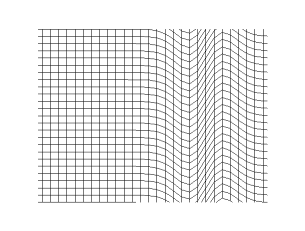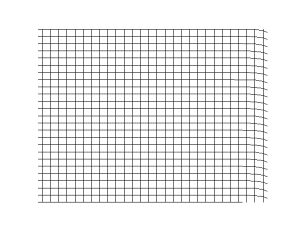
S waves are transverse waves, meaning that the direction of particle movement of an S wave is perpendicular to the direction of wave propagation, and the main restoring force comes from shear stress.[2] Therefore, S waves cannot propagate in liquids[3] with zero (or very low) viscosity; however, they may propagate in liquids with high viscosity.[4][5] Similarly, S waves cannot travel through gases.
The name secondary wave comes from the fact that they are the second type of wave to be detected by an earthquake seismograph, after the compressional primary wave, or P wave, because S waves travel more slowly in solids. Unlike P waves, S waves cannot travel through the molten outer core of the Earth, and this causes a shadow zone for S waves opposite to their origin. They can still propagate through the solid inner core: when a P wave strikes the boundary of molten and solid cores at an oblique angle, S waves will form and propagate in the solid medium. When these S waves hit the boundary again at an oblique angle, they will in turn create P waves that propagate through the liquid medium. This property allows seismologists to determine some physical properties of the Earth's inner core.[6]
History
[edit]In 1830, the mathematician Siméon Denis Poisson presented to the French Academy of Sciences an essay ("memoir") with a theory of the propagation of elastic waves in solids. In his memoir, he states that an earthquake would produce two different waves: one having a certain speed and the other having a speed . At a sufficient distance from the source, when they can be considered plane waves in the region of interest, the first kind consists of expansions and compressions in the direction perpendicular to the wavefront (that is, parallel to the wave's direction of motion); while the second consists of stretching motions occurring in directions parallel to the front (perpendicular to the direction of motion).[7]
Theory
[edit]Isotropic medium
[edit]
For the purpose of this explanation, a solid medium is considered isotropic if its strain (deformation) in response to stress is the same in all directions. Let be the displacement vector of a particle of such a medium from its "resting" position due elastic vibrations, understood to be a function of the rest position and time . The deformation of the medium at that point can be described by the strain tensor , the 3×3 matrix whose elements are
where denotes partial derivative with respect to position coordinate . The strain tensor is related to the 3×3 stress tensor by the equation
Here is the Kronecker delta (1 if , 0 otherwise) and and are the Lamé parameters ( being the material's shear modulus). It follows that
From Newton's law of inertia, one also gets where is the density (mass per unit volume) of the medium at that point, and denotes partial derivative with respect to time. Combining the last two equations one gets the seismic wave equation in homogeneous media
Using the nabla operator notation of vector calculus, , with some approximations, this equation can be written as
Taking the curl of this equation and applying vector identities, one gets
This formula is the wave equation applied to the vector quantity , which is the material's shear strain. Its solutions, the S waves, are linear combinations of sinusoidal plane waves of various wavelengths and directions of propagation, but all with the same speed . Assuming that the medium of propagation is linear, elastic, isotropic, and homogeneous, this equation can be rewritten as [8] where ω is the angular frequency and k is the wavenumber. Thus, .
Taking the divergence of seismic wave equation in homogeneous media, instead of the curl, yields a wave equation describing propagation of the quantity , which is the material's compression strain. The solutions of this equation, the P waves, travel at the faster speed .
The steady state SH waves are defined by the Helmholtz equation[9] where k is the wave number.
S waves in viscoelastic materials
[edit]Similar to in an elastic medium, in a viscoelastic material, the speed of a shear wave is described by a similar relationship , however, here, is a complex, frequency-dependent shear modulus and is the frequency dependent phase velocity.[8] One common approach to describing the shear modulus in viscoelastic materials is through the Voigt Model which states: , where is the stiffness of the material and is the viscosity.[8]
S wave technology
[edit]Magnetic resonance elastography
[edit]Magnetic resonance elastography (MRE) is a method for studying the properties of biological materials in living organisms by propagating shear waves at desired frequencies throughout the desired organic tissue.[10] This method uses a vibrator to send the shear waves into the tissue and magnetic resonance imaging to view the response in the tissue.[11] The measured wave speed and wavelengths are then measured to determine elastic properties such as the shear modulus. MRE has seen use in studies of a variety of human tissues including liver, brain, and bone tissues.[10]
See also
[edit]References
[edit]- ^ "Seismology | UPSeis | Michigan Tech". Michigan Technological University. Retrieved 2023-10-07.
- ^ "S wave". United States Geological Survey. Archived from the original on July 22, 2021.
- ^ "Why can't S-waves travel through liquids?". Earth Observatory of Singapore. Retrieved 2019-12-06.
- ^ Greenwood, Margaret Stautberg; Bamberger, Judith Ann (August 2002). "Measurement of viscosity and shear wave velocity of a liquid or slurry for on-line process control". Ultrasonics. 39 (9): 623–630. doi:10.1016/s0041-624x(02)00372-4. PMID 12206629.
- ^ "Do viscous fluids support shear waves propagation?". ResearchGate. Retrieved 2019-12-06.[unreliable source?]
- ^ "Lecture 16 Seismographs and the earth's interior". University of Illinois at Chicago. 17 July 1997. Archived from the original on 7 May 2002. Retrieved 8 June 2010.
- ^ Poisson, S. D. (1831). "Mémoire sur la propagation du mouvement dans les milieux élastiques" [Memoir on the propagation of motion in elastic media]. Mémoires de l'Académie des Sciences de l'Institut de France (in French). 10: 549–605. From p.595: "On verra aisément que cet ébranlement donnera naissance à deux ondes sphériques qui se propageront uniformément, l'une avec une vitesse a, l'autre avec une vitesse b ou a / √3" ... (One will easily see that this quake will give birth to two spherical waves that will be propagated uniformly, one with a speed a, the other with a speed b or a /√3 ... ) From p.602: ... "à une grande distance de l'ébranlement primitif, et lorsque les ondes mobiles sont devenues sensiblement planes dans chaque partie très-petite par rapport à leurs surfaces entières, il ne subsiste plus que des vitesses propres des molécules, normales ou parallèles à ces surfaces; les vitesses normal ayant lieu dans les ondes de la première espèce, où elles sont accompagnées de dilations qui leur sont proportionnelles, et les vitesses parallèles appartenant aux ondes de la seconde espèce, où elles ne sont accompagnées d'aucune dilatation ou condensation de volume, mais seulement de dilatations et de condensations linéaires." ( ... at a great distance from the original quake, and when the moving waves have become roughly planes in every tiny part in relation to their entire surface, there remain [in the elastic solid of the Earth] only the molecules' own speeds, normal or parallel to these surfaces; the normal speeds occur in waves of the first type, where they are accompanied by expansions that are proportional to them, and the parallel speeds belonging to waves of the second type, where they are not accompanied by any expansion or contraction of volume, but only by linear stretchings and squeezings.)
- ^ a b c Rouze; Deng; Trutna; Palmeri; Nightengale (May 2018). "Characterization of Viscoelastic Materials Using Group Shear Wave Speeds". IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 65 (5): 780–794. Bibcode:2018ITUFF..65..780R. doi:10.1109/TUFFC.2018.2815505. PMC 5972540. PMID 29733281.
- ^ Graff, Karl F. (2012-04-26). Wave Motion in Elastic Solids. Courier Corporation. ISBN 978-0-486-13957-9.
- ^ a b Tweten, Dennis J.; Okamoto, Ruth J.; Schmidt, John L.; Garbow, Joel R.; Bayly, Philip V. (November 2015). "Estimation of material parameters from slow and fast shear waves in an incompressible, transversely isotropic material". Journal of Biomechanics. 48 (15): 4002–4009. doi:10.1016/j.jbiomech.2015.09.009. PMC 4663187. PMID 26476762.
- ^ "MR Shear Wave Elastography". University of Utah Health. 10 November 2021.
Further reading
[edit]- Shearer, Peter (1999). Introduction to Seismology (1st ed.). Cambridge University Press. ISBN 0-521-66023-8.
- Aki, Keiiti; Richards, Paul G. (2002). Quantitative Seismology (2nd ed.). University Science Books. ISBN 0-935702-96-2.
- Fowler, C. M. R. (1990). The solid earth. Cambridge, UK: Cambridge University Press. ISBN 0-521-38590-3.
S-wave.