Hubbry Logo
Degree (angle)Degree (angle)Main
Open search
Degree (angle)
Community hub
Degree (angle)
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Contribute something
Degree (angle)
Degree (angle)
Degree (angle)
View on Wikipedia
from Wikipedia

Degree
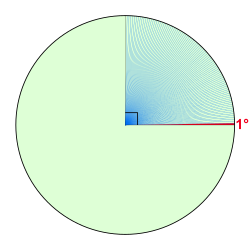One degree (shown in red) and eighty nine degrees (shown in blue). The lined area is a right angle.
General information
Unit systemNon-SI accepted unit
Unit ofAngle
Symbol°[1][2], deg[3]
Conversions
1°[1][2] in ...... is equal to ...
   turns   ⁠1/360⁠ turn
   radians   ⁠π/180⁠ rad ≈ 0.01745... rad
   milliradians   ⁠50π/9⁠ mrad ≈ 17.45... mrad
   gradians   ⁠10/9⁠g

A degree (in full, a degree of arc, arc degree, or arcdegree), usually denoted by ° (the degree symbol), is a measurement of a plane angle in which one full rotation is 360 degrees.[4]

It is not an SI unit—the SI unit of angular measure is the radian—but it is mentioned in the SI brochure as an accepted unit.[5] Because a full rotation equals 2π radians, one degree is equivalent to ⁠π/180⁠ radians.

History

[edit]
A circle with an equilateral chord (red). One sixtieth of this arc is a degree. Six such chords complete the circle.[6]

The original motivation for choosing the degree as a unit of rotations and angles is unknown. One theory states that it is related to the fact that 360 is approximately the number of days in a year. Ancient astronomers noticed that the sun, which follows through the ecliptic path over the course of the year, seems to advance in its path by approximately one degree each day. Some ancient calendars, such as the Persian calendar and the Babylonian calendar, used 360 days for a year. The use of a calendar with 360 days may be related to the use of sexagesimal numbers.[4]

Another theory is that the Babylonians subdivided the circle using the angle of an equilateral triangle as the basic unit, and further subdivided the latter into 60 parts following their sexagesimal numeric system.[7][8] The earliest trigonometry, used by the Babylonian astronomers and their Greek successors, was based on chords of a circle. A chord of length equal to the radius made a natural base quantity. One sixtieth of this, using their standard sexagesimal divisions, was a degree.

Aristarchus of Samos and Hipparchus seem to have been among the first Greek scientists to exploit Babylonian astronomical knowledge and techniques systematically.[9][10] Timocharis, Aristarchus, Aristillus, Archimedes, and Hipparchus were the first Greeks known to divide the circle in 360 degrees of 60 arc minutes.[citation needed] Eratosthenes used a simpler sexagesimal system dividing a circle into 60 parts.[citation needed]

Another motivation for choosing the number 360 may have been that it is readily divisible: 360 has 24 divisors,[note 1] making it one of only 7 numbers such that no number less than twice as much has more divisors (sequence A02182 in the OEIS).[11] Furthermore, it is divisible by every number from 1 to 10 except 7.[note 2] This property has many useful applications, such as dividing the world into 24 time zones, each of which is nominally 15° of longitude, to correlate with the established 24-hour day convention.

Finally, it may be the case that more than one of these factors has come into play. According to that theory, the number is approximately 365 because of the apparent movement of the sun against the celestial sphere, and that it was rounded to 360 for some of the mathematical reasons cited above.

Subdivisions

[edit]

For many practical purposes, a degree is a small enough angle that whole degrees provide sufficient precision. When this is not the case, as in astronomy or for geographic coordinates (latitude and longitude), degree measurements may be written using decimal degrees (DD notation); for example, 40.1875°.

Alternatively, the traditional sexagesimal unit subdivisions can be used: one degree is divided into 60 minutes (of arc), and one minute into 60 seconds (of arc). Use of degrees-minutes-seconds is also called DMS notation.[12] These subdivisions, also called the arcminute and arcsecond, are represented by a single prime (′) and double prime (″) respectively. For example, 40.1875° = 40° 11′ 15″. Additional precision can be provided using decimal fractions of an arcsecond.

Maritime charts are marked in degrees and decimal minutes to facilitate measurement; 1 minute of latitude is 1 nautical mile. The example above would be given as 40° 11.25′ (commonly written as 11′25 or 11′.25).[13]

The older system of thirds, fourths, etc., which continues the sexagesimal unit subdivision, was used by al-Kashi[citation needed] and other ancient astronomers, but is rarely used today. These subdivisions were denoted by writing the Roman numeral for the number of sixtieths in superscript: 1I for a "prime" (minute of arc), 1II for a second, 1III for a third, 1IV for a fourth, etc.[14] Hence, the modern symbols for the minute and second of arc, and the word "second" also refer to this system.[15]

SI prefixes can also be applied as in, e.g., millidegree, microdegree, etc.

Alternative units

[edit]
See also: Measuring angles
A chart to convert between degrees and radians

In most mathematical work beyond practical geometry, angles are typically measured in radians rather than degrees. This is for a variety of reasons; for example, the trigonometric functions have simpler and more "natural" properties when their arguments are expressed in radians. These considerations outweigh the convenient divisibility of the number 360. One complete turn (360°) is equal to 2π radians, so 180° is equal to π radians, or equivalently, the degree is a mathematical constant: 1° = π⁄180.

One turn (corresponding to a cycle or revolution) is equal to 360°.

With the invention of the metric system, based on powers of ten, there was an attempt to replace degrees by decimal "degrees" in France and nearby countries,[note 3] where the number in a right angle is equal to 100 gon with 400 gon in a full circle (1° = 10⁄9 gon). This was called grade (nouveau) or grad. Due to confusion with the existing term grad(e) in some northern European countries (meaning a standard degree, ⁠1/360⁠ of a turn), the new unit was called Neugrad in German (whereas the "old" degree was referred to as Altgrad), likewise nygrad in Danish, Swedish and Norwegian (also gradian), and nýgráða in Icelandic. To end the confusion, the name gon was later adopted for the new unit. Although this idea of metrification was abandoned by Napoleon, grades continued to be used in several fields and many scientific calculators support them. Decigrades (1⁄4,000) were used with French artillery sights in World War I.

An angular mil, which is most used in military applications, has at least three specific variants, ranging from 1⁄6,400 to 1⁄6,000. It is approximately equal to one milliradian (c. 1⁄6,283). A mil measuring 1⁄6,000 of a revolution originated in the imperial Russian army, where an equilateral chord was divided into tenths to give a circle of 600 units. This may be seen on a lining plane (an early device for aiming indirect fire artillery) dating from about 1900 in the St. Petersburg Museum of Artillery.

Conversion of common angles
Turns Radians Degrees Gradians
0 turn 0 rad 0° 0g
⁠1/72⁠ turn ⁠π/36⁠ or ⁠𝜏/72⁠ rad 5° ⁠5+5/9⁠g
⁠1/24⁠ turn ⁠π/12⁠ or ⁠𝜏/24⁠ rad 15° ⁠16+2/3⁠g
⁠1/16⁠ turn ⁠π/8⁠ or ⁠𝜏/16⁠ rad 22.5° 25g
⁠1/12⁠ turn ⁠π/6⁠ or ⁠𝜏/12⁠ rad 30° ⁠33+1/3⁠g
⁠1/10⁠ turn ⁠π/5⁠ or ⁠𝜏/10⁠ rad 36° 40g
⁠1/8⁠ turn ⁠π/4⁠ or ⁠𝜏/8⁠ rad 45° 50g
⁠1/2π or 𝜏⁠ turn 1 rad approx. 57.3° approx. 63.7g
⁠1/6⁠ turn ⁠π/3⁠ or ⁠𝜏/6⁠ rad 60° ⁠66+2/3⁠g
⁠1/5⁠ turn ⁠2π or 𝜏/5⁠ rad 72° 80g
⁠1/4⁠ turn ⁠π/2⁠ or ⁠𝜏/4⁠ rad 90° 100g
⁠1/3⁠ turn ⁠2π or 𝜏/3⁠ rad 120° ⁠133+1/3⁠g
⁠2/5⁠ turn ⁠4π or 2𝜏 or α/5⁠ rad 144° 160g
⁠1/2⁠ turn π or ⁠𝜏/2⁠ rad 180° 200g
⁠3/4⁠ turn ⁠3π or ρ/2⁠ or ⁠3𝜏/4⁠ rad 270° 300g
1 turn 𝜏 or 2π rad 360° 400g

See also

[edit]

Notes

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Degree (angle)

View on Grokipedia
from Grokipedia
A degree (symbol: °) is a unit of angular measurement defined as one three-hundred-sixtieth (1/360) of a full or . This unit divides the of a into 360 equal parts, each representing the subtended by the corresponding arc. The degree's origins trace back to ancient , where the sexagesimal (base-60) number system influenced the choice of 360 as the number of divisions for a , possibly approximating the number of days in a year or relating to the divisibility of 360 by many integers. This system facilitated astronomical calculations and timekeeping, with early uses appearing around 2000 BCE in Mesopotamian records. The degree symbol ° first appeared in modern printed form in the 1569 edition of Gemma Frisius's Arithmeticae practicae methodus facilis, evolving from earlier notations for small angles. In contemporary and , degrees are subdivided into 60 arcminutes (') and each arcminute into 60 arcseconds ('') for precision, mirroring the sexagesimal subdivisions used for time and geographic coordinates. While the —defined as the angle subtended by an arc equal in length to the radius—serves as the (SI) derived unit for plane angles, degrees remain prevalent in , , , , and everyday contexts due to their intuitive whole-number divisions. The conversion between units is given by 1° = π/180 radians, approximately 0.017453 radians. Degrees play a foundational role in , where functions like sine, cosine, and are tabulated and computed using degree measures, and in fields such as for celestial positioning and for rotational dynamics. Alternative angular units, like gradians (400 per ) or binary degrees, exist but see limited use compared to the widespread adoption of degrees.

Fundamentals

Definition

The degree (symbol: °) is a unit of plane angle measurement equal to 1/360 of a full rotation or circle. An angle is the measure of rotation between two rays or lines that meet at a common point, known as the vertex. Geometrically, one degree corresponds to the central angle subtended by an arc whose length is one three-hundred-sixtieth of the circumference of a circle. In angular measurement, rotations are typically considered positive when proceeding counterclockwise from a reference ray and negative when proceeding clockwise. For finer precision, the degree may be subdivided into 60 arcminutes and each arcminute into 60 arcseconds.

Properties

The degree, as an angular unit, is defined such that a complete around a circle measures exactly 360°, which corresponds precisely to 2π radians. However, because π is an , the conversion factor between degrees and radians—specifically π/180 radians per degree—is irrational, rendering the two units incommensurable; that is, no rational multiple of one unit (other than multiples of the full circle) will exactly match a rational multiple of the other. This property implies that angles measured in degrees cannot be expressed as exact rational multiples of radians except in the case of full rotations, affecting precision in certain mathematical computations involving both systems. In trigonometry, the sine, cosine, and tangent functions exhibit periodicity with a period of 360°, meaning that for any angle θ, sin(θ + 360° · k) = sin(θ), cos(θ + 360° · k) = cos(θ), and tan(θ + 360° · k) = tan(θ), where k is any integer. These functions are typically evaluated over the principal range of 0° to 360° for positive angles or -180° to 180° for signed angles, reflecting the full cycle of the unit circle. This periodicity arises from the circular nature of angles, allowing trigonometric values to repeat indefinitely. Coterminal angles are those that, when measured in degrees, differ by an multiple of 360° and thus share the same terminal side in standard position, representing equivalent directions of ; for instance, 30° and 390° (or 30° + 360°) are coterminal. angles, measuring greater than 180° but less than 360°, extend beyond a straight angle while remaining within one full , such as 270°. These concepts highlight the inherent in angular measurement modulo 360°. The additivity of angles in degrees ensures that the measure of a composite angle formed by adjacent angles equals the sum (or difference, for subtraction) of their individual measures, facilitating the analysis of rotations and geometric figures; for example, two adjacent 45° angles combine to form a 90° angle. This linear additivity holds for angles within the same plane and is fundamental to decomposing complex rotations into simpler components./05%3A_Trigonometric_Functions_of_Angles/5.02%3A_Angles)

Historical Development

Ancient Origins

The origins of the degree as an angular unit trace back to ancient , particularly the Babylonians, who around 2000 BCE employed a (base-60) numerical system inherited from the earlier Sumerians for astronomical calculations. This system facilitated precise divisions, as 60 has numerous factors, making it ideal for subdividing circles and time periods. Babylonian astronomers approximated the solar year as 360 days—close to the actual 365—and divided the , the apparent path of the Sun, into 360 equal parts to track celestial movements, establishing the foundational numerical basis for the degree. Mesopotamian influences extended to neighboring civilizations, including the , who integrated similar astronomical divisions into their decanal star system by the Middle Kingdom period (c. 2050–1710 BCE). Egyptian astronomers divided the 360-degree into 36 decans, each spanning 10 degrees, to mark nightly time intervals and seasonal changes, reflecting a shared cultural exchange in early Near Eastern astronomy. An Old Babylonian from approximately 1800 BCE, such as , exemplifies these early computational practices through tables of ratios for right-angled triangles, which underpinned later angular measurements in terms. The transition to formalized Greek usage occurred in the 2nd century BCE, when astronomer of adopted the Babylonian 360-part division of the circle, standardizing it for zodiacal measurements in his influential works on stellar positions and eclipses. This adoption preserved the roots, later extending to subdivisions like arcminutes and arcseconds for finer precision in Hellenistic astronomy.

Adoption and Evolution

The degree, originating from ancient Babylonian divisions of the circle, was adopted and systematized during the , reaching a pinnacle in Roman astronomy through Claudius Ptolemy's in the CE, where it served as the primary unit for specifying celestial coordinates, planetary longitudes, and latitudes in his geocentric model. Ptolemy's comprehensive tables of chord lengths for angles up to 180 degrees facilitated precise astronomical predictions, embedding the unit deeply in Greco-Roman scientific tradition. In the medieval Islamic world from the 9th to 11th centuries, scholars built upon this foundation, refining the degree's application in for advanced astronomical and geodesic purposes. , in particular, integrated degrees into his and methods, using them to compute sines and cosines for measuring the Earth's radius and resolving spherical triangles in works like Al-Qanun al-Mas'udi. Other figures, such as , further enhanced degree-based sine tables inherited from , promoting their use in Islamic observatories for eclipse predictions and determinations. By the European Renaissance, the degree achieved widespread adoption in and , driven by maritime expansion and the recovery of classical texts. Instruments like the measured stellar altitudes in degrees to calculate , enabling Portuguese and Spanish explorers to chart transoceanic routes with greater accuracy. Surveyors employed degree divisions in techniques, as seen in the practical of texts by authors like , solidifying the unit's role in and . The marked a phase of international for the degree, paralleling the metric system's global rollout, yet it was retained over the for its intuitive practicality in fields like astronomy and . Conferences such as the 1884 affirmed degree-based measurements, integrating them into standardized global frameworks. In the 1960s, the (SI) formally recognized the degree as an accepted non-SI unit for plane angles, equivalent to π/180 , while designating the as the SI coherent unit. Into the , the degree maintained persistence in applied contexts despite radians' dominance in higher , where the latter's dimensionless nature simplifies and series expansions. In digital computing, emerging from the mid-century, degrees influenced angular precision by standardizing input for and simulations—often converted internally to radians for efficient floating-point operations—balancing user familiarity with computational rigor.

Notation and Representation

Symbols and Abbreviations

The primary symbol for the degree in angular measurement is the superscript small circle °, known as the , which is encoded in as U+00B0. This symbol first appeared in modern printed works in the , notably in the 1569 revised edition of Gemma Frisius's Arithmeticae practicae methodus facilis, in an appendix by Jacques Peletier du Mans, where it denoted degrees in astronomical calculations. The degree is commonly abbreviated as "deg" in technical and , particularly when the cannot be rendered or for clarity in plain text. In many contexts, the ° is used directly adjacent to the numeral without a space, as in 90°, to indicate the unit succinctly. For plural forms, the full word "degrees" is standard in prose, while the ° applies to multiples without alteration, such as 360°. It is essential to distinguish the degree sign ° from similar characters like the masculine º (Unicode U+00BA), which is used in languages such as Spanish and to denote ordinal numbers (e.g., 1º for "first"). The degree sign is a simple, monoline without contrast or an "o" shape, whereas º often features subtle typographic variations like a lowered or styled "o". In digital typing and software rendering, the can be input via keyboard shortcuts (e.g., Alt+0176 on Windows) or entities like ° for web display. Common errors in digital environments include incorrect encoding leading to garbled output, such as "°" in legacy systems, which arises from mismatched character sets like ISO-8859-1 versus UTF-8. For instance, in angular notations involving subdivisions, it appears as 30° 15' to combine degrees and arcminutes.

Usage in Mathematical Expressions

In mathematical expressions, angles in degrees are conventionally expressed using postfix notation, where the degree ° immediately follows the numerical value without intervening space, adhering to standards for plane angle units. For instance, the equation for an angle θ measures 45 degrees as θ=45∘\theta = 45^\circ. In textual descriptions within proofs or explanations, may instead be spelled out as "degrees" to clarify the measure, such as "angle θ equals 45 degrees," avoiding the symbol for readability in non-equation contexts. Within , degree-based arguments are denoted directly in function calls, exemplified by sin⁡(30∘)\sin(30^\circ), which contrasts with the form sin⁡(π/6)\sin(\pi/6) for the same angle; this distinction ensures unambiguous computation, as calculators must be switched to degree mode to evaluate degree inputs correctly. Multi-angle expressions, such as those for coterminal angles sharing the same terminal side, employ the form θ+360∘n\theta + 360^\circ n, where nn is any , allowing representation of equivalent rotations. International standards, including ISO 80000-1 and the SI Brochure, mandate the ° symbol for degrees of plane angle with no space from the preceding number (e.g., 90∘90^\circ), distinguishing it from spaced usage in temperature scales like 25∘C25^\circ \text{C}. In modern academic writing, best practices recommend ∘^{\circ} for inline math mode in simple cases or the siunitx package's \si{\degree} command for precise unit handling in technical documents, ensuring typographic consistency across publications. For digital text, the character U+00B0 provides the , facilitating cross-platform rendering in mathematical software and markup.

Subdivisions

Arcminutes and Arcseconds

The degree is subdivided into 60 arcminutes, each denoted by a single prime symbol (′), providing a unit for measuring smaller angles with moderate precision. One arcminute equals 1/60 of a degree, or approximately 0.0167 degrees. Each arcminute is further divided into 60 arcseconds, denoted by a double prime symbol (″), resulting in 1 degree = 60′ = 3600″. This hierarchical division allows for expressing angular measurements with increasing accuracy, where arcseconds represent the smallest common subunit in this system. This subdivision scheme derives directly from the ancient Babylonian (base-60) numbering system, which influenced angular measurements in early and . Arcseconds, in particular, offer high precision equivalent to about 4.85 microradians, enabling fine distinctions in angular scale. In modern contexts, arcminutes and arcseconds are essential for specifying resolutions in , where instruments achieve angular separations as small as a few arcseconds to resolve fine details. Similarly, in , these units quantify the accuracy of devices like theodolites and total stations; for instance, a 1″ instrument provides precision suitable for measurements over distances of several kilometers, where 1″ corresponds to roughly 0.05 at 10 kilometers.

Sexagesimal Subdivision System

The sexagesimal subdivision system divides each degree of arc into 60 arcminutes (denoted as ' or arcmin), and each arcminute into 60 arcseconds (denoted as " or arcsec). This hierarchical structure, based on powers of 60, can be extended to higher subdivisions such as arcmilliseconds (1/60 arcsecond) or further if required for precise measurements. The choice of base 60 originates from ancient , where it was valued for its extensive divisibility—60 factors into 2² × 3 × 5, allowing clean divisions by 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, and 30 without producing repeating fractions in many cases. This property made it ideal for fractional representations in calculations involving circles and time, influencing its adoption for angular measures alongside the division of hours into minutes and seconds. An alternative to the system is the use of , which express angles as a single decimal value, such as 40.7128° for the approximate of . simplify storage and arithmetic operations in digital systems like GPS and GIS software, enabling straightforward computations and transformations without needing to handle multiple units. However, the format endures in traditional contexts due to its intuitive alignment with fractional divisions and historical precedence, with some fields showing resistance to full adoption of decimal systems despite their computational efficiency. Modern software often bridges the two through built-in conversions, such as transforming degrees-minutes-seconds (DMS) to for analysis. For instance, an of 1° 30' converts directly to 1.5° in form, illustrating the straightforward equivalence for common subdivisions.

Alternative Angular Units

Radian

The (symbol: rad) is the of plane , defined as the subtended at the center of a by an arc whose length equals the 's radius. This makes one approximately 57.2958 degrees, with a complete corresponding to exactly 2π2\pi , or roughly 6.2832 . The provides a natural, geometry-based measure tied directly to the 's properties, contrasting with the degree's arbitrary division of the full into 360 parts. The relationship between radians and degrees is given by the exact conversion factor π\pi radians = 180 degrees, so angles in degrees can be converted to radians by multiplying by π/180\pi/180./Book%3A_University_Physics_I_-Mechanics_Sound_Oscillations_and_Waves(OpenStax)/02%3A_Mathematical_Methods_and_Tools/2.01%3A_The_Radian_and_Degree_Measures) Introduced by James Thomson in 1871, the term "" derives from "" and was first used in academic contexts to promote a more intuitive angular unit; it was later formalized as an SI unit in 1960, transitioning from a supplementary to a derived unit in 1995 to reflect its dimensionless nature. A key advantage of the radian lies in its compatibility with and : for instance, the arc length formula simplifies to s=rθs = r \theta when θ\theta is in radians, avoiding extra conversion factors required with degrees, and trigonometric derivatives like ddθsin⁡θ=cos⁡θ\frac{d}{d\theta} \sin \theta = \cos \theta hold directly without scaling. As a ratio of two lengths (arc to radius), the is inherently dimensionless, equivalent to 1 in , which streamlines equations in physics and engineering. In modern applications, radians are preferred over degrees in physics for theoretical derivations and in software for computational efficiency, as most mathematical libraries implement natively in radians to align with these analytical benefits.

Gradian and Other Units

The , also known as the gon or grad, is an angular unit defined such that a full circle measures 400 gradians, with a equaling 100 gradians. This decimal-based system was introduced in during the development of the around 1795, aiming to align angular measurement with the decimal subdivisions used in linear metrics like the meter. It gained some adoption in fields requiring precise decimal calculations, particularly and , where right angles are naturally 100 units and further divisions into centigrades (0.01 gradian) facilitate computational ease. The conversion between degrees and gradians follows the ratio of their full-circle divisions: 1 degree equals 109\frac{10}{9} gradians, or approximately 1.111 gradians, while 1 equals 0.9 degrees. Despite its logical decimal structure, the gradian saw limited widespread use outside specialized European applications and has largely declined since the early , following the broader efforts that prioritized the in scientific contexts. Another alternative unit is the turn, which denotes a complete equivalent to 360 degrees or 400 gradians. This unit, sometimes called a or cycle, appears in and for describing full without fractional complexity, though it remains uncommon in standard measurements. Binary degrees, also referred to as brads or binary radians, subdivide a full circle into 256 equal parts, making 1 binary degree approximately 1.40625 degrees. Developed for computational efficiency in binary systems, they are employed in niche digital applications such as , , and , where powers of two align naturally with hardware representations. Historical and specialized units include the mil, prevalent in and sighting since the , where a full circle comprises 6400 mils for fine angular adjustments in targeting. Such units highlight past efforts to tailor angular measures to specific tools, like gunner protractors, but they have waned post-metrication in favor of more universal standards.

Applications

In Mathematics and Geometry

In geometry, the degree serves as a fundamental unit for measuring angles formed by intersecting lines or curves, particularly in polygons and circles. For instance, in regular polygons, the interior angles are calculated using the formula (n−2n)×180∘\left( \frac{n-2}{n} \right) \times 180^\circ, where nn is the number of sides; an equilateral triangle (n=3n=3) thus has each interior angle measuring 60∘60^\circ. In circles, the central angle subtended by an arc at the center equals the measure of the arc in degrees, with a full circle encompassing 360∘360^\circ. The inscribed angle theorem states that an angle inscribed in a circle, intercepting the same arc as a central angle, measures half the central angle; for example, if the central angle is 80∘80^\circ, the inscribed angle is 40∘40^\circ. In trigonometry, degrees define the standard position of angles on the unit circle, where the terminal side intersects the circle to yield coordinates (cos⁡θ,sin⁡θ)(\cos \theta, \sin \theta) for an angle θ∘\theta^\circ (with trigonometric functions evaluated in degree mode). Reference angles, the acute angles formed with the x-axis (between 0∘0^\circ and 90∘90^\circ), facilitate evaluation of trigonometric functions in other quadrants by relating them to principal values. Degrees are commonly used to solve triangles via the law of sines, asin⁡A∘=bsin⁡B∘=csin⁡C∘\frac{a}{\sin A^\circ} = \frac{b}{\sin B^\circ} = \frac{c}{\sin C^\circ}, and the law of cosines, c2=a2+b2−2abcos⁡C∘c^2 = a^2 + b^2 - 2ab \cos C^\circ, enabling determination of side lengths and angles in non-right triangles. For the equilateral triangle example, all angles are 60∘60^\circ, so sin⁡60∘=32\sin 60^\circ = \frac{\sqrt{3}}{2}
Add your contribution
Related Hubs
Contribute something
User Avatar
No comments yet.