Recent from talks
Nothing was collected or created yet.
Lucas number
View on WikipediaThis article includes a list of general references, but it lacks sufficient corresponding inline citations. (December 2019) |

The Lucas sequence is an integer sequence named after the mathematician François Édouard Anatole Lucas (1842–1891), who studied both that sequence and the closely related Fibonacci sequence. Individual numbers in the Lucas sequence are known as Lucas numbers. Lucas numbers and Fibonacci numbers form complementary instances of Lucas sequences.
The Lucas sequence has the same recursive relationship as the Fibonacci sequence, where each term is the sum of the two previous terms, but with different starting values.[1] This produces a sequence where the ratios of successive terms approach the golden ratio, and in fact the terms themselves are roundings of integer powers of the golden ratio.[2] The sequence also has a variety of relationships with the Fibonacci numbers, like the fact that adding any two Fibonacci numbers two terms apart in the Fibonacci sequence results in the Lucas number in between.[3]
The first few Lucas numbers are
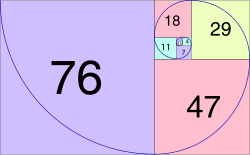
- 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, 9349, ... . (sequence A000032 in the OEIS)
which coincides for example with the number of independent vertex sets for cyclic graphs of length .[1]
Definition
[edit]As with the Fibonacci numbers, each Lucas number is defined to be the sum of its two immediately previous terms, thereby forming a Fibonacci integer sequence. The first two Lucas numbers are and , which differs from the first two Fibonacci numbers and . Though closely related in definition, Lucas and Fibonacci numbers exhibit distinct properties.
The Lucas numbers may thus be defined as follows:
(where n belongs to the natural numbers)
All Fibonacci-like integer sequences appear in shifted form as a row of the Wythoff array; the Fibonacci sequence itself is the first row and the Lucas sequence is the second row. Also like all Fibonacci-like integer sequences, the ratio between two consecutive Lucas numbers converges to the golden ratio.
Extension to negative integers
[edit]Using , one can extend the Lucas numbers to negative integers to obtain a doubly infinite sequence:
- ..., −11, 7, −4, 3, −1, 2, 1, 3, 4, 7, 11, ... (terms for are shown).
The formula for terms with negative indices in this sequence is
Relationship to Fibonacci numbers
[edit]
The Lucas numbers are related to the Fibonacci numbers by many identities. Among these are the following:
- , so .
- ; in particular, , so .
Their closed formula is given as:
where is the golden ratio. Alternatively, as for the magnitude of the term is less than 1/2, is the closest integer to or, equivalently, the integer part of , also written as .
Combining the above with Binet's formula,
a formula for is obtained:
For integers n ≥ 2, we also get:
with remainder R satisfying
- .
Lucas identities
[edit]Many of the Fibonacci identities have parallels in Lucas numbers. For example, the Cassini identity becomes
Also
where .
where except for .
For example if n is odd, and
Checking, , and
Generating function
[edit]Let
be the generating function of the Lucas numbers. By a direct computation,
which can be rearranged as
gives the generating function for the negative indexed Lucas numbers, , and
satisfies the functional equation
As the generating function for the Fibonacci numbers is given by
we have
which proves that
and
proves that
The partial fraction decomposition is given by
where is the golden ratio and is its conjugate.
This can be used to prove the generating function, as
Congruence relations
[edit]If is a Fibonacci number then no Lucas number is divisible by .
The Lucas numbers satisfy Gauss congruence. This implies that is congruent to 1 modulo if is prime. The composite values of which satisfy this property are known as Fibonacci pseudoprimes.
is congruent to 0 modulo 5.
Lucas primes
[edit]A Lucas prime is a Lucas number that is prime. The first few Lucas primes are
- 2, 3, 7, 11, 29, 47, 199, 521, 2207, 3571, 9349, 3010349, 54018521, 370248451, 6643838879, ... (sequence A005479 in the OEIS).
The indices of these primes are (for example, L4 = 7)
- 0, 2, 4, 5, 7, 8, 11, 13, 16, 17, 19, 31, 37, 41, 47, 53, 61, 71, 79, 113, 313, 353, 503, 613, 617, 863, 1097, 1361, 4787, 4793, 5851, 7741, 8467, ... (sequence A001606 in the OEIS).
As of September 2015[update], the largest confirmed Lucas prime is L148091, which has 30950 decimal digits.[4] As of August 2022[update], the largest known Lucas probable prime is L5466311, with 1,142,392 decimal digits.[5]
If Ln is prime then n is 0, prime, or a power of 2.[6] L2m is prime for m = 1, 2, 3, and 4 and no other known values of m.
Lucas polynomials
[edit]In the same way as Fibonacci polynomials are derived from the Fibonacci numbers, the Lucas polynomials are a polynomial sequence derived from the Lucas numbers.
Continued fractions for powers of the golden ratio
[edit]Close rational approximations for powers of the golden ratio can be obtained from their continued fractions.
For positive integers n, the continued fractions are:
- .
For example:
is the limit of
with the error in each term being about 1% of the error in the previous term; and
is the limit of
with the error in each term being about 0.3% that of the second previous term.
Applications
[edit]Lucas numbers are the second most common pattern in sunflowers after Fibonacci numbers, when clockwise and counter-clockwise spirals are counted, according to an analysis of 657 sunflowers in 2016.[7]
See also
[edit]References
[edit]- ^ a b Weisstein, Eric W. "Lucas Number". mathworld.wolfram.com. Retrieved 2020-08-11.
- ^ Parker, Matt (2014). "13". Things to Make and Do in the Fourth Dimension. Farrar, Straus and Giroux. p. 284. ISBN 978-0-374-53563-6.
- ^ Parker, Matt (2014). "13". Things to Make and Do in the Fourth Dimension. Farrar, Straus and Giroux. p. 282. ISBN 978-0-374-53563-6.
- ^ "The Top Twenty: Lucas Number". primes.utm.edu. Retrieved 6 January 2022.
- ^ "Henri & Renaud Lifchitz's PRP Top - Search by form". www.primenumbers.net. Retrieved 6 January 2022.
- ^ Chris Caldwell, "The Prime Glossary: Lucas prime" from The Prime Pages.
- ^ Swinton, Jonathan; Ochu, Erinma; null, null (2016). "Novel Fibonacci and non-Fibonacci structure in the sunflower: results of a citizen science experiment". Royal Society Open Science. 3 (5) 160091. Bibcode:2016RSOS....360091S. doi:10.1098/rsos.160091. PMC 4892450. PMID 27293788.
External links
[edit]- "Lucas polynomials", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Weisstein, Eric W. "Lucas Number". MathWorld.
- Weisstein, Eric W. "Lucas Polynomial". MathWorld.
- "The Lucas Numbers", Dr Ron Knott
- Lucas numbers and the Golden Section
- A Lucas Number Calculator can be found here.
- OEIS sequence A000032 (Lucas numbers beginning at 2)
Lucas number
View on GrokipediaDefinition and History
Definition
The Lucas numbers form an integer sequence defined by the recurrence relation with initial conditions and .[3][9] The first few terms of the sequence are , , , , , , , , , and so on (OEIS A000032).[10] The Lucas numbers constitute a particular instance of the more general Lucas sequences , obtained by setting the parameters and .[11] Like the Fibonacci numbers, the Lucas numbers obey the same linear recurrence but differ in their starting values.[3]History
The Lucas numbers are named after the French mathematician François Édouard Anatole Lucas (1842–1891), who first systematically studied the sequence in the 1870s as part of his investigations into integer sequences related to the Fibonacci numbers and applications in number theory.[12][13] Lucas's work on these sequences emerged during his broader research on primality testing, including methods for verifying Mersenne primes, which connect to the study of perfect numbers through the even perfect number theorem. In 1878, he published his seminal paper "Théorie des fonctions numériques simplement périodiques" in the American Journal of Mathematics, where he formalized the general class of Lucas sequences, including the specific case now known as the Lucas numbers, and introduced criteria for primality using these sequences—later refined into the Lucas-Lehmer test.[12][14] Following Lucas's death in 1891, the sequence gained wider recognition in the 20th century through recreational mathematics literature, which explored its properties alongside Fibonacci numbers in puzzles and patterns. The sequence was formally cataloged in the On-Line Encyclopedia of Integer Sequences (OEIS) upon its founding in 1964 by Neil Sloane, marking its integration into modern computational and combinatorial studies.[15][16]Mathematical Foundations
Closed-Form Expression
The closed-form expression for the Lucas number is given by Binet's formula: where is the golden ratio and is its conjugate.[9][17] This formula arises from solving the linear recurrence relation for , with initial conditions and . The characteristic equation is , which has roots and . The general solution is thus . Applying the initial conditions yields and . Since and , solving the system gives and .[17] The expression evaluates to an integer for all nonnegative integers , despite and being irrational algebraic conjugates in the quadratic field . This integer nature follows from the fact that the powers of these conjugates, when summed, lie in the rational subfield , and the sequence satisfies the integer-coefficient recurrence with integer initial values.[9][17] An equivalent form is , which highlights that is the exact value obtained without approximation. For , is also the nearest integer to , since . The Lucas numbers grow exponentially as for large , reflecting the dominant role of the golden ratio in the formula.[9][17]Relation to Fibonacci Numbers
The Lucas numbers and Fibonacci numbers are intimately connected through their shared linear recurrence relation. Both sequences satisfy the recurrence for , with the Fibonacci sequence defined by initial conditions , , and the Lucas sequence by , .[18] This common recurrence implies that they share the same characteristic equation , with roots (the golden ratio) and .[18] A direct explicit relation expresses each Lucas number as the sum of two Fibonacci numbers: for .[18] This formula highlights how Lucas numbers emerge from adjacent Fibonacci terms shifted by one index, illustrating a simple additive pattern between the sequences. For example, . Visually, this relation manifests in patterns where Lucas numbers approximate sums of every other Fibonacci number in certain geometric arrangements, such as tiled rectangles or spiral approximations, though the sequences interleave distinctly due to differing initial values.[18] The connection extends to matrix representations, where both sequences arise from powers of the companion matrix . Specifically, for , and the trace of this matrix equals , unifying the sequences through linear algebra.[19] Cassini-like identities further link the sequences. The standard Cassini identity for Fibonacci numbers states .[19] A related identity combining both is , which extends the Cassini form by incorporating the discriminant of the characteristic equation and reveals the interplay between the sequences' growth rates.[18]Sequence Extensions
Negative Indices
The Lucas sequence, defined by the recurrence for with initial conditions and , can be extended to negative indices by solving the recurrence relation in the reverse direction. Starting from these initial values, is found by rearranging the equation for : , so yields . Similarly, follows from : , so gives . Continuing, , and .[20][21] This backward extension preserves the same linear recurrence for all integers , resulting in the reflection formula for positive integers . This relation holds because the characteristic equation of the recurrence remains unchanged, and induction confirms it aligns with the computed values: for , ; for , ; for , . The formula can be derived by assuming the recurrence applies bidirectionally and verifying via the generating function or matrix representation of the sequence.[20][21] The closed-form Binet expression for Lucas numbers, where and , extends naturally to negative indices, but direct substitution confirms due to the properties and . This verification ensures the formula's consistency across all integers without altering the integer-valued nature of the sequence.[22][20] Regarding parity, the signs for negative indices alternate based on whether the absolute value of the index is even or odd: values at even negative indices (like , ) are positive, while those at odd negative indices (like , ) are negative, mirroring the positive sequence but with the sign flip encoded in . This pattern emerges directly from the reflection formula and the recurrence's linear structure.[21][20]Lucas Polynomials
The Lucas polynomials form a sequence of polynomials generalizing the Lucas numbers, defined by the recurrence relation for , with initial conditions and . These polynomials are monic of degree for , and they satisfy the same linear recurrence structure as the Lucas sequence but with coefficients depending on .[23] When evaluated at , the Lucas polynomials recover the standard Lucas numbers: , where denotes the -th Lucas number. For example, and higher-degree terms follow the pattern of expanding through the recurrence.[23] The ordinary generating function for the Lucas polynomials is This closed form arises from solving the recurrence and incorporating the initial conditions. The Lucas polynomials are of degree and possess roots that lie on the imaginary axis, specifically at for .[23] These roots are connected to the Chebyshev polynomials of the first kind via the relation , where is the -th Chebyshev polynomial, highlighting their trigonometric structure.[24]Identities and Properties
Fundamental Identities
The fundamental identities of Lucas numbers provide algebraic relations that connect terms within the sequence and link them to Fibonacci numbers. These identities are essential for deriving higher-level properties and have been established through methods such as mathematical induction and Binet's closed-form expression.[25] One key addition formula expresses in terms of Lucas and Fibonacci numbers: This symmetric form holds for positive integers and , and can be verified by direct computation for small values or proved using Binet's formulas for both sequences, where the powers of the golden ratio and its conjugate align to yield the relation. An equivalent expression is , which rearranges to highlight the product of Lucas terms adjusted by Fibonacci contributions.[25][26] The multiplication formula relates the product of two Lucas numbers to others in the sequence: This identity assumes and follows from the addition formula combined with the known relation ; a proof by induction on confirms it, with the base case reducing to , which aligns with the recurrence.[26] D'Ocagne's identity mixes Lucas and Fibonacci terms to yield another Fibonacci expression: For , this can be rearranged as , but the primary form is derived using Binet's formula, where the difference of powers simplifies due to the orthogonal properties of and its conjugate. The symmetric version holds similarly.[9] An adaptation of Catalan's identity for Lucas numbers generalizes the Cassini-like relation: This holds for integers , with the special case giving . Proofs proceed by induction on , leveraging the recurrence and the fundamental relation , or directly via Binet's formula, where the cross terms cancel to produce the Fibonacci square factor scaled by 5.[26]Generating Function
The ordinary generating function for the Lucas sequence , defined by , , and for , is given by for , where is the golden ratio.[27] To derive this, start with the recurrence relation and initial conditions. Multiply the recurrence by and sum over : The left side is . The first sum on the right is , and the second is . Substituting the initial values yields which simplifies to , solving for the stated formula.[28] This generating function relates closely to that of the Fibonacci sequence , where , , and the same recurrence holds, with The numerators differ due to the initial conditions: the Lucas numerator reflects , while the Fibonacci is simply .[27] The generating function connects to the closed-form Binet expression , where . Summing the geometric series gives Partial fraction decomposition confirms this equals , as the roots of the denominator are and .[27] Applications include extracting coefficients using the partial fractions above or via contour integrals around the poles at and , though the Binet form is more direct for computation. Generating functions also facilitate proofs of identities by series manipulation, such as multiplying by to recover the recurrence or deriving summation formulas through differentiation and integration.[28]Congruence Relations
The Lucas sequence is periodic modulo any positive integer , with the length of the minimal period denoted , analogous to the Pisano period for the Fibonacci sequence. This period satisfies whenever , but may differ otherwise; for example, for .[29] Representative examples illustrate this periodicity. Modulo 2, the sequence begins 1, 1, 0 and repeats every 3 terms: if , and otherwise.[30] Modulo 3, the sequence is 1, 0, 1, 1, 2, 0, 2, 2 and repeats every 8 terms.[31] For a prime , the rank of apparition (also called the entry point) is the smallest positive integer such that , provided such a exists. This is the law of appearance for Lucas numbers. For , . The prime 5 divides no Lucas number, so is undefined. For odd primes , always exists, divides (where is the Legendre symbol), and the period satisfies .[29] The primes for which exists (i.e., those dividing some ) form a set of asymptotic density .[32] Basic modular properties of Lucas numbers relate to quadratic residues. Specifically, if and only if divides . For example, if 5 is a quadratic residue modulo (so ), then divides , implying divides for some dividing . If instead , then divides . Additionally, for any odd prime , .[29][33]Special Lucas Numbers
Lucas Primes
A Lucas prime is defined as a Lucas number that is itself a prime number, where the Lucas sequence is given by , , and for .[34] While for prime has been of particular interest due to potential algebraic factorizations for composite indices, Lucas primes more generally refer to any prime regardless of whether is prime.[35] The known small Lucas primes occur at specific indices and provide examples of the sequence's primality patterns. These include:| Index | Lucas Prime |
|---|---|
| 0 | 2 |
| 2 | 3 |
| 4 | 7 |
| 5 | 11 |
| 7 | 29 |
| 8 | 47 |
| 11 | 199 |
| 13 | 521 |
| 16 | 2207 |
| 17 | 3571 |



































































![{\displaystyle \varphi ^{2n-1}=[L_{2n-1};L_{2n-1},L_{2n-1},L_{2n-1},\ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eea1fc49a65fe295a8893c405134849a8105f25e)
![{\displaystyle \varphi ^{2n}=[L_{2n}-1;1,L_{2n}-2,1,L_{2n}-2,1,L_{2n}-2,1,\ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24e6fa7e66de4d8247ff8981890b3c1828568a2f)
![{\displaystyle \varphi ^{5}=[11;11,11,11,\ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d92616182fb968582a30caa3c313bffb55be96b6)

![{\displaystyle \varphi ^{6}=[18-1;1,18-2,1,18-2,1,18-2,1,\ldots ]=[17;1,16,1,16,1,16,1,\ldots ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0620aa566c13841b0c2cb09ed64bb3cfde88bb77)

