Hubbry Logo
One- and two-tailed testsOne- and two-tailed testsMain
Open search
One- and two-tailed tests
Community hub
One- and two-tailed tests
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
One- and two-tailed tests
One- and two-tailed tests
One- and two-tailed tests
View on Wikipedia
from Wikipedia
A two-tailed test applied to the normal distribution.
A one-tailed test, showing the p-value as the size of one tail.

In statistical significance testing, a one-tailed test and a two-tailed test are alternative ways of computing the statistical significance of a parameter inferred from a data set, in terms of a test statistic. A two-tailed test is appropriate if the estimated value is greater or less than a certain range of values, for example, whether a test taker may score above or below a specific range of scores. This method is used for null hypothesis testing and if the estimated value exists in the critical areas, the alternative hypothesis is accepted over the null hypothesis. A one-tailed test is appropriate if the estimated value may depart from the reference value in only one direction, left or right, but not both.[1] An example can be whether a machine produces more than one-percent defective products. In this situation, if the estimated value exists in one of the one-sided critical areas, depending on the direction of interest (greater than or less than), the alternative hypothesis is accepted over the null hypothesis. Alternative names are one-sided and two-sided tests; the terminology "tail" is used because the extreme portions of distributions, where observations lead to rejection of the null hypothesis, are small and often "tail off" toward zero as in the normal distribution, colored in yellow, or "bell curve", pictured on the right and colored in green.

Applications

[edit]

One-tailed tests are used for asymmetric distributions that have a single tail, such as the chi-squared distribution, which are common in measuring goodness-of-fit, or for one side of a distribution that has two tails, such as the normal distribution, which is common in estimating location; this corresponds to specifying a direction. Two-tailed tests are only applicable when there are two tails, such as in the normal distribution, and correspond to considering either direction significant.[2][3]

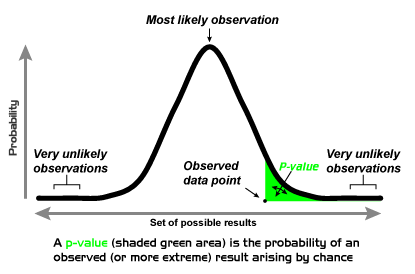
In the approach of Ronald Fisher, the null hypothesis H0 will be rejected when the p-value of the test statistic is sufficiently extreme (vis-a-vis the test statistic's sampling distribution) and thus judged unlikely to be the result of chance. This is usually done by comparing the resulting p-value with the specified significance level, denoted by , when computing the statistical significance of a parameter. In a one-tailed test, "extreme" is decided beforehand as either meaning "sufficiently small" or meaning "sufficiently large" – values in the other direction are considered not significant. One may report that the left or right tail probability as the one-tailed p-value, which ultimately corresponds to the direction in which the test statistic deviates from H0.[4] In a two-tailed test, "extreme" means "either sufficiently small or sufficiently large", and values in either direction are considered significant.[5] For a given test statistic, there is a single two-tailed test, and two one-tailed tests, one each for either direction. When provided a significance level , the critical regions would exist on the two tail ends of the distribution with an area of each for a two-tailed test. Alternatively, the critical region would solely exist on the single tail end with an area of for a one-tailed test. For a given significance level in a two-tailed test for a test statistic, the corresponding one-tailed tests for the same test statistic will be considered either twice as significant (half the p-value) if the data is in the direction specified by the test, or not significant at all (p-value above ) if the data is in the direction opposite of the critical region specified by the test.

For example, if flipping a coin, testing whether it is biased towards heads is a one-tailed test, and getting data of "all heads" would be seen as highly significant, while getting data of "all tails" would be not significant at all (p = 1). By contrast, testing whether it is biased in either direction is a two-tailed test, and either "all heads" or "all tails" would both be seen as highly significant data. In medical testing, while one is generally interested in whether a treatment results in outcomes that are better than chance, thus suggesting a one-tailed test; a worse outcome is also interesting for the scientific field, therefore one should use a two-tailed test that corresponds instead to testing whether the treatment results in outcomes that are different from chance, either better or worse.[6] In the archetypal lady tasting tea experiment, Fisher tested whether the lady in question was better than chance at distinguishing two types of tea preparation, not whether her ability was different from chance, and thus he used a one-tailed test.

Coin flipping example

[edit]
Main article: Checking whether a coin is fair

In coin flipping, the null hypothesis is a sequence of Bernoulli trials with probability 0.5, yielding a random variable X which is 1 for heads and 0 for tails, and a common test statistic is the sample mean (of the number of heads) If testing for whether the coin is biased towards heads, a one-tailed test would be used – only large numbers of heads would be significant. In that case a data set of five heads (HHHHH), with sample mean of 1, has a chance of occurring, (5 consecutive flips with 2 outcomes - ((1/2)^5 =1/32). This would have and would be significant (rejecting the null hypothesis) if the test was analyzed at a significance level of (the significance level corresponding to the cutoff bound). However, if testing for whether the coin is biased towards heads or tails, a two-tailed test would be used, and a data set of five heads (sample mean 1) is as extreme as a data set of five tails (sample mean 0). As a result, the p-value would be and this would not be significant (not rejecting the null hypothesis) if the test was analyzed at a significance level of .

History

[edit]
p-value of chi-squared distribution for different number of degrees of freedom

The p-value was introduced by Karl Pearson[7] in the Pearson's chi-squared test, where he defined P (original notation) as the probability that the statistic would be at or above a given level. This is a one-tailed definition, and the chi-squared distribution is asymmetric, only assuming positive or zero values, and has only one tail, the upper one. It measures goodness of fit of data with a theoretical distribution, with zero corresponding to exact agreement with the theoretical distribution; the p-value thus measures how likely the fit would be this bad or worse.

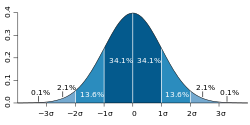
Normal distribution, showing two tails

The distinction between one-tailed and two-tailed tests was popularized by Ronald Fisher in the influential book Statistical Methods for Research Workers,[8] where he applied it especially to the normal distribution, which is a symmetric distribution with two equal tails. The normal distribution is a common measure of location, rather than goodness-of-fit, and has two tails, corresponding to the estimate of location being above or below the theoretical location (e.g., sample mean compared with theoretical mean). In the case of a symmetric distribution such as the normal distribution, the one-tailed p-value is exactly half the two-tailed p-value:[8]

Some confusion is sometimes introduced by the fact that in some cases we wish to know the probability that the deviation, known to be positive, shall exceed an observed value, whereas in other cases the probability required is that a deviation, which is equally frequently positive and negative, shall exceed an observed value; the latter probability is always half the former.

— Ronald Fisher, Statistical Methods for Research Workers

Fisher emphasized the importance of measuring the tail – the observed value of the test statistic and all more extreme – rather than simply the probability of specific outcome itself, in his The Design of Experiments (1935).[9] He explains this as because a specific set of data may be unlikely (in the null hypothesis), but more extreme outcomes likely, so seen in this light, the specific but not extreme unlikely data should not be considered significant.

Specific tests

[edit]

If the test statistic follows a Student's t-distribution in the null hypothesis – which is common where the underlying variable follows a normal distribution with unknown scaling factor, then the test is referred to as a one-tailed or two-tailed t-test. If the test is performed using the actual population mean and variance, rather than an estimate from a sample, it would be called a one-tailed or two-tailed Z-test.

The statistical tables for t and for Z provide critical values for both one- and two-tailed tests. That is, they provide the critical values that cut off an entire region at one or the other end of the sampling distribution as well as the critical values that cut off the regions (of half the size) at both ends of the sampling distribution.

See also

[edit]

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

One- and two-tailed tests

View on Grokipedia
from Grokipedia
In statistical hypothesis testing, one-tailed and two-tailed tests are procedures used to assess whether observed data provide sufficient evidence to reject a null hypothesis in favor of an alternative hypothesis, differing primarily in the directionality of the alternative hypothesis they evaluate. A one-tailed test, also known as a one-sided test, specifies a directional alternative hypothesis, such as a population mean being greater than or less than a hypothesized value, concentrating the rejection region in a single tail of the probability distribution. In contrast, a two-tailed test employs a non-directional alternative hypothesis, such as the mean differing from the hypothesized value in either direction, dividing the rejection region equally between both tails of the distribution. These tests are fundamental in fields like psychology, economics, and engineering for making inferences about population parameters from sample data. The choice between one-tailed and two-tailed tests hinges on the and theoretical expectations. One-tailed tests are appropriate when prior or the study's context justifies ignoring the possibility of an effect in the opposite direction, such as testing whether a new increases recovery rates without concern for decreases, thereby allocating the entire significance level (e.g., α = 0.05) to one tail for greater statistical power. However, two-tailed tests are the default in or when an effect could plausibly occur in either direction, as they provide a more conservative assessment by splitting α across both tails (e.g., 0.025 per tail), reducing the risk of overlooking unexpected results. Misapplying a one-tailed test to achieve significance or switching after initial results can lead to inflated error rates and is generally discouraged in rigorous statistical practice. In practice, the tests rely on test statistics like the z-score or , compared against critical values or via to determine significance. For a given test statistic, the in a two-tailed test is typically twice that of the corresponding one-tailed test, reflecting the broader rejection region. For example, in testing whether the mean hardness of a material exceeds 170 on the Brinell scale (two-tailed: H₀: μ = 170 vs. Hₐ: μ ≠ 170), a of 2.19 with 24 might yield a of 0.039, leading to rejection at α = 0.05, whereas a one-tailed version (Hₐ: μ > 170) would have a smaller p-value of approximately 0.0195. These methods assume normality or large sample sizes and are implemented in software like or SAS, but require careful specification of hypotheses before data collection to maintain validity.

Background Concepts

Hypothesis Testing Fundamentals

Hypothesis testing is a formal statistical procedure for making inferences about population parameters from sample data by evaluating the evidence against a hypothesized value or model, relying on the concept of to determine whether observed results are likely due to chance. This method allows researchers to test claims about a characteristic using probabilistic reasoning, where decisions are based on the likelihood of obtaining the sample under the assumption of the . The framework was formalized in the Neyman-Pearson approach, which emphasizes controlling error rates in evaluation. The standard steps in hypothesis testing include: formulating the (typically denoting no effect or difference) and the ; selecting a significance level α\alpha, which represents the acceptable probability of a Type I error; collecting a random sample and computing an appropriate from the data; determining the (the probability of observing data as extreme as or more extreme than the sample under the ) or identifying the critical value; and finally, making a decision to reject or fail to reject the based on whether the is less than α\alpha or the falls in the rejection region. These steps ensure a structured, objective process for , with α\alpha conventionally set at 0.05 to balance the risk of erroneous conclusions. A key aspect of hypothesis testing involves understanding potential errors: a Type I error occurs when the null hypothesis is incorrectly rejected (false positive), with its probability denoted by α\alpha, while a Type II error occurs when a false null hypothesis is not rejected (false negative), with probability β\beta. The significance level α\alpha directly controls the rate of Type I errors, safeguarding against overzealous rejection of the in scientific inquiry. The power of a test, defined as 1−β1 - \beta, measures its ability to detect a true effect when the holds, and is influenced by sample size, , and α\alpha. For large sample sizes, the provides the theoretical foundation for approximating the of the as normal, enabling the use of standard statistical tables and procedures even when the underlying distribution is unknown or non-normal.

Null and Alternative Hypotheses

In hypothesis testing, the , denoted H0H_0, represents the default assumption of no effect, no difference, or a specific in the . For instance, it might state that the equals a particular value, such as H0:μ=μ0H_0: \mu = \mu_0. This formulation originates from Ronald Fisher's development of significance testing, where the serves as a precise, testable benchmark against which observed data are evaluated. The , denoted H1H_1 or HaH_a, is the statement that contradicts the null and embodies the research claim or effect being investigated; it can be non-directional (indicating any difference) or directional (specifying a particular direction of effect). Introduced by and as a complement to Fisher's null framework, the alternative hypothesis guides the design of tests by specifying what deviation from the null is of interest. Hypotheses are classified as simple or composite based on whether they fully specify the of the data. A simple completely defines the distribution, such as H0:θ=θ0H_0: \theta = \theta_0 where the is fixed to a single value; the is conventionally simple to enable exact calculation of probabilities under it. In contrast, the is often composite, encompassing a range of values, like H1:θ≠θ0H_1: \theta \neq \theta_0, which includes multiple possible distributions. The must be falsifiable, meaning it can be disproven by data, but it is never proven true—only potentially supported by failure to reject it. This places the burden of proof on that rejects H0H_0 in favor of H1H_1, aligning with scientific principles of toward unproven effects. Standard notation distinguishes these as H0:θ=θ0H_0: \theta = \theta_0 for the null and H1:θ≠θ0H_1: \theta \neq \theta_0, θ>θ0\theta > \theta_0, or θ<θ0\theta < \theta_0 for the alternative, depending on the directionality.

Test Types

One-Tailed Tests

A one-tailed test, also referred to as a one-sided test, is a method of hypothesis testing where the alternative hypothesis posits a directional effect, specifically that a population parameter differs from the null value in one specified direction, such as H1:μ>μ0H_1: \mu > \mu_0 or H1:μ<μ0H_1: \mu < \mu_0. This contrasts with non-directional alternatives by focusing exclusively on deviations in the anticipated direction, which is established a priori based on theoretical or empirical grounds. For instance, in evaluating a new treatment, the hypothesis might test whether its efficacy exceeds a standard threshold, ignoring the possibility of inferiority. In a one-tailed test, the entire significance level α\alpha is allocated to the rejection region in one tail of the sampling distribution, rather than splitting it across both tails. For a test statistic ZZ that follows the standard normal distribution under the null hypothesis, rejection occurs if Z>zαZ > z_\alpha for an upper-tailed test (testing for a greater-than effect) or if Z<−zαZ < -z_\alpha for a lower-tailed test (testing for a less-than effect), where zαz_\alpha is the critical value such that the probability of exceeding it in the tail is α\alpha (e.g., z0.05=1.645z_{0.05} = 1.645). This asymmetric allocation concentrates the Type I error risk in the direction of interest. One-tailed tests provide a key advantage in statistical power: for a fixed α\alpha, they are more sensitive to detecting true effects in the specified direction than two-tailed tests, as the full α\alpha is not divided. However, this comes at the cost of zero power to detect effects in the opposite direction, potentially leading to overlooked bidirectional or contrary findings that could be scientifically relevant. Additionally, non-rejection of the null can be harder to interpret, as it may reflect either no effect or an effect in the untested direction. These tests are appropriate when prior evidence or theory strongly indicates a unidirectional effect, such as in non-inferiority trials where only improvement beyond a benchmark is of interest (e.g., a drug expected to increase a clinical parameter). They should be reserved for contexts where collective scientific or practical interest aligns exclusively with one direction, avoiding misuse driven by individual predictions.

Two-Tailed Tests

A two-tailed test is a type of hypothesis test designed to assess a non-directional alternative hypothesis, typically stated as H1:μ≠μ0H_1: \mu \neq \mu_0, where the goal is to determine if the population parameter differs from a specified value without assuming the direction of the difference. In such tests, the total significance level α\alpha is divided equally between the two tails of the underlying probability distribution, with α/2\alpha/2 allocated to each tail to form symmetric rejection regions. For a test statistic ZZ that follows a standard normal distribution under the , rejection of H0H_0 occurs if the absolute value of the statistic exceeds the critical value, as given by the rule: ∣Z∣>zα/2|Z| > z_{\alpha/2} where zα/2z_{\alpha/2} denotes the (1−α/2)(1 - \alpha/2)-th of the standard normal distribution. Two-tailed tests offer the advantage of detecting deviations from the in either direction, making them suitable when no prior directional assumption about the effect is justified. A key disadvantage is their reduced statistical power relative to one-tailed tests for detecting a specific directional effect, since the significance level is split across both tails. These tests are particularly appropriate in scenarios lacking strong theoretical or empirical guidance on the effect's direction, such as evaluating whether the of a differs from a hypothesized value in any way.

Examples and Illustrations

Coin Flipping Example

To illustrate the distinction between one-tailed and two-tailed tests, consider a classic scenario involving , which follows a . Suppose we want to test whether a is fair, meaning the probability of heads p=0.5p = 0.5. The is H0:p=0.5H_0: p = 0.5. For a two-tailed test, the alternative hypothesis is H1:p≠0.5H_1: p \neq 0.5, allowing detection of bias in either direction (more heads or more tails). For a one-tailed test, we might specify suspicion of bias toward heads, so H1:p>0.5H_1: p > 0.5, focusing only on excess heads. Imagine flipping the 100 times (n=100n = 100). Under H0H_0, we expect 50 heads on average. Suppose the observed outcome is 65 heads, an extreme result that might suggest bias. To assess this, we use the normal approximation to the , valid for large nn like 100, where the number of heads XX is approximately normal with np=50np = 50 and variance np(1−p)=25np(1-p) = 25, so standard deviation 25=5\sqrt{25} = 5
Add your contribution
Related Hubs
User Avatar
No comments yet.