Recent from talks
Nothing was collected or created yet.
Statistical hypothesis test
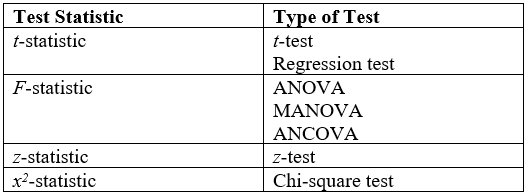
View on Wikipedia| Test Statistic | Type of Test |
|---|---|
| t-statistic | t-test Regression test |
| F-statistic | ANOVA MANOVA ANCOVA |
| z-statistic | z-test |
| x2-statistic | Chi-square test |
| Some of the most common test statistics and their corresponding statistical tests or models. | |
A statistical hypothesis test is a method of statistical inference used to decide whether the data provide sufficient evidence to reject a particular hypothesis. A statistical hypothesis test typically involves a calculation of a test statistic. Then a decision is made, either by comparing the test statistic to a critical value or equivalently by evaluating a p-value computed from the test statistic. Roughly 100 specialized statistical tests are in use and noteworthy.[1][2]
History
[edit]While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710),[3] followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see § Human sex ratio.
Choice of null hypothesis
[edit]Paul Meehl has argued that the epistemological importance of the choice of null hypothesis has gone largely unacknowledged. When the null hypothesis is predicted by theory, a more precise experiment will be a more severe test of the underlying theory. When the null hypothesis defaults to "no difference" or "no effect", a more precise experiment is a less severe test of the theory that motivated performing the experiment.[4] An examination of the origins of the latter practice may therefore be useful:
1778: Pierre Laplace compares the birthrates of boys and girls in multiple European cities. He states: "it is natural to conclude that these possibilities are very nearly in the same ratio". Thus, the null hypothesis in this case that the birthrates of boys and girls should be equal given "conventional wisdom".[5]
1900: Karl Pearson develops the chi squared test to determine "whether a given form of frequency curve will effectively describe the samples drawn from a given population." Thus the null hypothesis is that a population is described by some distribution predicted by theory. He uses as an example the numbers of five and sixes in the Weldon dice throw data.[6]
1904: Karl Pearson develops the concept of "contingency" in order to determine whether outcomes are independent of a given categorical factor. Here the null hypothesis is by default that two things are unrelated (e.g. scar formation and death rates from smallpox).[7] The null hypothesis in this case is no longer predicted by theory or conventional wisdom, but is instead the principle of indifference that led Fisher and others to dismiss the use of "inverse probabilities".[8]
Modern origins and early controversy
[edit]Modern significance testing is largely the product of Karl Pearson (p-value, Pearson's chi-squared test), William Sealy Gosset (Student's t-distribution), and Ronald Fisher ("null hypothesis", analysis of variance, "significance test"), while hypothesis testing was developed by Jerzy Neyman and Egon Pearson (son of Karl). Ronald Fisher began his life in statistics as a Bayesian (Zabell 1992), but Fisher soon grew disenchanted with the subjectivity involved (namely use of the principle of indifference when determining prior probabilities), and sought to provide a more "objective" approach to inductive inference.[9]
Fisher emphasized rigorous experimental design and methods to extract a result from few samples assuming Gaussian distributions. Neyman (who teamed with the younger Pearson) emphasized mathematical rigor and methods to obtain more results from many samples and a wider range of distributions. Modern hypothesis testing is an inconsistent hybrid of the Fisher vs Neyman/Pearson formulation, methods and terminology developed in the early 20th century.
Fisher popularized the "significance test". He required a null-hypothesis (corresponding to a population frequency distribution) and a sample. His (now familiar) calculations determined whether to reject the null-hypothesis or not. Significance testing did not utilize an alternative hypothesis so there was no concept of a Type II error (false negative).
The p-value was devised as an informal, but objective, index meant to help a researcher determine (based on other knowledge) whether to modify future experiments or strengthen one's faith in the null hypothesis.[10] Hypothesis testing (and Type I/II errors) was devised by Neyman and Pearson as a more objective alternative to Fisher's p-value, also meant to determine researcher behaviour, but without requiring any inductive inference by the researcher.[11][12]
Neyman & Pearson considered a different problem to Fisher (which they called "hypothesis testing"). They initially considered two simple hypotheses (both with frequency distributions). They calculated two probabilities and typically selected the hypothesis associated with the higher probability (the hypothesis more likely to have generated the sample). Their method always selected a hypothesis. It also allowed the calculation of both types of error probabilities.
Fisher and Neyman/Pearson clashed bitterly. Neyman/Pearson considered their formulation to be an improved generalization of significance testing (the defining paper[11] was abstract; Mathematicians have generalized and refined the theory for decades[13]). Fisher thought that it was not applicable to scientific research because often, during the course of the experiment, it is discovered that the initial assumptions about the null hypothesis are questionable due to unexpected sources of error. He believed that the use of rigid reject/accept decisions based on models formulated before data is collected was incompatible with this common scenario faced by scientists and attempts to apply this method to scientific research would lead to mass confusion.[14]
The dispute between Fisher and Neyman–Pearson was waged on philosophical grounds, characterized by a philosopher as a dispute over the proper role of models in statistical inference.[15]
Events intervened: Neyman accepted a position in the University of California, Berkeley in 1938, breaking his partnership with Pearson and separating the disputants (who had occupied the same building). World War II provided an intermission in the debate. The dispute between Fisher and Neyman terminated (unresolved after 27 years) with Fisher's death in 1962. Neyman wrote a well-regarded eulogy.[16] Some of Neyman's later publications reported p-values and significance levels.[17]
Null hypothesis significance testing (NHST)
[edit]The modern version of hypothesis testing is generally called the null hypothesis significance testing (NHST)[18] and is a hybrid of the Fisher approach with the Neyman-Pearson approach. In 2000, Raymond S. Nickerson wrote an article stating that NHST was (at the time) "arguably the most widely used method of analysis of data collected in psychological experiments and has been so for about 70 years" and that it was at the same time "very controversial".[18]
This fusion resulted from confusion by writers of statistical textbooks (as predicted by Fisher) beginning in the 1940s[19] (but signal detection, for example, still uses the Neyman/Pearson formulation). Great conceptual differences and many caveats in addition to those mentioned above were ignored. Neyman and Pearson provided the stronger terminology, the more rigorous mathematics and the more consistent philosophy, but the subject taught today in introductory statistics has more similarities with Fisher's method than theirs.[20]
Sometime around 1940,[19] authors of statistical text books began combining the two approaches by using the p-value in place of the test statistic (or data) to test against the Neyman–Pearson "significance level".
| # | Fisher's null hypothesis testing | Neyman–Pearson decision theory |
|---|---|---|
| 1 | Set up a statistical null hypothesis. The null need not be a nil hypothesis (i.e., zero difference). | Set up two statistical hypotheses, H1 and H2, and decide about α, β, and sample size before the experiment, based on subjective cost-benefit considerations. These define a rejection region for each hypothesis. |
| 2 | Report the exact level of significance (e.g. p = 0.051 or p = 0.049). Do not refer to "accepting" or "rejecting" hypotheses. If the result is "not significant", draw no conclusions and make no decisions, but suspend judgement until further data is available. | If the data falls into the rejection region of H1, accept H2; otherwise accept H1. Accepting a hypothesis does not mean that you believe in it, but only that you act as if it were true. |
| 3 | Use this procedure only if little is known about the problem at hand, and only to draw provisional conclusions in the context of an attempt to understand the experimental situation. | The usefulness of the procedure is limited among others to situations where you have a disjunction of hypotheses (e.g. either μ1 = 8 or μ2 = 10 is true) and where you can make meaningful cost-benefit trade-offs for choosing alpha and beta. |
Philosophy
[edit]Hypothesis testing and philosophy intersect. Inferential statistics, which includes hypothesis testing, is applied probability. Both probability and its application are intertwined with philosophy. Philosopher David Hume wrote, "All knowledge degenerates into probability." Competing practical definitions of probability reflect philosophical differences. The most common application of hypothesis testing is in the scientific interpretation of experimental data, which is naturally studied by the philosophy of science.
Fisher and Neyman opposed the subjectivity of probability. Their views contributed to the objective definitions. The core of their historical disagreement was philosophical.
Many of the philosophical criticisms of hypothesis testing are discussed by statisticians in other contexts, particularly correlation does not imply causation and the design of experiments. Hypothesis testing is of continuing interest to philosophers.[15][21]
Education
[edit]Statistics is increasingly being taught in schools with hypothesis testing being one of the elements taught.[22][23] Many conclusions reported in the popular press (political opinion polls to medical studies) are based on statistics. Some writers have stated that statistical analysis of this kind allows for thinking clearly about problems involving mass data, as well as the effective reporting of trends and inferences from said data, but caution that writers for a broad public should have a solid understanding of the field in order to use the terms and concepts correctly.[24][25] An introductory college statistics class places much emphasis on hypothesis testing – perhaps half of the course. Such fields as literature and divinity now include findings based on statistical analysis (see the Bible Analyzer). An introductory statistics class teaches hypothesis testing as a cookbook process. Hypothesis testing is also taught at the postgraduate level. Statisticians learn how to create good statistical test procedures (like z, Student's t, F and chi-squared). Statistical hypothesis testing is considered a mature area within statistics,[26] but a limited amount of development continues.
An academic study states that the cookbook method of teaching introductory statistics leaves no time for history, philosophy or controversy. Hypothesis testing has been taught as received unified method. Surveys showed that graduates of the class were filled with philosophical misconceptions (on all aspects of statistical inference) that persisted among instructors.[27] While the problem was addressed more than a decade ago,[28] and calls for educational reform continue,[29] students still graduate from statistics classes holding fundamental misconceptions about hypothesis testing.[30] Ideas for improving the teaching of hypothesis testing include encouraging students to search for statistical errors in published papers, teaching the history of statistics and emphasizing the controversy in a generally dry subject.[31]
Raymond S. Nickerson commented:
The debate about NHST has its roots in unresolved disagreements among major contributors to the development of theories of inferential statistics on which modern approaches are based. Gigerenzer et al. (1989) have reviewed in considerable detail the controversy between R. A. Fisher on the one hand and Jerzy Neyman and Egon Pearson on the other as well as the disagreements between both of these views and those of the followers of Thomas Bayes. They noted the remarkable fact that little hint of the historical and ongoing controversy is to be found in most textbooks that are used to teach NHST to its potential users. The resulting lack of an accurate historical perspective and understanding of the complexity and sometimes controversial philosophical foundations of various approaches to statistical inference may go a long way toward explaining the apparent ease with which statistical tests are misused and misinterpreted.[18]
Performing a frequentist hypothesis test in practice
[edit]The typical steps involved in performing a frequentist hypothesis test in practice are:
- Define a hypothesis (claim which is testable using data).
- Select a relevant statistical test with associated test statistic T.
- Derive the distribution of the test statistic under the null hypothesis from the assumptions. In standard cases this will be a well-known result. For example, the test statistic might follow a Student's t distribution with known degrees of freedom, or a normal distribution with known mean and variance.
- Select a significance level (α), the maximum acceptable false positive rate. Common values are 5% and 1%.
- Compute from the observations the observed value tobs of the test statistic T.
- Decide to either reject the null hypothesis in favor of the alternative or not reject it. The Neyman-Pearson decision rule is to reject the null hypothesis H0 if the observed value tobs is in the critical region, and not to reject the null hypothesis otherwise.[32]
Practical example
[edit]The difference in the two processes applied to the radioactive suitcase example (below):
- "The Geiger-counter reading is 10. The limit is 9. Check the suitcase."
- "The Geiger-counter reading is high; 97% of safe suitcases have lower readings. The limit is 95%. Check the suitcase."
The former report is adequate, the latter gives a more detailed explanation of the data and the reason why the suitcase is being checked.
Not rejecting the null hypothesis does not mean the null hypothesis is "accepted" per se (though Neyman and Pearson used that word in their original writings; see the Interpretation section).
The processes described here are perfectly adequate for computation. They seriously neglect the design of experiments considerations.[33][34]
It is particularly critical that appropriate sample sizes be estimated before conducting the experiment.
The phrase "test of significance" was coined by statistician Ronald Fisher.[35]
Interpretation
[edit]When the null hypothesis is true and statistical assumptions are met, the probability that the p-value will be less than or equal to the significance level is at most . This ensures that the hypothesis test maintains its specified false positive rate (provided that statistical assumptions are met).[36]
The p-value is the probability that a test statistic which is at least as extreme as the one obtained would occur under the null hypothesis. At a significance level of 0.05, a fair coin would be expected to (incorrectly) reject the null hypothesis (that it is fair) in 1 out of 20 tests on average. The p-value does not provide the probability that either the null hypothesis or its opposite is correct (a common source of confusion).[37]
If the p-value is less than the chosen significance threshold (equivalently, if the observed test statistic is in the critical region), then we say the null hypothesis is rejected at the chosen level of significance. If the p-value is not less than the chosen significance threshold (equivalently, if the observed test statistic is outside the critical region), then the null hypothesis is not rejected at the chosen level of significance.
In the "lady tasting tea" example (below), Fisher required the lady to properly categorize all of the cups of tea to justify the conclusion that the result was unlikely to result from chance. His test revealed that if the lady was effectively guessing at random (the null hypothesis), there was a 1.4% chance that the observed results (perfectly ordered tea) would occur.
Use and importance
[edit]Statistics are helpful in analyzing most collections of data. This is equally true of hypothesis testing which can justify conclusions even when no scientific theory exists. In the Lady tasting tea example, it was "obvious" that no difference existed between (milk poured into tea) and (tea poured into milk). The data contradicted the "obvious".
Real world applications of hypothesis testing include:[38]
- Testing whether more men than women suffer from nightmares
- Establishing authorship of documents
- Evaluating the effect of the full moon on behavior
- Determining the range at which a bat can detect an insect by echo
- Deciding whether hospital carpeting results in more infections
- Selecting the best means to stop smoking
- Checking whether bumper stickers reflect car owner behavior
- Testing the claims of handwriting analysts
Statistical hypothesis testing plays an important role in the whole of statistics and in statistical inference. For example, Lehmann (1992) in a review of the fundamental paper by Neyman and Pearson (1933) says: "Nevertheless, despite their shortcomings, the new paradigm formulated in the 1933 paper, and the many developments carried out within its framework continue to play a central role in both the theory and practice of statistics and can be expected to do so in the foreseeable future".
Significance testing has been the favored statistical tool in some experimental social sciences (over 90% of articles in the Journal of Applied Psychology during the early 1990s).[39] Other fields have favored the estimation of parameters (e.g. effect size). Significance testing is used as a substitute for the traditional comparison of predicted value and experimental result at the core of the scientific method. When theory is only capable of predicting the sign of a relationship, a directional (one-sided) hypothesis test can be configured so that only a statistically significant result supports theory. This form of theory appraisal is the most heavily criticized application of hypothesis testing.
Cautions
[edit]"If the government required statistical procedures to carry warning labels like those on drugs, most inference methods would have long labels indeed."[40] This caution applies to hypothesis tests and alternatives to them.
The successful hypothesis test is associated with a probability and a type-I error rate. The conclusion might be wrong.
The conclusion of the test is only as solid as the sample upon which it is based. The design of the experiment is critical. A number of unexpected effects have been observed including:
- The clever Hans effect. A horse appeared to be capable of doing simple arithmetic.
- The Hawthorne effect. Industrial workers were more productive in better illumination, and most productive in worse.
- The placebo effect. Pills with no medically active ingredients were remarkably effective.
A statistical analysis of misleading data produces misleading conclusions. The issue of data quality can be more subtle. In forecasting for example, there is no agreement on a measure of forecast accuracy. In the absence of a consensus measurement, no decision based on measurements will be without controversy.
Publication bias: Statistically nonsignificant results may be less likely to be published, which can bias the literature.
Multiple testing: When multiple true null hypothesis tests are conducted at once without adjustment, the overall probability of Type I error is higher than the nominal alpha level.[41]
Those making critical decisions based on the results of a hypothesis test are prudent to look at the details rather than the conclusion alone. In the physical sciences most results are fully accepted only when independently confirmed. The general advice concerning statistics is, "Figures never lie, but liars figure" (anonymous).
Definition of terms
[edit]The following definitions are mainly based on the exposition in the book by Lehmann and Romano:[36]
- Statistical hypothesis: A statement about the parameters describing a population (not a sample).
- Test statistic: A value calculated from a sample without any unknown parameters, often to summarize the sample for comparison purposes.
- Simple hypothesis: Any hypothesis which specifies the population distribution completely.
- Composite hypothesis: Any hypothesis which does not specify the population distribution completely.
- Null hypothesis (H0)
- Positive data: Data that enable the investigator to reject a null hypothesis.
- Alternative hypothesis (H1)

- Critical values of a statistical test are the boundaries of the acceptance region of the test.[42] The acceptance region is the set of values of the test statistic for which the null hypothesis is not rejected. Depending on the shape of the acceptance region, there can be one or more than one critical value.
- Region of rejection / Critical region: The set of values of the test statistic for which the null hypothesis is rejected.
- Power of a test (1 − β)
- Size: For simple hypotheses, this is the test's probability of incorrectly rejecting the null hypothesis. The false positive rate. For composite hypotheses this is the supremum of the probability of rejecting the null hypothesis over all cases covered by the null hypothesis. The complement of the false positive rate is termed specificity in biostatistics. ("This is a specific test. Because the result is positive, we can confidently say that the patient has the condition.") See sensitivity and specificity and type I and type II errors for exhaustive definitions.
- Significance level of a test (α)
- p-value
- Statistical significance test: A predecessor to the statistical hypothesis test (see the Origins section). An experimental result was said to be statistically significant if a sample was sufficiently inconsistent with the (null) hypothesis. This was variously considered common sense, a pragmatic heuristic for identifying meaningful experimental results, a convention establishing a threshold of statistical evidence or a method for drawing conclusions from data. The statistical hypothesis test added mathematical rigor and philosophical consistency to the concept by making the alternative hypothesis explicit. The term is loosely used for the modern version which is now part of statistical hypothesis testing.
- Conservative test: A test is conservative if, when constructed for a given nominal significance level, the true probability of incorrectly rejecting the null hypothesis is never greater than the nominal level.
- Exact test
A statistical hypothesis test compares a test statistic (z or t for examples) to a threshold. The test statistic (the formula found in the table below) is based on optimality. For a fixed level of Type I error rate, use of these statistics minimizes Type II error rates (equivalent to maximizing power). The following terms describe tests in terms of such optimality:
- Most powerful test: For a given size or significance level, the test with the greatest power (probability of rejection) for a given value of the parameter(s) being tested, contained in the alternative hypothesis.
- Uniformly most powerful test (UMP)
Nonparametric bootstrap hypothesis testing
[edit]Bootstrap-based resampling methods can be used for null hypothesis testing. A bootstrap creates numerous simulated samples by randomly resampling (with replacement) the original, combined sample data, assuming the null hypothesis is correct. The bootstrap is very versatile as it is distribution-free and it does not rely on restrictive parametric assumptions, but rather on empirical approximate methods with asymptotic guarantees. Traditional parametric hypothesis tests are more computationally efficient but make stronger structural assumptions. In situations where computing the probability of the test statistic under the null hypothesis is hard or impossible (due to perhaps inconvenience or lack of knowledge of the underlying distribution), the bootstrap offers a viable method for statistical inference.[43][44][45][46]
Examples
[edit]Human sex ratio
[edit]The earliest use of statistical hypothesis testing is generally credited to the question of whether male and female births are equally likely (null hypothesis), which was addressed in the 1700s by John Arbuthnot (1710),[47] and later by Pierre-Simon Laplace (1770s).[48]
Arbuthnot examined birth records in London for each of the 82 years from 1629 to 1710, and applied the sign test, a simple non-parametric test.[49][50][51] In every year, the number of males born in London exceeded the number of females. Considering more male or more female births as equally likely, the probability of the observed outcome is 0.582, or about 1 in 4,836,000,000,000,000,000,000,000; in modern terms, this is the p-value. Arbuthnot concluded that this is too small to be due to chance and must instead be due to divine providence: "From whence it follows, that it is Art, not Chance, that governs." In modern terms, he rejected the null hypothesis of equally likely male and female births at the p = 1/282 significance level.
Laplace considered the statistics of almost half a million births. The statistics showed an excess of boys compared to girls.[5] He concluded by calculation of a p-value that the excess was a real, but unexplained, effect.[52]
Lady tasting tea
[edit]In a famous example of hypothesis testing, known as the Lady tasting tea,[53] Dr. Muriel Bristol, a colleague of Fisher, claimed to be able to tell whether the tea or the milk was added first to a cup. Fisher proposed to give her eight cups, four of each variety, in random order. One could then ask what the probability was for her getting the number she got correct, but just by chance. The null hypothesis was that the Lady had no such ability. The test statistic was a simple count of the number of successes in selecting the 4 cups. The critical region was the single case of 4 successes of 4 possible based on a conventional probability criterion (< 5%). A pattern of 4 successes corresponds to 1 out of 70 possible combinations (p≈ 1.4%). Fisher asserted that no alternative hypothesis was (ever) required. The lady correctly identified every cup,[54] which would be considered a statistically significant result.
Courtroom trial
[edit]A statistical test procedure is comparable to a criminal trial; a defendant is considered not guilty as long as his or her guilt is not proven. The prosecutor tries to prove the guilt of the defendant. Only when there is enough evidence for the prosecution is the defendant convicted.
In the start of the procedure, there are two hypotheses : "the defendant is not guilty", and : "the defendant is guilty". The first one, , is called the null hypothesis. The second one, , is called the alternative hypothesis. It is the alternative hypothesis that one hopes to support.
The hypothesis of innocence is rejected only when an error is very unlikely, because one does not want to convict an innocent defendant. Such an error is called error of the first kind (i.e., the conviction of an innocent person), and the occurrence of this error is controlled to be rare. As a consequence of this asymmetric behaviour, an error of the second kind (acquitting a person who committed the crime), is more common.
| H0 is true Truly not guilty |
H1 is true Truly guilty | |
|---|---|---|
| Do not reject the null hypothesis Acquittal |
Right decision | Wrong decision Type II Error |
| Reject null hypothesis Conviction |
Wrong decision Type I Error |
Right decision |
A criminal trial can be regarded as either or both of two decision processes: guilty vs not guilty or evidence vs a threshold ("beyond a reasonable doubt"). In one view, the defendant is judged; in the other view the performance of the prosecution (which bears the burden of proof) is judged. A hypothesis test can be regarded as either a judgment of a hypothesis or as a judgment of evidence.
Clairvoyant card game
[edit]A person (the subject) is tested for clairvoyance. They are shown the back face of a randomly chosen playing card 25 times and asked which of the four suits it belongs to. The number of hits, or correct answers, is called X.
As we try to find evidence of their clairvoyance, for the time being the null hypothesis is that the person is not clairvoyant.[55] The alternative is: the person is (more or less) clairvoyant.
If the null hypothesis is valid, the only thing the test person can do is guess. For every card, the probability (relative frequency) of any single suit appearing is 1/4. If the alternative is valid, the test subject will predict the suit correctly with probability greater than 1/4. We will call the probability of guessing correctly p. The hypotheses, then, are:
- null hypothesis (just guessing)
and
- alternative hypothesis (true clairvoyant).
When the test subject correctly predicts all 25 cards, we will consider them clairvoyant, and reject the null hypothesis. Thus also with 24 or 23 hits. With only 5 or 6 hits, on the other hand, there is no cause to consider them so. But what about 12 hits, or 17 hits? What is the critical number, c, of hits, at which point we consider the subject to be clairvoyant? How do we determine the critical value c? With the choice c=25 (i.e. we only accept clairvoyance when all cards are predicted correctly) we're more critical than with c=10. In the first case almost no test subjects will be recognized to be clairvoyant, in the second case, a certain number will pass the test. In practice, one decides how critical one will be. That is, one decides how often one accepts an error of the first kind – a false positive, or Type I error. With c = 25 the probability of such an error is:
- ,
and hence, very small. The probability of a false positive is the probability of randomly guessing correctly all 25 times.
Being less critical, with c = 10, gives:
- .
Thus, c = 10 yields a much greater probability of false positive.
Before the test is actually performed, the maximum acceptable probability of a Type I error (α) is determined. Typically, values in the range of 1% to 5% are selected. (If the maximum acceptable error rate is zero, an infinite number of correct guesses is required.) Depending on this Type 1 error rate, the critical value c is calculated. For example, if we select an error rate of 1%, c is calculated thus:
- .
From all the numbers c, with this property, we choose the smallest, in order to minimize the probability of a Type II error, a false negative. For the above example, we select: .
Variations and sub-classes
[edit]Statistical hypothesis testing is a key technique of both frequentist inference and Bayesian inference, although the two types of inference have notable differences. Statistical hypothesis tests define a procedure that controls (fixes) the probability of incorrectly deciding that a default position (null hypothesis) is incorrect. The procedure is based on how likely it would be for a set of observations to occur if the null hypothesis were true. This probability of making an incorrect decision is not the probability that the null hypothesis is true, nor whether any specific alternative hypothesis is true. This contrasts with other possible techniques of decision theory in which the null and alternative hypothesis are treated on a more equal basis.
One naïve Bayesian approach to hypothesis testing is to base decisions on the posterior probability,[56][57] but this fails when comparing point and continuous hypotheses. Other approaches to decision making, such as Bayesian decision theory, attempt to balance the consequences of incorrect decisions across all possibilities, rather than concentrating on a single null hypothesis. A number of other approaches to reaching a decision based on data are available via decision theory and optimal decisions, some of which have desirable properties. Hypothesis testing, though, is a dominant approach to data analysis in many fields of science. Extensions to the theory of hypothesis testing include the study of the power of tests, i.e. the probability of correctly rejecting the null hypothesis given that it is false. Such considerations can be used for the purpose of sample size determination prior to the collection of data.
Neyman–Pearson hypothesis testing
[edit]An example of Neyman–Pearson hypothesis testing (or null hypothesis statistical significance testing) can be made by a change to the radioactive suitcase example. If the "suitcase" is actually a shielded container for the transportation of radioactive material, then a test might be used to select among three hypotheses: no radioactive source present, one present, two (all) present. The test could be required for safety, with actions required in each case. The Neyman–Pearson lemma of hypothesis testing says that a good criterion for the selection of hypotheses is the ratio of their probabilities (a likelihood ratio). A simple method of solution is to select the hypothesis with the highest probability for the Geiger counts observed. The typical result matches intuition: few counts imply no source, many counts imply two sources and intermediate counts imply one source. Notice also that usually there are problems for proving a negative. Null hypotheses should be at least falsifiable.
Neyman–Pearson theory can accommodate both prior probabilities and the costs of actions resulting from decisions.[58] The former allows each test to consider the results of earlier tests (unlike Fisher's significance tests). The latter allows the consideration of economic issues (for example) as well as probabilities. A likelihood ratio remains a good criterion for selecting among hypotheses.
The two forms of hypothesis testing are based on different problem formulations. The original test is analogous to a true/false question; the Neyman–Pearson test is more like multiple choice. In the view of Tukey[59] the former produces a conclusion on the basis of only strong evidence while the latter produces a decision on the basis of available evidence. While the two tests seem quite different both mathematically and philosophically, later developments lead to the opposite claim. Consider many tiny radioactive sources. The hypotheses become 0,1,2,3... grains of radioactive sand. There is little distinction between none or some radiation (Fisher) and 0 grains of radioactive sand versus all of the alternatives (Neyman–Pearson). The major Neyman–Pearson paper of 1933[11] also considered composite hypotheses (ones whose distribution includes an unknown parameter). An example proved the optimality of the (Student's) t-test, "there can be no better test for the hypothesis under consideration" (p 321). Neyman–Pearson theory was proving the optimality of Fisherian methods from its inception.
Fisher's significance testing has proven a popular flexible statistical tool in application with little mathematical growth potential. Neyman–Pearson hypothesis testing is claimed as a pillar of mathematical statistics,[60] creating a new paradigm for the field. It also stimulated new applications in statistical process control, detection theory, decision theory and game theory. Both formulations have been successful, but the successes have been of a different character.
The dispute over formulations is unresolved. Science primarily uses Fisher's (slightly modified) formulation as taught in introductory statistics. Statisticians study Neyman–Pearson theory in graduate school. Mathematicians are proud of uniting the formulations. Philosophers consider them separately. Learned opinions deem the formulations variously competitive (Fisher vs Neyman), incompatible[9] or complementary.[13] The dispute has become more complex since Bayesian inference has achieved respectability.
The terminology is inconsistent. Hypothesis testing can mean any mixture of two formulations that both changed with time. Any discussion of significance testing vs hypothesis testing is doubly vulnerable to confusion.
Fisher thought that hypothesis testing was a useful strategy for performing industrial quality control, however, he strongly disagreed that hypothesis testing could be useful for scientists.[10] Hypothesis testing provides a means of finding test statistics used in significance testing.[13] The concept of power is useful in explaining the consequences of adjusting the significance level and is heavily used in sample size determination. The two methods remain philosophically distinct.[15] They usually (but not always) produce the same mathematical answer. The preferred answer is context dependent.[13] While the existing merger of Fisher and Neyman–Pearson theories has been heavily criticized, modifying the merger to achieve Bayesian goals has been considered.[61]
Criticism
[edit]Much of the criticisms of statistical hypothesis testing can be summarized by the following issues:
- The interpretation of a p-value is dependent upon stopping rule and definition of multiple comparison. The former often changes during the course of a study and the latter is unavoidably ambiguous. (i.e. "p values depend on both the (data) observed and on the other possible (data) that might have been observed but weren't").[62]
- Confusion resulting (in part) from combining the methods of Fisher and Neyman–Pearson which are conceptually distinct.[59]
- Emphasis on statistical significance to the exclusion of estimation and confirmation by repeated experiments.[63]
- Rigidly requiring statistical significance as a criterion for publication, resulting in publication bias.[64] Most of the criticism is indirect. Rather than being wrong, statistical hypothesis testing is misunderstood, overused and misused.
- When used to detect whether a difference exists between groups, a paradox arises. As improvements are made to experimental design (e.g. increased precision of measurement and sample size), the test becomes more lenient. Unless one accepts the absurd assumption that all sources of noise in the data cancel out completely, the chance of finding statistical significance in either direction approaches 100%.[65] However, this absurd assumption that the mean difference between two groups cannot be zero implies that the data cannot be independent and identically distributed (i.i.d.) because the expected difference between any two subgroups of i.i.d. random variates is zero; therefore, the i.i.d. assumption is also absurd.
- Layers of philosophical concerns. The probability of statistical significance is a function of decisions made by experimenters/analysts.[66] If the decisions are based on convention they are termed arbitrary or mindless[67] while those not so based may be termed subjective. To minimize type II errors, large samples are recommended. In psychology practically all null hypotheses are claimed to be false for sufficiently large samples so "...it is usually nonsensical to perform an experiment with the sole aim of rejecting the null hypothesis."[68] "Statistically significant findings are often misleading" in psychology.[69] Statistical significance does not imply practical significance, and correlation does not imply causation. Casting doubt on the null hypothesis is thus far from directly supporting the research hypothesis.
- "[I]t does not tell us what we want to know".[70] Lists of dozens of complaints are available.[71][18][72]
Critics and supporters are largely in factual agreement regarding the characteristics of null hypothesis significance testing (NHST): While it can provide critical information, it is inadequate as the sole tool for statistical analysis. Successfully rejecting the null hypothesis may offer no support for the research hypothesis. The continuing controversy concerns the selection of the best statistical practices for the near-term future given the existing practices. However, adequate research design can minimize this issue. Critics would prefer to ban NHST completely, forcing a complete departure from those practices,[73] while supporters suggest a less absolute change.[citation needed]
Controversy over significance testing, and its effects on publication bias in particular, has produced several results. The American Psychological Association has strengthened its statistical reporting requirements after review,[74] medical journal publishers have recognized the obligation to publish some results that are not statistically significant to combat publication bias,[75] and a journal (Journal of Articles in Support of the Null Hypothesis) has been created to publish such results exclusively.[76] Textbooks have added some cautions,[77] and increased coverage of the tools necessary to estimate the size of the sample required to produce significant results. Few major organizations have abandoned use of significance tests although some have discussed doing so.[74] For instance, in 2023, the editors of the Journal of Physiology "strongly recommend the use of estimation methods for those publishing in The Journal" (meaning the magnitude of the effect size (to allow readers to judge whether a finding has practical, physiological, or clinical relevance) and confidence intervals to convey the precision of that estimate), saying "Ultimately, it is the physiological importance of the data that those publishing in The Journal of Physiology should be most concerned with, rather than the statistical significance."[78]
P-values are random variables[79]. Therefore, the decision of a statistical test is a random variable; to understand its stability, approaches including the following have been proposed:
- bootstrapping the "reproducibility probability" [80].
- Bootstrapping the sampling distribution of the p-values[81]
Alternatives
[edit]A unifying position of critics is that statistics should not lead to an accept-reject conclusion or decision, but to an estimated value with an interval estimate; this data-analysis philosophy is broadly referred to as estimation statistics. Estimation statistics can be accomplished with either frequentist[82] or Bayesian methods.[83][84]
Critics of significance testing have advocated basing inference less on p-values and more on confidence intervals for effect sizes for importance, prediction intervals for confidence, replications and extensions for replicability, meta-analyses for generality :.[85] But none of these suggested alternatives inherently produces a decision. Lehmann said that hypothesis testing theory can be presented in terms of conclusions/decisions, probabilities, or confidence intervals: "The distinction between the ... approaches is largely one of reporting and interpretation."[26]
Bayesian inference is one proposed alternative to significance testing. (Nickerson cited 10 sources suggesting it, including Rozeboom (1960)).[18] For example, Bayesian parameter estimation can provide rich information about the data from which researchers can draw inferences, while using uncertain priors that exert only minimal influence on the results when enough data is available. Psychologist John K. Kruschke has suggested Bayesian estimation as an alternative for the t-test[83] and has also contrasted Bayesian estimation for assessing null values with Bayesian model comparison for hypothesis testing.[84] Two competing models/hypotheses can be compared using Bayes factors.[86] Bayesian methods could be criticized for requiring information that is seldom available in the cases where significance testing is most heavily used. Neither the prior probabilities nor the probability distribution of the test statistic under the alternative hypothesis are often available in the social sciences.[18]
Advocates of a Bayesian approach sometimes claim that the goal of a researcher is most often to objectively assess the probability that a hypothesis is true based on the data they have collected.[87][88] Neither Fisher's significance testing, nor Neyman–Pearson hypothesis testing can provide this information, and do not claim to. The probability a hypothesis is true can only be derived from use of Bayes' Theorem, which was unsatisfactory to both the Fisher and Neyman–Pearson camps due to the explicit use of subjectivity in the form of the prior probability.[11][89] Fisher's strategy is to sidestep this with the p-value (an objective index based on the data alone) followed by inductive inference, while Neyman–Pearson devised their approach of inductive behaviour.
See also
[edit]- Statistics
- Behrens–Fisher problem
- Bootstrapping (statistics)
- Checking if a coin is fair
- Comparing means test decision tree
- Complete spatial randomness
- Counternull
- Falsifiability
- Fisher's method for combining independent tests of significance
- Granger causality
- Look-elsewhere effect
- Modifiable areal unit problem
- Modifiable temporal unit problem
- Multivariate hypothesis testing
- Omnibus test
- Dichotomous thinking
- Almost sure hypothesis testing
- Akaike information criterion
- Bayesian information criterion
- E-values
References
[edit]- ^ Lewis, Nancy D.; Lewis, Nigel Da Costa; Lewis, N. D. (2013). 100 Statistical Tests in R: What to Choose, how to Easily Calculate, with Over 300 Illustrations and Examples. Heather Hills Press. ISBN 978-1-4840-5299-0.
- ^ Kanji, Gopal K. (18 July 2006). 100 Statistical Tests. SAGE. ISBN 978-1-4462-2250-8.
- ^ Bellhouse, P. (2001), "John Arbuthnot", in Statisticians of the Centuries by C.C. Heyde and E. Seneta, Springer, pp. 39–42, ISBN 978-0-387-95329-8
- ^ Meehl, P (1990). "Appraising and Amending Theories: The Strategy of Lakatosian Defense and Two Principles That Warrant It" (PDF). Psychological Inquiry. 1 (2): 108–141. doi:10.1207/s15327965pli0102_1.
- ^ a b Laplace, P. (1778). "Mémoire sur les probabilités". Mémoires de l'Académie Royale des Sciences de Paris: 227–332. Reprinted in Laplace, P. (1878–1912). "Mémoire sur les probabilités (XIX, XX)". Oeuvres complètes de Laplace. Vol. 9. Gauthier-Villars. pp. 383–488. English translation: Laplace, P. (August 21, 2010). "Mémoire sur les probabilités" (PDF). Translated by Pulskam, Richard J. Archived from the original (PDF) on April 27, 2015.
- ^ Pearson, K (1900). "On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling" (PDF). The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 5 (50): 157–175. doi:10.1080/14786440009463897.
- ^ Pearson, K (1904). "On the Theory of Contingency and Its Relation to Association and Normal Correlation". Drapers' Company Research Memoirs Biometric Series. 1: 1–35.
- ^ Zabell, S (1989). "R. A. Fisher on the History of Inverse Probability". Statistical Science. 4 (3): 247–256. doi:10.1214/ss/1177012488. JSTOR 2245634.
- ^ a b Raymond Hubbard, M. J. Bayarri, P Values are not Error Probabilities Archived September 4, 2013, at the Wayback Machine. A working paper that explains the difference between Fisher's evidential p-value and the Neyman–Pearson Type I error rate .
- ^ a b Fisher, R (1955). "Statistical Methods and Scientific Induction" (PDF). Journal of the Royal Statistical Society, Series B. 17 (1): 69–78. doi:10.1111/j.2517-6161.1955.tb00180.x.
- ^ a b c d Neyman, J; Pearson, E. S. (January 1, 1933). "On the Problem of the most Efficient Tests of Statistical Hypotheses". Philosophical Transactions of the Royal Society A. 231 (694–706): 289–337. Bibcode:1933RSPTA.231..289N. doi:10.1098/rsta.1933.0009.
- ^ Goodman, S N (June 15, 1999). "Toward evidence-based medical statistics. 1: The P Value Fallacy". Ann Intern Med. 130 (12): 995–1004. doi:10.7326/0003-4819-130-12-199906150-00008. PMID 10383371. S2CID 7534212.
- ^ a b c d Lehmann, E. L. (December 1993). "The Fisher, Neyman–Pearson Theories of Testing Hypotheses: One Theory or Two?". Journal of the American Statistical Association. 88 (424): 1242–1249. doi:10.1080/01621459.1993.10476404.
- ^ Fisher, R N (1958). "The Nature of Probability" (PDF). Centennial Review. 2: 261–274.
We are quite in danger of sending highly trained and highly intelligent young men out into the world with tables of erroneous numbers under their arms, and with a dense fog in the place where their brains ought to be. In this century, of course, they will be working on guided missiles and advising the medical profession on the control of disease, and there is no limit to the extent to which they could impede every sort of national effort.
- ^ a b c Lenhard, Johannes (2006). "Models and Statistical Inference: The Controversy between Fisher and Neyman–Pearson". Br. J. Philos. Sci. 57: 69–91. doi:10.1093/bjps/axi152. S2CID 14136146.
- ^ Neyman, Jerzy (1967). "RA Fisher (1890—1962): An Appreciation". Science. 156 (3781): 1456–1460. Bibcode:1967Sci...156.1456N. doi:10.1126/science.156.3781.1456. PMID 17741062. S2CID 44708120.
- ^ Losavich, J. L.; Neyman, J.; Scott, E. L.; Wells, M. A. (1971). "Hypothetical explanations of the negative apparent effects of cloud seeding in the Whitetop Experiment". Proceedings of the National Academy of Sciences of the United States of America. 68 (11): 2643–2646. Bibcode:1971PNAS...68.2643L. doi:10.1073/pnas.68.11.2643. PMC 389491. PMID 16591951.
- ^ a b c d e f Nickerson, Raymond S. (2000). "Null Hypothesis Significance Tests: A Review of an Old and Continuing Controversy" (PDF). Psychological Methods. 5 (2): 241–301. doi:10.1037/1082-989X.5.2.241. PMID 10937333. S2CID 28340967. Archived from the original on 2000-02-23.
- ^ a b Halpin, P F; Stam, HJ (Winter 2006). "Inductive Inference or Inductive Behavior: Fisher and Neyman: Pearson Approaches to Statistical Testing in Psychological Research (1940–1960)". The American Journal of Psychology. 119 (4): 625–653. doi:10.2307/20445367. JSTOR 20445367. PMID 17286092.
- ^ Gigerenzer, Gerd; Zeno Swijtink; Theodore Porter; Lorraine Daston; John Beatty; Lorenz Kruger (1989). "Part 3: The Inference Experts". The Empire of Chance: How Probability Changed Science and Everyday Life. Cambridge University Press. pp. 70–122. ISBN 978-0-521-39838-1.
- ^ Mayo, D. G.; Spanos, A. (2006). "Severe Testing as a Basic Concept in a Neyman–Pearson Philosophy of Induction". The British Journal for the Philosophy of Science. 57 (2): 323–357. CiteSeerX 10.1.1.130.8131. doi:10.1093/bjps/axl003. S2CID 7176653.
- ^ Mathematics > High School: Statistics & Probability > Introduction Archived July 28, 2012, at archive.today Common Core State Standards Initiative (relates to USA students)
- ^ College Board Tests > AP: Subjects > Statistics The College Board (relates to USA students)
- ^ Huff, Darrell (1993). How to lie with statistics. New York: Norton. p. 8. ISBN 978-0-393-31072-6.'Statistical methods and statistical terms are necessary in reporting the mass data of social and economic trends, business conditions, "opinion" polls, the census. But without writers who use the words with honesty and readers who know what they mean, the result can only be semantic nonsense.'
- ^ Snedecor, George W.; Cochran, William G. (1967). Statistical Methods (6 ed.). Ames, Iowa: Iowa State University Press. p. 3. "...the basic ideas in statistics assist us in thinking clearly about the problem, provide some guidance about the conditions that must be satisfied if sound inferences are to be made, and enable us to detect many inferences that have no good logical foundation."
- ^ a b E. L. Lehmann (1997). "Testing Statistical Hypotheses: The Story of a Book". Statistical Science. 12 (1): 48–52. doi:10.1214/ss/1029963261.
- ^ Sotos, Ana Elisa Castro; Vanhoof, Stijn; Noortgate, Wim Van den; Onghena, Patrick (2007). "Students' Misconceptions of Statistical Inference: A Review of the Empirical Evidence from Research on Statistics Education" (PDF). Educational Research Review. 2 (2): 98–113. doi:10.1016/j.edurev.2007.04.001.
- ^ Moore, David S. (1997). "New Pedagogy and New Content: The Case of Statistics" (PDF). International Statistical Review. 65 (2): 123–165. doi:10.2307/1403333. JSTOR 1403333.
- ^ Hubbard, Raymond; Armstrong, J. Scott (2006). "Why We Don't Really Know What Statistical Significance Means: Implications for Educators". Journal of Marketing Education. 28 (2): 114–120. doi:10.1177/0273475306288399. hdl:2092/413. S2CID 34729227.
- ^ Sotos, Ana Elisa Castro; Vanhoof, Stijn; Noortgate, Wim Van den; Onghena, Patrick (2009). "How Confident Are Students in Their Misconceptions about Hypothesis Tests?". Journal of Statistics Education. 17 (2). doi:10.1080/10691898.2009.11889514.
- ^ Gigerenzer, G. (2004). "The Null Ritual What You Always Wanted to Know About Significant Testing but Were Afraid to Ask" (PDF). The SAGE Handbook of Quantitative Methodology for the Social Sciences. pp. 391–408. doi:10.4135/9781412986311. ISBN 9780761923596.
- ^ "Testing Statistical Hypotheses". Springer Texts in Statistics. 2005. doi:10.1007/0-387-27605-x. ISBN 978-0-387-98864-1. ISSN 1431-875X.
- ^ Hinkelmann, Klaus; Kempthorne, Oscar (2008). Design and Analysis of Experiments. Vol. I and II (Second ed.). Wiley. ISBN 978-0-470-38551-7.
- ^ Montgomery, Douglas (2009). Design and analysis of experiments. Hoboken, N.J.: Wiley. ISBN 978-0-470-12866-4.
- ^ R. A. Fisher (1925).Statistical Methods for Research Workers, Edinburgh: Oliver and Boyd, 1925, p.43.
- ^ a b Lehmann, E. L.; Romano, Joseph P. (2005). Testing Statistical Hypotheses (3E ed.). New York: Springer. ISBN 978-0-387-98864-1.
- ^ Nuzzo, Regina (2014). "Scientific method: Statistical errors". Nature. 506 (7487): 150–152. Bibcode:2014Natur.506..150N. doi:10.1038/506150a. hdl:11573/685222. PMID 24522584.
- ^ Richard J. Larsen; Donna Fox Stroup (1976). Statistics in the Real World: a book of examples. Macmillan. ISBN 978-0023677205.
- ^ Hubbard, R.; Parsa, A. R.; Luthy, M. R. (1997). "The Spread of Statistical Significance Testing in Psychology: The Case of the Journal of Applied Psychology". Theory and Psychology. 7 (4): 545–554. doi:10.1177/0959354397074006. S2CID 145576828.
- ^ Moore, David (2003). Introduction to the Practice of Statistics. New York: W.H. Freeman and Co. p. 426. ISBN 9780716796572.
- ^ Ranganathan, Priya; Pramesh, C. S; Buyse, Marc (April–June 2016). "Common pitfalls in statistical analysis: The perils of multiple testing". Perspect Clin Res. 7 (2): 106–107. doi:10.4103/2229-3485.179436. PMC 4840791. PMID 27141478.
- ^ Hughes, Ann J.; Grawoig, Dennis E. (1971). Statistics: A Foundation for Analysis. Reading, Mass.: Addison-Wesley. p. 191. ISBN 0-201-03021-7.
- ^ Hall, P. and Wilson, S.R., 1991. Two guidelines for bootstrap hypothesis testing. Biometrics, pp.757-762.
- ^ Tibshirani, R.J. and Efron, B., 1993. An introduction to the bootstrap. Monographs on statistics and applied probability, 57(1).
- ^ Martin, M.A., 2007. Bootstrap hypothesis testing for some common statistical problems: A critical evaluation of size and power properties. Computational Statistics & Data Analysis, 51(12), pp.6321-6342.
- ^ Horowitz, J.L., 2019. Bootstrap methods in econometrics. Annual Review of Economics, 11, pp.193-224. I'm
- ^ John Arbuthnot (1710). "An argument for Divine Providence, taken from the constant regularity observed in the births of both sexes" (PDF). Philosophical Transactions of the Royal Society of London. 27 (325–336): 186–190. doi:10.1098/rstl.1710.0011. S2CID 186209819.
- ^ Brian, Éric; Jaisson, Marie (2007). "Physico-Theology and Mathematics (1710–1794)". The Descent of Human Sex Ratio at Birth. Springer Science & Business Media. pp. 1–25. ISBN 978-1-4020-6036-6.
- ^ Conover, W.J. (1999), "Chapter 3.4: The Sign Test", Practical Nonparametric Statistics (Third ed.), Wiley, pp. 157–176, ISBN 978-0-471-16068-7
- ^ Sprent, P. (1989), Applied Nonparametric Statistical Methods (Second ed.), Chapman & Hall, ISBN 978-0-412-44980-2
- ^ Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty Before 1900. Harvard University Press. pp. 225–226. ISBN 978-0-67440341-3.
- ^ Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900. Cambridge, Mass: Belknap Press of Harvard University Press. p. 134. ISBN 978-0-674-40340-6.
- ^ Fisher, Sir Ronald A. (2000) [1935]. "Mathematics of a Lady Tasting Tea". In James Roy Newman (ed.). The World of Mathematics, volume 3 [Design of Experiments]. Courier Dover Publications. ISBN 978-0-486-41151-4. Originally from Fisher's book Design of Experiments.
- ^ Box, Joan Fisher (1978). R.A. Fisher, The Life of a Scientist. New York: Wiley. p. 134. ISBN 978-0-471-09300-8.
- ^ Jaynes, E. T. (2007). Probability theory : the logic of science (5. print. ed.). Cambridge [u.a.]: Cambridge Univ. Press. ISBN 978-0-521-59271-0.
- ^ Schervish, M (1996) Theory of Statistics, p. 218. Springer ISBN 0-387-94546-6
- ^ Kaye, David H.; Freedman, David A. (2011). "Reference Guide on Statistics". Reference Manual on Scientific Evidence (3rd ed.). Eagan, MN; Washington, D.C.: West National Academies Press. p. 259. ISBN 978-0-309-21421-6.
- ^ Ash, Robert (1970). Basic probability theory. New York: Wiley. ISBN 978-0471034506.Section 8.2
- ^ a b Tukey, John W. (1960). "Conclusions vs decisions". Technometrics. 26 (4): 423–433. doi:10.1080/00401706.1960.10489909. "Until we go through the accounts of testing hypotheses, separating [Neyman–Pearson] decision elements from [Fisher] conclusion elements, the intimate mixture of disparate elements will be a continual source of confusion." ... "There is a place for both "doing one's best" and "saying only what is certain," but it is important to know, in each instance, both which one is being done, and which one ought to be done."
- ^ Stigler, Stephen M. (August 1996). "The History of Statistics in 1933". Statistical Science. 11 (3): 244–252. doi:10.1214/ss/1032280216. JSTOR 2246117.
- ^ Berger, James O. (2003). "Could Fisher, Jeffreys and Neyman Have Agreed on Testing?". Statistical Science. 18 (1): 1–32. doi:10.1214/ss/1056397485.
- ^ Cornfield, Jerome (1976). "Recent Methodological Contributions to Clinical Trials" (PDF). American Journal of Epidemiology. 104 (4): 408–421. doi:10.1093/oxfordjournals.aje.a112313. PMID 788503.
- ^ Yates, Frank (1951). "The Influence of Statistical Methods for Research Workers on the Development of the Science of Statistics". Journal of the American Statistical Association. 46 (253): 19–34. doi:10.1080/01621459.1951.10500764. "The emphasis given to formal tests of significance throughout [R.A. Fisher's] Statistical Methods ... has caused scientific research workers to pay undue attention to the results of the tests of significance they perform on their data, particularly data derived from experiments, and too little to the estimates of the magnitude of the effects they are investigating." ... "The emphasis on tests of significance and the consideration of the results of each experiment in isolation, have had the unfortunate consequence that scientific workers have often regarded the execution of a test of significance on an experiment as the ultimate objective."
- ^ Begg, Colin B.; Berlin, Jesse A. (1988). "Publication bias: a problem in interpreting medical data". Journal of the Royal Statistical Society, Series A. 151 (3): 419–463. doi:10.2307/2982993. JSTOR 2982993. S2CID 121054702.
- ^ Meehl, Paul E. (1967). "Theory-Testing in Psychology and Physics: A Methodological Paradox" (PDF). Philosophy of Science. 34 (2): 103–115. doi:10.1086/288135. S2CID 96422880. Archived from the original (PDF) on December 3, 2013. Thirty years later, Meehl acknowledged statistical significance theory to be mathematically sound while continuing to question the default choice of null hypothesis, blaming instead the "social scientists' poor understanding of the logical relation between theory and fact" in "The Problem Is Epistemology, Not Statistics: Replace Significance Tests by Confidence Intervals and Quantify Accuracy of Risky Numerical Predictions" (Chapter 14 in Harlow (1997)).
- ^ Bakan, David (1966). "The test of significance in psychological research". Psychological Bulletin. 66 (6): 423–437. doi:10.1037/h0020412. PMID 5974619.
- ^ Gigerenzer, G (November 2004). "Mindless statistics". The Journal of Socio-Economics. 33 (5): 587–606. doi:10.1016/j.socec.2004.09.033.
- ^ Nunnally, Jum (1960). "The place of statistics in psychology". Educational and Psychological Measurement. 20 (4): 641–650. doi:10.1177/001316446002000401. S2CID 144813784.
- ^ Lykken, David T. (1991). "What's wrong with psychology, anyway?". Thinking Clearly About Psychology. 1: 3–39.
- ^ Jacob Cohen (December 1994). "The Earth Is Round (p < .05)". American Psychologist. 49 (12): 997–1003. doi:10.1037/0003-066X.49.12.997. S2CID 380942. This paper lead to the review of statistical practices by the APA. Cohen was a member of the Task Force that did the review.
- ^ Kline, Rex (2004). Beyond Significance Testing: Reforming Data Analysis Methods in Behavioral Research. Washington, D.C.: American Psychological Association. ISBN 9781591471189.
- ^ Branch, Mark (2014). "Malignant side effects of null hypothesis significance testing". Theory & Psychology. 24 (2): 256–277. doi:10.1177/0959354314525282. S2CID 40712136.
- ^ Hunter, John E. (January 1997). "Needed: A Ban on the Significance Test". Psychological Science. 8 (1): 3–7. doi:10.1111/j.1467-9280.1997.tb00534.x. S2CID 145422959.
- ^ a b Wilkinson, Leland (1999). "Statistical Methods in Psychology Journals; Guidelines and Explanations". American Psychologist. 54 (8): 594–604. doi:10.1037/0003-066X.54.8.594. S2CID 428023. "Hypothesis tests. It is hard to imagine a situation in which a dichotomous accept-reject decision is better than reporting an actual p value or, better still, a confidence interval." (p 599). The committee used the cautionary term "forbearance" in describing its decision against a ban of hypothesis testing in psychology reporting. (p 603)
- ^ "ICMJE: Obligation to Publish Negative Studies". Archived from the original on July 16, 2012. Retrieved September 3, 2012.
Editors should seriously consider for publication any carefully done study of an important question, relevant to their readers, whether the results for the primary or any additional outcome are statistically significant. Failure to submit or publish findings because of lack of statistical significance is an important cause of publication bias.
- ^ Journal of Articles in Support of the Null Hypothesis website: JASNH homepage. Volume 1 number 1 was published in 2002, and all articles are on psychology-related subjects.
- ^ Howell, David (2002). Statistical Methods for Psychology (5 ed.). Duxbury. p. 94. ISBN 978-0-534-37770-0.
- ^ Williams, S.; Carson, R.; Tóth, K. (October 10, 2023). "Moving beyond P values in The Journal of Physiology: A primer on the value of effect sizes and confidence intervals". J Physiol. 601 (23): 5131–5133. doi:10.1113/JP285575. PMID 37815959. S2CID 263827430.
- ^ P-Values are Random Variables Duncan J. Murdoch, Yu-Ling Tsai and James Adcock, The American Statistician, 2008, https://www.jstor.org/stable/27644033
- ^ Binhimd, Sulafah, and Bashair Almalki. "Bootstrap methods and reproducibility probability." American Scientific Research Journal for Engineering, Technology, and Sciences (ASRJETS) 59.1 (2019): 76-80.
- ^ P-Value Precision and Reproducibility" https://pmc.ncbi.nlm.nih.gov/articles/PMC3370685/
- ^ Ho, Joses; Tumkaya, Tayfun; Aryal, Sameer; Choi, Hyungwon; Claridge-Chang, Adam (June 19, 2019). "Moving beyond P values: data analysis with estimation graphics". Nature Methods. 16 (7): 565–566. doi:10.1038/s41592-019-0470-3. ISSN 1548-7091.
- ^ a b Kruschke, J K (July 9, 2012). "Bayesian Estimation Supersedes the T Test" (PDF). Journal of Experimental Psychology: General. 142 (2): 573–603. doi:10.1037/a0029146. PMID 22774788. S2CID 5610231.
- ^ a b Kruschke, J K (May 8, 2018). "Rejecting or Accepting Parameter Values in Bayesian Estimation" (PDF). Advances in Methods and Practices in Psychological Science. 1 (2): 270–280. doi:10.1177/2515245918771304. S2CID 125788648.
- ^ Armstrong, J. Scott (2007). "Significance tests harm progress in forecasting". International Journal of Forecasting. 23 (2): 321–327. CiteSeerX 10.1.1.343.9516. doi:10.1016/j.ijforecast.2007.03.004. S2CID 1550979.
- ^ Kass, R. E. (1993). Bayes factors and model uncertainty (PDF) (Report). Department of Statistics, University of Washington.
- ^ Rozeboom, William W (1960). "The fallacy of the null-hypothesis significance test" (PDF). Psychological Bulletin. 57 (5): 416–428. CiteSeerX 10.1.1.398.9002. doi:10.1037/h0042040. PMID 13744252. "...the proper application of statistics to scientific inference is irrevocably committed to extensive consideration of inverse [AKA Bayesian] probabilities..." It was acknowledged, with regret, that a priori probability distributions were available "only as a subjective feel, differing from one person to the next" "in the more immediate future, at least".
- ^ Berger, James (2006). "The Case for Objective Bayesian Analysis". Bayesian Analysis. 1 (3): 385–402. doi:10.1214/06-ba115. In listing the competing definitions of "objective" Bayesian analysis, "A major goal of statistics (indeed science) is to find a completely coherent objective Bayesian methodology for learning from data." The author expressed the view that this goal "is not attainable".
- ^ Aldrich, J (2008). "R. A. Fisher on Bayes and Bayes' theorem". Bayesian Analysis. 3 (1): 161–170. doi:10.1214/08-BA306.
Further reading
[edit]- Lehmann E.L. (1992) "Introduction to Neyman and Pearson (1933) On the Problem of the Most Efficient Tests of Statistical Hypotheses". In: Breakthroughs in Statistics, Volume 1, (Eds Kotz, S., Johnson, N.L.), Springer-Verlag. ISBN 0-387-94037-5 (followed by reprinting of the paper)
- Neyman, J.; Pearson, E.S. (1933). "On the Problem of the Most Efficient Tests of Statistical Hypotheses". Philosophical Transactions of the Royal Society A. 231 (694–706): 289–337. Bibcode:1933RSPTA.231..289N. doi:10.1098/rsta.1933.0009.
External links
[edit]- "Statistical hypotheses, verification of", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Bayesian critique of classical hypothesis testing
- Critique of classical hypothesis testing highlighting long-standing qualms of statisticians
- Statistical Tests Overview: How to choose the correct statistical test
- [1] Statistical Analysis based Hypothesis Testing Method in Biological Knowledge Discovery; Md. Naseef-Ur-Rahman Chowdhury, Suvankar Paul, Kazi Zakia Sultana
Online calculators
[edit]Statistical hypothesis test
View on GrokipediaFundamentals
Definition and Key Concepts
A statistical hypothesis test is a procedure in inferential statistics that uses sample data to evaluate the strength of evidence against a specified null hypothesis, typically in favor of an alternative hypothesis.[11] Hypotheses in this context are formal statements about unknown population parameters, such as means or proportions, rather than sample statistics, enabling researchers to draw conclusions about broader populations from limited data.[7] This approach plays a central role in inferential statistics by facilitating decision-making under uncertainty, distinct from parameter estimation, which focuses on approximating the value of a population parameter (e.g., via point or interval estimates) rather than deciding between competing claims.[12] The basic framework of a hypothesis test involves computing a test statistic from the sample data, which quantifies how far the observed results deviate from what would be expected under the null hypothesis.[11] This statistic is then compared to its sampling distribution—a theoretical distribution of possible values under the null—to determine the probability of observing such results by chance, leading to a decision rule for rejecting or retaining the null.[11] Concepts like p-values, which measure this probability, and significance levels provide thresholds for these decisions, though their interpretation remains a point of ongoing discussion.[4] The foundations of modern hypothesis testing trace back to Ronald Fisher's work in the 1920s, particularly his 1925 book Statistical Methods for Research Workers, where he introduced significance testing and p-values as tools for assessing evidence against a null hypothesis in experimental data, particularly in biology and agriculture.[13] However, Fisher did not fully formalize the dual-hypothesis framework or emphasize error control, which later developments addressed. Hypothesis tests are subject to two primary types of errors: a Type I error, or false positive, occurs when the null hypothesis is incorrectly rejected despite being true in the population, while a Type II error, or false negative, occurs when the null is not rejected despite being false.[7] These errors represent inherent trade-offs, as reducing the probability of a Type I error (controlled by the significance level α) typically increases the probability of a Type II error (β), and vice versa, depending on sample size, effect size, and test power; this framework was formalized by Jerzy Neyman and Egon Pearson in their 1933 paper on efficient tests.Null and Alternative Hypotheses
In statistical hypothesis testing, the null hypothesis, denoted , represents the default or baseline assumption that there is no effect, no relationship, or no difference between groups or variables in the population.[14] It is typically formulated as an equality statement involving population parameters, such as a mean or a proportion , reflecting the status quo or the absence of the phenomenon under investigation. This formulation allows the test to assess whether observed data provide sufficient evidence to challenge this assumption, thereby controlling the risk of incorrectly rejecting it when it is true.[15] The alternative hypothesis, denoted or , states the research claim or the presence of an effect, relationship, or difference that the investigator seeks to support.[14] It complements by specifying the opposite scenario and can be two-sided (e.g., , indicating a difference in either direction) or one-sided (e.g., or , indicating a directional effect). In the Neyman-Pearson framework, the alternative hypothesis guides the design of the test to maximize its power against , ensuring that the hypotheses together cover all possible outcomes.[15] Formulating hypotheses requires them to be mutually exclusive and collectively exhaustive, meaning exactly one must be true and they partition the parameter space without overlap or gaps.[3] They must also be testable through sample data and expressed specifically in terms of population parameters rather than sample statistics, enabling objective evaluation via statistical procedures. A classic example is testing the fairness of a coin, where assumes an equal probability of heads or tails, while posits bias in either direction.[3] The testing process seeks evidence to falsify , but if insufficient, is retained rather than proven, emphasizing the asymmetry in inference.[15]Historical Development
Early Foundations
The origins of statistical hypothesis testing trace back to the early 18th century, with John Arbuthnot's analysis of human sex ratios providing one of the first informal applications of probabilistic reasoning to test a hypothesis. In 1710, Arbuthnot examined christening records in London from 1629 to 1710 and observed a consistent excess of male births, calculating the probability under the assumption of equal likelihood for male or female births using binomial probabilities; he concluded that this pattern was unlikely to occur by chance alone, arguing for divine providence as the cause.[16] In the 19th century, Pierre-Simon Laplace advanced these ideas through his work on probability, applying it to assess the reliability of testimonies and to evaluate hypotheses in celestial mechanics. Laplace's Essai philosophique sur les probabilités (1814) included a chapter on the probabilities of testimonies, where he modeled the likelihood of multiple witnesses agreeing on an event under assumptions of independence and varying credibility, effectively using probability to test the hypothesis of truth versus error in reported facts.[17] Similarly, in his Mécanique céleste (1799–1825), Laplace employed inverse probability to test astronomical hypotheses, computing the probability that observed planetary perturbations were due to specific causes rather than random errors, thereby laying early groundwork for hypothesis evaluation in scientific data.[18] By the late 19th and early 20th centuries, more structured tests emerged, with Karl Pearson introducing the chi-squared goodness-of-fit test in 1900 to assess whether observed frequencies in categorical data deviated significantly from expected values under a hypothesized distribution. Pearson's criterion, detailed in his paper on deviations in correlated variables, provided a quantitative measure for judging if discrepancies could reasonably arise from random sampling, marking a key step toward formal statistical inference. William Sealy Gosset, working under the pseudonym "Student" at the Guinness brewery, developed the t-test in 1908 to handle small-sample inference in quality control, addressing the limitations of normal distribution assumptions for limited data on ingredient variability. Published in Biometrika, Gosset's method calculated the probable error of a mean using a t-distribution derived from small-sample simulations, enabling reliable testing of means without large datasets. In the 1920s, Jerzy Neyman and Egon Pearson began collaborating on likelihood-based approaches to hypothesis testing, with their 1928 paper introducing criteria using likelihood ratios to distinguish between hypotheses while controlling error rates. This early work in Biometrika explored test statistics that maximized discrimination between a null hypothesis and alternatives, predating their full unified formulation.[19] These foundational contributions established methods for probabilistic assessment and error control in data analysis but operated without a comprehensive theoretical framework, paving the way for Ronald Fisher's integration of significance testing concepts later in the decade.Modern Evolution and Debates
In the 1920s and 1930s, Ronald A. Fisher formalized the foundations of null hypothesis significance testing (NHST), introducing the null hypothesis as a baseline for assessing experimental outcomes and the p-value as a measure of the probability of observing data at least as extreme under that null assumption.[20] Fisher's seminal book, Statistical Methods for Research Workers (1925), popularized these concepts for practical use in scientific research, advocating fixed significance levels such as α = 0.05 as a convenient threshold for decision-making, though he emphasized reporting exact p-values over rigid cutoffs.[21] This approach framed hypothesis testing as a tool for inductive inference, drawing conclusions from sample data to broader populations without specifying alternatives.[20] The Neyman-Pearson framework emerged in the 1930s as a rival formulation, developed by Jerzy Neyman and Egon Pearson, which emphasized comparing the null hypothesis against a specific alternative to maximize the test's power—the probability of correctly rejecting a false null—while controlling the Type I error rate at a fixed α.[22] Unlike Fisher's focus on inductive inference from observed data, Neyman and Pearson adopted a behavioristic perspective, viewing tests as long-run decision procedures for repeated sampling, where errors of Type I (false rejection) and Type II (false acceptance) are balanced through power considerations.[23] This rivalry highlighted fundamental philosophical differences, with Neyman and Pearson critiquing Fisher's methods for lacking explicit alternatives and power analysis.[22] Early controversies unfolded in statistical journals during the 1930s, including exchanges in Biometrika, where critiques challenged Fisher's fiducial inference and randomization principles, prompting rebuttals that underscored tensions over test interpretation.[24] Fisher staunchly rejected power calculations, arguing they required assuming an unknown alternative distribution, rendering them impractical and misaligned with his evidential approach to p-values.[23] These debates, peaking around a 1934 Royal Statistical Society meeting, persisted amid personal animosities but spurred refinements in testing theory.[22] World War II accelerated the adoption of hypothesis testing in agriculture and industry, as Fisher's experimental designs and Neyman-Pearson procedures were applied to optimize resource allocation in wartime production and food security efforts, such as crop yield trials at institutions like Rothamsted Experimental Station.[25] Post-World War II, NHST spread widely to psychology and social sciences by the 1950s, becoming a standard for empirical validation in behavioral research despite ongoing theoretical disputes.[26] In the 1960s, psychologist Jacob Cohen critiqued its misuse in these fields, highlighting chronic underpowering of studies—often below 0.50 for detecting medium effects—which inflated Type II errors and undermined replicability in behavioral sciences. These concerns echoed earlier rivalries but gained traction amid growing empirical scrutiny. The debates' legacy persisted into the 21st century, influencing the American Statistical Association's 2019 statement on p-values, which clarified misconceptions (e.g., p-values do not measure null hypothesis probability) and linked NHST misapplications to the replication crisis across sciences.[27]Testing Procedure
Steps in Frequentist Hypothesis Testing
The frequentist hypothesis testing procedure consists of a series of well-defined steps designed to evaluate evidence against a null hypothesis using sample data, while controlling the risk of erroneous rejection (Type I error). This framework, formalized by Neyman and Pearson in their seminal work on optimal tests, balances error control with the power to detect true alternatives.[15] The process begins with Step 1: Stating the hypotheses. The null hypothesis posits no effect or a specific value for the population parameter (e.g., for the population mean ), while the alternative hypothesis (or ) specifies the opposite, such as a deviation from the null (e.g., for a two-sided test or for a one-sided test). These are framed in terms of unknown population parameters to link the test directly to inferential goals.[28] In Step 2: Choosing the significance level and considering power, the significance level is selected, typically 0.05, representing the maximum acceptable probability of rejecting when it is true (Type I error rate). This convention balances caution against over-sensitivity in decision-making. Additionally, the test's power (1 - , where is the Type II error rate) is considered during planning to ensure adequate detection of true alternatives, often guiding sample size determination.[29][30] Step 3: Selecting the test statistic and its distribution under involves choosing a statistic sensitive to deviations from , based on the data type and assumptions (e.g., normality). For testing a population mean with known variance, the z-statistic is used: where is the sample mean, is the hypothesized value, is the population standard deviation, and is the sample size. Under and the assumptions, this follows a standard normal distribution, enabling probabilistic assessment.[31] During Step 4: Computing the test statistic and finding the p-value or critical value, the observed sample data is plugged into the test statistic formula to obtain its value. The p-value is then calculated as the probability of observing a statistic at least as extreme under (using the sampling distribution, e.g., normal tables for z). Alternatively, critical values define the rejection boundaries (e.g., for , two-sided).[32] Step 5: Applying the decision rule compares the computed statistic or p-value to the threshold: reject if the p-value or if the statistic falls in the rejection region (e.g., beyond the critical values). Failure to reject indicates insufficient evidence against it, but does not prove it true. This binary decision maintains long-run frequency properties.[28] Finally, Step 6: Interpreting the results in context involves stating the conclusion (e.g., "There is sufficient evidence to reject at ") and relating it to the practical question. To provide additional insight, a confidence interval for the parameter can be constructed; if it excludes the null value, it aligns with rejection of , illustrating the duality between testing and interval estimation.[30]Significance Levels, P-Values, and Power
In statistical hypothesis testing, the significance level, denoted by α, represents the probability of committing a Type I error, which is the event of rejecting the null hypothesis H₀ when it is actually true. Formally, α = P(reject H₀ | H₀ is true). This threshold is chosen by the researcher prior to conducting the test and determines the critical region of the test statistic's distribution under H₀, typically the tails where extreme values lead to rejection. Common choices for α include 0.05, 0.01, and 0.10, reflecting a balance between controlling false positives and practical feasibility, though its selection is inherently arbitrary and context-dependent, as no universal value optimizes all scenarios.[15] The p-value, introduced by Ronald Fisher, quantifies the strength of evidence against H₀ provided by the observed data. It is defined as the probability of obtaining a test statistic at least as extreme as the one observed, assuming H₀ is true: p = P(T ≥ t_obs | H₀), where T is the test statistic and t_obs is its observed value. Unlike α, which is a fixed threshold set in advance, the p-value is a data-dependent measure that varies with the sample; a small p-value (e.g., less than 0.05) suggests the observed data are unlikely under H₀, providing evidence in favor of the alternative hypothesis H_a, but it does not directly indicate the probability that H₀ is true. The distinction lies in their roles: α governs the decision rule for rejection, while the p-value assesses compatibility of the data with H₀ without invoking a predefined cutoff.[33] Statistical power, a key concept in the Neyman-Pearson framework, is the probability of correctly rejecting H₀ when H_a is true, defined as 1 - β, where β = P(Type II error) = P(accept H₀ | H_a is true). For a simple case, such as a one-sided z-test for a mean with known variance, β can be expressed as the probability that the test statistic falls below the critical value under H_a: β = P(T < t_crit | H_a), where t_crit is determined by α from the distribution under H₀. Power depends on several factors, including sample size (larger n increases power by reducing variability), effect size (larger differences between H₀ and H_a enhance detectability), significance level α (higher α boosts power but raises Type I risk), and the variability in the data. In practice, power is often targeted at 0.80 or higher during study design to ensure adequate sensitivity.[15] The p-value and significance level α are interconnected through the decision process: rejection occurs if p ≤ α, meaning the observed extremity exceeds what α allows under H₀. Critical values derive from the tails of the test statistic's null distribution; for instance, in a standard normal test, the critical value for α = 0.05 (two-sided) is ±1.96, corresponding to the points where the cumulative probability covers 1 - α/2 in each tail. P-values inform the strength of evidence continuously—values near 0 indicate strong incompatibility with H₀, while those near 1 suggest consistency—allowing nuanced interpretation beyond binary reject/fail-to-reject decisions. Power complements these by evaluating the test's ability to detect true effects, with power curves illustrating how 1 - β varies with effect size or sample size for fixed α; for example, in a z-test, the curve shifts rightward as n decreases, showing reduced power for small effects.[29] To illustrate the p-value calculation, consider a two-sided z-test for a population mean μ with known σ, testing H₀: μ = μ₀ against H_a: μ ≠ μ₀. The test statistic is which follows a standard normal distribution N(0,1) under H₀. For an observed z_obs, the p-value is the probability of a |Z| at least as large as |z_obs| under N(0,1): where Φ is the cumulative distribution function of the standard normal. This derivation arises from the symmetry of the normal distribution: the one-tailed probability from |z_obs| to infinity is doubled for the two-sided case, capturing extremity in either direction. For example, if z_obs = 2.5, then Φ(2.5) ≈ 0.9938, so p ≈ 2 × (1 - 0.9938) = 0.0124, indicating strong evidence against H₀ at α = 0.05.[34] For power in this z-test setup, assume a one-sided alternative H_a: μ > μ₀ with effect size δ = (μ_a - μ₀)/σ. Under H_a, Z follows N(λ, 1) where λ = δ √n. The critical value z_crit = z_{1-α} from the standard normal (e.g., 1.645 for α = 0.05). Then, so power = 1 - Φ(z_{1-α} - δ √n). This formula highlights how power increases with δ and n, approaching 1 as λ grows large relative to z_{1-α}. Power curves, plotting 1 - β against δ for varying n, typically show sigmoid shapes, emphasizing the need for sufficient sample size to achieve desired power.[35]Illustrative Examples
Classic Statistical Examples
One of the most famous illustrations of hypothesis testing is Ronald Fisher's "Lady Tasting Tea" experiment, conducted in the 1920s with botanist Muriel Bristol, who claimed she could discern whether milk had been added to tea before or after the tea leaves. Fisher designed a randomized experiment with eight cups of tea: four prepared one way and four the other, presented in random order, requiring Bristol to identify the preparation method for each. The null hypothesis (H₀) posited no discriminatory ability, implying her identifications followed a random binomial distribution with success probability 0.5. If she correctly identified all eight, the exact p-value is the probability of this outcome or more extreme under H₀, calculated as 1 over the number of ways to choose 4 out of 8, or rejecting H₀ at the 5% significance level and demonstrating the power of exact binomial tests for small samples. This setup, detailed in Fisher's 1935 book The Design of Experiments, exemplifies controlled randomization and exact inference in hypothesis testing. Another seminal example is John Arbuthnot's 1710 analysis of human birth sex ratios in London, later extended with modern chi-squared tests to assess deviations from equality. Arbuthnot examined 82 years of christening records (1629–1710), observing 13,228 male births and 12,300 female births, and argued against a 50:50 expected ratio under H₀ of random sex determination, using a sign test on annual excesses of males. In contemporary reinterpretations, this data is tested via the chi-squared goodness-of-fit statistic: where observed (O) values are 13,228 males and 12,300 females, and expected (E) under H₀ totals 25,528 births at 12,764 each, yielding With 1 degree of freedom, this corresponds to a p-value of approximately 6.4 × 10^{-9}, strongly rejecting H₀ and highlighting early empirical challenges to probabilistic assumptions in biology. In parapsychology, J.B. Rhine's 1930s experiments on extrasensory perception (ESP) using Zener cards provide a classic z-test application for hit rates exceeding chance. Participants guessed symbols on decks of 25 cards (five each of five symbols), with H₀ assuming random guessing yields an expected 5 correct guesses (μ = 5, σ = √(25 × 0.2 × 0.8) = 2). Rhine reported subjects achieving, for instance, 7 or more hits in sessions; for 8 hits, the z-score is with a one-tailed p-value of about 0.0668, often failing to reject H₀ at α = 0.05 but illustrating the test's sensitivity to small deviations in large trials. These tests, aggregated over thousands of trials in Rhine's 1934 book Extra-Sensory Perception, underscored the z-test's role in evaluating binomial outcomes approximated as normal for n > 30. A common analogy framing hypothesis testing is the courtroom trial, where the null hypothesis H₀ represents the presumption of innocence, and the alternative H₁ suggests guilt based on evidence. The burden of proof lies with the prosecution to reject H₀, mirroring control of the Type I error rate (α, false conviction probability) at a low threshold like 5%, while accepting a higher Type II error (β, false acquittal) to protect the innocent. This analogy, popularized in Neyman and Pearson's 1933 formulation, emphasizes asymmetric error risks in decision-making under uncertainty.Practical Real-World Scenarios
In medical trials, hypothesis testing is routinely applied to assess drug efficacy, often using the null hypothesis that there is no difference in means between treatment and control groups, such as mean survival times or response rates. For instance, a two-sample t-test may compare average blood pressure reductions between a new antihypertensive drug and placebo, with rejection of indicating efficacy if the p-value is below the significance level.[36] Sample size calculations ensure adequate power, typically targeting 80% to detect a clinically meaningful effect size; for a two-sample t-test assuming equal variances and standard deviation of 10 mmHg, a 5 mmHg difference requires approximately 64 participants per group at .[37] In quality control, A/B testing evaluates manufacturing processes via the F-test for equality of variances, testing to ensure consistent output. For example, comparing steel rod diameters from two processes—one with 15 samples and variance 0.0025, the other with 20 samples and variance 0.0016—yields an F-statistic of 1.5625 (df = 14, 19), failing to reject at since 1.5625 < 2.42, confirming comparable process stability.[38] In social sciences, surveys on voter preferences employ proportion tests to compare group support, such as testing for Conservative party backing among those over 40 versus under 40. A 95% confidence interval for the difference in proportions might range from -0.05 to 0.15, indicating no significant disparity if the interval includes zero, as seen in UK polls where older voters showed slightly higher support but without statistical evidence at .[39] In economics, regression-based tests assess coefficient significance, with for predictors like unemployment rate changes on GDP growth under Okun's law. A model yields a t-statistic of -4.32 for , rejecting at (p < 0.01), supporting the inverse relationship across quarterly data from 2000–2020.[40] Recent advancements in the 2020s integrate hypothesis testing with machine learning for feature selection, using t-tests or ANOVA to identify significant predictors before model training, reducing dimensionality in high-dimensional datasets.[41] In big data contexts, adjusted levels control family-wise error rates during multiple tests, such as dividing 0.05 by the number of comparisons to mitigate false positives in genomic or sensor analyses.[42] A worked example from a hypothetical drug trial illustrates the two-sample t-test for efficacy on mean survival time (in months). Suppose 50 patients per group: treatment mean , SD ; control , SD . The t-statistic is with df ≈ 98. The p-value (two-tailed) is approximately 0.0002 < 0.05, rejecting of no difference and supporting improved efficacy.[36]Variations and Extensions
Parametric and Nonparametric Approaches
Parametric hypothesis tests assume that the data follow a specific probability distribution, typically the normal distribution, with known parameters such as mean and variance.[43] These tests are powerful when their assumptions hold, offering greater statistical efficiency in detecting true effects compared to alternatives.[44] Common examples include the z-test, used for comparing means when the population variance is known and the sample size is large; the t-test, applied for unknown variance with smaller samples; and analysis of variance (ANOVA), which extends the t-test to compare means across multiple groups under normality and equal variance assumptions.[45][46][47] In contrast, nonparametric hypothesis tests, also known as distribution-free tests, do not rely on assumptions about the underlying distribution of the data, making them suitable for ordinal data, small samples, or cases where normality is violated.[48] They focus on ranks or order statistics rather than raw values, providing robustness against outliers and non-normal distributions. Key examples are the Wilcoxon signed-rank test for paired samples, which assesses differences in medians by ranking absolute deviations; the Mann-Whitney U test for independent samples, evaluating whether one group's values tend to be larger than another's; and the Kolmogorov-Smirnov test, which compares the empirical cumulative distribution of a sample to a reference distribution.[48][49] The choice between parametric and nonparametric approaches depends on data type, sample size, and robustness needs; for instance, parametric tests are preferred for large, normally distributed interval data, while nonparametric tests suit skewed or categorical data.[50] To check normality assumptions for parametric tests, the Shapiro-Wilk test is commonly used, computing a statistic based on the correlation between ordered sample values and expected normal scores, with rejection of normality if the p-value is below a threshold like 0.05.[51] Within nonparametric methods, permutation tests form an important subclass, generating the null distribution by randomly reassigning labels or reshuffling data to compute exact p-values without distributional assumptions, particularly useful for complex designs.[52] Rank-based statistics often underpin these tests; for the Mann-Whitney U test, the statistic is calculated aswhere and are sample sizes, and is the sum of ranks for the first group, with the test proceeding by comparing this U to its null distribution.[53] Modern robust methods bridge parametric and nonparametric paradigms, such as those based on trimmed means, which reduce sensitivity to outliers by excluding a fixed proportion of extreme values before computing test statistics, enhancing reliability in hypothesis testing for contaminated data.[54] These approaches maintain efficiency under mild violations of normality while offering better control of Type I error rates than classical parametric tests in non-ideal conditions.[55]