Hubbry Logo
Statistical graphicsStatistical graphicsMain
Open search
Statistical graphics
Community hub
Statistical graphics
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Statistical graphics
Statistical graphics
Statistical graphics
View on Wikipedia
from Wikipedia
Part of a series on Statistics
Data and information visualization
Major dimensions
Important figures
Information graphic types
Related topics

Statistical graphics, also known as statistical graphical techniques, are graphics used in the field of statistics for data visualization.

Overview

[edit]

Whereas statistics and data analysis procedures generally yield their output in numeric or tabular form, graphical techniques allow such results to be displayed in some sort of pictorial form. They include plots such as scatter plots, histograms, probability plots, spaghetti plots, residual plots, box plots, block plots and biplots.[1]

Exploratory data analysis (EDA) relies heavily on such techniques. They can also provide insight into a data set to help with testing assumptions, model selection and regression model validation, estimator selection, relationship identification, factor effect determination, and outlier detection. In addition, the choice of appropriate statistical graphics can provide a convincing means of communicating the underlying message that is present in the data to others.[1]

Graphical statistical methods have four objectives:[2]

  • The exploration of the content of a data set
  • The use to find structure in data
  • Checking assumptions in statistical models
  • Communicate the results of an analysis.

If one is not using statistical graphics, then one is forfeiting insight into one or more aspects of the underlying structure of the data.

History

[edit]

Statistical graphics have been central to the development of science and date to the earliest attempts to analyse data. Many familiar forms, including bivariate plots, statistical maps, bar charts, and coordinate paper were used in the 18th century. Statistical graphics developed through attention to four problems:[3]

  • Spatial organization in the 17th and 18th century
  • Discrete comparison in the 18th and early 19th century
  • Continuous distribution in the 19th century and
  • Multivariate distribution and correlation in the late 19th and 20th century.

Since the 1970s statistical graphics have been re-emerging as an important analytic tool with the revitalisation of computer graphics and related technologies.[3]

Examples

[edit]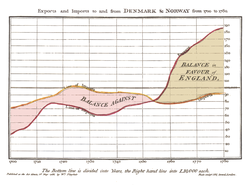
William Playfair's trade-balance time-series chart, published in his Commercial and Political Atlas, 1786
John Snow's Cholera map in dot style, 1854

Famous graphics were designed by:

See the plots page for many more examples of statistical graphics.

See also

[edit]

References

[edit]

Further reading

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Statistical graphics

View on Grokipedia
from Grokipedia
Statistical graphics are visual representations of quantitative and categorical designed to facilitate statistical , , and communication of insights through charts, graphs, plots, and diagrams. These tools encompass for discovering structures in raw data, visualization of statistical models to illustrate fitted relationships, and presentation graphics to convey results clearly and effectively. The history of statistical graphics traces back to ancient origins, such as primitive coordinate systems used by Nilotic surveyors around 1400 BC for land measurement, but modern forms emerged in the late 18th century with William Playfair's invention of the , , and in his 1786 Commercial and Political Atlas. The marked a "golden age" of innovation, featuring contributions like Florence Nightingale's coxcomb diagrams in 1858 to highlight mortality causes during the and Charles Minard's 1869 of Napoleon's Russian campaign, which integrated multiple variables to depict the disastrous retreat. In the , John Tukey's 1977 book emphasized graphics for hypothesis generation, while Edward Tufte's works, starting with The Visual Display of Quantitative Information in 1983, introduced principles like the data-ink ratio to maximize informational density and minimize non-essential elements. Key principles of effective statistical graphics prioritize human perceptual capabilities, such as detecting edges, motion, and color differences, to enable accurate comparisons and reveal both expected and unexpected patterns in data. Techniques include superposition for overlaying data layers, for side-by-side views, and dynamic methods like linking and brushing in interactive software to explore multivariate relationships. Common types encompass scatterplots for correlations, histograms for distributions, box plots for summaries of variability, and more advanced forms like or grand tours for high-dimensional data. With the advent of computing in the late , statistical graphics evolved from static paper-based displays to interactive, three-dimensional, and dynamic visualizations, supported by software such as and tools like XGobi for exploratory analysis. These advancements have expanded applications across fields like , , and , where aid in model validation through plots and in communicating complex findings to diverse audiences. Notable modern influences include Leland Wilkinson's 2005 grammar of framework, which formalizes the construction of visuals as a systematic . Overall, statistical graphics remain essential for transforming numerical data into intuitive, actionable knowledge while guarding against misinterpretation through rigorous design.

Introduction

Definition and Scope

Statistical graphics refer to the graphical representations of quantitative and categorical data designed to reveal patterns, trends, and relationships, with a primary emphasis on supporting statistical inference rather than mere aesthetic presentation. These visualizations transform complex numerical information into forms that facilitate the discovery and communication of insights derived directly from the data, enabling users to assess models, validate assumptions, and identify deviations from expected patterns. Unlike broader information visualization approaches that may prioritize storytelling or attention-grabbing elements, statistical graphics focus on accuracy and interpretability to aid in applied problem-solving. The scope of statistical graphics encompasses both static and dynamic plots that encode data through visual variables such as position, color, and size, allowing for the depiction of distributions, associations, and summaries in ways that support quantitative analysis. This includes a range of techniques rooted in perceptual principles, where elements like position along aligned scales are prioritized for their superior accuracy in human judgment over less precise encodings like area or color saturation. Graphical perception theory establishes a hierarchy of tasks, ranking position judgments highest, followed by length and angle, then area, volume, and shading, to guide the design of effective displays that minimize decoding errors. In contrast, non-statistical visuals such as infographics, which often integrate narrative or decorative components without rigorous data linkage, fall outside this scope. Originating in the alongside developments in and political arithmetic, statistical graphics evolved as tools for representing quantitative information amid growing data availability in science and , though their detailed historical progression extends beyond this foundational period. Within , they play roles in both exploratory contexts for pattern detection and confirmatory settings for testing, bridging with inferential conclusions.

Role in Data Analysis

Statistical graphics play a pivotal role in exploratory data analysis (EDA), where they enable analysts to generate hypotheses by revealing patterns, anomalies, and structures in data that might not be evident through numerical summaries alone. In EDA, graphics facilitate the initial interrogation of datasets, allowing for the identification of trends, clusters, and potential relationships without preconceived models, as pioneered by John Tukey's framework that emphasized visual techniques to probe data iteratively before formal statistical modeling. This approach contrasts with confirmatory analysis, where graphics validate hypotheses and test statistical inferences, such as through visual assessments of model fit or distribution assumptions. Beyond exploration and confirmation, statistical graphics are essential for communicating analytical findings, translating complex results into accessible visuals that support decision-making across disciplines like science, business, and policy. Graphics complement traditional statistical methods by enhancing the detection of outliers, distributional shapes, and correlations that numerical metrics might overlook or misrepresent. For instance, while like means and variances provide aggregated insights, plots allow for a more nuanced view of variability and interdependence, aiding in the refinement of analytical strategies. This integration leverages human , which excels at discerning subtle patterns in spatial arrangements, thereby reducing cognitive demands when processing large or multidimensional datasets. Research underscores that effective visualizations can uncover insights faster and with greater accuracy than tabular alone, as they align with innate abilities in and . In practical workflows, statistical graphics support testing by visualizing elements like distributions or test statistics against null expectations, helping to assess the robustness of inferences graphically rather than solely through computed values. Similarly, in model diagnostics, residual plots are routinely employed to evaluate assumptions such as , homoscedasticity, and ; deviations in these plots signal model inadequacies, prompting adjustments like transformations or alternative specifications. These graphical tools thus bridge exploratory insights with confirmatory rigor, ensuring that analyses are both intuitive and statistically sound.

Historical Development

Early Innovations

The origins of statistical graphics emerged in the late , primarily through the work of Scottish engineer and economist , who sought to make complex economic data more accessible. In 1785, Playfair invented the , first illustrated in a preliminary edition of his The Commercial and Political Atlas to compare Scotland's exports and imports over a one-year period. This innovation allowed for straightforward comparisons of discrete categories using horizontal or vertical bars proportional to values. One year later, in 1786, he introduced the in the formal edition of the same atlas, featuring 43 variants to depict time-series trends such as England's trade with and or national debts over decades. Playfair's designs emphasized the temporal dimension, connecting data points with lines to reveal patterns in economic fluctuations that tabular formats obscured. These early visualizations were bolstered by concurrent advances in and statistical methods, particularly those applied to astronomy and nascent demographic analysis. Pierre-Simon Laplace's , outlined in 1812, provided a theoretical foundation for representing aggregated data distributions graphically, influencing how variability in observations could be depicted. Similarly, developed the method of around 1795 and applied it to astronomical data, such as predicting the orbit of the Ceres in 1801 using sparse observations to minimize errors in plotted trajectories. These techniques enabled graphical smoothing and interpolation of celestial and earthly measurements, marking the integration of probabilistic models with visual representation in fields like astronomy, where scatter-like plots of star positions began to emerge. In demographics, early graphical methods similarly arose to map social patterns, drawing on statistical aggregation to visualize population trends and vital statistics. The 19th century saw further innovations in multivariate graphics, exemplified by French civil engineer Charles Minard's 1869 flow map of Napoleon's 1812 Russian campaign, which synthesized multiple variables into a single, intuitive depiction. The map traces the Grande Armée's advance and retreat across space, with path width varying to represent army size—from 422,000 troops at the start to 10,000 survivors—while incorporating time through a sequential timeline and temperature via a lower scale showing the severe winter drop during the return. This design highlighted catastrophic losses, such as halving the force at the River crossing, by blending geographic flow lines with quantitative scales for direction and magnitude. In the realm of public health and demographics, Florence Nightingale advanced statistical graphics in 1858 with her coxcomb diagrams, or polar area charts, to scrutinize mortality data from the Crimean War. Published in Notes on Matters Affecting the Health, Efficiency, and Hospital Administration of the British Army, these diagrams used wedge-shaped sectors radiating from a center to compare causes of death—blue for preventable diseases, red for wounds—across months, revealing that sickness caused over 16,000 deaths versus fewer than 4,000 from battle. The area of each wedge was proportional to mortality rates, with twelve diagrams illustrating the war's duration to underscore the impact of poor sanitation and advocate for reforms that subsequently reduced death rates by two-thirds. Nightingale's approach demonstrated graphics' persuasive power in demographic and epidemiological contexts, influencing policy through clear visual arguments for data-driven intervention.

20th-Century Advancements

In the early , advanced the use of scatterplots for visualizing correlations, building on earlier ideas by formalizing their role in statistical analysis. In his 1895 work Contributions to the Mathematical Theory of Evolution, Pearson introduced the product-moment correlation coefficient, which he illustrated using scatter diagrams to depict relationships between variables such as height and span in human measurements. By 1920, in Notes on the History of Correlation, he credited with originating the scatterplot but coined the term "scatter diagram" himself, emphasizing its utility in exploring distributions and regression lines. These contributions standardized scatterplots as essential tools for correlation visualization, influencing and beyond during the 1890s to 1920s. Mid-century developments were propelled by John Tukey's exploratory data analysis (EDA) framework, which emphasized graphical methods for uncovering data structures. Published in full in 1977 as , Tukey's work introduced the stem-and-leaf plot as a simple, data-preserving display that combines numerical summary with histogram-like visualization, allowing quick assessment of distributions and outliers. He also developed the —initially termed the "schematic plot"—to summarize univariate data via medians, quartiles, and fences for identifying extremes, promoting resistant and robust techniques over parametric assumptions. These innovations, refined through the 1970s, shifted statistical practice toward iterative, visual exploration. Theoretical foundations for graphical design emerged with Bertin's Semiology of Graphics in 1967, providing a systematic framework for visual representation. Bertin identified seven visual variables—position, size, shape, value, color, orientation, and texture—as building blocks for encoding in diagrams, networks, and maps, enabling effective communication of quantitative and qualitative information. Later, in the 1980s, Edward Tufte's The Visual Display of Quantitative Information (1983) articulated principles to enhance clarity and efficiency, including the data-ink ratio, defined as the proportion of used for versus non-essential elements, to maximize informational . Tufte also coined "" for decorative or misleading graphical elements that obscure , advocating their elimination to uphold graphical integrity. The advent of computers in the enabled dynamic graphics, exemplified by the PRIM-9 system developed by , Martin Friedman, and Mary Anne Fisherkeller. Conceived in 1972 at the Stanford Linear Accelerator Center, PRIM-9 allowed interactive manipulation of multivariate data in up to nine dimensions through operations like picturing (projecting views), (continuous turning of data clouds to reveal structures), isolation (selecting subsets), and masking (focusing on regions). This system marked a technological shift from static to interactive visualization, facilitating deeper of high-dimensional datasets on early computing hardware.

Fundamental Principles

Design Guidelines

Effective statistical graphics prioritize clarity and fidelity to the data by adhering to principles derived from and . A foundational guideline is to maximize the data-ink ratio, defined as the proportion of ink (or pixels) used to represent data relative to the total ink in the graphic, thereby minimizing non-essential elements like decorative frames or excessive gridlines. This approach, advocated by , ensures that the viewer's attention focuses on the information content rather than superfluous visuals. Similarly, graphical integrity requires representing data proportions accurately, such as through the lie factor metric, where the size of an effect in the graphic should match the size in the data (lie factor = 1); deviations, like those from truncated y-axes starting above zero, can distort perceptions of change magnitude. Selecting appropriate scales is crucial for accurate interpretation; linear scales suit data with comparable absolute differences, while logarithmic scales are preferable for datasets spanning orders of magnitude, such as patterns, to reveal relative changes without compressing low values. Perceptual accuracy further informs element choice, as outlined in the Cleveland-McGill hierarchy, which ranks graphical tasks by human decoding ease: position along a common scale (e.g., aligned dots) outperforms length judgments (e.g., bars), which in turn surpass angle, area, volume, or color saturation encodings. For instance, scatterplots leveraging position for both variables enable precise comparisons, whereas pie charts relying on area or color often lead to estimation errors. Accessibility enhances usability for diverse audiences, including those with color vision deficiencies affecting about 8% of men and 0.5% of women globally. Guidelines recommend color palettes tested for deuteranomaly (red-green confusion) using tools like color simulation, avoiding red-green pairings in favor of blue-orange schemes, and supplementing with patterns or textures. Labeling clarity supports this by employing fonts at least 10pt, direct data point annotations over remote legends when feasible, and hierarchical text sizing to guide the eye without clutter. Legend design should minimize by placing them adjacent to relevant elements, using consistent symbols matching the graphic, and limiting entries to 5-7 items; for complex cases, integrate labels directly into the plot to eliminate the need for cross-referencing. Small multiples, arrays of similar graphics varying by one data dimension, facilitate comparisons while adhering to these principles; the number of panels can be estimated as n=total data pointspoints per panel summaryn = \frac{\text{total data points}}{\text{points per panel summary}}, ensuring each mini-graphic retains sufficient detail without overwhelming the display.

Common Pitfalls

One common pitfall in statistical graphics is the use of dual-axis charts, which superimpose two variables on different y-scales, often creating spurious correlations that mislead viewers about relationships between variables. For instance, when one axis scales a rapidly increasing variable like revenue while the other shows a stable metric like user count, the visual alignment can imply causation or stronger association than exists, distorting statistical inference. Similarly, pie charts frequently distort proportions because human perception relies more on area or arc length than central angle, leading to inaccurate judgments of relative sizes, especially for slices differing by less than 30 degrees. Research shows that even subtle variations in pie chart design, such as exploded slices, exacerbate these perceptual errors, making comparisons unreliable. Statistical biases arise when graphics fail to represent data density or variability accurately, such as overplotting in scatterplots with dense datasets, where overlapping points obscure patterns and underestimate data volume. This issue is particularly problematic in large-scale visualizations, as it hides outliers or clusters, leading to underestimation of variance or false negatives in trend detection. Another bias occurs from ignoring uncertainty, as in bar or line charts without , which present point estimates as precise truths and inflate confidence in conclusions, potentially biasing decisions in fields like experimental science. Without such indicators, viewers cannot assess the reliability of trends, violating principles of statistical transparency. Ethical concerns emerge from deliberate manipulations like cherry-picking data ranges, where axes are truncated to start above zero, exaggerating differences and creating false impressions of significance. This practice selectively highlights favorable subsets, undermining trust and promoting biased narratives, as seen in reports that omit baseline context to amplify minor changes. Likewise, applying 3D effects to charts, such as rotated bars or pies, distorts perceived magnitudes through perspective illusion, making trends appear steeper or volumes larger than they are, which can mislead stakeholders on growth or comparisons. Such embellishments prioritize over accuracy, raising issues of in data presentation. To avoid these pitfalls, practitioners can follow a for graphical , including verifying that scales reflect the full distribution without , ensuring of quantities, and labeling all elements clearly to prevent misinterpretation. For example, confirm axes start at zero unless justified, test for perceptual distortions by comparing with alternative encodings like bar charts, and always include measures where variability exists. A notable case illustrating these risks is in graphics, where aggregated reverses subgroup trends, as in a visualization of treatment success rates that appears lower overall for one group due to uneven sample sizes, despite higher efficacy in each . This paradox, evident in stacked bar charts, underscores the need to disaggregate visually to reveal hidden confounders, preventing erroneous policy or scientific conclusions. These remedies align with broader guidelines by emphasizing proactive verification over reactive correction.

Types of Graphics

Univariate Displays

Univariate displays are graphical representations designed to visualize the distribution of a single variable, enabling analysts to examine its shape, central tendency, variability, and anomalies without relying solely on numerical summaries. These methods provide an intuitive overview of data characteristics that summary statistics, such as the mean or median, often obscure by aggregating information and potentially masking outliers or multimodal patterns. By preserving the raw structure of the data, univariate displays facilitate exploratory data analysis and reveal insights into skewness, spread, and modality that enhance understanding beyond point estimates. Histograms represent one of the core types of univariate displays, illustrating frequency distributions through adjacent bars where the height or area corresponds to the count of observations within predefined intervals, or bins. Coined by Karl Pearson in 1895, histograms partition the range of the variable into bins and tally occurrences to depict the empirical distribution. The construction of a histogram requires selecting an appropriate bin width to balance detail and smoothness; an optimal bin width kk can be approximated using Scott's rule: k=3.5σ/n1/3k = 3.5 \sigma / n^{1/3}, where σ\sigma is the sample standard deviation and nn is the sample size, minimizing the integrated mean squared error for normally distributed data. This rule, derived asymptotically, helps avoid under- or over-binning, which could respectively obscure or fragment the distribution. Density plots offer a smoothed alternative to histograms, estimating the via (KDE), which convolves the data with a kernel function to produce a continuous curve representing relative frequencies. Introduced by Emanuel Parzen in , KDE uses a bandwidth parameter analogous to bin width, applying a symmetric kernel (e.g., Gaussian) centered at each data point and scaled by the bandwidth to approximate the underlying density without discrete boundaries. This smoothing reveals the distribution's contour more fluidly than histograms, particularly for moderate to large datasets, though it requires careful bandwidth selection to prevent over- or under-smoothing. Box plots, another fundamental univariate display, summarize the distribution using and extremes, featuring a central box spanning the (from the first to third ), a line at the , and whiskers extending to the minimum and maximum non-outlier values. Developed by in his 1977 book , box plots highlight the (minimum, first , , third , maximum) while identifying outliers as points beyond 1.5 times the from the . They are particularly effective for comparing distributions across groups but focus on robust measures resistant to extreme values. Interpreting univariate displays involves assessing key distributional features: skewness (asymmetry toward higher or lower values, evident in elongated tails), modality (unimodal for single peaks or multimodal for multiple clusters), and spread (variability captured by range, , or density width). These visuals outperform like the and by revealing non-normality, such as heavy tails or gaps, which could mislead if data deviate from assumptions of or ; for instance, a skewed distribution might show a pulled toward the tail, while the display exposes the imbalance. Graphical methods thus promote deeper insight, allowing detection of anomalies or subpopulations that aggregated metrics overlook. Variations on these core types include dot plots, suitable for small datasets, which position dots along a scale to show individual values and their without binning. Popularized by William S. Cleveland in 1984, dot plots stack or points to visualize frequencies and clusters, avoiding the aggregation of histograms while maintaining clarity for up to a few hundred observations. plots extend plots by integrating , displaying a symmetric trace around the box to convey both and distributional shape in a compact form. Introduced by Hintze and Nelson in 1998, plots combine the quartile-based robustness of plots with the smoothness of estimates, enabling side-by-side comparisons of distribution contours.

Bivariate and Multivariate Plots

Bivariate plots visualize relationships between two variables, enabling the detection of patterns such as correlations or clusters. The scatterplot, a fundamental technique, plots data points as coordinates (x, y) to reveal linear or nonlinear associations. For instance, in exploratory data analysis, scatterplots allow assessment of correlation strength, often supplemented by a trend line fitted via linear regression, modeled as y=β0+β1x+ϵy = \beta_0 + \beta_1 x + \epsilon, where β0\beta_0 is the intercept, β1\beta_1 the slope, and ϵ\epsilon the error term. This approach highlights dependencies while incorporating univariate building blocks like marginal distributions along axes for context. For discrete bivariate data, heatmaps encode pairwise values as colored cells, with intensity representing magnitude, such as in correlation matrices to identify co-variation across variable pairs. Multivariate plots extend this to three or more variables, addressing the challenge of high dimensionality by projecting relationships into lower-dimensional views. Parallel coordinates represent each observation as a polygonal line intersecting parallel axes, one per variable, facilitating identification of patterns like clusters or outliers in high-dimensional spaces. Scatterplot matrices (SPLOMs) arrange multiple scatterplots in a grid, showing all pairwise bivariate relationships, which aids in detecting overall structure and potential . Advanced techniques further mitigate dimensionality issues. Contour plots depict continuous bivariate surfaces as level sets, where lines connect points of equal z-value from z=f(x,y)z = f(x, y), useful for visualizing or regression surfaces. Andrews' curves transform multivariate data into univariate functions, plotting each observation as f(t)=x12+∑m=1⌊(p−1)/2⌋[x2msin⁡(mt)+x2m+1cos⁡(mt)]f(t) = \frac{x_1}{\sqrt{2}} + \sum_{m=1}^{\lfloor (p-1)/2 \rfloor} \left[ x_{2m} \sin(m t) + x_{2m+1} \cos(m t) \right]
Add your contribution
Related Hubs
User Avatar
No comments yet.