Hubbry Logo
Contour lineContour lineMain
Open search
Contour line
Community hub
Contour line
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Contour line
Contour line
Contour line
View on Wikipedia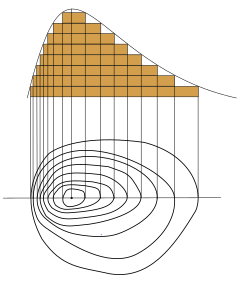
from Wikipedia
The bottom part of the diagram shows some contour lines with a straight line running through the location of the maximum value. The curve at the top represents the values along that straight line.
A three-dimensional surface, whose contour graph is below.
A two-dimensional contour graph of the three-dimensional surface in the above picture.

A contour line (also isoline, isopleth, isoquant or isarithm) of a function of two variables is a curve along which the function has a constant value, so that the curve joins points of equal value.[1][2] It is a plane section of the three-dimensional graph of the function parallel to the -plane. More generally, a contour line for a function of two variables is a curve connecting points where the function has the same particular value.[2]

In cartography, a contour line (often just called a "contour") joins points of equal elevation (height) above a given level, such as mean sea level.[3] A contour map is a map illustrated with contour lines, for example a topographic map, which thus shows valleys and hills, and the steepness or gentleness of slopes.[4] The contour interval of a contour map is the difference in elevation between successive contour lines.[5]

The gradient of the function is always perpendicular to the contour lines. When the lines are close together the magnitude of the gradient is large: the variation is steep. A level set is a generalization of a contour line for functions of any number of variables.

Contour lines are curved, straight or a mixture of both lines on a map describing the intersection of a real or hypothetical surface with one or more horizontal planes. The configuration of these contours allows map readers to infer the relative gradient of a parameter and estimate that parameter at specific places. Contour lines may be either traced on a visible three-dimensional model of the surface, as when a photogrammetrist viewing a stereo-model plots elevation contours, or interpolated from the estimated surface elevations, as when a computer program threads contours through a network of observation points of area centroids. In the latter case, the method of interpolation affects the reliability of individual isolines and their portrayal of slope, pits and peaks.[6]

History

[edit]
Edmond Halley's New and Correct Chart Shewing the Variations of the Compass (1701)

The idea of lines that join points of equal value was rediscovered several times. The oldest known isobath (contour line of constant depth) is found on a map dated 1584 of the river Spaarne, near Haarlem, by Dutchman Pieter Bruinsz.[7] In 1701, Edmond Halley used such lines (isogons) on a chart of magnetic variation.[8] The Dutch engineer Nicholas Cruquius drew the bed of the river Merwede with lines of equal depth (isobaths) at intervals of 1 fathom in 1727, and Philippe Buache used them at 10-fathom intervals on a chart of the English Channel that was prepared in 1737 and published in 1752. Such lines were used to describe a land surface (contour lines) in a map of the Duchy of Modena and Reggio by Domenico Vandelli in 1746, and they were studied theoretically by Ducarla in 1771, and Charles Hutton used them in the Schiehallion experiment. In 1791, a map of France by J. L. Dupain-Triel used contour lines at 20-metre intervals, hachures, spot-heights and a vertical section. In 1801, the chief of the French Corps of Engineers, Haxo, used contour lines at the larger scale of 1:500 on a plan of his projects for Rocca d'Anfo, now in northern Italy, under Napoleon.[9][10][11]

By around 1843, when the Ordnance Survey started to regularly record contour lines in Great Britain and Ireland, they were already in general use in European countries. Isobaths were not routinely used on nautical charts until those of Russia from 1834, and those of Britain from 1838.[9][12][13]

As different uses of the technique were invented independently, cartographers began to recognize a common theme, and debated what to call these "lines of equal value" generally. The word isogram (from Ancient Greek ἴσος (isos) 'equal' and γράμμα (gramma) 'writing, drawing') was proposed by Francis Galton in 1889 for lines indicating equality of some physical condition or quantity,[14] though isogram can also refer to a word without a repeated letter. As late as 1944, John K. Wright still preferred isogram, but it never attained wide usage. During the early 20th century, isopleth (πλῆθος, plethos, 'amount') was being used by 1911 in the United States, while isarithm (ἀριθμός, arithmos, 'number') had become common in Europe. Additional alternatives, including the Greek-English hybrid isoline and isometric line (μέτρον, metron, 'measure'), also emerged. Despite attempts to select a single standard, all of these alternatives have survived to the present.[15][16]

When maps with contour lines became common, the idea spread to other applications. Perhaps the latest to develop are air quality and noise pollution contour maps, which first appeared in the United States in approximately 1970, largely as a result of national legislation requiring spatial delineation of these parameters.

Types

[edit]

Contour lines are often given specific names beginning with "iso-" according to the nature of the variable being mapped, although in many usages the phrase "contour line" is most commonly used. Specific names are most common in meteorology, where multiple maps with different variables may be viewed simultaneously. The prefix "'iso-" can be replaced with "isallo-" to specify a contour line connecting points where a variable changes at the same rate during a given time period.

An isogon (from Ancient Greek γωνία (gonia) 'angle') is a contour line for a variable which measures direction. In meteorology and in geomagnetics, the term isogon has specific meanings which are described below. An isocline (κλίνειν, klinein, 'to lean or slope') is a line joining points with equal slope. In population dynamics and in geomagnetics, the terms isocline and isoclinic line have specific meanings which are described below.

Equidistant points

[edit]

A curve of equidistant points is a set of points all at the same distance from a given point, line, or polyline. In this case the function whose value is being held constant along a contour line is a distance function.

Isopleths

[edit]

In 1944, John K. Wright proposed that the term isopleth be used for contour lines that depict a variable which cannot be measured at a point, but which instead must be calculated from data collected over an area, as opposed to isometric lines for variables that could be measured at a point; this distinction has since been followed generally.[16][17] An example of an isopleth is population density, which can be calculated by dividing the population of a census district by the surface area of that district. Each calculated value is presumed to be the value of the variable at the centre of the area, and isopleths can then be drawn by a process of interpolation. The idea of an isopleth map can be compared with that of a choropleth map.[18][19]

In meteorology, the word isopleth is used for any type of contour line.[20]

Meteorology

[edit]
Isohyetal map of precipitation

Meteorological contour lines are based on interpolation of the point data received from weather stations and weather satellites. Weather stations are seldom exactly positioned at a contour line (when they are, this indicates a measurement precisely equal to the value of the contour). Instead, lines are drawn to best approximate the locations of exact values, based on the scattered information points available.

Meteorological contour maps may present collected data such as actual air pressure at a given time, or generalized data such as average pressure over a period of time, or forecast data such as predicted air pressure at some point in the future.

Thermodynamic diagrams use multiple overlapping contour sets (including isobars and isotherms) to present a picture of the major thermodynamic factors in a weather system.

Barometric pressure

[edit]
Video loop of isallobars showing the motion of a cold front

An isobar (from Ancient Greek βάρος (baros) 'weight') is a line of equal or constant pressure on a graph, plot, or map; an isopleth or contour line of pressure. More accurately, isobars are lines drawn on a map joining places of equal average atmospheric pressure reduced to sea level for a specified period of time. In meteorology, the barometric pressures shown are reduced to sea level, not the surface pressures at the map locations.[21] The distribution of isobars is closely related to the magnitude and direction of the wind field, and can be used to predict future weather patterns. Isobars are commonly used in television weather reporting.

Isallobars are lines joining points of equal pressure change during a specific time interval.[22] These can be divided into anallobars, lines joining points of equal pressure increase during a specific time interval,[23] and katallobars, lines joining points of equal pressure decrease.[24] In general, weather systems move along an axis joining high and low isallobaric centers.[25] Isallobaric gradients are important components of the wind as they increase or decrease the geostrophic wind.

An isopycnal is a line of constant density. An isoheight or isohypse is a line of constant geopotential height on a constant pressure surface chart. Isohypse and isoheight are simply known as lines showing equal pressure on a map.

[edit]
The 10 °C (50 °F) mean isotherm in July, marked by the red line, is commonly used to define the border of the Arctic region

An isotherm (from Ancient Greek θέρμη (thermē) 'heat') is a line that connects points on a map that have the same temperature. Therefore, all points through which an isotherm passes have the same or equal temperatures at the time indicated.[26][2] An isotherm at 0 °C is called the freezing level. The term lignes isothermes (or lignes d'égale chaleur) was coined by the Prussian geographer and naturalist Alexander von Humboldt, who as part of his research into the geographical distribution of plants published the first map of isotherms in Paris, in 1817.[27][28] According to Thomas Hankins, the Scottish engineer William Playfair's graphical developments greatly influenced Alexander von Humbolt's invention of the isotherm.[29] Humbolt later used his visualizations and analyses to contradict theories by Kant and other Enlightenment thinkers that non-Europeans were inferior due to their climate.[30]

An isocheim is a line of equal mean winter temperature, and an isothere is a line of equal mean summer temperature.

An isohel (ἥλιος, helios, 'Sun') is a line of equal or constant solar radiation.

An isogeotherm is a line of equal temperature beneath the Earth's surface.

Rainfall and air moisture

[edit]

An isohyet or isohyetal line (from Ancient Greek ὑετός (huetos) 'rain') is a line on a map joining points of equal rainfall in a given period. A map with isohyets is called an isohyetal map.

An isohume is a line of constant relative humidity, while an isodrosotherm (from Ancient Greek δρόσος (drosos) 'dew' and θέρμη (therme) 'heat') is a line of equal or constant dew point.

An isoneph is a line indicating equal cloud cover.

An isochalaz is a line of constant frequency of hail storms, and an isobront is a line drawn through geographical points at which a given phase of thunderstorm activity occurred simultaneously.

Snow cover is frequently shown as a contour-line map.

Wind

[edit]

An isotach (from Ancient Greek ταχύς (tachus) 'fast') is a line joining points with constant wind speed. In meteorology, the term isogon refers to a line of constant wind direction.

Freeze and thaw

[edit]

An isopectic line denotes equal dates of ice formation each winter, and an isotac denotes equal dates of thawing.

Physical geography and oceanography

[edit]

Elevation and depth

[edit]
Topographic map of Stowe, Vermont. The brown contour lines represent the elevation. The contour interval is 20 feet.

Contours are one of several common methods used to denote elevation or altitude and depth on maps. From these contours, a sense of the general terrain can be determined. They are used at a variety of scales, from large-scale engineering drawings and architectural plans, through topographic maps and bathymetric charts, up to continental-scale maps.

"Contour line" is the most common usage in cartography, but isobath for underwater depths on bathymetric maps and isohypse for elevations are also used.

In cartography, the contour interval is the elevation difference between adjacent contour lines. The contour interval should be the same over a single map. When calculated as a ratio against the map scale, a sense of the hilliness of the terrain can be derived.

Interpretation
[edit]

There are several rules to note when interpreting terrain contour lines:

  • The rule of Vs: sharp-pointed vees usually are in stream valleys, with the drainage channel passing through the point of the vee, with the vee pointing upstream. This is a consequence of erosion.
  • The rule of Os: closed loops are normally uphill on the inside and downhill on the outside, and the innermost loop is the highest area. If a loop instead represents a depression, some maps note this by short lines called hachures which are perpendicular to the contour and point in the direction of the low.[31] (The concept is similar to but distinct from hachures used in hachure maps.)
  • Spacing of contours: close contours indicate a steep slope; distant contours a shallow slope. Two or more contour lines merging indicates a cliff. By counting the number of contours that cross a segment of a stream, the stream gradient can be approximated.

Of course, to determine differences in elevation between two points, the contour interval, or distance in altitude between two adjacent contour lines, must be known, and this is normally stated in the map key. Usually contour intervals are consistent throughout a map, but there are exceptions. Sometimes intermediate contours are present in flatter areas; these can be dashed or dotted lines at half the noted contour interval. When contours are used with hypsometric tints on a small-scale map that includes mountains and flatter low-lying areas, it is common to have smaller intervals at lower elevations so that detail is shown in all areas. Conversely, for an island which consists of a plateau surrounded by steep cliffs, it is possible to use smaller intervals as the height increases.[32]

Electrostatics

[edit]

An isopotential map is a measure of electrostatic potential in space, often depicted in two dimensions with the electrostatic charges inducing that electric potential. The term equipotential line or isopotential line refers to a curve of constant electric potential. Whether crossing an equipotential line represents ascending or descending the potential is inferred from the labels on the charges. In three dimensions, equipotential surfaces may be depicted with a two dimensional cross-section, showing equipotential lines at the intersection of the surfaces and the cross-section.[citation needed]

The general mathematical term level set is often used to describe the full collection of points having a particular potential, especially in higher dimensional space.[citation needed]

Magnetism

[edit]
Isogonic lines for the year 2000. The agonic lines are thicker and labeled with "0".

In the study of the Earth's magnetic field, the term isogon or isogonic line refers to a line of constant magnetic declination, the variation of magnetic north from geographic north. An agonic line is drawn through points of zero magnetic declination. An isoporic line refers to a line of constant annual variation of magnetic declination .[33]

An isoclinic line connects points of equal magnetic dip, and an aclinic line is the isoclinic line of magnetic dip zero.

An isodynamic line (from δύναμις or dynamis meaning 'power') connects points with the same intensity of magnetic force.

Oceanography

[edit]

Besides ocean depth, oceanographers use contour to describe diffuse variable phenomena much as meteorologists do with atmospheric phenomena. In particular, isobathytherms are lines showing depths of water with equal temperature, isohalines show lines of equal ocean salinity, and isopycnals are surfaces of equal water density.

Geology

[edit]

Various geological data are rendered as contour maps in structural geology, sedimentology, stratigraphy and economic geology. Contour maps are used to show the below ground surface of geologic strata, fault surfaces (especially low angle thrust faults) and unconformities. Isopach maps use isopachs (lines of equal thickness) to illustrate variations in thickness of geologic units.

Environmental science

[edit]

In discussing pollution, density maps can be very useful in indicating sources and areas of greatest contamination. Contour maps are especially useful for diffuse forms or scales of pollution. Acid precipitation is indicated on maps with isoplats. Some of the most widespread applications of environmental science contour maps involve mapping of environmental noise (where lines of equal sound pressure level are denoted isobels[34]), air pollution, soil contamination, thermal pollution and groundwater contamination. By contour planting and contour ploughing, the rate of water runoff and thus soil erosion can be substantially reduced; this is especially important in riparian zones.

Ecology

[edit]

An isoflor is an isopleth contour connecting areas of comparable biological diversity. Usually, the variable is the number of species of a given genus or family that occurs in a region. Isoflor maps are thus used to show distribution patterns and trends such as centres of diversity.[35]

Social sciences

[edit]
From economics, an indifference map with three indifference curves shown. All points on a particular indifference curve have the same value of the utility function, whose values implicitly come out of the page in the unshown third dimension.

In economics, contour lines can be used to describe features which vary quantitatively over space. An isochrone shows lines of equivalent drive time or travel time to a given location and is used in the generation of isochrone maps. An isotim shows equivalent transport costs from the source of a raw material, and an isodapane shows equivalent cost of travel time.

A single production isoquant (convex) and a single isocost curve (linear). Labor usage is plotted horizontally and physical capital usage is plotted vertically.

Contour lines are also used to display non-geographic information in economics. Indifference curves (as shown at left) are used to show bundles of goods to which a person would assign equal utility. An isoquant (in the image at right) is a curve of equal production quantity for alternative combinations of input usages, and an isocost curve (also in the image at right) shows alternative usages having equal production costs.

In political science an analogous method is used in understanding coalitions (for example the diagram in Laver and Shepsle's work[36]).

In population dynamics, an isocline shows the set of population sizes at which the rate of change, or partial derivative, for one population in a pair of interacting populations is zero.

Statistics

[edit]

In statistics, isodensity lines [37] or isodensanes are lines that join points with the same value of a probability density. Isodensanes are used to display bivariate distributions. For example, for a bivariate elliptical distribution the isodensity lines are ellipses.

Thermodynamics, engineering, and other sciences

[edit]

Various types of graphs in thermodynamics, engineering, and other sciences use isobars (constant pressure), isotherms (constant temperature), isochors (constant specific volume), or other types of isolines, even though these graphs are usually not related to maps. Such isolines are useful for representing more than two dimensions (or quantities) on two-dimensional graphs. Common examples in thermodynamics are some types of phase diagrams.

Isoclines are used to solve ordinary differential equations.

In interpreting radar images, an isodop is a line of equal Doppler velocity, and an isoecho is a line of equal radar reflectivity.

In the case of hybrid contours, energies of hybrid orbitals and the energies of pure atomic orbitals are plotted. The graph obtained is called hybrid contour.

Other phenomena

[edit]

Algorithms

[edit]

Graphical design

[edit]
For features specific to topography, see Terrain cartography § Contour lines, and Topographic map § Conventions.

To maximize readability of contour maps, there are several design choices available to the map creator, principally line weight, line color, line type and method of numerical marking.

Line weight is simply the darkness or thickness of the line used. This choice is made based upon the least intrusive form of contours that enable the reader to decipher the background information in the map itself. If there is little or no content on the base map, the contour lines may be drawn with relatively heavy thickness. Also, for many forms of contours such as topographic maps, it is common to vary the line weight and/or color, so that a different line characteristic occurs for certain numerical values. For example, in the topographic map above, the even hundred foot elevations are shown in a different weight from the twenty foot intervals.

Line color is the choice of any number of pigments that suit the display. Sometimes a sheen or gloss is used as well as color to set the contour lines apart from the base map. Line colour can be varied to show other information.

Line type refers to whether the basic contour line is solid, dashed, dotted or broken in some other pattern to create the desired effect. Dotted or dashed lines are often used when the underlying base map conveys very important (or difficult to read) information. Broken line types are used when the location of the contour line is inferred.

Numerical marking is the manner of denoting the arithmetical values of contour lines. This can be done by placing numbers along some of the contour lines, typically using interpolation for intervening lines. Alternatively a map key can be produced associating the contours with their values.

If the contour lines are not numerically labeled and adjacent lines have the same style (with the same weight, color and type), then the direction of the gradient cannot be determined from the contour lines alone. However, if the contour lines cycle through three or more styles, then the direction of the gradient can be determined from the lines. The orientation of the numerical text labels is often used to indicate the direction of the slope.

Plan view versus profile view

[edit]
See also: Topographic profile

Most commonly contour lines are drawn in plan view, or as an observer in space would view the Earth's surface: ordinary map form. However, some parameters can often be displayed in profile view showing a vertical profile of the parameter mapped. Some of the most common parameters mapped in profile are air pollutant concentrations and sound levels. In each of those cases it may be important to analyze (air pollutant concentrations or sound levels) at varying heights so as to determine the air quality or noise health effects on people at different elevations, for example, living on different floor levels of an urban apartment. In actuality, both plan and profile view contour maps are used in air pollution and noise pollution studies.

Contour map labeled aesthetically in an "elevation up" manner.

Labeling contour maps

[edit]

Labels are a critical component of elevation maps. A properly labeled contour map helps the reader to quickly interpret the shape of the terrain. If numbers are placed close to each other, it means that the terrain is steep. Labels should be placed along a slightly curved line "pointing" to the summit or nadir, from several directions if possible, making the visual identification of the summit or nadir easy.[38][39] Contour labels can be oriented so a reader is facing uphill when reading the label.

Manual labeling of contour maps is a time-consuming process, however, there are a few software systems that can do the job automatically and in accordance with cartographic conventions, called automatic label placement.

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Contour line

View on Grokipedia
from Grokipedia
A contour line, also known as an isoline or level , is a connecting points of equal value on a two-dimensional representation, such as a or graph, where the value typically represents , , , or another measurable . In topographic mapping, contour lines specifically depict lines of equal above or below a reference datum, usually mean , allowing visualization of shape, slope steepness, and landforms like hills or depressions. These lines are fundamental to , enabling users to interpret three-dimensional landscapes on flat surfaces by showing how changes across space. In and , contour lines represent level sets of a function f(x,y)f(x, y), where the consists of all points (x,y)(x, y) such that f(x,y)=cf(x, y) = c for a constant cc, forming a analogous to a topographic chart of the function's graph. Key include that contour lines never cross each other, as each point on the has a unique or value, and closely spaced lines indicate steep gradients while widely spaced ones suggest gentle slopes or flat areas. Index contours, often bolder and labeled, mark every fifth line to aid readability, with contour intervals varying by terrain but commonly 10 or 20 feet (3 or 6 m) on U.S. 7.5-minute topographic maps. The concept of contour lines originated in the late 18th century, with British mathematician credited for their invention during the 1775–1776 in , where he used them to connect points of equal altitude and calculate the mountain's volume for determining Earth's density. Published by the Royal Society in 1778, Hutton's contour map of marked one of the earliest practical applications, laying the groundwork for modern surveying and topographic mapping techniques. Today, contour lines extend beyond geography to fields like for isobars, for bathymetric charts, and for visualizing data gradients, underscoring their versatility in scientific and technical visualization.

Fundamentals

Definition

A contour line is a along which every point has the same value of an underlying , such as or , on a two-dimensional representation of a continuous surface. These lines connect points of equal magnitude, effectively illustrating variations in the field without directly showing the third dimension. Unlike discrete data points, which represent isolated measurements, contour lines depict values across a continuous surface, bridging gaps between sampled locations to form a smooth, cohesive visualization. For instance, on topographic maps, contour lines join points of equal to reveal shape, while on weather maps, they connect areas of equal . This assumes a gradual change in the , enabling the representation of phenomena that vary smoothly over space. The terms isoline, isarithm, and isopleth are synonymous with contour line, though isarithms specifically denote lines based on actual point measurements, while isopleths may involve more interpretive averaging. Contour lines serve as a foundational tool for visualizing two-dimensional projections of three-dimensional surfaces or planar fields, essential for interpreting spatial data in various scientific contexts.

Mathematical Principles

Contour lines represent level sets of a scalar function f:R2→Rf: \mathbb{R}^2 \to \mathbb{R}, where the is defined by f(x,y)=cf(x, y) = c for some constant cc. These level sets partition the plane into regions where the function takes values above or below cc, serving as boundaries between areas of differing function values. Equivalently, the contour satisfies f(x,y)−c=0f(x, y) - c = 0, which describes an implicit curve in the plane. The gradient vector ∇f=(∂f∂x,∂f∂y)\nabla f = \left( \frac{\partial f}{\partial x}, \frac{\partial f}{\partial y} \right) at any point on the contour is perpendicular to the tangent vector of the curve, indicating the direction of steepest ascent for the function and thus the normal to the level set. This orthogonality follows from the chain rule: along the contour, the directional derivative in the tangent direction is zero, so ∇f⋅t=0\nabla f \cdot \mathbf{t} = 0 where t\mathbf{t} is the unit tangent. The magnitude of ∇f\nabla f determines the spacing between nearby contours, with closer lines corresponding to larger gradients and steeper changes. In discrete settings, such as sampled data points, contour positions are estimated via . Linear along edges between data points locates where the function crosses the level cc, by solving for the tt in f((1−t)p1+tp2)≈(1−t)f(p1)+tf(p2)=cf((1-t)\mathbf{p}_1 + t\mathbf{p}_2) \approx (1-t)f(\mathbf{p}_1) + t f(\mathbf{p}_2) = c. For regularly gridded data, extends this to quadrilaterals, approximating ff as a in both xx and yy directions within each cell to find intersection points. These methods assume piecewise linearity, providing a basic framework for constructing contours from sparse or grid-based samples. Contour lines apply specifically to scalar fields, distinguishing them from visualizations of vector fields, where analogous curves like streamlines trace the direction of the vector at each point rather than constant scalar values. In topography, for instance, elevation forms such a scalar field, with contours marking constant heights.

Key Properties

Contour lines exhibit a nesting property where contours of lower values enclose those of higher values in elevated terrains, such as hilltops represented by closed loops of progressively higher elevations toward the center, while the reverse occurs in depressions. This hierarchical enclosure reflects the monotonic increase or decrease in the underlying scalar field, allowing visualization of topographic highs and lows through concentric patterns. Contours of different values never intersect, as each line represents a unique level set in the continuous field, ensuring unambiguous representation of elevation changes. However, contours of the same value may merge or touch at saddle points, where the transitions between ridges and valleys without altering the constant value along the line. The spacing between adjacent contour lines indicates the local of the field: closely spaced lines denote steep changes, such as near cliffs, while widely spaced lines signify gentle slopes or flat areas. Uniform spacing corresponds to linear gradients, providing a direct visual cue for steepness without quantitative computation. Topologically, contour lines form closed curves around isolated features like summits or basins, or extend to map boundaries in unbounded regions, maintaining continuity across the represented domain. Depressions and summits are distinguished using hachures—short lines to the contour indicating direction into the feature—or other patterns on closed loops to denote inward descent or ascent. While contour lines approximate smooth, continuous scalar fields like elevation, they can appear jagged in areas of sparse data, reflecting limitations in sampling density rather than actual terrain irregularity.

Historical Development

Early Origins

In the 16th and 17th centuries, European artists and cartographers began producing sketches and charts that visually approximated varying depths and directions, foreshadowing contour techniques. Similarly, early nautical charts incorporated isogonic lines—contours of equal magnetic declination—to aid navigation; the earliest known example is Luís Teixeira's manuscript chart of circa 1585, which plotted these lines across the Atlantic and Indian Oceans for Portuguese sailors. A pivotal advancement came in 1701 with Edmond Halley's publication of the first printed explicit contour map, titled A New and Correct Chart Shewing the Variations of the Compass, which used curved isolines (isogones) to depict across the Atlantic Ocean, based on his voyages aboard HMS Paramour. This map not only improved maritime navigation by revealing systematic patterns in compass deviations but also demonstrated contours' utility for visualizing continuous spatial phenomena. These developments drew philosophical inspiration from Gottfried Wilhelm Leibniz's principle of continuity, articulated in works like his 1684 Nova Methodus, which posited that natural changes occur by degrees without abrupt leaps, enabling the spatial representation of gradual variations in phenomena such as or elevation. However, early applications remained and sporadic, constrained by rudimentary measurement tools like basic compasses and chains, which prevented comprehensive data gathering and standardized isoline construction.

18th-19th Century Advances

During the Enlightenment, French geographer Philippe Buache advanced the use of contour lines in the 1750s, notably with a 1752 chart of the that employed explicit contours at 10-fathom intervals to depict varying sea depths, building on his physiographic theories of interconnected watersheds and mountain systems as natural dividers. These works provided an early framework for visualizing hydrological and topographic divisions, influencing subsequent cartographic practices. Building on Edmond Halley's 1701 oceanic isogonic lines for , which marked the first printed use of such curves, a key development in topographic applications came from British mathematician . During the 1775–1776 in , Hutton used contour lines to connect points of equal altitude, enabling the calculation of the mountain's volume to determine Earth's . His contour map of , published by the Royal Society in 1778, represented one of the earliest practical uses of contours for . 19th-century innovations expanded contours beyond navigation to systematic scientific representation. German explorer pioneered their application in with his 1817 isotherm maps, the first to connect global points of equal temperature using isopleths derived from extensive observational data. These charts, published in Mémoires de physique et de chimie de la Société d'Arcueil, demonstrated contours' utility for abstracting environmental patterns, inspiring their adoption in diverse fields. Topographic mapping saw institutional milestones in the mid-19th century, with the British incorporating contours on its one-inch and six-inch scale maps starting in the 1830s, following accurate leveling surveys initiated in 1840 using Gravatt's improved level. This enabled the depiction of through spot heights and hachures supplemented by contours, standardizing their use across national surveys. , early contour rules emerged in 1853 amid Pacific Railroad Surveys conducted by the U.S. Army Corps of Topographical Engineers, where contours illustrated terrain profiles for route planning. These efforts relied on refined instruments, including Jesse Ramsden's 1787 precision for angular measurements and advanced leveling devices that achieved sub-foot accuracy in data. Contours extended to geology through William Smith's 1815 A Delineation of the Strata of , which included cross-sections employing stratigraphic layering to convey three-dimensional subsurface structures, akin to early contour-based visualization of rock units. Smith's hand-colored maps and sections, based on correlations, illustrated inclined strata dipping beneath younger layers, providing a foundational method for interpreting geological contours without explicit lines.

20th Century Standardization

In the early , the U.S. Geological Survey (USGS) played a pivotal role in standardizing contour lines for topographic mapping through detailed instructions that specified interval choices based on and map scale to ensure uniformity across national surveys. These guidelines, formalized in publications like the 1928 Topographic Instructions (reflecting practices from the mid-1920s), recommended intervals such as 20 feet for 1:62,500-scale maps in moderate areas and finer 5- or 10-foot intervals for flatter terrains, aiming to balance detail with readability while minimizing interpretive errors in elevation representation. This approach built on 19th-century foundations but emphasized scalable consistency for large-scale federal mapping programs. During , military applications accelerated contour line standardization, with Allied forces relying on detailed topographic maps featuring precise contours for terrain analysis, positioning, and . The U.S. Army Map Service and equivalents produced maps at scales like 1:50,000 with 10-meter intervals, incorporating brown hachuring for steep slopes to enhance rapid interpretation under combat conditions; post-war declassification of these maps facilitated civilian adoption by disseminating standardized contour techniques to international mapping agencies. The marked a transition toward digital precursors, as developed early computer programs for automated contour plotting from elevation data, enabling efficient generation of lines on System/360 mainframes and plotters for large-scale models. These tools, such as FORTRAN-based algorithms on the IBM 7094, automated the and drafting of contours, shifting from manual scribing to computational methods and laying groundwork for broader adoption in government and academic mapping. Global efforts in the 1970s, led by initiatives, promoted contour line standardization in developing regions through technical assistance programs and surveys like the 1974 World Cartography report, which advocated uniform topographic mapping at 1:50,000 scales with 10-meter intervals to support and . These initiatives addressed challenges such as inconsistent interval selection, which could lead to ambiguity in relief depiction, by recommending fixed intervals—e.g., 10 meters for 1:50,000 scales in varied terrains—to foster across national borders and reduce errors in cross-regional analysis.

Applications by Field

Cartography and Topography

In and , contour lines are essential for depicting the and of terrestrial landforms on , connecting points of equal above a reference level such as mean . These lines form closed, nested patterns that represent hills and valleys, with denser spacing indicating steeper . Index contours, which are bold or thicker lines labeled with specific values, occur at regular intervals—typically every fifth contour—to facilitate quick orientation, while intermediate contours are thinner lines between them that provide finer detail on the landscape's relief. Contour intervals, the vertical distance between adjacent lines, vary by scale and ; for standard USGS 1:24,000-scale maps, common intervals range from 5 to 50 feet in flatter areas, increasing to 80 or 100 feet in mountainous regions to balance clarity and detail. Supplementary or auxiliary contours, even thinner dashed lines, may be added between standard intervals in areas of subtle relief to enhance accuracy without overcrowding the . Hypsometric tints enhance topographic maps by applying graduated colors between contour lines to visually represent changes and provide shading, often using greens for lowlands, yellows for mid-s, and browns or reds for highlands. This layer-tinting technique, also known as coloring, aids in interpreting broad topographic patterns at a glance and is particularly useful in shaded- maps where contours alone might obscure subtle gradients. In USGS topographic maps, depressions—such as pits or sinks—are indicated by contour lines with short perpendicular tick marks called hachures pointing toward the lower , distinguishing them from rising . Supplementary depression contours can be included between primary lines to depict small-scale features within these lows. Bathymetric contours extend the principles of topographic mapping to underwater on coastal maps, outlining depths below in a manner analogous to contours above it, often integrated into hybrid bathymetric-topographic charts for nearshore areas. The USGS and NOAA collaborate on such representations, using contours at intervals like 10 or 20 feet near coastlines to map features such as shelves and canyons. In modern , contour lines are increasingly derived from Digital Elevation Models (DEMs), high-resolution raster datasets that model surfaces, allowing for automated generation and seamless integration of topographic and bathymetric data in digital mapping products. This approach maintains conceptual fidelity to traditional mapping while enabling scalable visualization for applications like and environmental assessment.

Meteorology

In meteorology, contour lines are essential for mapping and analyzing atmospheric variables on weather charts, enabling the visualization of , , and other fields to understand synoptic-scale patterns and short-term dynamics. These lines connect points of equal value, facilitating the identification of gradients that drive atmospheric motion. Unlike static representations, meteorological contours depict dynamic fields that evolve rapidly, aiding in the of systems such as cyclones and fronts. Isobars, or contours of constant , are a cornerstone of surface and upper-air maps, typically drawn at intervals of 4 millibars starting from 1000 millibars. Closed isobars encircling a central denote cyclones, where converging winds spiral inward, often associated with stormy conditions and . Conversely, closed high-pressure isobars surround anticyclones, featuring diverging winds that promote clear skies and . Isotherms represent contours of constant temperature and are used to delineate thermal gradients on surface and constant-pressure charts. Areas where isotherms are closely spaced indicate sharp temperature contrasts, often marking frontal boundaries between contrasting air masses, such as the leading edge of a cold front where cooler air advances. These tight spacings highlight zones of potential instability and weather activity, including cloud formation and precipitation. Other specialized contours include isohyets, which connect points of equal amounts to map rainfall distribution, and isotachs, lines of equal that reveal jet streams and areas of strong flow. Isohyets are particularly useful for assessing risks in regions of concentrated rainfall, while isotachs on upper-level charts identify maxima exceeding 100 knots, influencing development. Meteorological analysis employs rules based on contour patterns, such as the gradient wind approximation, which balances gradients, Coriolis forces, and curvature for near isobars in curved flows around . Troughs appear as elongated low-pressure areas without closed centers, promoting cyclonic circulation, while ridges are extended high-pressure features fostering anticyclonic . These structures guide the interpretation of directions, with mathematical gradients briefly informing the perpendicular relationship to flow. In , contour patterns on isobaric maps predict motion and ; for instance, geostrophic approximate actual flow parallel to isobars, with lows moving toward regions of falling pressure and highs toward rising pressure, enabling predictions of tracks and frontal passages.

and

In oceanography, contour lines are extensively used to represent underwater through bathymetric charts, where they depict lines of equal depth known as isobaths. These lines connect points of identical depth relative to a reference level, such as mean , and are crucial for and resource exploration. For instance, on nautical charts produced by organizations like the (NOAA), bathymetric contours are typically marked in feet or meters, with denser spacing indicating steeper seafloor gradients. Spot depths, or soundings, supplement these contours by providing precise depth measurements at specific locations, often obtained via or multibeam echosounders. Beyond depth, oceanographic applications extend contours to other physical properties of . Isohalines represent lines of equal , illustrating variations influenced by factors like , , and river inflows, which are vital for understanding ocean circulation and mixing processes. Similarly, isotherms delineate areas of constant , highlighting thermal fronts and stratification layers that affect marine ecosystems and patterns. These contours are derived from datasets collected by research vessels and buoys, as documented in reports from the Intergovernmental Oceanographic Commission (IOC). One of the earliest bathymetric charts was produced by in 1853, featuring rudimentary depth contours based on naval soundings. In , contour lines map surface features beyond elevation, such as and vegetation density, to analyze land-water interactions. Contours of connect areas with equivalent in the , aiding in assessments of risk and agricultural productivity; for example, satellite-derived data from NASA's (SMAP) mission visualizes these patterns across watersheds. Vegetation density contours, often expressed as (NDVI) isolines, reveal gradients in plant cover influenced by topography and climate, supporting . Additionally, contours delineate watershed divides by outlining drainage basins where elevation contours converge at ridgelines, facilitating hydrological modeling. Contour lines are instrumental in identifying seabed features by their characteristic bending and spacing patterns. Steep trenches, such as the , appear as tightly packed, V-shaped contours indicating rapid depth increases, while mid-ocean ridges exhibit broader, undulating lines reflecting gentler slopes and volcanic activity. These patterns, interpreted from global bathymetric datasets like those from the General Bathymetric Chart of the Oceans (GEBCO), enable geoscientists to map tectonic structures and potential mineral deposits. The integration of contour lines in coastal zones bridges hypsographic (land elevation) and bathymetric representations, creating seamless maps of the land-sea transition. In these areas, contours transition from positive elevations above to negative depths below, using a common datum to highlight features like continental shelves and submarine canyons. Such integrated visualizations, employed by the U.S. Geological Survey (USGS) in studies, underscore vulnerabilities to sea-level rise and inform efforts.

Geology and Environmental Sciences

In geology, isopach maps utilize contour lines to depict variations in the thickness of sedimentary strata or layers, aiding in the reconstruction of depositional environments and basin . These lines connect points of equal thickness, typically measured in feet or meters, and are essential for identifying thickening trends toward depocenters or thinning along basin margins. Similarly, structure contour maps represent subsurface horizons by connecting points of equal on a specific geologic surface, such as the top of a formation, to visualize folds, faults, and overall structural without direct surface exposure. These maps often reveal closed contours indicating structural basins or highs, which are critical for resource exploration. In environmental sciences, contour lines delineate potentiometric surfaces, which map the or level across , showing flow directions and recharge/discharge zones through lines of equal water elevation. These surfaces guide assessments of sustainability and migration, as water flows perpendicular to the contours from higher to lower heads. Isopleth maps further apply contours to represent spatial distributions of pollutant concentrations in or soil, such as equal lines of dissolved contaminants like nitrates or , facilitating plume delineation and remediation planning. Freeze-thaw boundaries in regions are mapped using isotherms, which are contour lines of equal , often the mean annual air (MAAT) at 0°C, to define the southern limit of continuous and transitions to discontinuous zones. These maps highlight areas vulnerable to thaw-induced and shifts, with isotherms shifting northward under warming climates. Tectonic applications employ isoseismal contours to map seismic intensity distributions from earthquakes, connecting points of equal shaking severity on scales like the Modified Mercalli Intensity, which reveal propagation patterns influenced by subsurface . Contours of fault displacements illustrate variations in slip along rupture planes, typically in meters, to quantify coseismic deformation and assess tectonic strain accumulation. In ecological contexts, contours of map acidity gradients across landscapes, using isopleths to identify zones suitable for specific plant communities or microbial activity, as pH influences nutrient availability and suitability. Similarly, erosion rate contours depict spatial variations in loss, often derived from models like the Universal Soil Loss Equation, to evaluate degradation hotspots and inform restoration by linking to vegetation cover and .

Other Disciplines

In physics, contour lines represent surfaces where the remains constant, forming perpendicular paths to lines in . These lines illustrate regions of equal for charges, aiding visualization of field behavior around conductors or point charges. Similarly, in magnetostatics, lines can be depicted as contours of the function, particularly in two-dimensional representations where they trace paths of constant . In the social sciences, contour lines, often termed isopleths, map continuous distributions such as , revealing gradients from urban cores to rural peripheries. They also delineate economic indicators, like income levels, through isolines that highlight spatial disparities in wealth across regions. In , density contours visualize distributions via , enclosing regions of high probabilistic density around data clusters. These contours, akin to topographic maps, facilitate identification of multimodal patterns or outliers in datasets like scatter plots of correlated variables. In , isotherms trace paths of constant on pressure-volume diagrams, while adiabats represent reversible processes without exchange, curving steeper than isotherms to show conservation. Phase diagrams employ these contours to demarcate boundaries between , , and gas states, with isotherms indicating equilibrium for phase transitions. In modern , contours of loss surfaces conceptually map optimization landscapes, where level sets reveal minima, maxima, and saddle points in high-dimensional parameter spaces during training.

Generation Methods

Manual Techniques

Manual techniques for generating contour lines rely on direct field measurements and hand-drafting to represent elevations on maps. These methods involve collecting spot elevations through traditional practices and then interpolating and sketching lines of equal elevation on paper. Predating widespread computer use, such approaches demanded precision and artistic judgment from surveyors and cartographers. Surveying for contour lines begins with establishing horizontal control using , where angles between known points are measured to determine positions accurately. Vertical control is achieved through leveling, employing instruments like automatic levels or theodolites to record elevations relative to a benchmark, yielding spot heights at intervals across the . These spot elevations form the foundational points for , at intervals appropriate to the map scale and terrain complexity. Once collected, spot elevations are plotted on scaled to the map's projection, with horizontal coordinates from and vertical values annotated at each point. The drafting process then connects these points with preliminary straight lines to outline elevation trends, followed by smoothing into continuous curves using tools like French curves or flexible splines to approximate natural flow without sharp angles. This hand-sketching ensures contours reflect realistic , such as closing in depressions or V-shapes in valleys. Interpolation between spot elevations is performed manually, often by calculating arithmetic means for linear segments—dividing the elevation difference proportionally along the distance between points—and adjusting for terrain steepness by narrowing on slopes and widening them on flats. Surveyors visually estimate adjustments to maintain uniform interval spacing, guided by rules like never crossing and always pointing upstream in valleys. Specialized tools enhance accuracy in manual contouring; the alidade, mounted on a plane table, allows sighting and plotting points directly in the field for real-time contour sketching. Planimeters are employed post-drafting to trace between contour lines and compute enclosed areas, useful for volume estimates in earthwork calculations. These techniques were the standard for topographic mapping through the mid-20th century, particularly in the United States Geological Survey's operations until the 1960s, and remain relevant today for remote fieldwork where digital tools are impractical.

Computational Algorithms

Computational algorithms for generating contour lines primarily operate on digital elevation models (DEMs) or raster data grids, enabling automated and scalable production of contours from large datasets. These methods interpolate values between known points to trace lines of equal value, contrasting with manual techniques by leveraging computational efficiency for high-resolution outputs. Key approaches include grid-based and vector-based interpolation, each suited to different data structures. Grid-based methods, such as the algorithm, process raster data by dividing the grid into squares and determining contour segments within each based on the values at the four corner . This algorithm examines 16 possible configurations of pixel values relative to a contour level, using a to connect equal-value points with line segments, effectively generating closed or open contours across the field. An extension to triangular grids, marching triangles, applies similar principles to irregularly spaced data, subdividing triangles and interpolating vertices on edges where the contour crosses. These methods are particularly efficient for uniform raster datasets like satellite-derived DEMs, producing vector contours directly from pixel interpolations. For vector interpolation from scattered point data, a common workflow involves constructing a to form a (TIN), followed by contour tracing along the edges of the triangles. The ensures that no point lies inside the of any triangle, maximizing the minimum angle and providing a robust for . Contour lines are then traced by identifying edges where interpolated values cross the desired level, connecting segments to form continuous polylines. This approach is advantageous for sparse or unevenly distributed data, as the TIN adapts to data density without introducing unnecessary nodes in flat areas. Seminal algorithms include CONREC, developed in 1987 for efficient contour plotting from gridded data, which subdivides each rectangular cell into triangles and computes linear interpolations to output contour segments for plotting. Modern TIN-based methods build on this by incorporating adaptive refinement, where triangle density increases in regions of high to capture detailed without excessive computation. For instance, TIN generation in GIS software often uses to create surfaces from which contours are extracted, supporting both raster-to-vector and point-cloud inputs. To handle errors and artifacts, such as jagged lines from discrete sampling or in steep , techniques are applied post-generation. These include low-pass filtering on the input raster or spline-based on contour polylines to reduce noise while preserving overall shape, often using constrained edges in the to enforce continuity. Adaptive interval selection further mitigates issues by dynamically adjusting contour spacing based on variability—closer intervals in rugged areas and sparser in flat regions—to balance detail and visual clarity without introducing errors. In geographic information systems (GIS), these algorithms are integrated into tools like ArcGIS's Contour function, which generates polylines from raster surfaces with options for smoothing and base intervals, facilitating applications in mapping and analysis. Recent advancements in the incorporate , particularly models like convolutional neural networks, to enhance contour generation from noisy or incomplete data, such as low-quality , by automatically vectorizing contours with improved accuracy over traditional methods.

Visualization and Design

Graphical Representation

Contour lines are rendered using distinct stylistic conventions to convey data clearly and aesthetically on maps and diagrams. Index contours, which highlight major intervals such as every fifth line, are typically depicted as thick, solid brown lines to emphasize key reference points and facilitate rapid orientation. Intermediate contours, filling the spaces between index lines, employ thinner solid brown lines for subtlety, while supplementary contours—representing half-intervals in detailed or flat terrains—are often dashed to denote approximate elevations without overwhelming the . These line styles, including variations in thickness for emphasis, enhance by prioritizing hierarchical in topographic representations. Color schemes play a crucial role in graphical representation, with contour lines themselves standardized in brown to symbolize terrestrial on topographic maps. Areas between are frequently filled with graduated hypsometric tints, progressing from dark greens at low elevations to yellows, browns, and whites at higher altitudes, creating a layered visual progression that intuitively communicates without relying solely on line density. This approach, rooted in principles of perceptual , uses monochromatic or analogous color families to maintain while delineating elevation bands effectively. Shading techniques further augment the two-dimensional rendering of contours to simulate three-dimensional form. Hillshading, which applies or colored overlays mimicking directional illumination from a hypothetical light source, casts shadows that align with contour patterns to evoke depth and . Contour-parallel patterns, such as short perpendicular ticks or hachures, can be integrated along lines to indicate aspect and steepness, providing an additional layer of topographic nuance while preserving the map's overall clarity. These methods balance functional depiction with artistic illusion, ensuring contours integrate seamlessly into the broader visual composition. Scale-dependent considerations are essential for effective rendering, particularly in managing density to prevent visual clutter. In flat terrains where contours cluster closely due to minimal elevation change, thinning techniques selectively omit intermediate or supplementary lines, opting for sparser representation to maintain legibility without sacrificing essential gradient information. This adaptive approach adjusts line frequency based on map scale and terrain variability, ensuring that steep areas retain detailed spacing while low-relief zones avoid overcrowding. The relative spacing of contours, where closer lines denote steeper gradients, thus serves as a subtle cue for terrain steepness in these designs. Accessibility in graphical representation addresses diverse user needs, including color vision deficiencies affecting a significant portion of the . High-contrast line styles, such as bold solids against backgrounds, combined with tint palettes avoiding red-green oppositions—favoring blue-yellow or monochromatic schemes—ensure distinguishability for color-blind viewers. In digital contexts, vector rendering of contour lines provides scalable, resolution-independent crispness ideal for interactive maps, whereas raster techniques excel for rendering shaded or tinted fills, allowing hybrid approaches that optimize both precision and visual appeal across devices.

Labeling Practices

Labeling practices for contour lines emphasize clarity, legibility, and minimal visual clutter to ensure users can quickly interpret without distraction. Contour values are placed directly on the lines, typically at midpoints between intersections or at bends where the line curves, allowing for straightforward association with the represented . This placement helps users trace the contour's path while identifying its value efficiently. To reduce redundancy and highlight significant elevation changes, index contours—thicker lines accentuating every fourth or fifth contour—are labeled with their elevation values, while intermediate contours are generally unlabeled unless supplementary detail is needed in flat or complex . Labeling occurs at frequent but spaced intervals along the line to avoid overcrowding, with figures oriented to read "uphill" in alignment with the contour's general direction. Key rules govern label positioning to preserve map integrity: labels must not cross other contours or features, as this could imply erroneous connections or obscure underlying details; instead, they are positioned to follow the line's flow without interruption. In densely packed areas where direct placement risks overlap, short leader lines—thin extensions from the contour to the —connect the annotation offset from the line, maintaining association while freeing space. Feature-specific annotations enhance precision for critical points. Spot elevations, marked as precise height values (often in black for verified accuracy to one-tenth the contour interval), are placed at summits, peaks, junctions, and edges to supplement contours where exact readings are essential. Depressions, shown with hachured contours (short ticks pointing inward), receive auxiliary labels at their lowest points to denote the depression's floor , typically prefixed with a minus sign or "below" for negative values relative to . Modern automated tools facilitate dynamic labeling in GIS software, employing algorithms that optimize positions by analyzing contour topology—such as constructing a contour tree to identify safe placement zones—and adjusting for overlap or in real time. These methods, rooted in computational , ensure labels adapt to varying scales and densities without manual intervention. USGS standards further specify that labels should be oriented parallel to the contours for intuitive reading, with figures sized and styled to integrate seamlessly with the map's brown contour scheme, promoting consistency across topographic products.

Plan and Profile Views

In topographic mapping, the plan view presents an overhead, two-dimensional representation of the , where contour lines form a complete network illustrating the of across a . This view allows users to visualize the horizontal layout of features such as hills, valleys, and ridges, providing a comprehensive overview of the surface morphology without distortion in the horizontal plane. Contour lines in plan view connect points of equal , enabling the inference of steepness through line spacing—closer lines indicate steeper gradients—while maintaining a consistent scale for navigation and broad-scale analysis. In contrast, the profile view offers a one-dimensional vertical cross-section along a specified line on the plan map, slicing through the contour network to depict elevation changes as a side-on graph of height versus horizontal distance. This representation reveals the true vertical profile of the terrain, such as the rise and fall along a transect, which is essential for understanding specific elevation variations that may not be immediately apparent in the plan view. Profiles are constructed by marking where the transect line intersects each contour and plotting those elevations, often resulting in a line graph that highlights peaks, troughs, and gradients. To convert from a plan view to a profile view, elevations are extracted along the chosen line by proportionally interpolating between contour intersections, assuming a linear change in height within each interval. For instance, if a line crosses midway between two contours separated by a 10-meter interval, the elevation at that point is estimated as halfway between the known values, ensuring a smooth approximation of the subsurface terrain. This interpolation method, while approximate, provides a reliable vertical slice for analysis. Plan views are particularly useful for , such as in or , where the full spatial context aids in route selection and feature identification, while profile views support applications like determining road grades or cut-and-fill volumes in projects. For example, engineers use profiles to calculate the percentage along a proposed alignment, ensuring safe and efficient design. However, plan views inherently lose the true vertical scale, compressing three-dimensional features into two dimensions and potentially underrepresenting steepness or depth, whereas profile views sacrifice horizontal context, limiting understanding of lateral relationships between features. To address these limitations, hybrid approaches in the 2020s have integrated (VR) and (AR) technologies, such as the AR Sandbox system, which overlays dynamic contour lines and elevation colors onto physical sand models in real time, allowing interactive three-dimensional exploration that combines plan and profile perspectives.

References

  1. https://support.esri.com/en-us/gis-dictionary/contour-line
  2. https://www.usgs.gov/faqs/what-a-topographic-map
  3. https://pubs.usgs.gov/gip/19/downloads/Chapter_3/Activities/Topographic_maps.pdf
  4. https://sites.math.duke.edu/education/ccp/materials/mvcalc/surfaces/surf5.html
  5. https://www.fsl.orst.edu/pnwerc/wrb/Atlas_web_compressed/Appendices/b.USGStopo_web.pdf
  6. https://pubs.usgs.gov/gip/TopographicMapSymbols/topomapsymbols.pdf
  7. https://www.tandfonline.com/doi/full/10.1080/17445647.2019.1582439
  8. https://profhorn.aos.wisc.edu/wxwise/contour/index.html
  9. https://www.sciencedirect.com/topics/mathematics/contour-line
  10. https://www.khanacademy.org/math/multivariable-calculus/thinking-about-multivariable-function/ways-to-represent-multivariable-functions/a/contour-maps
  11. https://www.qgistutorials.com/en/docs/3/interpolating_point_data.html
  12. https://gisgeography.com/contour-lines-topographic-map/
  13. https://support.esri.com/en-us/gis-dictionary/isoline
  14. https://www.khanacademy.org/math/multivariable-calculus/thinking-about-multivariable-function/visualizing-scalar-valued-functions/v/contour-plots
  15. https://ocw.mit.edu/courses/18-02sc-multivariable-calculus-fall-2010/85c1d85363d9808505351b571d2750aa_MIT18_02SC_notes_19.pdf
  16. https://blogs.reed.edu/projectproject/2017/07/10/level-sets-the-gradient-and-gradient-flow/
  17. https://mathweb.ucsd.edu/~gptesler/20c/slides/20c_dirderiv_f18-handout.pdf
  18. https://www.kgs.ku.edu/Tis/surf3/s3Cont2.html
  19. https://scholar.rose-hulman.edu/cgi/viewcontent.cgi?article=1313&context=rhumj
  20. https://vc.cs.ovgu.de/assets/publications/2008/Annen_2008_GraInt.pdf
  21. https://pubs.usgs.gov/gip/70043848/lesson-2.pdf
  22. https://www.ntc.blm.gov/krc/uploads/1050/bmr_sg.pdf
  23. http://www.nwcg.gov/course/ffm/mapping/55-contour-lines-and-intervals
  24. https://www.multires.caltech.edu/pubs/TerrRecon.pdf
  25. https://www.tandfonline.com/doi/abs/10.1080/03085694.2018.1450554
  26. https://academic.oup.com/astrogeo/article/42/1/1.23/270989
  27. https://plato.stanford.edu/entries/leibniz-physics/
  28. https://blogs.loc.gov/maps/2018/04/the-first-isothermic-world-maps/
  29. https://rmets.onlinelibrary.wiley.com/doi/10.1002/j.1477-8696.1967.tb02989.x
  30. https://maps.nls.uk/os/6inch/os_info4.html
  31. https://pubs.usgs.gov/circ/1341/pdf/circ_1341.pdf
  32. https://www.geosociety.org/gsatoday/archive/26/7/article/i1052-5173-26-7-4.htm
  33. https://pubs.usgs.gov/bul/0788e/report.pdf
  34. https://www.archives.gov/files/research/cartographic/cartographic-ww2-guide.pdf
  35. https://www.atu.edu/rotc/docs/7_fm3_25x26.pdf
  36. https://www.researchgate.net/publication/237169912_Three_computer_programs_for_contouring_map_data
  37. https://apps.dtic.mil/sti/tr/pdf/ADA088805.pdf
  38. https://unstats.un.org/unsd/methods/cartog/Americas/2/ECONF.71.3.pdf
  39. https://www.asprs.org/wp-content/uploads/pers/1985journal/apr/1985_apr_437-444.pdf
  40. https://originaloutdoors.co.uk/how-to-choose-the-right-map-scale-25k-40k-or-50k/
  41. https://www.rei.com/learn/expert-advice/topo-maps-how-to-use.html
  42. http://www.wvgs.wvnet.edu/www/maps/topomapsymbols_mapx1b.pdf
  43. https://www.esri.com/arcgis-blog/products/product/imagery/hypsometric-tinting
  44. https://www.usgs.gov/ngp-standards-and-specifications/us-topo-cartographic-specifications-elevation
  45. https://www.usgs.gov/faqs/where-can-i-find-bathymetric-data
  46. https://cmgds.marine.usgs.gov/catalog/science.php?thcode=2&term=80
  47. https://apps.nationalmap.gov/downloader/
  48. https://www.usgs.gov/programs/national-geospatial-program/topographic-maps
  49. https://www.noaa.gov/jetstream/wxmaps
  50. https://www.noaa.gov/jetstream/analyze-appair-pressure-map
  51. https://repository.library.noaa.gov/view/noaa/44567/noaa_44567_DS1.pdf
  52. https://repository.library.noaa.gov/view/noaa/28396/noaa_28396_DS1.pdf
  53. https://www.noaa.gov/jetstream/surface-temperature-map
  54. https://www.noaa.gov/jetstream/upper-air-charts/constant-pressure-charts-thickness
  55. https://www.noaa.gov/jetstream/appendix/weather-glossary-i
  56. https://www.noaa.gov/jetstream/upper-air-charts/common-features-of-constant-pressure-charts
  57. https://www.ess.uci.edu/~yu/class/ess55/lecture.4.motion.all.pdf
  58. https://www.wpc.ncep.noaa.gov/sfc/UASfcManualVersion1.pdf
  59. https://www.aoml.noaa.gov/ftp/hrd/annane/prelim_notes/nssfc5sm.pdf
  60. https://apps.nssl.noaa.gov/tgalarneau/webdocs/qghgttend-usersguide.pdf
  61. https://people.wou.edu/~taylors/es486_petro/in_class_isopach_willamette_aquifer_mckenzie_fan.pdf
  62. https://www.wsgs.wyo.gov/products/wsgs-n.d.-mp-05.pdf
  63. https://pubs.usgs.gov/sir/2006/5263/data/rd-00d-Warren_Maps_04.pdf
  64. https://people.wou.edu/~taylors/es486_petro/structure_contour_in_class.pdf
  65. https://courses.ems.psu.edu/earth111/node/932
  66. https://www.caee.utexas.edu/prof/maidment/tmpaper/spring98/landrum/map.htm
  67. https://pmc.ncbi.nlm.nih.gov/articles/PMC12216010/
  68. https://earth.yale.edu/sites/default/files/2025-08/Monteagudo_Daniel_Thesis%2520%25281%2529.pdf
  69. https://pubs.usgs.gov/pp/1223/report.pdf
  70. https://www.nap.edu/read/624/chapter/5
  71. https://www.epa.gov/sites/default/files/2014-03/documents/epa904r07001.pdf
  72. https://pmc.ncbi.nlm.nih.gov/articles/PMC8140410/
  73. https://pressbooks.uiowa.edu/clonedbook/chapter/equipotential-lines/
  74. https://pressbooks.online.ucf.edu/osuniversityphysics2/chapter/equipotential-surfaces-and-conductors/
  75. https://w3.pppl.gov/ppst/docs/ahsan2022pop.pdf
  76. https://digitalcommons.morris.umn.edu/cgi/viewcontent.cgi?article=2168&context=jmas
  77. https://www.journals.uchicago.edu/doi/pdfplus/10.1086/225953
  78. https://sites.stat.washington.edu/courses/stat527/s14/readings/Duong_R-vignette.pdf
  79. https://homepage.divms.uiowa.edu/~luke/classes/STAT7400-2023/_book/density-estimation-and-smoothing.html
  80. https://www.grc.nasa.gov/www/k-12/airplane/pvtsplot.html
  81. https://pressbooks.online.ucf.edu/osuniversityphysics2/chapter/thermodynamic-processes/
  82. https://www.csl.cornell.edu/~studer/papers/18NEURIPS_visualization.pdf
  83. https://pubs.usgs.gov/bul/0307/report.pdf
  84. https://www.e-education.psu.edu/natureofgeoinfo/c7_p6.html
  85. https://www.usgs.gov/educational-resources/topographic-mapping
  86. https://paulbourke.net/papers/conrec/
  87. https://books.google.com/books/about/Cartographic_Relief_Presentation.html?id=cVy1Ms43fFYC
  88. https://www.esri.com/arcgis-blog/products/arcgis-pro/mapping/designing-maps-for-colorblind-readability
  89. https://pubs.usgs.gov/circ/1955/0368/report.pdf
  90. https://www.e-education.psu.edu/geog486/node/557
  91. https://ngmdb.usgs.gov/fgdc_gds/geolsymstd/fgdc-geolsym-sec30.pdf
  92. https://cartogis.org/docs/proceedings/archive/auto-carto-7/pdf/automated-contour-labelling-and-the-contour-tree.pdf
  93. https://serc.carleton.edu/mathyouneed/slope/topoprofile.html
  94. https://archimash.com/articles/topography-contours-levels/
  95. https://getoutside.ordnancesurvey.co.uk/guides/advanced-contours-and-relief/
  96. https://web.cs.ucdavis.edu/~okreylos/ResDev/SARndbox/
Add your contribution
Related Hubs
User Avatar
No comments yet.