Recent from talks
Nothing was collected or created yet.
Infrared spectroscopy
View on Wikipedia
Infrared spectroscopy (IR spectroscopy or vibrational spectroscopy) is the measurement of the interaction of infrared radiation with matter by absorption, emission, or reflection. It is used to study and identify chemical substances or functional groups in solid, liquid, or gaseous forms. It can be used to characterize new materials or identify and verify known and unknown samples. The method or technique of infrared spectroscopy is conducted with an instrument called an infrared spectrometer (or spectrophotometer) which produces an infrared spectrum. An IR spectrum can be visualized in a graph of infrared light absorbance (or transmittance) on the vertical axis vs. frequency, wavenumber or wavelength on the horizontal axis. Typical units of wavenumber used in IR spectra are reciprocal centimeters, with the symbol cm−1. Units of IR wavelength are commonly given in micrometers (formerly called "microns"), symbol μm, which are related to the wavenumber in a reciprocal way. A common laboratory instrument that uses this technique is a Fourier transform infrared (FTIR) spectrometer. Two-dimensional IR is also possible as discussed below.
The infrared portion of the electromagnetic spectrum is usually divided into three regions; the near-, mid- and far- infrared, named for their relation to the visible spectrum. The higher-energy near-IR, approximately 14,000–4,000 cm−1 (0.7–2.5 μm wavelength) can excite overtone or combination modes of molecular vibrations. The mid-infrared, approximately 4,000–400 cm−1 (2.5–25 μm) is generally used to study the fundamental vibrations and associated rotational–vibrational structure. The far-infrared, approximately 400–10 cm−1 (25–1,000 μm) has low energy and may be used for rotational spectroscopy and low frequency vibrations. The region from 2–130 cm−1, bordering the microwave region, is considered the terahertz region and may probe intermolecular vibrations.[1] The names and classifications of these subregions are conventions, and are only loosely based on the relative molecular or electromagnetic properties.
Uses and applications
[edit]

Infrared spectroscopy is a simple and reliable technique widely used in both organic and inorganic chemistry, in research and industry. It is used in quality control, dynamic measurement, and monitoring applications such as the long-term unattended measurement of CO2 concentrations in greenhouses and growth chambers by infrared gas analyzers.[citation needed]
It is also used in forensic analysis in both criminal and civil cases, for example in identifying polymer degradation. It can be used in determining the blood alcohol content of a suspected drunk driver.
IR spectroscopy has been used in identification of pigments in paintings[2] and other art objects[3] such as illuminated manuscripts.[4]
Infrared spectroscopy is also useful in measuring the degree of polymerization in polymer manufacture. Changes in the character or quantity of a particular bond are assessed by measuring at a specific frequency over time. Instruments can routinely record many spectra per second in situ, providing insights into reaction mechanism (e.g., detection of intermediates) and reaction progress.[citation needed]
Infrared spectroscopy is utilized in the field of semiconductor microelectronics:[5] for example, infrared spectroscopy can be applied to semiconductors like silicon, gallium arsenide, gallium nitride, zinc selenide, amorphous silicon, silicon nitride, etc.
Another important application of infrared spectroscopy is in the food industry to measure the concentration of various compounds in different food products.[6][7]
Infrared spectroscopy is also used in gas leak detection devices such as the DP-IR and EyeCGAs.[8] These devices detect hydrocarbon gas leaks in the transportation of natural gas and crude oil.
Infrared spectroscopy is an important analysis method in the recycling process of household waste plastics, and a convenient stand-off method to sort plastic of different polymers (PET, HDPE, ...).[9]
Other developments include a miniature IR-spectrometer that's linked to a cloud based database and suitable for personal everyday use,[10] and NIR-spectroscopic chips[11] that can be embedded in smartphones and various gadgets.
In catalysis research it is a very useful tool to characterize the catalyst,[12][13][14] as well as to detect intermediates[15]
Infrared spectroscopy coupled with machine learning and artificial intelligence also has potential for rapid, accurate and non-invasive sensing of bacteria.[16] The complex chemical composition of bacteria, including nucleic acids, proteins, carbohydrates and fatty acids, results in high-dimensional datasets where the essential features are effectively hidden under the total spectrum. Extraction of the essential features therefore requires advanced statistical methods such as machine learning and deep-neural networks. The potential of this technique for bacteria classification have been demonstrated for differentiation at the genus,[17] species[18] and serotype[19] taxonomic levels, and it has also been shown promising for antimicrobial susceptibility testing,[20][21][22] which is important for many clinical settings where faster susceptibility testing would decrease unnecessary blind-treatment with broad-spectrum antibiotics. The main limitation of this technique for clinical applications is the high sensitivity to technical equipment and sample preparation techniques, which makes it difficult to construct large-scale databases. Attempts in this direction have however been made by Bruker with the IR Biotyper for food microbiology.[23]
Theory
[edit]
Infrared spectroscopy exploits the fact that molecules absorb frequencies that are characteristic of their structure. These absorptions occur at resonant frequencies, i.e. the frequency of the absorbed radiation matches the vibrational frequency. The energies are affected by the shape of the molecular potential energy surfaces, the masses of the atoms, and the associated vibronic coupling.[24]

In particular, in the Born–Oppenheimer and harmonic approximations (i.e. when the molecular Hamiltonian corresponding to the electronic ground state can be approximated by a harmonic oscillator in the neighbourhood of the equilibrium molecular geometry), the resonant frequencies are associated with the normal modes of vibration corresponding to the molecular electronic ground state potential energy surface. Thus, it depends on both the nature of the bonds and the mass of the atoms that are involved. Using the Schrödinger equation leads to the selection rule for the vibrational quantum number in the system undergoing vibrational changes:
The compression and extension of a bond may be likened to the behaviour of a spring, but real molecules are hardly perfectly elastic in nature. If a bond between atoms is stretched, for instance, there comes a point at which the bond breaks and the molecule dissociates into atoms. Thus real molecules deviate from perfect harmonic motion and their molecular vibrational motion is anharmonic. An empirical expression that fits the energy curve of a diatomic molecule undergoing anharmonic extension and compression to a good approximation was derived by P.M. Morse, and is called the Morse function. Using the Schrödinger equation leads to the selection rule for the system undergoing vibrational changes :
Number of vibrational modes
[edit]In order for a vibrational mode in a sample to be "IR active", it must be associated with changes in the molecular dipole moment. A permanent dipole is not necessary, as the rule requires only a change in dipole moment.[26]
A molecule can vibrate in many ways, and each way is called a vibrational mode. For molecules with N number of atoms, geometrically linear molecules have 3N – 5 degrees of vibrational modes, whereas nonlinear molecules have 3N – 6 degrees of vibrational modes (also called vibrational degrees of freedom). As examples linear carbon dioxide (CO2) has 3 × 3 – 5 = 4, while non-linear water (H2O), has only 3 × 3 – 6 = 3.[27]

Simple diatomic molecules have only one bond and only one vibrational band. If the molecule is symmetrical, e.g. N2, the band is not observed in the IR spectrum, but only in the Raman spectrum. Asymmetrical diatomic molecules, e.g. carbon monoxide (CO), absorb in the IR spectrum. More complex molecules have many bonds, and their vibrational spectra are correspondingly more complex, i.e. big molecules have many peaks in their IR spectra.
The atoms in a CH2X2 group, commonly found in organic compounds and where X can represent any other atom, can vibrate in nine different ways. Six of these vibrations involve only the CH2 portion: two stretching modes (ν): symmetric (νs) and antisymmetric (νas); and four bending modes: scissoring (δ), rocking (ρ), wagging (ω) and twisting (τ), as shown below. Structures that do not have the two additional X groups attached have fewer modes because some modes are defined by specific relationships to those other attached groups. For example, in water, the rocking, wagging, and twisting modes do not exist because these types of motions of the H atoms represent simple rotation of the whole molecule rather than vibrations within it. In case of more complex molecules, out-of-plane (γ) vibrational modes can be also present.[28]
Symmetry Direction |
Symmetric | Antisymmetric |
|---|---|---|
| Radial | 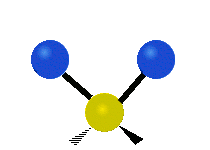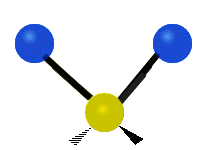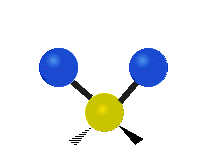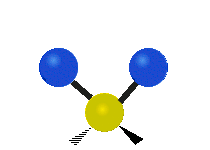 Symmetric stretching (νs) |
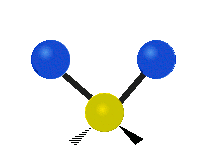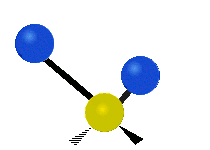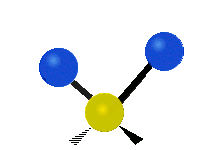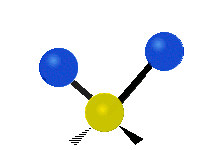 Antisymmetric stretching (νas) |
| Latitudinal |  Scissoring (δ) |
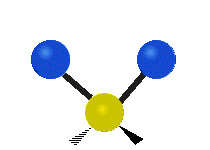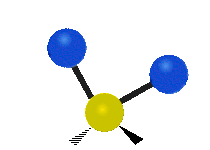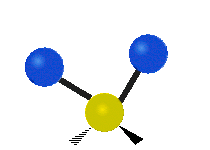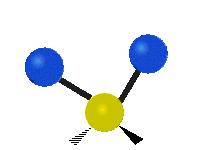 Rocking (ρ) |
| Longitudinal |  Wagging (ω) |
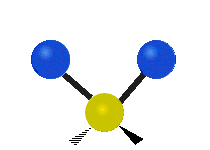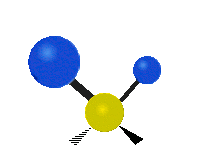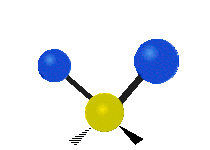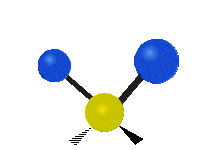 Twisting (τ) |
These figures do not represent the "recoil" of the C atoms, which, though necessarily present to balance the overall movements of the molecule, are much smaller than the movements of the lighter H atoms.
The simplest and most important or fundamental IR bands arise from the excitations of normal modes, the simplest distortions of the molecule, from the ground state with vibrational quantum number v = 0 to the first excited state with vibrational quantum number v = 1. In some cases, overtone bands are observed. An overtone band arises from the absorption of a photon leading to a direct transition from the ground state to the second excited vibrational state (v = 2). Such a band appears at approximately twice the energy of the fundamental band for the same normal mode. Some excitations, so-called combination modes, involve simultaneous excitation of more than one normal mode. The phenomenon of Fermi resonance can arise when two modes are similar in energy; Fermi resonance results in an unexpected shift in energy and intensity of the bands etc.[citation needed]
Practical IR spectroscopy
[edit]The infrared spectrum of a sample is recorded by passing a beam of infrared light through the sample. When the frequency of the IR matches the vibrational frequency of a bond or collection of bonds, absorption occurs. Examination of the transmitted light reveals how much energy was absorbed at each frequency (or wavelength). This measurement can be achieved by scanning the wavelength range using a monochromator. Alternatively, the entire wavelength range is measured using a Fourier transform instrument and then a transmittance or absorbance spectrum is extracted.
This technique is commonly used for analyzing samples with covalent bonds. The number of bands roughly correlates with symmetry and molecular complexity.
A variety of devices are used to hold the sample in the path of the IR beam These devices are selected on the basis of their transparency in the region of interest and their resilience toward the sample.
| material | transparency range (cm−1) | comment |
|---|---|---|
| Sodium chloride | 5000–650 | attacked (dissolved) by water, small alcohols, some amines |
| Calcium fluoride | 4200–1300 | insoluble in most solvents |
| Silver chloride | 5000–500 | attacked (dissolved) by amines, organosulfur compounds |

Sample preparation
[edit]Gas samples
[edit]Gaseous samples require a sample cell with a long pathlength to compensate for the diluteness. The pathlength of the sample cell depends on the concentration of the compound of interest. A simple glass tube with length of 5 to 10 cm equipped with infrared-transparent windows at both ends of the tube can be used for concentrations down to several hundred ppm. Sample gas concentrations well below ppm can be measured with a White's cell in which the infrared light is guided with mirrors to travel through the gas. White's cells are available with optical pathlength starting from 0.5 m up to hundred meters.[citation needed]
Liquid samples
[edit]Liquid samples can be sandwiched between two plates of a salt (commonly sodium chloride, or common salt, although a number of other salts such as potassium bromide or calcium fluoride are also used).[30] The plates are transparent to the infrared light and do not introduce any lines onto the spectra. With increasing technology in computer filtering and manipulation of the results, samples in solution can now be measured accurately (water produces a broad absorbance across the range of interest, and thus renders the spectra unreadable without this computer treatment).[citation needed]
Solid samples
[edit]Solid samples can be prepared in a variety of ways. One common method is to crush the sample with an oily mulling agent (usually mineral oil Nujol). A thin film of the mull is applied onto salt plates and measured. The second method is to grind a quantity of the sample with a specially purified salt (usually potassium bromide) finely (to remove scattering effects from large crystals). This powder mixture is then pressed in a mechanical press to form a translucent pellet through which the beam of the spectrometer can pass.[30] A third technique is the "cast film" technique, which is used mainly for polymeric materials. The sample is first dissolved in a suitable, non-hygroscopic solvent. A drop of this solution is deposited on the surface of a KBr or NaCl cell. The solution is then evaporated to dryness and the film formed on the cell is analysed directly. Care is important to ensure that the film is not too thick otherwise light cannot pass through. This technique is suitable for qualitative analysis. The final method is to use microtomy to cut a thin (20–100 μm) film from a solid sample. This is one of the most important ways of analysing failed plastic products for example because the integrity of the solid is preserved.[citation needed]
In photoacoustic spectroscopy the need for sample treatment is minimal. The sample, liquid or solid, is placed into the sample cup which is inserted into the photoacoustic cell which is then sealed for the measurement. The sample may be one solid piece, powder or basically in any form for the measurement. For example, a piece of rock can be inserted into the sample cup and the spectrum measured from it.[citation needed]
A useful way of analyzing solid samples without the need for cutting samples uses ATR or attenuated total reflectance spectroscopy. Using this approach, samples are pressed against the face of a single crystal. The infrared radiation passes through the crystal and only interacts with the sample at the interface between the two materials.[citation needed]
Comparing to a reference
[edit]
It is typical to record spectrum of both the sample and a "reference". This step controls for a number of variables, e.g. infrared detector, which may affect the spectrum. The reference measurement makes it possible to eliminate the instrument influence.[citation needed]
The appropriate "reference" depends on the measurement and its goal. The simplest reference measurement is to simply remove the sample (replacing it by air). However, sometimes a different reference is more useful. For example, if the sample is a dilute solute dissolved in water in a beaker, then a good reference measurement might be to measure pure water in the same beaker. Then the reference measurement would cancel out not only all the instrumental properties (like what light source is used), but also the light-absorbing and light-reflecting properties of the water and beaker, and the final result would just show the properties of the solute (at least approximately).[citation needed]
A common way to compare to a reference is sequentially: first measure the reference, then replace the reference by the sample and measure the sample. This technique is not perfectly reliable; if the infrared lamp is a bit brighter during the reference measurement, then a bit dimmer during the sample measurement, the measurement will be distorted. More elaborate methods, such as a "two-beam" setup (see figure), can correct for these types of effects to give very accurate results. The Standard addition method can be used to statistically cancel these errors.
Nevertheless, among different absorption-based techniques which are used for gaseous species detection, Cavity ring-down spectroscopy (CRDS) can be used as a calibration-free method. The fact that CRDS is based on the measurements of photon life-times (and not the laser intensity) makes it needless for any calibration and comparison with a reference [31]
Some instruments also automatically identify the substance being measured from a store of thousands of reference spectra held in storage.
FTIR
[edit]
Fourier transform infrared (FTIR) spectroscopy is a measurement technique that allows one to record infrared spectra. Infrared light is guided through an interferometer and then through the sample (or vice versa). A moving mirror inside the apparatus alters the distribution of infrared light that passes through the interferometer. The signal directly recorded, called an "interferogram", represents light output as a function of mirror position. A data-processing technique called Fourier transform turns this raw data into the desired result (the sample's spectrum): light output as a function of infrared wavelength (or equivalently, wavenumber). As described above, the sample's spectrum is always compared to a reference.[citation needed]
An alternate method for acquiring spectra is the "dispersive" or "scanning monochromator" method. In this approach, the sample is irradiated sequentially with various single wavelengths. The dispersive method is more common in UV-Vis spectroscopy, but is less practical in the infrared than the FTIR method. One reason that FTIR is favored is called "Fellgett's advantage" or the "multiplex advantage": The information at all frequencies is collected simultaneously, improving both speed and signal-to-noise ratio. Another is called "Jacquinot's Throughput Advantage": A dispersive measurement requires detecting much lower light levels than an FTIR measurement.[32] There are other advantages, as well as some disadvantages,[32] but virtually all modern infrared spectrometers are FTIR instruments.
Infrared microscopy
[edit]Various forms of infrared microscopy exist. These include IR versions of sub-diffraction microscopy[33] such as IR NSOM,[34] photothermal microspectroscopy, Nano-FTIR and atomic force microscope based infrared spectroscopy (AFM-IR).
Other methods in molecular vibrational spectroscopy
[edit]Infrared spectroscopy is not the only method of studying molecular vibrational spectra. Raman spectroscopy involves an inelastic scattering process in which only part of the energy of an incident photon is absorbed by the molecule, and the remaining part is scattered and detected. The energy difference corresponds to absorbed vibrational energy.[citation needed]
The selection rules for infrared and for Raman spectroscopy are different at least for some molecular symmetries, so that the two methods are complementary in that they observe vibrations of different symmetries.[citation needed]
Another method is electron energy loss spectroscopy (EELS), in which the energy absorbed is provided by an inelastically scattered electron rather than a photon. This method is useful for studying vibrations of molecules adsorbed on a solid surface.
Recently, high-resolution EELS (HREELS) has emerged as a technique for performing vibrational spectroscopy in a transmission electron microscope (TEM).[35] In combination with the high spatial resolution of the TEM, unprecedented experiments have been performed, such as nano-scale temperature measurements,[36][37] mapping of isotopically labeled molecules,[38] mapping of phonon modes in position- and momentum-space,[39][40] vibrational surface and bulk mode mapping on nanocubes,[41] and investigations of polariton modes in van der Waals crystals.[42] Analysis of vibrational modes that are IR-inactive but appear in inelastic neutron scattering is also possible at high spatial resolution using EELS.[43] In 2025, vibrational EELS was further extended to probe magnetic excitations (magnons) inside antiferromagnetic nanocrystals, achieving both nanometer spatial and millielectronvolt energy resolution.[44] Although the spatial resolution of HREELs is very high, the bands are extremely broad compared to other techniques.[35]
Another emerging method is optical force spectroscopy (OFS), which enables indirect mid-infrared vibrational spectroscopy by detecting the resonant optical forces acting on micro- and nanoparticles. Instead of recording absorption or scattering directly, OFS reconstructs vibrational spectra from force changes measured under a tunable mid-IR laser. Applications include label-free separation of particles based on vibrational signatures,[45] reconstruction of mid-IR spectra at the single-particle level,[46] and optical force chromatography of micro- nanospheres with specific functional groups.[47]
Computational infrared microscopy
[edit]By using computer simulations and normal mode analysis it is possible to calculate theoretical frequencies of molecules.[48]
Absorption bands
[edit]IR spectroscopy is often used to identify structures because functional groups give rise to characteristic bands both in terms of intensity and position (frequency). The positions of these bands are summarized in correlation tables as shown below.

Regions
[edit]A spectrograph is often interpreted as having two regions.[49]
- functional group region
In the functional region there are one to a few troughs per functional group.[49]
- fingerprint region
In the fingerprint region there are many troughs which form an intricate pattern which can be used like a fingerprint to determine the compound.[49]
Badger's rule
[edit]For many kinds of samples, the assignments are known, i.e. which bond deformation(s) are associated with which frequency. In such cases further information can be gleaned about the strength on a bond, relying on the empirical guideline called Badger's rule. Originally published by Richard McLean Badger in 1934,[50] this rule states that the strength of a bond (in terms of force constant) correlates with the bond length. That is, increase in bond strength leads to corresponding bond shortening and vice versa.
Isotope effects
[edit]The different isotopes in a particular species may exhibit different fine details in infrared spectroscopy. For example, the O–O stretching frequency (in reciprocal centimeters) of oxyhemocyanin is experimentally determined to be 832 and 788 cm−1 for ν(16O–16O) and ν(18O–18O), respectively.
By considering the O–O bond as a spring, the frequency of absorbance can be calculated as a wavenumber [= frequency/(speed of light)]
where k is the spring constant for the bond, c is the speed of light, and μ is the reduced mass of the A–B system:
( is the mass of atom ).
The reduced masses for 16O–16O and 18O–18O can be approximated as 8 and 9 respectively. Thus
The effect of isotopes, both on the vibration and the decay dynamics, has been found to be stronger than previously thought. In some systems, such as silicon and germanium, the decay of the anti-symmetric stretch mode of interstitial oxygen involves the symmetric stretch mode with a strong isotope dependence. For example, it was shown that for a natural silicon sample, the lifetime of the anti-symmetric vibration is 11.4 ps. When the isotope of one of the silicon atoms is increased to 29Si, the lifetime increases to 19 ps. In similar manner, when the silicon atom is changed to 30Si, the lifetime becomes 27 ps.[51]
Two-dimensional IR
[edit]Two-dimensional infrared correlation spectroscopy analysis combines multiple samples of infrared spectra to reveal more complex properties. By extending the spectral information of a perturbed sample, spectral analysis is simplified and resolution is enhanced. The 2D synchronous and 2D asynchronous spectra represent a graphical overview of the spectral changes due to a perturbation (such as a changing concentration or changing temperature) as well as the relationship between the spectral changes at two different wavenumbers.[citation needed]

Nonlinear two-dimensional infrared spectroscopy[52][53] is the infrared version of correlation spectroscopy. Nonlinear two-dimensional infrared spectroscopy is a technique that has become available with the development of femtosecond infrared laser pulses. In this experiment, first a set of pump pulses is applied to the sample. This is followed by a waiting time during which the system is allowed to relax. The typical waiting time lasts from zero to several picoseconds, and the duration can be controlled with a resolution of tens of femtoseconds. A probe pulse is then applied, resulting in the emission of a signal from the sample. The nonlinear two-dimensional infrared spectrum is a two-dimensional correlation plot of the frequency ω1 that was excited by the initial pump pulses and the frequency ω3 excited by the probe pulse after the waiting time. This allows the observation of coupling between different vibrational modes; because of its extremely fine time resolution, it can be used to monitor molecular dynamics on a picosecond timescale. It is still a largely unexplored technique and is becoming increasingly popular for fundamental research.
As with two-dimensional nuclear magnetic resonance (2DNMR) spectroscopy, this technique spreads the spectrum in two dimensions and allows for the observation of cross peaks that contain information on the coupling between different modes. In contrast to 2DNMR, nonlinear two-dimensional infrared spectroscopy also involves the excitation to overtones. These excitations result in excited state absorption peaks located below the diagonal and cross peaks. In 2DNMR, two distinct techniques, COSY and NOESY, are frequently used. The cross peaks in the first are related to the scalar coupling, while in the latter they are related to the spin transfer between different nuclei. In nonlinear two-dimensional infrared spectroscopy, analogs have been drawn to these 2DNMR techniques. Nonlinear two-dimensional infrared spectroscopy with zero waiting time corresponds to COSY, and nonlinear two-dimensional infrared spectroscopy with finite waiting time allowing vibrational population transfer corresponds to NOESY. The COSY variant of nonlinear two-dimensional infrared spectroscopy has been used for determination of the secondary structure content of proteins.[54]
See also
[edit]- Applied spectroscopy
- Astrochemistry
- Atomic and molecular astrophysics
- Atomic force microscopy based infrared spectroscopy (AFM-IR)
- Cosmochemistry
- Far-infrared astronomy
- Forensic chemistry
- Forensic engineering
- Forensic polymer engineering
- Infrared astronomy
- Infrared microscopy
- Infrared multiphoton dissociation
- Infrared photodissociation spectroscopy
- Infrared spectroscopy correlation table
- Infrared spectroscopy of metal carbonyls
- Near-infrared spectroscopy
- Nuclear resonance vibrational spectroscopy
- Photothermal microspectroscopy
- Raman spectroscopy
- Rotational-vibrational spectroscopy
- Time-resolved spectroscopy
- Vibrational spectroscopy of linear molecules
References
[edit]- ^ Zeitler JA, Taday PF, Newnham DA, Pepper M, Gordon KC, Rades T (February 2007). "Terahertz pulsed spectroscopy and imaging in the pharmaceutical setting--a review". The Journal of Pharmacy and Pharmacology. 59 (2): 209–23. doi:10.1211/jpp.59.2.0008. PMID 17270075. S2CID 34705104.
- ^ "Infrared Spectroscopy". ColourLex. 12 March 2021. Retrieved 19 January 2022.
- ^ Derrick MR, Stulik D, Landry JM (1999). Infrared Spectroscopy in Conservation Science (PDF). Scientific Tools for Conservation. Getty Publications. ISBN 0-89236-469-6.
- ^ Ricciardi P. "Unlocking the secrets of illuminated manuscripts". Retrieved 11 December 2015.
- ^ Lau WS (1999). Infrared characterization for microelectronics. World Scientific. ISBN 978-981-02-2352-6.
- ^ Osborne BG (2006). "Near-Infrared Spectroscopy in Food Analysis". Encyclopedia of Analytical Chemistry. John Wiley & Sons. doi:10.1002/9780470027318.a1018. ISBN 978-0-470-02731-8.
- ^ Villar A, Gorritxategi E, Aranzabe E, Fernández S, Otaduy D, Fernández LA (December 2012). "Low-cost visible-near infrared sensor for on-line monitoring of fat and fatty acids content during the manufacturing process of the milk". Food Chemistry. 135 (4): 2756–60. doi:10.1016/j.foodchem.2012.07.074. PMID 22980869.
- ^ www.TRMThemes.com, TRM Theme by. "Infrared (IR) / Optical Based Archives - Heath Consultants". Heath Consultants. Archived from the original on 2022-01-20. Retrieved 2016-04-12.
- ^ Becker, Wolfgang; Sachsenheimer, Kerstin; Klemenz, Melanie (2017). "Detection of Black Plastics in the Middle Infrared Spectrum (MIR) Using Photon Up-Conversion Technique for Polymer Recycling Process". Polymers. 9 (9). MDPI. doi:10.3390/polym9090435. PMC 6418689. PMID 30965736.
- ^ Perry, Tekla S. (2017-03-14). "What Happened When We Took the SCiO Food Analyzer Grocery Shopping". IEEE Spectrum: Technology, Engineering, and Science News. Retrieved 2017-03-23.
- ^ Coates, John (18 June 2014). "A Review of New Small-Scale Technologies for Near Infrared Measurements". American Pharmaceutical Review. Coates Consulting LLC. Retrieved 2017-03-23.
- ^ Boosa, Venu; Varimalla, Shirisha; Dumpalapally, Mahesh; Gutta, Naresh; Velisoju, Vijay Kumar; Nama, Narender; Akula, Venugopal (2021-09-05). "Influence of Brønsted acid sites on chemoselective synthesis of pyrrolidones over H-ZSM-5 supported copper catalyst". Applied Catalysis B: Environmental. 292 120177. Bibcode:2021AppCB.29220177B. doi:10.1016/j.apcatb.2021.120177. ISSN 0926-3373.
- ^ Fajdek-Bieda, Anna; Wróblewska, Agnieszka; Miądlicki, Piotr; Tołpa, Jadwiga; Michalkiewicz, Beata (2021-08-01). "Clinoptilolite as a natural, active zeolite catalyst for the chemical transformations of geraniol". Reaction Kinetics, Mechanisms and Catalysis. 133 (2): 997–1011. doi:10.1007/s11144-021-02027-3. ISSN 1878-5204. S2CID 236149569.
- ^ Azancot, Lola; Bobadilla, Luis F.; Centeno, Miguel A.; Odriozola, José A. (2021-05-15). "IR spectroscopic insights into the coking-resistance effect of potassium on nickel-based catalyst during dry reforming of methane". Applied Catalysis B: Environmental. 285 119822. Bibcode:2021AppCB.28519822A. doi:10.1016/j.apcatb.2020.119822. hdl:10261/251396. ISSN 0926-3373. S2CID 232627637.
- ^ Nuguid, Rob Jeremiah G.; Elsener, Martin; Ferri, Davide; Kröcher, Oliver (2021-12-05). "Operando diffuse reflectance infrared detection of cyanide intermediate species during the reaction of formaldehyde with ammonia over V2O5/WO3-TiO2". Applied Catalysis B: Environmental. 298 120629. doi:10.1016/j.apcatb.2021.120629. ISSN 0926-3373.
- ^ Sockalingum, G. D.; Bouhedja, W.; Pina, P.; Allouch, P.; Bloy, C.; Manfait, M. (February 1998). "FT-IR spectroscopy as an emerging method for rapid characterization of microorganisms". Cellular and Molecular Biology (Noisy-Le-Grand, France). 44 (1): 261–269. ISSN 0145-5680. PMID 9551657.
- ^ Helm, D.; Labischinski, H.; Schallehn, Gisela; Naumann, D. (1991-01-01). "Classification and identification of bacteria by Fourier-transform infrared spectroscopy". Microbiology. 137 (1): 69–79. doi:10.1099/00221287-137-1-69. ISSN 1350-0872. PMID 1710644.
- ^ Holt, C; Hirst, D; Sutherland, A; MacDonald, F (January 1995). "Discrimination of species in the genus Listeria by Fourier transform infrared spectroscopy and canonical variate analysis". Applied and Environmental Microbiology. 61 (1): 377–378. Bibcode:1995ApEnM..61..377H. doi:10.1128/aem.61.1.377-378.1995. ISSN 0099-2240. PMC 167294. PMID 7887620.
- ^ Campos, Joana; Sousa, Clara; Mourão, Joana; Lopes, João; Antunes, Patrícia; Peixe, Luísa (November 2018). "Discrimination of non-typhoid Salmonella serogroups and serotypes by Fourier Transform Infrared Spectroscopy: A comprehensive analysis". International Journal of Food Microbiology. 285: 34–41. doi:10.1016/j.ijfoodmicro.2018.07.005. PMID 30015261.
- ^ Sharaha, Uraib; Rodriguez-Diaz, Eladio; Sagi, Orli; Riesenberg, Klaris; Salman, Ahmad; Bigio, Irving J.; Huleihel, Mahmoud (July 2019). "Fast and reliable determination of Escherichia coli susceptibility to antibiotics: Infrared microscopy in tandem with machine learning algorithms". Journal of Biophotonics. 12 (7) e201800478. doi:10.1002/jbio.201800478. ISSN 1864-063X. PMID 30916881.
- ^ Wijesinghe, Hewa G. S.; Hare, Dominic J.; Mohamed, Ahmed; Shah, Alok K.; Harris, Patrick N. A.; Hill, Michelle M. (2021). "Detecting antimicrobial resistance in Escherichia coli using benchtop attenuated total reflectance-Fourier transform infrared spectroscopy and machine learning". The Analyst. 146 (20): 6211–6219. Bibcode:2021Ana...146.6211W. doi:10.1039/D1AN00546D. ISSN 0003-2654. PMID 34522918.
- ^ Suleiman, Manal; Abu-Aqil, George; Sharaha, Uraib; Riesenberg, Klaris; Lapidot, Itshak; Salman, Ahmad; Huleihel, Mahmoud (June 2022). "Infra-red spectroscopy combined with machine learning algorithms enables early determination of Pseudomonas aeruginosa's susceptibility to antibiotics". Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy. 274 121080. Bibcode:2022AcSpA.27421080S. doi:10.1016/j.saa.2022.121080. PMID 35248858.
- ^ "IR Biotyper® for Food Microbiology". www.bruker.com. Retrieved 2024-03-20.
- ^ Silverstein, Robert M.; Webster, Francis X.; Kiemle, David J.; Bryce, David L. (2016). Spectrometric Identification of Organic Compounds, 8th Edition. Wiley. ISBN 978-0-470-61637-6.
- ^ Banwell, Colin N. (1966). Fundamentals of molecular spectroscopy. European chemistry series. London: McGraw-Hill. ISBN 978-0-07-094020-8.
- ^ Atkins P, de Paula J (2002). Physical Chemistry (7th ed.). New York: W.H.Freeman. p. 513. ISBN 0-7167-3539-3.|quote=the electric dipole moment of the molecule must change when the atoms are displaced relative to one another
- ^ Atkins, Peter (1994). Physical Chemistry, 5th Edition. Freeman. p. 577.
- ^ Schrader B (1995). Infrared and Raman Spectroscopy: Methods and Applications. New York: VCH, Weinheim. p. 787. ISBN 978-3-527-26446-9.
- ^ Arnold J. Gordon; Richard A. Ford (1972). TheChemist's Companion. Wiley. p. 179.
- ^ a b Harwood LM, Moody CJ (1989). Experimental organic chemistry: Principles and Practice (Illustrated ed.). Wiley-Blackwell. p. 292. ISBN 978-0-632-02017-1.
- ^ Shadman S, Rose C, Yalin AP (2016). "Open-path cavity ring-down spectroscopy sensor for atmospheric ammonia". Applied Physics B. 122 (7): 194. Bibcode:2016ApPhB.122..194S. doi:10.1007/s00340-016-6461-5. S2CID 123834102.
- ^ a b Chromatography/Fourier transform infrared spectroscopy and its applications, by Robert White, p7
- ^ Pollock, Hubert M; Kazarian, S G (2014). "Microspectroscopy in the Mid-Infrared". In Meyers, Robert A. (ed.). Encyclopedia of Analytical Chemistry. John Wiley & Sons Ltd. pp. 1–26. doi:10.1002/9780470027318.a5609.pub2. ISBN 978-0-470-02731-8.
- ^ H M Pollock and D A Smith, The use of near-field probes for vibrational spectroscopy and photothermal imaging, in Handbook of vibrational spectroscopy, J.M. Chalmers and P.R. Griffiths (eds), John Wiley & Sons Ltd, Vol. 2, pp. 1472 - 1492 (2002)
- ^ a b Krivanek OL, Lovejoy TC, Dellby N, Aoki T, Carpenter RW, Rez P, et al. (October 2014). "Vibrational spectroscopy in the electron microscope". Nature. 514 (7521): 209–12. Bibcode:2014Natur.514..209K. doi:10.1038/nature13870. PMID 25297434. S2CID 4467249.
- ^ Idrobo JC, Lupini AR, Feng T, Unocic RR, Walden FS, Gardiner DS, et al. (March 2018). "Temperature Measurement by a Nanoscale Electron Probe Using Energy Gain and Loss Spectroscopy". Physical Review Letters. 120 (9) 095901. Bibcode:2018PhRvL.120i5901I. doi:10.1103/PhysRevLett.120.095901. PMID 29547334.
- ^ Lagos MJ, Batson PE (July 2018). "Thermometry with Subnanometer Resolution in the Electron Microscope Using the Principle of Detailed Balancing". Nano Letters. 18 (7): 4556–4563. Bibcode:2018NanoL..18.4556L. doi:10.1021/acs.nanolett.8b01791. PMID 29874456. S2CID 206748146.
- ^ Hachtel JA, Huang J, Popovs I, Jansone-Popova S, Keum JK, Jakowski J, et al. (February 2019). "Identification of site-specific isotopic labels by vibrational spectroscopy in the electron microscope". Science. 363 (6426): 525–528. Bibcode:2019Sci...363..525H. doi:10.1126/science.aav5845. PMID 30705191.
- ^ Hage FS, Nicholls RJ, Yates JR, McCulloch DG, Lovejoy TC, Dellby N, et al. (June 2018). "Nanoscale momentum-resolved vibrational spectroscopy". Science Advances. 4 (6) eaar7495. Bibcode:2018SciA....4.7495H. doi:10.1126/sciadv.aar7495. PMC 6018998. PMID 29951584.
- ^ Senga R, Suenaga K, Barone P, Morishita S, Mauri F, Pichler T (September 2019). "Position and momentum mapping of vibrations in graphene nanostructures". Nature. 573 (7773): 247–250. arXiv:1812.08294. Bibcode:2019Natur.573..247S. doi:10.1038/s41586-019-1477-8. PMID 31406319. S2CID 118999071.
- ^ Lagos MJ, Trügler A, Hohenester U, Batson PE (March 2017). "Mapping vibrational surface and bulk modes in a single nanocube". Nature. 543 (7646): 529–532. Bibcode:2017Natur.543..529L. doi:10.1038/nature21699. PMID 28332537. S2CID 4459728.
- ^ Govyadinov AA, Konečná A, Chuvilin A, Vélez S, Dolado I, Nikitin AY, et al. (July 2017). "Probing low-energy hyperbolic polaritons in van der Waals crystals with an electron microscope". Nature Communications. 8 (1) 95. arXiv:1611.05371. Bibcode:2017NatCo...8...95G. doi:10.1038/s41467-017-00056-y. PMC 5522439. PMID 28733660.
- ^ Venkatraman K, Levin BD, March K, Rez P, Crozier PA (2019). "Vibrational spectroscopy at atomic resolution with electron impact scattering". Nature Physics. 15 (12): 1237–1241. arXiv:1812.08895. Bibcode:2019NatPh..15.1237V. doi:10.1038/s41567-019-0675-5. S2CID 119452520.
- ^ Kepaptsoglou, Demie; Castellanos-Reyes, José Ángel; Kerrigan, Adam; Alves do Nascimento, Júlio; Zeiger, Paul M.; El hajraoui, Khalil; Idrobo, Juan Carlos; Mendis, Budhika G.; Bergman, Anders; Lazarov, Vlado K.; Rusz, Ján; Ramasse, Quentin M. (2025-07-23). "Magnon spectroscopy in the electron microscope". Nature. 644 (8075): 83–88. arXiv:2410.02908. Bibcode:2025Natur.644...83K. doi:10.1038/s41586-025-09318-y. ISSN 1476-4687. PMID 40702193.
- ^ Statsenko, Anna; Darmawan, Yoshua Albert; Fuji, Takao; Kudo, Tetsuhiro (2022-11-15). "Midinfrared Optical Manipulation Based on Molecular Vibrational Resonance". Physical Review Applied. 18 (5) 054041. Bibcode:2022PhRvP..18e4041S. doi:10.1103/PhysRevApplied.18.054041.
- ^ Darmawan, Y. Albert; Yanagishima, Taiki; Fuji, Takao; Kudo, Tetsuhiro (2025-07-15). "Proposed Method for Label-Free Separation and Infrared Spectroscopy of Carbonyl-Containing Micro- and Nanoparticles Using Mid-Infrared Optical Force". Analytical Chemistry. 97 (27): 14658–14665. Bibcode:2025AnaCh..9714658D. doi:10.1021/acs.analchem.5c02185. ISSN 0003-2700. PMID 40611653.
- ^ Darmawan, Yoshua Albert; Goto, Takuma; Yanagishima, Taiki; Fuji, Takao; Kudo, Tetsuhiro (2023-08-17). "Mid-Infrared Optical Force Chromatography of Microspheres Containing Siloxane Bonds". The Journal of Physical Chemistry Letters. 14 (32): 7306–7312. doi:10.1021/acs.jpclett.3c01679. PMID 37561048.
- ^ Henschel H, Andersson AT, Jespers W, Mehdi Ghahremanpour M, van der Spoel D (May 2020). "Theoretical Infrared Spectra: Quantitative Similarity Measures and Force Fields". Journal of Chemical Theory and Computation. 16 (5): 3307–3315. doi:10.1021/acs.jctc.0c00126. PMC 7304875. PMID 32271575.
- ^ a b c Smith JG (2011). "Chapter 13 Mass Spectrometry and Infrared Spectroscopy". In Hodge T, Nemmers D, Klein J (eds.). Organic chemistry (3rd ed.). New York, NY: McGraw-Hill. pp. 463–488. ISBN 978-0-07-337562-5. Archived from the original (Book) on 2018-06-28. Retrieved 2018-06-30.
- ^ Badger R (1934). "A Relation Between Internuclear Distances and Bond Force Constants" (PDF). The Journal of Chemical Physics. 2 (3): 128. Bibcode:1934JChPh...2..128B. doi:10.1063/1.1749433.
- ^ Kohli KK, Davies G, Vinh NQ, West D, Estreicher SK, Gregorkiewicz T, et al. (June 2006). "Isotope dependence of the lifetime of the vibration of oxygen in silicon". Physical Review Letters. 96 (22) 225503. Bibcode:2006PhRvL..96v5503K. doi:10.1103/PhysRevLett.96.225503. PMID 16803320.
- ^ Hamm P, Lim MH, Hochstrasser RM (1998). "Structure of the amide I band of peptides measured by femtosecond nonlinear-infrared spectroscopy". J. Phys. Chem. B. 102 (31): 6123–6138. doi:10.1021/jp9813286.
- ^ Mukamel S (2000). "Multidimensional femtosecond correlation spectroscopies of electronic and vibrational excitations". Annual Review of Physical Chemistry. 51 (1): 691–729. Bibcode:2000ARPC...51..691M. doi:10.1146/annurev.physchem.51.1.691. PMID 11031297. S2CID 31230696.
- ^ Demirdöven N, Cheatum CM, Chung HS, Khalil M, Knoester J, Tokmakoff A (June 2004). "Two-dimensional infrared spectroscopy of antiparallel beta-sheet secondary structure" (PDF). Journal of the American Chemical Society. 126 (25): 7981–90. Bibcode:2004JAChS.126.7981D. doi:10.1021/ja049811j. PMID 15212548.
External links
[edit]Infrared spectroscopy
View on GrokipediaBasic Principles
Definition and Scope
Infrared spectroscopy is a vibrational spectroscopic technique that measures the absorption, emission, or reflection of infrared radiation by matter, primarily corresponding to transitions between molecular vibrational energy levels.[8] This interaction occurs when infrared photons excite molecular bonds, causing stretches, bends, or other deformations that reveal structural information about the sample.[8] The technique is widely applied in chemistry, materials science, and biology to identify and characterize compounds based on their unique spectral fingerprints.[9] The scope of infrared spectroscopy encompasses the infrared region of the electromagnetic spectrum, which lies between visible light and microwaves, with wavelengths ranging from approximately 0.78 μm to 1000 μm.[10] This region is subdivided into near-infrared (NIR, 14000–4000 cm⁻¹ or 0.78–2.5 μm), mid-infrared (MIR, 4000–400 cm⁻¹ or 2.5–25 μm), and far-infrared (FIR, 400–10 cm⁻¹ or 25–1000 μm), where spectra are typically reported in wavenumbers (cm⁻¹) for convenience in relating energy to frequency.[11] The MIR region is most commonly used for probing fundamental vibrational modes of molecular bonds, while NIR captures overtones and combination bands, and FIR addresses low-energy lattice vibrations in solids.[11] The energies involved (roughly 1–15 kcal/mol) align closely with those required for molecular bond vibrations, enabling selective excitation without electronic transitions.[8] Key advantages of infrared spectroscopy include its non-destructive nature, allowing samples to be analyzed without alteration or consumption, and its ability to provide rapid identification of functional groups such as carbonyls, hydroxyls, and amines through characteristic absorption bands.[12] This makes it particularly valuable for qualitative and quantitative assessments in diverse fields, from pharmaceutical quality control to forensic analysis.[9]Historical Development
The discovery of infrared radiation is credited to British astronomer William Herschel, who in 1800 observed that the temperature of a thermometer increased when placed beyond the red end of the visible spectrum produced by sunlight passing through a prism, indicating the presence of invisible radiation with heating effects.[13] This finding laid the groundwork for infrared spectroscopy by establishing the existence of the infrared portion of the electromagnetic spectrum. Early efforts to measure infrared spectra were advanced by American physicist William Coblentz, who between 1905 and 1906 systematically recorded infrared absorption spectra of over 100 pure organic and inorganic substances using a bolometer detector and rock salt prism spectrometer.[14] His work, published in a seven-part series, provided the first comprehensive catalog of infrared spectra and demonstrated the technique's potential for identifying molecular structures, though limited by low resolution and sensitivity.[14] In the mid-20th century, technological improvements during and after World War II spurred the development of dispersive grating spectrometers, which replaced prisms with diffraction gratings for higher resolution in the 1940s and 1950s. Commercial instruments became available shortly after the war, with companies like Beckman Instruments and Perkin-Elmer introducing double-beam infrared spectrophotometers in the mid-1940s, enabling routine use in chemical analysis and accelerating adoption in industry and research.[15] The 1960s marked a revolutionary shift with the advent of Fourier transform infrared (FTIR) spectroscopy, leveraging Michelson interferometers to collect interferograms that are mathematically transformed into spectra via fast Fourier transform algorithms, offering superior speed, sensitivity, and resolution over dispersive methods.[16] French physicist Pierre Connes pioneered high-resolution FTIR applications, including planetary atmospheric spectra, while in the United States, Digilab released the first commercial FTIR spectrometer, the FTS-14, in 1970, equipped with minicomputers for data processing.[16] By the 1980s and 1990s, affordable microcomputers and detector arrays made FTIR the dominant technology, vastly expanding its accessibility.[15] In the 2010s, further integration of FTIR with microscopy and advanced computing enabled hyperspectral imaging for spatially resolved analysis at the micron scale, enhancing applications in materials science and biomedicine through automated data processing and multivariate analysis.[17]Theoretical Foundations
Molecular Vibrations and Modes
Molecules possess vibrational degrees of freedom arising from the relative motions of their atoms, which are probed by infrared spectroscopy through changes in dipole moments. For a molecule with atoms, there are total degrees of freedom, accounting for three-dimensional translations and rotations of the atoms. Three of these are translational degrees of freedom for the molecule as a whole, and two or three are rotational, leaving the remainder as vibrational degrees of freedom. Specifically, non-linear molecules have vibrational modes, while linear molecules have .[18] Vibrational modes are classified into stretching and bending types. Stretching modes involve changes in bond lengths and can be symmetric, where bonds lengthen and shorten in phase, or asymmetric, where they move out of phase. Bending modes involve changes in bond angles and include scissoring (atoms approach and separate like scissors), rocking (a group of atoms moves in opposite directions in a plane), wagging (out-of-plane motion perpendicular to the molecular plane), and twisting (rotation about a bond axis). For example, water (H₂O), a non-linear triatomic molecule with , exhibits three vibrational modes: a symmetric stretch, an asymmetric stretch, and a bending (scissoring) mode. Carbon dioxide (CO₂), a linear triatomic molecule with , has four vibrational modes: a symmetric stretch, an asymmetric stretch, and two degenerate bending modes.[19][1] These vibrational modes are described as normal modes, which represent independent, collective oscillations of the atoms where all parts of the molecule move in phase with the same frequency. In the harmonic oscillator approximation, valid for small-amplitude vibrations, each normal mode behaves like an independent harmonic oscillator. The vibrational frequency for a mode is approximated by where is the force constant of the bond or angle, and is the reduced mass of the oscillating units. This model assumes quadratic potential energy surfaces, simplifying the description of molecular vibrations.[20][21] Real molecules exhibit anharmonicity due to deviations from the ideal quadratic potential, particularly at larger amplitudes, leading to effects such as overtones (multiples of fundamental frequencies) and combination bands in infrared spectra. Anharmonicity arises from interactions between modes and finite bond lengths, causing the potential energy to include higher-order terms beyond the harmonic approximation.[21]Quantum Mechanical Basis
Infrared absorption arises from the quantization of molecular vibrational energy levels, which can be modeled using the quantum mechanical harmonic oscillator for diatomic or polyatomic bonds under the small-displacement approximation.[22] The potential energy of this model is parabolic, , where is the internuclear distance, is the equilibrium distance, and is the force constant. Solving the Schrödinger equation yields discrete energy levels given by where is the vibrational quantum number, is Planck's constant, and is the classical vibrational frequency, , with as the reduced mass.[22] In this ideal case, transitions between levels occur only for changes , corresponding to fundamental vibrational absorptions.[21] Real molecular bonds deviate from perfect harmonicity due to anharmonic effects, where the potential flattens at larger displacements and includes repulsive walls at short distances. The Morse potential provides a more accurate description: with as the dissociation energy from the bottom of the well and a parameter related to the curvature near equilibrium.[23] This model yields vibrational energy levels allowing for overtones at approximately and combination bands involving multiple modes, though these are weaker than fundamentals.[24] Anharmonicity also leads to dissociation at finite energy, limiting the number of bound states to roughly .[25] The interaction between molecules and infrared radiation is governed by time-dependent perturbation theory, where the oscillating electric field of the photon acts as a perturbation on the molecular Hamiltonian. Absorption occurs when the photon energy matches the energy difference between vibrational states, promoting the molecule from a lower to a higher level. The transition rate is derived using first-order time-dependent perturbation theory, yielding the probability per unit time proportional to the square of the matrix element of the perturbation Hamiltonian.[26] This formalism connects to Einstein's coefficients: the absorption coefficient (from initial state to final state ) determines the rate as , where is the radiation energy density at frequency , while the stimulated emission coefficient and spontaneous emission relate via . Both and depend on the dipole transition moment .[27] Infrared vibrational transitions typically span energies of 0.01–1 eV, corresponding to wavenumbers of 100–4000 cm⁻¹ in the mid-infrared region, where . This range aligns with the thermal energy at room temperature (~0.025 eV), enabling population of low-lying vibrational states and observable absorptions.Selection Rules and Intensity
In infrared spectroscopy, a vibrational transition is allowed only if it results in a change in the molecular dipole moment during the vibration. This condition, known as the gross selection rule for electric dipole transitions, requires that the derivative of the dipole moment μ with respect to the normal coordinate Q of the vibration be non-zero, i.e., .[1] Without this change, the interaction between the molecular vibration and the oscillating electric field of the infrared radiation is negligible, rendering the mode infrared-inactive. Within the harmonic oscillator approximation, the specific selection rule for vibrational quantum number v dictates that only fundamental transitions with are permitted, corresponding to excitations from the ground state (v=0) to the first excited state (v=1) or vice versa.[28] Anharmonicity relaxes this rule, allowing overtone transitions with (e.g., for the first overtone) and combination bands, though these are typically weaker due to smaller transition moments.[29] Symmetry considerations, analyzed through point group theory, further determine activity: a mode is IR-active if its symmetry species transforms like one of the dipole moment components (x, y, or z). For example, in linear CO₂ (D symmetry), the symmetric stretch () is inactive because it preserves the dipole moment, while the asymmetric stretch () is active as it induces a temporary dipole.[30] These rules build on the quantum energy levels of molecular vibrations, ensuring only compatible transitions contribute to the spectrum. The intensity of an IR absorption band reflects the strength of the transition and is quantified by the integrated absorbance , which is proportional to the square of the transition dipole moment matrix element multiplied by the population of the initial state, governed by the Boltzmann distribution.[8] Experimentally, this relates to concentration via the Beer-Lambert law: , where is the molar absorptivity (dependent on the transition moment), is the analyte concentration, and is the path length. Stronger dipole changes yield higher values, leading to more intense peaks, while thermal population effects favor lower-energy fundamentals over hot bands from excited initial states. IR spectral peaks exhibit characteristic shapes due to broadening mechanisms: homogeneous broadening from finite vibrational lifetimes produces Lorentzian profiles, while inhomogeneous effects like Doppler or environmental variations yield Gaussian profiles; real spectra often show Voigt profiles as convolutions of both. Lorentzian tails arise from lifetime uncertainty (), with full width at half maximum (FWHM) inversely proportional to lifetime, whereas Gaussian broadening reflects statistical distributions in velocity or solvation.[31] In the fingerprint region (typically below 1500 cm), numerous allowed vibrational modes overlap, producing complex, unique patterns that serve as molecular "fingerprints" for identification, as the interplay of active modes encodes structural details without isolated group assignments.[2] This utility stems from the density of IR-active fundamentals, bends, and interactions in polyatomic molecules, enabling comparison to reference spectra for compound verification.[32]Instrumentation
Dispersive Spectrometers
Dispersive spectrometers represent the traditional approach to infrared (IR) spectroscopy, employing optical elements to physically separate wavelengths of IR radiation before detection. These instruments scan across the spectrum sequentially, measuring intensity at individual wavelengths to construct the full spectrum point by point. Unlike interferometric methods, they rely on dispersion via prisms or diffraction gratings within a monochromator to achieve wavelength selection.[33] The primary components of a dispersive IR spectrometer include a broadband IR radiation source, a monochromator for dispersion, a detector for signal measurement, and a mechanical chopper for signal modulation. Common sources are the Globar, a silicon carbide rod heated electrically to 1300–1500 K, which emits continuous radiation peaking around 2 μm and covering approximately 0.5–50 μm,[34] and the Nernst glower, a cylindrical filament of rare earth oxides (such as zirconium, yttrium, and erbium oxides) heated to approximately 2000 K, providing emission from 0.5–25 μm with higher intensity in the mid-IR region.[35] The monochromator typically uses either prisms made of alkali halides like NaCl (effective for 2.5–15 μm but limited to resolutions of about 10 cm⁻¹ due to material dispersion) or reflection gratings (blazed for IR wavelengths, capable of resolutions down to ~1 cm⁻¹ across broader ranges). Detectors are thermal devices such as thermocouples, which generate a voltage from the temperature difference between an IR-absorbing hot junction and a reference cold junction, or bolometers, which measure resistance changes in a temperature-sensitive element (e.g., metal film or semiconductor) upon IR absorption. A rotating chopper wheel, operating at 5–30 Hz, modulates the IR beam to convert the signal to an alternating current, enabling lock-in amplification to distinguish it from ambient thermal noise.[36][37][38] In operation, IR radiation from the source passes through sample and reference compartments in a double-beam configuration to compensate for source fluctuations and solvent absorption. The beams then enter the monochromator, where the prism or grating disperses the radiation into its spectral components; a scanning mechanism rotates the dispersive element or adjusts entrance/exit slits to select successive narrow wavelength bands (typically 1–10 cm⁻¹ wide). The modulated beam at each selected wavelength reaches the detector, producing an electrical signal proportional to transmittance, which is recorded as the monochromator scans from ~4000 cm⁻¹ to 400 cm⁻¹. This sequential acquisition requires sensitive detectors due to the low photon flux in IR.[37][33] Dispersive spectrometers offer high spectral resolution in targeted narrow wavelength ranges, making them suitable for detailed studies of specific bands, with grating-based systems achieving ~1 cm⁻¹ resolution. However, their point-by-point scanning leads to slow acquisition times (often several minutes per spectrum) and lower signal-to-noise ratios compared to Fourier transform IR (FTIR) spectrometers, which benefit from multiplex detection. Historically, dispersive instruments dominated IR spectroscopy from their development in the mid-1940s through the 1970s, enabling widespread adoption in organic structural analysis, but they were largely supplanted by commercial FTIR systems in the late 1970s due to the latter's speed and sensitivity advantages. They remain in use today for specialized high-resolution applications, such as monitoring single IR wavelengths in kinetic studies or near-IR regions.[36][39][37]Fourier Transform Infrared (FTIR) Spectrometers
Fourier transform infrared (FTIR) spectrometers represent a significant advancement in infrared instrumentation, employing interferometry to measure spectra in the time domain before computationally converting data to the frequency domain. At the core of an FTIR spectrometer is the Michelson interferometer, which splits incoming infrared radiation from a broadband source using a beam splitter, directing one beam to a fixed mirror and the other to a moving mirror. The recombined beams interfere, producing an interferogram as a function of the optical path difference δ created by the moving mirror's translation. This interferogram I(δ) is mathematically described by the integral where B(ν) is the spectral intensity as a function of wavenumber ν.[40] To obtain the infrared spectrum, the interferogram undergoes a Fourier transform, yielding the intensity spectrum B(ν) via In practice, this is implemented using a discrete fast Fourier transform (FFT) algorithm on digitized interferogram data sampled at precise intervals, enabling efficient computation even for high-resolution spectra. Unlike dispersive spectrometers that sequentially scan wavelengths, FTIR captures the entire spectral range simultaneously in each interferogram measurement.[40][41] FTIR offers key advantages over dispersive methods, including the Fellgett or multiplex advantage, where all wavelengths contribute to the signal throughout the measurement, improving the signal-to-noise ratio (S/N) by a factor approximately proportional to the square root of the number of resolution elements for detector-noise-limited cases. Additionally, the Jacquinot or throughput advantage arises from the interferometer's slitless design, allowing a larger aperture and higher light collection efficiency—often 10 to 100 times greater than in dispersive systems—enhancing sensitivity for low-light samples. Rapid scanning of the moving mirror further enables high-speed data acquisition, with spectra collected in seconds.[41][42][43] The primary components of an FTIR spectrometer mirror those of dispersive instruments—such as the infrared source, sample compartment, and detector—but incorporate interferometer-specific elements like the beam splitter and mirrors, typically coated for infrared transmission. A helium-neon (HeNe) laser provides a monochromatic reference beam for precise zero-path-difference tracking, ensuring accurate sampling during mirror motion via interferogram modulation at the laser's frequency. Detectors commonly include deuterated triglycine sulfate (DTGS) pyroelectric sensors for room-temperature operation or mercury cadmium telluride (MCT) semiconductor detectors cooled with liquid nitrogen for faster response and higher sensitivity in the mid-infrared range.[44][45] To mitigate artifacts in the transformed spectrum, apodization applies a window function to the interferogram before Fourier transformation, tapering the data edges to suppress sidelobes from finite truncation while broadening the main lobe. Common functions include the Happ-Genzel (similar to a cosine bell) for balanced resolution and noise reduction or the Blackman-Harris for strong sidelobe suppression in quantitative analysis. This processing step is essential for producing clean, interpretable spectra without introducing excessive distortion.[46][47]Experimental Methods
Sample Preparation Techniques
Sample preparation in infrared (IR) spectroscopy is essential to ensure that the sample interacts effectively with the IR beam while minimizing artifacts and interferences, allowing for accurate transmission or reflection measurements across gas, liquid, and solid phases.[48] Traditional methods focus on creating thin, uniform sample layers or controlled environments to achieve optimal path lengths and avoid saturation of strong absorption bands. For gas samples, long-path gas cells with path lengths of 10 to 100 cm are commonly employed to enhance sensitivity for low-concentration analytes, typically fitted with NaCl windows that transmit mid-IR radiation effectively.[49] These cells allow the gas to flow through or be statically held, enabling the recording of absorption spectra as the IR beam passes multiple times via mirrors.[50] Pressure broadening effects must be considered, as increased gas pressure leads to collisional line broadening, which can alter spectral resolution and linewidths proportionally to pressure, often requiring operation at reduced pressures (e.g., 10-100 Torr) for sharp rotational-vibrational features.[51] Liquid samples are prepared as thin films sandwiched between two IR-transparent plates, such as KBr or NaCl, to achieve a path length of about 0.01-0.05 mm and prevent total absorption in strong bands like C-H stretches.[48] For non-volatile liquids, this method provides a simple transmission setup, though volatile solvents may require sealed cells to avoid evaporation.[52] Nujol mulls, involving dispersion in mineral oil between plates, are occasionally adapted for viscous liquids but are more standard for solids; they introduce C-H bands that must be subtracted. Attenuated total reflectance (ATR) techniques bypass extensive preparation for non-volatile liquids by directly placing the sample on a crystal surface, where the evanescent wave probes a shallow depth (typically 0.5-5 μm).[53] Solid samples often require dispersion in an IR-transparent matrix to form uniform mixtures for transmission analysis. The KBr pellet method involves grinding 1-2% by weight of the finely powdered sample (particle size <2 μm) with anhydrous KBr, then pressing at 10-15 tons to form a 1 mm thick, 13 mm diameter disk that is nearly transparent to IR.[54] This technique suits crystalline solids but demands dry conditions to avoid moisture artifacts. For powders and irregular solids, diffuse reflectance infrared Fourier transform spectroscopy (DRIFTS) collects scattered IR from the sample surface diluted in KBr (up to 5-10%), providing spectra without pressing and suitable for quantitative analysis of surface properties.[55] Polymers, which may not disperse well, can be analyzed via pyrolysis, where a small sample (1-10 mg) is heated to 500-800°C in a controlled furnace, volatilizing fragments for gas-phase IR detection with minimal initial preparation.[56] Common challenges in sample preparation include water interference, where atmospheric moisture or residual H₂O in samples produces broad OH stretching bands around 3700-3500 cm⁻¹ and bending at 1640 cm⁻¹, overlapping key functional group regions and necessitating dry nitrogen purging or desiccated environments.[57] Solvent subtraction is critical when using solutions, involving recording a background spectrum of the pure solvent and digitally removing its contributions to isolate analyte bands, though incomplete subtraction can introduce baseline distortions.[58] Since the early 2000s, diamond ATR crystals have become a dominant modern alternative, offering durable, high-pressure-resistant surfaces for minimal-preparation analysis of all sample types; a small amount of liquid, solid, or powder is simply pressed against the crystal, enabling rapid, non-destructive measurements with penetration depths of 1-3 μm and effective range down to 400 cm⁻¹.[59] This approach has largely supplanted traditional methods in routine labs due to its ease and reproducibility.[60]Spectral Acquisition and Analysis
Spectral acquisition in infrared (IR) spectroscopy begins with the collection of a background spectrum, also known as an empty cell or reference scan, which captures instrumental and environmental contributions such as solvent or atmospheric interferences.[61] This background is subtracted from the sample spectrum to isolate the analyte's signal, ensuring accurate representation of molecular vibrations.[61] Typical resolution settings range from 4 cm⁻¹ to 8 cm⁻¹, with 4 cm⁻¹ being common for routine analyses to balance detail and acquisition time without excessive broadening of peaks.[62] To enhance the signal-to-noise ratio (S/N), multiple scans—often 16 to 64—are averaged, as the S/N improves proportionally to the square root of the number of scans, reducing random noise while preserving spectral features.[63][64] Following acquisition, data processing refines the raw spectra for reliable interpretation. Baseline correction eliminates drifting offsets or sloping backgrounds caused by scattering or instrumental drift, using methods such as polynomial fitting or piecewise linear subtraction to flatten the spectrum without distorting peak shapes.[61] Smoothing reduces high-frequency noise via the Savitzky-Golay filter, which performs local least-squares polynomial fitting over a moving window (typically 11–21 points) to preserve peak widths and heights better than simple averaging.[65] Normalization scales the spectrum to a standard intensity, often to unit area or maximum absorbance, facilitating comparisons across samples.[66] Spectra are commonly converted from transmittance (T = I/I₀) to absorbance (A = -log₁₀ T) units, as absorbance follows a linear relationship with concentration per Beer's law, aiding quantitative work.[67] Qualitative analysis involves peak picking to identify absorption maxima corresponding to vibrational modes, followed by matching the overall "fingerprint" region (typically 1500–400 cm⁻¹) against reference libraries.[68] Automated algorithms detect peaks above a noise threshold, assigning wavenumbers and relative intensities for functional group inference.[68] Databases like the NIST Chemistry WebBook provide evaluated IR spectra for thousands of compounds, enabling hit-quality indexing via similarity metrics such as correlation coefficients to confirm molecular identities.[69] For quantitative analysis, Beer's law (A = ε b c, where ε is the molar absorptivity, b the path length, and c the concentration) underpins concentration determination from peak heights or areas at characteristic wavenumbers.[70] In multicomponent mixtures, least-squares deconvolution fits the observed spectrum as a linear combination of reference spectra, solving for individual concentrations while accounting for overlapping bands.[71] This method assumes additivity of absorbances and is effective for systems obeying the law, with matrix inversion or iterative algorithms minimizing residuals.[70][72] Common artifacts must be addressed to avoid misinterpretation. Atmospheric CO₂ and H₂O bands (e.g., CO₂ at ~2350 cm⁻¹ and H₂O at ~3400–3600 cm⁻¹ and 1600 cm⁻¹) are removed by subtracting a pre-recorded atmospheric spectrum or through instrument purging with dry nitrogen, ensuring they do not overlap sample features.[73] Stray light, which causes baseline elevation and reduced dynamic range, is corrected by measuring instrument response with a blocked beam and subtracting this scatter contribution, particularly important in dispersive systems.[74]Spectral Features
Absorption Regions and Bands
The infrared spectrum is conventionally divided into three primary regions based on wavelength or wavenumber: the near-infrared (NIR, approximately 14,000–4,000 cm⁻¹), mid-infrared (MIR, 4,000–400 cm⁻¹), and far-infrared (FIR, 400–10 cm⁻¹). The MIR region is the most widely utilized for molecular vibrational analysis, as it corresponds closely to the energies of fundamental vibrational transitions. Within the MIR, the higher-wavenumber portion from 4,000 to 1,500 cm⁻¹ is known as the group frequency region, where stretching vibrations involving light atoms, such as X-H bonds (X = C, N, O), dominate and provide initial clues to functional group presence. The lower MIR portion, from 1,500 to 600 cm⁻¹, constitutes the fingerprint region, characterized by complex skeletal bending, stretching, and deformation modes unique to the overall molecular structure, enabling compound identification through pattern matching. Below 600 cm⁻¹ in the FIR, absorption bands arise from heavy-atom motions, including metal-ligand vibrations in coordination compounds and lattice vibrations in solids./Spectroscopy/Vibrational_Spectroscopy/Infrared_Spectroscopy/Infrared_Spectroscopy)[1][75] In the NIR region, absorptions primarily result from overtones and combination bands of fundamental MIR vibrations, such as the first overtone of O-H stretching appearing around 6,800 cm⁻¹ (approximately twice the fundamental frequency near 3,400 cm⁻¹). These bands are inherently weaker—often 10 to 100 times less intense than fundamentals—due to the anharmonic nature of molecular potentials, which reduces transition probabilities for higher-order processes. Modern extensions into the low-wavenumber FIR and terahertz (THz) regime (down to 10 cm⁻¹ or ~0.3 THz) have expanded applications to phonon modes in crystalline materials, revealing low-energy collective vibrations not accessible in standard MIR measurements.[76][77][78] IR absorption bands exhibit characteristic shapes and widths influenced by molecular environment and relaxation processes. In condensed phases like liquids or solutions, typical band widths at half-height range from 10 to 20 cm⁻¹, arising from vibrational relaxation (on picosecond timescales) and rotational dephasing, which shorten the excited-state lifetime and broaden lines via the energy-time uncertainty principle. Asymmetry in band profiles often stems from Fermi resonance, where a fundamental vibration couples with a nearby overtone or combination band of similar energy and symmetry, leading to splitting and intensity redistribution. Solvent effects further modulate band characteristics; for instance, hydrogen bonding in protic solvents causes O-H stretching bands to shift to lower wavenumbers (e.g., from ~3,600 cm⁻¹ in dilute non-polar media to ~3,300 cm⁻¹ in water) and broaden significantly due to inhomogeneous broadening from varying hydrogen-bond strengths and rapid exchange dynamics.[79]/Spectroscopy/Vibrational_Spectroscopy/Vibrational_Modes/Combination_Bands_Overtones_and_Fermi_Resonances)[8]Characteristic Group Frequencies
Characteristic group frequencies in infrared spectroscopy correspond to the distinctive wavenumber ranges associated with the vibrational modes of specific functional groups, enabling the identification of molecular structures through spectral pattern matching. These absorptions are primarily due to stretching and bending vibrations of bonds, with stretching modes generally appearing at higher wavenumbers than deformations. The consistency of these frequencies across similar compounds makes them invaluable for qualitative analysis, often serving as the first step in interpreting an IR spectrum.[80] The diagnostic power lies in correlating observed peaks to known group frequencies, though exact positions can vary slightly based on molecular environment. For example, the C-H stretching vibrations distinguish between aliphatic and unsaturated hydrocarbons: alkanes absorb at 3000-2850 cm⁻¹, while aromatic C-H stretches occur at 3100-3000 cm⁻¹. Similarly, the carbonyl C=O stretch is a hallmark of ketones, aldehydes, and carboxylic derivatives, typically in the 1750-1650 cm⁻¹ range, with subtypes like esters at higher frequencies (~1735 cm⁻¹) and conjugated amides at lower (~1650 cm⁻¹). Hydroxyl O-H stretches provide another clear indicator, with free O-H in dilute solutions showing sharp peaks at 3650-3580 cm⁻¹ and hydrogen-bonded O-H in alcohols or phenols appearing as broad bands from 3550-3200 cm⁻¹.[81][1] The following table summarizes representative characteristic frequencies for common organic functional groups, focusing on stretching modes for diagnostic purposes:| Functional Group | Vibration Type | Wavenumber Range (cm⁻¹) | Typical Intensity | Notes/Example |
|---|---|---|---|---|
| Alkane C-H | Stretch | 3000–2850 | Strong (s) | Symmetric and asymmetric stretches in CH₃ and CH₂ groups. |
| Aromatic C-H | Stretch | 3100–3000 | Medium (m) | Often accompanied by =C-H bend at 900–700 cm⁻¹. |
| O-H (alcohols, phenols; H-bonded) | Stretch | 3550–3200 | Strong, broad (s, br) | Broadening due to hydrogen bonding; free O-H sharper at ~3600 cm⁻¹. |
| C=O (ketones) | Stretch | 1720–1700 | Strong (s) | Saturated acyclic; shifts lower with conjugation. |
| C=O (esters) | Stretch | 1750–1730 | Strong (s) | Higher frequency due to electronegative oxygen. |
| C=O (amides) | Stretch | 1680–1630 | Strong (s) | Lower due to resonance with N lone pair. |
| C≡C (alkynes) | Stretch | 2260–2190 | Variable (m-w) | Weak if symmetric; stronger in terminal alkynes. |
| C=C (alkenes) | Stretch | 1680–1620 | Variable (m-w) | Intensifies with conjugation. |












