Hubbry Logo
Thermodynamic processThermodynamic processMain
Open search
Thermodynamic process
Community hub
Thermodynamic process
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Thermodynamic process
Thermodynamic process
Thermodynamic process
View on Wikipedia
from Wikipedia
Thermodynamics
The classical Carnot heat engine
Branches
Laws
Systems
State
Processes
Cycles
System properties
Note: Conjugate variables in italics
Process functions
Functions of state
Material properties
Specific heat capacity 
Compressibility 
Thermal expansion 
Equations
Potentials
  • History
  • Culture
History
Philosophy
Theories
Key publications
Timelines
  • Art
  • Education
Scientists
Other

Classical thermodynamics considers three main kinds of thermodynamic processes: (1) changes in a system, (2) cycles in a system, and (3) flow processes.

(1) A Thermodynamic process is a process in which the thermodynamic state of a system is changed. A change in a system is defined by a passage from an initial to a final state of thermodynamic equilibrium. In classical thermodynamics, the actual course of the process is not the primary concern, and often is ignored. A state of thermodynamic equilibrium endures unchangingly unless it is interrupted by a thermodynamic operation that initiates a thermodynamic process. The equilibrium states are each respectively fully specified by a suitable set of thermodynamic state variables, that depend only on the current state of the system, not on the path taken by the processes that produce the state. In general, during the actual course of a thermodynamic process, the system may pass through physical states which are not describable as thermodynamic states, because they are far from internal thermodynamic equilibrium. Non-equilibrium thermodynamics, however, considers processes in which the states of the system are close to thermodynamic equilibrium, and aims to describe the continuous passage along the path, at definite rates of progress.

As a useful theoretical but not actually physically realizable limiting case, a process may be imagined to take place practically infinitely slowly or smoothly enough to allow it to be described by a continuous path of equilibrium thermodynamic states, when it is called a "quasi-static" process. This is a theoretical exercise in differential geometry, as opposed to a description of an actually possible physical process; in this idealized case, the calculation may be exact.

A really possible or actual thermodynamic process, considered closely, involves friction. This contrasts with theoretically idealized, imagined, or limiting, but not actually possible, quasi-static processes which may occur with a theoretical slowness that avoids friction. It also contrasts with idealized frictionless processes in the surroundings, which may be thought of as including 'purely mechanical systems'; this difference comes close to defining a thermodynamic process.[1]

(2) A cyclic process carries the system through a cycle of stages, starting and being completed in some particular state. The descriptions of the staged states of the system are not the primary concern. The primary concern is the sums of matter and energy inputs and outputs to the cycle. Cyclic processes were important conceptual devices in the early days of thermodynamical investigation, while the concept of the thermodynamic state variable was being developed.

(3) Defined by flows through a system, a flow process is a steady state of flows into and out of a vessel with definite wall properties. The internal state of the vessel contents is not the primary concern. The quantities of primary concern describe the states of the inflow and the outflow materials, and, on the side, the transfers of heat, work, and kinetic and potential energies for the vessel. Flow processes are of interest in engineering.

Kinds of process

[edit]

Cyclic process

[edit]

Defined by a cycle of transfers into and out of a system, a cyclic process is described by the quantities transferred in the several stages of the cycle. The descriptions of the staged states of the system may be of little or even no interest. A cycle is a sequence of a small number of thermodynamic processes that indefinitely often, repeatedly returns the system to its original state. For this, the staged states themselves are not necessarily described, because it is the transfers that are of interest. It is reasoned that if the cycle can be repeated indefinitely often, then it can be assumed that the states are recurrently unchanged. The condition of the system during the several staged processes may be of even less interest than is the precise nature of the recurrent states. If, however, the several staged processes are idealized and quasi-static, then the cycle is described by a path through a continuous progression of equilibrium states.

Flow process

[edit]

Defined by flows through a system, a flow process is a steady state of flow into and out of a vessel with definite wall properties. The internal state of the vessel contents is not the primary concern. The quantities of primary concern describe the states of the inflow and the outflow materials, and, on the side, the transfers of heat, work, and kinetic and potential energies for the vessel. The states of the inflow and outflow materials consist of their internal states, and of their kinetic and potential energies as whole bodies. Very often, the quantities that describe the internal states of the input and output materials are estimated on the assumption that they are bodies in their own states of internal thermodynamic equilibrium. Because rapid reactions are permitted, the thermodynamic treatment may be approximate, not exact.

A cycle of quasi-static processes

[edit]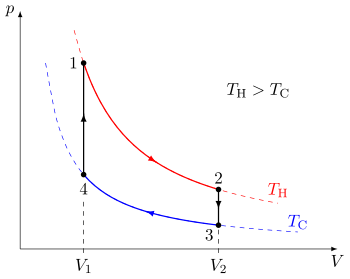
Main article: Stirling cycle
An example of a cycle of idealized thermodynamic processes which make up the Stirling cycle

A quasi-static thermodynamic process can be visualized by graphically plotting the path of idealized changes to the system's state variables. In the example, a cycle consisting of four quasi-static processes is shown. Each process has a well-defined start and end point in the pressure-volume state space. In this particular example, processes 1 and 3 are isothermal, whereas processes 2 and 4 are isochoric. The PV diagram is a particularly useful visualization of a quasi-static process, because the area under the curve of a process is the amount of work done by the system during that process. Thus work is considered to be a process variable, as its exact value depends on the particular path taken between the start and end points of the process. Similarly, heat may be transferred during a process, and it too is a process variable.

Conjugate variable processes

[edit]

It is often useful to group processes into pairs, in which each variable held constant is one member of a conjugate pair.

Pressure – volume

[edit]

The pressure–volume conjugate pair is concerned with the transfer of mechanical energy as the result of work.

  • An isobaric process occurs at constant pressure. An example would be to have a movable piston in a cylinder, so that the pressure inside the cylinder is always at atmospheric pressure, although it is separated from the atmosphere. In other words, the system is dynamically connected, by a movable boundary, to a constant-pressure reservoir.
  • An isochoric process is one in which the volume is held constant, with the result that the mechanical PV work done by the system will be zero. On the other hand, work can be done isochorically on the system, for example by a shaft that drives a rotary paddle located inside the system. It follows that, for the simple system of one deformation variable, any heat energy transferred to the system externally will be absorbed as internal energy. An isochoric process is also known as an isometric process or an isovolumetric process. An example would be to place a closed tin can of material into a fire. To a first approximation, the can will not expand, and the only change will be that the contents gain internal energy, evidenced by increase in temperature and pressure. Mathematically, . The system is dynamically insulated, by a rigid boundary, from the environment.

Temperature – entropy

[edit]

The temperature-entropy conjugate pair is concerned with the transfer of energy, especially for a closed system.

  • An isothermal process occurs at a constant temperature. An example would be a closed system immersed in and thermally connected with a large constant-temperature bath. Energy gained by the system, through work done on it, is lost to the bath, so that its temperature remains constant.
  • An adiabatic process is a process in which there is no matter or heat transfer, because a thermally insulating wall separates the system from its surroundings. For the process to be natural, either (a) work must be done on the system at a finite rate, so that the internal energy of the system increases; the entropy of the system increases even though it is thermally insulated; or (b) the system must do work on the surroundings, which then suffer increase of entropy, as well as gaining energy from the system.
  • An isentropic process is customarily defined as an idealized quasi-static reversible adiabatic process, of transfer of energy as work. Otherwise, for a constant-entropy process, if work is done irreversibly, heat transfer is necessary, so that the process is not adiabatic, and an accurate artificial control mechanism is necessary; such is therefore not an ordinary natural thermodynamic process.

Chemical potential - particle number

[edit]

The processes just above have assumed that the boundaries are also impermeable to particles. Otherwise, we may assume boundaries that are rigid, but are permeable to one or more types of particle. Similar considerations then hold for the chemical potential–particle number conjugate pair, which is concerned with the transfer of energy via this transfer of particles.

  • In a constant chemical potential process the system is particle-transfer connected, by a particle-permeable boundary, to a constant-μ reservoir.
  • The conjugate here is a constant particle number process. These are the processes outlined just above. There is no energy added or subtracted from the system by particle transfer. The system is particle-transfer-insulated from its environment by a boundary that is impermeable to particles, but permissive of transfers of energy as work or heat. These processes are the ones by which thermodynamic work and heat are defined, and for them, the system is said to be closed.

Thermodynamic potentials

[edit]

Any of the thermodynamic potentials may be held constant during a process. For example:

Polytropic processes

[edit]
Main article: Polytropic process

A polytropic process is a thermodynamic process that obeys the relation:

where P is the pressure, V is volume, n is any real number (the "polytropic index"), and C is a constant. This equation can be used to accurately characterize processes of certain systems, notably the compression or expansion of a gas, but in some cases, liquids and solids.

Processes classified by the second law of thermodynamics

[edit]

According to Planck, one may think of three main classes of thermodynamic process: natural, fictively reversible, and impossible or unnatural.[2][3]

Natural process

[edit]

Only natural processes occur in nature. For thermodynamics, a natural process is a transfer between systems that increases the sum of their entropies, and is irreversible.[2] Natural processes may occur spontaneously upon the removal of a constraint, or upon some other thermodynamic operation, or may be triggered in a metastable or unstable system, as for example in the condensation of a supersaturated vapour.[4] Planck emphasised the occurrence of friction as an important characteristic of natural thermodynamic processes that involve transfer of matter or energy between system and surroundings.

Effectively reversible process

[edit]

To describe the geometry of graphical surfaces that illustrate equilibrium relations between thermodynamic functions of state, no one can fictively think of so-called "reversible processes". They are convenient theoretical objects that trace paths across graphical surfaces. They are called "processes" but do not describe naturally occurring processes, which are always irreversible. Because the points on the paths are points of thermodynamic equilibrium, it is customary to think of the "processes" described by the paths as fictively "reversible".[2] Reversible processes are always quasistatic processes, but the converse is not always true.

Unnatural process

[edit]

Unnatural processes are logically conceivable but do not occur in nature. They would decrease the sum of the entropies if they occurred.[2]

Quasistatic process

[edit]
Main article: Quasistatic process

A quasistatic process is an idealized or fictive model of a thermodynamic "process" considered in theoretical studies. It does not occur in physical reality. It may be imagined as happening infinitely slowly so that the system passes through a continuum of states that are infinitesimally close to equilibrium.

See also

[edit]

References

[edit]

Further reading

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Thermodynamic process

View on Grokipedia
from Grokipedia
A thermodynamic process is the manner in which a changes from an initial state to a final state due to interactions with its surroundings, involving the transfer of , work, or both, while connecting equilibrium states. These processes are central to the field of , which studies the relationships between , work, , and energy in physical systems, governing phenomena from to phase changes in . Thermodynamic processes are classified based on constraints on system variables such as , , , or , and they can be reversible (occurring infinitely slowly through equilibrium states, allowing reversal without net change) or irreversible (involving finite rates and dissipative effects like ). A key subclass is the quasistatic process, which proceeds slowly enough for the system to remain in near-equilibrium at every stage, enabling ideal analysis with differential equations. Common types include:
  • Isothermal processes, where remains constant (ΔT = 0), often requiring exchange with a to maintain equilibrium, as in slow expansions of ideal gases following pV = constant.
  • Adiabatic processes, characterized by no (Q = 0), where work done changes and thus , leading to cooling during expansion or heating during compression.
  • Isobaric processes, with constant (P = constant), allowing and to vary proportionally via the .
  • Isochoric processes, where is fixed (V = constant), so changes in or occur without work, solely through addition or removal.
  • Additional specialized types, such as isentropic (constant , reversible and adiabatic), isenthalpic (constant , as in throttling), and polytropic (following PV^k = constant for some k), which generalize behaviors in engineering applications like turbines and compressors.
In practice, thermodynamic processes form the basis of cycles—closed paths returning the system to its initial state—such as the for maximum efficiency or the in steam power plants, enabling the conversion of into mechanical work while adhering to the . These concepts underpin technologies ranging from internal combustion engines to refrigeration systems, with process efficiency limited by the second law, which introduces as a measure of irreversibility.

Fundamentals

Definition and Characteristics

A thermodynamic process is defined as the change in the macroscopic state of a that occurs from one equilibrium state to another, typically involving transfers of in the form of or work. This evolution represents a sequence of events where the system's properties, such as , , and , vary between well-defined initial and final equilibrium conditions. Such processes are fundamental to , which studies transformations in physical systems, assuming the system can be isolated or interact with its surroundings in controlled ways. Key characteristics of thermodynamic processes include their representation as paths in the state space, where the state space is a multidimensional space defined by the system's thermodynamic variables like , , and . These paths trace the succession of equilibrium states through which the system passes during the change, distinguishing processes from static conditions like steady states, where no net change occurs over time. Processes can be idealized, such as those occurring infinitely slowly to maintain equilibrium at every step, or real, where finite rates lead to non-equilibrium transients; however, thermodynamic analysis often focuses on the initial and final states rather than microscopic fluctuations. This path-dependent nature underscores that the total energy exchange depends on the specific route taken in state space. The concept of thermodynamic processes originated in the 19th century, primarily through the foundational work of and William Thomson (), who developed the principles of and transformation amid the industrial era's focus on engines. , in his 1850 formulation, introduced key ideas around and work in cyclic processes, while Kelvin's 1851 contributions emphasized the impossibility of , laying the groundwork for modern . These developments built on earlier caloric theories but shifted emphasis to mechanical equivalents of . Understanding thermodynamic processes presupposes familiarity with basic thermodynamic systems—such as closed systems that exchange energy but not matter, or open systems that do both—and the notion of , where macroscopic properties are uniform and time-independent.

State Functions versus Path Functions

In thermodynamics, state functions are thermodynamic properties that depend solely on the current state of the system, independent of the path or history by which that state was reached. Examples include UU, TT, PP, VV, and SS. The change in a state function, such as ΔU=Ufinal−Uinitial\Delta U = U_\text{final} - U_\text{initial}, is thus determined only by the initial and final states, making it path-independent./Thermodynamics/Fundamentals_of_Thermodynamics/State_vs._Path_Functions) In contrast, path functions are quantities whose values depend on the specific or path taken between states. QQ and work WW are classic examples, as their magnitudes are given by integrals along the process path: Q=∫δQQ = \int \delta Q and W=∫δWW = \int \delta W, where the inexact differentials δQ\delta Q and δW\delta W reflect their . For instance, the heat transferred or work done to go from one state to another can vary significantly depending on whether the process is direct or involves intermediate steps, even if the endpoints are identical./Thermodynamics/Fundamentals_of_Thermodynamics/State_vs._Path_Functions) The distinction between state and path functions is central to of for closed s, which states that the change in equals the added minus the work done by the : ΔU=Q−W\Delta U = Q - W. Here, ΔU\Delta U is path-independent as a , while QQ and WW adjust accordingly to satisfy the equation for any path between the same states. In infinitesimal form, this becomes dU=δQ−δWdU = \delta Q - \delta W, where dUdU is an , highlighting how state changes are balanced by path-dependent transfers of . For example, compressing a gas slowly versus rapidly between the same initial and final volumes yields the same ΔU\Delta U but different values of QQ and WW.

Primary Classifications

Reversible and Irreversible Processes

A reversible thermodynamic process is an idealized process in which both the and its surroundings can be restored to their initial states without any net change in the , occurring infinitely slowly through a series of equilibrium states with no dissipative effects such as or unrestrained . In such processes, the remains in at every stage, allowing the direction of change to be reversed by an modification of the driving forces. This idealization serves as a limiting case for analyzing real processes, enabling the calculation of maximum work or potentials. In contrast, an irreversible thermodynamic process is a real-world process where the system and surroundings cannot be returned to their initial states without external intervention or net changes, typically due to finite gradients in temperature, pressure, or other potentials, leading to dissipative phenomena like friction, viscous flow, or spontaneous mixing. These processes generate entropy in the universe, making reversal impossible without additional work input that further increases total entropy. All actual physical processes are irreversible to some degree, as perfect equilibrium maintenance is unattainable in finite time. The criterion for reversibility is that the process must maintain throughout, which requires it to be quasi-static—proceeding through successive equilibrium states—but quasi-static conditions alone are insufficient without the absence of irreversibilities. Reversibility is tied to the second law of thermodynamics, where the total change of the universe is zero for reversible processes and positive for irreversible ones. A classic example is the expansion of an : in a reversible isothermal expansion, the gas expands slowly against a gradually decreasing external , maintaining equilibrium and allowing the piston to be pushed back to compress the gas to its original state without net change. Conversely, free expansion of the same gas into a is irreversible, as the gas rushes out spontaneously without doing work, generating through unrestrained molecular motion that cannot be undone without external effort. For reversible processes, the infinitesimal is related to change by δQrev=T dS\delta Q_\text{rev} = T \, dS where δQrev\delta Q_\text{rev} is the reversible , TT is the absolute temperature, and dSdS is the infinitesimal change of the . The second quantifies irreversibility through the total change of the : ΔSuniverse=ΔSsystem+ΔSsurroundings≥0\Delta S_\text{universe} = \Delta S_\text{system} + \Delta S_\text{surroundings} \geq 0 with equality holding only for reversible processes.

Quasi-static Processes

A quasi-static in thermodynamics is defined as one that proceeds sufficiently slowly such that the system remains in internal at every instant, passing through a continuous sequence of equilibrium states. This idealized process is approximated by an infinite number of infinitesimal steps, ensuring that deviations from equilibrium are negligible. Quasi-static processes exhibit well-defined paths in the thermodynamic state space because the system is always in a state describable by its equilibrium variables, such as , , and . While many quasi-static processes are reversible in the absence of dissipative effects like , others may be irreversible; for instance, a quasi-static compression involving sliding within the system generates and cannot be perfectly reversed. In calculations, quasi-static processes are often assumed to be reversible for simplicity when dissipation is minimal. These processes are typically represented as smooth, continuous curves on thermodynamic diagrams, such as pressure-volume (PV) or temperature-entropy (TS) plots, which illustrate the trajectory through state space. In practice, quasi-static approximations are valuable for analyzing real-world slow processes, like the gradual compression of a gas in a piston-cylinder assembly, where the system's response time is much shorter than the process duration. During a quasi-static process, state variables evolve continuously, allowing the work done due to volume changes to be calculated precisely. For such volume work, the expression is: W=∫P dVW = \int P \, dV where PP is the system's pressure and dVdV is the infinitesimal volume change./University_Physics_II_-Thermodynamics_Electricity_and_Magnetism(OpenStax)/03%3A_The_First_Law_of_Thermodynamics/3.05%3A_Thermodynamic_Processes)

Common Specific Processes

Isothermal Processes

An is a thermodynamic process in which the of the remains constant throughout the change in state. This constancy is typically maintained by placing the in with a large , or heat bath, at the same , allowing to flow as needed to counteract any temperature variations during expansion or compression. Such processes are fundamental in understanding heat engines and refrigeration cycles, where is essential for . For an ideal gas undergoing an isothermal process, the internal energy change is zero because the internal energy depends solely on temperature: ΔU=0\Delta U = 0. From the first law of thermodynamics, ΔU=Q−W\Delta U = Q - W, where WW is the work done by the system, it follows that the heat absorbed by the system equals the work done by it: Q=WQ = W. For a reversible isothermal expansion of an ideal gas, the work done by the system is given by W=nRTln⁡(VfVi),W = nRT \ln\left(\frac{V_f}{V_i}\right), where nn is the number of moles, RR is the gas constant, TT is the constant temperature, and VfV_f and ViV_i are the final and initial volumes, respectively. This expression arises from integrating the work differential dW=PdVdW = P dV using the ideal gas law P=nRT/VP = nRT / V. In the reversible case, the infinitesimal heat transfer is related to the entropy change by δQ=TdS\delta Q = T dS. Isothermal processes find applications in phase changes, such as or , where the remains fixed at the transition point (e.g., 100°C at standard for ) while is added or removed as . They also occur in slow expansions or compressions of gases in contact with thermal reservoirs, as in certain stages of heat engines or chemical reactors where precise prevents unwanted side reactions. On a - (PV) , an for an traces a following PV=nRTPV = nRT, reflecting the inverse relationship between and at constant . These processes can be quasi-static if performed slowly enough to maintain equilibrium at every stage.

Adiabatic Processes

An is a thermodynamic process in which no is transferred between the and its surroundings, denoted as Q=0Q = 0. According to the first law of thermodynamics, the change in ΔU\Delta U equals the negative of the work done by the , ΔU=−W\Delta U = -W, where work arises solely from changes in volume or other forms of energy transfer. For an undergoing such a , compression increases the as internal energy rises due to work done on the , while expansion decreases the as the gas performs work. In a reversible adiabatic process, which is typically modeled as quasi-static to maintain equilibrium, the process is isentropic, meaning the entropy change ΔS=0\Delta S = 0. For an , this leads to the relations TVγ−1=constantTV^{\gamma-1} = \text{constant} and PVγ=constantPV^\gamma = \text{constant}, where γ=Cp/Cv\gamma = C_p / C_v is the ratio of specific heats at constant pressure and volume, respectively. These equations derive from integrating under the assumption of reversibility, combining dU=CvdTdU = C_v dT with the . Irreversible adiabatic processes, in contrast, involve non-equilibrium conditions and generate . A classic example is the free expansion of an into a , where no work is done (W=0W = 0) and no is exchanged, resulting in ΔU=0\Delta U = 0 and thus a constant . Despite the volume increase, the lack of work or preserves the , which for an depends only on . Adiabatic processes find applications in rapid compressions within diesel engines, where fuel ignition occurs without significant loss during the compression stroke, enhancing . They also describe the of sound waves in air, which occurs nearly adiabatically due to the high relative to heat conduction. On a pressure-volume (PVPV) diagram, the path for a reversible adiabatic process appears as a steeper curve than that of a corresponding isothermal process, reflecting the greater pressure drop for a given volume change due to cooling during expansion. This steepness arises because the adiabatic condition prohibits heat addition to offset the temperature decrease.

Isobaric and Isochoric Processes

In , an maintains constant throughout, allowing to change as is added or removed, whereas an keeps fixed, resulting in variations with changes. These processes are fundamental in analyzing heat engines and chemical reactions, distinct from others by their constraints on or . On a pressure-volume (PV) diagram, an appears as a horizontal line, reflecting unchanged as expands or contracts, while an is a vertical line, indicating constant with shifts along the ordinate. For an , the work done by the system is given by W=PΔV,W = P \Delta V, where PP is the constant and ΔV\Delta V is the change; this equals the area under the horizontal line on the PV . From the first law of thermodynamics, ΔU=Q−W\Delta U = Q - W, the QQ at constant equals the change ΔH=ΔU+PΔV\Delta H = \Delta U + P \Delta V. For an , this simplifies to Q=n[Cp](/page/Molarheatcapacity)ΔTQ = n [C_p](/page/Molar_heat_capacity) \Delta T, where nn is the number of moles, CpC_p is the at constant , and ΔT\Delta T is the temperature change. Such processes commonly occur in open systems, such as heating a in an uncovered at , where expansion happens freely against constant external . In an isochoric process, no work is performed since ΔV=0\Delta V = 0, so W=0W = 0. Consequently, the first law yields Q=ΔUQ = \Delta U, the change in internal energy. For an ideal gas, ΔU=nCvΔT\Delta U = n C_v \Delta T, where CvC_v is the molar heat capacity at constant volume, thus Q=nCvΔTQ = n C_v \Delta T. This process is typical in rigid containers, like heating a gas confined in a fixed-volume tank, where all added heat increases internal energy without expansion work. For ideal gases, the heat capacities relate via Cp=Cv+RC_p = C_v + R, where RR is the , arising from the difference in work contributions between constant-pressure and constant-volume conditions. Isobaric and isochoric processes often combine in thermodynamic cycles to model efficient energy conversion.

Advanced Process Types

Cyclic Processes

A cyclic process in thermodynamics consists of a sequence of thermodynamic processes that form a closed loop in the state space, returning the system to its initial thermodynamic state after completion. This closure ensures that all state functions, such as internal energy UU, pressure PP, volume VV, temperature TT, and entropy SS, revert to their starting values. For a cyclic process in a closed system, the net change in internal energy is zero (ΔU=0\Delta U = 0), so the first law of thermodynamics implies that the net heat absorbed by the system equals the net work done by the system (Qnet=WnetQ_\text{net} = W_\text{net}). On a pressure-volume (PVPV) diagram, the net work output for a cycle is given by the area enclosed by the path; cycles traversed clockwise typically produce positive net work, as in heat engines. These processes are fundamental to devices like heat engines, which convert thermal energy to mechanical work, and refrigerators, which transfer heat against a temperature gradient using external work. Prominent examples include the , introduced by Sadi Carnot in 1824, which comprises two reversible isothermal processes and two reversible adiabatic processes operating between a hot reservoir at temperature ThT_h and a cold reservoir at TcT_c. Another is the , which models spark-ignition internal combustion engines and features two isochoric processes (one for heat addition via ) along with adiabatic compression and expansion. For heat engines, the is defined as η=Wnet/Qin\eta = W_\text{net} / Q_\text{in}, where QinQ_\text{in} is the heat input from the hot source; the achieves the maximum possible efficiency of η=1−Tc/Th\eta = 1 - T_c / T_h, setting an upper bound for all reversible engines operating between the same temperatures. Quasi-static cyclic processes are idealized cycles where each constituent process occurs infinitely slowly, maintaining the system in at every stage, which allows reversible operation and maximizes . In practice, real cycles approximate this through near-equilibrium steps, minimizing irreversibilities like or rapid changes. Such cycles are analyzed using thermodynamic potentials and diagrams to quantify performance metrics like work output and .

Flow Processes

Flow processes in thermodynamics occur in open systems, where mass crosses the system boundaries, allowing for the analysis of energy transfer accompanying fluid flow. These processes are typically analyzed using a , which is a fixed in space enclosing the of interest, enabling the application of conservation laws to account for mass inflow and outflow. Unlike closed systems, open systems in flow processes involve both energy and mass exchange, making a key property due to its inclusion of flow work. In steady flow processes, fluid properties remain constant over time at every point within the , and the is uniform across inlet and outlet sections. of thermodynamics for such processes, applied on a per-unit-mass basis, states that the change in plus changes in kinetic and equals the added minus the shaft work done: Δh+Δ(v22+gz)=q−ws\Delta h + \Delta \left( \frac{v^2}{2} + gz \right) = q - w_s, where hh is specific , vv is , zz is , gg is , qq is specific , and wsw_s is specific shaft work. This equation highlights how energy is conserved as fluid moves through devices, with negligible accumulation inside the under steady conditions. The rate form of the steady flow energy equation, suitable for continuous processes, is given by: m˙(h1+v122+gz1)+Q˙=m˙(h2+v222+gz2)+W˙\dot{m} \left( h_1 + \frac{v_1^2}{2} + g z_1 \right) + \dot{Q} = \dot{m} \left( h_2 + \frac{v_2^2}{2} + g z_2 \right) + \dot{W} where m˙\dot{m} is the , subscripts 1 and 2 denote inlet and outlet, Q˙\dot{Q} is the rate, and W˙\dot{W} is the work rate (typically shaft work). This formulation assumes one-dimensional flow and , facilitating calculations for applications. Unsteady flow processes involve time-dependent changes in properties within the , such as during transient operations where or accumulates. A common example is the filling of a , where incoming increases the 's and until equilibrium is reached, requiring integration of the general balance over time: ΔECV=Q−W+∑m˙i(hi+vi22+gzi)Δt−∑m˙e(he+ve22+gze)Δt\Delta E_{CV} = Q - W + \sum \dot{m}_i (h_i + \frac{v_i^2}{2} + g z_i) \Delta t - \sum \dot{m}_e (h_e + \frac{v_e^2}{2} + g z_e) \Delta t. These processes are analyzed by considering short time intervals to track variations in stored . Flow processes find widespread application in devices such as turbines, which extract work from expanding fluids; nozzles, which accelerate fluids by converting to ; and pumps, which impart energy to fluids via mechanical input. For ideal, incompressible, inviscid flows neglecting and , Bernoulli's equation provides a simplified : P1+12ρv12+ρgz1=P2+12ρv22+ρgz2P_1 + \frac{1}{2} \rho v_1^2 + \rho g z_1 = P_2 + \frac{1}{2} \rho v_2^2 + \rho g z_2, where PP is and ρ\rho is . Many practical flow analyses assume adiabatic conditions to isolate changes.

Polytropic Processes

A is a for an in which the PP and VV are related by PVn=constantPV^n = \text{constant}, where nn is the polytropic index, a constant that characterizes the specific path of the process. This relation generalizes several common thermodynamic processes and assumes a constant specific heat during the process, making it useful for modeling quasi-equilibrium changes in gas systems. The work done during a , calculated as the work by the , is given by W=P2V2−P1V11−nW = \frac{P_2 V_2 - P_1 V_1}{1 - n} for n≠1n \neq 1, where subscripts 1 and 2 denote initial and final states, respectively. For an , this integrates to W=RT1(1−(V1V2)n−1)n−1,W = \frac{ R T_1 \left(1 - \left(\frac{V_1}{V_2}\right)^{n-1}\right)}{n - 1}, where RR is the , T1T_1 is the initial , and the formula applies per mole (or scaled by the number of moles). These expressions derive from integrating W=∫P dVW = \int P \, dV using the polytropic relation and the PV=RTPV = RT (per mole). Special cases of polytropic processes correspond to specific values of the index nn: n=0n = 0 for isobaric (constant pressure), n=1n = 1 for isothermal (constant temperature), n=γn = \gamma for adiabatic (no , where γ=CP/CV\gamma = C_P / C_V is the ), and n=∞n = \infty for isochoric (constant volume). These cases unify simpler processes under the polytropic framework, with the index nn ranging typically from −∞-\infty to ∞\infty depending on the physical conditions. Polytropic processes find applications in , particularly in modeling compression and expansion in compressors and internal engines, where actual paths deviate from ideal isothermal or adiabatic conditions due to losses or inefficiencies. They approximate non-ideal behaviors in devices like reciprocating compressors, providing a practical way to calculate performance without assuming perfect reversibility. Heat transfer in a polytropic process follows from the first law of thermodynamics, Q=ΔU+WQ = \Delta U + W, where ΔU\Delta U is the change in internal energy. For an ideal gas, this yields Q=mCnΔTQ = m C_n \Delta T, with the polytropic specific heat Cn=(n−γ)R(γ−1)(n−1)C_n = \frac{(n - \gamma) R}{(\gamma - 1)(n - 1)} (per mole, or scaled by mass), where ΔT=T2−T1\Delta T = T_2 - T_1. This specific heat can be negative for 1<n<γ1 < n < \gamma, indicating heat removal during compression, which aligns with entropy considerations in such processes.

Processes and Conjugate Variables

Pressure-Volume Relations

In thermodynamics, pressure PP and volume VV form a conjugate pair of variables associated with mechanical work during processes involving volume changes. For a reversible process, the infinitesimal work done by the system is δW=P dV\delta W = P \, dV, where the positive sign indicates work performed by the system on its surroundings as volume increases. This relation arises because pressure exerts a force over the changing area of the system's boundary, such as in a piston-cylinder assembly, directly coupling the intensive variable PP to the extensive variable VV. Pressure-volume (PV) diagrams provide a graphical representation of thermodynamic processes by plotting PP against VV, allowing visualization of state changes and cycles. The area under the curve on a PV diagram quantifies the net work done by the system for a given path from initial volume ViV_i to final volume VfV_f, calculated as W=∫ViVfP dVW = \int_{V_i}^{V_f} P \, dV. For expansion processes, where dV>0dV > 0, the system performs positive work, as seen in the outward path of a cycle; conversely, compression (dV<0dV < 0) requires work input to the system. In reversible cases, the path follows equilibrium states, enabling precise computation via the integral; for example, in a linear pressure-volume relation like P=a+bVP = a + bV, the work simplifies to an algebraic expression derived from the trapezoidal area. However, irreversible processes, such as rapid expansions against a constant external pressure, do not trace a unique equilibrium curve on the PV diagram—instead, the effective work is often the rectangular area PextΔVP_{\text{ext}} \Delta V, which is less than the reversible value due to dissipative losses. These relations find practical application in devices like reciprocating pistons and internal combustion engines, where PV diagrams map the work output during strokes of expansion and compression. In a piston, the work during reversible isothermal expansion of an ideal gas follows W=nRTln⁡(Vf/Vi)W = nRT \ln(V_f / V_i), but real engines exhibit path deviations from ideality, reducing efficiency. For cyclic processes in engines, the enclosed area of the PV loop represents net work per cycle, guiding design optimizations for power output. The PV work term also connects to thermodynamic potentials, such as appearing in the differential form dU=T dS−P dVdU = T \, dS - P \, dV, where the negative sign accounts for work done by the system during expansion.

Temperature-Entropy Relations

In thermodynamics, temperature TT and entropy SS form a conjugate pair of variables, where temperature acts as the intensive "force" driving heat transfer and entropy as the extensive "displacement." For reversible processes, the infinitesimal heat transfer δQrev\delta Q_{\text{rev}} is related to the change in entropy by the equation δQrev=T dS,\delta Q_{\text{rev}} = T \, dS, which originates from the second law and defines entropy changes in equilibrium thermodynamics. This relation highlights how heat exchange at constant temperature contributes directly to entropy increase, distinguishing thermal processes from mechanical ones. Temperature-entropy (TS) diagrams provide a graphical representation of thermodynamic processes, plotting temperature on the vertical axis and entropy on the horizontal axis. Isentropic processes, such as reversible adiabatic expansions or compressions, appear as vertical lines because entropy remains constant (dS=0dS = 0). Isothermal processes, involving heat transfer at fixed temperature, are depicted as horizontal lines, with the length corresponding to the entropy change. The area under a curve on a TS diagram represents the heat transferred during the process, Q=∫T dSQ = \int T \, dS, offering a visual measure of thermal energy flow. A prominent example is the Carnot cycle, idealized for heat engines and refrigerators, which forms a rectangle on the TS diagram: two vertical isentropic legs connect two horizontal isothermal legs at high temperature ThT_h and low temperature TcT_c. During the isothermal expansion at ThT_h, heat QhQ_h is absorbed, increasing entropy by Qh/ThQ_h / T_h; the isentropic expansion lowers temperature without entropy change; isothermal compression at TcT_c rejects heat QcQ_c, decreasing entropy by Qc/TcQ_c / T_c; and isentropic compression returns to the initial state. This rectangular shape underscores the cycle's reversibility and maximum , given by η=1−Tc/Th\eta = 1 - T_c / T_h. In irreversible processes, such as those with finite temperature gradients, entropy generation occurs, causing the total entropy change ΔS>∫δQ/T\Delta S > \int \delta Q / T, leading to paths that deviate upward from reversible ones on the TS diagram and reduced . These relations are applied in analyzing heat engines and refrigeration cycles, where TS diagrams quantify efficiency limits and heat transfer requirements; for instance, in , the and condenser processes align with isothermal segments, optimizing . The total entropy change for any reversible process is calculated as ΔS=∫δQrevT,\Delta S = \int \frac{\delta Q_{\text{rev}}}{T}, with integration along the process path. For an ideal gas, entropy depends on both temperature and volume, yielding the differential form dS=CVT dT+RV dV,dS = \frac{C_V}{T} \, dT + \frac{R}{V} \, dV, where CVC_V is the heat capacity at constant volume and RR is the gas constant; integration provides explicit changes, such as ΔS=CVln⁡(T2/T1)+Rln⁡(V2/V1)\Delta S = C_V \ln(T_2 / T_1) + R \ln(V_2 / V_1) for processes between states 1 and 2. TS diagrams complement pressure-volume representations by emphasizing thermal aspects over mechanical work.

Chemical Potential and Particle Number

In thermodynamic processes involving open systems, the chemical potential μ\mu serves as the conjugate variable to the particle number NN, quantifying the change in the system's associated with adding or removing particles at constant and . This relationship manifests in the chemical work term δWchem=μ dN\delta W_{\text{chem}} = \mu \, dN, which accounts for the energy exchange due to particle transfer. The full differential form of the for such systems incorporates this term alongside thermal and mechanical contributions, expressed as dU=T dS−P dV+μ dN,dU = T \, dS - P \, dV + \mu \, dN, where TT is temperature, SS is entropy, PP is pressure, and VV is volume. This equation extends the first law of thermodynamics to scenarios where particle number is not conserved, enabling analysis of systems interacting with their surroundings through matter exchange. Processes driven by chemical potential gradients include diffusion, where particles move from regions of higher μ\mu to lower μ\mu to equalize potentials and maximize , as seen in the spontaneous mixing of gases or solutes. Chemical reactions also involve changes in NN for reacting , with the reaction proceeding in the direction that reduces the total free energy, guided by differences in μ\mu for reactants and products. Phase changes accompanied by , such as or dissolution, similarly rely on μ\mu equalization across phases, where the transferring particles adjust until their chemical potentials match in equilibrium. In the grand canonical ensemble, which models systems in contact with a , the particle number NN fluctuates around an average value determined by the fixed μ\mu, temperature, and volume. Equilibrium is achieved when μ\mu is uniform across connected systems, minimizing the grand potential and stabilizing particle exchange; fluctuations in NN arise from probabilistic variations but average to the value set by μ\mu. This framework is essential for understanding irreversible processes like those in non-equilibrium . Applications of these concepts appear in , where μ\mu differences drive ion transport in electrochemical cells, contributing to the cell potential via the . In , water flows across a from low to high solute concentration regions until the chemical potentials of the solvent equalize on both sides, generating . Battery reactions exemplify chemical work, as μ\mu gradients between electrodes, such as in lithium-ion systems, enable the conversion of to electrical work during discharge, with the voltage reflecting the μ\mu difference per transferred charge.

Thermodynamic Potentials in Processes

Internal Energy and Enthalpy

In thermodynamics, the internal energy UU represents the total microscopic energy of a system, encompassing kinetic and potential energies of its constituent particles, excluding macroscopic contributions like bulk kinetic or potential energy. For a closed system with fixed particle number, the differential form of the internal energy is given by the dU=T dS−P dVdU = T \, dS - P \, dV, where TT is , SS is , PP is , and VV is ; this expression arises from combining the first and second for reversible processes. The enthalpy HH, defined as H=U+PVH = U + P V, serves as a thermodynamic potential particularly suited for processes at constant pressure. Its differential form is dH=T dS+V dPdH = T \, dS + V \, dP, which follows directly from the definition of HH and the fundamental relation for UU. This form highlights enthalpy's utility, as at constant pressure (dP=0dP = 0), dH=T dS=δqdH = T \, dS = \delta q, equating the change in enthalpy to the heat transferred in reversible processes. Enthalpy is obtained via a Legendre transform of the with respect to volume, replacing VV as the independent variable with its conjugate PP, which facilitates analysis when pressure is controlled. In specific thermodynamic processes, these potentials simplify energy accounting. For an (dV=0dV = 0), dU=δq+δwdU = \delta q + \delta w reduces to ΔU=qV\Delta U = q_V since no work is done (δw=−P dV=0\delta w = -P \, dV = 0), making internal energy the direct measure of at constant volume. Conversely, in an (dP=0dP = 0), ΔH=qP\Delta H = q_P, so captures the heat transfer, accounting for both internal energy change and pressure-volume work. In adiabatic processes (δq=0\delta q = 0), conservation principles from imply ΔU=δw\Delta U = \delta w (with for work done by the system), preserving total through work alone. Applications of these potentials extend to practical contexts. In steady-flow processes, such as those in turbines or nozzles, the specific h=u+Pvh = u + P v (per unit mass) appears in the h1+v122+gz1=h2+v222+gz2+wsh_1 + \frac{v_1^2}{2} + g z_1 = h_2 + \frac{v_2^2}{2} + g z_2 + w_s, where flow work PvP v is incorporated naturally. For reactions at constant , the standard change ΔH\Delta H quantifies the heat released or absorbed, as qP=ΔHq_P = \Delta H, which is crucial for designing engines and reactors. These primary potentials, and , provide the foundational Legendre transforms for deriving free energies in systems involving or other constraints.

Free Energies

The Helmholtz free energy, denoted as FF, is defined as F=U−TSF = U - TS, where UU is the , TT is the , and SS is the . Its differential form is dF=−S dT−P dV+μ dNdF = -S \, dT - P \, dV + \mu \, dN, where PP is , VV is , μ\mu is the , and NN is the number of particles. At constant temperature and volume, the Helmholtz free energy reaches a minimum at , providing a criterion for stability in such conditions. The , denoted as GG, is defined as G=H−TSG = H - TS, where H=U+PVH = U + PV is the , equivalently expressed as G=U+PV−TSG = U + PV - TS. Its is dG=−S dT+V dP+μ dNdG = -S \, dT + V \, dP + \mu \, dN. At constant temperature and pressure, the Gibbs free energy minimizes at equilibrium, making it particularly useful for processes under these constraints. This form incorporates the term μ dN\mu \, dN to account for changes in particle number during chemical processes. In thermodynamic processes at constant , the change in ΔF\Delta F equals the maximum non--volume work that can be extracted from the system, ΔF=wmax⁡,non-PV\Delta F = w_{\max, \text{non-PV}}. For processes at constant and , the change in ΔG\Delta G determines spontaneity: if ΔG<0\Delta G < 0, the process is spontaneous. These relations stem from the second law, where free energies decrease during spontaneous processes at the respective constant conditions, reflecting the available work and directionality. Applications of Gibbs free energy include phase transitions, where equilibrium occurs when ΔG=0\Delta G = 0 between phases, such as at the melting or boiling point. In electrochemistry, the relation ΔG=−nFE\Delta G = -nFE links the free energy change to the cell potential EE, with nn as the number of electrons transferred and FF as Faraday's constant, quantifying the maximum electrical work in electrochemical cells.

Second Law Classifications

Spontaneous Processes

A spontaneous thermodynamic process is one that occurs naturally without external intervention, characterized by an increase in the of the universe, where ΔSuniverse>0\Delta S_{\text{universe}} > 0. This criterion stems from the second law of thermodynamics, which dictates that all spontaneous changes cause such an increase, driving systems toward greater disorder or equilibrium. Unlike idealized reversible processes, spontaneous processes are inherently irreversible, as reversing them would require work input to decrease universal , which violates the second law. In isolated systems, spontaneous processes proceed to maximize the total , as no or exchange occurs with the surroundings, leading to the highest probable state. For non-isolated systems, such as those in contact with a , spontaneity is instead governed by minimization of appropriate thermodynamic potentials like free energy, reflecting the entropy-driven tendency under constraints. Key examples include flowing spontaneously from a hotter object to a colder one, as articulated in the Clausius statement of the second law: heat cannot pass from a colder to a hotter body without external work. Similarly, the mixing of two gases in a occurs spontaneously due to increased from molecular dispersion, without any separating needed. These processes find applications in phenomena like , where particles spread from high to low concentration to increase , and in chemical reactions that proceed in direction when the overall change is positive, such as the of releasing and gases. In both cases, the directionality aligns with the second law's prohibition on decrease, ensuring that spontaneous events contribute to the universe's thermodynamic . At the boundary, reversible processes occur with ΔSuniverse=0\Delta S_{\text{universe}} = 0, representing equilibrium where no net spontaneous change happens without driving forces, allowing maximum in idealized cycles.

Non-spontaneous Processes

Non-spontaneous thermodynamic processes are those that lack a natural tendency to occur and would lead to a decrease in the of the (ΔSuniverse<0\Delta S_{\text{universe}} < 0) if attempted without external aid, effectively representing the reverse of spontaneous processes. The second law of thermodynamics prohibits such isolated occurrences, as it mandates that the of an isolated system cannot decrease, thereby requiring these processes to be driven by external work or coupling to compensating spontaneous reactions elsewhere. These processes are distinguished by their operation against natural gradients, such as temperature or chemical potential differences, and necessitate continuous energy input to proceed. A classic example is refrigeration, where heat is extracted from a colder region and transferred to a hotter one, defying the natural flow of heat from hot to cold; this requires mechanical work, as stated in the Clausius formulation of the second law. Another key example is electrolysis, which uses electrical energy to drive non-spontaneous reactions, such as the decomposition of water into hydrogen and oxygen gases, overcoming the positive Gibbs free energy change of the reaction. Under the second law, non-spontaneous processes cannot occur in isolated systems due to the entropy decrease they imply, but in open systems, they become viable through work input from external sources, ensuring the net ΔSuniverse>0\Delta S_{\text{universe}} > 0 when accounting for the broader context. This work often originates from spontaneous processes in other parts of the system or environment, allowing local order to form at the expense of greater disorder elsewhere. Practical applications encompass uphill chemical reactions, such as electrolytic metal refining or , and devices like heat pumps that move heat against thermal gradients for space heating. The performance of these systems is constrained by the Carnot limit, which defines the theoretical maximum based on the reservoirs involved, underscoring the second law's role in bounding real-world irreversibilities. Unlike spontaneous processes that align with equilibrium tendencies, non-spontaneous ones are inherently unnatural, sustaining non-equilibrium states by actively countering entropy's drive toward disorder. They often involve engineered cycles to integrate the required work efficiently within larger systems.

Effectively Reversible Processes

Real thermodynamic processes can approximate the reversible limit through quasistatic changes, where the system passes through near-equilibrium states with driving forces, resulting in negligible (ΔSuniverse≈0\Delta S_{\text{universe}} \approx 0). These are analyzed as reversible for calculations, such as in heat engines, despite minor irreversibilities, bridging idealized reversibility (ΔSuniverse=0\Delta S_{\text{universe}} = 0) and spontaneous irreversibility (ΔSuniverse≫0\Delta S_{\text{universe}} \gg 0). Examples include slow, frictionless expansions or phase changes at exact transition temperatures. changes are computed along hypothetical reversible paths: ΔS≈∫δQrevT\Delta S \approx \int \frac{\delta Q_{\text{rev}}}{T}.

References

  1. https://pressbooks.online.ucf.edu/osuniversityphysics2/chapter/thermodynamic-processes/
  2. https://phys.libretexts.org/Courses/University_of_California_Davis/UCD%253A_Physics_7A_-_General_Physics/04%253A_Models_of_Thermodynamics/4.05%253A_Thermodynamics_processes
  3. https://www.sciencedirect.com/topics/engineering/thermodynamic-process
  4. https://boulderschool.yale.edu/sites/default/files/files/Jarzynski-Boulder01.pdf
  5. https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node11.html
  6. https://eaglepubs.erau.edu/introductiontoaerospaceflightvehicles/chapter/thermodynamic-foundations/
  7. https://phys.uri.edu/gerhard/PHY525/tln79.pdf
  8. http://home.olemiss.edu/~cmpcs/engr321def.html
  9. https://plato.stanford.edu/archives/win2016/entries/time-thermo/
  10. https://pmc.ncbi.nlm.nih.gov/articles/PMC7516509/
  11. https://www.physics.ox.ac.uk/system/files/file_attachments/basic_thermo.pdf
  12. https://edu.rsc.org/feature/entropy-a-masterclass/2020134.article
  13. https://www.sfu.ca/~mbahrami/ENSC%20388/Notes/First%20Law%20of%20Thermodynamics_Closed%20Systems.pdf
  14. https://pressbooks.online.ucf.edu/osuniversityphysics2/chapter/reversible-and-irreversible-processes/
  15. https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node34.html
  16. https://www.usna.edu/Users/chemistry/morse/_files/documents/SC112-Chapter18/optional18.doc
  17. https://www.nsstc.uah.edu/mips/personnel/kevin/thermo/CHAP4notes.pdf
  18. https://users.wpi.edu/~sullivan/ES3001/Lectures/Entropy_ch05_2013.pdf
  19. https://pressbooks.online.ucf.edu/chemistryfundamentals/chapter/the-second-and-third-laws-of-thermodynamics/
  20. https://web.mit.edu/16.unified/www/FALL/thermodynamics/chapter_7.htm
  21. https://personal.colby.edu/personal/t/twshattu/PhysicalChemistryText/Part1/Ch11.pdf
  22. https://courses.physics.illinois.edu/phys213/su2023/prelecture6.pdf
  23. https://ocw.mit.edu/ans7870/16/16.unified/thermoF03/chapter_2.htm
  24. http://ui.adsabs.harvard.edu/abs/1960AmJPh..28..119T/abstract
  25. https://www.lehman.edu/faculty/dgaranin/Statistical_Thermodynamics/Thermodynamics.pdf
  26. https://farside.ph.utexas.edu/teaching/sm1/Thermalhtml/node37.html
  27. http://physics.bu.edu/~redner/211-sp06/class-thermodynamics/processes.html
  28. http://labman.phys.utk.edu/phys221core/modules/m10/processes.html
  29. https://personal.colby.edu/personal/t/twshattu/PhysicalChemistryText/Part1/Ch13.pdf
  30. https://scholar.harvard.edu/files/schwartz/files/9-phases.pdf
  31. http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/isoth.html
  32. https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node33.html
  33. https://chemistry.coe.edu/piper/posts/groves-thermo-kinetics/lecture_slides/AdiabaticProcesses_and_Heat_Engines_CHEM361A.pdf
  34. https://pressbooks.online.ucf.edu/osuniversityphysics2/chapter/adiabatic-processes-for-an-ideal-gas/
  35. https://web.mit.edu/16.unified/www/FALL/thermodynamics/thermo_7.htm
  36. https://web.pa.msu.edu/courses/2011fall/phy215/handouts/Thermodynamics_nq.pdf
  37. https://do-server1.sfs.uwm.edu/list/169H5013T3/ppt/115H42T/physics_notes__class__11-chapter__12_thermodynamics.pdf
  38. https://trace.tennessee.edu/cgi/viewcontent.cgi?article=1255&context=utk_chanhonoproj
  39. https://condor.depaul.edu/asarma/Teaching/Winter2012/PHY171/LEC171/feb20Lec15post.pdf
  40. https://pressbooks.online.ucf.edu/phy2053bc/chapter/the-first-law-of-thermodynamics-and-some-simple-processes/
  41. https://web.njit.edu/~tyson/P103_chapter12_TAT_wk6.pdf
  42. https://my.eng.utah.edu/~mse5032/classnote3.pdf
  43. http://nebula2.deanza.edu/~lanasheridan/4C/Phys4C-Lecture18.pdf
  44. https://pressbooks.uiowa.edu/clonedbook/chapter/the-first-law-of-thermodynamics-and-some-simple-processes/
  45. http://physics.bu.edu/~duffy/ns549_fall07_notes06/process_isochoric.html
  46. https://physics.uwyo.edu/~teyu/Ch19.pdf
  47. http://www.physics.gsu.edu/dhamala/Physics2211/Chapter16.pdf
  48. https://physicsx.erau.edu/Courses/CoursesS2025/PS208/Lectures/chapter_19.pdf
  49. https://www.lehman.edu/faculty/dgaranin/Statistical_Thermodynamics/PHY303-assignment-2-solutions.pdf
  50. https://eng.libretexts.org/Bookshelves/Introductory_Engineering/Basic_Engineering_Science_-_A_Systems_Accounting_and_Modeling_Approach_%28Richards%29/07%253A_Conservation_of_Energy/7.09%253A_Thermodynamic_Cycles
  51. http://physics.bu.edu/~redner/211-sp06/class-thermodynamics/process_cycle.html
  52. https://pressbooks.online.ucf.edu/thermorit/chapter/energy-balance-for-cycles/
  53. https://www3.nd.edu/~powers/ame.20231/carnot1897.pdf
  54. https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node26.html
  55. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Physical_Chemistry_%28Fleming%29/05%253A_The_Second_Law/5.02%253A_Heat_Engines_and_the_Carnot_Cycle
  56. https://phys.libretexts.org/Bookshelves/University_Physics/University_Physics_%28OpenStax%29/University_Physics_II_-_Thermodynamics_Electricity_and_Magnetism_%28OpenStax%29/03%253A_The_First_Law_of_Thermodynamics/3.05%253A_Thermodynamic_Processes
  57. https://www.eng.utah.edu/~mcmurtry/Notes/2300_les11.pdf
  58. https://ocw.mit.edu/ans7870/16/16.unified/thermoF03/chapter_6.htm
  59. https://www.purdue.edu/freeform/me200/wp-content/uploads/sites/29/2023/02/ME-200-Chapter-4.pdf
  60. https://eaglepubs.erau.edu/introductiontoaerospaceflightvehicles/chapter/conservation-of-energy-energy-equation-bernoullis-equation/
  61. http://www.physics.smu.edu/scalise/P3374/notes/polytropes.pdf
  62. https://www3.nd.edu/~powers/ame.20231/notes.pdf
  63. https://www.ocf.berkeley.edu/~rfu/notes/polytropic_processes
  64. https://users.wpi.edu/~sullivan/ES3001/Lectures/Chapter_4/ch04b-jms2013.pdf
  65. https://ps.uci.edu/~cyu/p214A/LectureNotes/Lecture2/html_version/
  66. https://courses.physics.ucsd.edu/2018/Spring/physics210a/LECTURES/SUM02.pdf
  67. http://www.chem.ucla.edu/~vinh/disc5.html
  68. https://physics.bu.edu/~duffy/EssentialPhysics/chapter15/section15dash2.pdf
  69. https://www3.nd.edu/~powers/ame.50531/notes.pdf
  70. https://ocw.mit.edu/courses/3-012-fundamentals-of-materials-science-fall-2005/4e66ccea9b9c9dcdb35d4c47cbb3ae78_lec04t.pdf
  71. https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node41.html
  72. http://nebula2.deanza.edu/~lanasheridan/4C/Phys4C-Lecture25-san.pdf
  73. https://webspace.clarkson.edu/projects/fluidflow/public_html/kam/courses/2005/es340/session-12.pdf
  74. https://ronney.usc.edu/AME436/Lecture7/AME436-S19-lecture7.pdf
  75. https://purdue.edu/freeform/me200/wp-content/uploads/sites/29/2023/03/ME-200-Chapter-6.pdf
  76. https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node40.html
  77. https://www2.chemistry.msu.edu/courses/CEM882/SS14/CourseNotes_part2.pdf
  78. https://phas.ubc.ca/~stamp/TEACHING/PHYS403/NOTES/1.pdf
  79. https://sites.esm.psu.edu/~vfm5153/TSM/lecture14.html
  80. https://www.physics.unlv.edu/~qzhu/Teaching/ThermalPhysics/Lec11.pdf
  81. https://dspace.mit.edu/bitstream/handle/1721.1/39424/133/2-141Fall-2002/NR/rdonlyres/Mechanical-Engineering/2-141Fall-2002/AA7ABFDB-317D-477A-BE2D-D94337845C7C/0/react_diffuse.pdf
  82. https://msecore.northwestern.edu/315/315text.xhtml
  83. https://scholar.harvard.edu/files/schwartz/files/7-ensembles.pdf
  84. https://itp.uni-frankfurt.de/~gros/Vorlesungen/TD/10_Grand_canonical_ensemble.pdf
  85. https://ocw.mit.edu/courses/3-012-fundamentals-of-materials-science-fall-2005/798d2e221c8f716e578bfd908383d9c6_lec13t.pdf
  86. https://www.princeton.edu/~akosmrlj/MAE545_S2018/lecture12-13_slides.pdf
  87. https://ceder.berkeley.edu/publications/2016_urban_li_computational_review_corrected.pdf
  88. https://mahi.ucsd.edu/Guy/sio224/thermo.pdf
  89. https://www.physics.rutgers.edu/~anirvans/611/lects/Notes.pdf
  90. https://ps.uci.edu/~cyu/p115A/LectureNotes/Lecture7/html_version/lecture7.html
  91. https://mcgreevy.physics.ucsd.edu/s12/lecture-notes/chapter05.pdf
  92. https://web.physics.wustl.edu/alford/physics/Legendre_introduction.pdf
  93. https://math.mit.edu/~hrm/papers/thermo7.pdf
  94. http://www.atmo.arizona.edu/students/courselinks/spring08/atmo336s1/courses/fall13/atmo551a/Site/ATMO_451a_551a_files/FirstLawThermodynamics.pdf
  95. https://web.mit.edu/16.unified/www/FALL/thermodynamics/notes/node15.html
  96. https://web.mit.edu/16.unified/www/FALL/thermodynamics/thermo_6.htm
  97. http://ch301.cm.utexas.edu/thermo/#enthalpy/enthalpy-all.php
  98. https://faculty.washington.edu/jcv2/CHEM452_WI2023/html/free_energy_and_equilibrium.html
  99. https://dev.housing.arizona.edu/helmholtz-free-energy
  100. https://schwartz.scholars.harvard.edu/file_url/168
  101. https://personal.colby.edu/personal/t/twshattu/PhysicalChemistryText/Part1/Ch16.pdf
  102. https://faculty.washington.edu/gdrobny/Lecture452_8.pdf
  103. https://cast.desu.edu/sites/cmnst/files/document/1/2015_trochapter17_free_energy_and_thermodynamics.pdf
  104. https://chem.libretexts.org/Courses/Mount_Royal_University/Chem_1202/Unit_7%253A_Principles_of_Thermodynamics/7.3%253A_Criteria_for_Spontaneous_Change%253A_The_Second_Law_of_Thermodynamics
  105. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%253A_General_Chemistry_%28Petrucci_et_al.%29/19%253A_Spontaneous_Change%253A_Entropy_and_Gibbs_Energy/19.4%253A_Criteria_for_Spontaneous_Change%253A_The_Second_Law_of_Thermodynamics
  106. https://openstax.org/books/physics/pages/12-3-second-law-of-thermodynamics-entropy
  107. https://openstax.org/books/university-physics-volume-2/pages/4-5-statements-of-the-second-law-of-thermodynamics
  108. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Thermodynamics/The_Four_Laws_of_Thermodynamics/Second_Law_of_Thermodynamics
  109. http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/seclaw.html
  110. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Chemistry_and_Chemical_Reactivity_(Kotz_et_al.)/19%3A_Electrochemistry/19.08%3A_Electrolysis-_Driving_Non-spontaneous_Chemical_Reactions_with_Electricity
  111. http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/heatpump.html
  112. https://courses.lumenlearning.com/suny-physics/chapter/15-5-applications-of-thermodynamics-heat-pumps-and-refrigerators/
  113. https://openstax.org/books/university-physics-volume-2/pages/4-2-reversible-and-irreversible-processes
  114. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Principles_of_Modern_Chemistry_(Oxtoby_et_al.)/Unit_4%3A_Equilibrium_in_Chemical_Reactions/13%3A_Spontaneous_Processes_and_Thermodynamic_Equilibrium/13.4%3A_Entropy_Changes_in_Reversible_Processes
Add your contribution
Related Hubs
User Avatar
No comments yet.