Adder (electronics)

George Stibitz invented the 2-bit binary adder (the Model K) in 1937.

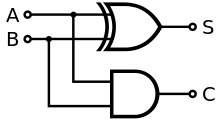
The half adder adds two single binary digits ${\displaystyle A}$ and ${\displaystyle B}$. It has two outputs, sum (${\displaystyle S}$) and carry (${\displaystyle C}$). The carry signal represents an overflow into the next digit of a multi-digit addition. The value of the sum is ${\displaystyle 2C+S}$. The simplest half-adder design, pictured on the right, incorporates an XOR gate for ${\displaystyle S}$ and an AND gate for ${\displaystyle C}$. The Boolean logic for the sum (in this case ${\displaystyle S}$) will be ${\displaystyle A\oplus B}$ whereas for the carry (${\displaystyle C}$) will be ${\displaystyle A\cdot B}$. With the addition of an OR gate to combine their carry outputs, two half adders can be combined to make a full adder.^[2]

The truth table for the half adder is:

Inputs		Outputs
A	B	Cout	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

Various half adder digital logic circuits:

• 
  Half adder in action.
• 
  Schematic of half adder implemented with one XOR gate and one AND gate.
• 
  Schematic of half adder implemented with five NAND gates.
• 
  Schematic symbol for a 1-bit half adder.

A full adder adds binary numbers and accounts for values carried in as well as out. A one-bit full-adder adds three one-bit numbers, often written as ${\displaystyle A}$, ${\displaystyle B}$, and ${\displaystyle C_{in}}$; ${\displaystyle A}$ and ${\displaystyle B}$ are the operands, and ${\displaystyle C_{in}}$ is a bit carried in from the previous less-significant stage.^[3] The circuit produces a two-bit output. Output carry and sum are typically represented by the signals ${\displaystyle C_{out}}$ and ${\displaystyle S}$, where the sum equals ${\displaystyle 2C_{out}+S}$. The full adder is usually a component in a cascade of adders, which add 8, 16, 32, etc. bit binary numbers.

A full adder can be implemented in many different ways such as with a custom transistor-level circuit or composed of other gates. The most common implementation is with:

${\displaystyle S=A\oplus B\oplus C_{in}}$

${\displaystyle C_{out}=(A\cdot B)+(C_{in}\cdot (A\oplus B))}$

The above expressions for ${\displaystyle S}$ and ${\displaystyle C_{in}}$ can be derived from using a Karnaugh map to simplify the truth table.

In this implementation, the final OR gate before the carry-out output may be replaced by an XOR gate without altering the resulting logic. This is because when A and B are both 1, the term ${\displaystyle (A\oplus B)}$ is always 0, and hence ${\displaystyle (C_{in}\cdot (A\oplus B))}$ can only be 0. Thus, the inputs to the final OR gate can never be both 1 (this is the only combination for which the OR and XOR outputs differ).

Due to the functional completeness property of the NAND and NOR gates, a full adder can also be implemented using nine NAND gates,^[4] or nine NOR gates.

Using only two types of gates is convenient if the circuit is being implemented using simple integrated circuit chips which contain only one gate type per chip.

A full adder can also be constructed from two half adders by connecting ${\displaystyle A}$ and ${\displaystyle B}$ to the input of one half adder, then taking its sum-output ${\displaystyle S}$ as one of the inputs to the second half adder and ${\displaystyle C_{in}}$ as its other input, and finally the carry outputs from the two half-adders are connected to an OR gate. The sum-output from the second half adder is the final sum output (${\displaystyle S}$) of the full adder and the output from the OR gate is the final carry output (${\displaystyle C_{out}}$). The critical path of a full adder runs through both XOR gates and ends at the sum bit ${\displaystyle S}$. Assumed that an XOR gate takes 1 delays to complete, the delay imposed by the critical path of a full adder is equal to:

${\displaystyle T_{\text{FA}}=2\cdot T_{\text{XOR}}=2D}$

The critical path of a carry runs through one XOR gate in adder and through 2 gates (AND and OR) in carry-block and therefore, if AND or OR gates take 1 delay to complete, has a delay of:

${\displaystyle T_{\text{c}}=T_{\text{XOR}}+T_{\text{AND}}+T_{\text{OR}}=D+D+D=3D}$

The truth table for the full adder is:

Inputs			Outputs
A	B	Cin	Cout	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

Inverting all inputs of a full adder also inverts all of its outputs, which can be used in the design of fast ripple-carry adders, because there is no need to invert the carry.^[5]

Various full adder digital logic circuits:

• 
  Full adder in action.
• 
  Schematic of full adder implemented with two XOR gates, two AND gates, one OR gate.
• 
  Schematic of full adder implemented with nine NAND gates.
• 
  Schematic of full adder implemented with nine NOR gates.
• 
  Full adder with inverted outputs with single-transistor carry propagation delay in CMOS^[5]
• 
  Schematic symbol for a 1-bit full adder with C_in and C_out drawn on sides of block to emphasize their use in a multi-bit adder

It is possible to create a logical circuit using multiple full adders to add N-bit numbers. Each full adder inputs a ${\displaystyle C_{in}}$, which is the ${\displaystyle C_{out}}$ of the previous adder. This kind of adder is called a ripple-carry adder (RCA), since each carry bit "ripples" to the next full adder. The first (and only the first) full adder may be replaced by a half adder (under the assumption that ${\displaystyle C_{in}=0}$).

The layout of a ripple-carry adder is simple, which allows fast design time; however, the ripple-carry adder is relatively slow, since each full adder must wait for the carry bit to be calculated from the previous full adder. The gate delay can easily be calculated by inspection of the full adder circuit. Each full adder requires three levels of logic. In a 32-bit ripple-carry adder, there are 32 full adders, so the critical path (worst case) delay is 3 (from input to ${\displaystyle C_{out}}$ of first adder) + 31 × 2 (for carry propagation in latter adders) = 65 gate delays.^[6] The general equation for the worst-case delay for a n-bit carry-ripple adder, accounting for both the sum and carry bits, is:

${\displaystyle T_{\text{CRA}}(n)=T_{\text{HA}}+(n-1)\cdot T_{\text{c}}+T_{\text{s}}=}$${\displaystyle T_{\text{FA}}+(n-1)\cdot T_{c}=}$${\displaystyle 3D+(n-1)\cdot 2D=(2n+1)\cdot D}$

A design with alternating carry polarities and optimized AND-OR-Invert gates can be about twice as fast.^[7][5]

To reduce the computation time, Weinberger and Smith invented a faster way to add two binary numbers by using carry-lookahead adders (CLA).^[8] They introduced two signals (${\displaystyle P}$ and ${\displaystyle G}$) for each bit position, based on whether a carry is propagated through from a less significant bit position (at least one input is a 1), generated in that bit position (both inputs are 1), or killed in that bit position (both inputs are 0). In most cases, ${\displaystyle P}$ is simply the sum output of a half adder and ${\displaystyle G}$ is the carry output of the same adder. After ${\displaystyle P}$ and ${\displaystyle G}$ are generated, the carries for every bit position are created.

Mere derivation of Weinberger-Smith CLA recurrence, are: Brent–Kung adder (BKA),^[9] and the Kogge–Stone adder (KSA).^[10][11] This was shown in Oklobdzija and Zeydel paper in IEEE Journal of Solid-State Circuits.^[12]

Some other multi-bit adder architectures break the adder into blocks. It is possible to vary the length of these blocks based on the propagation delay of the circuits to optimize computation time. These block based adders include the carry-skip (or carry-bypass) adder which will determine ${\displaystyle P}$ and ${\displaystyle G}$ values for each block rather than each bit, and the carry-select adder which pre-generates the sum and carry values for either possible carry input (0 or 1) to the block, using multiplexers to select the appropriate result when the carry bit is known.

By combining multiple carry-lookahead adders, even larger adders can be created. This can be used at multiple levels to make even larger adders. For example, the following adder is a 64-bit adder that uses four 16-bit CLAs with two levels of lookahead carry units.

Other adder designs include the carry-select adder, conditional sum adder, carry-skip adder, and carry-complete adder.

If an adding circuit is to compute the sum of three or more numbers, it can be advantageous to not propagate the carry result. Instead, three-input adders are used, generating two results: a sum and a carry. The sum and the carry may be fed into two inputs of the subsequent 3-number adder without having to wait for propagation of a carry signal. After all stages of addition, however, a conventional adder (such as the ripple-carry or the lookahead) must be used to combine the final sum and carry results.

A full adder can be viewed as a 3:2 lossy compressor: it sums three one-bit inputs and returns the result as a single two-bit number; that is, it maps 8 input values to 4 output values. (the term "compressor" instead of "counter" was introduced in^[13])Thus, for example, a binary input of 101 results in an output of 1 + 0 + 1 = 10 (decimal number 2). The carry-out represents bit one of the result, while the sum represents bit zero. Likewise, a half adder can be used as a 2:2 lossy compressor, compressing four possible inputs into three possible outputs.

Such compressors can be used to speed up the summation of three or more addends. If the number of addends is exactly three, the layout is known as the carry-save adder. If the number of addends is four or more, more than one layer of compressors is necessary, and there are various possible designs for the circuit: the most common are Dadda and Wallace trees. This kind of circuit is most notably used in multiplier circuits, which is why these circuits are also known as Dadda and Wallace multipliers.

Using only the Toffoli and CNOT quantum logic gates, it is possible to produce quantum full- and half-adders.^[14][15][16] The same circuits can also be implemented in classical reversible computation, as both CNOT and Toffoli are also classical logic gates.

Since the quantum Fourier transform has a low circuit complexity, it can efficiently be used for adding numbers as well.^[17][18][19]

Just as in Binary adders, combining two input currents effectively adds those currents together. Within the constraints of the hardware, non-binary signals (i.e. with a base higher than 2) can be added together to calculate a sum. Also known as a "summing amplifier",^[20] this technique can be used to reduce the number of transistors in an addition circuit.

• Binary multiplier
• Subtractor
• Electronic mixer — for adding analog signals