Hubbry Logo
Boiling pointBoiling pointMain
Open search
Boiling point
Community hub
Boiling point
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Boiling point
Boiling point
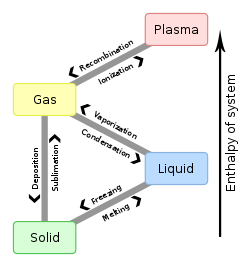
Boiling point
View on Wikipedia
from Wikipedia
Water boiling at 99.3 °C (210.8 °F) at 215 m (705 ft) elevation

The boiling point of a substance is the temperature at which the vapor pressure of a liquid equals the pressure surrounding the liquid[1][2] and the liquid changes into a vapor.

The boiling point of a liquid varies depending upon the surrounding environmental pressure. A liquid in a partial vacuum, i.e., under a lower pressure, has a lower boiling point than when that liquid is at atmospheric pressure. Because of this, water boils at 100°C (or with scientific precision: 99.97 °C (211.95 °F)) under standard pressure at sea level, but at 93.4 °C (200.1 °F) at 1,905 metres (6,250 ft)[3] altitude. For a given pressure, different liquids will boil at different temperatures.

The normal boiling point (also called the atmospheric boiling point or the atmospheric pressure boiling point) of a liquid is the special case in which the vapor pressure of the liquid equals the defined atmospheric pressure at sea level, one atmosphere.[4][5] At that temperature, the vapor pressure of the liquid becomes sufficient to overcome atmospheric pressure and allow bubbles of vapor to form inside the bulk of the liquid. The standard boiling point has been defined by IUPAC since 1982 as the temperature at which boiling occurs under a pressure of one bar.[6]

The heat of vaporization is the energy required to transform a given quantity (a mol, kg, pound, etc.) of a substance from a liquid into a gas at a given pressure (often atmospheric pressure).

Liquids may change to a vapor at temperatures below their boiling points through the process of evaporation. Evaporation is a surface phenomenon in which molecules located near the liquid's edge, not contained by enough liquid pressure on that side, escape into the surroundings as vapor. On the other hand, boiling is a process in which molecules anywhere in the liquid escape, resulting in the formation of vapor bubbles within the liquid.

Saturation temperature and pressure

[edit]
Demonstration of the lower boiling point of alcohol at lower pressure, achieved by using a vacuum pump.
Main article: Vapor–liquid equilibrium

A saturated liquid contains as much thermal energy as it can without boiling (or conversely a saturated vapor contains as little thermal energy as it can without condensing).

Saturation temperature means boiling point. The saturation temperature is the temperature for a corresponding saturation pressure at which a liquid boils into its vapor phase. The liquid can be said to be saturated with thermal energy. Any addition of thermal energy results in a phase transition.

If the pressure in a system remains constant (isobaric), a vapor at saturation temperature will begin to condense into its liquid phase as thermal energy (heat) is removed. Similarly, a liquid at saturation temperature and pressure will boil into its vapor phase as additional thermal energy is applied.

The boiling point corresponds to the temperature at which the vapor pressure of the liquid equals the surrounding environmental pressure. Thus, the boiling point is dependent on the pressure. Boiling points may be published with respect to the NIST, USA standard pressure of 101.325 kPa (1 atm), or the IUPAC standard pressure of 100.000 kPa (1 bar). At higher elevations, where the atmospheric pressure is much lower, the boiling point is also lower. The boiling point increases with increased pressure up to the critical point, where the gas and liquid properties become identical. The boiling point cannot be increased beyond the critical point. Likewise, the boiling point decreases with decreasing pressure until the triple point is reached. The boiling point cannot be reduced below the triple point.

If the heat of vaporization and the vapor pressure of a liquid at a certain temperature are known, the boiling point can be calculated by using the Clausius–Clapeyron equation, thus:

where:

is the boiling point at the pressure of interest,
is the ideal gas constant,
is the vapor pressure of the liquid,
is some pressure where the corresponding is known (usually data available at 1 atm or 100 kPa (1 bar)),
is the heat of vaporization of the liquid,
is the boiling temperature,
is the natural logarithm.

Saturation pressure is the pressure for a corresponding saturation temperature at which a liquid boils into its vapor phase. Saturation pressure and saturation temperature have a direct relationship: as saturation pressure is increased, so is saturation temperature.

If the temperature in a system remains constant (an isothermal system), vapor at saturation pressure and temperature will begin to condense into its liquid phase as the system pressure is increased. Similarly, a liquid at saturation pressure and temperature will tend to flash into its vapor phase as system pressure is decreased.

There are two conventions regarding the standard boiling point of water: The normal boiling point is commonly given as 100 °C (212 °F) (actually 99.97 °C (211.9 °F) following the thermodynamic definition of the Celsius scale based on the kelvin) at a pressure of 1 atm (101.325 kPa). The IUPAC-recommended standard boiling point of water at a standard pressure of 100 kPa (1 bar)[7] is 99.61 °C (211.3 °F).[6][8] For comparison, on top of Mount Everest, at 8,848 m (29,029 ft) elevation, the pressure is about 34 kPa (255 Torr)[9] and the boiling point of water is 71 °C (160 °F).[10] The Celsius temperature scale was defined until 1954 by two points: 0 °C being defined by the water freezing point and 100 °C being defined by the water boiling point at standard atmospheric pressure.

Relation between the normal boiling point and the vapor pressure of liquids

[edit]
A log-lin vapor pressure chart for various liquids

The higher the vapor pressure of a liquid at a given temperature, the lower the normal boiling point (i.e., the boiling point at atmospheric pressure) of the liquid.

The vapor pressure chart to the right has graphs of the vapor pressures versus temperatures for a variety of liquids.[11] As can be seen in the chart, the liquids with the highest vapor pressures have the lowest normal boiling points.

For example, at any given temperature, methyl chloride has the highest vapor pressure of any of the liquids in the chart. It also has the lowest normal boiling point (−24.2 °C), which is where the vapor pressure curve of methyl chloride (the blue line) intersects the horizontal pressure line of one atmosphere (atm) of absolute vapor pressure.

The critical point of a liquid is the highest temperature (and pressure) it will actually boil at.

See also Vapour pressure of water.

Boiling point of chemical elements

[edit]
Further information: List of chemical elements and Boiling points of the elements (data page)

The element with the lowest boiling point is helium. Both the boiling points of rhenium and tungsten exceed 5000 K at standard pressure; because it is difficult to measure extreme temperatures precisely without bias, both have been cited in the literature as having the higher boiling point.[12]

Boiling point as a reference property of a pure compound

[edit]

As can be seen from the above plot of the logarithm of the vapor pressure vs. the temperature for any given pure chemical compound, its normal boiling point can serve as an indication of that compound's overall volatility. A given pure compound has only one normal boiling point, if any, and a compound's normal boiling point and melting point can serve as characteristic physical properties for that compound, listed in reference books. The higher a compound's normal boiling point, the less volatile that compound is overall, and conversely, the lower a compound's normal boiling point, the more volatile that compound is overall. Some compounds decompose at higher temperatures before reaching their normal boiling point, or sometimes even their melting point. For a stable compound, the boiling point ranges from its triple point to its critical point, depending on the external pressure. Beyond its triple point, a compound's normal boiling point, if any, is higher than its melting point. Beyond the critical point, a compound's liquid and vapor phases merge into one phase, which may be called a superheated gas. At any given temperature, if a compound's normal boiling point is lower, then that compound will generally exist as a gas at atmospheric external pressure. If the compound's normal boiling point is higher, then that compound can exist as a liquid or solid at that given temperature at atmospheric external pressure, and will so exist in equilibrium with its vapor (if volatile) if its vapors are contained. If a compound's vapors are not contained, then some volatile compounds can eventually evaporate away in spite of their higher boiling points.

Boiling points of alkanes, alkenes, ethers, halogenoalkanes, aldehydes, ketones, alcohols and carboxylic acids as a function of molar mass

In general, compounds with ionic bonds have high normal boiling points, if they do not decompose before reaching such high temperatures. Many metals have high boiling points, but not all. Very generally—with other factors being equal—in compounds with covalently bonded molecules, as the size of the molecule (or molecular mass) increases, the normal boiling point increases. When the molecular size becomes that of a macromolecule, polymer, or otherwise very large, the compound often decomposes at high temperature before the boiling point is reached. Another factor that affects the normal boiling point of a compound is the polarity of its molecules. As the polarity of a compound's molecules increases, its normal boiling point increases, other factors being equal. Closely related is the ability of a molecule to form hydrogen bonds (in the liquid state), which makes it harder for molecules to leave the liquid state and thus increases the normal boiling point of the compound. Simple carboxylic acids dimerize by forming hydrogen bonds between molecules. A minor factor affecting boiling points is the shape of a molecule. Making the shape of a molecule more compact tends to lower the normal boiling point slightly compared to an equivalent molecule with more surface area.

Comparison of butane (C4H10) isomer boiling points
Common name n-butane isobutane
IUPAC name butane 2-methylpropane
Molecular
form
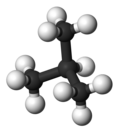
Boiling
point (°C) 		−0.5 −11.7
Comparison of pentane isomer boiling points
Common name n-pentane isopentane neopentane
IUPAC name pentane 2-methylbutane 2,2-dimethylpropane
Molecular
form
Boiling
point (°C) 		36.0 27.7 9.5
Binary boiling point diagram of two hypothetical only weakly interacting components without an azeotrope

Most volatile compounds (anywhere near ambient temperatures) go through an intermediate liquid phase while warming up from a solid phase to eventually transform to a vapor phase. By comparison to boiling, a sublimation is a physical transformation in which a solid turns directly into vapor, which happens in a few select cases such as with carbon dioxide at atmospheric pressure. For such compounds, a sublimation point is a temperature at which a solid turning directly into vapor has a vapor pressure equal to the external pressure.

Impurities and mixtures

[edit]

In the preceding section, boiling points of pure compounds were covered. Vapor pressures and boiling points of substances can be affected by the presence of dissolved impurities (solutes) or other miscible compounds, the degree of effect depending on the concentration of the impurities or other compounds. The presence of non-volatile impurities such as salts or compounds of a volatility far lower than the main component compound decreases its mole fraction and the solution's volatility, and thus raises the normal boiling point in proportion to the concentration of the solutes. This effect is called boiling point elevation. As a common example, salt water boils at a higher temperature than pure water.

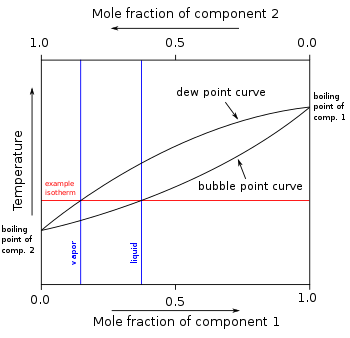
In other mixtures of miscible compounds (components), there may be two or more components of varying volatility, each having its own pure component boiling point at any given pressure. The presence of other volatile components in a mixture affects the vapor pressures and thus boiling points and dew points of all the components in the mixture. The dew point is a temperature at which a vapor condenses into a liquid. Furthermore, at any given temperature, the composition of the vapor is different from the composition of the liquid in most such cases. In order to illustrate these effects between the volatile components in a mixture, a boiling point diagram is commonly used. Distillation is a process of boiling and [usually] condensation which takes advantage of these differences in composition between liquid and vapor phases.

Boiling point of water with elevation

[edit]

Following is a table of the change in the boiling point of water with elevation, at intervals of 500 meters over the range of human habitation [the Dead Sea at −430.5 metres (−1,412 ft) to La Rinconada, Peru at 5,100 m (16,700 ft)], then of 1,000 meters over the additional range of uninhabited surface elevation [up to Mount Everest at 8,849 metres (29,032 ft)], along with a similar range in Imperial.

Boiling point of water
Elevation
(m)		 Boiling point
(°C) 		Elevation
(ft) 		Boiling point
(°F)
−500 101.6 −1,500 214.7
0 100.0 0 212.0
500 98.4 1,500 209.3
1,000 96.7 3,000 206.6
1,500 95.1 4,500 203.9
2,000 93.4 6,000 201.1
2,500 91.7 7,500 198.3
3,000 90.0 9,000 195.5
3,500 88.2 10,500 192.6
4,000 86.4 12,000 189.8
4,500 84.6 13,500 186.8
5,000 82.8 15,000 183.9
6,000 79.1 16,500 180.9
7,000 75.3 20,000 173.8
8,000 71.4 23,000 167.5
9,000 67.4 26,000 161.1
29,000 154.6

Element table

[edit]
Main article: Boiling points of the elements (data page)

See also

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Boiling point

View on Grokipedia
from Grokipedia
The boiling point of a substance is the temperature at which the vapor pressure of its liquid phase equals the pressure surrounding it, resulting in the formation of bubbles throughout the liquid and transition to the gaseous phase. The normal boiling point specifically refers to this temperature at standard atmospheric pressure of 1 atmosphere (760 mmHg or 101.3 kPa). This property serves as a key physical characteristic for identifying and characterizing pure substances in chemistry. The boiling point is highly sensitive to external ; as pressure decreases, the boiling point lowers because less is required for the vapor to match the surroundings, which is why water boils below 100°C at high altitudes. For pure liquids, boiling points are influenced by intermolecular forces, with stronger attractions—such as those from increased molecular weight, polarity, or —leading to higher boiling temperatures. For instance, branched hydrocarbons have lower boiling points than their linear isomers due to reduced surface area for van der Waals interactions, while polar molecules like water exhibit anomalously high boiling points from . In solutions, the boiling point typically elevates compared to the pure solvent, a colligative property dependent on the concentration and number of solute particles rather than their identity. This elevation, quantified by the formula ΔT_b = K_b × m × i (where K_b is the solvent's boiling point elevation constant, m is molality, and i is the van 't Hoff factor for particle dissociation), explains phenomena like the higher boiling point of saltwater. Boiling points are practically measured via techniques like the Thiele tube or distillation and play essential roles in processes such as purification, industrial separations, and phase diagrams.

Fundamentals of Boiling

Definition and Process

The boiling point of a is the at which the vapor pressure of the equals the surrounding pressure, typically at standard conditions, leading to a from to vapor throughout the bulk of the . This equilibrium condition allows vapor bubbles to form, grow, and detach from sites—such as microscopic crevices on the heating surface, impurities, or gas pockets trapped within the —initiating the boiling process. Once nucleated, these bubbles expand due to the input, rise through the due to , and release vapor at the surface, facilitating efficient . Boiling differs fundamentally from , as the latter is a slower, surface-limited process where individual molecules gain sufficient to escape the liquid-air interface without bubble formation, occurring at temperatures below the boiling point. In contrast, involves vigorous bubble generation and detachment across the volume, driven by the rapid phase change once the saturation temperature is reached. The first systematic investigations into the influence of pressure on boiling emerged in the 17th century through experiments by , who used an air pump to demonstrate that reducing lowers the boiling temperature of liquids like . Illustrations of the boiling process commonly depict vapor bubbles originating from nucleation sites at the bottom of a container, expanding as they ascend through the denser liquid, and rupturing at the to emit , highlighting the dynamic convective currents induced by the rising bubbles.

Saturation Temperature and Pressure

The saturation temperature, also known as the boiling point at a given , is defined as the at which the vapor of a equals the of the surrounding , allowing the and vapor phases to exist in . At this point, the can vaporize without further increase, as the rates of and balance. This equilibrium condition is fundamental to phase changes and is observed across various substances under controlled pressures. The boiling point of a varies inversely with external : higher pressures elevate the saturation temperature by requiring greater molecular energy to overcome the increased resistance to vapor formation, while lower pressures reduce it. For example, pressure cookers exploit this by sealing in to build , thereby raising the saturation temperature and enabling faster cooking at higher temperatures. In contrast, at high altitudes where drops, the saturation temperature decreases, prolonging cooking times; specifically, it falls by approximately 1°C for every 300 meters of elevation increase due to the reduced ambient . In a typical pressure-temperature for a pure substance, the saturation line—also called the vapor-liquid equilibrium curve—separates the and vapor regions, illustrating how saturation temperature changes with pressure along this boundary. This curve begins at the , the unique condition where solid, , and vapor phases coexist in equilibrium, and ends at the critical point, beyond which distinct liquid and vapor phases merge into a . The normal boiling point corresponds to the saturation temperature at standard atmospheric pressure of 1 atm.

Theoretical Relations

Normal Boiling Point

The normal boiling point of a is defined as the temperature at which its equals 101.325 kPa (1 atm), the , allowing the to transition to vapor throughout the bulk. Note that since 1982, IUPAC has recommended the at 1 bar (100 kPa) for conditions, which for is approximately 99.61 °C, differing slightly from the normal boiling point. This condition, denoted as TbT_b, represents the saturation temperature specifically at this benchmark and serves as a fundamental reference for comparing the volatility of substances under standardized conditions. The concept of the normal boiling point emerged in the as chemists and physicists sought consistent metrics for thermophysical properties, but it was formally standardized by the International Union of Pure and Applied Chemistry (IUPAC) in the to ensure uniformity in scientific data reporting. This adoption, detailed in IUPAC recommendations from 1994, emphasized the use of 101.325 kPa to align with historical conventions while facilitating reproducible measurements in . Prior to broader IUPAC codification, variations in definitions had led to inconsistencies in reported values, prompting the need for this precise benchmark. Measurement of the normal boiling point typically involves ebulliometric or dynamic techniques under controlled conditions to maintain exactly 101.325 kPa. In ebulliometry, the liquid is heated in a specialized apparatus like a Beckmann thermometer-equipped ebulliometer, where the steady-state is recorded as vapor recondenses, ensuring equilibrium at the target . methods, such as those using a simple or fractional column apparatus, observe the plateau during while barometric is monitored and adjusted if necessary to match 1 . These approaches prioritize purity and pressure control to achieve accuracy within 0.5–1 for most organic liquids. Values are conventionally reported in degrees (°C) or (K), with the latter preferred in thermodynamic calculations; for instance, the normal boiling point of is 100 °C, equivalent to 373.15 K. This unit choice reflects practical conventions, where °C aligns with historical scales, while K ensures additivity in equations without negative values.

Vapor Pressure Connection

The boiling point of a is defined as the at which its equals the surrounding external , marking the onset of where the and vapor phases are in equilibrium. This equilibrium condition arises because the represents the exerted by the escaping molecules, and when it matches the external , bubbles of vapor can form throughout the without restriction. The normal boiling point specifically refers to this when the external is 1 atm (101.325 kPa), serving as a standard reference for comparing substances. The temperature dependence of , which directly governs boiling behavior, is described by the Clausius-Clapeyron equation, derived from thermodynamic principles. The equation takes the form: ln⁡(P2P1)=−ΔHvapR(1T2−1T1)\ln\left(\frac{P_2}{P_1}\right) = -\frac{\Delta H_\text{vap}}{R} \left(\frac{1}{T_2} - \frac{1}{T_1}\right) where P1P_1 and P2P_2 are vapor pressures at absolute temperatures T1T_1 and T2T_2, ΔHvap\Delta H_\text{vap} is the enthalpy of vaporization, and RR is the gas constant. This relation quantifies how vapor pressure increases exponentially with temperature, explaining why boiling points rise with increasing external pressure. The derivation begins with the Clapeyron equation, dPdT=ΔHTΔV\frac{dP}{dT} = \frac{\Delta H}{T \Delta V}, which relates the slope of the phase boundary in the pressure-temperature diagram to the enthalpy change ΔH\Delta H and volume change ΔV\Delta V across the . For vaporization, ΔH=ΔHvap\Delta H = \Delta H_\text{vap} and ΔV≈Vvapor=RT/P\Delta V \approx V_\text{vapor} = RT/P from the , assuming the liquid volume is negligible compared to the vapor volume. Integrating this form, with the assumption of constant ΔHvap\Delta H_\text{vap}, yields the Clausius-Clapeyron equation. This approximation holds reasonably well for many substances over moderate temperature ranges but may deviate at high pressures or near critical points where ideality fails. In practice, the Clausius-Clapeyron equation enables predictions of boiling point shifts with pressure changes; for instance, it can estimate how the boiling point of decreases at high altitudes due to lower . For more accurate modeling over wider ranges, empirical correlations like the are often employed, given by: log⁡10P=A−BT+C\log_{10} P = A - \frac{B}{T + C} where PP is in mmHg, TT is in °C, and AA, BB, CC are substance-specific constants fitted to experimental data. This form provides a practical tool for engineering applications, such as processes, by offering a simple way to interpolate curves without relying solely on theoretical assumptions.

Boiling Points of Pure Substances

Chemical Elements

The normal boiling points of chemical elements, defined as the temperature at which their vapor pressure reaches 1 atm (101.325 kPa), vary dramatically across the periodic table, from cryogenic temperatures for light gases to over 5000 °C for refractory metals. These values serve as key physical properties for identifying elements and understanding their behavior in chemical processes. Boiling points exhibit distinct periodic trends influenced by bonding types and atomic structure. In groups of non-metals and metalloids, boiling points generally increase down the group due to larger atomic sizes leading to stronger van der Waals forces; for instance, noble gases show low values rising from helium at -268.9 °C to xenon at -108.1 °C. Metallic elements display higher boiling points overall, with transition metals like tungsten reaching 5555 °C owing to robust delocalized metallic bonding involving d-electrons. Anomalies occur, such as mercury's relatively low boiling point of 356.7 °C compared to neighboring transition metals, resulting from relativistic effects that contract the 6s orbital, reduce s-p orbital mixing, and weaken interatomic bonds. Measuring boiling points for reactive or volatile elements poses significant challenges. Alkali metals, highly reactive with oxygen and moisture, require inert atmospheres like or , often in sealed ampoules or gloveboxes to avoid oxidation during . Cryogenic elements and gases, such as or , demand specialized low-temperature setups like cryostats or dilution refrigerators to achieve and maintain sub-ambient conditions precisely, preventing contamination from atmospheric gases. The table below provides a comprehensive list of normal boiling points for all 118 elements, compiled from authoritative references including the CRC Handbook of Chemistry and Physics. Values are in °C; some for elements (atomic numbers 104–118) are theoretical estimates based on empirical trends and quantum calculations, as these elements have not been produced in sufficient quantities for direct measurement. For elements that sublime at 1 , the sublimation temperature is provided with a note.
Atomic NumberElementSymbolBoiling Point (°C)
1H-252.9
2He-268.9
3Li1342
4Be2470
5B3927
6CarbonC3642 (sublimes)
7N-195.8
8OxygenO-183.0
9F-188.1
10Ne-246.1
11SodiumNa883
12MagnesiumMg1090
13AluminumAl2467
14Si3265
15P280
16S444.6
17Cl-34.0
18Ar-185.8
19K759
20CalciumCa1484
21Sc2836
22Ti3287
23V3913
24Cr2671
25Mn2061
26IronFe2862
27Co2927
28Ni2913
29Cu2562
30Zn907
31Ga2204
32Ge2830
33As614 (sublimes)
34Se685
35Br59
36Kr-153.4
37Rb688
38Sr1382
39Y3338
40Zr4409
41Nb4742
42Mo4639
43Tc4538
44Ru3900
45Rh3695
46Pd2963
47SilverAg2162
48Cd767
49In2072
50TinSn2602
51Sb1587
52Te988
53IodineI184
54Xe-108.1
55CesiumCs671
56Ba1897
57La3464
58Ce3443
59Pr3520
60Nd3074
61Pm3000 (est.)
62Sm2076
63Eu1597
64Gd3273
65Tb3232
66Dy2567
67Ho2700
68Er2868
69Tm2540 (est.)
70Yb1196
71Lu3402
72Hf4602
73Ta5458
74W5555
75Re5596
76Os5012
77Ir4130
78Pt3825
79Au2856
80MercuryHg356.7
81Tl1473
82LeadPb1749
83Bi1564
84Po962
85At337 (est.)
86Rn-62
87Fr677 (est.)
88Ra1737 (est.)
89Ac3198
90Th4788
91Pa4171
92U4131
93Np4175
94Pu3228
95Am2607
96Cm3100 (est.)
97Bk2597 (est.)
98Cf1470 (est.)
99Es1087 (est.)
100Fm~1000 (est.)
101Md~1100 (est.)
102No~1800 (est.)
103Lr~1630 (est.)
104Rf~2100 (est.)
105DubniumDb~2200 (est.)
106SeaborgiumSg~2200 (est.)
107BohriumBh~2200 (est.)
108HassiumHs~480 (est.)
109MeitneriumMt~1800 (est.)
110DarmstadtiumDs~1500 (est.)
111RoentgeniumRg~1570 (est.)
112CoperniciumCn357 (est.)
113NihoniumNh~1400 (est.)
114FleroviumFl107 (est.)
115MoscoviumMc~1100 (est.)
116LivermoriumLv404 (est.)
117TennessineTs574 (est.)
118OganessonOg177 (est.)
Recent relativistic quantum calculations for superheavy elements like predict deviations from group trends; its estimated boiling point of 177 °C arises from enhanced stability and reduced volatility compared to lighter , based on simulations.

Reference Property for Compounds

The boiling point serves as a fundamental for identifying and characterizing pure chemical compounds, particularly in processes like and , where it helps confirm purity and distinguish between substances. For instance, the normal boiling point of at 78.37 °C allows it to be separated from , which boils at 100 °C, during simple , enabling verification of the compound's identity based on the observed temperature. In gas , the retention time of a compound correlates with its boiling point, providing a means to compare experimental data against known values for purity assessment and identification. Boiling points of pure organic compounds are extensively documented in authoritative , often with high precision to support accurate characterization. compiles experimental and predicted boiling points for thousands of compounds, drawing from peer-reviewed sources to ensure reliability. Similarly, the CRC Handbook of Chemistry and Physics lists boiling points for organic compounds to two decimal places (e.g., 0.01 °C precision) under standard conditions of 101.325 kPa, serving as a standard reference for laboratory and industrial applications. Despite its utility, the boiling point is not always unique for compound identification, as structural isomers can exhibit similar values, requiring combination with other properties like or for unambiguous characterization. For example, n-butanol and have boiling points of 117.7 °C and 107.9 °C, respectively, which are close enough to necessitate additional techniques for differentiation. Historically, boiling point measurements via played a pivotal role in 19th-century for classifying hydrocarbons, as demonstrated by Auguste Laurent's isolation of from fractions in the , which helped establish systematic categorization based on volatility. This approach facilitated the early structural elucidation of complex mixtures, laying groundwork for modern synthetic .

Influences on Boiling

Impurities and Mixtures

The presence of non-volatile impurities in a liquid solvent acts as a colligative property, lowering the vapor pressure of the solvent and thereby elevating the boiling point of the solution compared to the pure solvent. This elevation depends solely on the number of solute particles, not their identity, and is particularly relevant in processes like desalination where salts increase the energy required for vaporization. In multi-component mixtures of volatile liquids, the boiling behavior deviates from that of pure substances, often requiring to separate components as the composition and temperature vary during the process. For ideal mixtures, governs the total vapor pressure PtotalP_{\text{total}}, given by Ptotal=xAPA∗+xBPB∗P_{\text{total}} = x_A P_A^* + x_B P_B^* where xAx_A and xBx_B are the mole fractions of components A and B, and PA∗P_A^* and PB∗P_B^* are their pure-component vapor pressures at the given . The boiling point of the occurs when PtotalP_{\text{total}} equals the external PextP_{\text{ext}}, resulting in a temperature intermediate between those of the pure components, weighted by their mole fractions. Non-ideal mixtures can form azeotropes, which are constant-boiling compositions where the vapor phase has the same composition as the liquid, limiting separation by simple . Minimum-boiling azeotropes, such as the - system at 95.6% by mass boiling at 78.2°C (compared to 78.4°C for pure and 100°C for ), exhibit positive deviations from and lower boiling points than either component. Maximum-boiling azeotropes, conversely, show negative deviations and higher boiling points, as seen in systems like nitric acid-. Recent studies from the 2020s have advanced prediction and separation using simulations integrated with experimental data, improving accuracy for binary mixtures beyond traditional thermodynamic models. In biofuel production, overcoming ethanol-water remains critical; innovations like advanced hybrids and have reduced energy demands by up to 30% in ethanol dehydration processes since 2020. These developments, including , enable higher-purity while addressing sustainability challenges in azeotropic separations.

Boiling Point Elevation in Solutions

Boiling point elevation refers to the increase in the boiling point of a when a non-volatile solute is added, a colligative property dependent on the number of solute particles rather than their identity. For aqueous solutions, this elevation is quantified by the formula ΔTb=i⋅Kb⋅m\Delta T_b = i \cdot K_b \cdot m where ΔTb\Delta T_b is the boiling point elevation in °C, ii is the van't Hoff factor representing the effective number of particles per solute molecule, KbK_b is the ebullioscopic constant of the solvent (0.512 °C/kg/mol for water), and mm is the molality of the solution in mol/kg. This equation applies primarily to dilute solutions where solute-solvent interactions are minimal. In practical examples, seawater with approximately 0.6 molal NaCl equivalent (from 3.5% salinity) exhibits a boiling point of about 100.5°C at 1 atm, due to i≈2i \approx 2 for NaCl dissociation into Na⁺ and Cl⁻ ions, yielding ΔTb≈0.5\Delta T_b \approx 0.5 °C. Similarly, a 1 molal NaCl aqueous solution has a boiling point of approximately 101.0°C, as the elevation is ΔTb=2⋅0.512⋅1=1.024\Delta T_b = 2 \cdot 0.512 \cdot 1 = 1.024 °C. This phenomenon has applications in everyday cooking and . Adding salt to for boiling raises the slightly (e.g., by approximately 0.2–0.4°C for typical concentrations), which can enhance cooking efficiency once begins, though it marginally delays reaching the boil due to the higher required . In , in concentrated brines reduces in systems by lowering the driving force for , impacting energy costs in multi-effect . Several factors influence the accuracy of the elevation formula, particularly the van't Hoff factor ii. For electrolytes like NaCl, ii approaches the ideal value (e.g., 2) in dilute solutions but decreases in concentrated ones due to pairing, where oppositely charged ions associate and behave as fewer particles. Non-electrolytes, such as in aqueous solutions, have i=1i = 1 since they do not dissociate, resulting in elevation solely proportional to .

References

  1. https://chem.libretexts.org/Bookshelves/Organic_Chemistry/Organic_Chemistry_Lab_Techniques_(Nichols)/06:_Miscellaneous_Techniques/6.02:_Boiling_Point
  2. https://www.chem.purdue.edu/gchelp/liquids/boil.html
  3. https://www2.chemistry.msu.edu/faculty/reusch/virttxtjml/physprop.htm
  4. https://chem.libretexts.org/Bookshelves/Introductory_Chemistry/Introductory_Chemistry_(LibreTexts)/13:_Solutions/13.09:_Freezing_Point_Depression_and_Boiling_Point_Elevation
  5. https://ocw.mit.edu/courses/22-06-engineering-of-nuclear-systems-fall-2010/2e8614e58cc569d96acff67df51d9aef_MIT22_06F10_lec13.pdf
  6. https://adsabs.harvard.edu/full/2005ESASP1290..182T
  7. http://hyperphysics.phy-astr.gsu.edu/hbase/Kinetic/vappre.html
  8. https://van.physics.illinois.edu/ask/listing/1483
  9. https://academic.oup.com/book/44860/chapter/384801705
  10. https://www.engineersedge.com/thermodynamics/saturation.htm
  11. https://www.wartsila.com/encyclopedia/term/saturation-temperature
  12. https://www.nuclear-power.com/nuclear-engineering/materials-nuclear-engineering/properties-steam-what-is-steam/saturation-boiling-point/
  13. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_%28Physical_and_Theoretical_Chemistry%29/Physical_Properties_of_Matter/States_of_Matter/Phase_Transitions/Boiling
  14. https://www.seriouseats.com/how-pressure-cookers-work
  15. https://www.instrumentchoice.com.au/blogs/news/instrument-choice-experiment-does-altitude-impact-the-boiling-point-of-water
  16. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_%28Physical_and_Theoretical_Chemistry%29/Physical_Properties_of_Matter/States_of_Matter/Phase_Transitions/Phase_Diagrams
  17. https://goldbook.iupac.org/terms/view/N04211
  18. https://webbook.nist.gov/cgi/cbook.cgi?ID=C7732185&Type=TBOIL
  19. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Physical_Chemistry_%28LibreTexts%29/23%253A_Phase_Equilibria/23.04%253A_The_Clausius-Clapeyron_Equation
  20. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_%28Physical_and_Theoretical_Chemistry%29/Physical_Properties_of_Matter/States_of_Matter/Phase_Transitions/Clausius-Clapeyron_Equation
  21. https://chemed.chem.purdue.edu/genchem/topicreview/bp/ch14/clausius.php
  22. https://eng.libretexts.org/Bookshelves/Chemical_Engineering/Distillation_Science_%28Coleman%29/02%253A_Vapor_Pressure
  23. https://pmc.ncbi.nlm.nih.gov/articles/PMC11033562/
  24. https://webbook.nist.gov/chemistry/guide/
  25. https://webbook.nist.gov/chemistry/
  26. https://www.knowledgedoor.com/2/elements_handbook/boiling_point.html
  27. https://www.chemistryworld.com/news/relativity-behind-mercurys-liquidity/6297.article
  28. https://tsapps.nist.gov/publication/get_pdf.cfm?pub_id=956838
  29. https://pubchem.ncbi.nlm.nih.gov/compound/Carbon
  30. https://onlinelibrary.wiley.com/doi/10.1002/anie.202011976
  31. https://pubchem.ncbi.nlm.nih.gov/compound/Ethanol#section=Boiling-Point
  32. https://pubchem.ncbi.nlm.nih.gov/
  33. https://dl.icdst.org/pdfs/files/415f61e9082c7d23df09fb15605aa59d.pdf
  34. https://chem.libretexts.org/Bookshelves/General_Chemistry/Book%253A_Structure_and_Reactivity_in_Organic_Biological_and_Inorganic_Chemistry_%28Schaller%29/I%253A__Chemical_Structure_and_Properties/07%253A_Structure-Property_Relationships/7.08%253A_Comparing_Properties_of_Isomers
  35. https://www.journals.uchicago.edu/doi/pdfplus/10.1086/350538
  36. https://wou.edu/chemistry/courses/online-chemistry-textbooks/ch105-consumer-chemistry/ch105-chapter-7/
  37. https://chem.libretexts.org/Bookshelves/General_Chemistry/Chem1_%28Lower%29/08%253A_Solutions/8.04%253A_Colligative_Properties-_Boiling_Point_Elevation_and_Freezing_Point_Depression
  38. https://www.thoughtco.com/understanding-boiling-point-elevation-609180
  39. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_%28Physical_and_Theoretical_Chemistry%29/Equilibria/Physical_Equilibria/Raoults_Law_and_Ideal_Mixtures_of_Liquids
  40. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_%28Physical_and_Theoretical_Chemistry%29/Equilibria/Physical_Equilibria/Fractional_Distillation_of_Non-ideal_Mixtures_%28Azeotropes%29
  41. https://www.chemguide.co.uk/physical/phaseeqia/nonideal.html
  42. https://pubs.aip.org/aip/jcp/article/161/3/034111/3303346/Integrating-molecular-dynamics-simulations-and
  43. https://onlinelibrary.wiley.com/doi/full/10.1002/eng2.70451
  44. https://www.sciencedirect.com/science/article/abs/pii/S0263876222002383
  45. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%253A_Chemistry_-_The_Central_Science_(Brown_et_al.)/13%3A_Properties_of_Solutions/13.05%3A_Colligative_Properties
  46. https://www.chemteam.info/Solutions/BP-elevation-probs1-to-10.html
  47. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%253A_General_Chemistry_(Petrucci_et_al.)/13%3A_Solutions_and_their_Physical_Properties/13.08%253A_Freezing-Point_Depression_and_Boiling-Point_Elevation_of_Nonelectrolyte_Solutions
  48. https://www.sciencedirect.com/science/article/pii/S0011916421000266
  49. https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%253A_General_Chemistry_(Petrucci_et_al.)/13%3A_Solutions_and_their_Physical_Properties/13.09%3A_Solutions_of_Electrolytes
Add your contribution
Related Hubs
User Avatar
No comments yet.