Recent from talks
Nothing was collected or created yet.
Phase space
View on Wikipedia

| Differential equations |
|---|
| Scope |
| Classification |
| Solution |
| People |
The phase space of a physical system is the set of all possible physical states of the system when described by a given parameterization. Each possible state corresponds uniquely to a point in the phase space. For mechanical systems, the phase space usually consists of all possible values of the position and momentum parameters. It is the direct product of direct space and reciprocal space.[clarification needed] The concept of phase space was developed in the late 19th century by Ludwig Boltzmann, Henri Poincaré, and Josiah Willard Gibbs.[1]
Principles
[edit]In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space; a one-dimensional system is called a phase line, while a two-dimensional system is called a phase plane. For every possible state of the system or allowed combination of values of the system's parameters, a point is included in the multidimensional space. The system's evolving state over time traces a path (a phase-space trajectory for the system) through the high-dimensional space. The phase-space trajectory represents the set of states compatible with starting from one particular initial condition, located in the full phase space that represents the set of states compatible with starting from any initial condition. As a whole, the phase diagram represents all that the system can be, and its shape can easily elucidate qualities of the system that might not be obvious otherwise. A phase space may contain a great number of dimensions. For instance, a gas containing many molecules may require a separate dimension for each particle's x, y and z positions and momenta (6 dimensions for an idealized monatomic gas), and for more complex molecular systems additional dimensions are required to describe vibrational modes of the molecular bonds, as well as spin around 3 axes. Phase spaces are easier to use when analyzing the behavior of mechanical systems restricted to motion around and along various axes of rotation or translation – e.g. in robotics, like analyzing the range of motion of a robotic arm or determining the optimal path to achieve a particular position/momentum result.

Conjugate momenta
[edit]In classical mechanics, any choice of generalized coordinates qi for the position (i.e. coordinates on configuration space) defines conjugate generalized momenta pi, which together define co-ordinates on phase space. More abstractly, in classical mechanics phase space is the cotangent bundle of configuration space, and in this interpretation the procedure above expresses that a choice of local coordinates on configuration space induces a choice of natural local Darboux coordinates for the standard symplectic structure on a cotangent space.
Statistical ensembles in phase space
[edit]The motion of an ensemble of systems in this space is studied by classical statistical mechanics. The local density of points in such systems obeys Liouville's theorem, and so can be taken as constant. Within the context of a model system in classical mechanics, the phase-space coordinates of the system at any given time are composed of all of the system's dynamic variables. Because of this, it is possible to calculate the state of the system at any given time in the future or the past, through integration of Hamilton's or Lagrange's equations of motion.
In low dimensions
[edit]For simple systems, there may be as few as one or two degrees of freedom. One degree of freedom occurs when one has an autonomous ordinary differential equation in a single variable, with the resulting one-dimensional system being called a phase line, and the qualitative behaviour of the system being immediately visible from the phase line. The simplest non-trivial examples are the exponential growth model/decay (one unstable/stable equilibrium) and the logistic growth model (two equilibria, one stable, one unstable).
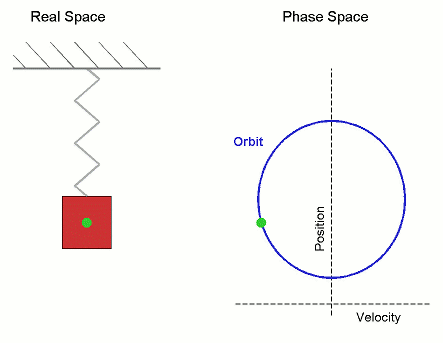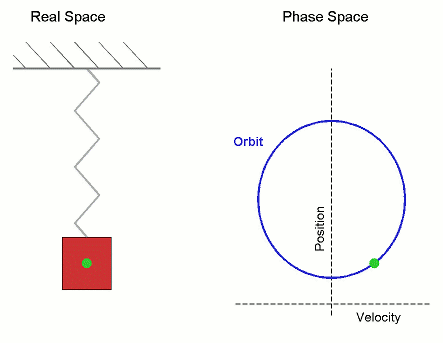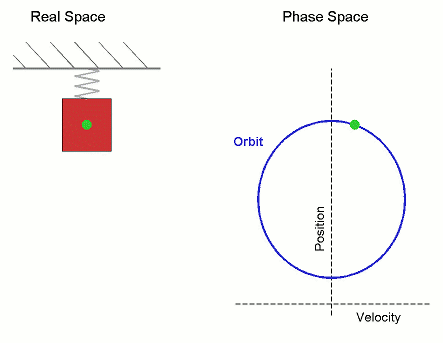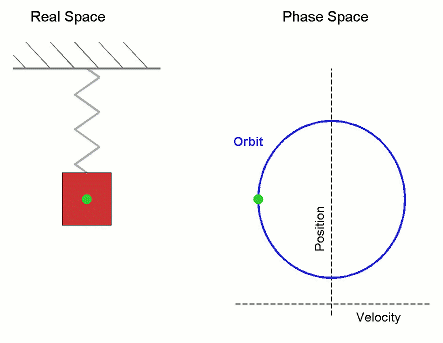
The phase space of a two-dimensional system is called a phase plane, which occurs in classical mechanics for a single particle moving in one dimension, and where the two variables are position and velocity. In this case, a sketch of the phase portrait may give qualitative information about the dynamics of the system, such as the limit cycle of the Van der Pol oscillator shown in the diagram.
Here the horizontal axis gives the position, and vertical axis the velocity. As the system evolves, its state follows one of the lines (trajectories) on the phase diagram.

Related concepts
[edit]Phase plot
[edit]A plot of position and momentum variables as a function of time is sometimes called a phase plot or a phase diagram. However the latter expression, "phase diagram", is more usually reserved in the physical sciences for a diagram showing the various regions of stability of the thermodynamic phases of a chemical system, which consists of pressure, temperature, and composition.
Phase portrait
[edit]

In mathematics, a phase portrait is a geometric representation of the orbits of a dynamical system in the phase plane. Each set of initial conditions is represented by a different point or curve.
Phase portraits are an invaluable tool in studying dynamical systems. They consist of a plot of typical trajectories in the phase space. This reveals information such as whether an attractor, a repellor or limit cycle is present for the chosen parameter value. The concept of topological equivalence is important in classifying the behaviour of systems by specifying when two different phase portraits represent the same qualitative dynamic behavior. An attractor is a stable point which is also called a "sink". The repeller is considered as an unstable point, which is also known as a "source".
A phase portrait graph of a dynamical system depicts the system's trajectories (with arrows) and stable steady states (with dots) and unstable steady states (with circles) in a phase space. The axes are of state variables.Phase integral
[edit]In classical statistical mechanics (continuous energies) the concept of phase space provides a classical analog to the partition function (sum over states) known as the phase integral.[2] Instead of summing the Boltzmann factor over discretely spaced energy states (defined by appropriate integer quantum numbers for each degree of freedom), one may integrate over continuous phase space. Such integration essentially consists of two parts: integration of the momentum component of all degrees of freedom (momentum space) and integration of the position component of all degrees of freedom (configuration space). Once the phase integral is known, it may be related to the classical partition function by multiplication of a normalization constant representing the number of quantum energy states per unit phase space. This normalization constant is simply the inverse of the Planck constant raised to a power equal to the number of degrees of freedom for the system.[3]
Applications
[edit]

Chaos theory
[edit]Classic examples of phase diagrams from chaos theory are:
- the Lorenz attractor
- population growth (i.e. logistic map)
- parameter plane of complex quadratic polynomials with Mandelbrot set.
Quantum mechanics
[edit]In quantum mechanics, the coordinates p and q of phase space normally become Hermitian operators in a Hilbert space.
But they may alternatively retain their classical interpretation, provided functions of them compose in novel algebraic ways (through Groenewold's 1946 star product). This is consistent with the uncertainty principle of quantum mechanics. Every quantum mechanical observable corresponds to a unique function or distribution on phase space, and conversely, as specified by Hermann Weyl (1927) and supplemented by John von Neumann (1931); Eugene Wigner (1932); and, in a grand synthesis, by H. J. Groenewold (1946). With J. E. Moyal (1949), these completed the foundations of the phase-space formulation of quantum mechanics, a complete and logically autonomous reformulation of quantum mechanics.[4] (Its modern abstractions include deformation quantization and geometric quantization.)
Expectation values in phase-space quantization are obtained isomorphically to tracing operator observables with the density matrix in Hilbert space: they are obtained by phase-space integrals of observables, with the Wigner quasi-probability distribution effectively serving as a measure.
Thus, by expressing quantum mechanics in phase space (the same ambit as for classical mechanics), the Weyl map facilitates recognition of quantum mechanics as a deformation (generalization) of classical mechanics, with deformation parameter ħ/S, where S is the action of the relevant process. (Other familiar deformations in physics involve the deformation of classical Newtonian into relativistic mechanics, with deformation parameter v/c;[citation needed] or the deformation of Newtonian gravity into general relativity, with deformation parameter Schwarzschild radius/characteristic dimension.)[citation needed]
Classical expressions, observables, and operations (such as Poisson brackets) are modified by ħ-dependent quantum corrections, as the conventional commutative multiplication applying in classical mechanics is generalized to the noncommutative star-multiplication characterizing quantum mechanics and underlying its uncertainty principle.
Thermodynamics and statistical mechanics
[edit]In thermodynamics and statistical mechanics contexts, the term "phase space" has two meanings: for one, it is used in the same sense as in classical mechanics. If a thermodynamic system consists of N particles, then a point in the 6N-dimensional phase space describes the dynamic state of every particle in that system, as each particle is associated with 3 position variables and 3 momentum variables. In this sense, as long as the particles are distinguishable, a point in phase space is said to be a microstate of the system. (For indistinguishable particles a microstate consists of a set of N! points, corresponding to all possible exchanges of the N particles.) N is typically on the order of the Avogadro number, thus describing the system at a microscopic level is often impractical. This leads to the use of phase space in a different sense.
The phase space can also refer to the space that is parameterized by the macroscopic states of the system, such as pressure, temperature, etc. For instance, one may view the pressure–volume diagram or temperature–entropy diagram as describing part of this phase space. A point in this phase space is correspondingly called a macrostate. There may easily be more than one microstate with the same macrostate. For example, for a fixed temperature, the system could have many dynamic configurations at the microscopic level. When used in this sense, a phase is a region of phase space where the system in question is in, for example, the liquid phase, or solid phase, etc.
Since there are many more microstates than macrostates, the phase space in the first sense is usually a manifold of much larger dimensions than in the second sense. Clearly, many more parameters are required to register every detail of the system down to the molecular or atomic scale than to simply specify, say, the temperature or the pressure of the system.
Optics
[edit]Phase space is extensively used in nonimaging optics,[5] the branch of optics devoted to illumination. It is also an important concept in Hamiltonian optics.
Medicine
[edit]In medicine and bioengineering, the phase space method is used to visualize multidimensional physiological responses.[6][7]
See also
[edit]- Configuration space (mathematics)
- Minisuperspace
- Phase line, 1-dimensional case
- Phase plane, 2-dimensional case
- Phase portrait
- Phase space method
- Parameter space
- Separatrix
- Applications
- Optical phase space
- State space (controls) for information about state space (similar to phase state) in control engineering.
- State space for information about state space with discrete states in computer science.
- Molecular dynamics
- Mathematics
- Physics
- Classical mechanics
- Hamiltonian mechanics
- Lagrangian mechanics
- State space (physics) for information about state space in physics
- Phase-space formulation of quantum mechanics
- Characteristics in phase space of quantum mechanics
References
[edit]- ^ Nolte, D. D. (2010). "The tangled tale of phase space". Physics Today. 63 (4): 33–38. Bibcode:2010PhT....63d..33N. doi:10.1063/1.3397041. S2CID 17205307.
- ^ Laurendeau, Normand M. (2005). Statistical Thermodynamics: Fundamentals and Applications. New York: Cambridge University Press. ISBN 0-521-84635-8.
- ^ Vu-Quoc, L. (2008). "Configuration integral". Archived from the original on April 28, 2012.
- ^ Curtright, T. L.; Zachos, C. K. (2012). "Quantum Mechanics in Phase Space". Asia Pacific Physics Newsletter. 01: 37–46. arXiv:1104.5269. doi:10.1142/S2251158X12000069. S2CID 119230734.
- ^ Chaves, Julio (2015). Introduction to Nonimaging Optics, Second Edition. CRC Press. ISBN 978-1482206739.
- ^ Klabukov, I.; Tenchurin, T.; Shepelev, A.; Baranovskii, D.; Mamagulashvili, V.; Dyuzheva, T.; Krasilnikova, O.; Balyasin, M.; Lyundup, A.; Krasheninnikov, M.; Sulina, Y.; Gomzyak, V.; Krasheninnikov, S.; Buzin, A.; Zayratyants, G. (2023). "Biomechanical Behaviors and Degradation Properties of Multilayered Polymer Scaffolds: The Phase Space Method for Bile Duct Design and Bioengineering". Biomedicines. 11 (3): 745. doi:10.3390/biomedicines11030745. ISSN 2227-9059. PMC 10044742. PMID 36979723.
- ^ Kirkland, M.A. (2004). "A phase space model of hemopoiesis and the concept of stem cell renewal". Experimental Hematology. 32 (6): 511–519. doi:10.1016/j.exphem.2004.02.013. hdl:10536/DRO/DU:30101092. ISSN 0301-472X. PMID 15183891.
Further reading
[edit]- Nolte, D. D. (2015). Introduction to Modern Dynamics: Chaos, Networks, Space and Time. Oxford University Press. ISBN 978-0-19-965703-2.
- Nolte, D. D. (2018). Galileo Unbound: A Path Across Life, the Universe and Everything. Oxford University Press. ISBN 978-0-19-880584-7.
External links
[edit]- "Phase space", Encyclopedia of Mathematics, EMS Press, 2001 [1994]