Recent from talks
Nothing was collected or created yet.
Frequency modulation
View on Wikipedia| Passband modulation |
|---|
 |
| Analog modulation |
| Digital modulation |
| Hierarchical modulation |
| Spread spectrum |
| See also |
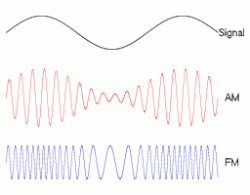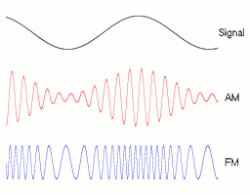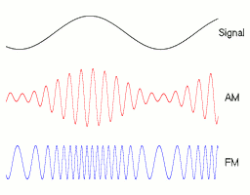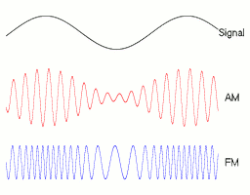

Frequency modulation (FM) is a signal modulation technique used in electronic communication, originally for transmitting messages with a radio wave. In frequency modulation a carrier wave is varied in its instantaneous frequency in proportion to a property, primarily the instantaneous amplitude, of a message signal, such as an audio signal.[1] The technology is used in telecommunications, radio broadcasting, signal processing, and computing.
In analog frequency modulation, such as radio broadcasting of voice and music, the instantaneous frequency deviation, i.e. the difference between the frequency of the carrier and its center frequency, has a functional relation to the modulating signal amplitude.
Digital data can be encoded and transmitted with a type of frequency modulation known as frequency-shift keying (FSK), in which the instantaneous frequency of the carrier is shifted among a set of frequencies. The frequencies may represent digits, such as 0 and 1. FSK is widely used in computer modems such as fax modems, telephone caller ID systems, garage door openers, and other low-frequency transmissions.[2] Radioteletype also uses FSK.[3]
Frequency modulation is widely used for FM radio broadcasting. It is also used in telemetry, radar, seismic prospecting, and monitoring newborns for seizures via EEG,[4] two-way radio systems, sound synthesis, magnetic tape-recording systems and some video-transmission systems. In radio transmission, an advantage of frequency modulation is that it has a larger signal-to-noise ratio and therefore rejects radio frequency interference better than an equal power amplitude modulation (AM) signal. For this reason, most music is broadcast over FM radio.
Frequency modulation and phase modulation are the two complementary principal methods of angle modulation; phase modulation is often used as an intermediate step to achieve frequency modulation. These methods contrast with amplitude modulation, in which the amplitude of the carrier wave varies, while the frequency and phase remain constant.
FM Signal
[edit]According to Nahin, "To apply the baseband signal of a microphone output directly to the transmitter antenna won't work, because ...a quarter-wavelength antenna at audio frequencies is physically enormous. To have a reasonably sized antenna requires a transmitter signal at frequencies considerably higher than those of the bandwidth spectrum; that is, the baseband spectrum must be upshifted to the radio frequencies."[5] This is called signal modulation. According to Bertrand, "Frequency modulation is a method of modulating a carrier wave whereby the modulating audio causes the instantaneous frequency of the carrier to change. Without modulation, an FM transmitter produces a single carrier frequency."[6]
The FM signal produced by a sinusoidal carrier of frequency ωc, modulated by an audio tone of frequency ωa with amplitude A, can be written as:[5]
We need the instantaneous frequency, which describes a frequency varying above and below the carrier frequency at the audio tone frequency, which we derive by using Carson's time derivative method:[5]
The amplitude factor kAωa defines the maximum Frequency deviation around ωc. Dividing by ωa, gives us the modulation index kA,[5] which "is the ratio of the amount of frequency deviation to the audio modulating frequency."[6]
While most of the energy of the signal is contained within fc ± fΔ, it can be shown by Fourier analysis that a wider range of frequencies is required to precisely represent an FM signal. The frequency spectrum of an actual FM signal has components extending infinitely, although their amplitude decreases and higher-order components are often neglected in practical design problems.[7]
Sinusoidal baseband signal
[edit]Mathematically, a baseband modulating signal may be approximated by a sinusoidal continuous wave signal with a frequency fm. This method is also named as single-tone modulation. The integral of such a signal is:
In this case, the expression for y(t) above simplifies to:[8]
where the amplitude of the modulating sinusoid is represented in the peak deviation (see frequency deviation).
The harmonic distribution of a sine wave carrier modulated by such a sinusoidal signal can be represented with Bessel functions; this provides the basis for a mathematical understanding of frequency modulation in the frequency domain.[8]
Modulation index
[edit]As in other modulation systems, the modulation index indicates by how much the modulated variable varies around its unmodulated level. It relates to variations in the carrier frequency:
where is the highest frequency component present in the modulating signal xm(t), and is the peak frequency-deviation – i.e. the maximum deviation of the instantaneous frequency from the carrier frequency. For a sine wave modulation, the modulation index is seen to be the ratio of the peak frequency deviation of the carrier wave to the frequency of the modulating sine wave.[9]
If , the modulation is called narrowband FM (NFM), and its bandwidth is approximately . Sometimes modulation index is considered NFM and other modulation indices are considered wideband FM (WFM or FM).[8]
For digital modulation systems, for example, binary frequency shift keying (BFSK), where a binary signal modulates the carrier, the modulation index is given by:
where is the symbol period, and is used as the highest frequency of the modulating binary waveform by convention, even though it would be more accurate to say it is the highest fundamental of the modulating binary waveform. In the case of digital modulation, the carrier is never transmitted. Rather, one of two frequencies is transmitted, either or , depending on the binary state 0 or 1 of the modulation signal.
If , the modulation is called wideband FM and its bandwidth is approximately . While wideband FM uses more bandwidth, it can improve the signal-to-noise ratio significantly; for example, doubling the value of , while keeping constant, results in an eight-fold improvement in the signal-to-noise ratio.[10] (Compare this with chirp spread spectrum, which uses extremely wide frequency deviations to achieve processing gains comparable to traditional, better-known spread-spectrum modes).
With a tone-modulated FM wave, if the modulation frequency is held constant and the modulation index is increased, the (non-negligible) bandwidth of the FM signal increases but the spacing between spectra remains the same; some spectral components decrease in strength as others increase. If the frequency deviation is held constant and the modulation frequency increased, the spacing between spectra increases.
Frequency modulation can be classified as narrowband if the change in the carrier frequency is about the same as the signal frequency, or as wideband if the change in the carrier frequency is much higher (modulation index > 1) than the signal frequency.[11] For example, narrowband FM (NFM) is used for two-way radio systems such as Family Radio Service, in which the carrier is allowed to deviate only 2.5 kHz above and below the center frequency with speech signals of no more than 3.5 kHz bandwidth. Wideband FM is used for FM broadcasting, in which music and speech are transmitted with up to 75 kHz deviation from the center frequency and carry audio with up to a 20 kHz bandwidth and subcarriers up to 92 kHz.
Bessel functions
[edit]
In his 1922 FM paper, Carson pointed out an infinite number of side frequencies are generated when a carrier frequency is modulated by a signal frequency, the amplitudes expressed as Bessel functions. The separation is determined by the frequency of the modulating signal, and the amplitude dependent upon the modulation index. A table of Bessel functions of the first kind is used to determine the side frequency amplitudes.[6][5]: 214
For the case of a carrier modulated by a single sine wave, the resulting frequency spectrum can be calculated using Bessel functions of the first kind, as a function of the sideband number and the modulation index. The carrier and sideband amplitudes are illustrated for different modulation indices of FM signals. For particular values of the modulation index, the carrier amplitude becomes zero and all the signal power is in the sidebands.[7]
Since the sidebands are on both sides of the carrier, their count is doubled, and then multiplied by the modulating frequency to find the bandwidth. For example, 3 kHz deviation modulated by a 2.2 kHz audio tone produces a modulation index of 1.36. Suppose that we limit ourselves to only those sidebands that have a relative amplitude of at least 0.01. Then, examining the chart shows this modulation index will produce three sidebands. These three sidebands, when doubled, gives us (6 × 2.2 kHz) or a 13.2 kHz required bandwidth.
| Modulation index |
Sideband amplitude | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Carrier | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| 0.00 | 1.00 | ||||||||||||||||
| 0.25 | 0.98 | 0.12 | |||||||||||||||
| 0.5 | 0.94 | 0.24 | 0.03 | ||||||||||||||
| 1.0 | 0.77 | 0.44 | 0.11 | 0.02 | |||||||||||||
| 1.5 | 0.51 | 0.56 | 0.23 | 0.06 | 0.01 | ||||||||||||
| 2.0 | 0.22 | 0.58 | 0.35 | 0.13 | 0.03 | ||||||||||||
| 2.40483 | 0.00 | 0.52 | 0.43 | 0.20 | 0.06 | 0.02 | |||||||||||
| 2.5 | −0.05 | 0.50 | 0.45 | 0.22 | 0.07 | 0.02 | 0.01 | ||||||||||
| 3.0 | −0.26 | 0.34 | 0.49 | 0.31 | 0.13 | 0.04 | 0.01 | ||||||||||
| 4.0 | −0.40 | −0.07 | 0.36 | 0.43 | 0.28 | 0.13 | 0.05 | 0.02 | |||||||||
| 5.0 | −0.18 | −0.33 | 0.05 | 0.36 | 0.39 | 0.26 | 0.13 | 0.05 | 0.02 | ||||||||
| 5.52008 | 0.00 | −0.34 | −0.13 | 0.25 | 0.40 | 0.32 | 0.19 | 0.09 | 0.03 | 0.01 | |||||||
| 6.0 | 0.15 | −0.28 | −0.24 | 0.11 | 0.36 | 0.36 | 0.25 | 0.13 | 0.06 | 0.02 | |||||||
| 7.0 | 0.30 | 0.00 | −0.30 | −0.17 | 0.16 | 0.35 | 0.34 | 0.23 | 0.13 | 0.06 | 0.02 | ||||||
| 8.0 | 0.17 | 0.23 | −0.11 | −0.29 | −0.10 | 0.19 | 0.34 | 0.32 | 0.22 | 0.13 | 0.06 | 0.03 | |||||
| 8.65373 | 0.00 | 0.27 | 0.06 | −0.24 | −0.23 | 0.03 | 0.26 | 0.34 | 0.28 | 0.18 | 0.10 | 0.05 | 0.02 | ||||
| 9.0 | −0.09 | 0.25 | 0.14 | −0.18 | −0.27 | −0.06 | 0.20 | 0.33 | 0.31 | 0.21 | 0.12 | 0.06 | 0.03 | 0.01 | |||
| 10.0 | −0.25 | 0.04 | 0.25 | 0.06 | −0.22 | −0.23 | −0.01 | 0.22 | 0.32 | 0.29 | 0.21 | 0.12 | 0.06 | 0.03 | 0.01 | ||
| 12.0 | 0.05 | −0.22 | −0.08 | 0.20 | 0.18 | −0.07 | −0.24 | −0.17 | 0.05 | 0.23 | 0.30 | 0.27 | 0.20 | 0.12 | 0.07 | 0.03 | 0.01 |
Carson's rule
[edit]A rule of thumb, Carson's rule states that the frequency-modulated signal lies within a bandwidth of:[8]: 146
where , as defined above, is the peak deviation of the instantaneous frequency from the center carrier frequency , is the modulation index which is the ratio of frequency deviation to highest frequency in the modulating signal, and is the highest frequency in the modulating signal. Carson's rule can only be applied to sinusoidal signals. For non-sinusoidal signals:
where W is the highest frequency in the modulating signal but non-sinusoidal in nature and D is the Deviation ratio which is the ratio of frequency deviation to highest frequency of modulating non-sinusoidal signal.
Noise reduction
[edit]FM provides improved signal-to-noise ratio (SNR), as compared for example with AM. Compared with an optimum AM scheme, FM typically has poorer SNR below a certain signal level called the noise threshold, but above a higher level – the full improvement or full quieting threshold – the SNR is much improved over AM. The improvement depends on modulation level and deviation. For typical voice communications channels, improvements are typically 5–15 dB. FM broadcasting using wider deviation can achieve even greater improvements. Additional techniques, such as pre-emphasis of higher audio frequencies with corresponding de-emphasis in the receiver, are generally used to improve overall SNR in FM circuits. Since FM signals have constant amplitude, FM receivers normally have limiters that remove AM noise, further improving SNR.[12][13]
Implementation
[edit]Modulation
[edit]FM signals can be generated using either direct or indirect frequency modulation:
- Direct FM modulation can be achieved by directly feeding the modulating audio voltage into a voltage-controlled oscillator.[6]
- For indirect FM modulation, the message signal is integrated to generate a phase-modulated signal. This is used to modulate a crystal-controlled oscillator, and the result is passed through a frequency multiplier to produce an FM signal. In this modulation, narrowband FM is generated leading to wideband FM later and hence the modulation is known as indirect FM modulation.[14]
Demodulation
[edit]
Many FM detector circuits exist. A common method for recovering the information signal is through a Foster–Seeley discriminator or ratio detector. A phase-locked loop can be used as an FM demodulator.[6]: 415–419 Slope detection demodulates an FM signal by using a tuned circuit which has its resonant frequency slightly offset from the carrier. The input FM wave of constant amplitude and instantaneous frequency, is converted to an FM wave with instantaneous frequency and instantaneous amplitude, which is then sent to an envelop detector.[5]: 224–228 AM receivers may detect some FM transmissions by this means, although it does not provide an efficient means of detection for FM broadcasts.
In software-defined radio implementations, the demodulation may be carried out by using the Hilbert transform (implemented as a filter) to recover the instantaneous phase, and thereafter differentiating this phase (using another filter) to recover the instantaneous frequency. Alternatively, a complex mixer followed by a bandpass filter may be used to translate the signal to baseband, and then proceeding as before. For sampled signals, phase detection, and therefore frequency modulation detection, can be approximated by taking the IQ (complex) sample and multiplying it with the complex conjugate of the previous IQ sample, .[15] If the demodulated signal is sampled at or above Nyquist, this allows for recovery of near-instantaneous phase changes.
Applications
[edit]Doppler effect
[edit]In 1968, Schnitzler noted certain bats lower the animal echolocation emission frequency by 13 to 16 kHz, compensating for Doppler shifts caused by the bat’s own movement. Doppler shift compensation, dynamic frequency modulation, ensures that the returning echo frequency is optimally adjusted for the bat's auditory fovea.[16][17]
Magnetic tape storage
[edit]FM is also used at intermediate frequencies by analog VCR systems (including VHS) to record the luminance (black and white) portions of the video signal. Commonly, the chrominance component is recorded as a conventional AM signal, using the higher-frequency FM signal as bias. FM is the only feasible method of recording the luminance ("black-and-white") component of video to (and retrieving video from) magnetic tape without distortion; video signals have a large range of frequency components – from a few hertz to several megahertz, too wide for equalizers to work with due to electronic noise below −60 dB. FM also keeps the tape at saturation level, acting as a form of noise reduction; a limiter can mask variations in playback output, and the FM capture effect removes print-through and pre-echo. A continuous pilot-tone, if added to the signal – as was done on V2000 and many Hi-band formats – can keep mechanical jitter under control and assist timebase correction.
These FM systems are unusual, in that they have a ratio of carrier to maximum modulation frequency of less than two; contrast this with FM audio broadcasting, where the ratio is around 10,000. Consider, for example, a 6-MHz carrier modulated at a 3.5-MHz rate; by Bessel analysis, the first sidebands are on 9.5 and 2.5 MHz and the second sidebands are on 13 MHz and −1 MHz. The result is a reversed-phase sideband on +1 MHz; on demodulation, this results in unwanted output at 6 – 1 = 5 MHz. The system must be designed so that this unwanted output is reduced to an acceptable level.[18]
Sound
[edit]FM is also used at audio frequencies to synthesize sound. This technique, known as FM synthesis, was popularized by early digital synthesizers and became a standard feature in several generations of personal computer sound cards.
Radio
[edit]
Edwin Howard Armstrong (1890–1954) was an American electrical engineer who invented wideband frequency modulation (FM) radio.[19] He patented the regenerative circuit in 1914, the superheterodyne receiver in 1918 and the super-regenerative circuit in 1922.[20] Armstrong presented his paper, "A Method of Reducing Disturbances in Radio Signaling by a System of Frequency Modulation", (which first described FM radio) before the New York section of the Institute of Radio Engineers on November 6, 1935. The paper was published in 1936.[21]
As the name implies, wideband FM (WFM) requires a wider signal bandwidth than amplitude modulation by an equivalent modulating signal; this also makes the signal more robust against noise and interference. Frequency modulation is also more robust against signal-amplitude-fading phenomena. As a result, FM was chosen as the modulation standard for high frequency, high fidelity radio transmission, hence the term "FM radio" (although for many years the BBC called it "VHF radio" because commercial FM broadcasting uses part of the VHF band – the FM broadcast band). FM receivers employ a special detector for FM signals and exhibit a phenomenon known as the capture effect, in which the tuner "captures" the stronger of two stations on the same frequency while rejecting the other (compare this with a similar situation on an AM receiver, where both stations can be heard simultaneously). Frequency drift or a lack of selectivity may cause one station to be overtaken by another on an adjacent channel. Frequency drift was a problem in early (or inexpensive) receivers; inadequate selectivity may affect any tuner.
A wideband FM signal can also be used to carry a stereo signal; this is done with multiplexing and demultiplexing before and after the FM process. The FM modulation and demodulation process is identical in stereo and monaural processes.
FM is commonly used at VHF radio frequencies for high-fidelity broadcasts of music and speech. In broadcast services, where audio fidelity is important, wideband FM is generally used. Analog TV sound is also broadcast using FM. Narrowband FM is used for voice communications in commercial and amateur radio settings. In two-way radio, narrowband FM (NBFM) is used to conserve bandwidth for land mobile, marine mobile and other radio services.
A high-efficiency radio-frequency switching amplifier can be used to transmit FM signals (and other constant-amplitude signals). For a given signal strength (measured at the receiver antenna), switching amplifiers use less battery power and typically cost less than a linear amplifier. This gives FM another advantage over other modulation methods requiring linear amplifiers, such as AM and QAM.
There are reports that on October 5, 1924, Professor Mikhail A. Bonch-Bruevich, during a scientific and technical conversation in the Nizhny Novgorod Radio Laboratory, reported about his new method of telephony, based on a change in the period of oscillations. Demonstration of frequency modulation was carried out on the laboratory model.[22]
Hearing assistive technology
[edit]Frequency modulated systems are a widespread and commercially available assistive technology that make speech more understandable by improving the signal-to-noise ratio in the user's ear. They are also called auditory trainers, a term which refers to any sound amplification system not classified as a hearing aid. They intensify signal levels from the source by 15 to 20 decibels.[23] FM systems are used by hearing-impaired people as well as children whose listening is affected by disorders such as auditory processing disorder or ADHD.[24] For people with sensorineural hearing loss, FM systems result in better speech perception than hearing aids. They can be coupled with behind-the-ear hearing aids to allow the user to alternate the setting.[25] FM systems are more convenient and cost-effective than alternatives such as cochlear implants, but many users use FM systems infrequently due to their conspicuousness and need for recharging.[26]
See also
[edit]- Continuous-wave frequency-modulated radar
- Chirp
- FM stereo
- FM-UWB (FM and Ultra Wideband)
- History of radio
- Modulation, for a list of other modulation techniques
References
[edit]- ^ Smith, Robert H. (1993). Machines and Inventions. Alexandria, VA: Time Life. p. 85. ISBN 0-8094-9704-2.
- ^ Gibilisco, Stan (2002). Teach yourself electricity and electronics. McGraw-Hill Professional. p. 477. ISBN 978-0-07-137730-0.
morse-code frequency-shift-keying sent-using-fsk.
- ^ Rutledge, David B. (1999). The Electronics of Radio. Cambridge University Press. p. 310. ISBN 978-0-521-64645-1.
- ^ B. Boashash, editor, Time-Frequency Signal Analysis and Processing – A Comprehensive Reference, Elsevier Science, Oxford, 2003; ISBN 0-08-044335-4
- ^ a b c d e f Nahin, Paul (2024). The Mathematical Radio: Inside the Magic of AM, FM, and Single-Sideband. Princeton: Princeton University Press. pp. 74, 210–213. ISBN 9780691235318.
- ^ a b c d e Bertrand, Ron (2022). Radio Handbook. pp. 405, 408–409. ISBN 9798362553722.
- ^ a b T.G. Thomas, S. C. Sekhar Communication Theory, Tata-McGraw Hill 2005, ISBN 0-07-059091-5 p. 136
- ^ a b c d Gibson, Jerry (1993). Principles of Digital and Analog Communications. New York: Macmillan Publishing Company. pp. 143–144. ISBN 0023418605.
- ^ "Frequency Modulation (FM): Basics and Applications". IB-Lenhardt AG. Retrieved 2025-07-16.
- ^ Der, Lawrence. "Frequency Modulation (FM) Tutorial" (PDF). Silicon Laboratories. S2CID 48672999. Archived from the original (PDF) on 2014-10-21. Retrieved 17 October 2019.
- ^ Lathi, B. P. (1968). Communication Systems, pp. 214–17. New York: John Wiley and Sons, ISBN 0-471-51832-8.
- ^ H. P. Westman, ed. (1970). Reference Data for Radio Engineers (Fifth ed.). Howard W. Sams & Co. pp. 21–11.
- ^ Alan Bloom (2010). "Chapter 8. Modulation". In H. Ward Silver; Mark J. Wilson (eds.). The ARRL Handbook for Radio Communications. American Radio Relay League. p. 8.7. ISBN 978-0-87259-146-2.
- ^ Haykin, Simon [Ed]. (2001). Communication Systems, 4th ed.
- ^ Shima, James Michael (1995). FM Demodulation Using a Digital Radio and Digital Signal Processing. University of Florida.
- ^ Schnitzler, HU; Denzinger, A (2011). "Auditory fovea and Doppler shift compensation: adaptations for flutter detection in echolocating bats using CF-FM signals". Journal of Comparative Physiology A. 197 (5). Journal Comparative Physiology A 197: 541–559. doi:10.1007/s00359-010-0569-6. PMID 20857119. Retrieved 28 October 2025.
- ^ Schnitzler, Hans-Ulrich (1968). "Die Ultraschall-Ortungslaute der Hufeisen-Fledermäuse (Chiroptera-Rhinolophidae) in verschiedenen Orientierungssituationen". Zeitschrift Für Vergleichende Physiologie. 57 (4): 376–408. doi:10.1007/BF00303062. Retrieved 28 October 2025.
- ^ "FM Systems Of Exceptional Bandwidth" Proc. IEEE vol. 112, no. 9, p. 1664, September 1965
- ^ A. Michael Noll (2001). Principles of modern communications technology. Artech House. p. 104. ISBN 978-1580532846.
- ^ US 1342885
- ^ Armstrong, E. H. (May 1936). "A Method of Reducing Disturbances in Radio Signaling by a System of Frequency Modulation". Proceedings of the IRE. 24 (5). IRE: 689–740. Bibcode:1936PIRE...24..689A. doi:10.1109/JRPROC.1936.227383. S2CID 43628076.
- ^ Ф. Лбов. Новая система радиофона «Радиолюбитель». – 1924. – № 6. – С. 86.
- ^ ASHA Ad Hoc Committee on FM Systems (2002) [Original March 1994]. Guidelines for Fitting and Monitoring FM Systems (Technical report) (Revised ed.). American Speech–Language–Hearing Association. doi:10.1044/policy.GL2002-00010.
- ^ Schafer, Erin C.; Bryant, Danielle; Sanders, Katie; Baldus, Nicole; Algier, Katherine; Lewis, Audrey; Traber, Jordan; Layden, Paige; Amin, Aneeqa (June 1, 2014). "Fitting and Verification of Frequency Modulation on Children with Normal Hearing". Journal of the American Academy of Audiology. 25 (6): 529–540. doi:10.3766/jaaa.25.6.3. ISSN 1050-0545. PMID 25313543. EBSCOhost 107832936.
- ^ Lewis, M. Samantha; Crandall, Carl C.; Valente, Michael; Enrietto Horn, Jane (2004). "Speech perception in noise: directional microphones versus frequency modulation (FM) systems". Journal of the American Academy of Audiology. 15 (6): 426–439. doi:10.3766/jaaa.15.6.4. PMID 15341224.
- ^ McArdle, Rachel; Abrams, Harvey B.; Hnath Chisholm, Theresa (2005). "When Hearing Aids Go Bad: An FM Success Story". Journal of the American Academy of Audiology. 16 (10): 809–821. doi:10.3766/jaaa.16.10.5. PMID 16515133. EBSCOhost 106441304.
Further reading
[edit]- Carlson, A. Bruce (2001). Communication Systems. Science/Engineering/Math (4th ed.). McGraw-Hill. ISBN 978-0-07-011127-1.
- Frost, Gary L. (2010). Early FM Radio: Incremental technology in twentieth-century America. Baltimore, MD: Johns Hopkins University Press. ISBN 978-0-8018-9440-4.
- Seymour, Ken (2005) [1996]. "Frequency Modulation". The Electronics Handbook (2nd ed.). CRC Press. pp. 1188–1200. ISBN 0-8493-8345-5.
External links
[edit]- Analog Modulation online interactive demonstration using Python in Google Colab Platform, by C Foh.
Frequency modulation
View on GrokipediaFundamentals
Definition and Principles
Frequency modulation (FM) is a modulation technique in which the instantaneous frequency of a high-frequency sinusoidal carrier wave is varied in accordance with the instantaneous amplitude of a message signal, while the amplitude of the carrier remains constant.[7] This variation, known as frequency deviation, is directly proportional to the amplitude of the message signal m(t), which is typically bandlimited to a maximum frequency W.[8] The core principle of FM lies in encoding information through these frequency changes rather than alterations in amplitude or phase directly, providing a means to transmit analog signals over radio frequencies with potential advantages in noise resilience. Developed by Edwin Howard Armstrong in the early 1930s, FM represented a significant advancement in radio communication, particularly for broadcasting applications.[9] To understand FM, it is essential to first grasp the basics of a carrier wave, which is an unmodulated sinusoidal signal of the form , where is the carrier amplitude and is the carrier frequency, typically in the radio spectrum (e.g., MHz range).[10] The message signal m(t), often normalized such that , drives the modulation process. The general time-domain expression for an FM signal is given by where is the frequency deviation constant (in Hz per unit amplitude of m(t)), determining the sensitivity of frequency changes to the message.[11] The phase term represents the cumulative frequency deviation up to time t.[12] The instantaneous frequency of the FM signal, , is defined as the time derivative of the total phase divided by , yielding .[10] This shows that the deviation from the carrier frequency, , directly mirrors the message amplitude, with the maximum deviation . FM is classified into narrowband FM (NBFM) and wideband FM (WBFM) based on the deviation ratio .[8] In NBFM, , meaning the frequency deviation is small compared to the message bandwidth, resulting in a spectrum similar to amplitude modulation with minimal sidebands.[13] Conversely, WBFM features , producing a wider spectrum with many sidebands, as pioneered by Armstrong for improved signal quality in broadcasting.[9]Comparison to Amplitude Modulation
In amplitude modulation (AM), the information signal modulates the amplitude of a high-frequency carrier wave while keeping the frequency constant, resulting in a transmitted signal of the form , where is the carrier amplitude, is the amplitude sensitivity, is the message signal, and is the carrier frequency; this structure causes the signal power to vary with the message content.[14] In contrast, frequency modulation (FM) encodes the information by varying the instantaneous frequency of the carrier around proportional to , producing a constant-amplitude envelope that remains unaffected by amplitude fluctuations, such as those introduced by noise or interference.[15] This fundamental difference makes AM vulnerable to amplitude-based distortions, whereas FM's constant envelope allows demodulators to ignore amplitude variations, focusing solely on frequency deviations. A key distinction lies in bandwidth usage: AM requires a bandwidth of approximately , where is the bandwidth of the message signal, as the modulation produces upper and lower sidebands symmetric around the carrier.[16] FM, however, demands wider bandwidth, estimated by Carson's rule as approximately , with representing the peak frequency deviation, often significantly larger than in wideband applications to achieve noise suppression.[17] The development of FM stemmed from efforts to overcome AM's susceptibility to noise in early radio broadcasting; inventor Edwin Howard Armstrong, motivated by the persistent static and interference plaguing AM systems, demonstrated wideband FM in 1933 as a method to drastically reduce such disturbances by shifting modulation to the frequency domain.[18][19] This innovation traded increased bandwidth for superior signal quality, providing a higher signal-to-noise ratio (SNR) under noisy channel conditions, particularly when the modulation index is high enough to exploit frequency discrimination in receivers.[15]Mathematical Theory
Sinusoidal Baseband Signal
In frequency modulation (FM), a common case for analysis is when the baseband modulating signal is a single-tone sinusoid, given by , where is the amplitude and is the modulating frequency.[20] This assumption simplifies the derivation of the modulated signal's characteristics while illustrating core principles of FM, where the carrier frequency varies proportionally with the modulating signal.[17] The instantaneous phase of the FM signal under this sinusoidal modulation is expressed as , with as the carrier frequency and denoting the modulation index.[20] Here, quantifies the extent of phase deviation induced by the modulation. The resulting FM waveform is then , where is the carrier amplitude, producing a signal whose phase term incorporates the sinusoidal variation.[20] This form arises from integrating the instantaneous frequency deviation, as established in early theoretical work on modulation. The maximum frequency deviation from the carrier, , is defined as , where is the frequency sensitivity constant (in hertz per unit of modulating signal amplitude).[17] This deviation represents the peak excursion of the instantaneous frequency above or below . In the time domain, the instantaneous frequency swings symmetrically around the carrier frequency , reaching at the positive peaks of and at the negative peaks.[11] This symmetric oscillation results in a waveform where the carrier's zero-crossings adjust periodically, reflecting the modulating sinusoid's influence without altering the amplitude.[20]Modulation Index
In frequency modulation (FM), the modulation index, denoted as , is a dimensionless parameter that quantifies the degree of frequency deviation relative to the modulating signal's frequency. It is defined as the ratio of the peak frequency deviation to the modulating frequency , expressed as . This can also be written as , where is the frequency sensitivity constant (in hertz per unit amplitude of the modulating signal) and is the amplitude of the modulating signal.[21][22][23] Physically, characterizes the extent of phase deviation in the FM waveform. For small values where , the modulation approximates narrowband FM (NBFM), producing sidebands akin to those in amplitude modulation with minimal additional spectral components. In contrast, when , it results in wideband FM (WBFM), generating multiple significant sidebands that expand the signal's frequency occupancy.[24][25][22] As increases, the FM signal's spectrum broadens due to the proliferation of higher-order sidebands, but this also enhances noise immunity by trading bandwidth for improved signal-to-noise ratio in the demodulated output, up to the point where threshold effects may limit benefits. In FM receivers, the capture effect—wherein the stronger signal suppresses weaker interferers—is influenced by , as larger indices strengthen the dominant signal's deviation relative to noise or competing signals, aiding performance in multipath or interference-prone environments.[6][26][27] A representative example occurs in commercial FM broadcasting, where the standard peak deviation is 75 kHz and the maximum audio modulating frequency is 15 kHz, yielding . This value ensures wideband operation for high-fidelity audio transmission while balancing spectral efficiency.[21][28][29]Bessel Functions and Spectrum
The spectrum of a frequency-modulated signal with a sinusoidal baseband signal is derived using the Jacobi-Anger expansion, which decomposes the modulated waveform into an infinite series of harmonic components. For an FM signal expressed as , where is the carrier amplitude, is the carrier frequency, is the modulating frequency, and is the modulation index, the expansion yields: with denoting the Bessel functions of the first kind of integer order .[22] This representation shows that the FM spectrum comprises a discrete carrier tone at frequency with amplitude , accompanied by pairs of upper and lower sidebands at frequencies (for ) each with amplitude . The coefficients for negative satisfy , ensuring symmetric sideband amplitudes.[30] The magnitudes of the Bessel functions exhibit distinct behavior depending on . The zeroth-order term starts at 1 for and decreases with increasing , oscillating and passing through zero at values such as , , and , where the carrier component disappears entirely. Higher-order terms for initially grow with before oscillating, with significant contributions typically limited to orders ; beyond this, the coefficients decay asymptotically as for large . For instance, at , the carrier is near zero (), while sidebands up to the fifth order dominate the spectrum. The approximate values of are summarized below:| Order | |
|---|---|
| 0 | -0.178 |
| 1 | -0.328 |
| 2 | 0.047 |
| 3 | 0.365 |
| 4 | 0.391 |
| 5 | 0.262 |
| 6 | 0.131 |
| 7 | 0.053 |































![{\displaystyle x[n]\cdot {\overline {x[n-1]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c02d0f694209d31ac9b9330e2b942318578fa50)