Recent from talks
Nothing was collected or created yet.
Solubility
View on Wikipedia


In chemistry, solubility is the ability of a substance, the solute, to form a solution with another substance, the solvent. Insolubility is the opposite property, the inability of the solute to form such a solution.
The extent of the solubility of a substance in a specific solvent is generally measured as the concentration of the solute in a saturated solution, one in which no more solute can be dissolved.[1] At this point, the two substances are said to be at the solubility equilibrium. For some solutes and solvents, there may be no such limit, in which case the two substances are said to be "miscible in all proportions" (or just "miscible").[2]
The solute can be a solid, a liquid, or a gas, while the solvent is usually solid or liquid. Both may be pure substances, or may themselves be solutions. Gases are always miscible in all proportions, except in very extreme situations,[3] and a solid or liquid can be "dissolved" in a gas only by passing into the gaseous state first.
The solubility mainly depends on the composition of solute and solvent (including their pH and the presence of other dissolved substances) as well as on temperature and pressure. The dependency can often be explained in terms of interactions between the particles (atoms, molecules, or ions) of the two substances, and of thermodynamic concepts such as enthalpy and entropy.
Under certain conditions, the concentration of the solute can exceed its usual solubility limit. The result is a supersaturated solution, which is metastable and will rapidly exclude the excess solute if a suitable nucleation site appears.[4]
The concept of solubility does not apply when there is an irreversible chemical reaction between the two substances, such as the reaction of calcium hydroxide with hydrochloric acid; even though one might say, informally, that one "dissolved" the other. The solubility is also not the same as the rate of solution, which is how fast a solid solute dissolves in a liquid solvent. This property depends on many other variables, such as the physical form of the two substances and the manner and intensity of mixing.
The concept and measure of solubility are extremely important in many sciences besides chemistry, such as geology, biology, physics, and oceanography, as well as in engineering, medicine, agriculture, and even in non-technical activities like painting, cleaning, cooking, and brewing. Most chemical reactions of scientific, industrial, or practical interest only happen after the reagents have been dissolved in a suitable solvent. Water is by far the most common such solvent.
The term "soluble" is sometimes used for materials that can form colloidal suspensions of very fine solid particles in a liquid.[5] The quantitative solubility of such substances is generally not well-defined, however.
Quantification of solubility
[edit]The solubility of a specific solute in a specific solvent is generally expressed as the concentration of a saturated solution of the two.[1] Any of the several ways of expressing concentration of solutions can be used, such as the mass, volume, or amount in moles of the solute for a specific mass, volume, or mole amount of the solvent or of the solution.
Per quantity of solvent
[edit]In particular, chemical handbooks often express the solubility as grams of solute per 100 millilitres of solvent (g/(100 mL), often written as g/100 ml), or as grams of solute per decilitre of solvent (g/dL); or, less commonly, as grams of solute per litre of solvent (g/L). The quantity of solvent can instead be expressed in mass, as grams of solute per 100 grams of solvent (g/(100 g), often written as g/100 g), or as grams of solute per kilogram of solvent (g/kg). The number may be expressed as a percentage in this case, and the abbreviation "w/w" may be used to indicate "weight per weight".[6] (The values in g/L and g/kg are similar for water, but that may not be the case for other solvents.)
Alternatively, the solubility of a solute can be expressed in moles instead of mass. For example, if the quantity of solvent is given in kilograms, the value is the molality of the solution (mol/kg).
Per quantity of solution
[edit]The solubility of a substance in a liquid may also be expressed as the quantity of solute per quantity of solution, rather than of solvent. For example, following the common practice in titration, it may be expressed as moles of solute per litre of solution (mol/L), the molarity of the latter.
In more specialized contexts the solubility may be given by the mole fraction (moles of solute per total moles of solute plus solvent) or by the mass fraction at equilibrium (mass of solute per mass of solute plus solvent). Both are dimensionless numbers between 0 and 1 which may be expressed as percentages (%).
Liquid and gaseous solutes
[edit]For solutions of liquids or gases in liquids, the quantities of both substances may be given volume rather than mass or mole amount; such as litre of solute per litre of solvent, or litre of solute per litre of solution. The value may be given as a percentage, and the abbreviation "v/v" for "volume per volume" may be used to indicate this choice.
Conversion of solubility values
[edit]Conversion between these various ways of measuring solubility may not be trivial, since it may require knowing the density of the solution — which is often not measured, and cannot be predicted. While the total mass is conserved by dissolution, the final volume may be different from both the volume of the solvent and the sum of the two volumes.[7]
Moreover, many solids (such as acids and salts) will dissociate in non-trivial ways when dissolved; conversely, the solvent may form coordination complexes with the molecules or ions of the solute. In those cases, the sum of the moles of molecules of solute and solvent is not really the total moles of independent particles solution. To sidestep that problem, the solubility per mole of solution is usually computed and quoted as if the solute does not dissociate or form complexes—that is, by pretending that the mole amount of solution is the sum of the mole amounts of the two substances.
Qualifiers used to describe extent of solubility
[edit]The extent of solubility ranges widely, from infinitely soluble (without limit, i.e. miscible[2]) such as ethanol in water, to essentially insoluble, such as titanium dioxide in water. A number of other descriptive terms are also used to qualify the extent of solubility for a given application. For example, U.S. Pharmacopoeia gives the following terms, according to the mass msv of solvent required to dissolve one unit of mass msu of solute:[8] (The solubilities of the examples are approximate, for water at 20–25 °C.)
| Term | Range (msv/msu) | Example | g/dL | msv/msu |
|---|---|---|---|---|
| Very soluble | <1 | calcium nitrate | 158.7 | 0.63 |
| Freely soluble | 1 to 10 | calcium chloride | 65 | 1.54 |
| Soluble | 10 to 30 | sodium oxalate | 3.9 | 26 |
| Sparingly soluble | 30 to 100 | |||
| Slightly soluble | 100 to 1000 | calcium sulfate | 0.21 | 490 |
| Very slightly soluble | 1000 to 10,000 | dicalcium phosphate | 0.02 | 5000 |
| Practically insoluble or insoluble | ≥ 10,000 | barium sulfate | 0.000245 | 409000 |
The thresholds to describe something as insoluble, or similar terms, may depend on the application. For example, one source states that substances are described as "insoluble" when their solubility is less than 0.1 g per 100 mL of solvent.[9]
Molecular view
[edit]Solubility occurs under dynamic equilibrium, which means that solubility results from the simultaneous and opposing processes of dissolution and phase joining (e.g. precipitation of solids). A stable state of the solubility equilibrium occurs when the rates of dissolution and re-joining are equal, meaning the relative amounts of dissolved and non-dissolved materials are equal. If the solvent is removed, all of the substance that had dissolved is recovered.
The term solubility is also used in some fields where the solute is altered by solvolysis. For example, many metals and their oxides are said to be "soluble in hydrochloric acid", although in fact the aqueous acid irreversibly degrades the solid to give soluble products. Most ionic solids dissociate when dissolved in polar solvents. In those cases where the solute is not recovered upon evaporation of the solvent, the process is referred to as solvolysis. The thermodynamic concept of solubility does not apply straightforwardly to solvolysis.
When a solute dissolves, it may form several species in the solution. For example, an aqueous solution of cobalt(II) chloride can afford [Co(H2O)6]2+, [CoCl(H2O)5]+, CoCl2(H2O)2, each of which interconverts.
Factors affecting solubility
[edit]Solubility is defined for specific phases. For example, the solubility of aragonite and calcite in water are expected to differ, even though they are both polymorphs of calcium carbonate and have the same chemical formula.[clarification needed]
The solubility of one substance in another is determined by the balance of intermolecular forces between the solvent and solute, and the entropy change that accompanies the solvation. Factors such as temperature and pressure will alter this balance, thus changing the solubility.
Solubility may also strongly depend on the presence of other species dissolved in the solvent, for example, complex-forming anions (ligands) in liquids. Solubility will also depend on the excess or deficiency of a common ion in the solution[clarification needed], a phenomenon known as the common-ion effect. To a lesser extent, solubility will depend on the ionic strength of solutions. The last two effects can be quantified using the equation for solubility equilibrium.
For a solid that dissolves in a redox reaction, solubility is expected to depend on the potential (within the range of potentials under which the solid remains the thermodynamically stable phase). For example, solubility of gold in high-temperature water is observed to be almost an order of magnitude higher (i.e. about ten times higher) when the redox potential is controlled using a highly oxidizing Fe3O4-Fe2O3 redox buffer than with a moderately oxidizing Ni-NiO buffer.[10]

Solubility (metastable, at concentrations approaching saturation) also depends on the physical size of the crystal or droplet of solute (or, strictly speaking, on the specific surface area or molar surface area of the solute).[11] For quantification, see the equation in the article on solubility equilibrium. For highly defective crystals, solubility may increase with the increasing degree of disorder. Both of these effects occur because of the dependence of solubility constant on the Gibbs energy of the crystal. The last two effects, although often difficult to measure, are of practical importance.[citation needed] For example, they provide the driving force for precipitate aging (the crystal size spontaneously increasing with time).
Temperature
[edit]The solubility of a given solute in a given solvent is function of temperature. Depending on the change in enthalpy (ΔH) of the dissolution reaction, i.e., on the endothermic (ΔH > 0) or exothermic (ΔH < 0) character of the dissolution reaction, the solubility of a given compound may increase or decrease with temperature. The van 't Hoff equation relates the change of solubility equilibrium constant (Ksp) to temperature change and to reaction enthalpy change.
- For most solids and liquids, their solubility increases with temperature because their dissolution reaction is endothermic (ΔH > 0).[12] In liquid water at high temperatures, (e.g. that approaching the critical temperature), the solubility of ionic solutes tends to decrease due to the change of properties and structure of liquid water; the lower dielectric constant results in a less polar solvent and in a change of hydration energy affecting the ΔG of the dissolution reaction.
- Gaseous solutes exhibit more complex behavior with temperature. As the temperature is raised, gases usually become less soluble in water (exothermic dissolution reaction related to their hydration) (to a minimum, which is below 120 °C for most permanent gases[13]), but more soluble in organic solvents (endothermic dissolution reaction related to their solvation).[12]
The chart shows solubility curves for some typical solid inorganic salts in liquid water (temperature is in degrees Celsius, i.e. kelvins minus 273.15).[14] Many salts behave like barium nitrate and disodium hydrogen arsenate, and show a large increase in solubility with temperature (ΔH > 0). Some solutes (e.g. sodium chloride in water) exhibit solubility that is fairly independent of temperature (ΔH ≈ 0). A few, such as calcium sulfate (gypsum) and cerium(III) sulfate, become less soluble in water as temperature increases (ΔH < 0).[15] This is also the case for calcium hydroxide (portlandite), whose solubility at 70 °C is about half of its value at 25 °C. The dissolution of calcium hydroxide in water is also an exothermic process (ΔH < 0). As dictated by the van 't Hoff equation and Le Chatelier's principle, low temperatures favor dissolution of Ca(OH)2. Portlandite solubility increases at low temperature. This temperature dependence is sometimes referred to as "retrograde" or "inverse" solubility.[citation needed] Occasionally, a more complex pattern is observed, as with sodium sulfate, where the less soluble decahydrate crystal (mirabilite) loses water of crystallization at 32 °C to form a more soluble anhydrous phase (thenardite) with a smaller change in Gibbs free energy (ΔG) in the dissolution reaction.[citation needed]
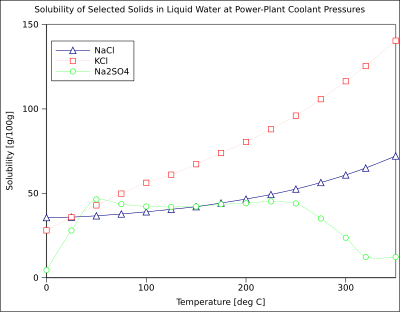
The solubility of organic compounds nearly always increases with temperature. The technique of recrystallization, used for purification of solids, depends on a solute's different solubilities in hot and cold solvent. A few exceptions exist, such as certain cyclodextrins.[16]
Pressure
[edit]For condensed phases (solids and liquids), the pressure dependence of solubility is typically weak and usually neglected in practice. Assuming an ideal solution, the dependence can be quantified as:
where the index iterates the components, is the mole fraction of the -th component in the solution, is the pressure, the index refers to constant temperature, is the partial molar volume of the -th component in the solution, is the partial molar volume of the -th component in the dissolving solid, and is the universal gas constant.[17]
The pressure dependence of solubility does occasionally have practical significance. For example, precipitation fouling of oil fields and wells by calcium sulfate (which decreases its solubility with decreasing pressure) can result in decreased productivity with time.
Solubility of gases
[edit]Henry's law is used to quantify the solubility of gases in solvents. The solubility of a gas in a solvent is directly proportional to the partial pressure of that gas above the solvent. This relationship is similar to Raoult's law and can be written as:
where is a temperature-dependent constant (for example, 769.2 L·atm/mol for dioxygen (O2) in water at 298 K), is the partial pressure (in atm), and is the concentration of the dissolved gas in the liquid (in mol/L).
The solubility of gases is sometimes also quantified using Bunsen solubility coefficient.
In the presence of small bubbles, the solubility of the gas does not depend on the bubble radius in any other way than through the effect of the radius on pressure (i.e. the solubility of gas in the liquid in contact with small bubbles is increased due to pressure increase by Δp = 2γ/r; see Young–Laplace equation).[18]
Henry's law is valid for gases that do not undergo change of chemical speciation on dissolution. Sieverts' law shows a case when this assumption does not hold.
The carbon dioxide solubility in seawater is also affected by temperature, pH of the solution, and by the carbonate buffer. The decrease of solubility of carbon dioxide in seawater when temperature increases is also an important retroaction factor (positive feedback) exacerbating past and future climate changes as observed in ice cores from the Vostok site in Antarctica. At the geological time scale, because of the Milankovich cycles, when the astronomical parameters of the Earth orbit and its rotation axis progressively change and modify the solar irradiance at the Earth surface, temperature starts to increase. When a deglaciation period is initiated, the progressive warming of the oceans releases CO2 into the atmosphere because of its lower solubility in warmer sea water. In turn, higher levels of CO2 in the atmosphere increase the greenhouse effect and carbon dioxide acts as an amplifier of the general warming.
Polarity
[edit]A popular aphorism used for predicting solubility is "like dissolves like" also expressed in the Latin language as "Similia similibus solventur".[19] This statement indicates that a solute will dissolve best in a solvent that has a similar chemical structure to itself, based on favorable entropy of mixing. This view is simplistic, but it is a useful rule of thumb. The overall solvation capacity of a solvent depends primarily on its polarity.[a] For example, a very polar (hydrophilic) solute such as urea is very soluble in highly polar water, less soluble in fairly polar methanol, and practically insoluble in non-polar solvents such as benzene. In contrast, a non-polar or lipophilic solute such as naphthalene is insoluble in water, fairly soluble in methanol, and highly soluble in non-polar benzene.[20]

In even more simple terms a simple ionic compound (with positive and negative ions) such as sodium chloride (common salt) is easily soluble in a highly polar solvent (with some separation of positive (δ+) and negative (δ-) charges in the covalent molecule) such as water, as thus the sea is salty as it accumulates dissolved salts since early geological ages.
The solubility is favored by entropy of mixing (ΔS) and depends on enthalpy of dissolution (ΔH) and the hydrophobic effect. The free energy of dissolution (Gibbs energy) depends on temperature and is given by the relationship: ΔG = ΔH – TΔS. Smaller ΔG means greater solubility.
Chemists often exploit differences in solubilities to separate and purify compounds from reaction mixtures, using the technique of liquid-liquid extraction. This applies in vast areas of chemistry from drug synthesis to spent nuclear fuel reprocessing.
Rate of dissolution
[edit]Dissolution is not an instantaneous process. The rate of solubilization (in kg/s) is related to the solubility product and the surface area of the material. The speed at which a solid dissolves may depend on its crystallinity or lack thereof in the case of amorphous solids and the surface area (crystallite size) and the presence of polymorphism. Many practical systems illustrate this effect, for example in designing methods for controlled drug delivery. In some cases, solubility equilibria can take a long time to establish (hours, days, months, or many years; depending on the nature of the solute and other factors).
The rate of dissolution can be often expressed by the Noyes–Whitney equation or the Nernst and Brunner equation[21] of the form:
where:
- = mass of dissolved material
- = time
- = surface area of the interface between the dissolving substance and the solvent
- = diffusion coefficient
- = thickness of the boundary layer of the solvent at the surface of the dissolving substance
- = mass concentration of the substance on the surface
- = mass concentration of the substance in the bulk of the solvent
For dissolution limited by diffusion (or mass transfer if mixing is present), is equal to the solubility of the substance. When the dissolution rate of a pure substance is normalized to the surface area of the solid (which usually changes with time during the dissolution process), then it is expressed in kg/m2s and referred to as "intrinsic dissolution rate". The intrinsic dissolution rate is defined by the United States Pharmacopeia.
Dissolution rates vary by orders of magnitude between different systems. Typically, very low dissolution rates parallel low solubilities, and substances with high solubilities exhibit high dissolution rates, as suggested by the Noyes-Whitney equation.
Theories of solubility
[edit]Solubility product
[edit]Solubility constants are used to describe saturated solutions of ionic compounds of relatively low solubility (see solubility equilibrium). The solubility constant is a special case of an equilibrium constant. Since it is a product of ion concentrations in equilibrium, it is also known as the solubility product. It describes the balance between dissolved ions from the salt and undissolved salt. The solubility constant is also "applicable" (i.e. useful) to precipitation, the reverse of the dissolving reaction. As with other equilibrium constants, temperature can affect the numerical value of solubility constant. While the solubility constant is not as simple as solubility, the value of this constant is generally independent of the presence of other species in the solvent.
Other theories
[edit]The Flory–Huggins solution theory is a theoretical model describing the solubility of polymers. The Hansen solubility parameters and the Hildebrand solubility parameters are empirical methods for the prediction of solubility. It is also possible to predict solubility from other physical constants such as the enthalpy of fusion.
The octanol-water partition coefficient, usually expressed as its logarithm (Log P), is a measure of differential solubility of a compound in a hydrophobic solvent (1-octanol) and a hydrophilic solvent (water). The logarithm of these two values enables compounds to be ranked in terms of hydrophilicity (or hydrophobicity).
The energy change associated with dissolving is usually given per mole of solute as the enthalpy of solution.
Applications
[edit]Solubility is of fundamental importance in a large number of scientific disciplines and practical applications, ranging from ore processing and nuclear reprocessing to the use of medicines, and the transport of pollutants.
Solubility is often said to be one of the "characteristic properties of a substance", which means that solubility is commonly used to describe the substance, to indicate a substance's polarity, to help to distinguish it from other substances, and as a guide to applications of the substance. For example, indigo is described as "insoluble in water, alcohol, or ether but soluble in chloroform, nitrobenzene, or concentrated sulfuric acid".[22]
Solubility of a substance is useful when separating mixtures. For example, a mixture of salt (sodium chloride) and silica may be separated by dissolving the salt in water, and filtering off the undissolved silica. The synthesis of chemical compounds, by the milligram in a laboratory, or by the ton in industry, both make use of the relative solubilities of the desired product, as well as unreacted starting materials, byproducts, and side products to achieve separation.
Another example of this is the synthesis of benzoic acid from phenylmagnesium bromide and dry ice. Benzoic acid is more soluble in an organic solvent such as dichloromethane or diethyl ether, and when shaken with this organic solvent in a separatory funnel, will preferentially dissolve in the organic layer. The other reaction products, including the magnesium bromide, will remain in the aqueous layer, clearly showing that separation based on solubility is achieved. This process, known as liquid–liquid extraction, is an important technique in synthetic chemistry. Recycling is used to ensure maximum extraction.
Differential solubility
[edit]In flowing systems, differences in solubility often determine the dissolution-precipitation driven transport of species. This happens when different parts of the system experience different conditions. Even slightly different conditions can result in significant effects, given sufficient time.
For example, relatively low solubility compounds are found to be soluble in more extreme environments, resulting in geochemical and geological effects of the activity of hydrothermal fluids in the Earth's crust. These are often the source of high quality economic mineral deposits and precious or semi-precious gems. In the same way, compounds with low solubility will dissolve over extended time (geological time), resulting in significant effects such as extensive cave systems or Karstic land surfaces.
Solubility of ionic compounds in water
[edit]Some ionic compounds (salts) dissolve in water, which arises because of the attraction between positive and negative charges (see: solvation). For example, the salt's positive ions (e.g. Ag+) attract the partially negative oxygen atom in H2O. Likewise, the salt's negative ions (e.g. Cl−) attract the partially positive hydrogens in H2O. Note: the oxygen atom is partially negative because it is more electronegative than hydrogen, and vice versa (see: chemical polarity).
- AgCl(s) ⇌ Ag+(aq) + Cl−(aq)
However, there is a limit to how much salt can be dissolved in a given volume of water. This concentration is the solubility and related to the solubility product, Ksp. This equilibrium constant depends on the type of salt (AgCl vs. NaCl, for example), temperature, and the common ion effect.
One can calculate the amount of AgCl that will dissolve in 1 liter of pure water as follows:
- Ksp = [Ag+] × [Cl−] / M2 (definition of solubility product; M = mol/L)
- Ksp = 1.8 × 10−10 (from a table of solubility products)
[Ag+] = [Cl−], in the absence of other silver or chloride salts, so
- [Ag+]2 = 1.8 × 10−10 M2
- [Ag+] = 1.34 × 10−5 mol/L
The result: 1 liter of water can dissolve 1.34 × 10−5 moles of AgCl at room temperature. Compared with other salts, AgCl is poorly soluble in water. For instance, table salt (NaCl) has a much higher Ksp = 36 and is, therefore, more soluble. The following table gives an overview of solubility rules for various ionic compounds.
| Easily soluble | Limited solubility or insoluble[23] |
|---|---|
| Group I and NH4+ compounds (except lithium phosphate) | Carbonates (except Group I, NH4+ and uranyl compounds) |
| Nitrates | Sulfites (except Group I and NH4+ compounds) |
| Acetates (ethanoates) (except Ag+ compounds) | Phosphates (except Group I and NH4+ compounds (excluding Li+)) |
| Chlorides (chlorates and perchlorates), bromides and iodides (except Ag+, Pb2+, Cu+ and Hg22+) | Hydroxides and oxides (except Group I, NH4+, Ba2+, Sr2+ and Tl+) |
| Sulfates (except Ag+, Pb2+, Ba2+, Sr2+ and Ca2+) | Sulfides (except Group I, Group II and NH4+ compounds) |
Solubility of organic compounds
[edit]The principle outlined above under polarity, that like dissolves like, is the usual guide to solubility with organic systems. For example, petroleum jelly will dissolve in gasoline because both petroleum jelly and gasoline are non-polar hydrocarbons. It will not, on the other hand, dissolve in ethyl alcohol or water, since the polarity of these solvents is too high. Sugar will not dissolve in gasoline, since sugar is too polar in comparison with gasoline. A mixture of gasoline and sugar can therefore be separated by filtration or extraction with water.
Solid solution
[edit]This term is often used in the field of metallurgy to refer to the extent that an alloying element will dissolve into the base metal without forming a separate phase. The solvus or solubility line (or curve) is the line (or lines) on a phase diagram that give the limits of solute addition. That is, the lines show the maximum amount of a component that can be added to another component and still be in solid solution. In the solid's crystalline structure, the 'solute' element can either take the place of the matrix within the lattice (a substitutional position; for example, chromium in iron) or take a place in a space between the lattice points (an interstitial position; for example, carbon in iron).
In microelectronic fabrication, solid solubility refers to the maximum concentration of impurities one can place into the substrate.
In solid compounds (as opposed to elements), the solubility of a solute element can also depend on the phases separating out in equilibrium. For example, amount of Sn soluble in the ZnSb phase can depend significantly on whether the phases separating out in equilibrium are (Zn4Sb3+Sn(L)) or (ZnSnSb2+Sn(L)).[24] Besides these, the ZnSb compound with Sn as a solute can separate out into other combinations of phases after the solubility limit is reached depending on the initial chemical composition during synthesis. Each combination produces a different solubility of Sn in ZnSb. Hence solubility studies in compounds, concluded upon the first instance of observing secondary phases separating out might underestimate solubility.[25] While the maximum number of phases separating out at once in equilibrium can be determined by the Gibb's phase rule, for chemical compounds there is no limit on the number of such phase separating combinations itself. Hence, establishing the "maximum solubility" in solid compounds experimentally can be difficult, requiring equilibration of many samples. If the dominant crystallographic defect (mostly interstitial or substitutional point defects) involved in the solid-solution can be chemically intuited beforehand, then using some simple thermodynamic guidelines can considerably reduce the number of samples required to establish maximum solubility.[26]
Incongruent dissolution
[edit]Many substances dissolve congruently (i.e. the composition of the solid and the dissolved solute stoichiometrically match). However, some substances may dissolve incongruently, whereby the composition of the solute in solution does not match that of the solid. This solubilization is accompanied by alteration of the "primary solid" and possibly formation of a secondary solid phase. However, in general, some primary solid also remains and a complex solubility equilibrium establishes. For example, dissolution of albite may result in formation of gibbsite.[27]
- NaAlSi3O8(s) + H+ + 7H2O ⇌ Na+ + Al(OH)3(s) + 3H4SiO4.
In this case, the solubility of albite is expected to depend on the solid-to-solvent ratio. This kind of solubility is of great importance in geology, where it results in formation of metamorphic rocks.
In principle, both congruent and incongruent dissolution can lead to the formation of secondary solid phases in equilibrium. So, in the field of Materials Science, the solubility for both cases is described more generally on chemical composition phase diagrams.
Solubility prediction
[edit]Solubility is a property of interest in many aspects of science, including but not limited to: environmental predictions, biochemistry, pharmacy, drug-design, agrochemical design, and protein ligand binding. Aqueous solubility is of fundamental interest owing to the vital biological and transportation functions played by water.[28][29][30] In addition, to this clear scientific interest in water solubility and solvent effects; accurate predictions of solubility are important industrially. The ability to accurately predict a molecule's solubility represents potentially large financial savings in many chemical product development processes, such as pharmaceuticals.[31] In the pharmaceutical industry, solubility predictions form part of the early stage lead optimisation process of drug candidates. Solubility remains a concern all the way to formulation.[31] A number of methods have been applied to such predictions including quantitative structure–activity relationships (QSAR), quantitative structure–property relationships (QSPR) and data mining. These models provide efficient predictions of solubility and represent the current standard. The draw back such models is that they can lack physical insight. A method founded in physical theory, capable of achieving similar levels of accuracy at an sensible cost, would be a powerful tool scientifically and industrially.[32][33][34][35]
Methods founded in physical theory tend to use thermodynamic cycles, a concept from classical thermodynamics. The two common thermodynamic cycles used involve either the calculation of the free energy of sublimation (solid to gas without going through a liquid state) and the free energy of solvating a gaseous molecule (gas to solution), or the free energy of fusion (solid to a molten phase) and the free energy of mixing (molten to solution). These two process are represented in the following diagrams.


These cycles have been used for attempts at first principles predictions (solving using the fundamental physical equations) using physically motivated solvent models,[33] to create parametric equations and QSPR models[36][34] and combinations of the two.[34] The use of these cycles enables the calculation of the solvation free energy indirectly via either gas (in the sublimation cycle) or a melt (fusion cycle). This is helpful as calculating the free energy of solvation directly is extremely difficult. The free energy of solvation can be converted to a solubility value using various formulae, the most general case being shown below, where the numerator is the free energy of solvation, R is the gas constant and T is the temperature in kelvins.[33]
Well known fitted equations for solubility prediction are the general solubility equations. These equations stem from the work of Yalkowsky et al.[37][38] The original formula is given first, followed by a revised formula which takes a different assumption of complete miscibility in octanol.[38]
These equations are founded on the principles of the fusion cycle.
See also
[edit]- Apparent molar property – Difference in properties of one mole of substance in a mixture vs. an ideal solution
- Biopharmaceutics Classification System – System to differentiate drugs on the basis of their solubility and permeability
- Dühring's rule – Rule in thermodynamics
- Fajans–Paneth–Hahn Law – Chemistry rule concerning co-precipitation and adsorption
- Flexible SPC water model – Aspect of computational chemistry
- Henry's law – Gas law regarding proportionality of dissolved gas
- Hot water extraction – Method of carpet cleaning
- Hydrotrope
- Micellar solubilization – Process of incorporating the solubilizate into or onto micelles
- Raoult's law – Law of thermodynamics for vapour pressure of a mixture
- Rate of solution – Capacity of a substance to dissolve in a homogeneous way
- Solubility equilibrium – Thermodynamic equilibrium between a solid and a solution of the same compound
- Van 't Hoff equation – Relation between temperature and the equilibrium constant of a chemical reaction
Notes
[edit]- ^ The solvent polarity is defined as its solvation power according to Reichardt.
References
[edit]- ^ a b IUPAC, Compendium of Chemical Terminology, 5th ed. (the "Gold Book") (2025). Online version: (2006–) "Solubility". doi:10.1351/goldbook.S05740
- ^ a b Clugston, M.; Fleming, R. (2000). Advanced Chemistry (1st ed.). Oxford: Oxford Publishing. p. 108.
- ^ J. de Swaan Arons and G. A. M. Diepen (1966): "Gas—Gas Equilibria". Journal of Chemical Physics, volume 44, issue 6, page 2322. doi:10.1063/1.1727043
- ^ Tomlinson, Charles (1868-01-01). "On Supersaturated Saline Solutions". Philosophical Transactions of the Royal Society of London. 158: 659–673. doi:10.1098/rstl.1868.0028. ISSN 0261-0523. S2CID 110079029.
- ^ Claudius Kormann, Detlef W. Bahnemann, and Michael R. Hoffmann (1988): "Preparation and characterization of quantum-size titanium dioxide". Journal of Physical Chemistry,volume 92, issue 18, pages 5196–5201. doi:10.1021/j100329a027
- ^ Abler (2021): "W/W (Weight/Weight)". Online page at Abler Help Center. Accessed on 2021-11-26.
- ^ I. Lee and J. Lee (2012): "Measurement of mixing ratio and volume change of ethanol-water binary mixtures using suspended microchannel resonators". SENSORS, volume 2012, pages 1-3. doi:10.1109/ICSENS.2012.6411272.
- ^ "Pharmacopeia of the United States of America, 32nd revision, and the National Formulary, 27th edition", 2009, pp.1 to 12.
- ^ Rogers, Elizabeth; Stovall, Iris (2000). "Fundamentals of Chemistry: Solubility". Department of Chemistry. University of Wisconsin. Archived from the original on 13 April 2015. Retrieved 22 April 2015.
- ^ I.Y. Nekrasov (1996). Geochemistry, Mineralogy and Genesis of Gold Deposits. Taylor & Francis. pp. 135–136. ISBN 978-90-5410-723-1.
- ^ Hefter, G. T.; Tomkins, R. P. T., eds. (2003). The Experimental Determination of Solubilities. Wiley-Blackwell. ISBN 978-0-471-49708-0.
- ^ a b John W. Hill, Ralph H. Petrucci, General Chemistry, 2nd edition, Prentice Hall, 1999.
- ^ P. Cohen, ed. (1989). The ASME Handbook on Water Technology for Thermal Power Systems. The American Society of Mechanical Engineers. p. 442.
- ^ Handbook of Chemistry and Physics (27th ed.). Cleveland, Ohio: Chemical Rubber Publishing Co. 1943.
- ^ "What substances, such as cerium sulfate, have a lower solubility when they are heated?". Scientific American. Retrieved 28 May 2014.
- ^ Salvatore Filippone, Frank Heimanna and André Rassat (2002). "A highly water-soluble 2+1 b-cyclodextrin–fullerene conjugate". Chem. Commun. 2002 (14): 1508–1509. doi:10.1039/b202410a. PMID 12189867.
- ^ E.M. Gutman (1994). Mechanochemistry of Solid Surfaces. World Scientific Publishing Co.
- ^ G.W. Greenwood (1969). "The Solubility of Gas Bubbles". Journal of Materials Science. 4 (4): 320–322. Bibcode:1969JMatS...4..320G. doi:10.1007/BF00550401. S2CID 93098036.
- ^ Kenneth J. Williamson (1994). Macroscale and Microscale Organic Experiments (2nd ed.). Lexington, Massachusetts: D. C, Heath. p. 40. ISBN 978-0-669-19429-6.
- ^ Merck Index (7th ed.). Merck & Co. 1960.
- ^ Dokoumetzidis, Aristides; Macheras, Panos (2006). "A century of dissolution research: From Noyes and Whitney to the Biopharmaceutics Classification System". Int. J. Pharm. 321 (1–2): 1–11. doi:10.1016/j.ijpharm.2006.07.011. PMID 16920290.
- ^ El-Mansy, Mohamed & Yahia, Ibrahim S. & Alfaify, Sa. (2015). Conformational and Vibrational Properties of Indigo Dye: DFT Approach. Organo Opto-Electronics An International Journal. 3. 1-9.
- ^ C. Houk; R. Post, eds. (1997). Chemistry, Concept and Problems. John Wiley & Sons. p. 121. ISBN 978-0-471-12120-6.
- ^ Wood, Maxwell; Toriyama, Michael; Dugar, Shristi; Male, James; Anand, Shashwat; Stevanović, Vladan; Snyder, Jeff (2020). "Phase Boundary Mapping of Tin-Doped ZnSb Reveals Thermodynamic Route to High Thermoelectric Efficiency". Advanced Energy Materials. 11 (20). doi:10.1002/aenm.202100181. S2CID 234807088.
- ^ Tang, Yinglu; Hanus, Riley; Chen, Sin-wen; Snyder, Jeff (2015). "Solubility design leading to high figure of merit in low-cost Ce-CoSb3 skutterudites". Nature Communications. 6 (7584): 7584. Bibcode:2015NatCo...6.7584T. doi:10.1038/ncomms8584. PMC 4518255. PMID 26189943.
- ^ Anand, Shashwat; Wolverton, Chris; Snyder, Jeff (2022). "Thermodynamic Guidelines for Maximum Solubility". Chemistry of Materials. 34 (4): 1638–1648. doi:10.1021/acs.chemmater.1c03715. S2CID 246516386.
- ^ O.M. Saether; P. de Caritat, eds. (1997). Geochemical processes, weathering and groundwater recharge in catchments. Rotterdam: Taylor & Francis. p. 6. ISBN 978-90-5410-641-8.
- ^ Skyner, R.; McDonagh, J. L.; Groom, C. R.; van Mourik, T.; Mitchell, J. B. O. (2015). "A Review of Methods for the Calculation of Solution Free Energies and the Modelling of Systems in Solution" (PDF). Phys Chem Chem Phys. 17 (9): 6174–91. Bibcode:2015PCCP...17.6174S. doi:10.1039/C5CP00288E. PMID 25660403.
- ^ Tomasi, J.; Mennucci, B.; Cammi, R. (2005). "Quantum Mechanical Continuum Solvation Models". Chemical Reviews. 105 (8): 2999–3093. doi:10.1021/cr9904009. PMID 16092826.
- ^ Cramer, C. J.; Truhlar, D. G. (1999). "Implicit Solvation Models: Equilibria, Structure, Spectra, and Dynamics". Chemical Reviews. 99 (8): 2161–2200. doi:10.1021/cr960149m. PMID 11849023.
- ^ a b Abramov, Y. A. (2015). "Major Source of Error in QSPR Prediction of Intrinsic Thermodynamic Solubility of Drugs: Solid vs Nonsolid State Contributions?". Molecular Pharmaceutics. 12 (6): 2126–2141. doi:10.1021/acs.molpharmaceut.5b00119. PMID 25880026.
- ^ McDonagh, J. L. (2015). Computing the Aqueous solubility of Organic Drug-Like Molecules and Understanding Hydrophobicity (Thesis). University of St Andrews. hdl:10023/6534.
- ^ a b c Palmer, D. S.; McDonagh, J. L.; Mitchell, J. B. O.; van Mourik, T.; Fedorov, M. V. (2012). "First-Principles Calculation of the Intrinsic Aqueous Solubility of Crystalline Druglike Molecules". Journal of Chemical Theory and Computation. 8 (9): 3322–3337. doi:10.1021/ct300345m. hdl:10023/25470. PMID 26605739. S2CID 26334468.
- ^ a b c McDonagh, J. L.; Nath, N.; De Ferrari, L.; van Mourik, T.; Mitchell, J. B. O. (2014). "Uniting Cheminformatics and Chemical Theory To Predict the Intrinsic Aqueous Solubility of Crystalline Druglike Molecules". Journal of Chemical Information and Modeling. 54 (3): 844–856. doi:10.1021/ci4005805. PMC 3965570. PMID 24564264.
- ^ Lusci, A.; Pollastri, G.; Baldi, P. (2013). "Deep Architectures and Deep Learning in Chemoinformatics: The Prediction of Aqueous Solubility for Drug-Like Molecules". Journal of Chemical Information and Modeling. 53 (7): 1563–1575. doi:10.1021/ci400187y. PMC 3739985. PMID 23795551.
- ^ Ran, Y.; N. Jain; S.H. Yalkowsky (2001). "Prediction of Aqueous Solubility of Organic Compounds by the General Solubility Equation (GSE)". Journal of Chemical Information and Modeling. 41 (5): 1208–1217. doi:10.1021/ci010287z. PMID 11604020.
- ^ Yalkowsky, S.H.; Valvani, S.C. (1980). "Solubility and partitioning I: solubility of nonelectrolytes in water". Journal of Pharmaceutical Sciences. 69 (8): 912–922. doi:10.1002/jps.2600690814. PMID 7400936.
- ^ a b Jain, N.; Yalkowsky, S.H. (2001). "Estimation of the aqueous solubility I: application to organic nonelectrolytes". Journal of Pharmaceutical Sciences. 90 (2): 234–252. doi:10.1002/1520-6017(200102)90:2<234::aid-jps14>3.0.co;2-v. PMID 11169540.
External links
[edit]Solubility
View on GrokipediaFundamentals of Solubility
Definition and Basic Principles
Solubility refers to the maximum amount of a solute that can dissolve in a given quantity of solvent under specified conditions of temperature, pressure, and composition, resulting in the formation of a saturated solution where the solution is in dynamic equilibrium with any undissolved solute. This property is fundamental to understanding solution formation and is expressed quantitatively as the analytical composition of the saturated solution, often in terms of concentration, mass per volume, or mole fraction.[1] The process of dissolution represents a physical equilibrium, in which the rate of solute particles entering the solution equals the rate at which they crystallize out, maintaining a constant solute concentration once saturation is reached./Equilibria/Solubilty/Solubility_and_Factors_Affecting_Solubility) The concept of solubility has evolved through historical observations and formal definitions. Early insights into gas solubility were provided by English chemist William Henry in the early 19th century, who through systematic experiments demonstrated the proportional relationship between gas pressure and its solubility in liquids, laying groundwork for later quantitative studies.[9] Over time, these empirical foundations led to modern standardization by the International Union of Pure and Applied Chemistry (IUPAC), which defines solubility precisely to account for diverse solute-solvent systems and conditions, ensuring consistency in scientific communication and application.[1] To describe the extent of solubility, qualitative terms are commonly used based on approximate thresholds in grams of solute per 100 mL of solvent at standard conditions: substances are considered soluble if exceeding 1 g/100 mL, sparingly soluble if between 0.1 and 1 g/100 mL, and insoluble if less than 0.1 g/100 mL.[10] [11] For instance, sodium chloride (NaCl) exemplifies high solubility in water, dissolving at about 36 g/100 mL at 25°C, enabling its widespread use in aqueous solutions.[12] In contrast, silver chloride (AgCl) is insoluble, with a solubility of only approximately 0.00019 g/100 mL at 25°C, which underlies its precipitation in qualitative analysis.[13] These qualifiers help predict behavior in chemical processes without requiring exact measurements.Molecular View of Dissolution
The dissolution of a solute in a solvent occurs at the molecular level through the process of solvation, where solute particles are surrounded and stabilized by solvent molecules, forming new intermolecular interactions that replace the original solute-solute attractions.[14] For ionic solutes in polar solvents like water, this involves strong ion-dipole forces, in which the partial charges on the solvent molecules align with the full charges on the ions, effectively pulling them apart from the solid lattice.[15] In cases of non-ionic solutes, weaker van der Waals forces or dipole-dipole interactions may contribute to solvation, facilitating the integration of the solute into the solvent structure.[14] A key aspect of dissolution is the energy balance between breaking solute-solute bonds and forming solute-solvent bonds; for ionic solids, this pits the lattice energy—the energy required to separate ions in the crystal—against the hydration energy released when ions interact with water molecules.[16] If the hydration energy sufficiently offsets the lattice energy, the process becomes energetically favorable, though the overall spontaneity depends on the Gibbs free energy change, given by where represents the enthalpy change (primarily from net energy shifts in bond breaking and forming), is the entropy change (reflecting increased disorder from dispersing solute particles), and is the absolute temperature.[17] Negative indicates a spontaneous dissolution, with entropy often playing a crucial role in overcoming any endothermic enthalpy contributions.[17] In the solvation shell, or solvent cage, solvent molecules form a structured layer around the solute, dynamically orienting to maximize favorable interactions; for example, water molecules arrange with their oxygen atoms facing Na ions and hydrogen atoms toward Cl ions, creating a hydration sphere that stabilizes the ions in solution.[18] This cage formation enhances solubility by isolating solute particles and preventing recombination, while the solvent's polarity is essential, as it enables the "like dissolves like" principle where solutes with similar intermolecular forces to the solvent are more readily solvated.[19]Quantification of Solubility
Measures per Solvent or Solution
Solubility is often quantified relative to the amount of solvent used, providing a measure independent of the total solution volume. One common expression is grams of solute per 100 grams of solvent (g/100 g), which directly indicates the mass ratio and is particularly useful for comparing solubilities across different solvents without considering density variations. Another key unit is molality (m), defined as the number of moles of solute per kilogram of solvent, which normalizes concentrations based on solvent mass and remains constant despite changes in solution volume. For instance, the solubility of potassium nitrate (KNO₃) in water at 25°C is approximately 38 g per 100 g of water, highlighting its high solubility in this metric.[20] In contrast, measures expressed per quantity of solution account for the total mixture and are suited for volumetric analyses or reactions in fixed volumes. Grams of solute per 100 milliliters of solution (g/100 mL) is a practical unit for laboratory preparations, as it aligns with common measurement tools like pipettes and reflects the density of the solution implicitly.[19] Molarity (M), or moles of solute per liter of solution, facilitates stoichiometric calculations in chemical reactions, while mole fraction (X), the ratio of moles of solute to total moles in the solution, offers a dimensionless scale ideal for thermodynamic discussions. The same KNO₃ solubility at 25°C corresponds to approximately 35 g/100 mL of solution, though exact values depend on whether expressed per solvent mass or solution volume. This approximation holds better for dilute systems where solution density ≈1 g/mL.[20] Each unit has specific advantages depending on the context; for example, molality is preferred for colligative properties like boiling point elevation because it is unaffected by temperature-induced volume changes, unlike molarity, which varies with solution density.[3] Mole fraction, meanwhile, simplifies Raoult's law applications by being independent of the solvent's mass or volume. For ionic compounds, saturation equilibrium is conceptually bounded by the solubility product constant (Ksp), an equilibrium constant that equals the product of ion concentrations (in moles per liter) raised to their stoichiometric powers in a saturated solution.[21] This value serves as a limit indicating the maximum solubility under ideal conditions, with lower Ksp values signifying poorer solubility, though it applies primarily to sparingly soluble salts and assumes no common ion effects or complex formations.[21]Handling Liquid and Gaseous Solutes
Liquid solutes are handled differently in solubility quantification due to their fluid nature, which allows for complete miscibility or partial mixing without the need to disrupt a rigid structure. Miscibility refers to the ability of two or more liquids to form a homogeneous solution in all proportions, as seen in the ethanol-water system where polar interactions enable full dissolution.[22] In contrast, limited solubility occurs when liquids do not mix completely, such as oil and water, where nonpolar hydrocarbons separate into distinct layers due to unfavorable interactions.[22] Common units for expressing the solubility of liquid solutes include volume percent (v/v), defined as the volume of solute per 100 volumes of solution, and mole fraction, which represents the ratio of moles of solute to total moles in the mixture.[19][23] Gaseous solutes are quantified primarily through their equilibrium distribution between the gas phase and the liquid solvent, often expressed in volume/volume (V/V) terms or as a function of partial pressure. Henry's law provides the fundamental relationship, stating that at constant temperature, the solubility of a gas in a liquid is directly proportional to the partial pressure of the gas above the liquid: where is the Henry's law constant, which varies with temperature and the gas-solvent pair.[24] This constant can be expressed in units such as atm/mol or mol/(L·atm), allowing conversion between concentration and pressure.[25] A practical example is the dissolution of carbon dioxide (CO₂) in carbonated beverages, where high pressure during bottling increases , dissolving CO₂ to create fizz upon opening as pressure drops and the gas escapes.[26] Unlike solid solutes, which require energy to overcome lattice energy for dissolution, liquid and gaseous solutes lack a crystalline lattice, so their solubility emphasizes equilibrium partitioning driven by intermolecular forces and phase distribution.[27][28] This partitioning reflects a dynamic balance where the solute distributes between phases based on solubility parameters, without the enthalpic barrier of lattice disruption characteristic of solids.[29]Unit Conversions and Equivalents
Converting between different units of solubility is essential for comparing data across scientific literature, engineering applications, and regulatory standards, as solubility is often reported in context-specific formats such as mass per mass, moles per volume, or mole fractions.[30] Common conversions involve transforming molality (moles of solute per kilogram of solvent) to molarity (moles of solute per liter of solution) or mass-based units like grams of solute per 100 grams of solvent to mole fraction. These transformations require knowledge of molar masses, solution densities, and sometimes approximations for dilute solutions.[31] The conversion from molality to molarity accounts for the volume of the solution, which depends on the solvent's density and the solute's contribution to the total mass. For dilute aqueous solutions, an approximation is M ≈ m (since 1 kg water ≈ 1 L). For more accurate results, especially in concentrated solutions, the full calculation uses the actual solution density (): where is molarity in mol/L, is molality in mol/kg, is solution density in g/mL, and is the molar mass of the solute in g/mol. This incorporates the total mass and volume of the solution.[31] Similarly, converting from grams of solute per 100 grams of solvent (g/100 g) to mole fraction () involves calculating the moles of each component. The mole fraction of the solute is given by: where and are the moles of solute and solvent, respectively, determined from their masses and molar masses. For example, if 36 g of solute is dissolved in 100 g of solvent, divide each mass by the appropriate molar mass to find the moles, then apply the formula.[30] A practical example is the solubility of sodium chloride (NaCl) in water at 25°C, reported as 36 g NaCl per 100 g water.[12] First, convert to molality: moles of NaCl = 36 g / 58.44 g/mol ≈ 0.616 mol; molality = 0.616 mol / 0.100 kg = 6.16 m. To find molarity, note the total mass of solution = 136 g and density of the saturated solution ≈ 1.202 g/mL, so volume ≈ 136 g / 1.202 g/mL ≈ 0.113 L; thus, ≈ 0.616 mol / 0.113 L ≈ 5.4 M.[12] This conversion highlights the need for solution density, which is often assumed as 1 g/mL for dilute cases but leads to errors in concentrated solutions like this one.[32] In different systems, particularly for trace solubilities, parts per million (ppm) is widely used, defined as milligrams of solute per kilogram of solution (or equivalently, g/g for mass basis). This unit is common in environmental contexts, such as assessing pollutant solubility in water bodies, where concentrations below 1 mg/L (≈ 1 ppm assuming density ≈ 1 g/mL) indicate trace levels.[33] For instance, the solubility of sparingly soluble salts like lead(II) sulfate in natural waters is often expressed in ppm to evaluate environmental risks.[34] Errors in unit conversions can arise from variations in temperature and solution density, which affect both the reported solubility and the conversion factors. Solubility itself often changes with temperature (e.g., increasing for most solids in water), and density decreases as temperature rises, potentially introducing up to 5-10% error in molarity calculations if not adjusted.[35] For precise work, use temperature-specific density values and re-evaluate solubility data at the exact conditions.[36]Factors Influencing Solubility
Temperature Dependence
The solubility of solid solutes in liquid solvents generally varies with temperature, depending on whether the dissolution process is endothermic or exothermic. In endothermic dissolution, where the process absorbs heat, solubility increases as temperature rises, shifting the equilibrium toward greater dissolution to absorb the added thermal energy. For instance, the solubility of potassium nitrate (KNO₃) in water exemplifies this trend, increasing from about 13 g per 100 mL at 0°C to 247 g per 100 mL at 100°C.[37] Conversely, exothermic dissolution releases heat, leading to decreased solubility with increasing temperature as the system shifts to counteract the added heat by favoring the undissolved state. Calcium hydroxide (Ca(OH)₂) in water demonstrates this behavior, with solubility dropping from 0.173 g per 100 mL at 20°C to 0.066 g per 100 mL at 100°C. This temperature dependence can be understood through Le Chatelier's principle, which predicts that the equilibrium position will adjust to minimize changes in conditions. For dissolution, the process is treated as a reversible equilibrium: solute(s) ⇌ solute(aq) + heat (for exothermic) or solute(s) + heat ⇌ solute(aq) (for endothermic). Increasing temperature thus drives endothermic equilibria forward, enhancing solubility, while opposing exothermic ones, reducing it./Equilibria/Solubilty/Temperature_Effects_on_Solubility) Quantitatively, the relationship between temperature and solubility is described by the van't Hoff equation, derived from the temperature dependence of the equilibrium constant (here, related to the solubility product or saturation concentration). The equation is: where is the enthalpy change of dissolution, is the gas constant, and is the absolute temperature. Integrating this form allows prediction of how solubility varies with temperature, assuming is constant; a positive (endothermic) yields increasing with , while negative (exothermic) yields decreasing ./26%3A_Chemical_Equilibrium/26.07%3A_The_van_%27t_Hoff_Equation) Exceptions to these patterns occur, particularly with hydrated salts undergoing phase transitions. For example, sodium sulfate decahydrate (Na₂SO₄·10H₂O) exhibits retrograde solubility above approximately 32°C, where its solubility peaks and then slightly decreases due to dehydration and transition to the anhydrous form, altering the effective dissolution thermodynamics.Pressure Effects
The solubility of gases in liquids is significantly influenced by pressure, as described by Henry's law, which states that at constant temperature, the solubility of a gas in a liquid is directly proportional to the partial pressure of the gas above the liquid:where is the Henry's law constant, typically expressed in units such as mol/L/atm or mol/L/bar.[38] This relationship arises from the increased frequency of gas molecule collisions with the liquid surface under higher pressure, leading to greater dissolution until equilibrium is reached./Physical_Properties_of_Matter/Solutions_and_Mixtures/Ideal_Solutions/Dissolving_Gases_In_Liquids_Henrys_Law) For instance, the solubility of oxygen in human blood, which follows Henry's law, approximately doubles when the total pressure increases from 1 atm to 2 atm, assuming the partial pressure of oxygen also doubles in compressed air; this enhances oxygen delivery but is limited by blood's low baseline solubility of about 0.003 mL O₂/100 mL blood/mm Hg at 37°C.[39] Henry's law constants for common gases vary widely; for oxygen in water at 25°C, is approximately 0.0013 mol/L/atm, while for carbon dioxide it is higher at 0.034 mol/L/atm, reflecting differences in gas-liquid interactions.[40] In contrast, the solubility of liquids in liquids and solids in liquids exhibits minimal dependence on pressure under normal conditions, due to the low compressibility of these phases, which results in negligible changes in molar volume during dissolution./13:_Solutions/13.04:_Effects_of_Temperature_and_Pressure_on_Solubility) However, under extreme pressures, such as those encountered in deep-sea environments (up to several hundred atm) or industrial high-pressure processes, solubility of solids can increase slightly if the partial molar volume of the solute in solution is less than in the solid phase, as predicted by thermodynamic relations.[41] A practical application of pressure effects on gas solubility is in scuba diving, where increased ambient pressure at depth raises the solubility of nitrogen in blood and tissues according to Henry's law; upon rapid ascent and pressure reduction, dissolved nitrogen forms bubbles, potentially causing decompression sickness if not managed through staged decompression stops.[42]
























