Three-dimensional space

Books XI to XIII of Euclid's Elements dealt with three-dimensional geometry. Book XI develops notions of perpendicularity and parallelism of lines and planes, and defines solids including parallelepipeds, pyramids, prisms, spheres, octahedra, icosahedra and dodecahedra. Book XII develops notions of similarity of solids. Book XIII describes the construction of the five regular Platonic solids in a sphere.

In the 17th century, three-dimensional space was described with Cartesian coordinates, with the advent of analytic geometry developed by René Descartes in his work La Géométrie and Pierre de Fermat in the manuscript Ad locos planos et solidos isagoge (Introduction to Plane and Solid Loci), which was unpublished during Fermat's lifetime. However, only Fermat's work dealt with three-dimensional space.

In the 19th century, developments of the geometry of three-dimensional space came with William Rowan Hamilton's development of the quaternions. In fact, it was Hamilton who coined the terms scalar and vector, and they were first defined within his geometric framework for quaternions. Three dimensional space could then be described by quaternions ${\displaystyle q=a+ui+vj+wk}$ which had vanishing scalar component, that is, ${\displaystyle a=0}$. While not explicitly studied by Hamilton, this indirectly introduced notions of basis, here given by the quaternion elements ${\displaystyle i,j,k}$, as well as the dot product and cross product, which correspond to (the negative of) the scalar part and the vector part of the product of two vector quaternions.

It was not until Josiah Willard Gibbs that these two products were identified in their own right, and the modern notation for the dot and cross product were introduced in his classroom teaching notes, found also in the 1901 textbook Vector Analysis written by Edwin Bidwell Wilson based on Gibbs' lectures.

Also during the 19th century came developments in the abstract formalism of vector spaces, with the work of Hermann Grassmann and Giuseppe Peano, the latter of whom first gave the modern definition of vector spaces as an algebraic structure.

Geometry
Projecting a sphere to a plane
Branches Euclidean Non-Euclidean Elliptic Spherical Hyperbolic Non-Archimedean geometry Projective Affine Synthetic Analytic Algebraic Arithmetic Diophantine Differential Riemannian Symplectic Discrete differential Complex Finite Discrete/Combinatorial Digital Convex Computational Fractal Incidence Noncommutative geometry Noncommutative algebraic geometry
Concepts Features Dimension Straightedge and compass constructions Angle Curve Diagonal Orthogonality (Perpendicular) Parallel Vertex Congruence Similarity Symmetry
Zero-dimensional Point
One-dimensional Line segment ray Curve Length
Two-dimensional Surface Plane Area Polygon Triangle Altitude Hypotenuse Pythagorean theorem Quadrilateral Parallelogram Square Rectangle Rhombus Rhomboid Trapezoid Kite Circle Diameter Circumference Area
Three-dimensional Volume Polyhedron Platonic Solid Tetrahedron cuboid Cube Octahedron Dodecahedron Icosahedron Pyramid Solid of revolution Sphere Cylinder Cone
Four-/other-dimensional Tesseract Hypersphere
Geometers
by name Aida Aryabhata Ahmes Alhazen Apollonius Archimedes Atiyah Baudhayana Bolyai Brahmagupta Cartan Chern Coxeter Descartes Euclid Euler Gauss Gromov Hilbert Huygens Jyeṣṭhadeva Kātyāyana Khayyám Klein Lobachevsky Manava Minkowski Minggatu Pascal Pythagoras Parameshvara Poincaré Riemann Sakabe Sijzi al-Tusi Veblen Virasena Yang Hui al-Yasamin Zhang List of geometers
by period BCE Ahmes Baudhayana Manava Pythagoras Euclid Archimedes Apollonius 1–1400s Zhang Kātyāyana Aryabhata Brahmagupta Virasena Alhazen Sijzi Khayyám al-Yasamin al-Tusi Yang Hui Parameshvara 1400s–1700s Jyeṣṭhadeva Descartes Pascal Huygens Minggatu Euler Sakabe Aida 1700s–1900s Gauss Lobachevsky Bolyai Riemann Klein Poincaré Hilbert Minkowski Cartan Veblen Coxeter Chern Present day Atiyah Gromov
v t e

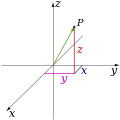
In mathematics, analytic geometry (also called Cartesian geometry) describes every point in three-dimensional space by means of three coordinates. Three coordinate axes are given, each perpendicular to the other two at the origin, the point at which they cross. They are usually labeled x, y, and z. Relative to these axes, the position of any point in three-dimensional space is given by an ordered triple of real numbers, each number giving the distance of that point from the origin measured along the given axis, which is equal to the distance of that point from the plane determined by the other two axes.^[5]

Other popular methods of describing the location of a point in three-dimensional space include cylindrical coordinates and spherical coordinates, though there are an infinite number of possible methods. For more, see Euclidean space.

Below are images of the above-mentioned systems.

• 
  Cartesian coordinate system
• 
  Cylindrical coordinate system
• 
  Spherical coordinate system

Two distinct points always determine a (straight) line. Three distinct points are either collinear or determine a unique plane. On the other hand, four distinct points can either be collinear, coplanar, or determine the entire space.

Two distinct lines can either intersect, be parallel or be skew. Two parallel lines, or two intersecting lines, lie in a unique plane, so skew lines are lines that do not meet and do not lie in a common plane.

Two distinct planes can either meet in a common line or are parallel (i.e., do not meet). Three distinct planes, no pair of which are parallel, can either meet in a common line, meet in a unique common point, or have no point in common. In the last case, the three lines of intersection of each pair of planes are mutually parallel.

A line can lie in a given plane, intersect that plane in a unique point, or be parallel to the plane. In the last case, there will be lines in the plane that are parallel to the given line.

A hyperplane is a subspace of one dimension less than the dimension of the full space. The hyperplanes of a three-dimensional space are the two-dimensional subspaces, that is, the planes. In terms of Cartesian coordinates, the points of a hyperplane satisfy a single linear equation, so planes in this 3-space are described by linear equations. A line can be described by a pair of independent linear equations—each representing a plane having this line as a common intersection.

Varignon's theorem states that the midpoints of any quadrilateral in ${\displaystyle \mathbb {R} ^{3}}$ form a parallelogram, and hence are coplanar.

A sphere in 3-space (also called a 2-sphere because it is a 2-dimensional object) consists of the set of all points in 3-space at a fixed distance r from a central point P. The solid enclosed by the sphere is called a ball (or, more precisely a 3-ball).

The volume of the ball is given by

$${\displaystyle V={\frac {4}{3}}\pi r^{3},}$$ and the surface area of the sphere is $${\displaystyle A=4\pi r^{2}.}$$ Another type of sphere arises from a 4-ball, whose three-dimensional surface is the 3-sphere: points equidistant to the origin of the euclidean space R⁴. If a point has coordinates, P(x, y, z, w), then x² + y² + z² + w² = 1 characterizes those points on the unit 3-sphere centered at the origin.

This 3-sphere is an example of a 3-manifold: a space which is 'looks locally' like 3-D space. In precise topological terms, each point of the 3-sphere has a neighborhood which is homeomorphic to an open subset of 3-D space.

In three dimensions, there are nine regular polytopes: the five convex Platonic solids and the four nonconvex Kepler-Poinsot polyhedra.

Regular polytopes in three dimensions

Class	Platonic solids					Kepler-Poinsot polyhedra
Symmetry	Td	Oh		Ih
Coxeter group	A3, [3,3]	B3, [4,3]		H3, [5,3]
Order	24	48		120
Regular polyhedron	{3,3}	{4,3}	{3,4}	{5,3}	{3,5}	{5/2,5}	{5,5/2}	{5/2,3}	{3,5/2}

A surface generated by revolving a plane curve about a fixed line in its plane as an axis is called a surface of revolution. The plane curve is called the generatrix of the surface. A section of the surface, made by intersecting the surface with a plane that is perpendicular (orthogonal) to the axis, is a circle.

Simple examples occur when the generatrix is a line. If the generatrix line intersects the axis line, the surface of revolution is a right circular cone with vertex (apex) the point of intersection. However, if the generatrix and axis are parallel, then the surface of revolution is a circular cylinder.

In analogy with the conic sections, the set of points whose Cartesian coordinates satisfy the general equation of the second degree, namely, $${\displaystyle Ax^{2}+By^{2}+Cz^{2}+Fxy+Gyz+Hxz+Jx+Ky+Lz+M=0,}$$ where A, B, C, F, G, H, J, K, L and M are real numbers and not all of A, B, C, F, G and H are zero, is called a quadric surface.^[6]

There are six types of non-degenerate quadric surfaces:

1. Ellipsoid
2. Hyperboloid of one sheet
3. Hyperboloid of two sheets
4. Elliptic cone
5. Elliptic paraboloid
6. Hyperbolic paraboloid

The degenerate quadric surfaces are the empty set, a single point, a single line, a single plane, a pair of planes or a quadratic cylinder (a surface consisting of a non-degenerate conic section in a plane π and all the lines of R³ through that conic that are normal to π).^[6] Elliptic cones are sometimes considered to be degenerate quadric surfaces as well.

Both the hyperboloid of one sheet and the hyperbolic paraboloid are ruled surfaces, meaning that they can be made up from a family of straight lines. In fact, each has two families of generating lines, the members of each family are disjoint and each member one family intersects, with just one exception, every member of the other family.^[7] Each family is called a regulus.

Another way of viewing three-dimensional space is found in linear algebra, where the idea of independence is crucial. Space has three dimensions because the length of a box is independent of its width or breadth. In the technical language of linear algebra, space is three-dimensional because every point in space can be described by a linear combination of three independent vectors.

A vector can be pictured as an arrow. The vector's magnitude is its length, and its direction is the direction the arrow points. A vector in ${\displaystyle \mathbb {R} ^{3}}$ can be represented by an ordered triple of real numbers. These numbers are called the components of the vector.

The dot product of two vectors A = [A₁, A₂, A₃] and B = [B₁, B₂, B₃] is defined as:^[8]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =A_{1}B_{1}+A_{2}B_{2}+A_{3}B_{3}=\sum _{i=1}^{3}A_{i}B_{i}.}$

The magnitude of a vector A is denoted by ||A||. The dot product of a vector A = [A₁, A₂, A₃] with itself is

${\displaystyle \mathbf {A} \cdot \mathbf {A} =\|\mathbf {A} \|^{2}=A_{1}^{2}+A_{2}^{2}+A_{3}^{2},}$

which gives

${\displaystyle \|\mathbf {A} \|={\sqrt {\mathbf {A} \cdot \mathbf {A} }}={\sqrt {A_{1}^{2}+A_{2}^{2}+A_{3}^{2}}},}$

the formula for the Euclidean length of the vector.

Without reference to the components of the vectors, the dot product of two non-zero Euclidean vectors A and B is given by^[9]

${\displaystyle \mathbf {A} \cdot \mathbf {B} =\|\mathbf {A} \|\,\|\mathbf {B} \|\cos \theta ,}$

where θ is the angle between A and B.

The cross product or vector product is a binary operation on two vectors in three-dimensional space and is denoted by the symbol ×. The cross product A × B of the vectors A and B is a vector that is perpendicular to both and therefore normal to the plane containing them. It has many applications in mathematics, physics, and engineering.

In function language, the cross product is a function ${\displaystyle \times :\mathbb {R} ^{3}\times \mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}}$.

The components of the cross product are ${\displaystyle \mathbf {A} \times \mathbf {B} =[A_{2}B_{3}-B_{2}A_{3},A_{3}B_{1}-B_{3}A_{1},A_{1}B_{2}-B_{1}A_{2}]}$, and can also be written in components, using Einstein summation convention as ${\displaystyle (\mathbf {A} \times \mathbf {B} )_{i}=\varepsilon _{ijk}A_{j}B_{k}}$ where ${\displaystyle \varepsilon _{ijk}}$ is the Levi-Civita symbol. It has the property that ${\displaystyle \mathbf {A} \times \mathbf {B} =-\mathbf {B} \times \mathbf {A} }$.

Its magnitude is related to the angle ${\displaystyle \theta }$ between ${\displaystyle \mathbf {A} }$ and ${\displaystyle \mathbf {B} }$ by the identity $${\displaystyle \left\|\mathbf {A} \times \mathbf {B} \right\|=\left\|\mathbf {A} \right\|\cdot \left\|\mathbf {B} \right\|\cdot \left|\sin \theta \right|.}$$

The space and product form an algebra over a field, which is not commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket. Specifically, the space together with the product, ${\displaystyle (\mathbb {R} ^{3},\times )}$ is isomorphic to the Lie algebra of three-dimensional rotations, denoted ${\displaystyle {\mathfrak {so}}(3)}$. In order to satisfy the axioms of a Lie algebra, instead of associativity the cross product satisfies the Jacobi identity. For any three vectors ${\displaystyle \mathbf {A} ,\mathbf {B} }$ and ${\displaystyle \mathbf {C} }$

$${\displaystyle \mathbf {A} \times (\mathbf {B} \times \mathbf {C} )+\mathbf {B} \times (\mathbf {C} \times \mathbf {A} )+\mathbf {C} \times (\mathbf {A} \times \mathbf {B} )=0}$$

One can in n dimensions take the product of n − 1 vectors to produce a vector perpendicular to all of them. But if the product is limited to non-trivial binary products with vector results, it exists only in three and seven dimensions.^[10]

It can be useful to describe three-dimensional space as a three-dimensional vector space ${\displaystyle V}$ over the real numbers. This differs from ${\displaystyle \mathbb {R} ^{3}}$ in a subtle way. By definition, there exists a basis ${\displaystyle {\mathcal {B}}=\{e_{1},e_{2},e_{3}\}}$ for ${\displaystyle V}$. This corresponds to an isomorphism between ${\displaystyle V}$ and ${\displaystyle \mathbb {R} ^{3}}$: the construction for the isomorphism is found here. However, there is no 'preferred' or 'canonical basis' for ${\displaystyle V}$.

On the other hand, there is a preferred basis for ${\displaystyle \mathbb {R} ^{3}}$, which is due to its description as a Cartesian product of copies of ${\displaystyle \mathbb {R} }$, that is, ${\displaystyle \mathbb {R} ^{3}=\mathbb {R} \times \mathbb {R} \times \mathbb {R} }$. This allows the definition of canonical projections, ${\displaystyle \pi _{i}:\mathbb {R} ^{3}\rightarrow \mathbb {R} }$, where ${\displaystyle 1\leq i\leq 3}$. For example, ${\displaystyle \pi _{1}(x_{1},x_{2},x_{3})=x}$. This then allows the definition of the standard basis ${\displaystyle {\mathcal {B}}_{\text{Standard}}=\{E_{1},E_{2},E_{3}\}}$ defined by $${\displaystyle \pi _{i}(E_{j})=\delta _{ij}}$$ where ${\displaystyle \delta _{ij}}$ is the Kronecker delta. Written out in full, the standard basis is $${\displaystyle E_{1}={\begin{pmatrix}1\\0\\0\end{pmatrix}},E_{2}={\begin{pmatrix}0\\1\\0\end{pmatrix}},E_{3}={\begin{pmatrix}0\\0\\1\end{pmatrix}}.}$$

Therefore ${\displaystyle \mathbb {R} ^{3}}$ can be viewed as the abstract vector space, together with the additional structure of a choice of basis. Conversely, ${\displaystyle V}$ can be obtained by starting with ${\displaystyle \mathbb {R} ^{3}}$ and 'forgetting' the Cartesian product structure, or equivalently the standard choice of basis.

As opposed to a general vector space ${\displaystyle V}$, the space ${\displaystyle \mathbb {R} ^{3}}$ is sometimes referred to as a coordinate space.^[11]

Physically, it is conceptually desirable to use the abstract formalism in order to assume as little structure as possible if it is not given by the parameters of a particular problem. For example, in a problem with rotational symmetry, working with the more concrete description of three-dimensional space ${\displaystyle \mathbb {R} ^{3}}$ assumes a choice of basis, corresponding to a set of axes. But in rotational symmetry, there is no reason why one set of axes is preferred to say, the same set of axes which has been rotated arbitrarily. Stated another way, a preferred choice of axes breaks the rotational symmetry of physical space.

Computationally, it is necessary to work with the more concrete description ${\displaystyle \mathbb {R} ^{3}}$ in order to do concrete computations.

A more abstract description still is to model physical space as a three-dimensional affine space ${\displaystyle E(3)}$ over the real numbers. This is unique up to affine isomorphism. It is sometimes referred to as three-dimensional Euclidean space. Just as the vector space description came from 'forgetting the preferred basis' of ${\displaystyle \mathbb {R} ^{3}}$, the affine space description comes from 'forgetting the origin' of the vector space. Euclidean spaces are sometimes called Euclidean affine spaces for distinguishing them from Euclidean vector spaces.^[12]

This is physically appealing as it makes the translation invariance of physical space manifest. A preferred origin breaks the translational invariance.

The above discussion does not involve the dot product. The dot product is an example of an inner product. Physical space can be modelled as a vector space which additionally has the structure of an inner product. The inner product defines notions of length and angle (and therefore in particular the notion of orthogonality). For any inner product, there exist bases under which the inner product agrees with the dot product, but again, there are many different possible bases, none of which are preferred. They differ from one another by a rotation, an element of the group of rotations SO(3).

In a rectangular coordinate system, the gradient of a (differentiable) function ${\displaystyle f:\mathbb {R} ^{3}\rightarrow \mathbb {R} }$ is given by

${\displaystyle \nabla f={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} +{\frac {\partial f}{\partial z}}\mathbf {k} }$

and in index notation is written

$${\displaystyle (\nabla f)_{i}=\partial _{i}f.}$$

The divergence of a (differentiable) vector field F = U i + V j + W k, that is, a function ${\displaystyle \mathbf {F} :\mathbb {R} ^{3}\rightarrow \mathbb {R} ^{3}}$, is equal to the scalar-valued function:

${\displaystyle \operatorname {div} \,\mathbf {F} =\nabla \cdot \mathbf {F} ={\frac {\partial U}{\partial x}}+{\frac {\partial V}{\partial y}}+{\frac {\partial W}{\partial z}}.}$

In index notation, with Einstein summation convention this is $${\displaystyle \nabla \cdot \mathbf {F} =\partial _{i}F_{i}.}$$

Expanded in Cartesian coordinates (see Del in cylindrical and spherical coordinates for spherical and cylindrical coordinate representations), the curl ∇ × F is, for F composed of [F_x, F_y, F_z]:

${\displaystyle {\begin{vmatrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\\\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\\\F_{x}&F_{y}&F_{z}\end{vmatrix}}}$

where i, j, and k are the unit vectors for the x-, y-, and z-axes, respectively. This expands as follows:^[13]

${\displaystyle \left({\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\right)\mathbf {i} +\left({\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}\right)\mathbf {j} +\left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\right)\mathbf {k} .}$

In index notation, with Einstein summation convention this is $${\displaystyle (\nabla \times \mathbf {F} )_{i}=\epsilon _{ijk}\partial _{j}F_{k},}$$ where ${\displaystyle \epsilon _{ijk}}$ is the totally antisymmetric symbol, the Levi-Civita symbol.

For some scalar field f : U ⊆ Rⁿ → R, the line integral along a piecewise smooth curve C ⊂ U is defined as

${\displaystyle \int \limits _{C}f\,ds=\int _{a}^{b}f(\mathbf {r} (t))|\mathbf {r} '(t)|\,dt.}$

where r: [a, b] → C is an arbitrary bijective parametrization of the curve C such that r(a) and r(b) give the endpoints of C and ${\displaystyle a<b}$.

For a vector field F : U ⊆ Rⁿ → Rⁿ, the line integral along a piecewise smooth curve C ⊂ U, in the direction of r, is defined as

${\displaystyle \int \limits _{C}\mathbf {F} (\mathbf {r} )\cdot \,d\mathbf {r} =\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt.}$

where · is the dot product and r: [a, b] → C is a bijective parametrization of the curve C such that r(a) and r(b) give the endpoints of C.

A surface integral is a generalization of multiple integrals to integration over surfaces. It can be thought of as the double integral analog of the line integral. To find an explicit formula for the surface integral, we need to parameterize the surface of interest, S, by considering a system of curvilinear coordinates on S, like the latitude and longitude on a sphere. Let such a parameterization be x(s, t), where (s, t) varies in some region T in the plane. Then, the surface integral is given by

${\displaystyle \iint _{S}f\,\mathrm {d} S=\iint _{T}f(\mathbf {x} (s,t))\left\|{\partial \mathbf {x} \over \partial s}\times {\partial \mathbf {x} \over \partial t}\right\|\mathrm {d} s\,\mathrm {d} t}$

where the expression between bars on the right-hand side is the magnitude of the cross product of the partial derivatives of x(s, t), and is known as the surface element. Given a vector field v on S, that is a function that assigns to each x in S a vector v(x), the surface integral can be defined component-wise according to the definition of the surface integral of a scalar field; the result is a vector.

A volume integral is an integral over a three-dimensional domain or region. When the integrand is trivial (unity), the volume integral is simply the region's volume.^[14][1] It can also mean a triple integral within a region D in R³ of a function ${\displaystyle f(x,y,z),}$ and is usually written as:

${\displaystyle \iiint \limits _{D}f(x,y,z)\,dx\,dy\,dz.}$

The fundamental theorem of line integrals, says that a line integral through a gradient field can be evaluated by evaluating the original scalar field at the endpoints of the curve.

Let ${\displaystyle \varphi :U\subseteq \mathbb {R} ^{n}\to \mathbb {R} }$. Then

${\displaystyle \varphi \left(\mathbf {q} \right)-\varphi \left(\mathbf {p} \right)=\int _{\gamma [\mathbf {p} ,\,\mathbf {q} ]}\nabla \varphi (\mathbf {r} )\cdot d\mathbf {r} .}$

Stokes' theorem relates the surface integral of the curl of a vector field F over a surface Σ in Euclidean three-space to the line integral of the vector field over its boundary ∂Σ:

${\displaystyle \iint _{\Sigma }\nabla \times \mathbf {F} \cdot \mathrm {d} \mathbf {\Sigma } =\oint _{\partial \Sigma }\mathbf {F} \cdot \mathrm {d} \mathbf {r} .}$

Suppose V is a subset of ${\displaystyle \mathbb {R} ^{n}}$ (in the case of n = 3, V represents a volume in 3D space) which is compact and has a piecewise smooth boundary S (also indicated with ∂V = S). If F is a continuously differentiable vector field defined on a neighborhood of V, then the divergence theorem says:^[15]

${\displaystyle \iiint _{V}\left(\mathbf {\nabla } \cdot \mathbf {F} \right)\,dV=}$ ${\displaystyle \scriptstyle S}$ ${\displaystyle (\mathbf {F} \cdot \mathbf {n} )\,dS.}$

The left side is a volume integral over the volume V, the right side is the surface integral over the boundary of the volume V. The closed manifold ∂V is quite generally the boundary of V oriented by outward-pointing normals, and n is the outward pointing unit normal field of the boundary ∂V. (dS may be used as a shorthand for ndS.)

Three-dimensional space has a number of topological properties that distinguish it from spaces of other dimension numbers. For example, at least three dimensions are required to tie a knot in a piece of string.^[16]

In differential geometry the generic three-dimensional spaces are 3-manifolds, which locally resemble ${\displaystyle {\mathbb {R} }^{3}}$.

Many ideas of dimension can be tested with finite geometry. The simplest instance is PG(3,2), which has Fano planes as its 2-dimensional subspaces. It is an instance of Galois geometry, a study of projective geometry using finite fields. Thus, for any Galois field GF(q), there is a projective space PG(3,q) of three dimensions. For example, any three skew lines in PG(3,q) are contained in exactly one regulus.^[17]

• 3D rotation
  • Rotation formalisms in three dimensions
• Dimensional analysis
• Distance from a point to a plane
• Four-dimensional space
• Skew lines § Distance
• Three-dimensional graph
• Solid geometry
• Terms of orientation