Hubbry Logo
Atomic physicsAtomic physicsMain
Open search
Atomic physics
Community hub
Atomic physics
logo
7 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Atomic physics
Atomic physics
Atomic physics
View on Wikipedia
from Wikipedia
Modern physics

Schrödinger and Einstein field equations
Founders
Concepts
Branches
Scientists
Categories

Atomic physics is the field of physics that studies atoms as an isolated system of electrons and an atomic nucleus. Atomic physics typically refers to the study of atomic structure and the interaction between atoms.[1] It is primarily concerned with the way in which electrons are arranged around the nucleus and the processes by which these arrangements change. This comprises ions, neutral atoms and, unless otherwise stated, it can be assumed that the term atom includes ions.

The term atomic physics can be associated with nuclear power and nuclear weapons, due to the synonymous use of atomic and nuclear in standard English. Physicists distinguish between atomic physics—which deals with the atom as a system consisting of a nucleus and electrons—and nuclear physics, which studies nuclear reactions and special properties of atomic nuclei.

As with many scientific fields, strict delineation can be highly contrived and atomic physics is often considered in the wider context of atomic, molecular, and optical physics. As a result, atomic physics research groups are usually classified as such.

Isolated atoms

[edit]

Atomic physics primarily considers atoms in isolation. Atomic models will consist of a single nucleus that may be surrounded by one or more bound electrons. It is not concerned with the formation of molecules (although much of the physics is identical), nor does it examine atoms in a solid state as condensed matter. It is concerned with processes such as ionization and excitation by photons or collisions with atomic particles.

While modelling atoms in isolation may not seem realistic, if one considers atoms in a gas or plasma then the time-scales for atom-atom interactions are huge in comparison to the atomic processes that are generally considered. This means that the individual atoms can be treated as if each were in isolation, as the vast majority of the time they are. By this consideration, atomic physics provides the underlying theory in plasma physics and atmospheric physics, even though both deal with very large numbers of atoms.

Electronic configuration

[edit]

Electrons form notional shells around the nucleus. These are normally in a ground state but can be excited by the absorption of energy from light (photons), magnetic fields, or interaction with a colliding particle (typically ions or other electrons).

In the Bohr model, the transition of an electron with n=3 to the shell n=2 is shown, where a photon is emitted. An electron from shell (n=2) must have been removed beforehand by ionization

Electrons that populate a shell are said to be in a bound state. The energy necessary to remove an electron from its shell (taking it to infinity) is called the binding energy. Any quantity of energy absorbed by the electron in excess of this amount is converted to kinetic energy according to the conservation of energy. The atom is said to have undergone the process of ionization.

If the electron absorbs a quantity of energy less than the binding energy, it will be transferred to an excited state. After a certain time, the electron in an excited state will "jump" (undergo a transition) to a lower state. In a neutral atom, the system will emit a photon of the difference in energy, since energy is conserved.

If an inner electron has absorbed more than the binding energy (so that the atom ionizes), then a more outer electron may undergo a transition to fill the inner orbital. In this case, a visible photon or a characteristic X-ray is emitted, or a phenomenon known as the Auger effect may take place, where the released energy is transferred to another bound electron, causing it to go into the continuum. The Auger effect allows one to multiply ionize an atom with a single photon.

There are rather strict selection rules as to the electronic configurations that can be reached by excitation by light –however, there are no such rules for excitation by collision processes.

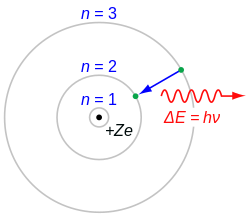
Bohr model of the atom

[edit]

The Bohr model, proposed by Niels Bohr in 1913, is a revolutionary theory describing the structure of the hydrogen atom. It introduced the idea of quantized orbits for electrons, combining classical and quantum physics.

Key Postulates of the Bohr Model
  1. Electrons Move in Circular Orbits
    • Electrons revolve around the nucleus in fixed, circular paths called orbits or energy levels.
    • These orbits are stable and do not radiate energy.
  2. Quantization of Angular Momentum:
    • The angular momentum of an electron is quantized and given by: where:
      : electron mass
      : velocity of the electron
      : radius of the orbit
      : reduced Planck constant ()
      : principal quantum number, representing the orbit
  3. Energy Levels
    • Each orbit has a specific energy. The total energy of an electron in the th orbit is: where  is the ground-state energy of the hydrogen atom.
  4. Emission or Absorption of Energy
    • Electrons can transition between orbits by absorbing or emitting energy equal to the difference between the energy levels: where:
      : the Planck constant.
      : frequency of emitted/absorbed radiation.
      : final and initial energy levels.

History and developments

[edit]
Main article: Atomic theory

One of the earliest steps towards atomic physics was the recognition that matter was composed of atoms. It forms a part of the texts written in 6th century BC to 2nd century BC, such as those of Democritus or Vaiśeṣika Sūtra written by Kaṇāda.[2][3] This theory was later developed in the modern sense of the basic unit of a chemical element by the British chemist and physicist John Dalton in the 18th century.[4] At this stage, it was not clear what atoms were, although they could be described and classified by their properties (in bulk). The invention of the periodic system of elements by Dmitri Mendeleev was another great step forward.

The true beginning of atomic physics is marked by the discovery of spectral lines and attempts to describe the phenomenon, most notably by Joseph von Fraunhofer.[5] The study of these lines led to the Bohr atom model and to the birth of quantum mechanics. In seeking to explain atomic spectra, an entirely new mathematical model of matter was revealed. As far as atoms and their electron shells were concerned, not only did this yield a better overall description, i.e. the atomic orbital model, but it also provided a new theoretical basis for chemistry (quantum chemistry) and spectroscopy.[6]

Since the Second World War, both theoretical and experimental fields have advanced at a rapid pace. This can be attributed to progress in computing technology, which has allowed larger and more sophisticated models of atomic structure and associated collision processes.[7][8] Similar technological advances in accelerators, detectors, magnetic field generation and lasers have greatly assisted experimental work.

Beyond the well-known phenomena which can be described with regular quantum mechanics chaotic processes[9] can occur which need different descriptions.

Significant atomic physicists

[edit]
Pre quantum mechanics
Post quantum mechanics

See also

[edit]

Bibliography

[edit]

References

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Atomic physics

View on Grokipedia
from Grokipedia
Atomic physics is the branch of physics that studies the structure and behavior of atoms, focusing on the quantum mechanical interactions between , the , and electromagnetic fields. It examines phenomena such as levels, electron configurations, spectral lines, and processes like excitation, , and radiative transitions. This field provides foundational insights into the quantum nature of matter at the atomic scale, bridging microscopic atomic properties with observable macroscopic effects like chemical bonding and light emission. The historical development of atomic physics accelerated in the early following the discovery of the by J.J. Thomson in 1897, which challenged classical models and led to the of the atom. Ernest Rutherford's 1911 gold foil experiment revealed the dense , prompting Niels Bohr's 1913 model that incorporated quantized orbits to explain hydrogen's . The advent of in the , through contributions from Schrödinger, Heisenberg, and Dirac, enabled precise descriptions of multi-electron atoms and relativistic effects. In modern atomic physics, advances in laser cooling and trapping techniques allow atoms to be manipulated at temperatures near , enabling studies of ultracold gases and quantum degenerate states such as Bose-Einstein condensates. Research explores interactions in optical lattices to simulate complex , including and , while precision tests fundamental constants and searches for . Key applications include atomic clocks for timekeeping with unprecedented accuracy, quantum sensors for inertial navigation and detection, and platforms for processing.

Fundamentals

Definition and Scope

Atomic physics is the branch of physics dedicated to the study of the structure, properties, and interactions of atoms, with a primary focus on electrons bound to the . This field examines atoms as isolated systems, investigating phenomena such as electron-nuclear interactions and the quantum states of atomic electrons. It deliberately excludes in-depth analyses of molecular formations, where interatomic bonds dominate, and , which concerns the nucleus's internal composition and strong force interactions. A key aspect of atomic physics is its role as a foundational testing ground for , where theoretical frameworks can be rigorously tested against experimental observations. The , consisting of a single proton and , exemplifies this simplicity, enabling exact solutions to the and providing benchmarks for quantum theory's predictions on energy levels and wave functions. Central questions driving atomic physics research include the mechanisms by which atoms emit and absorb —manifesting as discrete lines from electronic transitions between quantized energy levels—and the stability of orbits or configurations that prevent classical collapse into the nucleus. Additionally, the field elucidates the atomic basis of matter's composition, revealing how elemental building blocks determine the chemical and physical properties of substances.

Basic Components of Atoms

Atoms are composed of three fundamental subatomic particles: protons, neutrons, and electrons. The nucleus at the center of the atom contains protons and neutrons, which together account for nearly all of the atom's . Protons carry a positive of +1 (e = 1.602 176 634 × 10⁻¹⁹ C) and have a mass of approximately 1.007 276 u (unified atomic mass units), where 1 u = 1.660 539 066 60 × 10⁻²⁷ kg. Neutrons are electrically neutral and have a slightly larger mass of about 1.008 665 u. Surrounding the nucleus is a of electrons, each with a negative charge of -1 e and a much smaller mass of roughly 0.000 549 u, or about 1/1836 that of a proton. The following table summarizes the key properties of these particles:
ParticleChargeMass (u)Location
Proton+1 e1.007 276Nucleus
Neutron01.008 665Nucleus
Electron-1 e0.000 549Electron cloud
The atomic number Z, defined as the number of protons in the nucleus, uniquely identifies the chemical element and determines its position in the periodic table. The mass number A is the total number of protons and neutrons (nucleons) in the nucleus. Atoms of the same element with the same Z but different A due to varying numbers of neutrons are called isotopes. The electromagnetic force, arising from the Coulomb attraction between the positively charged protons in the nucleus and the negatively charged electrons, is the dominant interaction that binds electrons to the atom, maintaining its overall stability. Within the nucleus, protons and neutrons are bound by the strong nuclear force, a short-range interaction much stronger than electromagnetism but operating on scales outside the primary focus of atomic physics./Book%3A_University_Physics_III_-Optics_and_Modern_Physics(OpenStax)/10%3A__Nuclear_Physics/10.03%3A_Nuclear_Binding_Energy) The scale of binding energies underscores the distinction between atomic and nuclear phenomena. Electrons are bound to the nucleus with energies typically on the order of electronvolts (eV); for example, the of the —the energy required to remove its single —is 13.598 44 eV. In contrast, the within the nucleus is on the order of millions of electronvolts (MeV) per , with an average of about 8 MeV for stable nuclei, reflecting the vastly stronger forces at play./Book%3A_University_Physics_III_-Optics_and_Modern_Physics(OpenStax)/10%3A__Nuclear_Physics/10.03%3A_Nuclear_Binding_Energy) Electron configurations serve as a key organizing principle for understanding how electrons occupy orbitals around the nucleus.

Historical Development

Early Models and Experiments

The foundations of atomic physics were laid in the early with John Dalton's atomic theory, first detailed in his 1808 publication A New System of Chemical Philosophy. Dalton proposed that all matter consists of tiny, indivisible particles called atoms, which are indestructible and unchangeable in chemical reactions, with atoms of the same element possessing identical masses and those of different elements having distinct masses. He further asserted that chemical compounds form when atoms combine in simple whole-number ratios by weight, providing a quantitative basis for understanding chemical reactions and . This theory revolutionized chemistry by shifting from qualitative descriptions to a particle-based framework, though it initially assumed atoms as the ultimate indivisible units. By the late 19th century, experiments began to reveal that atoms were not indivisible, starting with the study of in vacuum tubes. In 1897, J.J. Thomson demonstrated that these rays consisted of streams of negatively charged particles, which he termed "corpuscles" (later known as electrons), with a mass-to-charge ratio about 1/1836 that of a . This discovery implied the existence of subatomic structure, challenging Dalton's indivisibility postulate. Concurrently, in 1896, accidentally observed that salts emitted invisible capable of penetrating black paper and exposing photographic plates, even without exposure to light, marking the first evidence of spontaneous atomic disintegration. Building on this, Marie and isolated two highly radioactive elements from pitchblende in 1898: , about 400 times more active than , announced in July; and , identified in December, which exhibited even greater intensity and was chemically similar to . These findings, published in Comptes Rendus, introduced the term "" and suggested that certain atoms could undergo spontaneous transformation, further eroding the notion of atomic permanence. In response to the electron's discovery, Thomson proposed the "plum pudding" model of the atom in 1904, envisioning a uniform sphere of positive charge in which electrons were embedded like plums in a pudding, ensuring overall neutrality and stability through electrostatic equilibrium. To quantify the electron's properties, Robert Millikan conducted the oil-drop experiment in 1909, ionizing tiny oil droplets and measuring their terminal velocities in an to determine that the elementary charge e is 1.602 × 10-19 C, confirming electrons as discrete units of charge. However, these early models faced significant limitations: Dalton's theory could not account for subatomic particles or , while Thomson's model failed to explain the long-term stability of atoms, as orbiting electrons should radiate energy and spiral inward according to , and it predicted a continuous rather than the observed discrete atomic lines. These shortcomings highlighted the need for new experimental and theoretical approaches to atomic structure.

Key Theoretical Advances

The foundations of modern atomic physics were laid in the early through a series of theoretical breakthroughs that introduced quantum concepts to explain atomic phenomena. In 1900, proposed the quantum hypothesis to resolve the in , positing that energy is emitted and absorbed in discrete packets, or quanta, given by the relation E=hνE = h\nu, where hh is Planck's constant and ν\nu is the . This idea marked the birth of quantum theory and paved the way for the concept of photons as fundamental particles of light. Building on Planck's work, in 1905 explained the by treating light as composed of discrete quanta, or photons, each carrying energy E=hνE = h\nu. He demonstrated that the ejection of electrons from a metal surface occurs only when the exceeds the material's , with the maximum of emitted electrons linearly dependent on frequency, independent of light intensity. This particle-like behavior of light provided empirical support for quantization and earned Einstein the in 1921. In 1924, extended wave-particle duality to matter, hypothesizing that particles like possess wave properties characterized by a de Broglie λ=h/p\lambda = h / p, where pp is . This duality suggested that in atoms could be described as standing waves, influencing subsequent quantum models and experimentally verified through . introduced the wave equation in 1926, providing a mathematical framework for applicable to atomic systems. The time-independent , H^ψ=Eψ\hat{H} \psi = E \psi, where H^\hat{H} is the Hamiltonian operator, ψ\psi is the wave function, and EE is the energy eigenvalue, describes stationary states and enables solutions for bound orbits. This formulation shifted atomic theory from classical to probabilistic interpretations, with the wave function encoding probability densities for positions. Complementing Schrödinger's approach, formulated the in 1927, stating that the product of uncertainties in position and satisfies ΔxΔp≥ℏ/2\Delta x \Delta p \geq \hbar / 2, where ℏ=h/2π\hbar = h / 2\pi. This fundamental limit implies that electrons cannot be precisely localized in atoms without disturbing their , challenging classical determinism and underscoring the inherent indeterminacy of quantum measurements. Finally, developed the relativistic quantum equation for electrons in 1928, combining with through the , (iℏγμ∂μ−mc)ψ=0(i \hbar \gamma^\mu \partial_\mu - m c) \psi = 0, where γμ\gamma^\mu are Dirac matrices, mm is , and cc is the . This first-order accurately predicts electron spin and in atomic spectra, while implying the existence of . These advances collectively enabled precise descriptions of atomic spectra and electronic transitions.

Atomic Models

Rutherford and Classical Models

The , conducted between 1909 and 1913 at the under Ernest Rutherford's supervision, involved bombarding thin metal foils—primarily —with alpha particles from a radioactive source such as . and directed the alpha particles at the foil and detected their paths using a zinc sulfide screen viewed through a , revealing that while most particles passed through undeflected, approximately 1 in 8,000 were scattered by large angles, with some rebounding nearly 180 degrees back toward the source. These observations, detailed in their 1909 paper on and subsequent 1913 report on deflection laws, contradicted J.J. Thomson's , which distributed positive charge uniformly throughout the atom, as such large deflections would require an intense, localized . In 1911, Rutherford interpreted these results in his seminal paper, proposing the nuclear model of the atom: a minuscule, dense nucleus bearing the atom's positive charge and nearly all its , surrounded by electrons orbiting at a distance, much like planets . To explain the , Rutherford derived a formula for the differential cross-section per unit , dσdΩ∝1sin⁡4(θ/2),\frac{d\sigma}{d\Omega} \propto \frac{1}{\sin^4 (\theta / 2)}, where θ\theta is the scattering angle, assuming Coulomb repulsion between the incoming alpha particle and the nucleus. This prediction aligned closely with Geiger and Marsden's measurements, confirming that the probability of large-angle scattering decreased sharply with increasing θ\theta, and it implied a nuclear radius on the order of 10−1410^{-14} meters—far smaller than the atomic radius of about 10−1010^{-10} meters. Rutherford emphasized the model's simplicity, likening the electrons' orbits to planetary motion under central force, but acknowledged its classical electromagnetic foundations. Despite its explanatory power for scattering, the Rutherford model faced fundamental challenges within classical physics. Orbiting electrons, undergoing centripetal acceleration, would continuously radiate electromagnetic energy according to Larmor's formula, P=23e2a2c3,P = \frac{2}{3} \frac{e^2 a^2}{c^3}, where PP is the radiated power, ee the electron charge, aa its acceleration, and cc the speed of light (in cgs units). This energy loss would cause the orbits to decay rapidly, spiraling the electrons into the nucleus within approximately 10−810^{-8} seconds, rendering atoms unstable and incompatible with observed atomic persistence. The solar system analogy, while intuitive for stable gravitational orbits, failed here due to the radiative effects of charged particles, highlighting the need for a non-classical description to resolve these instabilities.

Bohr Model

The Bohr model, proposed by Danish physicist in 1913, provides a semi-classical framework for understanding the structure of hydrogen-like atoms, incorporating elements of with ad hoc quantum conditions to resolve inconsistencies in earlier planetary models. The model assumes that electrons orbit the nucleus in specific, stable paths without radiating electromagnetic energy, contrary to classical electrodynamics predictions. Bohr's model rests on three key postulates. First, electrons revolve around the positively charged nucleus in stationary orbits where they do not lose energy through radiation. Second, the angular momentum of the electron in these orbits is quantized, given by L=nℏ,L = n \hbar, where n=1,2,3,…n = 1, 2, 3, \dots is a positive integer (the principal quantum number) and ℏ=h/2π\hbar = h / 2\pi is the reduced Planck's constant. Third, transitions between stationary orbits involve the absorption or emission of photons with energy equal to the difference between the levels, ΔE=hν\Delta E = h \nu, where ν\nu is the frequency of the radiation. From these postulates, the orbital radius and levels can be derived for the (with nuclear charge Z=1Z = 1). Balancing the classical with the attraction yields the for the nn-th orbit as rn=n2[a0](/page/Bohrradius),r_n = n^2 [a_0](/page/Bohr_radius), where a0=0.529 A˚a_0 = 0.529 \, \AA (the ) is the ground-state (n=1n=1) . The corresponding levels are En=−13.6 eVn2,E_n = -\frac{13.6 \, \mathrm{eV}}{n^2}, negative due to the , with the ground state (n=1n=1) at E1=−13.6 eVE_1 = -13.6 \, \mathrm{eV}. The model predicts the atomic spectrum of through transitions between these quantized levels, producing distinct series of emission lines. The () corresponds to transitions to n1=1n_1 = 1, the (visible) to n1=2n_1 = 2, and the Paschen series () to n1=3n_1 = 3, with higher n2>n1n_2 > n_1. These lines follow the : 1[λ](/page/Lambda)=R(1n12−1n22),\frac{1}{[\lambda](/page/Lambda)} = R \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right), where R≈1.097×107 m−1R \approx 1.097 \times 10^7 \, \mathrm{m}^{-1} is the for and λ\lambda is the . Among its successes, the Bohr model quantitatively explains the observed of , matching the positions of lines in the Balmer, Lyman, and other series without adjustable parameters beyond the known constants. It also correctly predicts the of as 13.6 eV, the energy required to excite the from the to infinity. Despite these achievements, the model has significant limitations. It fails to describe the spectra of multi-electron atoms, where electron-electron interactions are not accounted for. Additionally, it does not explain the in hydrogen's spectrum arising from relativistic effects and spin-orbit coupling. The model also overlooks the wave nature of electrons, treating them solely as particles in fixed orbits.

Quantum Mechanical Description

The quantum mechanical description of atoms fundamentally relies on the time-independent , which governs the behavior of in the potential field of the nucleus. For the , consisting of a single in the potential of a proton, the equation is solved exactly in spherical coordinates, yielding the energy eigenvalues and wavefunctions that characterize the bound states. The Hamiltonian operator includes the of the and the attractive potential, leading to separable solutions in radial and angular parts. The solutions introduce four quantum numbers: the principal quantum number n=1,2,3,…n = 1, 2, 3, \dots, which determines the energy levels En=−13.6 eVn2E_n = -\frac{13.6 \, \text{eV}}{n^2}; the azimuthal quantum number l=0,1,…,n−1l = 0, 1, \dots, n-1, describing the orbital angular momentum; the magnetic quantum number ml=−l,−l+1,…,lm_l = -l, -l+1, \dots, l, specifying the projection of angular momentum along a quantization axis; and the spin magnetic quantum number ms=±12m_s = \pm \frac{1}{2}, accounting for the electron's intrinsic spin. These quantum numbers arise naturally from the boundary conditions and separability of the Schrödinger equation, with nn emerging from the radial quantization, ll and mlm_l from the angular part, and msm_s incorporated via the spin degree of freedom. The atomic wavefunctions for hydrogen-like atoms are expressed as ψnlml(r,θ,ϕ)=Rnl(r)Ylml(θ,ϕ)\psi_{nlm_l}(r, \theta, \phi) = R_{nl}(r) Y_{lm_l}(\theta, \phi), where Rnl(r)R_{nl}(r) is the radial function involving associated and an , and Ylml(θ,ϕ)Y_{lm_l}(\theta, \phi) are representing the angular dependence. The probability density ∣ψnlml∣2|\psi_{nlm_l}|^2 gives the likelihood of finding the at a position, replacing classical trajectories with a probabilistic interpretation central to . This structure ensures orthogonality among states with different quantum numbers, forming a complete basis for the . For multi-electron atoms, the , formulated in 1925, states that no two can occupy the same , meaning they cannot share identical values of nn, ll, mlm_l, and msm_s. This principle, derived from the antisymmetry of the fermionic wavefunction under particle exchange, prevents electron collapse into the lowest energy state and explains the filling of atomic shells, underpinning the structure of the periodic table. Exact solutions for multi-electron systems are intractable due to electron-electron interactions, necessitating approximation methods. The variational method provides an upper bound to the ground-state energy by minimizing the expectation value of the Hamiltonian with respect to a parameterized trial wavefunction, such as a of basis functions; for example, in the , trial functions incorporating inter-electron distance yield energies accurate to within 1% of the exact value. A more systematic approach for multi-electron atoms is the Hartree-Fock method, which approximates the many-body wavefunction as a of single-particle orbitals to satisfy antisymmetry and incorporates exchange effects. Introduced by in 1928 as a self-consistent field where each moves in the mean potential created by others, it was refined by Fock in 1930 to include the full antisymmetrization via determinants, leading to self-consistent equations solved iteratively for orbital energies and densities. This method captures the essential electronic structure, with typical errors in ground-state energies of a few percent for light atoms, forming the basis for more advanced post-Hartree-Fock techniques. Electron configurations, specifying how electrons occupy these quantum states according to the , follow directly from the quantum mechanical framework and .

Electronic Structure

Electron Configurations

Electron configurations describe the distribution of in the atomic orbitals of an atom in its , governed by fundamental quantum mechanical principles that dictate the order and arrangement of electron occupancy. These configurations arise from the interplay of the , which limits each orbital to a maximum of two electrons with opposite spins, and the tendency for electrons to occupy the lowest available energy levels. The resulting arrangements explain many periodic properties of elements, such as chemical reactivity and spectral characteristics. The , formulated by in the early 1920s, states that electrons fill atomic orbitals in order of increasing energy, starting from the lowest energy subshell. This building-up process follows the Madelung rule, where the energy order is determined by the sum of the principal quantum number nn and the ll (i.e., n+ln + l rule), with subshells of equal n+ln + l filled by increasing nn. The standard filling sequence begins with the 1s orbital, followed by 2s, 2p, 3s, 3p, 4s, 3d, 4p, and so on, leading to configurations like that of as 1s22s22p61s^2 2s^2 2p^6. This principle provides a predictive framework for neutral atoms but assumes non-relativistic conditions and neglects electron-electron interactions in multi-electron atoms for the basic order. Complementing the Aufbau principle are Hund's rules, proposed by Friedrich Hund in 1925, which determine the arrangement of electrons within degenerate orbitals of the same subshell. The first rule specifies that the ground state has the maximum possible total spin quantum number SS, achieved by placing electrons in degenerate orbitals with parallel spins to maximize multiplicity 2S+12S + 1. The second rule states that for states with the same SS, the one with the maximum total orbital angular momentum quantum number LL is lowest in energy. These rules minimize electron repulsion by maximizing spin alignment and orbital separation, as seen in the p2p^2 configuration where electrons occupy separate pxp_x, pyp_y, or pzp_z orbitals with parallel spins rather than pairing in one. The third rule, concerning total angular momentum J=L+SJ = L + S, applies to states with less than half-filled shells where J=∣L−S∣J = |L - S| is favored, though it is less directly tied to configuration filling. Representative examples illustrate these principles. For helium (Z=2), the configuration is 1s21s^2, with both electrons paired in the lowest-energy orbital, yielding a singlet ground state. Carbon (Z=6) follows as 1s22s22p21s^2 2s^2 2p^2, where the two 2p electrons occupy separate orbitals with parallel spins per Hund's first rule, resulting in a . These configurations are experimentally verified through and ionization data. Exceptions to the Aufbau order occur in transition metals due to the close energy proximity of 4s and 3d orbitals, where exchange energy and stability favor alternative arrangements. Chromium (Z=24) adopts [Ar]4s13d5[Ar] 4s^1 3d^5 instead of the expected [Ar]4s23d4[Ar] 4s^2 3d^4, achieving a half-filled 3d subshell, which lowers the overall through greater exchange stabilization among the five unpaired 3d electrons compared to four paired and unpaired in the predicted form. Similar exceptions appear in ([Ar]4s13d10[Ar] 4s^1 3d^{10}) for a fully filled 3d subshell. These deviations highlight that while the Aufbau provides a guideline, full configuration energies require accounting for electron correlation. Electron configurations also give rise to term symbols in the Russell-Saunders (LS) coupling scheme, which describes the possible angular momentum states of the atom. Introduced by Henry Norris Russell and Frederick Albert Saunders in 1925, term symbols are denoted as 2S+1LJ^{2S+1}L_J, where LL is represented by (S for 0, P for 1, D for 2, etc.), SS is the total spin, and JJ is the total . For multi-electron atoms, the ground state term is determined by applied to the valence configuration. Oxygen (Z=8), with 1s22s22p41s^2 2s^2 2p^4 or equivalently 2p42p^4 in the valence shell, has a ground state term symbol of 3P^3P (with J=2,1,0J=2,1,0 levels), arising from two unpaired 2p electrons with parallel spins (S=1S=1) and L=1L=1. This triplet P state is the lowest energy due to maximum multiplicity and appropriate LL. Term symbols are essential for classifying atomic states but assume coupling, valid for lighter elements. Ionization potentials, the energy required to remove an from the neutral atom, exhibit trends tied to electron configurations and increase generally with Z across a period due to rising effective nuclear charge ZeffZ_{eff}, which binds valence electrons more tightly. For instance, first ionization energies rise from (5.39 eV) to (21.56 eV) in period 2, reflecting fuller shells and higher ZeffZ_{eff}. Down a group, ionization energies decrease as valence electrons occupy larger orbitals farther from the nucleus, reducing ZeffZ_{eff}. Exceptions occur at half-filled or filled subshells, like nitrogen's higher value than oxygen due to stability of the half-filled 2p^3 configuration. These trends are quantified in atomic databases and underpin periodic table organization.

Atomic Orbitals and Shells

Atomic orbitals describe the spatial distribution of electron probability density in an atom and emerge as solutions to the Schrödinger equation for the hydrogen atom. These wave functions are characterized by four quantum numbers derived from the separable solutions of the equation. The principal quantum number n=1,2,3,…n = 1, 2, 3, \dots governs the orbital's energy and average radial extent from the nucleus. The azimuthal quantum number l=0,1,…,n−1l = 0, 1, \dots, n-1 determines the orbital's angular momentum and shape, with l=0l = 0 corresponding to s orbitals, l=1l = 1 to p orbitals, l=2l = 2 to d orbitals, and l=3l = 3 to f orbitals. The magnetic quantum number ml=−l,…,0,…,+lm_l = -l, \dots, 0, \dots, +l specifies the orbital's orientation relative to an external magnetic field. The spin quantum number ms=+12m_s = +\frac{1}{2} or −12-\frac{1}{2} accounts for the electron's intrinsic angular momentum. The angular part of the wave function dictates the orbital shapes: s orbitals are spherically symmetric around the nucleus, p orbitals form dumbbell-shaped lobes along the x, y, or z axes, and d orbitals display more complex cloverleaf or double-dumbbell configurations in the xy, yz, xz, x²-y², or z² planes. Additionally, the radial introduces nodes—regions of zero probability—with the number of radial nodes given by n−l−1n - l - 1, such that higher-n s orbitals (l=0) exhibit more spherical nodes than p or d orbitals of the same n. In the , orbital energies depend solely on n, rendering all subshells within a given shell degenerate. In multi-electron atoms, however, electron-electron repulsions disrupt this degeneracy, causing energies to increase with l for fixed n (s < p < d < f) due to differences in radial distribution and interaction strengths. Principal quantum numbers define atomic shells, traditionally labeled K (n=1), L (n=2), M (n=3), N (n=4), O (n=5), P (n=6), and Q (n=7) in X-ray spectroscopy notation, with each shell corresponding to a period in the periodic table. The maximum electron capacity of the nth shell is 2n22n^2, arising from the , which prohibits two electrons from sharing identical quantum numbers, allowing 2 electrons per orbital across all possible l and m_l values. In multi-electron atoms, shielding occurs as inner-shell electrons screen outer electrons from the full nuclear charge, reducing the effective nuclear charge Zeff=Z−σZ_{\text{eff}} = Z - \sigma (where σ\sigma is the shielding constant). Penetration refers to how closely an orbital approaches the nucleus, with s orbitals (l=0) penetrating more effectively than p (l=1), d (l=2), or f (l=3) orbitals due to their concentrated probability near the nucleus, resulting in weaker shielding and stronger nuclear attraction for s electrons. For example, 2s electrons penetrate the 1s core more than 2p electrons, lowering their energy relative to 2p. This interplay of penetration and shielding primarily dictates subshell energy ordering beyond hydrogen-like systems.

Multi-Electron Atoms

In multi-electron atoms, the presence of electron-electron interactions complicates the exact solution of the Schrödinger equation, necessitating approximate methods to describe the electronic structure. Unlike the hydrogen atom, where a single electron orbits the nucleus in a Coulomb potential, multi-electron systems involve mutual repulsions that lead to complex many-body effects, requiring approximations to achieve tractable calculations. The central field approximation, developed by Douglas Hartree, simplifies the problem by assuming each electron moves independently in a spherically symmetric effective potential generated by the nucleus and the average charge distribution of all other electrons. This approach replaces the full interacting Hamiltonian with a set of single-particle equations, yielding self-consistent orbitals that approximate the atomic wavefunction. In this framework, the effective potential for the radial motion of an electron includes the nuclear attraction, the mean-field repulsion from other electrons, and the centrifugal barrier, expressed as Veff(r)=−Zr+VH(r)+l(l+1)ℏ22mr2,V_{\mathrm{eff}}(r) = -\frac{Z}{r} + V_{\mathrm{H}}(r) + \frac{l(l+1)\hbar^2}{2mr^2}, where ZZ is the atomic number, VH(r)V_{\mathrm{H}}(r) is the Hartree potential from the averaged electron density, ll is the orbital angular momentum quantum number, ℏ\hbar is the reduced Planck's constant, and mm is the electron mass (in atomic units, the constants simplify accordingly). This approximation captures the gross features of atomic structure but neglects detailed correlations between electrons. Within the central field approximation, the electron-electron repulsion is treated as a mean-field potential, but the instantaneous correlations—where electrons avoid each other more than the average—remain unaccounted for, resulting in the correlation energy, defined as the difference between the exact ground-state energy and the mean-field energy. This correlation energy arises from perturbations beyond the independent-particle model and is typically a small but crucial fraction (on the order of 1% or less) of the total binding energy, essential for accurate predictions of atomic properties like ionization potentials. The Hartree-Fock method refines the central field by incorporating an exchange term due to the antisymmetry of the fermionic wavefunction. The exchange interaction stems from the Pauli exclusion principle, requiring the total wavefunction to be antisymmetric under electron exchange, which introduces a non-classical term in the effective potential that lowers the energy for states with parallel spins in degenerate orbitals, as seen in Hund's rules for ground-state multiplicities. This effect, first elucidated by Werner Heisenberg in his treatment of the helium atom, manifests as an effective attraction between electrons with parallel spins, stabilizing configurations like the triplet state over the singlet in equivalent orbitals. Vladimir Fock formalized this in the antisymmetrized product of orbitals, leading to the Hartree-Fock equations that include both direct (Coulomb) and exchange integrals. Relativistic effects begin to play a role in multi-electron atoms, particularly for heavier elements, previewed by the fine structure constant α≈1/137\alpha \approx 1/137, which parametrizes the strength of quantum electrodynamic interactions. Key corrections include the mass-velocity term, arising from the relativistic increase in electron mass at high velocities near the nucleus, contributing to the overall fine structure splitting observed in atomic spectra. These effects scale with (Zα)2(Z\alpha)^2 and are incorporated perturbatively in non-relativistic treatments. To achieve higher accuracy beyond the single-determinant Hartree-Fock approximation, configuration interaction (CI) methods mix multiple Slater determinants corresponding to different electron configurations, capturing dynamic correlation through linear combinations of excited states. This approach, pioneered in early calculations for light atoms like helium, systematically reduces the correlation energy error by allowing the wavefunction to adjust for instantaneous electron positions, though it scales poorly with atomic number due to the exponential growth in configurations.

Spectral Properties

Atomic Spectra

Atomic spectra refer to the discrete patterns of wavelengths observed in the emission or absorption of light by atoms, contrasting sharply with the continuous spectra produced by hot, dense sources like blackbody radiation. In the mid-19th century, chemists and pioneered spectroscopy by passing light from heated elements through prisms, revealing sharp emission lines unique to each element rather than a smooth continuum. These line spectra arise from electrons transitioning between discrete energy levels in atoms, producing photons of specific energies corresponding to the differences between those levels./Text/6:_The_Structure_of_Atoms/6.3:_Atomic_Line_Spectra_and_Niels_Bohr) The quantized nature of atomic energy levels was experimentally confirmed in 1914 through the Franck-Hertz experiment, where electrons accelerated through mercury vapor lost energy in discrete steps of about 4.9 eV, matching the energy difference between the ground and first excited states of mercury atoms. This inelastic collision process demonstrated that atoms cannot absorb or emit arbitrary amounts of energy but only specific quanta, providing direct evidence against classical theories and supporting the emerging quantum model. The experiment involved measuring current drops in a vacuum tube as electron energy increased, with peaks recurring at multiples of the excitation energy. The hydrogen atom exhibits particularly simple line spectra, organized into series such as the Balmer series in the visible range, discovered empirically by Johann Balmer in 1885 through a formula relating wavelengths to integer values. Balmer observed four prominent lines at 656.3 nm (Hα), 486.1 nm (Hβ), 434.0 nm (Hγ), and 410.2 nm (Hδ), corresponding to transitions from higher principal quantum numbers n2>2n_2 > 2 to the n1=2n_1 = 2 level. In 1888, generalized this into a formula applicable to all series, including the (n1=1n_1 = 1) and Paschen series (n1=3n_1 = 3): 1λ=R∞(1n12−1n22),\frac{1}{\lambda} = R_\infty \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right), where λ\lambda is the wavelength, R∞≈1.097×107R_\infty \approx 1.097 \times 10^7 m−1^{-1} is the Rydberg constant for infinite nuclear mass, and n1<n2n_1 < n_2 are principal quantum numbers. Each series converges to a limit as n2→∞n_2 \to \infty, marking the ionization energy from the n1n_1 level, with the Lyman limit at 91.2 nm corresponding to transitions to the ground state. These jumps between principal quantum numbers explain the discrete spacing of lines, becoming denser near the series limits./01:_The_Dawn_of_the_Quantum_Theory/1.05:_The_Rydberg_Formula_and_the_Hydrogen_Atomic_Spectrum) Alkali metals, with a single valence electron outside a closed shell, display relatively simple spectra dominated by s-to-p transitions, producing prominent resonance lines. For sodium, the characteristic D-lines at 588.995 nm (D2) and 589.592 nm (D1) result from 3p to 3s transitions, observed as a bright yellow doublet in flame tests and responsible for the yellow color of sodium vapor lamps. These lines were first identified by Bunsen and Kirchhoff in 1860 as matching absorption features in the solar spectrum, confirming sodium's presence in the Sun's atmosphere. Similar s-p transitions occur in other alkali atoms, such as the principal series in potassium and rubidium, though with more complexity due to fine structure. The intensity of spectral lines reflects the population of energy levels and transition rates, while their width arises from various broadening mechanisms. Natural broadening, the fundamental limit set by the finite lifetime τ\tau of excited states, gives a Lorentzian profile with full width at half maximum Γ=1/τ\Gamma = 1/\tau in angular frequency units, stemming from the Heisenberg uncertainty principle ΔEΔt≥ℏ/2\Delta E \Delta t \geq \hbar/2. Doppler broadening, due to thermal motion of atoms, produces a Gaussian profile superimposed on the natural width, with the linewidth ΔνD=(2ν0/c)(kT/m)ln⁡2\Delta \nu_D = (2 \nu_0 / c) \sqrt{(kT / m) \ln 2}
Add your contribution
Related Hubs
User Avatar
No comments yet.