Indeterminate form

In calculus, it is usually possible to compute the limit of the sum, difference, product, quotient or power of two functions by taking the corresponding combination of the separate limits of each respective function. For example,

${\begin{aligned}\lim _{x\to c}{\bigl (}f(x)+g(x){\bigr )}&=\lim _{x\to c}f(x)+\lim _{x\to c}g(x),\\[3mu]\lim _{x\to c}{\bigl (}f(x)g(x){\bigr )}&=\lim _{x\to c}f(x)\cdot \lim _{x\to c}g(x),\end{aligned}}$

and likewise for other arithmetic operations; this is sometimes called the algebraic limit theorem. However, certain combinations of particular limiting values cannot be computed in this way, and knowing the limit of each function separately does not suffice to determine the limit of the combination. In these particular situations, the limit is said to take an indeterminate form, described by one of the informal expressions

${\frac {0}{0}},~{\frac {\infty }{\infty }},~0\times \infty ,~\infty -\infty ,~0^{0},~1^{\infty },{\text{ or }}\infty ^{0},$

among a wide variety of uncommon others, where each expression stands for the limit of a function constructed by an arithmetical combination of two functions whose limits respectively tend to ⁠ $0,$ ⁠ ⁠ $1,$ ⁠ or ⁠ $\infty$ ⁠ as indicated.^[1]

A limit taking one of these indeterminate forms might tend to zero, might tend to any finite value, might tend to infinity, or might diverge, depending on the specific functions involved. A limit which unambiguously tends to infinity, for instance ${\textstyle \lim _{x\to 0}1/x^{2}=\infty ,}$ is not considered indeterminate.^[2] The term was originally introduced by Cauchy's student Moigno in the middle of the 19th century.

The most common example of an indeterminate form is the quotient of two functions each of which converges to zero. This indeterminate form is denoted by $0/0$ . For example, as $x$ approaches $0,$ the ratios $x/x^{3}$ , $x/x$ , and $x^{2}/x$ go to $\infty$ , $1$ , and $0$ respectively. In each case, if the limits of the numerator and denominator are substituted, the resulting expression is $0/0$ , which is indeterminate. In this sense, $0/0$ can take on the values $0$ , $1$ , or $\infty$ , by appropriate choices of functions to put in the numerator and denominator. A pair of functions for which the limit is any particular given value may in fact be found. Even more surprising, perhaps, the quotient of the two functions may in fact diverge, and not merely diverge to infinity. For example, $x\sin(1/x)/x$ .

So the fact that two functions $f(x)$ and $g(x)$ converge to $0$ as $x$ approaches some limit point $c$ is insufficient to determine the limit

$\lim _{x\to c}{\frac {f(x)}{g(x)}}.$

An expression that arises by ways other than applying the algebraic limit theorem may have the same form of an indeterminate form. However it is not appropriate to call an expression "indeterminate form" if the expression is made outside the context of determining limits. An example is the expression $0^{0}$ . Whether this expression is left undefined, or is defined to equal $1$ , depends on the field of application and may vary between authors. For more, see the article Zero to the power of zero. Note that $0^{\infty }$ and other expressions involving infinity are not indeterminate forms.

Some examples and non-examples

Indeterminate form 0/0

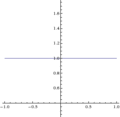
Fig. 1: y = ⁠x/x⁠
Fig. 2: y = ⁠x²/x⁠
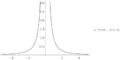
Fig. 3: y = ⁠sin x/x⁠
Fig. 4: y = ⁠x − 49/√x − 7⁠ (for x = 49)
Fig. 5: y = ⁠ax/x⁠ where a = 2
Fig. 6: y = ⁠x/x³⁠

The indeterminate form $0/0$ is particularly common in calculus, because it often arises in the evaluation of derivatives using their definition in terms of limit.

As mentioned above,

\lim _{x\to 0}{\frac {x}{x}}=1,\qquad

(see fig. 1)

while

\lim _{x\to 0}{\frac {x^{2}}{x}}=0,\qquad

(see fig. 2)

This is enough to show that $0/0$ is an indeterminate form. Other examples with this indeterminate form include

\lim _{x\to 0}{\frac {\sin(x)}{x}}=1,\qquad

(see fig. 3)

and

\lim _{x\to 49}{\frac {x-49}{{\sqrt {x}}\,-7}}=14,\qquad

(see fig. 4)

Direct substitution of the number that $x$ approaches into any of these expressions shows that these are examples correspond to the indeterminate form $0/0$ , but these limits can assume many different values. Any desired value $a$ can be obtained for this indeterminate form as follows:

\lim _{x\to 0}{\frac {ax}{x}}=a.\qquad

(see fig. 5)

The value $\infty$ can also be obtained (in the sense of divergence to infinity):

\lim _{x\to 0}{\frac {x}{x^{3}}}=\infty .\qquad

(see fig. 6)

Indeterminate form 0⁰

Graph of

y = x 0

Graph of

y = 0 x

The following limits illustrate that the expression $0^{0}$ is an indeterminate form: ${\begin{aligned}\lim _{x\to 0^{+}}x^{0}&=1,\\\lim _{x\to 0^{+}}0^{x}&=0.\end{aligned}}$

Thus, in general, knowing that $\textstyle \lim _{x\to c}f(x)\;=\;0$ and $\textstyle \lim _{x\to c}g(x)\;=\;0$ is not sufficient to evaluate the limit $\lim _{x\to c}f(x)^{g(x)}.$

If the functions $f$ and $g$ are analytic at $c$ , and $f$ is positive for $x$ sufficiently close (but not equal) to $c$ , then the limit of $f(x)^{g(x)}$ will be $1$ .^[3] Otherwise, use the transformation in the table below to evaluate the limit.

Expressions that are not indeterminate forms

The expression $1/0$ is not commonly regarded as an indeterminate form, because if the limit of $f(x)/g(x)$ as $g(x)\rightarrow 0$ exists then there is no ambiguity as to its value, as it always diverges. Specifically, with the constraint that $f(x)$ approaches $1$ and $g(x)$ approaches $0,$ we may choose $f$ and $g$ so that:

$f(x)/g(x)$ approaches $+\infty$
$f(x)/g(x)$ approaches $-\infty$
The limit fails to exist.

In each case the absolute value $|f(x)/g(x)|$ approaches $+\infty$ , and so the quotient $f(x)/g(x)$ must diverge, in the sense of the extended real numbers (in the framework of the projectively extended real line, the limit is the unsigned infinity $\infty$ in all three cases^[4]). Similarly, any expression of the form $a/0$ with $a\neq 0$ (including $a=+\infty$ and $a=-\infty$ ) is not an indeterminate form, since a quotient giving rise to such an expression will always diverge.

The expression $0^{\infty }$ is not an indeterminate form. The expression $0^{+\infty }$ obtained from considering $\lim _{x\to c}f(x)^{g(x)}$ gives the limit $0,$ provided that $f(x)$ remains nonnegative as $x$ approaches $c$ . The expression $0^{-\infty }$ is similarly equivalent to $1/0$ ; if $f(x)>0$ as $x$ approaches $c$ , the limit comes out as $+\infty$ .

To see why, let $L=\lim _{x\to c}f(x)^{g(x)},$ where $\lim _{x\to c}{f(x)}=0,$ and $\lim _{x\to c}{g(x)}=\infty .$ By taking the natural logarithm of both sides and using $\lim _{x\to c}\ln {f(x)}=-\infty ,$ we get that $\ln L=\lim _{x\to c}({g(x)}\times \ln {f(x)})=\infty \times {-\infty }=-\infty ,$ which means that $L={e}^{-\infty }=0.$

Evaluating indeterminate forms

The adjective indeterminate does not imply that the limit does not exist, as many of the examples above show. In many cases, algebraic elimination, L'Hôpital's rule, or other methods can be used to manipulate the expression so that the limit can be evaluated.

Equivalent infinitesimal

When two variables $\alpha$ and $\beta$ converge to zero at the same limit point and $\textstyle \lim {\frac {\beta }{\alpha }}=1$ , they are called equivalent infinitesimal (equiv. $\alpha \sim \beta$ ).

Moreover, if variables $\alpha '$ and $\beta '$ are such that $\alpha \sim \alpha '$ and $\beta \sim \beta '$ , then: $\lim {\frac {\beta }{\alpha }}=\lim {\frac {\beta '}{\alpha '}}$

Here is a brief proof:

Suppose there are two equivalent infinitesimals $\alpha \sim \alpha '$ and $\beta \sim \beta '$ .

$\lim {\frac {\beta }{\alpha }}=\lim {\frac {\beta \beta '\alpha '}{\beta '\alpha '\alpha }}=\lim {\frac {\beta }{\beta '}}\lim {\frac {\alpha '}{\alpha }}\lim {\frac {\beta '}{\alpha '}}=\lim {\frac {\beta '}{\alpha '}}$

For the evaluation of the indeterminate form $0/0$ , one can make use of the following facts about equivalent infinitesimals (e.g., $x\sim \sin x$ if x becomes closer to zero):^[5]

${\begin{aligned}x&\sim \sin x,\\x&\sim \arcsin x,\\x&\sim \sinh x,\\x&\sim \tan x,\\x&\sim \arctan x,\\x&\sim \ln(1+x),\\1-\cos x&\sim {\frac {x^{2}}{2}},\\\cosh x-1&\sim {\frac {x^{2}}{2}},\\a^{x}-1&\sim x\ln a,\\e^{x}-1&\sim x,\\(1+x)^{a}-1&\sim ax.\end{aligned}}$

For example:

${\begin{aligned}\lim _{x\to 0}{\frac {1}{x^{3}}}\left[\left({\frac {2+\cos x}{3}}\right)^{x}-1\right]&=\lim _{x\to 0}{\frac {e^{x\ln {\frac {2+\cos x}{3}}}-1}{x^{3}}}\\&=\lim _{x\to 0}{\frac {1}{x^{2}}}\ln {\frac {2+\cos x}{3}}\\&=\lim _{x\to 0}{\frac {1}{x^{2}}}\ln \left({\frac {\cos x-1}{3}}+1\right)\\&=\lim _{x\to 0}{\frac {\cos x-1}{3x^{2}}}\\&=\lim _{x\to 0}-{\frac {x^{2}}{6x^{2}}}\\&=-{\frac {1}{6}}\end{aligned}}$

In the 2nd equality, $e^{y}-1\sim y$ where $y=x\ln {2+\cos x \over 3}$ as y become closer to 0 is used, and $y\sim \ln {(1+y)}$ where $y={{\cos x-1} \over 3}$ is used in the 4th equality, and $1-\cos x\sim {x^{2} \over 2}$ is used in the 5th equality.

L'Hôpital's rule

L'Hôpital's rule is a general method for evaluating the indeterminate forms $0/0$ and $\infty /\infty$ . This rule states that (under appropriate conditions)

$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {f'(x)}{g'(x)}},$

where $f'$ and $g'$ are the derivatives of $f$ and $g$ . (Note that this rule does not apply to expressions $\infty /0$ , $1/0$ , and so on, as these expressions are not indeterminate forms.) These derivatives will allow one to perform algebraic simplification and eventually evaluate the limit.

L'Hôpital's rule can also be applied to other indeterminate forms, using first an appropriate algebraic transformation. For example, to evaluate the form 0⁰:

$\ln \lim _{x\to c}f(x)^{g(x)}=\lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}.$

The right-hand side is of the form $\infty /\infty$ , so L'Hôpital's rule applies to it. Note that this equation is valid (as long as the right-hand side is defined) because the natural logarithm (ln) is a continuous function; it is irrelevant how well-behaved $f$ and $g$ may (or may not) be as long as $f$ is asymptotically positive. (the domain of logarithms is the set of all positive real numbers.)

Although L'Hôpital's rule applies to both $0/0$ and $\infty /\infty$ , one of these forms may be more useful than the other in a particular case (because of the possibility of algebraic simplification afterwards). One can change between these forms by transforming $f/g$ to $(1/g)/(1/f)$ .

List of indeterminate forms

The following table lists the most common indeterminate forms and the transformations for applying l'Hôpital's rule.

Indeterminate form	Conditions	Transformation to $0/0$	Transformation to $\infty /\infty$
${\frac {0}{0}}$	$\lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=0\!$	—	$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {1/g(x)}{1/f(x)}}\!$
${\frac {\infty }{\infty }}$	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}{\frac {f(x)}{g(x)}}=\lim _{x\to c}{\frac {1/g(x)}{1/f(x)}}\!$	—
$0\cdot \infty$	$\lim _{x\to c}f(x)=0,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}f(x)g(x)=\lim _{x\to c}{\frac {f(x)}{1/g(x)}}\!$	$\lim _{x\to c}f(x)g(x)=\lim _{x\to c}{\frac {g(x)}{1/f(x)}}\!$
$\infty -\infty$	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}(f(x)-g(x))=\lim _{x\to c}{\frac {1/g(x)-1/f(x)}{1/(f(x)g(x))}}\!$	$\lim _{x\to c}(f(x)-g(x))=\ln \lim _{x\to c}{\frac {e^{f(x)}}{e^{g(x)}}}\!$
$0^{0}$	$\lim _{x\to c}f(x)=0^{+},\lim _{x\to c}g(x)=0\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$
$1^{\infty }$	$\lim _{x\to c}f(x)=1,\ \lim _{x\to c}g(x)=\infty \!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$
$\infty ^{0}$	$\lim _{x\to c}f(x)=\infty ,\ \lim _{x\to c}g(x)=0\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {g(x)}{1/\ln f(x)}}\!$	$\lim _{x\to c}f(x)^{g(x)}=\exp \lim _{x\to c}{\frac {\ln f(x)}{1/g(x)}}\!$

References

Citations

^ Varberg, Purcell & Rigdon (2007), p. 423, 429, 430, 431, 432.
^ Weisstein, Eric W. "Indeterminate". Wolfram MathWorld. Retrieved 2019-12-02.
^ Rotando, Louis M.; Korn, Henry (January 1977). "The indeterminate form 0⁰". Mathematics Magazine. 50 (1): 41–42. doi:10.2307/2689754. JSTOR 2689754.
^ "Undefined vs Indeterminate in Mathematics". Cut The Knot. Retrieved 2019-12-02.
^ "Table of equivalent infinitesimals" (PDF). Vaxa Software.

Bibliographies

Varberg, Dale E.; Purcell, Edwin J.; Rigdon, Steven E. (2007). Calculus (9th ed.). Pearson Prentice Hall. ISBN 978-0131469686.

[FOOTNOTEVarbergPurcellRigdon2007423,_429,_430,_431,_432-1] Varberg, Purcell & Rigdon (2007), p. 423, 429, 430, 431, 432.

[:1-2] Weisstein, Eric W. "Indeterminate". Wolfram MathWorld. Retrieved 2019-12-02.

[3] Rotando, Louis M.; Korn, Henry (January 1977). "The indeterminate form 0⁰". Mathematics Magazine. 50 (1): 41–42. doi:10.2307/2689754. JSTOR 2689754.

[:3-4] "Undefined vs Indeterminate in Mathematics". Cut The Knot. Retrieved 2019-12-02.

[5] "Table of equivalent infinitesimals" (PDF). Vaxa Software.

[1]

[2]

[3]

[4]

[5]

Form	Typical Limit Behaviors	Brief Origin
$\frac{0}{0}$	Finite value, $\pm \infty$ , or oscillation	Limits of quotients where numerator and denominator both approach 0.^[1]
$\frac{\infty}{\infty}$	Finite value, $\pm \infty$ , or oscillation (includes $\frac{\infty}{-\infty}$ variant)	Limits of quotients where numerator and denominator both approach $\pm \infty$ .^[1]
$0 \cdot \infty$	Finite value, $\pm \infty$ , or oscillation	Products where one factor approaches 0 and the other $\pm \infty$ .^[1]
$\infty - \infty$	Finite value, $\pm \infty$ , or oscillation	Differences where both terms approach $\pm \infty$ .^[1]
$0^0$	Finite value (often 1), 0, or oscillation	Exponential limits where base approaches 0 and exponent approaches 0.
$\infty^0$	Finite value, 0, $\pm \infty$ , or oscillation	Exponential limits where base approaches $\pm \infty$ and exponent approaches 0.^[1]
$1^\infty$	Finite value (often e or 1), $\pm \infty$ , or oscillation	Exponential limits where base approaches 1 and exponent approaches $\pm \infty$ .

History

Indeterminate form

Recent from talks

Recent from talks

Contribute something

Contribute something

Media Pages

Timelines

Articles

Notes collections

Notes

Notes

Days in Chronicle

Indeterminate form

Some examples and non-examples

Indeterminate form 0/0

Indeterminate form 00

Expressions that are not indeterminate forms

Evaluating indeterminate forms

Equivalent infinitesimal

L'Hôpital's rule

List of indeterminate forms

See also

References

Citations

Bibliographies

Indeterminate form

Basic Concepts

Definition

Context in Calculus

Examples of Indeterminate Forms

The 0/0 Form

The ∞/∞ Form

The 0^0 Form

Other Forms

Non-Indeterminate Expressions

Definite Forms

Distinguishing Features

Evaluation Methods

L'Hôpital's Rule

Equivalent Infinitesimals

Algebraic and Series Techniques

Add your contribution

Related Hubs

Contribute something

Indeterminate form 0⁰