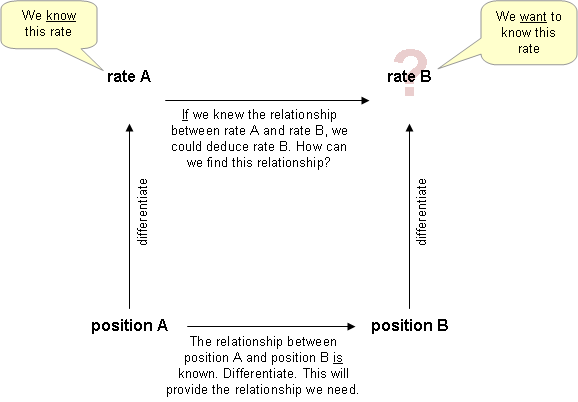
In differential calculus, related rates problems involve finding a rate at which a quantity changes by relating that quantity to other quantities whose rates of change are known. The rate of change is usually with respect to time. Because science and engineering often relate quantities to each other, the methods of related rates have broad applications in these fields. Differentiation with respect to time or one of the other variables requires application of the chain rule, since most problems involve several variables.

Fundamentally, if a function ${\displaystyle F}$ is defined such that ${\displaystyle F=f(x)}$, then the derivative of the function ${\displaystyle F}$ can be taken with respect to another variable. We assume ${\displaystyle x}$ is a function of ${\displaystyle t}$, i.e. ${\displaystyle x=g(t)}$. Then ${\displaystyle F=f(g(t))}$, so

Written in Leibniz notation, this is:

Thus, if it is known how ${\displaystyle x}$ changes with respect to ${\displaystyle t}$, then we can determine how ${\displaystyle F}$ changes with respect to ${\displaystyle t}$ and vice versa. We can extend this application of the chain rule with the sum, difference, product and quotient rules of calculus, etc.

For example, if ${\displaystyle F(x)=G(y)+H(z)}$ then

The most common way to approach related rates problems is the following:

Errors in this procedure are often caused by plugging in the known values for the variables before (rather than after) finding the derivative with respect to time. Doing so will yield an incorrect result, since if those values are substituted for the variables before differentiation, those variables will become constants; and when the equation is differentiated, zeroes appear in places of all variables for which the values were plugged in.

A 10-meter ladder is leaning against the wall of a building, and the base of the ladder is sliding away from the building at a rate of 3 meters per second. How fast is the top of the ladder sliding down the wall when the base of the ladder is 6 meters from the wall?