Hubbry Logo
Nuclear physicsNuclear physicsMain
Open search
Nuclear physics
Community hub
Nuclear physics
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Nuclear physics
Nuclear physics
Nuclear physics
View on Wikipedia
from Wikipedia
Nuclear physics
Models of the nucleus
Nuclides' classification
Nuclear stability
Radioactive decay
Nuclear fission
Capturing processes
High-energy processes
Nucleosynthesis and
nuclear astrophysics
High-energy nuclear physics
Scientists

Nuclear physics is the field of physics that studies atomic nuclei and their constituents and interactions, in addition to the study of other forms of nuclear matter.

Nuclear physics should not be confused with atomic physics, which studies the atom as a whole, including its electrons.

Discoveries in nuclear physics have led to applications in many fields such as nuclear power, nuclear weapons, nuclear medicine and magnetic resonance imaging, industrial and agricultural isotopes, ion implantation in materials engineering, and radiocarbon dating in geology and archaeology. Such applications are studied in the field of nuclear engineering.

Particle physics evolved out of nuclear physics and the two fields are typically taught in close association. Nuclear astrophysics, the application of nuclear physics to astrophysics, is crucial in explaining the inner workings of stars and the origin of the chemical elements.

History

[edit]
Henri Becquerel
Since the 1920s, cloud chambers played an important role of particle detectors and eventually lead to the discovery of positron, muon and kaon.

The history of nuclear physics as a discipline distinct from atomic physics, starts with the discovery of radioactivity by Henri Becquerel in 1896,[1] made while investigating phosphorescence in uranium salts.[2] The discovery of the electron by J. J. Thomson[3] a year later was an indication that the atom had internal structure. At the beginning of the 20th century the accepted model of the atom was J. J. Thomson's "plum pudding" model in which the atom was a positively charged ball with smaller negatively charged electrons embedded inside it.

In the years that followed, radioactivity was extensively investigated, notably by Marie Curie, a Polish physicist whose maiden name was Sklodowska, Pierre Curie, Ernest Rutherford and others. By the turn of the century, physicists had also discovered three types of radiation emanating from atoms, which they named alpha, beta, and gamma radiation. Experiments by Otto Hahn in 1911 and by James Chadwick in 1914 discovered that the beta decay spectrum was continuous rather than discrete. That is, electrons were ejected from the atom with a continuous range of energies, rather than the discrete amounts of energy that were observed in gamma and alpha decays. This was a problem for nuclear physics at the time, because it seemed to indicate that energy was not conserved in these decays.

The 1903 Nobel Prize in Physics was awarded jointly to Becquerel, for his discovery and to Marie and Pierre Curie for their subsequent research into radioactivity. Rutherford was awarded the Nobel Prize in Chemistry in 1908 for his "investigations into the disintegration of the elements and the chemistry of radioactive substances".

In 1905, Albert Einstein formulated the idea of mass–energy equivalence. While the work on radioactivity by Becquerel and Marie Curie predates this, an explanation of the source of the energy of radioactivity would have to wait for the discovery that the nucleus itself was composed of smaller constituents, the nucleons.

Rutherford discovers the nucleus

[edit]

In 1906, Ernest Rutherford published "Retardation of the a Particle from Radium in passing through matter."[4] Hans Geiger expanded on this work in a communication to the Royal Society[5] with experiments he and Rutherford had done, passing alpha particles through air, aluminum foil and gold leaf. More work was published in 1909 by Geiger and Ernest Marsden,[6] and further greatly expanded work was published in 1910 by Geiger.[7] In 1911–1912 Rutherford went before the Royal Society to explain the experiments and propound the new theory of the atomic nucleus as we now understand it.

Published in 1909,[8] with the eventual classical analysis by Rutherford published May 1911,[9][10][11][12] the key preemptive experiment was performed during 1909,[9][13][14][15] at the University of Manchester. Ernest Rutherford's assistant, Professor [15] Johannes [14] "Hans" Geiger, and an undergraduate, Marsden,[15] performed an experiment in which Geiger and Marsden under Rutherford's supervision fired alpha particles (helium 4 nuclei[16]) at a thin film of gold foil. The plum pudding model had predicted that the alpha particles should come out of the foil with their trajectories being at most slightly bent. But Rutherford instructed his team to look for something that shocked him to observe: a few particles were scattered through large angles, even completely backwards in some cases. He likened it to firing a bullet at tissue paper and having it bounce off. The discovery, with Rutherford's analysis of the data in 1911, led to the Rutherford model of the atom, in which the atom had a very small, very dense nucleus containing most of its mass, and consisting of heavy positively charged particles with embedded electrons in order to balance out the charge (since the neutron was unknown). As an example, in this model (which is not the modern one) nitrogen-14 consisted of a nucleus with 14 protons and 7 electrons (21 total particles) and the nucleus was surrounded by 7 more orbiting electrons.

Eddington and stellar nuclear fusion

[edit]

Around 1920, Arthur Eddington anticipated the discovery and mechanism of nuclear fusion processes in stars, in his paper The Internal Constitution of the Stars.[17][18] At that time, the source of stellar energy was a complete mystery; Eddington correctly speculated that the source was fusion of hydrogen into helium, liberating enormous energy according to Einstein's equation E = mc2. This was a particularly remarkable development since at that time fusion and thermonuclear energy, and even that stars are largely composed of hydrogen (see metallicity), had not yet been discovered.

Studies of nuclear spin

[edit]

The Rutherford model worked quite well until studies of nuclear spin were carried out by Franco Rasetti at the California Institute of Technology in 1929. By 1925 it was known that protons and electrons each had a spin of ±+1⁄2. In the Rutherford model of nitrogen-14, 20 of the total 21 nuclear particles should have paired up to cancel each other's spin, and the final odd particle should have left the nucleus with a net spin of 1⁄2. Rasetti discovered, however, that nitrogen-14 had a spin of 1.

James Chadwick discovers the neutron

[edit]
Main article: Discovery of the neutron

In 1932 Chadwick realized that radiation that had been observed by Walther Bothe, Herbert Becker, Irène and Frédéric Joliot-Curie was actually due to a neutral particle of about the same mass as the proton, that he called the neutron (following a suggestion from Rutherford about the need for such a particle).[19] In the same year Dmitri Ivanenko suggested that there were no electrons in the nucleus — only protons and neutrons — and that neutrons were spin 1⁄2 particles, which explained the mass not due to protons. The neutron spin immediately solved the problem of the spin of nitrogen-14, as the one unpaired proton and one unpaired neutron in this model each contributed a spin of 1⁄2 in the same direction, giving a final total spin of 1.

With the discovery of the neutron, scientists could at last calculate what fraction of binding energy each nucleus had, by comparing the nuclear mass with that of the protons and neutrons which composed it. Differences between nuclear masses were calculated in this way. When nuclear reactions were measured, these were found to agree with Einstein's calculation of the equivalence of mass and energy to within 1% as of 1934.

Proca's equations of the massive vector boson field

[edit]

Alexandru Proca was the first to develop and report the massive vector boson field equations and a theory of the mesonic field of nuclear forces. Proca's equations were known to Wolfgang Pauli[20] who mentioned the equations in his Nobel address, and they were also known to Yukawa, Wentzel, Taketani, Sakata, Kemmer, Heitler, and Fröhlich who appreciated the content of Proca's equations for developing a theory of the atomic nuclei in Nuclear Physics.[21][22][23][24][25]

Yukawa's meson postulated to bind nuclei

[edit]

In 1935 Hideki Yukawa[26] proposed the first significant theory of the strong force to explain how the nucleus holds together. In the Yukawa interaction a virtual particle, later called a meson, mediated a force between all nucleons, including protons and neutrons. This force explained why nuclei did not disintegrate under the influence of proton repulsion, and it also gave an explanation of why the attractive strong force had a more limited range than the electromagnetic repulsion between protons. Later, the discovery of the pi meson showed it to have the properties of Yukawa's particle.

With Yukawa's papers, the modern model of the atom was complete. The center of the atom contains a tight ball of neutrons and protons, which is held together by the strong nuclear force, unless it is too large. Unstable nuclei may undergo alpha decay, in which they emit an energetic helium nucleus, or beta decay, in which they eject an electron (or positron). After one of these decays the resultant nucleus may be left in an excited state, and in this case it decays to its ground state by emitting high-energy photons (gamma decay).

The study of the strong and weak nuclear forces (the latter explained by Enrico Fermi via Fermi's interaction in 1934) led physicists to collide nuclei and electrons at ever higher energies. This research became the science of particle physics, the crown jewel of which is the standard model of particle physics, which describes the strong, weak, and electromagnetic forces.

Modern nuclear physics

[edit]
Main articles: Liquid-drop model, Nuclear shell model, and Nuclear structure

A heavy nucleus can contain hundreds of nucleons. This means that with some approximation it can be treated as a classical system, rather than a quantum-mechanical one. In the resulting liquid-drop model,[27] the nucleus has an energy that arises partly from surface tension and partly from electrical repulsion of the protons. The liquid-drop model is able to reproduce many features of nuclei, including the general trend of binding energy with respect to mass number, as well as the phenomenon of nuclear fission.

Superimposed on this classical picture, however, are quantum-mechanical effects, which can be described using the nuclear shell model, developed in large part by Maria Goeppert Mayer[28] and J. Hans D. Jensen.[29] Nuclei with certain "magic" numbers of neutrons and protons are particularly stable, because their shells are filled.

Other more complicated models for the nucleus have also been proposed, such as the interacting boson model, in which pairs of neutrons and protons interact as bosons.

Ab initio methods try to solve the nuclear many-body problem from the ground up, starting from the nucleons and their interactions.[30]

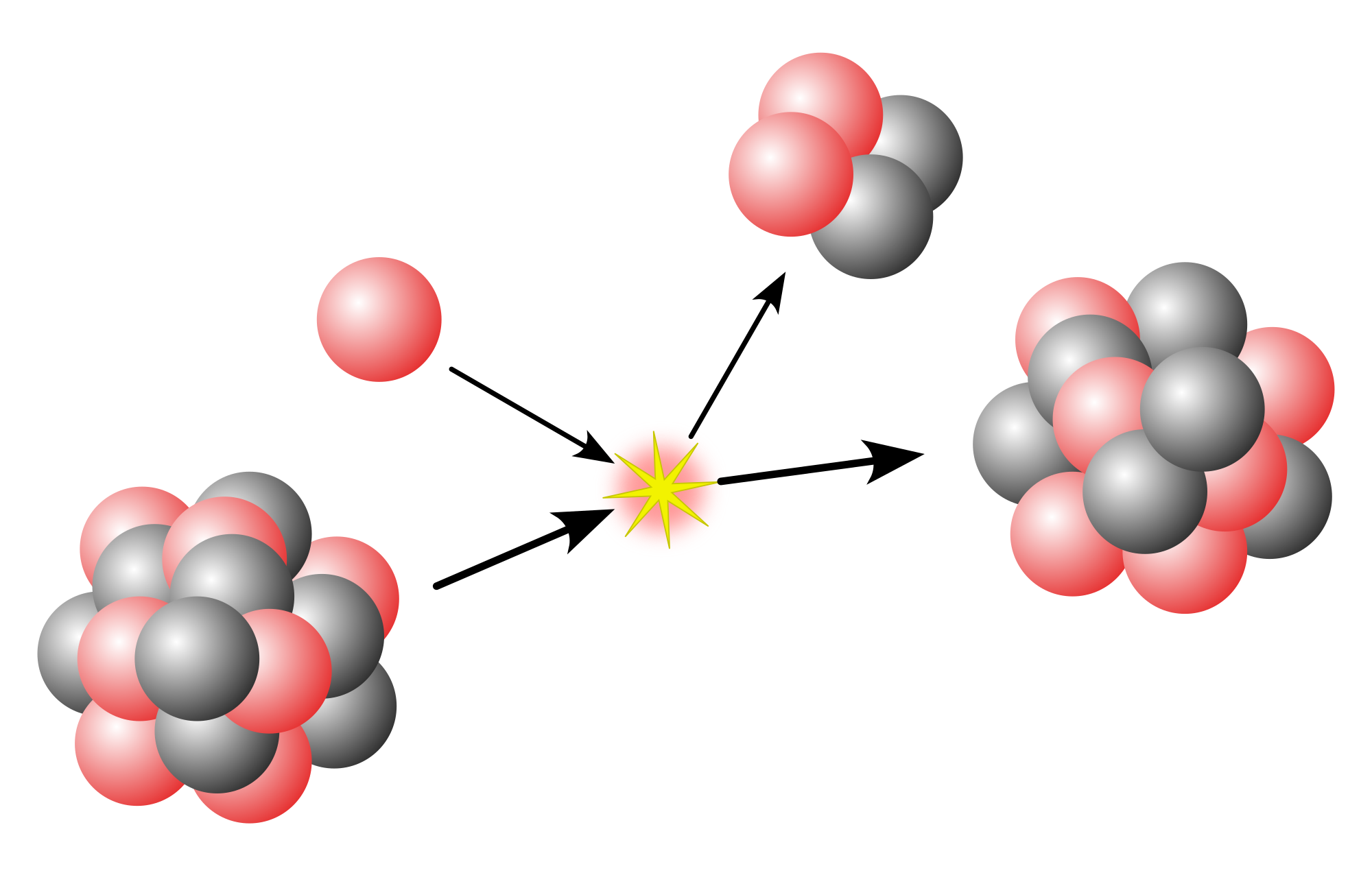
Much of current research in nuclear physics relates to the study of nuclei under extreme conditions such as high spin and excitation energy. Nuclei may also have extreme shapes (similar to that of Rugby balls or even pears) or extreme neutron-to-proton ratios. Experimenters can create such nuclei using artificially induced fusion or nucleon transfer reactions, employing ion beams from an accelerator. Beams with even higher energies can be used to create nuclei at very high temperatures, and there are signs that these experiments have produced a phase transition from normal nuclear matter to a new state, the quark–gluon plasma, in which the quarks mingle with one another, rather than being segregated in triplets as they are in neutrons and protons.

Nuclear decay

[edit]
Main articles: Radioactivity and Valley of stability

Eighty elements have at least one stable isotope which is never observed to decay, amounting to a total of about 251 stable nuclides. However, thousands of isotopes have been characterized as unstable. These "radioisotopes" decay over time scales ranging from fractions of a second to trillions of years. Plotted on a chart as a function of atomic and neutron numbers, the binding energy of the nuclides forms what is known as the valley of stability. Stable nuclides lie along the bottom of this energy valley, while increasingly unstable nuclides lie up the valley walls, that is, have weaker binding energy.

The most stable nuclei fall within certain ranges or balances of composition of neutrons and protons: too few or too many neutrons (in relation to the number of protons) will cause it to decay. For example, in beta decay, a nitrogen-16 atom (7 protons, 9 neutrons) is converted to an oxygen-16 atom (8 protons, 8 neutrons)[31] within a few seconds of being created. In this decay a neutron in the nitrogen nucleus is converted by the weak interaction into a proton, an electron and an antineutrino. The element is transmuted to another element, with a different number of protons.

In alpha decay, which typically occurs in the heaviest nuclei, the radioactive element decays by emitting a helium nucleus (2 protons and 2 neutrons), giving another element, plus helium-4. In many cases this process continues through several steps of this kind, including other types of decays (usually beta decay) until a stable element is formed.

In gamma decay, a nucleus decays from an excited state into a lower energy state, by emitting a gamma ray. The element is not changed to another element in the process (no nuclear transmutation is involved).

Other more exotic decays are possible (see the first main article). For example, in internal conversion decay, the energy from an excited nucleus may eject one of the inner orbital electrons from the atom, in a process which produces high speed electrons but is not beta decay and (unlike beta decay) does not transmute one element to another.

Nuclear fusion

[edit]

In nuclear fusion, two low-mass nuclei come into very close contact with each other so that the strong force fuses them. It requires a large amount of energy for the strong or nuclear forces to overcome the electrical repulsion between the nuclei in order to fuse them; therefore nuclear fusion can only take place at very high temperatures or high pressures. When nuclei fuse, a very large amount of energy is released and the combined nucleus assumes a lower energy level. The binding energy per nucleon increases with mass number up to nickel-62. Stars like the Sun are powered by the fusion of four protons into a helium nucleus, two positrons, and two neutrinos. The uncontrolled fusion of hydrogen into helium is known as thermonuclear runaway. A frontier in current research at various institutions, for example the Joint European Torus (JET) and ITER, is the development of an economically viable method of using energy from a controlled fusion reaction. Nuclear fusion is the origin of the energy (including in the form of light and other electromagnetic radiation) produced by the core of all stars including our own Sun.

Nuclear fission

[edit]

Nuclear fission is the reverse process to fusion. For nuclei heavier than nickel-62 the binding energy per nucleon decreases with the mass number. It is therefore possible for energy to be released if a heavy nucleus breaks apart into two lighter ones.

The process of alpha decay is in essence a special type of spontaneous nuclear fission. It is a highly asymmetrical fission because the four particles which make up the alpha particle are especially tightly bound to each other, making production of this nucleus in fission particularly likely.

From several of the heaviest nuclei whose fission produces free neutrons, and which also easily absorb neutrons to initiate fission, a self-igniting type of neutron-initiated fission can be obtained, in a chain reaction. Chain reactions were known in chemistry before physics, and in fact many familiar processes like fires and chemical explosions are chemical chain reactions. The fission or "nuclear" chain-reaction, using fission-produced neutrons, is the source of energy for nuclear power plants and fission-type nuclear bombs, such as those detonated in Hiroshima and Nagasaki, Japan, at the end of World War II. Heavy nuclei such as uranium and thorium may also undergo spontaneous fission, but they are much more likely to undergo decay by alpha decay.

For a neutron-initiated chain reaction to occur, there must be a critical mass of the relevant isotope present in a certain space under certain conditions. The conditions for the smallest critical mass require the conservation of the emitted neutrons and also their slowing or moderation so that there is a greater cross-section or probability of them initiating another fission. In two regions of Oklo, Gabon, Africa, natural nuclear fission reactors were active over 1.5 billion years ago.[32] Measurements of natural neutrino emission have demonstrated that around half of the heat emanating from the Earth's core results from radioactive decay. However, it is not known if any of this results from fission chain reactions.[33]

Production of "heavy" elements

[edit]
Main article: nucleosynthesis

According to the theory, as the Universe cooled after the Big Bang it eventually became possible for common subatomic particles as we know them (neutrons, protons and electrons) to exist. The most common particles created in the Big Bang which are still easily observable to us today were protons and electrons (in equal numbers). The protons would eventually form hydrogen atoms. Almost all the neutrons created in the Big Bang were absorbed into helium-4 in the first three minutes after the Big Bang, and this helium accounts for most of the helium in the universe today (see Big Bang nucleosynthesis).

Some relatively small quantities of elements beyond helium (lithium, beryllium, and perhaps some boron) were created in the Big Bang, as the protons and neutrons collided with each other, but all of the "heavier elements" (carbon, element number 6, and elements of greater atomic number) that we see today, were created inside stars during a series of fusion stages, such as the proton–proton chain, the CNO cycle and the triple-alpha process. Progressively heavier elements are created during the evolution of a star.

Energy is only released in fusion processes involving smaller atoms than iron because the binding energy per nucleon peaks around iron (56 nucleons). Since the creation of heavier nuclei by fusion requires energy, nature resorts to the process of neutron capture. Neutrons (due to their lack of charge) are readily absorbed by a nucleus. The heavy elements are created by either a slow neutron capture process (the so-called s-process) or the rapid, or r-process. The s process occurs in thermally pulsing stars (called AGB, or asymptotic giant branch stars) and takes hundreds to thousands of years to reach the heaviest elements of lead and bismuth. The r-process is thought to occur in supernova explosions, which provide the necessary conditions of high temperature, high neutron flux and ejected matter. These stellar conditions make the successive neutron captures very fast, involving very neutron-rich species which then beta-decay to heavier elements, especially at the so-called waiting points that correspond to more stable nuclides with closed neutron shells (magic numbers).

See also

[edit]

References

[edit]

Bibliography

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Nuclear physics

View on Grokipedia
from Grokipedia
Nuclear physics is the branch of that investigates the structure, stability, reactions, and decay of atomic nuclei, along with the protons and neutrons that constitute them and the that binds these particles against electrostatic repulsion. This discipline explores phenomena occurring at scales of femtometers within the nucleus, distinct from atomic physics which focuses on electron orbits, and relies on empirical data from accelerators, detectors, and theoretical models grounded in and . The field emerged in the late 19th century with Henri Becquerel's 1896 discovery of natural radioactivity in uranium salts, revealing unseen nuclear processes, followed by Ernest Rutherford's 1911 gold foil experiment that demonstrated the nucleus as a dense, positively charged core comprising most atomic mass. Pivotal advancements include James Chadwick's 1932 identification of the neutron as a neutral nuclear constituent, resolving mass discrepancies in isotopes, and the 1938 observation of uranium fission by Otto Hahn and Fritz Strassmann, which unleashed chain reactions powering both nuclear reactors and atomic bombs. Nuclear physics underpins critical technologies, including fission-based electricity generation that provides about 10% of global power while emitting no carbon dioxide during operation, production of radioisotopes for medical imaging and cancer therapy via targeted radiation, and elucidation of stellar fusion processes that forge elements heavier than helium. Defining challenges encompass accurately modeling the many-body strong interaction, which resists exact solutions due to computational complexity, and probing exotic nuclei near the drip lines to test limits of stability, with recent anomalies like unexpected energy shifts in heavy isotopes questioning established shell models. These pursuits drive ongoing experiments at facilities like those of the Department of Energy, advancing fundamental understanding and practical innovations amid debates over nuclear energy's safety and waste management.

Historical Development

Early Radioactivity and Nucleus Discovery (1896–1920s)

In February 1896, Henri Becquerel observed that uranium salts emitted rays capable of penetrating black paper and exposing a photographic plate, initially hypothesizing a connection to phosphorescence excited by sunlight. Further experiments on March 1, 1896, confirmed the emission occurred spontaneously without external stimulation, marking the discovery of radioactivity as an inherent atomic property. Becquerel's findings demonstrated that uranium emitted penetrating radiation continuously, independent of temperature or chemical form, with intensity proportional to uranium content. Building on Becquerel's work, Pierre and Marie Curie systematically investigated pitchblende ore, which exhibited higher radioactivity than its uranium content suggested. In July 1898, they announced the discovery of polonium, an element 400 times more active than uranium, named after Marie's native Poland. By December 1898, they identified radium, approximately two million times more radioactive than uranium, through laborious chemical separations yielding milligram quantities from tons of ore. These isolations established radioactivity as an atomic phenomenon tied to specific elements, prompting the term "radioactive elements" for substances decaying via emission. Ernest Rutherford, collaborating with Frederick Soddy, classified radioactive emissions into three types between 1899 and 1903. Alpha rays, deflected by electric and magnetic fields toward the negative plate but less than beta rays, were identified as doubly ionized helium atoms (He²⁺) with mass about 4 amu and charge +2e. Beta rays behaved as negatively charged particles with mass near that of electrons (cathode ray particles discovered by J.J. Thomson in 1897), penetrating farther than alphas. Gamma rays, discovered in 1900 from radium decay, showed no deflection in fields, indicating neutral, high-energy electromagnetic radiation akin to X-rays but more penetrating. Rutherford and Soddy's studies revealed sequential decay chains, with alpha emission transmuting elements by reducing atomic number by 2 and mass by 4, explaining observed half-lives and new species formation. J.J. Thomson's 1904 plum pudding model described the atom as a uniform sphere of positive charge, roughly 10⁻¹⁰ m in diameter, with electrons embedded like plums to maintain neutrality, consistent with observed atomic masses and electron counts. This diffuse structure accounted for minimal scattering in early experiments but predicted uniform deflection for charged probes. In 1909–1911, Rutherford, with Hans Geiger and Ernest Marsden, directed alpha particles from radium at thin gold foil (about 10⁻⁷ m thick). Contrary to Thomson's model, most particles passed undeflected, but approximately 1 in 8000 scattered by over 90 degrees, and some backscattered, implying atoms contain a minuscule, dense core (radius <10⁻¹⁴ m) bearing positive charge and most mass. Rutherford's 1911 analysis, using hyperbolic trajectories under Coulomb scattering, estimated the nucleus radius as 10,000 times smaller than the atom's, with charge Ze where Z is atomic number. This nuclear model supplanted the plum pudding view, positing electrons orbiting a central nucleus, laying groundwork for later quantum refinements by 1920.

Neutron Identification and Pre-Fission Era (1930–1938)

In 1930, German physicists Walther Bothe and Herbert Becker bombarded beryllium nuclei with alpha particles from polonium, observing a highly penetrating neutral radiation that produced coincidence counts with secondary particles but resisted absorption by materials that stopped charged particles or typical gamma rays; they interpreted this as gamma radiation of unprecedented energy exceeding 10 MeV. In 1932, French physicists Irène and Frédéric Joliot replicated and extended these results, noting that the radiation ejected protons from paraffin wax with kinetic energies up to approximately 5 MeV, which implied incident gamma photons of around 50 MeV to satisfy Compton scattering kinematics—a value far beyond contemporary theoretical limits for nuclear gamma emission. James Chadwick, working at the Cavendish Laboratory under Ernest Rutherford, investigated these findings in early 1932 by directing the beryllium-alpha radiation onto paraffin and measuring recoil proton energies via ionization in air; the maximum proton energy of 5.7 MeV could not be reconciled with high-energy gamma rays under Compton or photoelectric effects, as it required impossible photon momenta without violating conservation laws. Chadwick proposed instead a neutral particle with mass comparable to the proton (approximately 1 atomic mass unit), dubbing it the "neutron" for its lack of charge and role in ejecting protons via elastic collisions; momentum and energy conservation fit precisely with this hypothesis, and subsequent scattering experiments on nitrogen and other gases confirmed the neutron's neutrality and mass. Chadwick announced the discovery in a letter to Nature on February 27, 1932, followed by a detailed paper in the Proceedings of the Royal Society, resolving anomalies in isotopic masses and nuclear binding while earning him the 1935 Nobel Prize in Physics. The neutron's identification enabled rapid advances in nuclear transmutations. In December 1931, Harold Urey isolated deuterium (heavy hydrogen isotope-2) via fractional distillation and electrolysis, its mass-2 nucleus interpreted by Rutherford as a proton bound to a neutron, providing early empirical support for composite nuclei beyond protons alone. In April 1932, John Cockcroft and Ernest Walton at Cavendish used a high-voltage electrostatic accelerator to propel protons at 700 keV onto lithium-7 targets, detecting alpha particles with 8 MeV energy via scintillation screens, confirming the endothermic reaction 7Li+p→24He^7\mathrm{Li} + \mathrm{p} \to 2 ^4\mathrm{He} and demonstrating artificial nuclear disintegration with energy release as predicted by Weizsäcker's semi-empirical mass formula— the first such feat without relying on natural radioactive sources. These proton-lithium collisions released neutrons, further validating Chadwick's particle in reaction products. By 1934, neutron applications expanded nuclear synthesis. Irène and Frédéric Joliot induced artificial radioactivity by bombarding boron-10 with polonium alphas, yielding unstable nitrogen-13 (half-life 10 minutes) that decayed via positron emission to carbon-13 plus a neutrino, as 10B+α→13N∗+n^{10}\mathrm{B} + \alpha \to ^{13}\mathrm{N}^* + \mathrm{n}, followed by 13N→13C+e++νe^{13}\mathrm{N} \to ^{13}\mathrm{C} + e^+ + \nu_e; similar positrons arose from aluminum and magnesium transmutations, marking the first human-created radioisotopes and earning the 1935 Nobel Prize in Chemistry. Enrico Fermi's group in Rome, using radium-beryllium neutron sources, systematically irradiated elements from hydrogen to uranium, inducing radioactivity in over 60 species and classifying activities by half-life; crucially, in October 1934, they found that neutrons slowed by elastic scattering in paraffin or water (thermalizing to ~0.025 eV) exhibited cross-sections for capture up to 100–1000 times higher than fast neutrons (~1 MeV), enhancing reaction probabilities via lowered centrifugal barriers in s-wave interactions. These slow-neutron effects underpinned Fermi's 1934–1937 investigations into heavy-element transmutations, where uranium bombarded with moderated neutrons produced new beta-emitters (e.g., 13-second, 2.3-minute, 40-second activities), initially ascribed to transuranic elements beyond neptunium rather than fission fragments, as isotopic assignments favored sequential neutron capture and beta decay over symmetric splitting. Complementary theoretical progress included Hideki Yukawa's 1935 meson-exchange model for the strong nuclear force mediating proton-neutron binding, positing a massive particle (~200 proton masses) to confine the short-range force within ~10^{-15} m, anticipating pion discovery. By 1938, refined neutron spectroscopy and cross-section measurements, often via cloud chambers tracking recoil ions, solidified the neutron as the glue resolving nuclear stability puzzles, setting the stage for fission's elucidation without yet revealing chain-reaction potential.

Fission Discovery and World War II Mobilization (1938–1945)

In late 1938, German chemists Otto Hahn and Fritz Strassmann bombarded uranium atoms with neutrons and detected lighter elements, including barium, which indicated the nucleus had split into fragments rather than merely transmuting. Lise Meitner, who had collaborated with Hahn but fled Nazi Germany due to her Jewish ancestry, and her nephew Otto Frisch provided the theoretical interpretation during a walk in Sweden over Christmas 1938, calculating that the process released approximately 200 million electron volts per fission event and proposing it resembled biological fission, a term Frisch formalized as "nuclear fission" in early 1939. Their explanation, published in Nature on February 11, 1939, highlighted the potential for a self-sustaining chain reaction if neutrons from fission could induce further splits, releasing vast energy from uranium-235. The discovery rapidly alarmed émigré physicists fearing Nazi weaponization, as Germany's Uranverein program had begun exploring uranium in April 1939. Leo Szilard, recognizing the military implications, drafted a letter signed by Albert Einstein on August 2, 1939, warning President Franklin D. Roosevelt that German scientists might achieve chain reactions in a large uranium mass, producing bombs of "unimaginable power," and urging U.S. government funding for uranium research and isotope separation. Delivered on October 11, 1939, amid war's outbreak, it prompted Roosevelt to form the Advisory Committee on Uranium, initially allocating $6,000 for fission studies at universities like Columbia, where Enrico Fermi demonstrated uranium-graphite chain reaction hints by 1940. By mid-1941, British MAUD Committee reports confirmed a uranium bomb's feasibility with 10-25 pounds of U-235, accelerating U.S. efforts despite skepticism over scale. In June 1942, the U.S. Army Corps of Engineers assumed control under Brigadier General Leslie Groves, rebranding as the Manhattan Engineer District with a $2 billion budget (equivalent to about $30 billion in 2023 dollars), employing 130,000 personnel across sites including Oak Ridge, Tennessee, for electromagnetic and gaseous diffusion uranium enrichment; Hanford, Washington, for plutonium production via reactors; and Los Alamos, New Mexico, laboratory directed by J. Robert Oppenheimer for bomb design. Fermi's team achieved the first controlled chain reaction on December 2, 1942, in Chicago Pile-1, a 40-foot graphite-moderated uranium pile under the University of Chicago's Stagg Field, sustaining neutron multiplication for 28 minutes and validating reactor scalability. Parallel advances addressed fissile material scarcity: Oak Ridge's calutrons produced sufficient U-235 by 1945, while Hanford's B Reactor yielded plutonium-239, though its spontaneous fission necessitated an implosion lens design over simpler gun-type assembly. Oppenheimer's team, including physicists like Richard Feynman and Edward Teller, overcame implosion symmetry challenges through hydrodynamical modeling and high-explosive tests. The Trinity test on July 16, 1945, detonated a 21-kiloton plutonium device at Alamogordo, New Mexico, confirming viability with a yield from rapid supercritical assembly, though initial fears of atmospheric ignition proved unfounded via prior calculations. This culminated in Little Boy (uranium gun-type, 15 kilotons) dropped on Hiroshima on August 6, 1945, and Fat Man (plutonium implosion, 21 kilotons) on Nagasaki on August 9, ending organized Japanese resistance by August 15. Allied intelligence verified Germany's program stalled early due to resource diversion and misprioritization, never nearing a bomb.

Post-War Expansion and Cold War Accelerators (1946–1980s)

Following World War II, nuclear physics research expanded significantly under substantial government patronage, particularly in the United States, where the Atomic Energy Act of 1946 established the Atomic Energy Commission (AEC) to oversee atomic energy development, including fundamental research into nuclear structure and reactions. The AEC allocated millions in funding annually to national laboratories and universities, recognizing nuclear physics' dual role in weapons advancement and basic science, with nuclear physics emerging as the primary beneficiary of federal support amid Cold War priorities. This era saw the founding of facilities like Brookhaven National Laboratory in 1947, initially focused on civilian nuclear applications but quickly incorporating accelerator-based experiments to probe nuclear forces and isotopic properties. Internationally, similar expansions occurred, though constrained by geopolitical tensions, with Soviet facilities emphasizing parallel accelerator developments for nuclear studies. Accelerator technology advanced rapidly to achieve higher energies needed for detailed nuclear investigations, building on wartime innovations. The 184-inch synchrocyclotron at the University of California, Berkeley, achieved first operation in November 1946, modulating frequency to compensate for relativistic effects and accelerating deuterons to 190 MeV or alpha particles to 380 MeV, which enabled pioneering scattering experiments revealing nuclear potential shapes and reaction mechanisms. Shortly thereafter, Brookhaven's Cosmotron, a weak-focusing proton synchrotron with a 75-foot diameter and 2,000-ton magnet array, reached 3 GeV in 1952—the world's first GeV-scale machine—facilitating nuclear emulsion studies and pion production for meson-nuclear interactions. These instruments shifted research from low-energy spectroscopy to high-energy collisions, yielding data on nuclear excitation and fission barriers under extreme conditions. The 1950s and 1960s brought even larger synchrotrons tailored for nuclear physics, exemplified by Berkeley's Bevatron, operational from 1954 and designed to deliver 6.2 GeV protons, which supported heavy-ion beam lines and experiments on hypernuclei formation and nuclear matter compressibility. Heavy-ion accelerators proliferated for fusion reaction studies and exotic nuclei synthesis; Yale's heavy-ion linear accelerator (HILAC), commissioned in 1958, produced beams of ions like carbon and oxygen up to 5 MeV per nucleon, advancing understanding of nuclear shell closures and collective rotations. Berkeley's Super Heavy Ion Linear Accelerator (SuperHILAC), upgraded in the mid-1960s to energies exceeding 10 MeV per nucleon, coupled with cyclotrons for tandem operation, enabled the creation of superheavy elements and detailed fission dynamics measurements. Cold War competition spurred this scale-up, with U.S. facilities outpacing rivals in energy and beam quality, though limited exchanges occurred, such as Soviet invitations to their IHEP accelerator in the 1970s for joint nuclear beam tests. By the 1970s and into the 1980s, accelerator complexes integrated multiple stages for precision nuclear astrophysics and reaction rate determinations, with Brookhaven's Alternating Gradient Synchrotron (1959 onward) and planned Relativistic Heavy Ion Collider laying groundwork for quark-gluon plasma probes mimicking early universe conditions. Funding peaked under AEC successors like the Department of Energy, sustaining operations despite shifting priorities toward particle physics, as nuclear data informed weapons simulations and reactor safety without direct testing. This period's accelerators not only refined models of nuclear binding and decay but also highlighted tensions between open science and classified applications, with declassification of select results gradually broadening global access.

Fundamental Concepts

Atomic Nucleus Composition and Sizes

The atomic nucleus is composed of protons and neutrons, collectively termed nucleons. Protons carry a positive electric charge equal in magnitude to the elementary charge e, while neutrons possess no electric charge. The number of protons, denoted Z, defines the atomic number and thus the chemical element, whereas the total number of nucleons A = Z + N (with N the neutron number) approximates the atomic mass. These constituents are bound by the strong nuclear force, which overcomes the electrostatic repulsion between protons. Nuclear sizes are characterized by an effective radius R, empirically related to the mass number by R = r_0 A^{1/3}, where r_0 is a constant. For the root-mean-square charge radius, r_0 ≈ 1.2 fm, while the matter radius yields a slightly larger value of approximately 1.4 fm. This scaling arises from the near-constant nuclear density of about 0.17 nucleons per fm³, implying nuclear volume proportional to A. Actual nuclear density profiles exhibit a diffuse surface, but the A^{1/3} dependence holds well for A ≳ 10, with deviations for very light nuclei. For example, the proton (A=1) has a charge radius of roughly 0.84 fm, while heavier nuclei like uranium-238 (A=238) extend to about 7.4 fm. These dimensions, orders of magnitude smaller than atomic radii (~10²–10³ times), underscore the nucleus's extreme density, exceeding that of ordinary matter by a factor of ~10¹⁴.

Nuclear Binding Energy and Semi-Empirical Relations

The nuclear binding energy of an atom is the minimum energy required to separate its nucleus into its constituent protons and neutrons, equivalent to the energy released when the nucleus forms from those free nucleons. This energy arises from the mass defect, the difference between the mass of the isolated nucleons and the measured mass of the nucleus, converted via Einstein's relation E=mc2E = mc^2. The binding energy BB for a nucleus with mass number AA, atomic number ZZ, and neutron number N=A−ZN = A - Z is given by
B=[Zmp+Nmn−(mA−Zme)]c2,B = \left[ Z m_p + N m_n - (m_A - Z m_e) \right] c^2,
where mpm_p is the proton mass, mnm_n the neutron mass, mAm_A the atomic mass (including electrons), and mem_e the electron mass; the electron masses nearly cancel for neutral atoms, making the approximation valid since atomic binding energies are negligible compared to nuclear scales. Binding energies per nucleon peak around iron-56 at approximately 8.8 MeV, explaining its relative abundance in stellar nucleosynthesis as the point of maximum stability. To approximate binding energies without detailed quantum calculations, the semi-empirical mass formula (SEMF), also known as the Bethe-Weizsäcker formula, expresses B(Z,A)B(Z, A) as a sum of terms capturing bulk nuclear properties:
B(Z,A)=avA−asA2/3−acZ(Z−1)A1/3−asym(A−2Z)2A+δ,B(Z, A) = a_v A - a_s A^{2/3} - a_c \frac{Z(Z-1)}{A^{1/3}} - a_{sym} \frac{(A - 2Z)^2}{A} + \delta,
where coefficients aia_i are empirically fitted to experimental mass data, and δ\delta accounts for pairing effects. This liquid-drop-inspired model treats the nucleus as a charged incompressible fluid, balancing attractive strong forces against repulsive Coulomb interactions, and succeeds in reproducing measured binding energies to within a few percent for medium-to-heavy nuclei. The volume term avAa_v A represents the dominant attractive binding from short-range strong nuclear forces, with each nucleon interacting with roughly 12 neighbors in a saturated nuclear density of about 0.170.17 nucleons per fm³, yielding av≈15.5a_v \approx 15.5 MeV. The negative surface term −asA2/3-a_s A^{2/3} corrects for reduced coordination at the nuclear surface, analogous to surface tension in liquids, with as≈13a_s \approx 13--1818 MeV reflecting edge effects that lower density slightly outward. The Coulomb term −acZ(Z−1)/A1/3-a_c Z(Z-1)/A^{1/3} quantifies electrostatic repulsion among protons, modeled as a uniformly charged sphere of radius R≈1.2A1/3R \approx 1.2 A^{1/3} fm, giving ac≈0.72a_c \approx 0.72 MeV derived from ac=35e24πϵ0R0a_c = \frac{3}{5} \frac{e^2}{4\pi \epsilon_0 R_0} with proton charge ee. The asymmetry term −asym(A−2Z)2/A-a_{sym} (A - 2Z)^2 / A penalizes deviations from N≈ZN \approx Z, arising from the Pauli exclusion principle and isospin symmetry in the strong force, which favors balanced proton-neutron ratios; asym≈23a_{sym} \approx 23 MeV drives neutron excess in heavy nuclei to minimize Coulomb energy. The pairing term δ\delta (often ±ap/A3/4\pm a_p / A^{3/4} or ±12/A1/2\pm 12 / A^{1/2} MeV, with ap≈34a_p \approx 34 MeV) provides a small correction for quantum pairing: positive for even-even nuclei (paired protons and neutrons), zero for odd-AA, and negative for odd-odd, reflecting enhanced stability from Cooper-pair-like correlations in the nuclear superfluid. These terms, when fitted to datasets like the Atomic Mass Evaluation, predict fission barriers and beta-decay energies, though deviations near shell closures highlight the model's macroscopic limitations.
TermCoefficient (MeV)Physical Origin
Volumeav≈15.5a_v \approx 15.5Strong force saturation
Surfaceas≈13a_s \approx 13--1818Boundary effects
Coulombac≈0.72a_c \approx 0.72Proton repulsion
Asymmetryasym≈23a_{sym} \approx 23Isospin imbalance
Pairingδ≈±12/A\delta \approx \pm 12 / \sqrt{A}Nucleon pairing

Strong Nuclear Force and Residual Interactions

The strong nuclear force, also known as the strong interaction, is the fundamental force responsible for binding quarks into protons, neutrons, and other hadrons, as well as mediating the residual interactions that hold atomic nuclei together. It operates at subatomic scales through the exchange of massless gluons between quarks carrying color charge, a property analogous to electric charge but involving three types (red, green, blue) and their anticolors, leading to color confinement where quarks are never observed in isolation. Described by quantum chromodynamics (QCD), the theory predicts asymptotic freedom at high energies (short distances), where the force weakens, allowing perturbative calculations, but strong coupling at low energies (nuclear scales), necessitating non-perturbative methods like lattice QCD for accurate modeling. The force's strength, characterized by the QCD coupling constant α_s ≈ 1 at energy scales of ~1 GeV relevant to nuclear physics, vastly exceeds that of electromagnetism (α_em ≈ 1/137), enabling it to overcome proton-proton Coulomb repulsion within nuclei. At the scale of nucleons (protons and neutrons), separated by ~1–2 femtometers (fm), the strong force manifests as the residual strong interaction, an effective two-body potential arising from the incomplete cancellation of gluon exchanges between the constituent quarks of adjacent nucleons. This residual force is mediated primarily by the exchange of light mesons—virtual particles such as pions (π⁺, π⁻, π⁰ with mass ~140 MeV/c²), rho mesons (ρ with mass ~770 MeV/c²), and others—emitted from one nucleon and absorbed by another, transmitting momentum and binding the nucleus. The dominant one-pion-exchange (OPE) contribution yields a spin-dependent Yukawa potential of the form V(r) ≈ -(g_πNN² / 4π) (τ₁·τ₂) (σ₁·σ₂) (e^{-μ r}/r), where g_πNN ≈ 13.5 is the pion-nucleon coupling constant, τ and σ are isospin and spin operators, μ = m_π c / ℏ ≈ 0.7 fm⁻¹ sets the range to ~1.4 fm (the pion's Compton wavelength), and the tensor term (S_{12}) introduces quadrupole deformation crucial for nuclear deformation. Shorter-range components from heavier mesons like rho provide repulsion at r < 0.5 fm, preventing collapse, while multi-pion exchanges and gluon-mediated core effects refine the potential in modern chiral effective field theories. Key properties of the residual strong force include its short range (confined to ~2–3 fm, beyond which it drops exponentially, unlike the long-range electromagnetic force), approximate charge independence (similar strength for proton-proton, neutron-neutron, and proton-neutron pairs, reflecting isospin SU(2) symmetry treating protons and neutrons as states of the nucleon), and saturation (each nucleon interacts strongly with only nearest neighbors, ~4–12 in a nucleus, explaining nuclear matter density ~0.17 nucleons/fm³ without unbounded attraction). These features ensure nuclear stability against electromagnetic repulsion, which at nuclear distances (~1 fm) exerts a Coulomb barrier of ~0.7 Z₁ Z₂ MeV (for protons), countered by the strong force's ~10–100 MeV well depth per nucleon pair. Violations of charge independence, observed at ~1% level in scattering experiments (e.g., np vs. pp cross sections differing by ~few mb at 10–100 MeV), arise from electromagnetic corrections, quark mass differences (m_d > m_u by ~2–5 MeV), and pion cloud effects, quantifiable in precision lattice QCD simulations. The force's tensor and spin-orbit components drive phenomena like deuteron quadrupole moment (Q_d ≈ 0.286 fm²) and magic numbers in shell structure.

Theoretical Models of the Nucleus

Liquid Drop Model and Fission Barriers

The liquid drop model portrays the atomic nucleus as a charged, incompressible droplet of nuclear matter, where nucleons interact via short-range attractive forces analogous to molecular cohesion in liquids, opposed by long-range Coulomb repulsion among protons. This macroscopic approach, formalized by Niels Bohr in 1936, captures bulk nuclear properties without resolving individual nucleon motions, emphasizing surface tension, volume saturation, and electrostatic effects as dominant contributors to stability. The model's predictive power derives from the semi-empirical mass formula (SEMF), proposed by Carl Friedrich von Weizsäcker in 1935, which approximates the binding energy B(A,Z)B(A, Z) for a nucleus with mass number AA and proton number ZZ: B(A,Z)=avA−asA2/3−acZ(Z−1)A1/3−aa(A−2Z)24A±apA−1/2,B(A, Z) = a_v A - a_s A^{2/3} - a_c \frac{Z(Z-1)}{A^{1/3}} - a_a \frac{(A-2Z)^2}{4A} \pm a_p A^{-1/2}, with fitted coefficients: volume term av≈15.5a_v \approx 15.5 MeV reflecting strong force saturation; surface term as≈16.8a_s \approx 16.8 MeV accounting for reduced coordination at the boundary; Coulomb term ac≈0.717a_c \approx 0.717 MeV quantifying electrostatic destabilization; asymmetry term aa≈23.285a_a \approx 23.285 MeV penalizing neutron-proton imbalance due to Pauli exclusion in the strong force; and pairing term ap≈12a_p \approx 12 MeV favoring even-even configurations via residual interactions. These parameters, derived from mass spectrometry data across nuclides, enable computation of nuclear masses and stabilities with errors under 1% for most species. Applied to fission, the model reveals instability in heavy nuclei where Coulomb energy exceeds surface binding, quantified by the fissility parameter x=acZ22asAx = \frac{a_c Z^2}{2 a_s A}; for x>1x > 1, spontaneous division occurs, though observed fission requires x≈0.7−1x \approx 0.7-1 due to deformation barriers. The SEMF predicts a fissionability limit near Z2/A≈50Z^2/A \approx 50, aligning with actinide behavior, as deformation lowers surface energy while initially increasing Coulomb repulsion less rapidly. Fission barriers in the liquid drop framework denote the potential energy maximum along the deformation path from spherical ground state to scission, computed by minimizing SEMF energy at fixed volume under elongation (e.g., via quadrupole parameter β2\beta_2). Bohr and Wheeler's 1939 analysis expanded the model to dynamical deformations, estimating the saddle-point barrier as Bf≈Esaddle−EgroundB_f \approx E_{\rm saddle} - E_{\rm ground}, where saddle configurations feature neck formation and reduced Coulomb self-energy; for uranium isotopes, macroscopic barriers range 15-25 MeV, scaling as Bf∝A−1/3(1−2x)3/2B_f \propto A^{-1/3} (1 - 2x)^{3/2} in simplified approximations. This overestimates empirical thresholds (e.g., 5-6 MeV for neutron-induced fission in 235U^{235}\mathrm{U}) by neglecting shell structure, yet provides the baseline for macroscopic-microscopic refinements.

Independent Particle Shell Model

The independent particle shell model describes atomic nuclei as systems of non-interacting protons and neutrons occupying quantized energy levels in a central mean-field potential, analogous to electron shells in atoms but accounting for the short-range strong nuclear force. This approximation assumes each nucleon moves independently in an average potential generated by the nuclear core, with shell closures occurring at specific "magic numbers" of protons or neutrons—2, 8, 20, 28, 50, 82, and 126—beyond which nuclei display exceptional stability, lower binding energy per nucleon deviations, and reduced cross sections for certain reactions. Formulated in 1949 by Maria Goeppert Mayer and J. Hans D. Jensen, the model resolved discrepancies in earlier attempts by incorporating a strong spin-orbit coupling term into the single-particle Hamiltonian, which splits degenerate orbital levels and aligns predicted shell gaps with empirical magic numbers observed in nuclear binding energies and decay rates since the 1930s. Mayer's work, building on harmonic oscillator potentials modified by spin-orbit interactions, quantitatively reproduced the sequence of magic numbers, while Jensen emphasized isospin symmetry between protons and neutrons; their contributions earned the 1963 Nobel Prize in Physics. The mean-field potential is typically parameterized as a Woods-Saxon form, V(r)=−V0/(1+exp⁡((r−R)/a))V(r) = -V_0 / (1 + \exp((r - R)/a)), with depth V0≈50V_0 \approx 50 MeV, radius R≈1.25A1/3R \approx 1.25 A^{1/3} fm (where AA is the mass number), and diffuseness a≈0.65a \approx 0.65 fm, augmented by a spin-orbit term Vls(l⋅s)/r dV/drV_{ls} (\mathbf{l} \cdot \mathbf{s}) / r \, dV/dr of strength Vls≈20−25V_{ls} \approx 20-25 MeV to prioritize high-jj subshells for filling. Single-particle wave functions are solutions to the Schrödinger equation in this potential, yielding quantum numbers nn, ll, jj, and mjm_j, with the Pauli exclusion principle enforcing maximum occupancy of 2j+12j + 1 per subshell. For ground states near closed shells, the model predicts the total angular momentum JJ as that of the unpaired valence nucleon, matching observed spins and parities for odd-AA nuclei, such as J=5/2+J = 5/2^+ for 17^{17}O from the d5/2d_{5/2} neutron level. Magnetic moments are approximated via the Schmidt lines, μ=j\mu = j (in nuclear magnetons) for l=0l = 0 or j=l+1/2j = l + 1/2, though deviations arise from meson-exchange currents and configuration mixing. Excited states emerge from particle-hole excitations across shell gaps, with selection rules from angular momentum conservation. Limitations include neglect of two-body residual interactions, which drive pairing correlations (reducing excitation energies by ~1-2 MeV via BCS-like gaps) and collective rotations/vibrations in non-spherical nuclei, necessitating extensions like the interacting shell model with configuration interaction. Despite approximations, the model underpins ab initio calculations using realistic nucleon-nucleon potentials, achieving spectroscopic quality for light nuclei up to A≈16A \approx 16.

Collective and Microscopic Models

The collective model, pioneered by Aage Bohr and Ben Roy Mottelson in 1952–1953, treats the nucleus as a deformable fluid exhibiting coherent motion among many nucleons, rather than independent particle behavior. This approach extends the liquid drop model by incorporating quadrupole deformations, surface vibrations, and rotations, successfully accounting for the low-lying excitation spectra in heavy, deformed nuclei such as rare-earth isotopes. For axially symmetric deformations, the model predicts rotational energy levels following the rigid rotor formula EJ=ℏ22IJ(J+1)E_J = \frac{\hbar^2}{2\mathcal{I}} J(J+1), where I\mathcal{I} is the moment of inertia and JJ the total angular momentum, matching experimental spacings in bands observed via Coulomb excitation and inelastic scattering experiments from the 1950s onward. Vibrational modes, modeled as quantized surface oscillations, describe spherical nuclei like those near 208^{208}Pb, with characteristic 2+→0+2^+ \to 0^+ transitions at energies around 1–2 MeV, as verified in gamma-ray spectroscopy data. The model's parameters, including deformation β\beta and triaxiality γ\gamma, are fitted to empirical moments and transition probabilities, enabling predictions of electromagnetic decay rates via the rotational model's intensity rules, such as enhanced E2E2 transitions within bands by factors of 10310^3–10410^4 over single-particle estimates. Limitations arise in transitional regions, where anharmonicity and particle-core coupling require extensions like the variable moment of inertia or cranking models, introduced in the 1960s to incorporate Coriolis effects and align quasiparticles. Empirical validation includes the prediction of backbending in moment-of-inertia curves for high-spin states in nuclei like 158^{158}Dy, observed in heavy-ion fusion-evaporation reactions by the mid-1970s. Microscopic models derive nuclear properties from realistic two- and three-body nucleon-nucleon interactions, often using many-body techniques to solve the Schrödinger equation for AA nucleons. The Hartree-Fock-Bogoliubov approximation, developed in the 1950s–1960s, generates self-consistent mean fields from effective potentials like Skyrme or Gogny forces, yielding single-particle orbitals and pairing gaps that reproduce binding energies within 1–2 MeV for medium-mass nuclei. Beyond mean-field, random-phase approximation (RPA) incorporates residual interactions to describe collective excitations, deriving giant resonances like the isoscalar giant quadrupole at 14–16 MeV from particle-hole correlations, consistent with electron scattering data from accelerators such as those at SLAC in the 1970s. Ab initio methods, such as no-core shell model or chiral effective field theory, achieve parameter-free calculations for light nuclei (A≤16A \leq 16) using bare nucleon potentials renormalized via similarity renormalization group, predicting ground-state energies and electromagnetic moments with accuracies better than 1% for 4^4He and 16^{16}O as of 2020s benchmarks. These contrast with collective phenomenology by explicitly including tensor forces and three-body effects, revealing emergent collectivity—e.g., quadrupole correlations arising from T=0T=0 neutron-proton pairs—without ad hoc deformation variables. Configuration-interaction approaches, like the projected shell model, bridge gaps by diagonalizing valence spaces over deformed bases, reproducing rotational bands in rare earths with reduced χ2\chi^2 fits to data under 1 for E2E2 probabilities. Efforts to unify the paradigms include microscopic derivations of the Bohr-Mottelson Hamiltonian via RPA or time-dependent density functional theory, projecting collective operators onto shell-model configurations to justify irrotational flow assumptions and predict shape coexistence in nuclei like 78^{78}Kr, where prolate and oblate minima differ by 0.5–1 MeV in energy landscapes from constrained Hartree-Fock calculations. Such hybrid frameworks highlight that collective modes emerge from correlated many-body dynamics, with deformation parameters β2≈0.2\beta_2 \approx 0.2–0.3 correlating to microscopic quadrupole moments Q∼10Q \sim 10–100 eb in even-even nuclei, as cross-verified by lifetime measurements and ab initio extrapolations.

Nuclear Stability and Decay Modes

Alpha, Beta, and Gamma Decay Mechanisms

Alpha decay involves the spontaneous emission of an alpha particle, consisting of two protons and two neutrons bound as a helium-4 nucleus (^4_2He), from an unstable parent nucleus, primarily in heavy nuclides with atomic numbers Z > 82. This process reduces the proton-to-neutron ratio in the daughter nucleus, enhancing stability against electrostatic repulsion among protons. The decay is described by the reaction ^{A}{Z}X \to ^{A-4}{Z-2}Y + ^4_2He + Q, where Q is the disintegration energy, typically 4-9 MeV for common emitters like uranium-238 (Q = 4.27 MeV). Classically, alpha emission is prohibited by the Coulomb barrier, which exceeds the available kinetic energy of the alpha particle; the barrier height for typical separations is on the order of 20-30 MeV, far above Q. Quantum mechanically, the process proceeds via tunneling: the alpha particle, assumed preformed within the nucleus due to strong nuclear correlations, penetrates the barrier with a transmission probability governed by the Gamow factor, approximately \exp(-2\pi \eta), where \eta = (2\mu Z_d Z_\alpha e^2 / \hbar v)^{1/2} involves the reduced mass \mu, charges Z_d and Z_\alpha, and velocity v of the alpha. This semiclassical model, developed by Gamow in 1928, accurately predicts half-lives ranging from microseconds to billions of years, correlating logarithmically with Q and barrier penetrability. Beta decay encompasses processes mediated by the weak nuclear interaction, altering the nucleon flavor without changing the nucleon number A but shifting Z by \pm 1. In beta-minus decay (n \to p + e^- + \bar{\nu}_e), a neutron transforms into a proton, electron, and electron antineutrino, occurring in neutron-rich nuclei to increase the proton fraction; the free neutron lifetime is 879.4 \pm 0.6 seconds. Beta-plus decay (p \to n + e^+ + \nu_e) converts a proton to a neutron, positron, and neutrino in proton-rich nuclei, with the process requiring sufficient Q > 1.022 MeV to account for positron-electron annihilation. The weak force, characterized by charged current interactions via W^\pm bosons (mass ~80 GeV/c^2), violates parity and operates at femtometer scales with coupling strength ~10^{-5} times the strong force. The beta spectrum is continuous due to three-body kinematics, with maximum electron energies up to several MeV (e.g., 18.6 MeV for neutron decay endpoint, though modulated by nuclear matrix elements). Fermi's golden rule describes the transition rate as proportional to the phase space integral \int p_e^2 (Q - E_e)^2 dE_e, weighted by nuclear form factors; allowed transitions (ΔJ=0 or 1, no parity change) dominate via vector-axial vector currents conserved in the standard model. Electron capture, a competing beta process, involves orbital electron absorption (p + e^- \to n + \nu_e), prevalent in high-Z nuclei where Q is low. Gamma decay is the electromagnetic deexcitation of an excited nuclear state to a lower-energy state, emitting a high-energy photon (γ) with no change in Z or A, often following alpha or beta decay. The transition energy E_γ matches the level spacing, typically 10 keV to 10 MeV, with wavelengths ~10^{-12} to 10^{-10} m. Represented as ^{A}{Z}X^* \to ^{A}{Z}X + \gamma, the process obeys multipole selection rules: electric 2^L pole (EL) for parity-preserving ΔJ = L (even L) or L\pm1 (odd L), magnetic (ML) for parity-changing, with lowest multipoles (E1, M1) fastest due to radiation ~ (kR)^{2L} suppression for higher L, where k is photon wave number and R nuclear radius. Weisskopf-Weisskopf single-particle estimates yield lifetimes τ ≈ (ħ / E_γ^3) (E_γ R / ħ c)^{2L-1} / constants, but collective effects enhance rates in deformed nuclei; hindered transitions (e.g., spin-forbidden) extend lifetimes to nanoseconds. Internal conversion competes at low E_γ, where the nucleus ejects an orbital electron instead of radiating, with probability increasing for high-Z and inner shells. Gamma rays carry angular momentum and parity from the nuclear transition, enabling spectroscopy of level schemes.

Spontaneous Fission and Cluster Decay

Spontaneous fission represents a quantum tunneling process in which a heavy atomic nucleus divides into two fragments of comparable mass, typically accompanied by the release of 2–4 neutrons and subsequent gamma radiation, without requiring external excitation. This decay mode becomes observable in actinides and transactinides with atomic numbers Z > 82, where the fission barrier height decreases sufficiently to allow appreciable tunneling probability despite the nucleus's overall stability against induced fission. The theoretical foundation rests on the liquid drop model, augmented by shell corrections, which predicts the barrier as arising from competition between surface tension-like binding and Coulomb repulsion; for spontaneous events, the tunneling action integral through this barrier determines the half-life, often exceeding 10^{15} years for lighter actinides like uranium-238 but shortening dramatically for superheavies. The discovery of spontaneous fission occurred in 1940 when Georgy Flerov and Konstantin Petrzhak detected rare fission events in uranium-238 using ionization chamber measurements, attributing them to intrinsic instability rather than cosmic ray induction, with an estimated half-life of approximately 10^{16} years for this mode—far longer than the 4.47 × 10^9-year alpha decay half-life, yielding a branching ratio below 10^{-6}. In heavier isotopes, such as californium-252, spontaneous fission dominates with a partial half-life of about 2.6 years and a branching ratio approaching 3% relative to total decay, making it a practical neutron source due to ~3–4 neutrons emitted per event. Plutonium-240 exhibits a spontaneous fission branching ratio of roughly 5.7 × 10^{-5}, influencing nuclear fuel reactivity through accumulated fragments and neutrons. Experimental branching ratios for such isotopes are measured via high-precision mass spectrometry and fission track detection, revealing systematics where even-Z, even-N configurations enhance stability against fission. Cluster decay, a rarer intermediate process between alpha emission and full spontaneous fission, entails the tunneling of a preformed light cluster (e.g., ^{14}C or ^{20}O) from the parent nucleus, leaving a doubly magic or near-magic daughter. Predicted theoretically in the 1980s via analytic superposition of fission and alpha modes in the liquid drop framework, it was first experimentally confirmed in 1984 through observation of ^{14}C emission from ^{223}Ra, with a partial half-life of 10^{15} years and branching ratio of ~10^{-10} relative to alpha decay. Subsequent detections include ^{20}O from ^{222,224}Ra, ^{23}F from ^{231}Pa, and heavier clusters like ^{32}Si from thorium isotopes, all with branching ratios below 10^{-12}, verified using magnetic spectrometers and silicon detectors at facilities like ISOLDE. These decays probe nuclear structure via cluster preformation probabilities, modeled as solutions to the Schrödinger equation with mass asymmetry coordinates, where hindrance factors relative to alpha decay reflect shell effects and barrier penetrability. Unlike binary spontaneous fission, cluster modes favor asymmetric splits due to Q-value maximization near closed shells, with experimental yields constrained by Geiger-Nuttall-like relations adjusted for cluster inertia.

Stability Criteria: Magic Numbers and Drip Lines

Nuclei display enhanced stability when the proton number ZZ or neutron number NN reaches specific values known as magic numbers: 2, 8, 20, 28, 50, 82, and 126. These configurations correspond to complete filling of nuclear energy levels in the shell model, resulting in closed shells that confer greater resistance to decay and fission compared to neighboring nuclides. Empirical evidence includes abrupt changes in the binding energy per nucleon, elevated first excited-state energies (e.g., higher 2+2^+ levels in even-even nuclei), and minima in neutron-capture cross-sections at these numbers. The shell model, formulated by Maria Goeppert Mayer and J. Hans D. Jensen in 1949, accounts for these by incorporating a spin-orbit coupling term in the nucleon mean-field potential, which splits degenerate levels and yields the observed sequence. Double magic numbers, where both ZZ and NN are magic (e.g., 48^{48}Ca with Z=20Z=20, N=28N=28; 208^{208}Pb with Z=82Z=82, N=126N=126), exhibit particularly robust stability, with binding energies exceeding those predicted by semi-empirical mass formulas by several MeV and decay half-lives orders of magnitude longer than adjacent isotopes. In neutron-deficient or neutron-rich regions, shell closures can shift; for instance, experiments at GSI confirmed a new subshell closure at N=32N=32 in 54^{54}Ca, altering single-particle energies near the drip lines. The drip lines delineate the boundaries of bound nuclear matter on the chart of nuclides, defined as loci where the one-neutron separation energy SnS_n or one-proton separation energy SpS_p equals zero. Beyond the neutron drip line, adding a neutron results in an unbound state, leading to prompt neutron emission and continuum resonances rather than discrete bound levels; the proton drip line similarly marks proton-unbound limits, though it resides closer to the valley of stability due to Coulomb repulsion increasing proton separation barriers. For light elements, drip-line positions are experimentally mapped, such as 8^8He (N=6N=6) approaching the neutron drip line for Z=2Z=2, while heavier cases rely on predictions from density functional theory or shell-model extrapolations, with the neutron drip line for Z≈100Z \approx 100 estimated around N≈180N \approx 180. Nuclei near the drip lines often display exotic phenomena, including halo structures where valence nucleons occupy high-ll orbitals with extended wavefunctions (e.g., the two-neutron halo in 11^{11}Li, where Sn≈0.2S_n \approx 0.2 MeV), low-lying resonances, and enhanced two-proton or di-neutron emission channels. Magic numbers influence drip-line positions by stabilizing shell closures, potentially creating "islands of inversion" where deformed configurations compete with spherical ones, as observed in mid-mass neutron-rich isotopes. Experimental probes, such as knockout reactions at facilities like RIKEN or NSCL, measure separation energies to refine these boundaries, revealing deviations from liquid-drop predictions due to shell effects.

Nuclear Reactions and Processes

Reaction Kinematics and Cross Sections

In nuclear reactions, kinematics describes the conservation of energy and momentum for incoming projectiles and target nuclei interacting to produce outgoing particles. For a two-body reaction a+A→b+Ba + A \to b + B, the Q-value determines the energetics: Q=[ma+mA−mb−mB]c2Q = [m_a + m_A - m_b - m_B] c^2, where masses are atomic or nuclear as appropriate, and cc is the speed of light. Positive Q indicates an exothermic reaction releasing kinetic energy to products, while negative Q signifies endothermic processes requiring input energy. In the laboratory frame, where the target is at rest, the kinetic energy relation is Q=Tb+TB−TaQ = T_b + T_B - T_a, with TT denoting kinetic energies. For endothermic reactions (Q < 0), a threshold incident kinetic energy TthT_{th} is required in the laboratory frame to enable the reaction, given by Tth=−Q(1+mamA)T_{th} = -Q \left(1 + \frac{m_a}{m_A}\right), assuming non-relativistic conditions where projectile mass mam_a is much less than target mass mAm_A. This threshold arises because excess kinetic energy in the center-of-mass frame must compensate for the energy deficit. Momentum conservation further constrains outgoing particle directions and energies, often solved via quadratic equations for energies as functions of scattering angles. Kinematic analyses distinguish between the laboratory frame, where the target is stationary and measurements occur, and the center-of-mass frame, where total momentum vanishes, simplifying isotropic angular distributions and theoretical calculations. Transformations between frames involve boosting along the beam direction; for non-relativistic cases, outgoing lab angles θlab\theta_{lab} relate to center-of-mass angles θCM\theta_{CM} by tan⁡θlab=sin⁡θCMcos⁡θCM+mb/mB\tan \theta_{lab} = \frac{\sin \theta_{CM}}{\cos \theta_{CM} + m_b / m_B} for equal masses or adjusted ratios. In relativistic regimes, Lorentz transformations apply, altering energies and angles based on the center-of-mass velocity v=plabc2/(Elab+mAc2)v = p_{lab} c^2 / (E_{lab} + m_A c^2). Nuclear cross sections quantify reaction probabilities, defined as the effective interaction area per target nucleus such that the reaction rate equals incident flux times target density times cross section σ\sigma. Units are typically in barns (1 b = 10^{-24} cm²), with subdivisions like millibarns (mb) for finer scales. Total cross sections sum all possible outcomes, while partial cross sections specify channels (e.g., elastic, inelastic); differential cross sections dσ/dΩd\sigma / d\Omega describe angular dependence. Cross sections are measured experimentally by detecting reaction products from a known beam flux incident on a thin target, using σ=N/(ϕnt)\sigma = N / (\phi n t), where NN is detected events, ϕ\phi is particle flux, nn is areal target density, and tt is exposure time; for angular distributions, dσ/dΩ=Nq/(QnxΔΩ)d\sigma / d\Omega = N q / (Q n x \Delta \Omega), with qq elementary charge, QQ collected beam charge, and xx target thickness. Values vary strongly with incident energy, exhibiting resonances from compound nucleus formation or thresholds, and are tabulated in databases like those from the National Nuclear Data Center for applications in reactors and astrophysics.

Induced Fission and Chain Reactions

Induced fission refers to the splitting of a heavy atomic nucleus into two or more lighter nuclei triggered by the absorption of an incident particle, most commonly a neutron. This process was first observed in 1938 when Otto Hahn and Fritz Strassmann irradiated uranium with neutrons and detected lighter elements like barium among the products, a finding later theoretically explained by Lise Meitner and Otto Robert Frisch as nuclear fission. In the paradigmatic case of uranium-235 (U-235), a thermal neutron is absorbed, forming an excited uranium-236 (U-236) compound nucleus with approximately 6.5 MeV of excitation energy, which exceeds the fission barrier of about 5.5-6 MeV, leading to asymmetric scission into fission fragments such as barium-141 and krypton-92, accompanied by the release of 2 to 3 prompt neutrons and gamma rays. The total energy released per fission event is roughly 200 MeV, with about 168 MeV appearing as kinetic energy of the fragments, converted to heat via Coulomb interactions in a medium. The neutrons emitted during induced fission enable the possibility of a self-sustaining nuclear chain reaction, wherein each fission event produces sufficient neutrons to induce further fissions in neighboring fissile nuclei. For U-235, the average number of prompt neutrons released per fission (ν) is approximately 2.43 for thermal neutron-induced fission, though including delayed neutrons from precursor isotopes raises the effective total to about 2.5. The sustainability of the chain reaction is quantified by the effective neutron multiplication factor, k_eff, defined as the ratio of the number of neutrons in one generation to the previous generation, accounting for production by fission, absorption without fission, leakage, and other losses. A system is subcritical if k_eff < 1 (neutron population decreases), critical if k_eff = 1 (steady-state), and supercritical if k_eff > 1 (exponential growth), with the latter enabling explosive energy release in nuclear weapons or controlled power generation in reactors via neutron moderators, reflectors, and absorbers like cadmium or boron to adjust reactivity. Fissile isotopes such as U-235, uranium-233 (U-233), and plutonium-239 (Pu-239) are particularly amenable to induced fission by low-energy neutrons due to their low fission barriers post-neutron capture, whereas uranium-238 (U-238) primarily undergoes radiative capture unless fast neutrons (above ~1 MeV) are employed. Criticality requires achieving a sufficient mass and geometry to minimize neutron leakage, known as the critical mass; for bare U-235, this is about 52 kg for a sphere, reducible with tampers or reflectors. In practice, nuclear reactors maintain k_eff slightly above 1 during operation, relying on delayed neutrons (about 0.65% of total for U-235) for stability, as prompt neutrons alone would yield a much higher β_eff ≈ 0.0065, allowing seconds-scale response times for control systems. This controlled chain reaction underpins nuclear power, where sustained fissions generate heat for steam turbines, contrasting with the rapid, uncontrolled supercritical assembly in fission bombs.

Fusion Reactions and Barriers

Nuclear fusion reactions unite light atomic nuclei to form heavier ones, converting mass into energy via the binding energy curve, where the binding energy per nucleon peaks around iron-56. This process requires overcoming mutual electrostatic repulsion, quantified as the Coulomb barrier with height VC=14πϵ0Z1Z2e2R1+R2V_C = \frac{1}{4\pi\epsilon_0} \frac{Z_1 Z_2 e^2}{R_1 + R_2}, typically 0.5–5 MeV for light nuclei pairs like proton-proton or deuterium-tritium, depending on charges Z1,Z2Z_1, Z_2 and radii R1,R2≈1.2A1/3R_1, R_2 \approx 1.2 A^{1/3} fm. Quantum tunneling circumvents classical requirements for energies exceeding VCV_C, with probability governed by the Gamow factor G(E)∝exp⁡(−2πZ1Z2e2hv)G(E) \propto \exp\left( - \frac{2\pi Z_1 Z_2 e^2}{h v} \right), where vv is relative velocity; this yields a reaction rate peaking at the Gamow energy E0=(πZ1Z2e22ℏ)2m1m2m1+m2kT2E_0 = \left( \frac{\pi Z_1 Z_2 e^2}{2 \hbar} \right)^2 \frac{m_1 m_2}{m_1 + m_2} kT^2, balancing tunneling enhancement and Boltzmann suppression in thermal plasmas. For deuterium-tritium (D-T) fusion, 2H+3H→4He(3.5 MeV)+n(14.1 MeV)^2\mathrm{H} + ^3\mathrm{H} \to ^4\mathrm{He}(3.5\,\mathrm{MeV}) + \mathrm{n}(14.1\,\mathrm{MeV}), the barrier is ~0.4 MeV, cross-section peaks at ~5 barns near 100 keV center-of-mass energy, and total Q-value is 17.6 MeV, making it optimal for terrestrial reactors due to lower ignition temperature ~10–20 keV versus ~100 keV for proton-proton. In stellar interiors, the proton-proton chain dominates for low-mass stars, initiating with p+p→2H+e++νep + p \to ^2\mathrm{H} + e^+ + \nu_e (weak interaction, Q=1.44 MeV, barrier ~0.5 MeV), followed by charged particle captures requiring tunneling through higher effective barriers from lower Z but thermal velocities at millions of Kelvin. Heavier cycles like CNO face steeper barriers from higher Z catalysts, shifting peaks to greater temperatures ~15–20 MK. Additional barriers include angular momentum (centrifugal) for l>0 partial waves and nuclear structure effects like resonances boosting cross-sections, as in D-T's 3/2+ state. Net fusion power demands ignition, where alpha heating sustains against losses, per nτETi≳5×1021n \tau_E T_i \gtrsim 5 \times 10^{21} keV·s·m^{-3} for D-T at ~10 keV ion TiT_i, requiring densities ~10^{20} m^{-3} and confinement ~1 s or equivalents in inertial schemes. Sub-barrier fusion enhances via multi-body effects or screening in dense , but remains exponentially sensitive to .

Nucleosynthesis and Cosmic Origins

Big Bang Nucleosynthesis and Light Elements

(BBN) refers to the formation of light atomic nuclei in the early , occurring approximately 10 seconds to 20 minutes after the , when the ranged from about 10^9 to 10^7 (corresponding to energies of ~0.1–1 MeV). During this , the transitioned from a dominated by photons, electrons, protons, and neutrons to one where stable nuclei could form without immediate . The process is governed by the expansion rate, set by the Hubble parameter and influenced by the energy density (primarily from relativistic particles), and the baryon-to-photon ratio η ≈ 6 × 10^{-10}, which determines the scarcity of baryons relative to photons. BBN primarily synthesizes deuterium (D), helium-3 (^3He), helium-4 (^4He), and lithium-7 (^7Li), with trace amounts of beryllium-7 decaying to lithium-7; heavier elements are negligible due to the brief timescale and lack of stable intermediates beyond ^4He. The neutron-to-proton (n/p) ratio is established by weak interactions (e.g., n ↔ p + e^- + ν̄_e), which maintain equilibrium until freeze-out at ~1 MeV, yielding n/p ≈ exp(-Δm/m_e) ≈ 1/6, where Δm is the neutron-proton . Subsequent neutron ( ~880 s) reduces this to ~1/7 by the onset of nucleosynthesis, providing the neutrons needed for . A limitation is the deuterium bottleneck: the low binding energy of deuterium (2.2 MeV) makes it vulnerable to photodissociation by the abundant high-energy photons (η^{-1} ≈ 10^{10} photons per baryon), delaying significant nucleus formation until T ~ 0.08 MeV, when the deuterium abundance suffices to initiate rapid reactions. Once broken, this bottleneck allows swift : p + D → ^3He + γ, D + D → ^3He + n or ^4He + γ, and nearly all available neutrons capture into ^4He (binding energy 28.3 MeV, highly stable), resulting in a ^4He fraction Y_p ≈ 2(n/p)/(1 + n/p) ≈ 0.25. Residual unprocessed protons dominate as ^1H (~75% by ), with leftover deuterium and ^3He from incomplete pairings. Standard BBN predictions, computed using nuclear reaction networks sensitive to η, the neutron lifetime τ_n, and extra radiation (e.g., from neutrinos), yield primordial abundances that align well with observations for most elements. For ^4He, Y_p ≈ 0.247 ± 0.003 matches extragalactic H II region measurements of ~0.244–0.248 after corrections for stellar production. Deuterium, fragile and not produced post-BBN, shows D/H ≈ (2.45 ± 0.05) × 10^{-5} from quasar absorption lines, consistent with theory. ^3He abundances are harder to isolate primordially due to stellar processing but support BBN within uncertainties. However, ^7Li exhibits a tension: predictions of ^7Li/H ≈ (4–5) × 10^{-10} exceed halo star observations of ~1.6 × 10^{-10} by a factor of ~3–4, potentially indicating gaps in nuclear rates, diffusion in stars, or new physics like non-standard neutrino interactions, though no consensus resolution exists. These abundances constrain cosmology: BBN-derived η_b h^2 ≈ 0.008–0.025 overlaps with cosmic microwave background (CMB) measurements from Planck (η_b h^2 ≈ 0.0224), validating the hot Big Bang model and limiting extra relativistic degrees of freedom (ΔN_eff < 0.3–1). Updates to input parameters, such as τ_n = 879.4 ± 0.6 s from 2021 measurements, refine predictions but do not resolve the lithium discrepancy. BBN's success as a probe relies on well-calibrated low-energy nuclear cross-sections from laboratory experiments, underscoring its empirical foundation over alternative cosmologies lacking quantitative light-element predictions.

Stellar Fusion and s-Process

In stars with masses above approximately 0.08 solar masses, nuclear fusion begins with the proton-proton (pp) chain or the CNO cycle, converting hydrogen into helium and releasing energy that balances gravitational contraction. The pp chain dominates in low-mass stars like the Sun, involving sequential proton captures and beta decays to form helium-4, with a core temperature around 15 million Kelvin required for ignition. In more massive stars exceeding 1.3 solar masses, the CNO cycle prevails due to higher temperatures (above 17 million Kelvin), cycling carbon, nitrogen, and oxygen as catalysts in a closed loop that fuses four protons into helium-4 more efficiently. These hydrogen-burning phases constitute over 90% of a star's lifetime on the main sequence. Post-main-sequence evolution involves helium fusion ignited at core temperatures of about 100 million Kelvin via the triple-alpha process, where three helium-4 nuclei combine to form carbon-12, subsequently capturing additional alphas to produce oxygen-16, neon-20, and magnesium-24. In stars above 8 solar masses, advanced burning stages occur in onion-like shells: carbon burning at 600 million Kelvin yields neon and magnesium; neon burning at 1.2 billion Kelvin produces oxygen and magnesium; oxygen burning at 1.5 billion Kelvin forms silicon and sulfur; and silicon burning at 3 billion Kelvin builds the iron-peak nuclei through photodisintegrations and alpha captures. Iron-56 marks the endpoint of exothermic fusion, as further captures require energy input, leading to core collapse in massive stars. The s-process, or slow neutron-capture process, operates in asymptotic giant branch (AGB) stars of low to intermediate mass (1-8 solar masses) during thermal pulses in the helium-burning shell, where neutron densities remain low (around 10^7 neutrons per cubic centimeter) such that capture timescales exceed most beta-decay half-lives, allowing the nucleosynthesis path to follow the valley of beta stability. Primary neutron sources are the 13C(α,n)16O reaction, activated during convective mixing that dredges up protons to form 13C pockets, and the 22Ne(α,n)25Mg reaction during hotter pulses above 300 million Kelvin; the former dominates the bulk s-process yield. Starting from iron-peak seed nuclei, successive neutron captures and intervening beta decays build heavier isotopes up to bismuth-209, with branching points at unstable nuclei like 85Kr determining isotopic ratios; this process accounts for roughly half of the galactic abundances of elements heavier than iron up to lead. Observational constraints from presolar grains and barium stars confirm AGB origins, though uncertainties in neutron release and mixing persist.

Rapid Processes: r-Process and Heavy Element Formation

The r-process, or rapid neutron-capture process, is a nucleosynthesis pathway in which atomic nuclei rapidly capture free neutrons at rates exceeding the timescales of subsequent beta decays, leading to the formation of extremely neutron-rich isotopes that decay toward stability. This process builds heavy elements beyond the iron peak (Z > 26), for approximately half of all nuclei heavier than iron, particularly those with mass numbers A > 130, such as , and . Neutron densities in r-process environments reach 10^{20}-10^{30} neutrons per cm³, with capture times on the order of milliseconds, the production of over 50 neutrons per nucleus before beta decay intervenes. The mechanism proceeds in phases: an initial freeze-out from nuclear statistical equilibrium where (n,γ) captures dominate over photodisintegrations, followed by a neutron-capture on seed nuclei (typically iron-group ), and concluding with decays that shift the decay toward observed abundances. Theoretical models predict a characteristic abundance peaking around A ≈ 80 (third r-process peak) and A ≈ 130 (second peak), modulated by neutron separation energies and shell effects near magic numbers like N=82 and N=126. Uncertainties persist in nuclear physics inputs, such as neutron-capture cross-sections and fission barriers for superheavy nuclei, which influence yields of actinides like thorium-232 and uranium-238. Primary astrophysical sites for the r-process are binary mergers, where dynamical and neutrino-driven provide the requisite extreme fluxes during the collision and post-merger . Ejected material masses range from 0.01 to 0.1 solar masses, with electron fractions Ye ≈ 0.05-0.3 favoring neutron-rich conditions; mergers occurring at Galactic rates of 10-100 per million years suffice to explain cosmic r-process enrichment. While core-collapse supernovae were once favored, simulations indicate insufficient neutron richness in neutrino-driven for robust r-process yields, limiting their contribution; alternative sites like collapsars or magneto-rotational supernovae remain marginal. Observational confirmation emerged from the gravitational wave event GW170817 on August 17, 2017, involving a neutron star merger at 40 Mpc , whose electromagnetic counterpart AT2017gfo exhibited powered by of r-process nuclides. features, including a blue-to-red color over days and tentative of lines, indicated lanthanide-poor and -rich ejecta components, with total r-process mass ≈ 0.05 M⊙ matching model predictions for elements up to the actinides. Isotopic anomalies in ultra-metal-poor stars, such as high [Eu/Fe] ratios, further support rare, high-yield events like mergers over frequent supernova contributions. These data resolve long-standing debates, affirming mergers as the dominant source while highlighting needs for refined nuclear mass measurements to match observed abundance patterns.

Experimental Techniques and Facilities

Particle Accelerators and Beams

Particle accelerators are devices that use electromagnetic fields to accelerate charged particles, such as protons, electrons, or heavy ions, to high energies for inducing reactions and studying properties. In physics, these instruments produce particle beams with precisely controlled energies, typically ranging from kiloelectronvolts (keV) to gigaelectronvolts (GeV) per , enabling experiments on , reactions, and exotic nuclei. The beams collide with fixed or other beams, revealing details about forces, binding energies, and decay modes through the of reaction products. The principles rely on Lorentz force acceleration: electric fields provide longitudinal boosts, while magnetic fields constrain transverse motion to prevent beam divergence. Early electrostatic accelerators, like the Cockcroft-Walton generator operational in 1932 at 700 keV, achieved the first artificial nuclear transmutation by bombarding lithium with protons, producing alpha particles as predicted by quantum tunneling theory. Van de Graaff generators, introduced in the 1930s, generated up to several MV through charge accumulation on high-voltage electrodes, powering tandem accelerators that strip and reaccelerate ions for nuclear reaction studies up to 20-30 MeV. These constant-potential machines remain useful for low-energy precision experiments due to their stable beams and simplicity. Cyclotrons, pioneered by in with a keV prototype to 1.22 MeV protons by , employ a fixed to induce spiral trajectories and radiofrequency (RF) oscillating at the for repeated accelerations across a central gap. Fixed-frequency operation limits energies to non-relativistic regimes, but frequency-modulated synchrocyclotrons and superconducting variants extend capabilities to 100-500 MeV/nucleon for heavy ions, as in facilities producing beams for fusion-like reactions or spallation neutron sources. Beam intensities reach 10^14 particles per second, with emittance minimized by careful ion source design and bunching. Linear accelerators (linacs) propel particles along straight paths using sequential RF cavities, where phased electromagnetic waves synchronize with particle velocity for efficient energy gain without radiation losses inherent in curved paths. Proton linacs, such as the 800 MeV facility at Los Alamos operational since 1947, deliver high-current beams (up to 1 mA) for nuclear physics and isotope production, while heavy-ion linacs like those at GSI achieve velocities near the speed of light for relativistic reactions. Superconducting RF technology, advanced since the 1970s, reduces power consumption and enables continuous-wave operation, supporting beam energies over 100 MeV/A with pulse lengths of microseconds. Synchrotrons, developed , circulate particles in rings with ramped matching increasing and RF cavities for phased , allowing GeV-scale energies in compact designs. In nuclear physics, synchrotrons like the Alternating Gradient Synchrotron (AGS) at Brookhaven, operational since 1960 at up to 24 GeV for protons, drive heavy-ion collisions mimicking interactions, while booster rings enhance for rare-isotope (RIB) production via projectile fragmentation. properties include low emittance (<1 mm mrad) via strong focusing and polarization preservation up to 70% for spin-dependent studies. Storage rings further enable internal target experiments with cooled beams, extending interaction times for precision measurements. Beam lines transport accelerated particles from the accelerator to experimental stations using quadrupole and dipole magnets for focusing and steering, with diagnostics like Faraday cups measuring current and profile monitors assessing emittance. In nuclear applications, beams are often degraded or purified for specific reactions, such as inverse kinematics where heavy projectiles hit light targets to study astrophysically relevant captures. Radioactive ion beams, generated via in-flight separation or isotope separation on-line (ISOL), extend studies to unstable nuclei near drip lines, with facilities achieving 10^6-10^9 ions per second. Challenges include beam loss from scattering and activation, mitigated by vacuum systems at 10^{-10} mbar and radiation shielding.

Detection Methods: Gamma Spectroscopy and Tracking

Gamma-ray spectroscopy identifies and characterizes nuclear excited states by measuring the discrete energies of gamma rays emitted during de-excitation cascades following nuclear reactions or decays. The technique relies on detectors that record the full energy deposition of incident gamma rays, producing photopeak spectra where peak positions correspond to transition energies, typically in the range of 10 keV to 10 MeV, with intensities reflecting branching ratios. High-purity germanium (HPGe) detectors dominate due to their superior energy resolution, achieving approximately 2 keV full width at half maximum (FWHM) at 1.33 MeV, enabling the resolution of closely spaced nuclear levels separated by as little as 1-2 keV. Interactions occur primarily via Compton scattering, photoelectric absorption, and pair production; only events with complete energy deposition contribute to the photopeak, while partial depositions form a Compton continuum that limits efficiency in traditional setups. In nuclear physics experiments, such as in-beam spectroscopy with particle accelerators, gamma spectroscopy maps level schemes, determines spin-parity assignments, and measures lifetimes via Doppler-shift attenuation methods. Arrays of multiple HPGe detectors, often arranged in geometries approaching 4π solid angle coverage, enhance detection efficiency and angular correlation analysis; for instance, escape-suppressed setups use anti-Compton shields of bismuth germanate (BGO) scintillators to veto incomplete energy events, improving peak-to-total ratios to over 60%. Calibration involves standard sources like ^{60}Co (1.17 and 1.33 MeV lines) or ^{152}Eu, ensuring absolute energy accuracy to within 0.1 keV. Gamma-ray tracking advances spectroscopy by reconstructing the trajectories of individual gamma rays within highly segmented HPGe detectors, mitigating Compton background through event-by-event analysis. In tracking arrays like GRETINA or the planned GRETA, each gamma interaction sequence—scattering points and energies—is digitized with sub-millimeter position resolution using digital signal processing and machine learning algorithms for pattern recognition. This yields photopeak efficiencies exceeding 40% for a full 4π array at 1 MeV, compared to 10-20% in conventional clover detectors, while providing Doppler correction via interaction positions for reaction kinematics reconstruction. The method exploits the kinematics of Compton scattering, solving for scattering angles and energies to discriminate valid full-energy events from escapes or multi-gamma pileup. Tracking enables high-fold coincidence studies in exotic nuclei produced at facilities like FRIB, resolving complex decay schemes in neutron-rich isotopes where traditional methods suffer from low efficiency. For example, GRETA's design incorporates 36 large-volume segmented germanium crystals, achieving angular resolutions of 1°-5° and enabling gamma-gamma angular correlations with uncertainties below 1°. Challenges include high data rates (up to 10^6 events/s) requiring front-end electronics with 100 MHz sampling and real-time tracking algorithms, as demonstrated in GRETINA deployments since 2012. These systems thus extend nuclear structure studies to weaker transitions and higher excitation energies, up to 20-30 MeV, critical for understanding shell evolution and collectivity.

Key Facilities: RHIC, FAIR, and Recent Upgrades

The Relativistic Heavy Ion Collider (RHIC) at Brookhaven National Laboratory in Upton, New York, is a 3.8-kilometer circumference superconducting accelerator ring operational since 2000, designed to collide heavy ions such as gold nuclei at energies up to 100 GeV per nucleon pair to recreate quark-gluon plasma conditions from the early universe microseconds after the Big Bang. It achieves collision rates exceeding 10 billion per second for gold ions, enabling studies of quantum chromodynamics under extreme temperatures and densities exceeding 10^12 K, where quarks and gluons transition from confinement in hadrons to a deconfined state. RHIC also uniquely operates as a polarized proton collider with beam polarizations up to 70%, facilitating spin-dependent interaction probes, including the first polarized proton collisions at 500 GeV center-of-mass energy. The Facility for Antiproton and Ion Research (FAIR), under construction at the GSI Helmholtz Centre for Heavy Ion Research in Darmstadt, Germany, comprises an international accelerator complex centered on the SIS100 synchrotron with a 100 Tm magnetic rigidity and 1,100-meter circumference, capable of accelerating ions up to uranium at intensities up to 10^11 particles per pulse and antiprotons to 15 GeV. Upon completion, FAIR will deliver beams 1,000 times more intense than prior facilities, supporting experiments on nuclear matter at high baryon densities, including heavy-ion collisions mimicking neutron star cores via facilities like the Compressed Baryonic Matter (CBM) detector. It extends GSI's existing infrastructure, with Phase 0 operations leveraging current accelerators for precursor experiments since 2018. Recent upgrades at RHIC for the Beam Energy Scan (BES) Phase II, initiated in 2019, include electron cooling via the Low-Energy RHIC Electron Cooler (LEReC), which uses 1-5 MeV electron bunches to reduce ion beam emittance by factors of 2-3, enabling luminosity increases up to 10 times at energies below 7.7 GeV per nucleon for probing QCD phase transitions near the critical point. Additional enhancements encompass 9 MHz radiofrequency cavities for bunch shortening and stochastic cooling improvements, yielding gold-gold luminosities over 10^30 cm^-2 s^-1 in 2020-2024 runs, with data accumulation projected at 20 billion events by 2025 before RHIC's reconfiguration into the Electron-Ion Collider. For FAIR, construction milestones include SIS100 magnet series production completion by 2024 and transport line commissioning by late 2025, advancing toward beam operations in 2027 and full user experiments by 2028, enhancing heavy-ion collision capabilities at 2-8 GeV per nucleon for baryon-rich matter studies. These developments prioritize empirical validation of phase diagrams through higher precision data, countering prior limitations in statistics and beam quality.

Practical Applications

Nuclear Power Generation: Reactors and Fuel Cycles

Nuclear power generation utilizes controlled nuclear fission chain reactions within reactors to release thermal energy, which drives steam turbines for electricity production. The process begins with neutrons inducing fission in fissile nuclei, primarily uranium-235, liberating approximately 200 MeV per fission event—over a million times the energy of chemical reactions—while emitting 2-3 additional neutrons to propagate the chain reaction. To sustain a steady-state reaction without criticality excursion, reactors incorporate neutron moderators to thermalize fast fission neutrons (reducing their energy from ~2 MeV to ~0.025 eV), increasing the fission cross-section of uranium-235 from about 1 barn to 580 barns, and control rods composed of neutron-absorbing materials like boron-10 or cadmium to adjust the neutron multiplication factor (k-effective) near unity. Most operational reactors are thermal neutron designs, classified by moderator and coolant types. Pressurized water reactors (PWRs), comprising about 70% of global capacity as of 2024, employ ordinary water (H2O) as both moderator and coolant, maintained at 15-16 MPa to suppress boiling and transfer heat via a secondary loop. Boiling water reactors (BWRs) allow core boiling to generate steam directly, simplifying design but requiring separation of radioactive steam. Heavy-water moderated reactors, such as CANDU types, use deuterium oxide (D2O), which has lower neutron absorption (due to deuterium's lack of a large upscatter cross-section), enabling fission with unenriched natural uranium (0.7% U-235). Gas-cooled reactors, like advanced gas-cooled (AGR) variants, use graphite moderation and CO2 coolant for higher thermal efficiency (~41% vs. 33% for PWRs). Fast neutron reactors bypass moderation, relying on high-energy neutrons (~0.1-1 MeV) to sustain fission in plutonium-239 or uranium-238, with breeding ratios exceeding 1.0 to convert fertile U-238 into fissile Pu-239 via neutron capture and beta decay (half-life of Pu-239 precursor Np-239 is 2.36 days). This design minimizes long-lived actinide waste but requires liquid metal coolants like sodium for heat removal due to poor moderation by coolants. Experimental prototypes, such as Russia's BN-800 operational since 2016, demonstrate closed-cycle potential with breeding ratios up to 1.1. The nuclear fuel cycle integrates reactor physics with material processing. Front-end stages involve mining uranium ore (global identified resources ~6 million tonnes U as of 2023), milling to yellowcake (U3O8), conversion to UF6 gas, enrichment via gaseous diffusion or centrifugation to 3-5% U-235 for light-water reactors (LWRs), and fabrication into UO2 pellets clad in zircaloy rods. During irradiation, ~3-5% of U-235 fissions, producing Pu-239 (from 30% of captures in U-238) and accumulating fission products that absorb neutrons, necessitating fuel shuffling or replacement after 3-6 years. Open (once-through) cycles discard spent fuel after cooling, leaving ~95% recoverable uranium (mostly U-238) and 1% plutonium, with direct disposal in geologic repositories like Finland's Onkalo (under construction since 2004). Closed cycles reprocess via PUREX solvent extraction to separate uranium (~96%), plutonium (~1%), and waste, recycling Pu and U into mixed oxide (MOX) fuel (typically 5-7% PuO2 in UO2) for LWRs or breeders, potentially extracting 30-60 times more energy per tonne of uranium while reducing high-level waste volume by 90%. France's La Hague facility reprocessed ~1,100 tonnes annually as of 2023, but proliferation risks from separated plutonium have limited adoption; the U.S. halted commercial reprocessing in 1977 under Carter policy, citing safeguards concerns. In breeders, the cycle achieves near-complete actinide burnup, transmuting minor actinides like americium-241 (half-life 432 years) via fast-spectrum fission.

Nuclear Weapons: Physics of Detonation and Yields

Nuclear weapons derive their explosive power from controlled nuclear reactions that release vast amounts of energy through fission or fusion processes, far exceeding chemical explosives. In fission-based devices, a supercritical mass of fissile material, such as uranium-235 or plutonium-239, sustains an exponential chain reaction where neutrons split atomic nuclei, producing additional neutrons and energy via the conversion of a small fraction of mass into kinetic energy, heat, and radiation per Einstein's mass-energy equivalence. The critical mass required for this chain reaction varies with factors including material purity, density, geometry, and neutron reflectors; for bare plutonium-239, it is approximately 10 kilograms under ideal compression, but practical designs account for predetonation risks and inefficiencies. Only about 1-2% of the fissile material typically fissions before hydrodynamic disassembly limits the reaction, yielding energies equivalent to thousands of tons of TNT. Fission weapon detonation typically employs either gun-type or implosion assemblies to rapidly achieve supercriticality. The gun-type design, suitable for highly enriched uranium-235 due to its lower spontaneous fission rate, propels a subcritical "bullet" into a subcritical "target" using conventional explosives, forming a supercritical mass in microseconds; the Little Boy bomb, detonated over Hiroshima on August 6, 1945, used this method with about 64 kilograms of uranium, achieving a yield of approximately 15 kilotons of TNT equivalent from the fission of roughly 1 kilogram of material. Implosion designs, necessary for plutonium-239's higher neutron emission, symmetrically compress a subcritical spherical pit using precisely timed high-explosive lenses to increase density by a factor of two or more, initiating the chain reaction; the Fat Man bomb, dropped on Nagasaki on August 9, 1945, employed this with 6.2 kilograms of plutonium, yielding about 21 kilotons of TNT. These designs ensure the reaction's prompt supercritical phase dominates, with neutron multiplication factors exceeding unity by orders of magnitude before expansion quenches the process. Yields are quantified in TNT equivalents, where 1 kiloton corresponds to 4.184 × 10¹² joules, derived from empirical blast measurements, radiochemical analysis of fission products, and seismic data; for instance, Little Boy's yield was calculated from canister pressure gauges and structural damage patterns in Hiroshima. Fission yields are inherently limited to around 500 kilotons maximum due to the finite fissile material and disassembly timescales, though boosting with fusion fuels like deuterium-tritium enhances efficiency by supplying additional neutrons, increasing fission by 20-50% in modern primaries. Thermonuclear weapons amplify yields through multi-stage designs, where a fission primary generates X-rays that ablate and compress a secondary fusion stage containing lithium deuteride, igniting deuterium-tritium fusion at temperatures exceeding 100 million Kelvin and densities of 100-1000 times liquid state. The primary's fission (typically 10-20 kilotons) triggers the secondary via radiation implosion, with fusion releasing 17.6 MeV per deuterium-tritium reaction—primarily as high-energy neutrons that induce further fission in a uranium-238 tamper, contributing up to 50-80% of total yield in some designs. The first such device, Ivy Mike tested on November 1, 1952, yielded 10.4 megatons, demonstrating scalable multi-megaton potentials limited mainly by delivery constraints rather than physics. Overall yields thus derive from fission (primary and tamper), fusion, and neutron-induced reactions, with efficiencies approaching 1-5% mass-to-energy conversion in optimized systems.

Medical Isotopes, Imaging, and Therapy

Medical isotopes are radionuclides produced through nuclear reactions, primarily in research reactors via neutron-induced fission or in particle accelerators like cyclotrons via charged-particle bombardment. Fission of uranium-235 in reactors yields molybdenum-99 (Mo-99), the precursor to technetium-99m (Tc-99m), which accounts for approximately 85% of diagnostic nuclear medicine procedures worldwide, enabling over 40 million scans annually. Cyclotrons produce shorter-lived isotopes such as fluorine-18 (F-18) and gallium-68 (Ga-68) through proton or deuteron irradiation of targets, supporting positron emission tomography (PET) and offering on-site generation to mitigate supply chain vulnerabilities. Global production of Mo-99 remains dependent on a handful of aging reactors, leading to recurrent shortages, such as the 2024 disruption from reactor maintenance that threatened up to 50% reduction in Tc-99m availability. In nuclear imaging, single-photon emission computed tomography (SPECT) utilizes gamma-emitting isotopes like Tc-99m, which decays by isomeric transition with a 140 keV photon suitable for collimated detection in Anger cameras, reconstructing 3D distributions of radiotracers bound to physiological targets such as myocardial perfusion or bone metastases. Positron emission tomography (PET) employs positron emitters like F-18 (half-life 110 minutes), where beta-plus decay leads to electron-positron annihilation producing two 511 keV photons detected in coincidence to localize metabolic activity with higher sensitivity than SPECT, as in FDG-PET for oncology staging. Hybrid SPECT/CT and PET/CT systems integrate anatomical computed tomography for attenuation correction and precise localization, enhancing diagnostic accuracy in cardiology and neurology. Radionuclide therapy delivers targeted radiation via isotopes conjugated to biomolecules, exploiting selective uptake in diseased tissues. Beta-emitting lutetium-177 (Lu-177, half-life 6.7 days) is used in peptide receptor radionuclide therapy (PRRT) with DOTATATE for somatostatin receptor-positive neuroendocrine tumors, achieving progression-free survival extensions in phase III trials. Alpha emitters like actinium-225 (Ac-225, half-life 10 days) provide high linear energy transfer for DNA double-strand breaks in prostate cancer via PSMA-targeted conjugates, yielding PSA response rates of 40-60% in metastatic cases, though limited by supply constraints from generator-based production. These therapies minimize off-target damage compared to external beam radiation, with dosimetry guided by pre-therapeutic imaging analogs.

Recent Advances

Inertial and Magnetic Confinement Fusion Progress (2020s)

In December 2022, the National Ignition Facility (NIF) at Lawrence Livermore National Laboratory achieved the first controlled fusion experiment to reach scientific breakeven, producing 3.15 megajoules (MJ) of fusion energy output from 2.05 MJ of laser energy delivered to the target, yielding an energy gain factor (Q) of 1.5. This inertial confinement fusion (ICF) milestone, using indirect-drive implosions with a hohlraum, marked the ignition threshold where fusion reactions self-heat the plasma core, surpassing prior yields like the 1.3 MJ achieved in 2021 and over 150 kilojoules in optimized high-foot pulse experiments by 2020. Peer-reviewed analyses confirmed the target gain exceeded unity, though overall system efficiency remains below breakeven due to laser inefficiencies. Subsequent NIF experiments in 2023 and 2024 demonstrated repeatability, with multiple ignitions achieving similar or higher yields under varied conditions, advancing understanding of hydrodynamic instabilities and mix in implosions. Private sector ICF efforts, such as Xcimer Energy's diode-pumped solid-state laser demonstrations, targeted cost reductions toward $40 per megawatt-hour by leveraging higher repetition rates and efficiency improvements over NIF's flashlamp systems. In magnetic confinement fusion (MCF), the Joint European Torus (JET) set a modern energy record in 2022 operations, sustaining a plasma with 59 MJ of fusion energy over five seconds at a peak power approaching 16 megawatts, achieving a transient Q of approximately 0.67—building on its 1997 benchmark but with deuterium-tritium fuel for relevance to future reactors. The ITER project, a multinational tokamak under construction in France, progressed toward first plasma by the late 2020s despite delays, designed for sustained Q=10 with 500 MW output from 50 MW input heating, emphasizing steady-state operation via advanced divertors and superconducting magnets. Private MCF ventures accelerated in the 2020s, with over $6 billion in global fusion investments by 2024 enabling high-temperature superconducting magnets for compact tokamaks. Commonwealth Fusion Systems' SPARC device, backed by $3 billion, aims for net energy gain (Q>1) by 2026 using rare-earth barium copper oxide magnets enabling stronger fields in smaller volumes. Similarly, Tokamak Energy pursued spherical tokamaks for commercialization by the 2030s, achieving plasma temperatures over 100 million kelvin in prototypes, while stellarator designs like those from private startups advanced via optimized coil geometries for quasi-symmetry and reduced disruptions. Innovations in magnetic mirrors also reached first plasma milestones in 2024, offering simpler geometries for potential hybrid fission-fusion applications.

Nuclear Clocks and Precision Timekeeping

Nuclear clocks represent an emerging of timekeeping devices that exploit hyperfine transitions within atomic nuclei, rather than electronic transitions used in conventional atomic clocks. These transitions occur on energy scales determined by and electromagnetic nuclear forces, rendering them inherently less susceptible to perturbations from external , , and temperature variations that affect valence electrons. The primary candidate for practical implementation is the low-lying isomeric state in thorium-229 (), with an energy of approximately 8.4 electronvolts, corresponding to a vacuum-ultraviolet of about 148 nanometers. This energy level enables optical excitation, a prerequisite for high- interrogation akin to optical atomic clocks. The 229mTh isomer's ranges from seconds to hours, depending on the host , providing a narrow linewidth for exceeding that of current atomic standards, which achieve fractional uncertainties around 10^{-18}. Nuclear clocks could surpass this by orders of magnitude due to the nucleus's from environmental noise, potentially relative at 10^{-19} or better over extended averaging times. In September 2024, researchers at institutions including NIST and Ludwig directly measured the 229mTh clock in a calcium fluoride host using a vacuum-ultraviolet comb, achieving a precision of 0.04 parts per million and confirming the at 2.2 \times 10^{15} Hz relative to an atomic reference. This milestone validated internal and external clock configurations, where the former loads the isomer via nuclear excitation and the latter via electronic shelving, demonstrating coherence times suitable for locking to the . Advancements in sample preparation have addressed radioactivity concerns inherent to thorium. In December 2024, teams at UCLA and developed thin films of thorium tetrafluoride (ThF_4), requiring 1,000 times less material than bulk crystals while reducing by embedding ions in low-radioactivity matrices, facilitating safer laboratory handling and scalability. optical excitation of the isomer was achieved in April 2024, marking progress toward prototype integration with frequency combs for absolute frequency referencing. These developments position nuclear clocks for applications beyond timekeeping, including stringent tests of , variations in fundamental constants like the (with 229mTh sensitivity coefficients exceeding those of atomic transitions), and detection of via anomalous frequency drifts. Challenges persist, including the need for higher efficiencies, suppression of transitions that broaden the signal, and mitigation of effects in isolated ions. Ongoing efforts at facilities like PTB and UNSW aim to construct fully operational prototypes by the late 2020s, potentially redefining the second if proves superior to optical clocks, which currently hold with inaccuracies of one second per 40 billion years. Empirical validation requires long-term comparisons, but causal insensitivity of radii to atomic-scale perturbations underpins theoretical expectations of enhanced resilience.

Exotic Nuclei Studies and Ab Initio Computations

Exotic nuclei, characterized by extreme neutron-to-proton ratios approaching the or proton drip lines, exhibit structural phenomena such as configurations and altered shell closures that conventional nuclear models. These nuclei, often short-lived with half-lives on the of milliseconds or less, provide insights into nuclear forces at the limits of stability and inform processes like rapid in . Experimental production relies on radioactive ion beams at facilities like the (FRIB), where fragmentation and reactions generate isotopes of stable beams. Recent experiments have mapped regions near the neutron drip line, revealing new isotopes and decay properties. In December 2022, FRIB's inaugural experiment identified five previously neutron-rich isotopes—^{28}, ^{29}, ^{31}, ^{32}, and ^{33}—lying close to the line with approximately 28 neutrons, using fast-beam techniques and invariant-mass . mass measurements of proton--line nuclei, such as those conducted in 2024, have confirmed proton structures in species like ^{8} and highlighted mirror-symmetry breaking due to effects. advancements, including collinear resonance ionization, have enabled ground-state properties like in exotic chains such as mercury isotopes, as demonstrated in 2020 studies at using accelerated ^{206} beams and detectors. nuclei, exemplified by two-neutron halos in ^{11}Li or proton halos in ^{8}, manifest as spatially extended weakly bound valence nucleons, with breakup reactions and invariant-mass spectrometry quantifying their low binding energies, often below 0.5 MeV per nucleon. These findings underscore deviations from mean-field predictions, such as the "island of inversion" around N=20 in magnesium isotopes, where deformation persists to the line. Ab initio computations, grounded in quantum chromodynamics-derived effective theories like chiral EFT, solve the nuclear from first principles without adjustable parameters beyond low-energy constants fitted to few-body . These methods employ techniques such as the in-medium similarity (IMSRG), coupled-cluster , and no-core to compute ground-state energies, radii, and spectra for light to medium-mass nuclei, incorporating two-, three-, and higher-body forces systematically. Recent developments include local chiral N^3LO nucleon-nucleon potentials applied in 2024 to intermediate-mass nuclei, yielding binding energies accurate to within 1% for A<16 systems when combined with three-body forces. For exotic nuclei, ab initio predictions delineate the neutron drip line, forecasting anomalies like the sudden shift in ^{54}Ca due to enhanced correlations, and quantify uncertainties from truncated chiral orders, typically at the 0.5-1 MeV level for binding energies. Integration of ab initio results with experiments validates interactions and probes open questions, such as the emergence of halos from ab initio wave functions showing extended asymptotic tails. Calculations using chiral EFT have reproduced excited states in drip-line nuclei via pathways like multi-nucleon transfer, as explored in 2023 National Superconducting Cyclotron Laboratory experiments on rare isotopes. Ongoing challenges include scaling to heavier systems and incorporating continuum effects for unbound states, addressed by Gamow IMSRG extensions for resonant spectra. These computations, leveraging increased supercomputing resources, now predict electroweak properties and reaction cross-sections, aiding interpretations of data from facilities like FRIB and .

Controversies and Empirical Debates

Radiation Risks: Linear No-Threshold Critique

The linear no-threshold (LNT) posits that induces cancer proportionally to dose, with no safe exposure level below which harm is absent, a model adopted in regulatory frameworks since the for . This extrapolates risks from high-dose observations, such as survivors receiving over 100 mSv, to low doses under 100 mSv, despite biological indicating non-linear responses including and adaptive that mitigate low-level . Critics argue the LNT overestimates risks at environmentally relevant doses, fostering unnecessary public and constraining technologies like , as epidemiological often reveal no detectable cancer excess or even reduced mortality in low-dose cohorts. Historical analysis reveals foundational errors in LNT's development, including misinterpretations of early mouse mutagenesis studies by Russell, which ignored spontaneous mutation rates and dose-rate effects, leading to erroneous adoption over threshold models in reports like BEIR I (). Calabrese's archival documents how key proponents suppressed contrary data, such as dose-rate findings showing no genetic harm at low chronic exposures, prioritizing precautionary linearity amid secrecy rather than empirical fidelity. These origins undermine LNT's scientific legitimacy, as subsequent toxicological tests—comparing it against or alternatives—demonstrate its to predict outcomes in over ,000 low-dose experiments across , where sub-toxic exposures frequently enhance via upregulated repair pathways. Epidemiological critiques highlight LNT's discord with human data; for instance, cohorts of nuclear workers cumulatively exposed to 10-50 mSv show no consistent solid cancer elevation, with meta-analyses indicating risks indistinguishable from background or protective effects against non-cancer mortality. Studies like INWORKS (2023), claiming a 52% per-Gy solid cancer mortality increase, rely on broad dose bins and fail to disaggregate confounders like smoking or lifestyle, yielding confidence intervals overlapping zero at doses below 100 mSv and ignoring null findings in similar worker populations. Atomic bomb survivor analyses at low doses (<100 mSv) similarly detect no excess leukemia or solid tumors after adjusting for dosimetry uncertainties, supporting threshold models where risks plateau near natural background levels (2-3 mSv/year). Radon-exposed miners and radium dial workers provide high-dose validation but falter at chronic low exposures, where LNT predictions exceed observed incidences by factors of 10-100. Alternative paradigms, such as , posit that low doses (<10 mSv) activate protective responses like and of damaged cells, yielding J-shaped dose-response curves with net benefits observed in studies of irradiated mammals and human ecologies (e.g., high-background areas in , with cancer rates below global norms). Calabrese's synthesis of thousands of endpoint evaluations affirms in 36% of cases LNT's in under %, challenging the model's universality. Regulatory persistence with LNT, despite petitions to bodies like the U.S. citing these discrepancies, reflects institutional over causal , amplifying costs in avoidance and policies without commensurate . Transitioning to dose- and endpoint-specific assessments, informed by , would better align protection with verifiable hazards.

Nuclear Waste Management: Long-Term Storage Facts

High-level nuclear waste, primarily spent fuel and vitrified reprocessing residues, requires isolation from the biosphere for periods exceeding 10,000 years due to radionuclides like plutonium-239 with half-lives of approximately 24,100 years. Deep geological repositories, sited in stable formations such as granite, salt, or clay, employ multiple barriers—including corrosion-resistant copper or steel canisters, bentonite clay buffers, and low-permeability host rock—to prevent radionuclide migration, with engineered systems designed to maintain integrity against seismic, hydrological, and geochemical stressors. Empirical modeling and natural analogs, such as ancient uranium deposits undisturbed for millions of years, support containment efficacy, projecting individual radiation doses from repositories far below natural background levels (e.g., less than 0.1 millisievert per year at repository boundaries). Finland's Onkalo , excavated 400-520 into crystalline at Olkiluoto, represents the first operational deep geological for , with a first encapsulation trial completed in March 2025 and operations anticipated to commence following final licensing by the and in 2025. Designed for 6,500 tons of from Finnish reactors, Onkalo uses copper-overpack canisters emplaced in deposition tunnels, sealed with , leveraging Finland's transparent siting involving to achieve regulatory approval absent in more politicized programs. In contrast, the lacks a permanent repository for commercial spent fuel, with approximately 80,000 tons currently stored in dry casks and pools at 77 sites, despite the Waste Isolation Pilot Plant (WIPP) successfully disposing of 200,000 cubic meters of transuranic defense waste in salt beds since 1999 without radionuclide releases to the environment. The proposed Yucca Mountain repository in Nevada, characterized over decades at a cost exceeding $15 billion, was deemed viable for 70,000 tons by the Regulatory Commission in 2010 but halted by executive action, illustrating political impediments over technical barriers. The volume of high-level nuclear waste remains modest relative to outputs from fossil fuels; all spent fuel generated by U.S. nuclear plants since 1950 equates to roughly 80,000 metric tons—occupying a volume akin to a football field piled 10 yards high—while annual coal combustion ash exceeds 100 million metric tons, containing heavy metals like arsenic and mercury that leach into groundwater without comparable regulatory isolation. Over five decades of interim storage worldwide, no fatalities or significant environmental releases have occurred from managed nuclear waste, contrasting with thousands of annual deaths from air pollution by coal and other sources. A 2014 incident at WIPP involving a chemical reaction released minor airborne contaminants, contained within the facility with no off-site impact, underscoring robust monitoring but highlighting human factors in operations. International Atomic Energy Agency assessments affirm geological disposal as technically proven, with risks dominated by retrievability concerns rather than failure probabilities, though public opposition, often amplified by institutional biases favoring intermittent renewables, has delayed implementations despite empirical demonstrations of safety.

Energy Policy: Reliability vs. Intermittent Alternatives

Nuclear power plants operate as baseload providers with capacity factors averaging 92.7% in the United States in 2023, meaning they generate near continuously except for scheduled . This reliability stems from the physics of controlled reactions, which produce steady thermal output independent of or diurnal cycles, enabling nuclear to supply consistent to grids. In , wind and photovoltaic systems exhibit capacity factors of 35.0% and 23.2% respectively in the same year, reflecting their dependence on meteorological conditions. Intermittent renewables necessitate backup capacity or to maintain stability, as output can drop to during calm periods or at night, requiring overbuild factors of 2-3 times in some scenarios to achieve equivalent firm . These integration costs, including balancing for unpredictability and additional , are often excluded from (LCOE) calculations, leading to understated system-wide expenses estimated at 20-50% higher for high-renewable grids without sufficient dispatchable sources. peaker plants or hydroelectric reserves typically fill gaps, increasing emissions during high-demand lulls in renewable output, as observed in California's where midday solar surpluses force curtailments followed by evening ramp-ups. Empirical grid data underscores nuclear's role in reliability: U.S. Department of Energy analyses show nuclear plants deliver over 90% of potential output annually, outperforming wind and solar by factors of 2.5-3, reducing forced outage rates and enhancing overall system inertia against frequency fluctuations. In France, where nuclear constitutes about 70% of electricity generation, the grid maintains high reliability metrics with low outage durations, exporting surplus power during periods of low domestic demand. Germany's Energiewende policy, emphasizing wind and solar post-nuclear phase-out, has correlated with elevated wholesale prices and import dependence—including nuclear electricity from neighbors—during renewable droughts, though major blackouts have been averted through interconnections and gas backups. Policy debates center on causal trade-offs: prioritizing intermittents without scaled storage (current global capacity insufficient for seasonal gaps) risks supply volatility, as evidenced by ' 2021 freeze exposing renewable shortfalls amid baseload failures. 's , with reserves supporting decades of at full load, contrasts with the land-intensive required for renewables to output, informing arguments for hybrid approaches where nuclear anchors grids amid renewable . Mainstream assessments from like the IEA often underweight these intermittency penalties due to modeling assumptions favoring subsidized renewables, yet raw operational data from independent agencies affirm nuclear's empirical edge in dispatchable, low-carbon reliability.

References

  1. https://physics.uiowa.edu/nuclear-and-particle-physics
  2. https://physics.illinois.edu/research/groups-and-centers/nuclear-physics
  3. https://www.energy.gov/science/np/nuclear-physics
  4. https://www.iop.org/about/iop-history/100th-anniversary/100-incredible-years/nuclear-physics
  5. https://www.physics.ucla.edu/~moszkowski/earlynp/earlynp.htm
  6. https://faculty.wcas.northwestern.edu/infocom/Ideas/nuc_timeline.html
  7. https://www.nap.edu/read/6288/chapter/10
  8. https://www.unh.edu/inquiryjournal/blog/2021/03/nuclear-physics-applications-through-lens-undergraduate-research
  9. https://www.frontiersin.org/journals/physics/articles/10.3389/fphy.2018.00078/full
  10. https://scitechdaily.com/scientists-uncover-mysterious-nuclear-bump-that-challenges-current-physics-models/
  11. https://www.aps.org/apsnews/2008/02/becquerel-discovers-radioactivity
  12. https://timeline.web.cern.ch/becquerel-discovers-radioactivity
  13. https://www2.lbl.gov/abc/wallchart/chapters/03/4.html
  14. https://www.nobelprize.org/prizes/themes/marie-and-pierre-curie-and-the-discovery-of-polonium-and-radium/
  15. https://history.aip.org/exhibits/curie/resbr2.htm
  16. https://www.nobelprize.org/prizes/chemistry/1908/rutherford/facts/
  17. https://radioactivity.eu.com/articles/phenomenon/three_radiations
  18. https://rinconeducativo.org/en/recursos-educativos/alpha-beta-gamma-particles-great-discovery-rutherford-soddy/
  19. http://large.stanford.edu/courses/2017/ph241/sivulka2/
  20. https://history.aip.org/exhibits/rutherford/sections/alpha-particles-atom.html
  21. https://chemed.chem.purdue.edu/genchem/history/gold.html
  22. https://royalsocietypublishing.org/doi/10.1098/rspa.1932.0112
  23. https://www.nobelprize.org/prizes/physics/1935/chadwick/biographical/
  24. https://www.aps.org/apsnews/2007/05/may-1932-chadwick-discovery-neutron
  25. https://www.ebsco.com/research-starters/history/chadwick-discovers-neutron
  26. https://www.nature.com/articles/129649a0
  27. https://history.aip.org/exhibits/mod/fission/fission1/02.html
  28. https://www.nobelprize.org/prizes/chemistry/1935/joliot-curie/lecture/
  29. https://link.springer.com/article/10.1007/s11224-024-02283-8
  30. https://arxiv.org/abs/2507.16928
  31. https://world-nuclear.org/information-library/current-and-future-generation/outline-history-of-nuclear-energy
  32. https://www.sciencedirect.com/science/article/pii/S1631070517300993
  33. https://www.aps.org/apsnews/2007/12/december-1938-discovery-nuclear-fission
  34. https://www.sciencehistory.org/education/scientific-biographies/otto-hahn-lise-meitner-and-fritz-strassmann/
  35. https://axial.acs.org/nuclear-chemistry/lise-meitner-and-the-discovery-of-nuclear-fission-politics-persecution-and-the-prize
  36. https://ahf.nuclearmuseum.org/ahf/history/nuclear-fission/
  37. https://ahf.nuclearmuseum.org/ahf/key-documents/einstein-szilard-letter/
  38. http://www.fdrlibrary.marist.edu/archives/pdfs/docsworldwar.pdf
  39. https://www.nps.gov/mapr/learn/historyculture/timeline.htm
  40. https://www.atomicarchive.com/history/manhattan-project/chronology.html
  41. https://news.uchicago.edu/explainer/first-nuclear-reactor-explained
  42. https://ahf.nuclearmuseum.org/ahf/history/trinity-test-1945/
  43. https://www.eia.gov/kids/history-of-energy/timelines/nuclear.php
  44. https://www.jdmartin.org/nuclear-high-energy-and-solid-state-physics
  45. https://www.bnl.gov/about/history/accelerators.php
  46. https://chemistry.berkeley.edu/news/cyclotrons-history-berkeley
  47. https://newscenter.lbl.gov/2009/11/11/farewell-to-the-bevatron-1954-1993/
  48. https://wlab.yale.edu/about/history
  49. https://pubs.aip.org/physicstoday/article/73/10/12/853152/Cold-War-particle-physics-collaborations
  50. https://www.nrc.gov/reading-rm/basic-ref/students/science-101/what-is-an-atom
  51. https://www.vanderbilt.edu/AnS/Chemistry/courses/chem104/experiment1/composition/composition.htm
  52. https://www.arpansa.gov.au/understanding-radiation/what-is-radiation/ionising-radiation/atomic-structure
  53. https://web.physics.wustl.edu/~wimd/N19-01.pdf
  54. https://physics.stackexchange.com/questions/624022/what-r-0-in-the-nucleus-radius-equation
  55. https://phys.libretexts.org/Bookshelves/Nuclear_and_Particle_Physics/Introduction_to_Applied_Nuclear_Physics_(Cappellaro)/01%3A_Introduction_to_Nuclear_Physics/1.02%3A_Binding_energy_and_Semi-empirical_mass_formula
  56. https://www2.lbl.gov/abc/wallchart/chapters/04/0.html
  57. https://doi.org/10.1103/physrevlett.99.022001
  58. http://hyperphysics.phy-astr.gsu.edu/hbase/Forces/funfor.html
  59. https://www.nuclear-power.com/nuclear-power/reactor-physics/atomic-nuclear-physics/fundamental-interactions-fundamental-forces/strong-interaction-strong-force/nuclear-force-residual-strong-force/
  60. https://doi.org/10.1103/PhysRev.78.135
  61. https://arxiv.org/pdf/1708.02198
  62. https://openmedscience.com/the-liquid-drop-model-a-cornerstone-of-nuclear-physics/
  63. https://www.nuclear-power.com/nuclear-power/fission/weizsaecker-formula-semi-empirical-mass-formula/
  64. https://link.aps.org/doi/10.1103/PhysRevC.79.054327
  65. http://hyperphysics.phy-astr.gsu.edu/hbase/Nuclear/shell2.html
  66. https://www.nobelprize.org/prizes/physics/1963/mayer/facts/
  67. https://www.aps.org/apsnews/2008/08/goeppert-mayer-nuclear-shell-model
  68. https://phys.libretexts.org/Bookshelves/Nuclear_and_Particle_Physics/Introduction_to_Applied_Nuclear_Physics_(Cappellaro)/05%3A_Nuclear_Structure/5.03%3A_Nuclear_Models
  69. https://indico.ictp.it/event/7641/session/21/contribution/46/material/0/0.pdf
  70. https://link.aps.org/doi/10.1103/RevModPhys.77.427
  71. https://arxiv.org/pdf/2203.04460
  72. https://iopscience.iop.org/article/10.1088/0034-4885/48/10/003
  73. https://www.nobelprize.org/prizes/physics/1975/press-release/
  74. https://link.springer.com/chapter/10.1007/978-3-642-60970-1_7
  75. https://phys.libretexts.org/Bookshelves/Nuclear_and_Particle_Physics/Nuclear_and_Particle_Physics_%28Walet%29/04%253A_Nuclear_Models
  76. https://arxiv.org/html/2506.15406v1
  77. https://link.aps.org/doi/10.1103/PhysRevC.82.024309
  78. https://link.springer.com/article/10.1140/epja/s10050-022-00834-3
  79. https://www2.lbl.gov/abc/wallchart/chapters/03/1.html
  80. http://physics.bu.edu/~duffy/sc546_notes09/alpha_decay.html
  81. http://hyperphysics.phy-astr.gsu.edu/hbase/Nuclear/alptun.html
  82. http://web.mit.edu/8.13/www/JLExperiments/JLExp45.pdf
  83. https://www.energy.gov/science/doe-explainsthe-weak-force
  84. http://hyperphysics.phy-astr.gsu.edu/hbase/Nuclear/beta.html
  85. https://physics.lbl.gov/shapiro/Physics226/lecture14.pdf
  86. https://www2.lbl.gov/abc/wallchart/chapters/03/3.html
  87. https://ocw.mit.edu/courses/22-02-introduction-to-applied-nuclear-physics-spring-2012/0dedac3694d87c637b6214fd85c9eec9_MIT22_02S12_lec_ch7.pdf
  88. http://web1.eng.famu.fsu.edu/~dommelen/quantum/style_a/ntgd.html
  89. https://inpp.ohio.edu/~meisel/PHYS7501/file/Lecture9_GammaDecay_PHYS7501_F2021_ZM.pdf
  90. https://www.nndc.bnl.gov/nudat3/guide/spontaneousfission.html
  91. https://ncsp.llnl.gov/sites/ncsp/files/2021-05/la-14098.pdf
  92. https://link.aps.org/doi/10.1103/PhysRev.58.89.2
  93. https://www.osti.gov/servlets/purl/10187072
  94. https://link.aps.org/doi/10.1103/PhysRevC.98.034612
  95. https://www.sciencedirect.com/science/article/pii/S0375947423001902
  96. https://www.nature.com/articles/s41598-020-65585-x
  97. https://link.aps.org/doi/10.1103/PhysRevC.111.064603
  98. https://www.physics.ucla.edu/~moszkowski/mgm/mgmagnos.htm
  99. https://www.eurekalert.org/news-releases/1090551
  100. https://phys.libretexts.org/Bookshelves/Nuclear_and_Particle_Physics/Nuclear_and_Particle_Physics_(Walet)/04:_Nuclear_Models/4.01:_Nuclear_Shell_Model
  101. https://cerncourier.com/a/gsi-reveals-new-magic-numbers-in-nuclei/
  102. https://cerncourier.com/a/the-drip-line-nuclei-on-the-edge-of-stability/
  103. https://link.aps.org/doi/10.1103/RevModPhys.84.567
  104. https://www.sciencedirect.com/science/article/abs/pii/S0146641007000956
  105. https://cds.cern.ch/record/241958/files/Record241958.pdf
  106. https://trace.tennessee.edu/cgi/viewcontent.cgi?referer=&httpsredir=1&article=2610&context=utk_chanhonoproj
  107. https://www.mdpi.com/2624-8174/4/2/35
  108. https://ocw.mit.edu/courses/22-01-introduction-to-nuclear-engineering-and-ionizing-radiation-fall-2016/resources/the-q-equation2014the-most-general-nuclear-reaction/
  109. https://phys.libretexts.org/Bookshelves/Nuclear_and_Particle_Physics/Nuclear_and_Particle_Physics_(Walet)/09%3A_Relativistic_Kinematics/9.03%3A_Transformations_between_CM_and_lab_frame
  110. https://facultystaff.richmond.edu/~ggilfoyl/research/nuclearCrossSections.pdf
  111. https://www.energy.gov/science/doe-explainsnuclear-fission
  112. https://nrl.mit.edu/reactor/fission-process/
  113. https://world-nuclear.org/information-library/nuclear-fuel-cycle/introduction/physics-of-nuclear-energy
  114. https://www.nrc.gov/reading-rm/basic-ref/glossary/chain-reaction
  115. https://www.nuclear-power.com/nuclear-power/reactor-physics/nuclear-fission-chain-reaction/reactor-criticality/
  116. https://www.nrc.gov/reading-rm/basic-ref/glossary/fissionable-material
  117. https://www.lanl.gov/media/publications/actinide-research-quarterly/1123-calculating-criticality
  118. http://hyperphysics.phy-astr.gsu.edu/hbase/NucEne/fusion.html
  119. http://hyperphysics.phy-astr.gsu.edu/hbase/NucEne/coubar.html
  120. https://www.iaea.org/topics/energy/fusion/background
  121. https://www.osti.gov/servlets/purl/4215203
  122. https://lorenanderson.faculty.wvu.edu/files/d/2a1369c0-0ffa-453c-9f6f-9bc58e783d2c/astr702_nuclear_fusion.pdf
  123. http://faculty.tamuc.edu/cbertulani/cab/Lectures/FusionReactions.pdf
  124. http://hyperphysics.phy-astr.gsu.edu/hbase/NucEne/lawson.html
  125. https://www1.grc.nasa.gov/wp-content/uploads/TP-20205001617-Theory-Paper-Final.pdf
  126. https://pdg.lbl.gov/2024/reviews/rpp2024-rev-bbang-nucleosynthesis.pdf
  127. https://arxiv.org/abs/2409.06015
  128. https://map.gsfc.nasa.gov/universe/bb_tests_ele.html
  129. http://astro1.physics.utoledo.edu/~megeath/ph6820/lecture26_ph6820.pdf
  130. https://ned.ipac.caltech.edu/level5/Sept16/Rauscher/Rauscher4.html
  131. https://www.cod.edu/faculty/websites/fazzinid/astro1124/pdf/astro1124lec18.pdf
  132. https://www.annualreviews.org/doi/pdf/10.1146/annurev-nucl-102422-080857
  133. https://www.aanda.org/articles/aa/full_html/2022/01/aa39318-20/aa39318-20.html
  134. https://www.aanda.org/articles/aa/full_html/2023/02/aa44926-22/aa44926-22.html
  135. https://link.aps.org/doi/10.1103/RevModPhys.93.015002
  136. https://www.aanda.org/articles/aa/full_html/2018/12/aa34079-18/aa34079-18.html
  137. https://ntrs.nasa.gov/api/citations/19980007188/downloads/19980007188.pdf
  138. https://ui.adsabs.harvard.edu/abs/1991PhR...208..267C/abstract
  139. https://ned.ipac.caltech.edu/level5/Sept01/Meyer/Meyer3.html
  140. https://www.astro.princeton.edu/~burrows/classes/514/papers/cowan.r-process.phys.repts.pdf
  141. https://greta.lbl.gov/greta-science-case/r-process
  142. https://ui.adsabs.harvard.edu/abs/2025Univ...11..229B/abstract
  143. https://iopscience.iop.org/article/10.1086/312343/fulltext/
  144. https://academic.oup.com/mnras/article/529/2/1154/7608534
  145. https://www.astro.princeton.edu/~burrows/classes/514/papers/thielemann.r-process.sites.pdf
  146. https://link.aps.org/doi/10.1103/Physics.17.s122
  147. https://www.science.org/doi/10.1126/science.aap9580
  148. https://iopscience.iop.org/article/10.3847/1538-4357/ad1193
  149. https://arxiv.org/abs/1901.09044
  150. https://www.sciencedirect.com/science/article/abs/pii/S0003491619302180
  151. https://home.cern/science/accelerators/how-accelerator-works
  152. http://www.iaea.org/newscenter/news/what-are-particle-accelerators
  153. https://uspas.fnal.gov/materials/11ODU/Lecture1a_Intro_to_Accelerators.pdf
  154. https://cds.cern.ch/record/261062/files/p1_2.pdf
  155. https://www.energy.gov/articles/how-particle-accelerators-work
  156. http://www.iaea.org/newscenter/news/what-is-a-cyclotron
  157. https://uspas.fnal.gov/materials/09VU/Lecture1a.pdf
  158. https://www.isotopes.gov/accelerator-facilities
  159. https://www.sciencedirect.com/topics/chemistry/gamma-spectroscopy
  160. https://chem.libretexts.org/Bookshelves/Analytical_Chemistry/Physical_Methods_in_Chemistry_and_Nano_Science_%28Barron%29/01%253A_Elemental_Analysis/1.17%253A_Principles_of_Gamma-ray_Spectroscopy_and_Applications_in_Nuclear_Forensics
  161. https://iopscience.iop.org/article/10.1088/1742-6596/420/1/012156
  162. https://www.physics.rutgers.edu/~eandrei/389/gamma.pdf
  163. https://www.sciencedirect.com/science/article/pii/S0168900213000508
  164. http://www.mi.infn.it/~wieland/paper_wieland/gamm_ray_tracking_arrays_prog_part_phys_2001.pdf
  165. https://joint-research-centre.ec.europa.eu/system/files/2016-06/JRC-ITU-handbook4c-2010_0.pdf
  166. https://greta.lbl.gov/
  167. https://frib.msu.edu/news-center/news/berkeley-lab-article-spotlights-gamma-ray-energy-tracking-array
  168. https://ns.ph.liv.ac.uk/~ajb/summerschool/files/Simpson_Eberth_Prog_PArt_Nuc_Phys_2008.pdf
  169. https://link.springer.com/article/10.1140/epja/s10050-020-00132-w
  170. https://newscenter.lbl.gov/2018/11/07/greta-better-gamma-ray-detector/
  171. https://oxfordre.com/physics/display/10.1093/acrefore/9780190871994.001.0001/acrefore-9780190871994-e-93
  172. https://www.bnl.gov/rhic/
  173. https://www.bnl.gov/rhic/physics.php
  174. https://www.bnl.gov/newsroom/news.php?a=222486
  175. https://www.gsi.de/en/researchaccelerators/fair
  176. https://www.gsi.de/en/researchaccelerators/fair/research
  177. https://www.gsi.de/en/start/news/details/2025/07/10/wichtige-beschluesse-zur-inbetriebnahme-der-fair-anlage
  178. https://arxiv.org/abs/1810.04767
  179. https://www.rhichome.bnl.gov/RHIC/Runs/RhicRun21AuAu.pdf
  180. https://link.aps.org/doi/10.1103/PhysRevAccelBeams.25.051001
  181. https://arxiv.org/abs/2510.14948
  182. https://indico.gsi.de/event/21768/contributions/87323/attachments/52142/77781/20250715_RRB-Meeting_v02_final.pdf
  183. https://www.researchgate.net/publication/351636167_Heavy-Ion_Collisions_at_FAIR-NICA_Energies
  184. https://www.energy.gov/ne/articles/nuclear-101-how-does-nuclear-reactor-work
  185. https://world-nuclear.org/information-library/nuclear-fuel-cycle/nuclear-power-reactors/nuclear-power-reactors
  186. https://world-nuclear.org/information-library/current-and-future-generation/fast-neutron-reactors
  187. https://world-nuclear.org/information-library/nuclear-fuel-cycle/introduction/nuclear-fuel-cycle-overview
  188. https://world-nuclear.org/information-library/nuclear-fuel-cycle/fuel-recycling/processing-of-used-nuclear-fuel
  189. https://www.acq.osd.mil/ncbdp/nm/NMHB2020rev/chapters/chapter13.html
  190. https://www.nuclearweaponarchive.org/Nwfaq/Nfaq4-1.html
  191. https://physics.info/weapons/
  192. https://www.lanl.gov/media/publications/the-vault/1023-a-tale-of-two-bomb-designs
  193. https://chem.libretexts.org/Courses/Furman_University/CHM101%253A_Chemistry_and_Global_Awareness_%28Gordon%29/06%253A_Nuclear_Weapons-_Fission_and_Fusion/6.04%253A_The_Manhattan_Project_-_Critical_Mass_and_Bomb_Construction
  194. https://www.osti.gov/opennet/manhattan-project-history/Science/BombDesign/gun-type.html
  195. https://www.britannica.com/technology/nuclear-weapon/Gun-assembly-implosion-and-boosting
  196. http://large.stanford.edu/courses/2018/ph241/cheng2/docs/malik.pdf
  197. https://ee.stanford.edu/~hellman/sts152_02/handout02.pdf
  198. https://armscontrolcenter.org/fact-sheet-thermonuclear-weapons/
  199. https://www.britannica.com/technology/thermonuclear-bomb
  200. https://www-pub.iaea.org/MTCD/Publications/PDF/trs465_web.pdf
  201. https://www.jacc.org/doi/10.1016/j.jcmg.2008.12.013
  202. https://www.iaea.org/newscenter/news/what-is-a-cyclotron
  203. https://www.murr.missouri.edu/reliability-in-a-challenged-global-supply-chain/
  204. https://www.ncbi.nlm.nih.gov/books/NBK559013/
  205. https://www.ncbi.nlm.nih.gov/books/NBK582124/
  206. https://tech.snmjournals.org/content/36/1/1
  207. https://pmc.ncbi.nlm.nih.gov/articles/PMC9607057/
  208. https://ejnmmipharmchem.springeropen.com/articles/10.1186/s41181-024-00239-1
  209. https://pmc.ncbi.nlm.nih.gov/articles/PMC12468063/
  210. https://lasers.llnl.gov/science/achieving-fusion-ignition
  211. https://www.energy.gov/articles/doe-national-laboratory-makes-history-achieving-fusion-ignition
  212. https://www.llnl.gov/article/48866/three-peer-reviewed-papers-highlight-scientific-results-national-ignition-facility-record
  213. https://www.epj-conferences.org/articles/epjconf/pdf/2024/20/epjconf_lnes2024_00013.pdf
  214. https://link.aps.org/doi/10.1103/PhysRevLett.132.065102
  215. https://thefusionreport.substack.com/p/xcimer-energy-achieves-inertial-fusion
  216. https://www.iter.org/few-lines
  217. https://www.iter.org/fusion-energy/60-years-progress
  218. https://www.innovationnewsnetwork.com/fusion-energy-explained-powering-the-future-of-clean-energy/58361/
  219. https://theconversation.com/billions-in-private-cash-is-flooding-into-fusion-power-will-it-pay-off-266354
  220. https://www.fusionindustryassociation.org/wp-content/uploads/2024/07/2024-annual-global-fusion-industry-report.pdf
  221. https://world-nuclear.org/information-library/current-and-future-generation/nuclear-fusion-power
  222. https://www.popularmechanics.com/science/energy/a61711423/magnetic-mirror-fusion-breakthrough/
  223. https://www.nist.gov/news-events/news/2024/09/major-leap-nuclear-clock-paves-way-ultraprecise-timekeeping
  224. https://www.nature.com/articles/s41586-024-07839-6
  225. https://physics.aps.org/articles/v17/71
  226. https://newsroom.ucla.edu/releases/thorium-film-could-replace-crystals-in-atomic-clocks-of-the-near-future
  227. https://jila.colorado.edu/news-events/articles/building-safer-and-more-affordable-nuclear-clock
  228. https://www.nature.com/articles/s41467-025-64191-7
  229. https://phys.org/news/2025-07-dark-side-scientists-nuclear-clock.html
  230. https://www.unsw.edu.au/research/nuclear-innovation-centre/research/projects/thorium-229-nuclear-clock
  231. https://www.nature.com/articles/d41586-024-02865-w
  232. https://www.osti.gov/servlets/purl/1886251
  233. https://www.anl.gov/article/the-next-frontier-in-nuclear-physics
  234. https://physicsworld.com/a/five-new-exotic-nuclei-revealed-in-first-experiment-at-frib/
  235. https://www.techexplorist.com/first-precise-mass-measurements-several-exotic-atomic-nuclei/94237/
  236. https://arxiv.org/abs/2209.15228
  237. https://www.anl.gov/pse/article/a-pioneering-exploration-of-exotic-nuclei
  238. https://indico.phy.anl.gov/event/25/attachments/139/444/augusto_macchiavelli_jps.pdf
  239. https://arxiv.org/pdf/2212.11064
  240. https://link.springer.com/article/10.1007/s41365-024-01585-0
  241. https://link.aps.org/doi/10.1103/PhysRevC.109.064316
  242. https://indico.mitp.uni-mainz.de/event/380/contributions/4777/attachments/3437/4384/hhergert_bormio2024_web.pdf
  243. https://www.frontiersin.org/journals/physics/articles/10.3389/fphy.2023.1098262/full
  244. https://arxiv.org/html/2510.11038v1
  245. https://www.energy.gov/science/np/articles/novel-way-get-excited-states-exotic-nuclei
  246. https://www.energy.gov/science/np/articles/ab-initio-methods-help-scientists-make-sense-complex-particle-collisions
  247. https://pmc.ncbi.nlm.nih.gov/articles/PMC6043938/
  248. https://www.sciencedirect.com/science/article/pii/S0009279718310858
  249. https://phys.org/news/2017-01-calabrese-lnt-toxicology.html
  250. https://pubmed.ncbi.nlm.nih.gov/27974149/
  251. https://www.sciencedirect.com/science/article/abs/pii/S0009279722002691
  252. https://pmc.ncbi.nlm.nih.gov/articles/PMC1299203/
  253. https://pmc.ncbi.nlm.nih.gov/articles/PMC12033839/
  254. https://www.bmj.com/content/382/bmj-2022-074520
  255. https://bioone.org/journals/Radiation-Research/volume-182/issue-5/RR13829.1/Estimating-Risk-of-Low-Radiation-Doses--A-Critical-Review/10.1667/RR13829.1.full
  256. https://www.sciencedirect.com/science/article/abs/pii/S0013935121003352
  257. https://www.federalregister.gov/documents/2021/08/17/2021-17475/linear-no-threshold-model-and-standards-for-protection-against-radiation
  258. https://journals.sagepub.com/doi/10.1177/15593258251367588
  259. https://www-pub.iaea.org/MTCD/Publications/PDF/TRS413_web.pdf
  260. https://www.nucnet.org/news/finland-completes-key-trial-for-world-s-first-deep-geological-nuclear-waste-repository-3-2-2025
  261. https://www.ans.org/news/2025-07-25/article-7222/deep-geologic-repository-progress2025-update/
  262. https://wipp.energy.gov/wipp-site.asp
  263. https://republicans-energycommerce.house.gov/yucca-mountain
  264. https://www.nrc.gov/reading-rm/doc-collections/fact-sheets/yucca-license-review
  265. https://world-nuclear.org/information-library/nuclear-fuel-cycle/nuclear-waste/radioactive-wastes-myths-and-realities
  266. http://www.iaea.org/newscenter/news/finlands-spent-fuel-repository-a-game-changer-for-the-nuclear-industry-director-general-grossi-says
  267. https://www.eia.gov/electricity/annual/html/epa_04_08_b.html
  268. https://www.energy.gov/ne/articles/nuclear-power-most-reliable-energy-source-and-its-not-even-close
  269. https://www.resources.org/common-resources/what-are-costs-and-values-wind-and-solar-power-how-are-they-changing/
  270. https://www.instituteforenergyresearch.org/renewable/media-misleads-the-public-on-wind-and-solar-powers-cost-and-environmental-impacts/
  271. https://www.fraserinstitute.org/commentary/solar-and-wind-power-are-expensive
  272. https://energytalkingpoints.com/other-countries-80-percent/
  273. https://energytransition.org/2015/06/germany-reliant-on-foreign-nuclear-power/
  274. https://www.cleanenergywire.org/factsheets/blackout-or-gas-shortage-how-would-germany-deal-energy-emergency
  275. https://www.sciencedirect.com/science/article/abs/pii/S2211339822000880
  276. https://www.iea.org/data-and-statistics/charts/monthly-wind-capacity-factors-in-the-united-states-summer-2023
Add your contribution
Related Hubs
User Avatar
No comments yet.