Hubbry Logo
Visible spectrumVisible spectrumMain
Open search
Visible spectrum
Community hub
Visible spectrum
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Visible spectrum
Visible spectrum
Visible spectrum
View on Wikipedia
from Wikipedia
White light is dispersed by a glass prism into the colors of the visible spectrum.

The visible spectrum is the band of the electromagnetic spectrum that is visible to the human eye. Electromagnetic radiation in this range of wavelengths is called visible light (or simply light). The optical spectrum is sometimes considered to be the same as the visible spectrum, but some authors define the term more broadly, to include the ultraviolet and infrared parts of the electromagnetic spectrum as well, known collectively as optical radiation.[1][2]

A typical human eye will respond to wavelengths from about 380 to about 750 nanometers.[3] In terms of frequency, this corresponds to a band in the vicinity of 400–790 terahertz. These boundaries are not sharply defined and may vary per individual.[4] Under optimal conditions, these limits of human perception can extend to 310 nm (ultraviolet) and 1100 nm (near infrared).[5][6][7]

The spectrum does not contain all the colors that the human visual system can distinguish. Unsaturated colors such as pink, or purple variations like magenta, for example, are absent because they can only be made from a mix of multiple wavelengths. Colors containing only one wavelength are also called pure colors or spectral colors.[8][9]

Visible wavelengths pass largely unattenuated through the Earth's atmosphere via the "optical window" region of the electromagnetic spectrum. An example of this phenomenon is when clean air scatters blue light more than red light, and so the midday sky appears blue (apart from the area around the Sun which appears white because the light is not scattered as much). The optical window is also referred to as the "visible window" because it overlaps the human visible response spectrum. The near infrared (NIR) window lies just out of the human vision, as well as the medium wavelength infrared (MWIR) window, and the long-wavelength or far-infrared (LWIR or FIR) window, although other animals may perceive them.[2][4]

Spectral colors

[edit]
sRGB rendering of the spectrum of visible light
sRGB rendering of the spectrum of visible light
Color Wave­length
(nm) 		Fre­quen­cy
(THz) 		Photon energy
(eV)
  violet
 380–450 670–790 2.75–3.26
  blue
 450–485 620–670 2.56–2.75
  cyan
 485–500 600–620 2.48–2.56
  green
 500–565 530–600 2.19–2.48
  yellow
 565–590 510–530 2.10–2.19
  orange
 590–625 480–510 1.98–2.10
  red
 625–750 400–480 1.65–1.98
Main article: Spectral color

Colors that can be produced by visible light of a narrow band of wavelengths (monochromatic light) are called spectral colors. The various color ranges indicated in the illustration are an approximation: The spectrum is continuous, with no clear boundaries between one color and the next.[10]

History

[edit]
Newton's color circle, from Opticks of 1704, showing the colors he associated with musical notes. The spectral colors from red to violet are divided by the notes of the musical scale, starting at D. The circle completes a full octave, from D to D. Newton's circle places red, at one end of the spectrum, next to violet, at the other. This reflects the fact that non-spectral purple colors are observed when red and violet light are mixed.

In the 13th century, Roger Bacon theorized that rainbows were produced by a similar process to the passage of light through glass or crystal.[11]

In the 17th century, Isaac Newton discovered that prisms could disassemble and reassemble white light, and described the phenomenon in his book Opticks. He was the first to use the word spectrum (Latin for "appearance" or "apparition") in this sense in print in 1671 in describing his experiments in optics. Newton observed that, when a narrow beam of sunlight strikes the face of a glass prism at an angle, some is reflected and some of the beam passes into and through the glass, emerging as different-colored bands. Newton hypothesized light to be made up of "corpuscles" (particles) of different colors, with the different colors of light moving at different speeds in transparent matter, red light moving more quickly than violet in glass. The result is that red light is bent (refracted) less sharply than violet as it passes through the prism, creating a spectrum of colors.

Newton's observation of prismatic colors (David Brewster 1855)

Newton originally divided the spectrum into six named colors: red, orange, yellow, green, blue, and violet. He later added indigo as the seventh color since he believed that seven was a perfect number as derived from the ancient Greek sophists, of there being a connection between the colors, the musical notes, the known objects in the Solar System, and the days of the week.[12] The human eye is relatively insensitive to indigo's frequencies, and some people who have otherwise-good vision cannot distinguish indigo from blue and violet. For this reason, some later commentators, including Isaac Asimov,[13] have suggested that indigo should not be regarded as a color in its own right but merely as a shade of blue or violet. Evidence indicates that what Newton meant by "indigo" and "blue" does not correspond to the modern meanings of those color words. Comparing Newton's observation of prismatic colors with a color image of the visible light spectrum shows that "indigo" corresponds to what is today called blue, whereas his "blue" corresponds to cyan.[14][15][16]

In the 18th century, Johann Wolfgang von Goethe wrote about optical spectra in his Theory of Colours. Goethe used the word spectrum (Spektrum) to designate a ghostly optical afterimage, as did Schopenhauer in On Vision and Colors. Goethe argued that the continuous spectrum was a compound phenomenon. Where Newton narrowed the beam of light to isolate the phenomenon, Goethe observed that a wider aperture produces not a spectrum but rather reddish-yellow and blue-cyan edges with white between them. The spectrum appears only when these edges are close enough to overlap.

In the early 19th century, the concept of the visible spectrum became more definite, as light outside the visible range was discovered and characterized by William Herschel (infrared) and Johann Wilhelm Ritter (ultraviolet), Thomas Young, Thomas Johann Seebeck, and others.[17] Young was the first to measure the wavelengths of different colors of light, in 1802.[18]

The connection between the visible spectrum and color vision was explored by Thomas Young and Hermann von Helmholtz in the early 19th century. Their theory of color vision correctly proposed that the eye uses three distinct receptors to perceive color.

Limits to visible range

[edit]
See also: Color vision § Physiology of color perception
Photopic (black) and scotopic (green) luminous efficiency functions. The horizontal axis is wavelength in nm. See luminous efficiency function for more info.

The visible spectrum is limited to wavelengths that can both reach the retina and trigger visual phototransduction (excite a visual opsin). Insensitivity to UV light is generally limited by transmission through the lens. Insensitivity to IR light is limited by the spectral sensitivity functions of the visual opsins. The range is defined psychometrically by the luminous efficiency function, which accounts for all of these factors. In humans, there is a separate function for each of two visual systems, one for photopic vision, used in daylight, which is mediated by cone cells, and one for scotopic vision, used in dim light, which is mediated by rod cells. Each of these functions have different visible ranges. However, discussion on the visible range generally assumes photopic vision.

Atmospheric transmission

[edit]

The visible range of most animals evolved to match the optical window, which is the range of light that can pass through the atmosphere. The ozone layer absorbs almost all UV light (below 315 nm).[19] However, this only affects cosmic light (e.g. sunlight), not terrestrial light (e.g. Bioluminescence).

Ocular transmission

[edit]
Cumulative transmission spectra of light as it passes through the ocular media, namely after the cornea (blue), before the lens (red), after the lens (gray) and before the retina (orange). The solid lines are for a 4.5 year old eye. The dashed orange line is for a 53 year old eye, and dotted for a 75 year old eye, indicating the effect of lens yellowing.)

Before reaching the retina, light must first transmit through the cornea and lens. UVB light (< 315 nm) is filtered mostly by the cornea, and UVA light (315–400 nm) is filtered mostly by the lens.[20] The lens also yellows with age, attenuating transmission most strongly at the blue part of the spectrum.[20] This can cause xanthopsia as well as a slight truncation of the short-wave (blue) limit of the visible spectrum. Subjects with aphakia are missing a lens, so UVA light can reach the retina and excite the visual opsins; this expands the visible range and may also lead to cyanopsia.

Opsin absorption

[edit]

Each opsin has a spectral sensitivity function, which defines how likely it is to absorb a photon of each wavelength. The luminous efficiency function is approximately the superposition of the contributing visual opsins. Variance in the position of the individual opsin spectral sensitivity functions therefore affects the luminous efficiency function and the visible range. For example, the long-wave (red) limit changes proportionally to the position of the L-opsin. The positions are defined by the peak wavelength (wavelength of highest sensitivity), so as the L-opsin peak wavelength blue shifts by 10 nm, the long-wave limit of the visible spectrum also shifts 10 nm. Large deviations of the L-opsin peak wavelength lead to a form of color blindness called protanomaly and a missing L-opsin (protanopia) shortens the visible spectrum by about 30 nm at the long-wave limit. Forms of color blindness affecting the M-opsin and S-opsin do not significantly affect the luminous efficiency function nor the limits of the visible spectrum.

Different definitions

[edit]

Regardless of actual physical and biological variance, the definition of the limits is not standard and will change depending on the industry. For example, some industries may be concerned with practical limits, so would conservatively report 420–680 nm,[21][22] while others may be concerned with psychometrics and achieving the broadest spectrum would liberally report 380–750, or even 380–800 nm.[23][24] The luminous efficiency function in the NIR does not have a hard cutoff, but rather an exponential decay, such that the function's value (or vision sensitivity) at 1,050 nm is about 109 times weaker than at 700 nm; much higher intensity is therefore required to perceive 1,050 nm light than 700 nm light.[25]

Vision outside the visible spectrum

[edit]

Under ideal laboratory conditions, subjects may perceive infrared light up to at least 1,064 nm.[25] While 1,050 nm NIR light can evoke red, suggesting direct absorption by the L-opsin, there are also reports that pulsed NIR lasers can evoke green, which suggests two-photon absorption may be enabling extended NIR sensitivity.[25]

Similarly, young subjects may perceive ultraviolet wavelengths down to about 310–313 nm,[26][27][28] but detection of light below 380 nm may be due to fluorescence of the ocular media, rather than direct absorption of UV light by the opsins. As UVA light is absorbed by the ocular media (lens and cornea), it may fluoresce and be released at a lower energy (longer wavelength) that can then be absorbed by the opsins. For example, when the lens absorbs 350 nm light, the fluorescence emission spectrum is centered on 440 nm.[29]

Non-visual light detection

[edit]

In addition to the photopic and scotopic systems, humans have other systems for detecting light that do not contribute to the primary visual system. For example, melanopsin has an absorption range of 420–540 nm and regulates circadian rhythm and other reflexive processes.[30] Since the melanopsin system does not form images, it is not strictly considered vision and does not contribute to the visible range.

In non-humans

[edit]
See also: Evolution of color vision

The visible spectrum is defined as that visible to humans, but the variance between species is large. Not only can cone opsins be spectrally shifted to alter the visible range, but vertebrates with 4 cones (tetrachromatic) or 2 cones (dichromatic) relative to humans' 3 (trichromatic) will also tend to have a wider or narrower visible spectrum than humans, respectively.

Vertebrates tend to have 1-4 different opsin classes:[19]

  • longwave sensitive (LWS) with peak sensitivity between 500–570 nm,
  • middlewave sensitive (MWS) with peak sensitivity between 480–520 nm,
  • shortwave sensitive (SWS) with peak sensitivity between 415–470 nm, and
  • violet/ultraviolet sensitive (VS/UVS) with peak sensitivity between 355–435 nm.

Testing the visual systems of animals behaviorally is difficult, so the visible range of animals is usually estimated by comparing the peak wavelengths of opsins with those of typical humans (S-opsin at 420 nm and L-opsin at 560 nm).

Mammals

[edit]

Most mammals have retained only two opsin classes (LWS and VS), due likely to the nocturnal bottleneck. However, old world primates (including humans) have since evolved two versions in the LWS class to regain trichromacy.[19] Unlike most mammals, rodents' UVS opsins have remained at shorter wavelengths. Along with their lack of UV filters in the lens, mice have a UVS opsin that can detect down to 340 nm. While allowing UV light to reach the retina can lead to retinal damage, the short lifespan of mice compared with other mammals may minimize this disadvantage relative to the advantage of UV vision.[31] Dogs have two cone opsins at 429 nm and 555 nm, so see almost the entire visible spectrum of humans, despite being dichromatic.[32] Horses have two cone opsins at 428 nm and 539 nm, yielding a slightly more truncated red vision.[33]

Birds

[edit]
See also: Bird vision § Ultraviolet sensitivity

Most other vertebrates (birds, lizards, fish, etc.) have retained their tetrachromacy, including UVS opsins that extend further into the ultraviolet than humans' VS opsin.[19] The sensitivity of avian UVS opsins vary greatly, from 355–425 nm, and LWS opsins from 560–570 nm.[34] This translates to some birds with a visible spectrum on par with humans, and other birds with greatly expanded sensitivity to UV light. The LWS opsin of birds is sometimes reported to have a peak wavelength above 600 nm, but this is an effective peak wavelength that incorporates the filter of avian oil droplets.[34] The peak wavelength of the LWS opsin alone is the better predictor of the long-wave limit. A possible benefit of avian UV vision involves sex-dependent markings on their plumage that are visible only in the ultraviolet range.[35][36]

Fish

[edit]
See also: Vision in fish § Ultraviolet

Teleosts (bony fish) are generally tetrachromatic. The sensitivity of fish UVS opsins vary from 347-383 nm, and LWS opsins from 500-570 nm.[37] However, some fish that use alternative chromophores can extend their LWS opsin sensitivity to 625 nm.[37] The popular belief that the common goldfish is the only animal that can see both infrared and ultraviolet light[38] is incorrect, because goldfish cannot see infrared light.[39]

Invertebrates

[edit]

The visual systems of invertebrates deviate greatly from vertebrates, so direct comparisons are difficult. However, UV sensitivity has been reported in most insect species.[40] Bees and many other insects can detect ultraviolet light, which helps them find nectar in flowers. Plant species that depend on insect pollination may owe reproductive success to their appearance in ultraviolet light rather than how colorful they appear to humans. Bees' long-wave limit is at about 590 nm.[41] Mantis shrimp exhibit up to 14 opsins, enabling a visible range of less than 300 nm to above 700 nm.[19]

Thermal vision

[edit]
Main article: Infrared sensing in snakes

Some snakes can "see"[42] radiant heat at wavelengths between 5 and 30 μm to a degree of accuracy such that a blind rattlesnake can target vulnerable body parts of the prey at which it strikes,[43] and other snakes with the organ may detect warm bodies from a meter away.[44] It may also be used in thermoregulation and predator detection.[45][46]

Spectroscopy

[edit]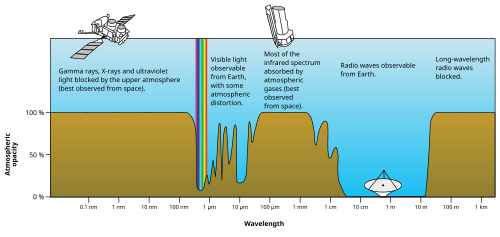
Earth's atmosphere partially or totally blocks some wavelengths of electromagnetic radiation, but in visible light it is mostly transparent
Main article: Spectroscopy

Spectroscopy is the study of objects based on the spectrum of color they emit, absorb or reflect. Visible-light spectroscopy is an important tool in astronomy (as is spectroscopy at other wavelengths), where scientists use it to analyze the properties of distant objects. Chemical elements and small molecules can be detected in astronomical objects by observing emission lines and absorption lines. For example, helium was first detected by analysis of the spectrum of the Sun. The shift in frequency of spectral lines is used to measure the Doppler shift (redshift or blueshift) of distant objects to determine their velocities towards or away from the observer. Astronomical spectroscopy uses high-dispersion diffraction gratings to observe spectra at very high spectral resolutions.

See also

[edit]
English Wikisource has original text related to this article:
Wikimedia Commons has media related to Visible spectrum.

References

[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Visible spectrum

View on Grokipedia
from Grokipedia
The visible spectrum is the band of with wavelengths detectable by the , typically ranging from about 380 to 740 nanometers. This narrow portion of the broader corresponds to that appears as a continuous sequence of colors, from violet at the shorter wavelengths to at the longer ones. The perceives these wavelengths as distinct hues, enabling essential for daily perception and interaction with the environment. The exact boundaries vary slightly among individuals. The visible spectrum was first systematically studied by in 1666–1667, who used prisms to show that white light is composed of a mixture of colors.

Basic Concepts

Definition and Scope

The visible spectrum encompasses the segment of the detectable by the , comprising with wavelengths roughly from 380 to 700 nanometers and corresponding frequencies of approximately 430 to 790 terahertz. This range defines the boundaries of light that humans perceive as colors, from violet at the shorter wavelengths to at the longer ones. Within the broader , the visible spectrum lies between the region (shorter wavelengths, higher frequencies) and the region (longer wavelengths, lower frequencies), occupying a narrow band amid radio waves, microwaves, X-rays, and gamma rays. in this spectrum exhibits dual properties as electromagnetic waves, characterized by oscillating electric and magnetic fields, and as discrete packets of energy called photons, whose interactions with determine visibility. The detectability of these wavelengths stems from the sensitivity of retinal photoreceptors, which absorb photons in this range to initiate visual signaling. Visible light represents only a minuscule portion of the entire , accounting for about 0.0035% of its total span. This limited fraction underscores the specificity of human vision to a precise subset of , enabling perception of phenomena such as the pure spectral colors produced by isolating individual wavelengths, like the violet of nm or the of nm.

Wavelength and Frequency Ranges

The visible spectrum encompasses electromagnetic waves with wavelengths ranging approximately from 380 nanometers (nm) in the violet region to 700 nm in the region, though these boundaries can vary slightly based on conventional definitions and measurement contexts. Wavelengths in this range are typically expressed in nanometers, a unit equal to 10−910^{-9} meters, which provides a convenient scale for the short distances involved in visible propagation. The corresponding frequencies for these wavelengths span from about 430 terahertz (THz) for red light to 790 THz for violet light, reflecting the inverse relationship between wavelength (λ\lambda) and frequency (ff) governed by the fundamental equation c=λfc = \lambda f, where cc is the speed of light in vacuum, approximately 3×1083 \times 10^8 m/s. Frequencies in the visible spectrum are commonly measured in terahertz, where 1 THz equals 101210^{12} hertz (Hz). This inverse proportionality means that shorter wavelengths correspond to higher frequencies, positioning the visible spectrum within the broader between (higher frequency, shorter wavelength) and (lower frequency, wavelength) regions. To illustrate, consider a wavelength of 500 nm, typical for green : f=cλ=3×108 m/s500×10−9 m=6×1014 Hz≈600 THz.f = \frac{c}{\lambda} = \frac{3 \times 10^8 \, \mathrm{m/s}}{500 \times 10^{-9} \, \mathrm{m}} = 6 \times 10^{14} \, \mathrm{Hz} \approx 600 \, \mathrm{THz}. This calculation demonstrates how the speed of constant links the two measures, allowing conversion between and for any point in the . The boundaries of the visible are not sharply defined but exhibit a gradual transition, influenced by the sensitivity curves that characterize detection thresholds across the range. These conventions establish the core extent of visible while acknowledging inherent variations in practical applications.

Spectral Colors

Characteristics and Production

Spectral colors are defined as consisting of a single within the visible range, resulting in pure hues without any mixing of other wavelengths. These colors exhibit maximum saturation and intensity for their respective hues, as the absence of additional spectral components ensures no dilution of the dominant wavelength's purity. Each specific wavelength corresponds to a distinct hue; for example, light at approximately 450 nm appears , while 550 nm appears . Spectral colors can be produced through various methods that isolate or generate monochromatic light. Prisms achieve this via dispersion, where the refractive index of the material varies with , causing different colors to bend at slightly different angles and separate spatially. gratings function similarly but more precisely by exploiting , diffracting light into spectral orders based on , often providing higher resolution than prisms. Lasers serve as direct sources of highly monochromatic , emitting coherent at a precise through , enabling the production of pure spectral colors with narrow linewidths. A foundational demonstration of spectral color production came from Isaac Newton's prism experiments in the 1660s and 1670s, where he decomposed white into a continuous of colors, showing that white is a composite of all visible wavelengths rather than a singular entity. This revealed the spectrum's continuity across wavelengths from approximately 380 to 700 nm. The physical basis for prism-based separation lies in dispersion, quantified by the angular separation δθ between , approximated as δθ ≈ (dn/dλ) Δλ times a geometry factor dependent on the prism's apex and incidence, where n is the and λ is . This differential bending arises because shorter (e.g., ) experience higher refractive indices in most materials, leading to greater deviation than longer (e.g., ).

Human Perception of Pure Spectral Colors

Human trichromatic color vision relies on three types of cone photoreceptors in the retina: short-wavelength-sensitive (S) cones, medium-wavelength-sensitive (M) cones, and long-wavelength-sensitive (L) cones. These cones enable the perception of color by comparing their relative activation levels in response to incoming light, allowing the visual system to distinguish hues across the visible spectrum. Spectral colors, being monochromatic wavelengths, stimulate these cones in distinct patterns; for instance, shorter wavelengths around 400-450 nm predominantly activate S cones to produce violet hues, while medium wavelengths near 500-570 nm balance M-cone stimulation for green perceptions, and longer wavelengths above 620 nm primarily engage L cones for red sensations. The further shapes this , positing that color information is processed along antagonistic channels—red versus and blue versus —which prevent certain hue combinations from being perceived simultaneously. As a result, impossible colors such as reddish-green cannot occur because spectral lights eliciting (e.g., 630 nm) and (e.g., 500 nm) activate opposing channels, and no single stimulus can engage both positively. Similarly, the endpoints, like extreme violet and , resist exact matching by additive mixtures of other colors due to the unique stimulation profiles at these boundaries, highlighting the limits of human hue . In , the spectral locus illustrates these pure colors as a boundary curve on the CIE 1931 xy chromaticity diagram, which models human color perception based on standardized observer data; points along this locus represent the most saturated hues achievable, enclosing the of all perceivable colors. Overall, while the can distinguish approximately one million color variations through interactions, spectral colors embody the purest forms without desaturation, serving as perceptual anchors in this vast space.

Historical Development

Early Observations and Theories

Ancient civilizations observed rainbows and halos as striking atmospheric phenomena, often interpreting them through a mix of natural and supernatural lenses. In , , in his work (c. 350 BCE), provided one of the earliest systematic natural explanations, attributing the formation of rainbows to the reflection of in clouds and distinguishing them from halos, which he described as circular reflections around the sun or moon due to denser atmospheric moisture. He posited that these effects arose from the interaction of sight with solar rays refracted in misty air, marking a shift toward empirical observation over purely mythical accounts, though such events retained cultural significance as portents in Greek and other traditions. In ancient China, scholars like (c. 470–391 BCE) laid foundational work in through the Mohist school, discussing the of , shadow formation, and early principles related to reflection and in texts such as the Mozi. By the 11th century, Shen Kua further advanced these ideas in his (1088 CE), describing optical phenomena including the pinhole camera's inversion of images and observations on that demonstrated 's bending through media, contributing to understandings of how behaves in forming visual effects like those in rainbows. Medieval Islamic scholars built on these foundations with rigorous experimentation. (Alhazen, 965–1040 CE), in his seminal (completed c. 1021 CE), systematically analyzed and reflection, explaining the rainbow's colors as resulting from sunlight's , internal reflection, and dispersion within spherical water droplets in the atmosphere. His work emphasized quantitative measurements of light paths and refuted earlier notions of light emission from the eye, establishing as a mathematical science and influencing later European thought. In the 17th century, advanced a mechanistic particle theory of in La Dioptrique (1637), proposing that consisted of straight-moving particles whose speed varied in different media, causing and enabling the 's formation through successive refractions and reflections in raindrops. This corpuscular model aimed to explain color emergence geometrically but assumed colors arose from particle modifications during propagation. A pivotal breakthrough came in 1666 when conducted prism experiments, demonstrating that white is inherently composite, decomposing into a of distinct colors upon passing through a prism, thereby refuting prevailing "modification" theories that light's hue was altered by the medium rather than revealed in its primal form. Newton's findings, detailed in his (1704), included a color circle arranging the spectral hues—, orange, , , , , violet—in a circular sequence to illustrate their relational harmonies and transitions, profoundly shaping subsequent .

Modern Scientific Advancements

In the early 19th century, Thomas Young's in 1801 provided compelling evidence for the wave nature of light by demonstrating interference patterns when visible light passed through two closely spaced slits, challenging the particle theory dominant at the time. This work laid foundational insights into the propagation of visible wavelengths as waves. Building on this, Joseph von Fraunhofer's observations in 1814 revealed dark absorption lines in the solar spectrum, now known as , which indicated selective absorption by atmospheric and stellar elements, advancing the understanding of spectral composition in the visible range. By 1865, James Clerk Maxwell's electromagnetic theory unified electricity and magnetism, positing that visible light consists of transverse electromagnetic waves propagating at the , thereby integrating the visible spectrum into the broader electromagnetic framework. The transition to the 20th century marked a with Max Planck's quantum hypothesis in 1900, which resolved the problem by proposing that light energy is emitted and absorbed in discrete quanta, or packets, rather than continuously, fundamentally altering the conceptualization of visible light interactions. Extending this idea, Albert Einstein's 1905 explanation of the demonstrated that light behaves as particles—later termed photons—ejecting electrons from metals only when photon energy exceeds a threshold corresponding to visible or frequencies, earning him the 1921 and solidifying the wave-particle duality of visible spectrum radiation. Instrumental developments in the 1920s included the creation of early spectrophotometers, such as visual models by Keuffel & Esser and , which enabled precise measurement of absorption and transmission across visible wavelengths, facilitating quantitative spectral analysis in laboratories. In 1931, the International Commission on Illumination (CIE) established standardized color-matching functions based on human observer data, defining the CIE 1931 XYZ color space to quantify visible spectrum colors through tristimulus values, which remains the basis for modern . Molecular biology intersected with spectral understanding in the 1960s through the identification of opsins—protein components of visual photopigments—as key molecules absorbing specific visible wavelengths in photoreceptor cells, linking quantum-level light detection to biochemical signaling in vision. More recently, advancements in light-emitting diode (LED) technology during the 2000s have allowed for engineered emission spectra tailored to precise visible wavelengths, enabling applications in tunable lighting and displays with high color fidelity and efficiency.

Boundaries of Visibility

Physical and Environmental Limits

The transmission of through Earth's atmosphere significantly constrains the observable visible spectrum, primarily due to scattering and absorption processes that preferentially affect shorter . by air molecules, which dominates for particles much smaller than the of , scatters shorter wavelengths more intensely than longer ones, resulting in the characteristic color of the and a narrowing of the effective visible range toward the red end under clear conditions. This scattering follows a wavelength dependence described by the cross-section σ∝1λ4\sigma \propto \frac{1}{\lambda^4}, where λ\lambda is the , for particles much smaller than λ\lambda. The atmosphere's overall transmission window extends approximately from 300 nm to 1100 nm, encompassing , visible, and near- regions, but the visible portion (roughly 380–750 nm) is further delimited by these effects, with increased at the blue-violet edge due to the λ−4\lambda^{-4} law. in the strongly absorbs radiation below about 300 nm, effectively blocking shorter wavelengths from reaching the surface and defining the lower atmospheric boundary for visible . At the infrared edge, contributes to absorption in the near-infrared (beyond 700 nm), subtly influencing the upper limit of the visible spectrum by attenuating longer wavelengths near the boundary. Within the ocular media, the lens and other transparent structures impose additional physical limits on transmission, absorbing light below 400 nm and above 700 nm due to inherent molecular properties. Age-related yellowing of the lens, resulting from accumulation of chromophores, further reduces transmission in the blue-violet (around 400–450 nm), shifting the perceived lower limit toward longer wavelengths and diminishing color discrimination in older individuals. Environmental variations also alter the visible spectrum's boundaries. In settings, water molecules preferentially absorb longer wavelengths, causing a blue shift where reds fade rapidly with depth, making the effective visible range appear more dominated beyond a few meters. At high altitudes, reduced atmospheric density leads to less overall, allowing clearer transmission of wavelengths and enhancing the visibility of the full visible spectrum compared to .

Biological Limits in Human Vision

The human visible spectrum is primarily determined by the spectral sensitivities of the retinal photoreceptors, particularly the three types of cone cells that mediate color vision under normal lighting conditions. These cones contain opsin proteins that absorb light at distinct wavelength peaks: short-wavelength-sensitive (S) cones peak at approximately 420 nm in the violet-blue range, medium-wavelength-sensitive (M) cones at about 530 nm in the green range, and long-wavelength-sensitive (L) cones at around 560 nm in the yellow-green range. The sensitivity curves for these cones, often represented by the Smith-Pokorny fundamentals derived from color-matching experiments, overlap significantly, enabling the trichromatic basis of human color perception within the broader visible range. While the peak sensitivities of the cones align closely with the conventional visible spectrum of 400–700 nm, the effective detection threshold for human vision extends more broadly, from approximately 360 nm in the ultraviolet to 830 nm in the near-infrared, though perception is achromatic and weak at these extremes. Sensitivity drops sharply outside the 380–750 nm range, where the photopic luminous efficiency function V(λ), standardized by the CIE in 1924, quantifies the relative brightness perception based on cone responses, with V(λ) approaching zero beyond these limits. Under low-light (scotopic) conditions, rod photoreceptors dominate, with their sensitivity peaking at 498 nm and extending slightly into the near-infrared up to about 800 nm at threshold levels, though still far below cone-mediated visibility. A key physiological adaptation influencing spectral boundaries is the Purkinje shift, where in dim illumination, the transition from cone- to rod-dominated vision shifts peak sensitivity from the yellow-green (around 555 nm) to the (around 500 nm), enhancing detection of shorter wavelengths as become active. This reflects the ' higher sensitivity to light compared to reds, optimizing low-light vision but reducing color discrimination. Individual variations can alter these limits; for instance, while most humans are trichromats, some women carry genes for a fourth type, potentially enabling and expanded color discrimination beyond standard trichromatic boundaries, though functional tetrachromacy remains exceedingly rare.

Individual and Definitional Variations

The visible spectrum's boundaries are not universally fixed but vary according to definitional standards in scientific and technical contexts. The (CIE) commonly defines the range as approximately 380 to 780 nm, encompassing the wavelengths to which the average is sensitive under standard viewing conditions. In contrast, some sources adopt a stricter range of 400 to 700 nm to focus on the core wavelengths producing distinct spectral colors, excluding marginal sensitivities at the violet and extremes. The ASTM E308 standard for extends the practical measurement range to 360–830 nm to account for instrumental needs in computing object colors from spectral data, though human perception tapers off beyond 780 nm. Individual variations in perceiving the visible spectrum arise from physiological differences, altering the effective range for specific people. Color vision deficiencies, affecting an estimated 300 million individuals worldwide, can shift perceptual boundaries; for instance, protanomaly reduces sensitivity to longer red wavelengths (around 620–700 nm), making reds appear dimmer or confused with greens, effectively narrowing the red end of the spectrum. With aging, the eye's lens yellows due to accumulated UV exposure and oxidative changes, increasingly absorbing shorter blue-violet wavelengths (below 450 nm) and reducing transmission by up to 20–30% in those over 70, thereby compressing the blue boundary of visibility. These differences build on baseline human biology but highlight how personal factors modify the spectrum's experiential limits. Cultural and linguistic influences further diversify how the visible spectrum is segmented and perceived. Languages vary in their color categorization; for example, some, like certain Indigenous Australian tongues, lack distinct terms for and , leading speakers to group those wavelengths (450–570 nm) together and exhibit slower discrimination in perceptual tasks compared to languages with separate terms. This relativity affects not just naming but attentional focus on spectral regions, as demonstrated in where linguistic structure influences color boundary judgments.

Vision Across Species

Mammals and Invertebrates

Most mammals exhibit dichromatic vision, relying on two types of cone photoreceptors sensitive to short-wavelength (blue-violet) and medium-to-long-wavelength (green-yellow) light, which limits their color discrimination compared to the trichromatic vision of s. This adaptation is prevalent in most mammalian , particularly among nocturnal or crepuscular lineages that prioritize low-light sensitivity over broad spectral range. For example, dogs possess cones peaking at 429 nm (blue-violet) and 555 nm (yellow-green), enabling perception across much of the human visible spectrum (roughly 400–600 nm) but rendering reds and greens indistinguishable, often appearing as shades of yellow or gray. Similarly, cats have peak sensitivities at 454 nm (blue) and 561 nm (green-yellow), with a functional range of about 450–650 nm, though their vision extends slightly into wavelengths below 400 nm due to lens transparency. In contrast, many , including humans, have evolved trichromatic vision through a third cone type sensitive to long wavelengths (), enhancing detection and social signaling in diurnal environments. This shift represents an exception among mammals, where the majority retain the ancestral dichromatic system shaped by a nocturnal evolutionary bottleneck during the era, when early mammals avoided diurnal predators by becoming active at night. During this period, ancestral mammals lost ultraviolet-sensitive cones (SWS1 functionality), reducing their spectral range to favor rod-dominated retinas for ; however, some , such as mice and rats, have retained UV sensitivity peaking around 360 nm, aiding in detecting markings and enhancing contrast in low-light . Invertebrates often possess more expansive or specialized visible spectrum perception, frequently incorporating ultraviolet sensitivity absent in most mammals. Insects like bees exhibit trichromatic vision with photoreceptors tuned to ultraviolet (peaking ~340 nm), blue (~430 nm), and green (~540 nm), spanning approximately 300–650 nm; this allows them to detect nectar guides and patterns on flowers that appear as contrasting UV-reflective bullseyes invisible to humans. Butterflies demonstrate even greater diversity, with vision extending from 300–700 nm supported by 5–6 receptor types in many species, including UV, violet, blue, green, and red-sensitive classes, which facilitate mate selection, host plant identification, and evasion of predators through enhanced color discrimination. Cephalopod mollusks, such as , also perceive a broad spectrum within 300–700 nm via a single type peaking around 480 nm, but they uniquely detect polarized light patterns—changes in light wave orientation scattered by or prey—enhancing object detection and in marine environments where color cues alone are insufficient. This polarization sensitivity, with thresholds as low as 1° contrast, compensates for their achromatic vision and underscores evolutionary adaptations to underwater .

Birds and Fish

Birds possess tetrachromatic , featuring four types of cone photoreceptors sensitive to (UV), short-wavelength (violet or ), medium-wavelength (), and long-wavelength () , spanning approximately 300–700 nm. This expanded spectral range allows birds to perceive UV patterns invisible to humans, which play crucial roles in ecological behaviors such as mate selection and ; for instance, female zebra finches use UV reflectance in male to assess potential mates. Unique adaptations like colored oil droplets in the cones act as spectral filters, sharpening color discrimination by narrowing the bandwidth of reaching each photoreceptor and enhancing contrast against natural backgrounds. Consequently, birds can distinguish far more colors than humans, enabling finer detection of subtle environmental cues. In parrots, the long-wavelength-sensitive cones peak at around 570 nm, optimizing sensitivity to reddish hues that signal ripe fruit, which supports their frugivorous diet by facilitating the identification of nutritious food sources in forest canopies. Many surface-dwelling exhibit trichromatic vision with cones sensitive to , and wavelengths, covering roughly 400–700 nm, which aligns with the broader available in shallow, well-lit waters. In contrast, like the have adapted to dim, -dominated environments through blue-shifted visual s, with rod and sensitivities peaking at approximately 478–485 nm, effectively losing sensitivity to both UV and longer wavelengths beyond 600 nm. This narrowing of the spectral range, often to just two types, prioritizes maximal capture in the prevalent penetrating deeper waters while sacrificing color complexity for enhanced low-light performance. Adaptive features such as UV-blocking lenses in many clear-water species further protect tissues from harmful short-wavelength radiation while maintaining focus on visible signals essential for navigation and prey detection.

Specialized Non-Visible Extensions

Certain animals possess specialized photoreceptive mechanisms that extend sensitivity beyond the visible spectrum (approximately 400–700 nm), enabling detection of (UV) or (IR) light for , , or physiological regulation, often without forming coherent images like those produced by vision. These extensions rely on proteins—light-sensitive G protein-coupled receptors—that bind chromophores to initiate phototransduction, but they function in non-ocular tissues or as supplementary systems distinct from image-forming vision. Birds and insects utilize UV-sensitive opsins (e.g., short-wavelength-sensitive type 1, SWS1) for environmental navigation, where UV reflectance patterns reveal otherwise invisible cues such as flower nectaries or trail markers. In birds, tetrachromatic vision incorporates UV alongside violet, green, and red channels, aiding mate selection and prey detection, though this represents an extension rather than a standalone non-visual sense. Insects, including bees and butterflies, employ UV opsins peaking around 340–370 nm to orient during flight and locate resources, with UV acting as a distinct "color" channel in their compound eyes. Arctic reindeer (Rangifer tarandus), uniquely among mammals, detect UV up to ~320 nm via rod and cone responses, allowing differentiation of lichens and vegetation against snow, which reflects up to 90% of incident UV light—critical for foraging in low-visibility winter conditions. This capability arises from permeable ocular media rather than dedicated UV opsins, enhancing contrast without specialized non-ocular detectors. IR detection in reptiles and mammals occurs via thermal sensing organs that transduce heat as neural signals, bypassing photochemical opsins entirely and producing no visual images. Pit vipers (e.g., rattlesnakes in Crotalinae) sense mid-IR wavelengths (7.5–15 μm, or 7,500–15,000 nm) through loreal pit organs—cavities between the eye and nostril containing a thin, heat-absorbent innervated by trigeminal . These pits function as thermal imagers, detecting prey gradients up to 1 m away with a sensitivity threshold of ~27–29°C, integrating signals in the optic tectum to overlay thermal maps onto visual input for strike accuracy. Vampire bats (Desmodus rotundus) similarly employ nasal pit organs with ion channels tuned for IR (peaking ~8–10 μm), enabling localization of blood vessels in hosts from 20 cm away; this modifies an ancestral heat-pain receptor for precise thermolocation during nocturnal feeding. Non-image-forming photoreception further extends through intrinsically photosensitive mechanisms in non-retinal tissues, regulating behaviors and without . (OPN4), a bistable peaking at ~480 nm in the spectrum, mediates circadian entrainment in vertebrates by suppressing in ipRGCs and signaling the , with UV contributions enhancing non-visual light detection in some species. Fish exhibit dermal photosensitivity via opsins embedded in skin chromatophores, as in (Lachnolaimus maximus), where SWS1 opsins (~415 nm peak) provide feedback on pigmentation shifts for , filtering light through overlying pigments to modulate color change without eye involvement. In (Carassius auratus), the hosts photoreceptive cells with rod-like opsins sensitive to broader wavelengths, including near-IR extensions via A2-based pigments, contributing to photoperiodic rhythms rather than vision. These systems underscore chemosensory or irradiance-detecting roles, contrasting image-forming processes by prioritizing intensity over pattern.

Scientific Applications

Spectroscopy Techniques

Spectroscopy techniques in the visible spectrum exploit the interaction of with to determine material composition, primarily through emission and absorption processes occurring between approximately 400 and 700 nm. involves exciting atoms to higher energy states, causing them to emit at discrete wavelengths characteristic of the element, producing line spectra. For instance, the sodium D-lines at 589 nm serve as a prominent example of such emissions, arising from transitions in the sodium atom's ./08%3A_An_Introduction_to_Optical_Atomic_Spectroscopy/8.01%3A_Optical_Atomic_Spectra) Absorption spectroscopy, conversely, measures the attenuation of visible light as it passes through a sample, where molecules or atoms absorb specific wavelengths corresponding to electronic transitions. This is governed by the Beer-Lambert law, expressed as A=ϵclA = \epsilon c l, where AA is the , ϵ\epsilon is the molar absorptivity, cc is the concentration, and ll is the path length. Visible-specific methods include tests, which identify metal ions by their characteristic emission colors when introduced into a ; copper compounds, for example, produce a green emission in the 500–570 nm range due to excited electron transitions. photometry extends this principle quantitatively, measuring the intensity of emitted light from and alkaline earth metals like sodium and in a controlled to determine their concentrations in samples./Spectroscopy/Electronic_Spectroscopy/Electronic_Spectroscopy_Basics/The_Beer-Lambert_Law)/Descriptive_Chemistry/Elements_Organized_by_Block/1_s-Block_Elements/Group_1%3A_The_Alkali_Metals/2Reactions_of_the_Group_1_Elements/_Tests) These techniques find broad applications in scientific fields. In astronomy, visible line spectra enable by analyzing absorption and emission features, such as Balmer lines, to infer , composition, and evolutionary stage. In environmental monitoring, absorption at around 680 nm by in vegetation allows of plant health and stress levels via spectroscopic . Visible spectroscopy instruments typically achieve resolutions of about 0.1 nm, enabling precise identification of spectral features, and the method is one of the most widely used in routine laboratory analyses across chemistry, , and .

Colorimetry and Standards

Colorimetry provides a standardized framework for quantifying colors within the visible spectrum through numerical representations that correlate with human perception. The International Commission on Illumination (CIE) established the foundational CIE 1931 XYZ color space based on experimental color-matching functions derived from human observers. These functions, denoted as xˉ(λ)\bar{x}(\lambda), yˉ(λ)\bar{y}(\lambda), and zˉ(λ)\bar{z}(\lambda), describe the spectral sensitivity of the human visual system to red, green, and blue primaries, respectively. For a light source with spectral power distribution P(λ)P(\lambda), the tristimulus values XX, YY, and ZZ are computed via integration: X=∫P(λ)xˉ(λ) dλ,Y=∫P(λ)yˉ(λ) dλ,Z=∫P(λ)zˉ(λ) dλ,\begin{align*} X &= \int P(\lambda) \bar{x}(\lambda) \, d\lambda, \\ Y &= \int P(\lambda) \bar{y}(\lambda) \, d\lambda, \\ Z &= \int P(\lambda) \bar{z}(\lambda) \, d\lambda, \end{align*} where the integrals span the visible wavelengths, typically from 380 nm to 780 nm, and normalization ensures YY corresponds to luminance. This system enables device-independent color specification, essential for cross-media consistency in industries like printing and textiles. Key standards facilitate transformations between color representations and . The CIE RGB color space, an early model using real primaries, is converted to the XYZ space via a linear that accounts for the primaries' chromaticities and : (XYZ)=(0.41847−0.15866−0.082835−0.0911690.252430.0157080.00092090−0.00254980.17860)(RGB),\begin{pmatrix} X \\ Y \\ Z \end{pmatrix} = \begin{pmatrix} 0.41847 & -0.15866 & -0.082835 \\ -0.091169 & 0.25243 & 0.015708 \\ 0.00092090 & -0.0025498 & 0.17860 \end{pmatrix} \begin{pmatrix} R \\ G \\ B \end{pmatrix},
Add your contribution
Related Hubs
User Avatar
No comments yet.