Recent from talks
Nothing was collected or created yet.
Ambiguity
View on Wikipedia

Ambiguity is the type of meaning in which a phrase, statement, or resolution is not explicitly defined, making for several interpretations; others describe it as a concept or statement that has no real reference. A common aspect of ambiguity is uncertainty. It is thus an attribute of any idea or statement whose intended meaning cannot be definitively resolved, according to a rule or process with a finite number of steps. The prefix ambi- reflects the idea of "two", as in "two meanings".
The concept of ambiguity is generally contrasted with vagueness. In ambiguity, specific and distinct interpretations are permitted (although some may not be immediately obvious), whereas with vague information it is difficult to form any interpretation at the desired level of specificity.
Linguistic forms
[edit]Lexical ambiguity is contrasted with semantic ambiguity.[citation needed] The former represents a choice between a finite number of known and meaningful context-dependent interpretations. The latter represents a choice between any number of possible interpretations, none of which may have a standard agreed-upon meaning. This form of ambiguity is closely related to vagueness.
Ambiguity in human language is argued to reflect principles of efficient communication.[2][3] Languages that communicate efficiently will avoid sending information that is redundant with information provided in the context. This can be shown mathematically to result in a system that is ambiguous when context is neglected. In this way, ambiguity is viewed as a generally useful feature of a linguistic system.
Linguistic ambiguity can be a problem in law, because the interpretation of written documents and oral agreements is often of paramount importance.

Pepe vio a Pablo enfurecido.
Interpretation 1: When Pepe was angry, then he saw Pablo.
Interpretation 2: Pepe saw that Pablo was angry.
Here, the syntactic tree in the figure represents interpretation 2.
Lexical ambiguity
[edit]The lexical ambiguity of a word or phrase applies to it having more than one meaning in the language to which the word belongs.[4] "Meaning" here refers to whatever should be represented by a good dictionary. For instance, the word "bank" has several distinct lexical definitions, including "financial institution" and "edge of a river". Or consider "apothecary". One could say, "I bought herbs from the apothecary". This could mean one actually spoke to the apothecary (pharmacist) or went to the apothecary (pharmacy).
The context in which an ambiguous word is used often makes it clearer which of the meanings is intended. If, for instance, someone says, "I put $100 in the bank", most people would not think someone used a shovel to dig in the mud. However, some linguistic contexts do not provide sufficient information to make a used word clearer.
Lexical ambiguity can be addressed by algorithmic methods that automatically associate the appropriate meaning with a word in context, a task referred to as word-sense disambiguation.
The use of multi-defined words requires the author or speaker to clarify their context and sometimes elaborate on their specific intended meaning (in which case, a less ambiguous term should have been used). The goal of clear, concise communication is that the receiver(s) have no misunderstanding about what was meant to be conveyed. An exception to this could include a politician whose "weasel words" and obfuscation are necessary to gain support from multiple constituents with mutually exclusive conflicting desires from their candidate of choice. Ambiguity is a powerful tool of political science.
More problematic are words whose multiple meanings express closely related concepts. "Good", for example, can mean "useful" or "functional" (That's a good hammer), "exemplary" (She's a good student), "pleasing" (This is good soup), "moral" (a good person versus the lesson to be learned from a story), "righteous", etc. "I have a good daughter" is not clear about which sense is intended. The various ways to apply prefixes and suffixes can also create ambiguity ("unlockable" can mean "capable of being opened" or "impossible to lock").
Semantic and syntactic ambiguity
[edit]
Semantic ambiguity occurs when a word, phrase, or sentence, taken out of context, has more than one interpretation. In "We saw her duck" (example due to Richard Nordquist), the words "her duck" can refer either:
- To the person's bird (the noun "duck", modified by the possessive pronoun "her"), or
- To a motion she made (the verb "duck", the subject of which is the objective pronoun "her", object of the verb "saw").[5]
Syntactic ambiguity arises when a sentence can have two (or more) different meanings because of the structure of the sentence—its syntax. This is often due to a modifying expression, such as a prepositional phrase, the application of which is unclear. In the sentence "He ate the cookies on the couch", for example, could mean that he ate the cookies that were on the couch (as opposed to those that were on the table), or it could mean that he was sitting on the couch when he ate the cookies. The sentence "To get in, you will need an entrance fee of $10 or your voucher and your drivers' license." could mean that you need EITHER ten dollars OR BOTH your voucher and your license, or it could mean that you need your license AND you need EITHER ten dollars OR a voucher. Only rewriting the sentence or placing appropriate punctuation can resolve a syntactic ambiguity.[5] For the notion of, and theoretic results about, syntactic ambiguity in artificial, formal languages (such as computer programming languages), see Ambiguous grammar.
Usually, semantic and syntactic ambiguity occur in the same sentence. The sentence "We saw her duck" is also syntactically ambiguous. Conversely, a sentence like "He ate the cookies on the couch" is also semantically ambiguous. Rarely, but occasionally, the different parsings of a syntactically ambiguous phrase result in the same meaning. For example, the command "Cook, cook!" can be parsed as "Cook (noun used as vocative), cook (imperative verb form)!", but also as "Cook (imperative verb form), cook (noun used as vocative)!". It is more common that a syntactically unambiguous phrase has a semantic ambiguity; for example, the lexical ambiguity in "Your boss is a funny man" is purely semantic, leading to the response "Funny ha-ha or funny peculiar?"
Spoken language can contain many more types of ambiguities that are called phonological ambiguities, where there is more than one way to compose a set of sounds into words, such as "ice cream" and "I scream". Such ambiguity is generally resolved according to the context. A mishearing of such, based on incorrectly resolved ambiguity, is called a mondegreen.
Philosophy
[edit]Philosophers (and other users of logic) spend a lot of time and effort searching for and removing (or intentionally adding) ambiguity in arguments because it can lead to incorrect conclusions and can be used to deliberately conceal bad arguments. For example, a politician might say, "I oppose taxes which hinder economic growth", an example of a glittering generality. Some will think they oppose taxes in general because they hinder economic growth. Others may think they oppose only those taxes that they believe will hinder economic growth. In writing, the sentence can be rewritten to reduce possible misinterpretation, either by adding a comma after "taxes" (to convey the first sense), or by changing "which" to "that" (to convey the second sense), or by rewriting it in other ways. The devious politician hopes that each constituent will interpret the statement in the most desirable way, and think the politician supports everyone's opinion. However, the opposite can also be true—an opponent can turn a positive statement into a bad one if the speaker uses ambiguity (intentionally or not). The logical fallacies of amphiboly and equivocation rely heavily on the use of ambiguous words and phrases.
In continental philosophy (particularly phenomenology and existentialism), there is much greater tolerance of ambiguity, as it is generally seen as an integral part of the human condition. Martin Heidegger argued that the relation between the subject and object is ambiguous, as is the relation of mind and body and part and whole. In Heidegger's phenomenology, Dasein is always in a meaningful world, but there is always an underlying background for every instance of signification. Thus, although some things may be certain, they have little to do with Dasein's sense of care and existential anxiety, e.g., in the face of death. In calling his work Being and Nothingness an "essay in phenomenological ontology" Jean-Paul Sartre follows Heidegger in defining the human essence as ambiguous, or relating fundamentally to such ambiguity. Simone de Beauvoir tries to base an ethics on Heidegger's and Sartre's writings (The Ethics of Ambiguity), where she highlights the need to grapple with ambiguity:
as long as there have been philosophers and they have thought, most of them have tried to mask it ... And the ethics which they have proposed to their disciples has always pursued the same goal. It has been a matter of eliminating the ambiguity by making oneself pure inwardness or pure externality, by escaping from the sensible world or being engulfed by it, by yielding to eternity or enclosing oneself in the pure moment.
Ethics cannot be based on the authoritative certainty given by mathematics and logic, or prescribed directly from the empirical findings of science. She states: "Since we do not succeed in fleeing it, let us, therefore, try to look the truth in the face. Let us try to assume our fundamental ambiguity. It is in the knowledge of the genuine conditions of our life that we must draw our strength to live and our reason for acting".
Literature and rhetoric
[edit]In literature and rhetoric, ambiguity can be a useful tool. Groucho Marx's classic joke depends on a grammatical ambiguity for its humor, for example: "Last night I shot an elephant in my pajamas. How he got in my pajamas, I'll never know". Songs and poetry often rely on ambiguous words for artistic effect, as in the song title "Don't It Make My Brown Eyes Blue" (where "blue" can refer to the color or to sadness).
In the narrative, ambiguity can be introduced in several ways: motive, plot, and character. F. Scott Fitzgerald uses the latter type of ambiguity with notable effect in his novel The Great Gatsby.
Mathematical notation
[edit]Mathematical notation is a helpful tool that eliminates a lot of misunderstandings associated with natural language in physics and other sciences. Nonetheless, there are still some inherent ambiguities due to lexical, syntactic, and semantic reasons that persist in mathematical notation.
Names of functions
[edit]The ambiguity in the style of writing a function should not be confused with a multivalued function, which can (and should) be defined in a deterministic and unambiguous way. Several special functions still do not have established notations. Usually, the conversion to another notation requires scaling the argument or the resulting value; sometimes, the same name of the function is used, causing confusion. Examples of such under-established functions:
- Sinc function
- Elliptic integral of the third kind; translating elliptic integral form from MAPLE to Mathematica, one should replace the second argument with its square; dealing with complex values, this may cause problems.
- Exponential integral[6]
- Hermite polynomial[6]: 775
Expressions
[edit]Ambiguous expressions often appear in physical and mathematical texts. It is common practice to omit multiplication signs in mathematical expressions. Also, it is common to give the same name to a variable and a function, for example, . Then, if one sees , there is no way to distinguish whether it means multiplied by , or function evaluated at argument equal to . In each case of use of such notations, the reader is supposed to be able to perform the deduction and reveal the true meaning.
Creators of algorithmic languages try to avoid ambiguities. Many algorithmic languages (C++ and Fortran) require the character * as a symbol of multiplication. The Wolfram Language used in Mathematica allows the user to omit the multiplication symbol but requires square brackets to indicate the argument of a function; square brackets are not allowed for grouping of expressions. Fortran, in addition, does not allow the use of the same name (identifier) for different objects, for example, a function and a variable; in particular, the expression is qualified as an error.
The order of operations may depend on the context. In most programming languages, the operations of division and multiplication have equal priority and are executed from left to right. Until the last century, many editorials assumed that multiplication is performed first, for example, is interpreted as ; in this case, the insertion of parentheses is required when translating the formulas to an algorithmic language. In addition, it is common to write an argument of a function without parentheses, which also may lead to ambiguity. In the scientific journal style, one uses Roman letters to denote elementary functions, whereas variables are written using italics. For example, in mathematical journals the expression does not denote the sine function but the product of the three variables , , , although in the informal notation of a slide presentation it may stand for .
Commas in multi-component subscripts and superscripts are sometimes omitted; this is also potentially ambiguous notation. For example, in the notation , the reader can only infer from the context whether it means a single-index object, taken with the subscript equal to the product of variables , and , or it is an indication of a trivalent tensor.
Examples of potentially confusing ambiguous mathematical expressions
[edit]An expression such as can be understood to mean either or . Often the author's intention can be understood from the context, in cases where only one of the two makes sense, but an ambiguity like this should be avoided, for example by writing or .
The expression means in several texts, though it might be thought to mean , since commonly means . Conversely, might seem to mean , as this exponentiation notation usually denotes function iteration: in general, means . However, for trigonometric and hyperbolic functions, this notation conventionally means exponentiation of the result of function application.
The expression can be interpreted as meaning ; however, it is more commonly understood to mean .
Notations in quantum optics and quantum mechanics
[edit]It is common to define the coherent states in quantum optics with and states with a fixed number of photons with . Then, there is an "unwritten rule": the state is coherent if there are more Greek characters than Latin characters in the argument and -photon state if the Latin characters dominate. The ambiguity becomes even worse, if is used for the states with a certain value of the coordinate and means the state with a certain value of the momentum, which may be used in books on quantum mechanics. Such ambiguities easily lead to confusions, especially if some normalized adimensional, dimensionless variables are used. Expression may mean a state with a single photon, or the coherent state with mean amplitude equal to 1, or state with momentum equal to unity, and so on. The reader is supposed to guess from the context.
Ambiguous terms in physics and mathematics
[edit]Some physical quantities do not yet have established notations; their value (and sometimes even dimension, as in the case of the Einstein coefficients) depends on the system of notations. Many terms are ambiguous. Each use of an ambiguous term should be preceded by the definition suitable for a specific case. Just like Ludwig Wittgenstein states in Tractatus Logico-Philosophicus: "... Only in the context of a proposition has a name meaning."[7]
A highly confusing term is gain. For example, the sentence "the gain of a system should be doubled", without context, means close to nothing.
- It may mean that the ratio of the output voltage of an electric circuit to the input voltage should be doubled.
- It may mean that the ratio of the output power of an electric or optical circuit to the input power should be doubled.
- It may mean that the gain of the laser medium should be doubled, for example, doubling the population of the upper laser level in a quasi-two-level system (assuming negligible absorption of the ground state).
The term intensity is ambiguous when applied to light. The term can refer to any of irradiance, luminous intensity, radiant intensity, or radiance, depending on the background of the person using the term.
Also, confusions may be related to the use of atomic percent as a measure of concentration of a dopant or resolution of an imaging system as a measure of the size of the smallest detail that can be resolved at the background of statistical noise. See also Accuracy and precision.
The Berry paradox arises as a result of systematic ambiguity in the meaning of terms such as "definable" or "nameable". Terms of this kind give rise to vicious circle fallacies. Other terms with this type of ambiguity are: satisfiable, true, false, function, property, class, relation, cardinal, and ordinal.[8]
Mathematical interpretation of ambiguity
[edit]
In mathematics and logic, ambiguity can be considered to be an instance of the logical concept of underdetermination—for example, leaves open what the value of is—while overdetermination, except when like , is a self-contradiction, also called inconsistency, paradoxicalness, or oxymoron, or in mathematics, an inconsistent system—such as , which has no solution.
Logical ambiguity and self-contradiction are analogous to visual ambiguity and impossible objects, such as the Necker cube and impossible cube, or many of the drawings of M. C. Escher.[9]
Constructed language
[edit]Some languages have been created with the intention of avoiding ambiguity, especially lexical ambiguity. Lojban and Loglan are two related languages that have been created for this, focusing chiefly on syntactic ambiguity. The languages can be both spoken and written. These languages are intended to provide greater technical precision over natural languages, although historically, such attempts at language improvement have been criticized. Languages composed from many diverse sources contain much ambiguity and inconsistency. The many exceptions to syntax and semantic rules are time-consuming and difficult to learn.
Biology
[edit]In structural biology, ambiguity has been recognized as a problem for studying protein conformations.[10] The analysis of a protein's three-dimensional structure consists in dividing the macromolecule into subunits called domains. The difficulty of this task arises from the fact that different definitions of what a domain is can be used (e.g., folding autonomy, function, thermodynamic stability, or domain motions), which sometimes results in a single protein having different—yet equally valid—domain assignments.
Christianity and Judaism
[edit]Christianity and Judaism employ the concept of paradox synonymously with "ambiguity". Many Christians and Jews endorse Rudolf Otto's description of the sacred as 'mysterium tremendum et fascinans,' the awe-inspiring mystery that fascinates humans.[dubious – discuss] The orthodox Catholic writer G. K. Chesterton regularly employed paradox to tease out the meanings in common concepts that he found ambiguous or to reveal meaning often overlooked or forgotten in common phrases: the title of one of his most famous books, Orthodoxy (1908), itself employed such a paradox.[11]
Music
[edit]In music, pieces or sections that confound expectations and may be, or are, interpreted simultaneously in different ways are ambiguous. Examples being some polytonality, polymeter, other ambiguous meters or rhythms, and ambiguous phrasing, or (Stein 2005, p. 79) any aspect of music. The music of Africa is often purposely ambiguous. To quote Sir Donald Francis Tovey (1935, p. 195), "Theorists are apt to vex themselves with vain efforts to remove uncertainty just where it has a high aesthetic value."
Visual art
[edit]
In visual art, certain images are visually ambiguous, such as the Necker cube, which can be interpreted in two ways. Perceptions of such objects remain stable for a time, then may flip, a phenomenon called multistable perception. The opposite of such ambiguous images are impossible objects.[12]
Social psychology and the bystander effect
[edit]In social psychology, ambiguity is a factor used in determining people's responses to various situations. High levels of ambiguity in an emergency (e.g., an unconscious man lying on a park bench) make witnesses less likely to offer any sort of assistance, due to the fear that they may have misinterpreted the situation and acted unnecessarily. Alternately, non-ambiguous emergencies (e.g., an injured person verbally asking for help) elicit more consistent intervention and assistance. With regard to the bystander effect, studies have shown that emergencies deemed ambiguous trigger the appearance of the classic bystander effect (wherein more witnesses decrease the likelihood of them helping) far more than non-ambiguous emergencies.[13]
Computer science
[edit]In computer science, the SI prefixes kilo-, mega-, and giga- were historically used in certain contexts to mean either the first three powers of 1024 (1024, 10242, and 10243), contrary to the metric system, in which these units unambiguously mean one thousand, one million, and one billion. This usage is particularly prevalent with electronic memory devices (e.g., DRAM) addressed directly by a binary machine register where a decimal interpretation makes no practical sense.
Subsequently, the Ki-, Mi-, and Gi- prefixes were introduced so that binary prefixes could be written explicitly, also rendering k, M, and G unambiguous in texts conforming to the new standard—this led to a new ambiguity in engineering documents lacking outward trace of the binary prefixes (indicating the new style) as to whether the usage of k, M, and G remains ambiguous (old style) or not (new style). 1 M (where M is ambiguously 1000000 or 1048576) is less uncertain than the engineering value 1.0×106 (defined to designate the interval 950000 to 1050000). As non-volatile storage devices begin to exceed 1 GB in capacity (where the ambiguity begins to routinely impact the second significant digit), GB and TB almost always mean 109 and 1012 bytes.
See also
[edit]- Abbreviation
- Ambiguity (law)
- Ambiguity tolerance–intolerance
- Amphibology
- Decision problem
- Double entendre
- Equivocation
- Essentially contested concept
- Fallacy
- Formal fallacy
- Golden hammer
- Informal fallacy
- Pleonasm
- Semantics
- Uncertainty
- Volatility, uncertainty, complexity and ambiguity
- Word-sense disambiguation
References
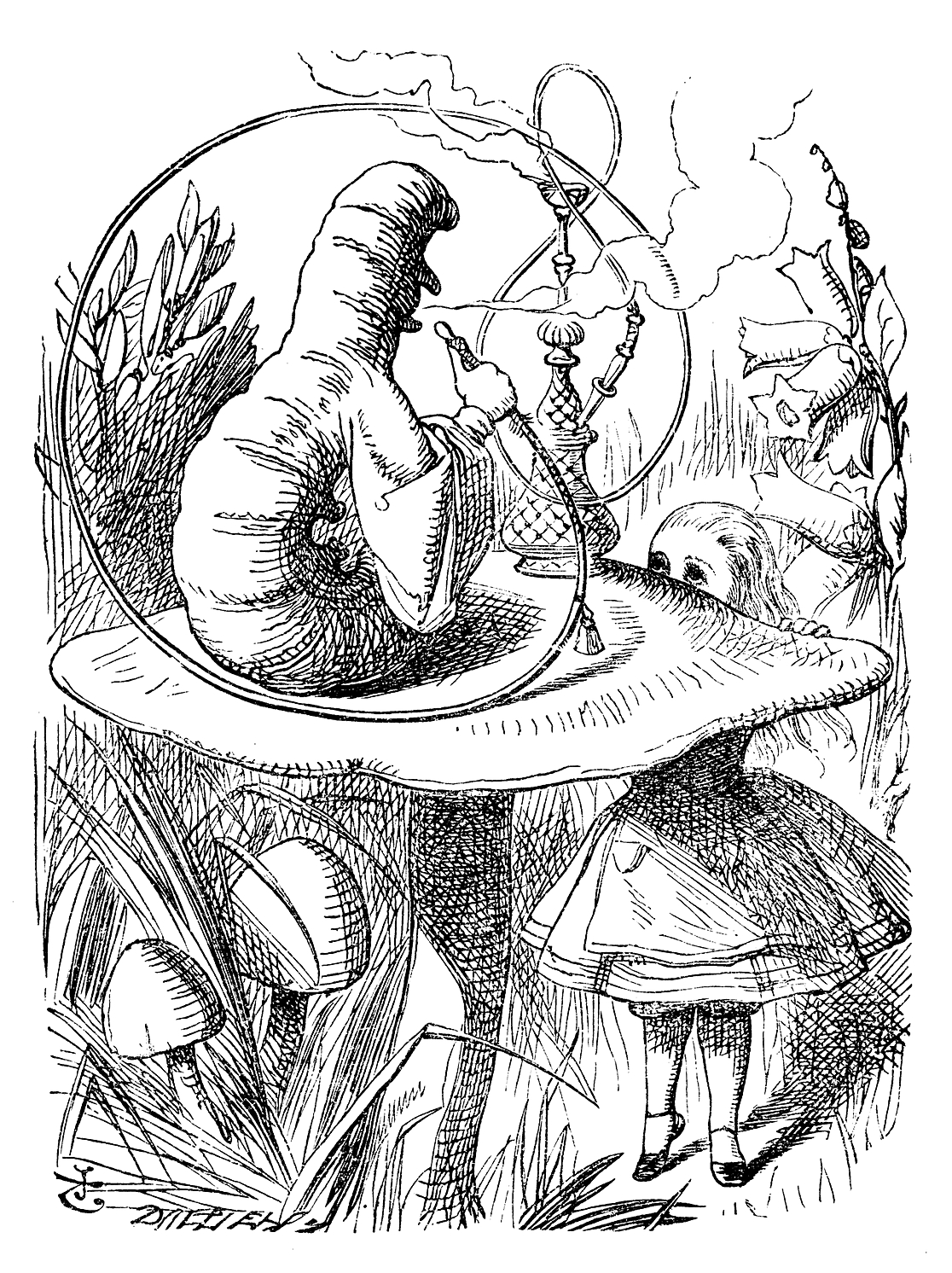
[edit]- ^ "And do you see its long nose and chin? At least, they look exactly like a nose and chin, that is don't they? But they really are two of its legs. You know a Caterpillar has got quantities of legs: you can see more of them, further down." Carroll, Lewis. The Nursery "Alice". Dover Publications (1966), p 27.
- ^ Piantadosi, Steven; Tily, Hal; Gibson, Edward (2012). "The communicative function of ambiguity in language". Cognition. 122 (3): 280–291. doi:10.1016/j.cognition.2011.10.004. hdl:1721.1/102465. PMID 22192697. S2CID 13726095.
- ^ Finn, Emily (19 January 2012). "The advantage of ambiguity". MIT Press.
- ^ Steven L. Small; Garrison W Cottrell; Michael K Tanenhaus (22 October 2013). Lexical Ambiguity Resolution: Perspective from Psycholinguistics, Neuropsychology and Artificial Intelligence. Elsevier Science. ISBN 978-0-08-051013-2.
- ^ a b Critical Thinking, 10th ed., Ch 3, Moore, Brooke N. and Parker, Richard. McGraw-Hill, 2012
- ^ a b Abramovits, M.; Stegun, I. Handbook on mathematical functions. p. 228.
- ^ Wittgenstein, Ludwig (1999). Tractatus Logico-Philosophicus. Dover Publications Inc. p. 39. ISBN 978-0-486-40445-5.
- ^ Russell/Whitehead, Principia Mathematica
- ^ Goldstein, Laurence (1996). "Reflexivity, Contradiction, Paradox and M. C. Escher". Leonardo. 29 (4): 299–308. doi:10.2307/1576313. JSTOR 1576313. S2CID 191403643.
- ^ a b Postic, Guillaume; Ghouzam, Yassine; Chebrek, Romain; Gelly, Jean-Christophe (2017). "An ambiguity principle for assigning protein structural domains". Science Advances. 3 (1) e1600552. Bibcode:2017SciA....3E0552P. doi:10.1126/sciadv.1600552. ISSN 2375-2548. PMC 5235333. PMID 28097215.
- ^ Chesterton, G. K., Orthodoxy, especially p. 32
- ^ Seckel, Al (2009). Optical Illusions: The Science of Visual Perception. Canada: Firefly Books Ltd. ISBN 978-1-55407-172-2.
- ^ Mason, David; Allen, Bem P. (1976). "The Bystander Effect as a Function of Ambiguity and Emergency Character". The Journal of Social Psychology. 100: 145–146. doi:10.1080/00224545.1976.9711917.
External links
[edit] Media related to Ambiguity at Wikimedia Commons
Media related to Ambiguity at Wikimedia Commons- Zalta, Edward N. (ed.). "Ambiguity". Stanford Encyclopedia of Philosophy.
- Ambiguity at the Indiana Philosophy Ontology Project
- Ambiguity at PhilPapers
- Collection of Ambiguous or Inconsistent/Incomplete Statements
- Leaving out ambiguities when writing
Ambiguity
View on GrokipediaAmbiguity denotes the property of a linguistic expression, mathematical formula, or other sign wherein multiple legitimate interpretations coexist, engendering interpretive uncertainty distinct from vagueness.[1][2] In linguistics, it primarily arises through lexical ambiguity, where a single word admits polysemous senses (e.g., "bank" as financial institution or river edge); syntactic ambiguity, stemming from structural parse alternatives (e.g., "flying planes can be dangerous" parsed as subject modification or object, or "I saw her duck" interpreted as observing her lowering her head or seeing her pet duck); semantic ambiguity involving propositional underdetermination; and pragmatic ambiguity from contextual inference variability.[3][4] Empirical investigations reveal that controlled ambiguity facilitates efficient communication by enabling concise reuse of versatile linguistic units, as listeners disambiguate via context without necessitating exhaustive specification.[5][6] Conversely, unresolved ambiguity in domains like mathematics—such as operator precedence in "a/bc" yielding a/(b*c) or (a/b)/c—or requirements engineering precipitates errors and miscommunication, underscoring the causal role of precise conventions in mitigating interpretive divergence.[7] Philosophically, ambiguity challenges formal semantics by necessitating models that accommodate multiple logical forms per surface structure, influencing theories of compositionality and reference.[2]
Definition and Conceptual Foundations
Core Definition and Distinctions
Ambiguity denotes a property of linguistic expressions, mathematical symbols, or communicative acts wherein multiple distinct interpretations are semantically permissible, arising from the expression possessing more than one viable semantic value or structural configuration.[8] In formal terms, an ambiguous expression fails the "one meaning per context" criterion, allowing for discrete alternatives that cannot be resolved without additional contextual disambiguation, as opposed to expressions with a singular, fixed denotation.[9] This phenomenon manifests across domains such as natural language, where words like "light" can denote electromagnetic radiation or minimal weight, and logic, where operator precedence may yield differing computational outcomes.[8] Central distinctions separate ambiguity from related indeterminacies. Vagueness involves fuzzy or gradient predicates lacking precise boundaries, such as the sorites paradox in terms like "heap," where incremental changes do not trigger abrupt shifts in truth value, whereas ambiguity entails sharply delineated, mutually exclusive interpretations without such gradience.[1] [8] For example, the sentence "Flying planes can be dangerous" is syntactically ambiguous (planes that fly versus the act of flying planes), yielding complete alternative parses, unlike the vague predicate "bald," which permits borderline cases but no fully discrete meanings.[1] Epistemic uncertainty, by contrast, arises from incomplete knowledge about a determinate fact, independent of the expression's inherent multiplicity; an ambiguous term remains so even under full information, as the alternatives persist linguistically.[8] Ambiguity further contrasts with generality or polysemy in non-discrete senses, where a term's broad applicability does not produce incompatible readings but rather overlapping extensions.[8] In philosophical logic, ambiguity underpins fallacies like equivocation, where substitution of meanings mid-argument invalidates inference, distinguishing it from mere imprecision.[10] Detection often relies on tests such as contradictory entailments across interpretations (e.g., an ambiguous sentence entailing both P and not-P under different readings) or zeugma incompatibility, confirming structural multiplicity over mere underspecification.[11]Types of Ambiguity
Lexical ambiguity arises when a single word or morpheme possesses multiple distinct meanings, often due to homonymy (unrelated meanings) or polysemy (related senses). For example, the English word "bat" can refer to a flying mammal or a piece of sports equipment used in baseball.[8] This type is rooted in the lexicon, where entries share phonetic or orthographic forms but diverge semantically. Morphological ambiguity, a subtype, occurs when affixes or inflections allow multiple grammatical interpretations, such as the English suffix "-s" functioning as a plural marker (e.g., "dogs"), a possessive (e.g., "dog's"), or a third-person singular verb marker (e.g., "runs").[9] Syntactic ambiguity, also known as structural ambiguity, emerges from multiple possible grammatical parses of a phrase or sentence, yielding differing logical forms. A classic example is "Superfluous hair remover," interpretable as a hair-removal product that is unnecessary or a product removing superfluous hair.[8] Subtypes include phrasal attachment ambiguities (e.g., modifier attachment to different heads) and scope ambiguities involving quantifiers (e.g., "Every linguist read a book" allowing either every linguist read some book or there exists a book read by every linguist).[8] In logical and mathematical contexts, this extends to operator precedence or grouping, as in the expression "a/bc," which could mean (a/b)c or a/(bc) without parentheses.[8] Semantic ambiguity involves deeper interpretive layers beyond syntax, such as collective versus distributive readings (e.g., "The boys carried the piano" as jointly or individually) or referential ambiguities in anaphora (e.g., unclear pronoun antecedents). Scope ambiguities, often semantic in nature, highlight quantifier interactions, as in "Some boys ate all the cookies," where "all" may scope over or under "some."[8] Pragmatic ambiguity pertains to context-sensitive uses, including speech act indeterminacy or presuppositional variability. For instance, uttering "The cops are coming" might convey a warning, assertion of fact, or expression of relief, depending on speaker intent and situational factors.[8][9] This type underscores how ambiguity persists even after resolving lexical and syntactic issues, influenced by implicatures or felicity conditions rather than encoded meaning alone.[8] Other classifications include elliptical ambiguity (incomplete constructions with recoverable but uncertain elements, e.g., "Dan did, too," ambiguous on what action) and idiomatic ambiguity (literal versus figurative readings, e.g., "kick the bucket" as literal death or idiom for dying). These types often intersect, complicating resolution in natural language processing and philosophical analysis.Relation to Vagueness and Uncertainty
Ambiguity, vagueness, and uncertainty each generate interpretive challenges in language and reasoning, but they differ in their underlying mechanisms. Ambiguity arises when a linguistic expression admits multiple discrete, structurally distinct interpretations, such as lexical polysemy (e.g., "bank" referring to a financial institution or river edge) or syntactic parsing alternatives (e.g., "flying planes can be dangerous" interpretable as planes that fly or the act of flying them).[1] This form of multiplicity often permits disambiguation through context, yielding precise resolutions for each possible meaning.[1] Vagueness, by contrast, involves predicates lacking sharp boundaries in their application, leading to borderline cases where no clear yes/no assignment holds, as in the sorites paradox concerning heaps (e.g., removing one grain from a heap eventually yields non-heaps without a precise threshold).[12] Unlike ambiguity's discrete options, vagueness features continuous gradience and resists exhaustive partitioning, often invoking higher-order vagueness where boundary indeterminacy itself blurs.[12] Philosophers like Timothy Williamson argue that vagueness manifests in epistemic uncertainty over application—knowable in principle but practically elusive due to the predicate's inherent imprecision—rather than semantic multiplicity.[13] Uncertainty encompasses both, but extends to epistemic or probabilistic gaps beyond linguistic structure, such as incomplete evidence about which ambiguous reading or vague application prevails in a scenario.[1] Ambiguity induces uncertainty resolvable by selecting among fixed alternatives, whereas vagueness embeds uncertainty in the semantics itself, potentially requiring non-classical logics (e.g., fuzzy or supervaluationist) to model tolerance principles without contradiction.[14] Empirical studies in communication support this: groups converge on vague terms to manage variability in reference, incurring coordination costs distinct from ambiguity's disambiguation overhead.[15] Thus, while ambiguity and vagueness both undermine univocal truth-values, ambiguity aligns with structural underdetermination and vagueness with boundary indeterminacy, each contributing uniquely to broader uncertainty in inference and decision-making.[1][12]Historical Development
Ancient Origins in Rhetoric and Logic
In ancient Greek intellectual traditions, ambiguity first gained systematic attention through the practices of sophists and the analytical responses of philosophers like Plato and Aristotle in the 5th and 4th centuries BCE. Sophists, itinerant teachers such as Protagoras (c. 490–420 BCE) and Gorgias (c. 483–375 BCE), emphasized rhetorical skill in public discourse and education, often deploying arguments that hinged on verbal pliability—including equivocation and multiple interpretations—to achieve persuasive effects or to demonstrate the relativity of truth, as critiqued by Plato for prioritizing seeming over being.[16] [17] This approach contributed to early recognition of ambiguity as a tool for eristic debate, where opponents could exploit linguistic flexibility to appear victorious without substantive resolution.[18] Aristotle (384–322 BCE), building on these foundations, provided the earliest formal classification of ambiguities as sources of logical error in his Sophistical Refutations (c. 350 BCE), part of the Organon. He identified paralogisms—fallacious refutations—arising from homonymia (equivocation), where a single term bears unrelated meanings (e.g., "bank" as river edge or financial institution), and amphiboly, stemming from syntactic constructions permitting dual readings (e.g., phrases interpretable as modifying different elements).[19] [8] Aristotle further delineated related fallacies of composition (treating a whole as summed parts) and division (treating parts as a unified whole), attributing their deceptive power to sophistic exploitation in dialectical encounters, which mimic valid reasoning but collapse under scrutiny.[20] He prescribed resolutions, such as substituting opposites to test meanings or clarifying grammatical relations, emphasizing that true dialectic demands precision to avoid such traps.[19] In rhetorical contexts, Aristotle addressed ambiguity as a stylistic vice in his Rhetoric (c. 350 BCE), advising speakers to eschew ambiguous diction for clarity unless intentional obscurity aids irony, jest, or deliberate misleading, as in cases where "those who have nothing to say but are pretending to mean something" use it to feign depth.[21] Plato, in dialogues such as the Euthydemus (c. 380 BCE), dramatized sophistic fallacies reliant on lexical shifts and propositional ambiguities, portraying them as eristic games that undermine genuine inquiry by allowing premises to slide between senses without detection.[22] These treatments established ambiguity not merely as a linguistic quirk but as a causal factor in erroneous inference and persuasive manipulation, influencing subsequent logical and rhetorical traditions by privileging disambiguation for reliable knowledge.[8]Modern Theories from Empson to Contemporary Philosophy
William Empson's Seven Types of Ambiguity, published in 1930, systematized literary ambiguity by delineating seven escalating forms, from basic metaphorical comparisons implying alternative attributes to advanced cases where a word or phrase sustains mutually irreconcilable readings, such that the statement holds as true under one view yet false or void under another.[23] Empson contended that these layers, often arising from syntactic flexibility or lexical polysemy, amplify poetry's emotional and intellectual impact by engaging readers in active interpretive tension.[24] His analysis drew on close examinations of English poets like Shakespeare and Donne, positing ambiguity not as flaw but as deliberate artistry fostering "alternative reactions to the same words."[25] Empson's framework exerted lasting influence on New Criticism, a mid-20th-century school emphasizing textual autonomy and meticulous explication to reveal ambiguities as sources of aesthetic richness, evident in works by Cleanth Brooks and John Crowe Ransom who adapted it for practical criticism. Yet, later evaluations highlighted limitations, such as imprecise boundaries between ambiguity and simple multiple meanings, potentially inflating subjective interpretations over textual evidence.[26] This critique paralleled broader philosophical scrutiny, where Empson's intuitive typology yielded to rigorous semantic dissections. In post-World War II philosophy of language, analytic thinkers reframed ambiguity as a structural feature demanding resolution for precise reference and compositionality, contrasting Empson's celebratory stance. Drawing from Frege's 1892 distinction between sense and reference, philosophers like W.V.O. Quine in his 1960 Word and Object explored radical indeterminacy, arguing that translational ambiguities undermine fixed meanings across languages, though resolvable via behavioral evidence rather than innate polysemy.[27] Syntactic ambiguities, such as scopal variations in quantifiers (e.g., "every man loves a woman" permitting universal or existential scopes), furnished empirical tests for generative grammar's hierarchical structures, as Noam Chomsky's 1957 Syntactic Structures demonstrated through transformations that disambiguate surface forms.[27] Contemporary philosophy distinguishes ambiguity—discrete, context-independent multiplicities—from vagueness's gradual indeterminacy, attributing the former to lexical underspecification or parsing alternatives, as Chris Kennedy outlined in 2009, where empirical psycholinguistic data reveal rapid disambiguation via prosody or inference.[1] Paul Grice's 1975 cooperative principle further posits that ambiguities persist for efficiency, resolved pragmatically through implicatures without semantic overhaul, balancing clarity against expressive economy.[1] Donald Davidson's 1978 essays extended this by viewing metaphor as controlled ambiguity, where literal falsity prompts novel interpretations grounded in causal speaker intentions, eschewing Empson-style free association for truth-conditional anchors. These developments underscore ambiguity's role in modeling natural language's robustness, informed by computational simulations showing minimal processing costs for common cases.[27]Linguistic Aspects
Lexical and Semantic Ambiguity
Lexical ambiguity arises when a word or morpheme has multiple distinct senses or lexical entries, permitting more than one interpretation of its use in context. This phenomenon stems from homonymy, where words share form but not etymology or meaning (e.g., "bat" as a flying mammal or a sports implement), or polysemy, where a single lexical entry encompasses related but distinct senses (e.g., "head" as part of the body or leader of a group).[8] In sentence processing, such ambiguity triggers multiple semantic representations until disambiguated by context, as evidenced in psycholinguistic studies showing delayed resolution for homonymous words compared to unambiguous controls.[28] Semantic ambiguity, encompassing lexical cases as a subtype, occurs when an expression admits multiple truth-conditional interpretations due to the composition of meanings, independent of syntactic structure.[29] For instance, phrases involving relational terms like "outrun" can yield distinct readings based on whether the ambiguity lies in scope or predicate interpretation, though pure semantic cases often overlap with logical forms (e.g., "Every farmer who owns a donkey beats it" allowing quantifier scope variations).[8] Unlike syntactic ambiguity, which involves parse tree multiplicity, semantic ambiguity persists even in syntactically unique structures, as confirmed by formal semantic tests where expressions fail single-meaning assignment without pragmatic intrusion.[11] Empirical measures, such as variability in gloss assignments across dictionaries, quantify semantic ambiguity by sense frequency, revealing that high-ambiguity words like "run" (over 600 senses in some corpora) complicate automated natural language processing.[30] Distinguishing the two, lexical ambiguity is narrowly tied to individual lexical items' multiplicity, resolvable via sense selection, whereas semantic ambiguity may emerge compositionally from interactions among unambiguous elements, though in practice, most natural language instances trace to lexical sources.[31] This interplay underlies challenges in machine translation and comprehension models, where failure to model lexical-semantic branching leads to error rates exceeding 20% in ambiguous contexts, per benchmark evaluations.[32] Resolution strategies include contextual priming, as neural imaging shows preferential activation of dominant senses in supportive sentences, minimizing interpretive load.[28]Syntactic Ambiguity
Syntactic ambiguity, also termed structural ambiguity, occurs when a sentence's grammatical structure permits multiple parse trees, resulting in distinct meanings from alternative syntactic analyses.[33][34] This phenomenon arises primarily from the arrangement of words into grammatical combinations that allow more than one valid interpretation, often due to limited syntactic markers in English such as sparse inflections.[33] In the framework of transformational generative grammar, syntactic ambiguity manifests when a single surface structure derives from multiple underlying deep structures.[34] Common triggers include ambiguous prepositional phrase (PP) attachment, where a PP may modify the preceding verb or noun phrase, as in "I saw the man with the telescope," which can mean observing using a telescope or observing a man possessing one.[35] Another classic example is "I saw her duck," which can mean either "I witnessed her lowering her head" (with "duck" as a verb) or "I witnessed her pet duck" (with "duck" as a noun object), demonstrating how differing syntactic parses arise from alternative category assignments and structures.[36] Coordination ambiguity presents another type, where the scope of conjunctions is unclear, for example, in "Mr. Stone was a professor and a dramatist of great fame," interpretable as both professions sharing great fame or only the dramatist doing so.[34][37] Noun phrase bracketing ambiguity involves uncertain grouping, such as in "flying planes can be dangerous," where "flying" may modify "planes" (airplanes in flight) or serve as a subject (the act of piloting is hazardous).[34] Adjective or adverbial modifier placement can also induce ambiguity, like "There stood a big brick house at the foot of the hill," where "big" could describe "brick house" or "house" alone.[34] Dangling modifiers contribute further, as in "Staggering along the road, I saw a familiar form," potentially implying the speaker staggers rather than the form.[33] Such ambiguities challenge sentence processing, often leading to garden path effects where initial parses require revision upon encountering disambiguating elements.[38] In natural language processing and psycholinguistics, they highlight the incremental nature of human parsing, influenced by factors like verb bias and contextual cues to favor one resolution.[39] Efforts to mitigate syntactic ambiguity in formal communication include rephrasing for explicit attachments, though it persists in everyday English due to its reliance on context for disambiguation.[40][33]Efforts to Minimize in Constructed Languages
Loglan, developed by James Cooke Brown starting in 1955 at Indiana University, represents an early systematic effort to construct a language with minimal syntactic ambiguity, motivated by the Sapir-Whorf hypothesis and the goal of enabling precise, testable scientific discourse. The language employs a predicate-based grammar where sentences map directly to logical structures, using explicit markers for argument positions and relations to avoid parsing uncertainties common in natural languages, such as prepositional phrase attachment ambiguities. This design ensures that each grammatically valid sentence corresponds to a unique logical form, as verified through formal rule sets. Lojban, a successor to Loglan initiated in 1987 by the Logical Language Group amid disputes over Loglan's intellectual property, refines these principles into a fully formalized system with an unambiguous grammar proven parsable by computer tools like YACC.[41] Lojban's structure relies on predicate logic, featuring 1,300 root words (gismu) for predicates and structural particles (cmavo) that delimit sumti (arguments) and specify connections, eliminating syntactic ambiguities like those in English phrases such as "flying planes can be dangerous," which could parse as modifiers or subjects.[42] For instance, Lojban requires explicit bridi (predicate-argument) framing, with markers like "be" for complex sumti grouping, ensuring unique parse trees for every valid utterance. The language's phonetic and morphological rules further reduce homophony risks, with voiced stops distinguished from voiceless and syllable boundaries unambiguous via consonant clusters limited to specific pairs. Ithkuil, created by John Quijada and first detailed in 2004, pursues ambiguity minimization through extreme morphological precision rather than strict logic, incorporating over 90 affixes to encode semantic nuances like evidentiality, perspective, and agentivity in a single word. This approach condenses expressions to minimize polysemy and interpretive latitude; for example, verb forms specify whether an action is deliberate or accidental, and nouns denote exact configurations, reducing reliance on context for disambiguation. Revised in 2011 and 2023, Ithkuil prioritizes expressive density, with a core inventory of 58 consonants and 26 vowels enabling compact forms that convey what might require ambiguous clauses in natural languages. These languages demonstrate trade-offs: while achieving syntactic unambiguity, they demand learner mastery of rigid rules, limiting adoption, as Lojban's speaker community remains under 1,000 active users as of 2023. Semantic ambiguity persists to some degree via flexible predicate interpretations, addressed in Lojban through a dictionary of precise place structures, but full elimination proves challenging without exhaustive predication.Philosophical and Logical Perspectives
Avoidance in Formal Logic
In formal logic, ambiguity is systematically avoided through the use of artificial symbolic languages with rigid syntax and semantics, contrasting with the inherent vagueness of natural language expressions. Symbols for propositions, predicates, connectives, and quantifiers are assigned fixed interpretations, while grammatical rules—such as mandatory parentheses for grouping and variable binding—enforce unique parse trees and scopes, ensuring that every well-formed formula corresponds to precisely one meaning. This approach traces to efforts in the late 19th and early 20th centuries to rigorize inference and mathematics, where natural language's polysemy, scope errors, and pragmatic inferences could lead to paradoxes or invalid deductions.[43][44] Gottlob Frege's Begriffsschrift (1879) pioneered this by devising a "concept-script" notation that depicted logical structure visually, using indentations and lines to represent implications and quantifications without verbal ambiguity; Frege explicitly criticized natural language for allowing "equivocation" that obscures thought-content, insisting on a "judgeable content" expressed univocally to facilitate exact proof. Building on this, propositional logic defines connectives via truth tables: for instance, conjunction (∧) is true only when both operands are true, disjunction (∨) true if at least one is true, and material implication (→) false solely when the antecedent is true and consequent false—tabular enumeration exhausts all cases (2^n rows for n atoms), preempting disputes over inclusive versus exclusive "or" or counterfactual readings in English.[45][46] Predicate logic further mitigates referential and quantificational ambiguities by introducing variables, predicates (e.g., P(x) for "x is prime"), and explicit quantifiers: ∀x (universal, binding all domain elements) and ∃x (existential, asserting at least one satisfier), with scope delimited by parentheses to avoid natural language's "every...some" reversals. For example, ∀x ∃y (x < y) asserts a total order exists (true over positives), while ∃y ∀x (x < y) claims a maximum (false over positives); formal binding rules and prenex normal form standardize order, rendering such distinctions mechanically verifiable unlike ambiguous sentences like "Every boy loves some girl," which could imply varying distributions.[47][48] These mechanisms extend to higher-order logics and type theories (e.g., Church's simply typed λ-calculus, 1940), where types prevent illicit substitutions (no "quantifying into" subjects), and to automated theorem provers that parse formulas deterministically. While primitives remain subject to axiomatic choice and metalogical undecidability (per Gödel, 1931), the syntax-semantics divide ensures syntactic unambiguity, enabling mechanical validation over interpretive latitude.[49]Embrace in Rhetorical and Hermeneutic Traditions
In rhetorical traditions, ambiguity has been selectively embraced through specific figures of speech that leverage multiple interpretations for persuasive or ornamental impact, despite a general preference for clarity in forensic and deliberative oratory. Amphiboly, involving syntactic ambiguity that allows a phrase to convey dual meanings via grammatical structure, serves to intrigue audiences or underscore irony, as seen in classical examples where sentence construction deliberately obscures intent to heighten engagement. Antanaclasis employs a word's repeated use with shifting semantic senses, creating layered wit or emphasis, such as in proverbial turns where homonyms pivot meanings mid-discourse. Quintilian, in his Institutio Oratoria (completed circa 95 CE), permits such ambiguities in jest or epigrammatic flourishes to evoke secondary connotations without falsity, though he warns against their overuse in formal argumentation to avoid ethical lapses or misinterpretation.[50] Later rhetorical analyses highlight strategic ambiguity's utility in aligning divergent audiences, as when vague phrasing accommodates multiple interpretive frames to foster consensus without explicit concession. Empirical studies of organizational discourse confirm that rhetors deploy such tactics to enable collective action amid conflicting interests, evidenced by case analyses where ambiguous appeals sustained alliances longer than precise but divisive statements.[51][52] Hermeneutic traditions, particularly in philosophical variants, position ambiguity as a generative condition of understanding rather than a flaw to eradicate. Hans-Georg Gadamer, in Truth and Method (1960), contends that interpretive fusion of horizons thrives on language's inherent polysemy and historical indeterminacy, where ambiguous texts invite ongoing dialogic participation over fixed resolution. This view frames ambiguity as productive, mirroring the open-endedness of tradition-bound inquiry, with Gadamer emphasizing everyday speech's semantic fluidity as a conduit for authentic encounter.[53][54] Paul Ricoeur complements this by analyzing metaphor and narrative as mechanisms that harness ambiguity's tension—semantic dissonance yielding novel referential insights—thus advancing hermeneutic arcs from suspicion to restitution. In Ricoeur's model, metaphorical innovation, rooted in Aristotle's notions of likeness amid dissimilarity, produces meaning through interpretive labor that embraces rather than suppresses equivocation, as documented in analyses of symbolic discourse where unresolved ambiguities foster ethical and existential depth.[55][56]Criticisms and Debates on Clarity vs. Richness
Analytic philosophers and logicians criticize ambiguity as a barrier to precise reasoning, arguing that it enables fallacies like equivocation, where terms shift meanings mid-argument, thereby undermining the validity of inferences in natural language.[8] This perspective holds that regimentation—translating ambiguous expressions into unambiguous formal systems—is essential for philosophical progress, as ambiguity obscures causal relations and empirical verification.[8] For example, in evaluating arguments, multiple legitimate interpretations of a sign can prevent consensus on truth values, prompting demands for disambiguation to prioritize clarity over interpretive multiplicity.[8] In rhetorical and hermeneutic traditions, however, ambiguity is defended for its capacity to enrich discourse, allowing texts to sustain layered meanings that foster deeper engagement and persuasive power.[57] Proponents contend that eliminating ambiguity in pursuit of logical purity strips language of its pragmatic and contextual vitality, reducing philosophy to mechanical analysis that neglects human interpretive horizons.[58] This view posits that richness arises from ambiguity's ability to evoke multiple facets of experience, akin to how poetic language achieves insight through elastic concepts rather than rigid definitions.[59] Debates intensify over whether overemphasizing clarity fosters sterile semantic disputes—endlessly parsing terms without advancing substantive knowledge—or if tolerating richness invites deliberate obscurity that evades falsifiability.[60] Analytic critics of hermeneutic approaches charge that ambiguity's embrace can devolve into unverifiable relativism, prioritizing evocative prose over testable claims, while defenders of richness counter that analytic disambiguation overlooks the embedded ambiguities in everyday cognition, potentially distorting real-world applications. Empirical studies in cognitive linguistics suggest natural language tolerates ambiguity for efficiency, supporting a balanced view where clarity resolves core propositions but richness preserves expressive utility.[8]Mathematical and Formal Interpretations
Ambiguous Notations and Expressions
In mathematics, ambiguous notations and expressions arise primarily from unresolved operator precedence, implied operations, and inconsistent conventions for grouping, leading to multiple possible interpretations without explicit parentheses. These ambiguities persist despite conventions like PEMDAS (parentheses, exponents, multiplication/division, addition/subtraction), which do not universally address cases such as implied multiplication or juxtaposed terms. For instance, the expression lacks a standard resolution, with some interpreting it as (left-associative, yielding ) and others as (grouping the denominator, yielding ).[61] This issue stems from the absence of a defined precedence between explicit division and adjacent multiplication, a gap noted in pedagogical discussions where human intuition often favors denominator grouping but computational tools may not.[62] Implied multiplication, denoted by juxtaposition (e.g., ), exacerbates such problems by conventionally taking precedence over explicit division in many educational contexts, interpreting it as rather than . This convention, rooted in algebraic traditions where variables are treated as grouped units, conflicts with strict left-to-right evaluation in some programming languages and calculators, leading to discrepancies like those in the debated expression , which yields 9 under implied precedence but 1 otherwise.[63] Historical evolution of order of operations, formalized in the 19th century, aimed to reduce but did not eliminate these inconsistencies, as early texts varied in handling juxtaposed terms.[64] In trigonometric notation, expressions like are prone to misinterpretation, potentially read as instead of the intended , a half-angle formula component. This arises from ambiguous exponent scoping and division precedence, where the superscript applies only to sine without clear boundaries for the subsequent operator; explicit parentheses are required for precision in identities such as .[65] Similar issues occur in higher-order notations, such as tensor components , where subscript placement ambiguously indicates covariance without specified metric conventions, relying on contextual summation rules like Einstein notation for resolution.[66] Mathematicians mitigate these through rigorous definitions and parentheses, as ambiguity undermines proof validity, though informal sketches tolerate it for brevity.[67]Resolutions in Quantum and Physics Contexts
In quantum mechanics, operator ordering ambiguities emerge when quantizing classical Hamiltonians containing products of non-commuting observables, such as position and momentum , where . For a classical term like , possible quantum counterparts include , , or the symmetrized Weyl-ordered form , each yielding distinct spectra and dynamics unless constrained.[68] These ambiguities can alter physical predictions, as seen in the anharmonic oscillator where different orderings shift energy levels by terms proportional to . Resolutions often invoke covariance under canonical transformations or hermiticity requirements, ensuring the operator is self-adjoint; for instance, in curved spacetime, the geometric calculus uniquely factors the Laplacian-Beltrami operator as , eliminating ad hoc choices by aligning with differential geometry.[69] Path integral quantization further mitigates this by employing the Trotter product formula, which discretizes the evolution operator and converges to a symmetric ordering independent of intermediate choices for smooth potentials.[70] In gauge theories, particularly ultrastrong-coupling cavity quantum electrodynamics (QED), ambiguities arise from incomplete truncation of the Hilbert space in light-matter Hamiltonians, violating gauge invariance under transformations like the Göppert-Mayer or Power-Zienau-Woolley gauges. This leads to spurious results, such as non-physical ground-state degeneracies or incorrect ultrastrong-coupling spectra. A general resolution, derived in 2019, constructs gauge-invariant Hamiltonians via a unitary transformation that disentangles photonic and material degrees of freedom while projecting onto the physical subspace, applicable to arbitrary truncations and couplings exceeding unity.[71] For molecular cavity QED, a 2020 framework resolves these by explicitly constraining interaction terms through a unitary operator, preserving multipolar gauge invariance and enabling accurate simulations of polaritonic states without dipole approximations.[72] Empirical validation comes from matching experimental cavity-modified molecular spectra, where unresolved ambiguities previously overestimated Rabi splittings by factors of 2–3.[73] In quantum cosmology, such as the Wheeler-DeWitt equation, operator ordering affects minisuperspace models with matter fields like dust, introducing ambiguities in kinetic terms that influence singularity resolution or inflationary dynamics. Constraints from quantum fluctuations or third quantization limit viable orderings, with sharply peaked wavefunctions minimizing ordering imprints to below observational thresholds in perfect-fluid universes.[74] These resolutions prioritize empirical consistency, such as reproducing cosmic microwave background anisotropies, over arbitrary symmetrizations. Notational ambiguities in physical expressions, like in spin-1/2 rotation probabilities or neutrino oscillations, are conventionally resolved as via explicit parentheses or context from trigonometric identities, ensuring unitarity in matrix elements.[75]Ambiguous Terms and Their Implications
In mathematics, certain terms exhibit polysemy, allowing multiple distinct interpretations within the discipline, which necessitates contextual disambiguation to maintain rigor. For instance, the term "normal" applies to diverse concepts such as a normal distribution in probability theory, a normal matrix satisfying in linear algebra, and a normal subgroup of a group where for all .[76] Similarly, "regular" denotes a regular polygon with equal sides and angles, a regular language accepted by a finite automaton in computer science, and a regular function in algebraic geometry satisfying certain smoothness conditions.[77] These overloaded usages stem from historical development and analogy across subfields, but without explicit qualification, they risk conflation in interdisciplinary work or introductory texts.[78] Such ambiguities carry implications for precision and error propagation in formal reasoning. In proofs or derivations, misinterpreting a term can invalidate conclusions; for example, assuming "normal" implies commutativity in a matrix context might lead to incorrect eigenvalue computations, as normal matrices are diagonalizable over the complex numbers but not all matrices are normal.[76] Empirical studies of student discourse reveal that unresolved term ambiguity fosters misconceptions, with learners projecting everyday meanings onto technical ones, such as equating "average" solely with arithmetic mean while overlooking median or mode in statistics.[79] In computational implementations, this extends to software where ambiguous terms in input specifications yield divergent outputs, as seen in parsing "regular expression" versus "regular polyhedron" in algorithmic design.[62] Furthermore, in foundational mathematics, ambiguous terms challenge the completeness of axiomatic systems by introducing vagueness that formal languages seek to eliminate through strict syntax. Solomon Feferman notes that while informal mathematical language thrives on syntactic ambiguity for conciseness—allowing efficient expression of complex ideas—it undermines machine verification and automated theorem proving, where unique denotations are paramount.[80] This tension implies a trade-off: ambiguity accelerates human intuition but demands rigorous context or reformulation for verifiability, as evidenced by regional definitional variances like "trapezoid" (exactly one pair of parallel sides in U.S. usage versus at least one elsewhere), potentially altering geometric proofs or classifications.[78] Resolving these requires explicit scoping, such as prefixing with qualifiers (e.g., "Lie group normal"), underscoring the discipline's reliance on convention over inherent clarity.[81]Applications in Decision Theory and Economics
Ambiguity Aversion
Ambiguity aversion denotes the tendency of decision-makers to prefer prospects with objectively known probabilities of outcomes over those with equivalent expected values but unknown or ambiguous probabilities.[82] This behavior contrasts with risk aversion, which involves aversion to variance under known probabilities, as ambiguity aversion specifically penalizes uncertainty about the likelihoods themselves rather than the variability of payoffs.[83] Empirical observations indicate that a majority of individuals exhibit this aversion, with approximately 58% displaying ambiguity-averse preferences in controlled choice tasks involving financial outcomes, while about 30% show ambiguity-seeking behavior under similar conditions.[84] Theoretical models formalize ambiguity aversion through frameworks that relax standard expected utility assumptions, such as the maxmin expected utility model proposed by Gilboa and Schmeidler in 1989, where agents evaluate prospects using the minimum possible expected value across a set of plausible probability distributions to account for ambiguity.[85] Alternative representations include variational preferences or smooth ambiguity models, which incorporate ambiguity attitudes via parameters that weight ambiguous events more pessimistically than known risks.[82] These models predict that ambiguity-averse agents will underweight ambiguous assets, leading to suboptimal diversification in portfolios compared to ambiguity-neutral benchmarks.[86] In economic contexts, ambiguity aversion explains several observed anomalies, including reduced participation in stock markets and lower allocations to equities or foreign assets, as investors perceive market returns as ambiguously distributed despite historical data.[87] It also drives preferences for established brands over innovative but uncertain alternatives, where quality signals reduce perceived ambiguity about performance.[88] Household-level studies confirm negative correlations between ambiguity aversion measures and equity holdings, suggesting it contributes to the equity premium puzzle by amplifying demands for compensation beyond mere risk.[87] Furthermore, in contract design, ambiguity aversion diminishes the value of detailed but probabilistically ambiguous clauses, potentially leading to simpler agreements.[89] Critiques of the ambiguity aversion literature highlight interpretive challenges, as behaviors attributed to ambiguity may stem from other primitives like model misspecification or source-dependence preferences, where credibility of probability assessments influences choices.[85] Experimental evidence, while robust in laboratory settings, shows variability across domains, with ambiguity aversion intensifying for gains but sometimes reversing for losses or when competence in the ambiguous domain is high.[90] These findings underscore that ambiguity aversion is not a monolithic trait but context-dependent, informing policy designs that mitigate ambiguity to encourage uptake in areas like insurance or innovation adoption.[91]Ellsberg Paradox and Experimental Evidence
The Ellsberg paradox, introduced by Daniel Ellsberg in 1961, demonstrates a violation of subjective expected utility theory by highlighting individuals' aversion to ambiguity—situations with unknown probabilities—distinct from aversion to known risks. In the core setup, an urn contains 90 balls: 30 red and 60 either black or yellow in an unknown proportion. Subjects choose between two bets of equal stakes: winning if a red ball is drawn (known probability of 30/90 or 1/3) versus winning if a black ball is drawn (unknown probability between 0 and 60/90). A second paired choice involves winning if a yellow ball is drawn (unknown probability, complementary to black within the 60) versus winning if a non-yellow ball is drawn (red or black, with probability 1 minus the unknown yellow probability). Typical preferences favor the black bet over the red bet and the non-yellow bet over the yellow bet. These choices imply inconsistent subjective probabilities: preferring black over red suggests a subjective probability for black exceeding 1/3, while preferring non-yellow over yellow suggests a probability for yellow below 1/3, which contradicts the fixed relationship where yellow probability equals 2/3 minus black probability. This inconsistency breaches Savage's sure-thing principle, which requires preferences to depend only on unambiguous outcomes.[92] Ellsberg's informal experiments, conducted with small groups of decision theorists and economists at RAND Corporation and Harvard University between 1957 and 1961, yielded near-unanimous results: approximately 80% to 100% of participants across tested cohorts exhibited the paradoxical preferences, consistently avoiding the more ambiguous options despite equal expected values under probabilistic neutrality. These findings, derived from hypothetical choices rather than incentivized draws, underscored a behavioral distinction between "risk" (objective probabilities) and "ambiguity" (subjective uncertainty about probabilities), prompting Ellsberg to argue that Savage's axioms fail to capture real decision-making under ignorance.[92][93] Subsequent incentivized laboratory experiments have robustly replicated the paradox, confirming ambiguity aversion as a prevalent phenomenon. For example, in controlled studies using real monetary payoffs, 70% to 90% of subjects display the inconsistent preferences, with aversion strongest for prospects where ambiguity cannot be resolved by additional information. Meta-analyses of Ellsberg-style tasks across diverse populations, including students and professionals, report average ambiguity aversion rates around 75%, persisting even after instructions explaining the paradox, though awareness can modestly reduce it without elimination. These results hold across variations, such as multi-urn setups or dynamic updates, and extend to non-monetary domains like delays or losses, indicating ambiguity aversion as a robust deviation from Bayesian updating rather than mere computational error or alternative utility representations. Theoretical responses, including maxmin expected utility models, accommodate the behavior but require additional parameters beyond standard expected utility.[82][89][94]Legal Interpretations
Ambiguity in Statutes and Contracts
In statutory interpretation, ambiguity arises when the plain text of a law admits of more than one reasonable meaning, prompting courts to apply interpretive canons to discern legislative intent while adhering to textual primacy. Under common principles in U.S. law, judges first examine the statute's ordinary meaning in context; if ambiguity persists, they may consider surrounding provisions, purpose, and structure before resorting to extrinsic aids like legislative history, though textualist approaches limit the latter to avoid judicial overreach.[95] For criminal statutes, the rule of lenity mandates resolving genuine ambiguities in favor of the defendant to ensure fair notice and avoid expanding penalties beyond clear legislative authorization, as affirmed in cases like Wooden v. United States (2022), where the Supreme Court invoked lenity to interpret "occasions" under the Armed Career Criminal Act narrowly.[96] This canon reflects a first-principles commitment to limiting government power through precise enactment, countering tendencies in expansive readings that could stem from purposivist biases in judicial or academic commentary. A notable example of statutory ambiguity is Bond v. United States (2014), where the Court found the Chemical Weapons Convention Implementation Act's definition of "chemical weapon" ambiguous when applied to a woman's use of a mild irritant against a rival, rejecting a broad reading that would federalize trivial acts absent clear congressional intent.[97] Courts also employ substantive canons, such as the presumption against surplusage—interpreting terms to give effect to all provisions—or the avoidance of absurdity, though the latter is invoked sparingly to prevent subjective rewriting under guise of clarification.[98] These tools prioritize empirical fidelity to enacted text over speculative policy goals, acknowledging that legislative ambiguity often signals deliberate delegation or oversight rather than invitation for judicial policymaking. In contract law, ambiguity occurs when a term is reasonably susceptible to multiple interpretations, assessed objectively from the parties' manifested intentions rather than subjective understandings, with courts considering the contractual context and commercial purpose.[99] The contra proferentem doctrine resolves such ambiguities against the drafter, incentivizing precise drafting and protecting non-drafting parties from adhesive terms, particularly in standard-form agreements like insurance policies.[100] Parol evidence may admit extrinsic evidence for latent ambiguities—those not apparent on the face but revealed by external facts—but not to contradict integrated writings, preserving the contract's reliability as a bargained-for exchange.[101] The landmark case Raffles v. Wichelhaus (1864) illustrates latent ambiguity: a contract for cotton "to arrive ex Peerless from Bombay" failed due to two ships named Peerless departing months apart, with each party intending a different vessel, resulting in no mutual assent and thus no enforceable agreement absent evidence resolving the discrepancy.[102] Courts avoid rewriting contracts to impose outcomes but may imply reasonable terms under the business efficacy doctrine if essential gaps exist, though persistent ambiguity can render provisions void or trigger renegotiation, underscoring the causal role of clear language in enforcing voluntary obligations.[103] Empirical studies of litigation data confirm that ambiguous drafting correlates with higher dispute rates, validating first-principles emphasis on definiteness for predictable commerce.[104]Canons of Construction and Judicial Approaches
Canons of construction refer to a set of interpretive rules employed by courts to resolve ambiguities in statutory language, drawing from linguistic, contextual, and substantive principles. These canons, often traced to common-law traditions and elaborated in works like Antonin Scalia and Bryan Garner's Reading Law: The Interpretation of Legal Texts (2012), prioritize textual fidelity over external policy considerations when statutory text admits multiple reasonable readings.[105][95] For instance, the ordinary-meaning canon directs courts to apply the plain, contemporary meaning of words as understood by a reasonable reader at the time of enactment, unless context indicates otherwise; in Caminetti v. United States (1917), the Supreme Court interpreted "immoral purposes" in the Mann Act according to dictionary definitions rather than evolving moral standards.[106][95] Other semantic canons address structural ambiguities. The surplusage canon avoids constructions rendering any word superfluous, as seen in Lamie v. United States Trustee (2004), where the Court rejected an interpretation nullifying statutory language authorizing debtor representation by non-attorneys.[95] The expressio unius est exclusio alterius canon infers exclusion from deliberate omission, exemplified in Federal Maritime Commission v. South Carolina Ports Authority (2002), where silence on state sovereign immunity in a federal statute precluded its application.[106] The ejusdem generis rule limits general terms following specifics to the same class, as in Circuit City Stores, Inc. v. Adams (2001), confining exemptions in the Federal Arbitration Act to employment contracts akin to maritime and transportation workers.[95] Substantive canons, applied more cautiously, include the rule of lenity, resolving criminal ambiguities in favor of defendants, as in United States v. Santos (2008), which narrowed "proceeds" in money-laundering statutes to avoid overreach.[95] Judicial philosophies shape canon application amid ambiguity. Textualism, championed by Justice Scalia, insists on objective textual meaning without recourse to legislative history or purpose unless text demands it, arguing purposivism risks judicial policymaking; in FDA v. Brown & Williamson Tobacco Corp. (2000), textualists rejected agency deference expanding FDA jurisdiction beyond statutory text.[95] Purposivism, favored by Justice Breyer, integrates statutory purpose and context, including committee reports, to effectuate legislative goals, as in King v. Burwell (2015), where purpose justified reading Affordable Care Act subsidies broadly despite textual awkwardness.[95] Originalism, overlapping with textualism, anchors meaning to ratification-era understandings, though debates persist on historical evidence reliability.[107] Courts often weigh canons against each other, favoring those aligning with constitutional avoidance—interpreting ambiguities to evade serious doubts—per the constitutional-doubt canon in Almendarez-Torres v. United States (1998).[106] In contract interpretation, ambiguities trigger rules ascertaining parties' mutual intent, diverging from statutory focus on legislative text. Courts first apply the plain-meaning rule; if extrinsic evidence reveals patent ambiguity (obvious on face), or latent (contextual), parol evidence becomes admissible to clarify, as under Uniform Commercial Code § 2-202, which permits course-of-dealing proof without varying terms.[108] The contra proferentem doctrine resolves drafting ambiguities against the drafter, promoting fairness, as in California cases like Moss v. Minor Properties, Inc. (1995), penalizing boilerplate exclusions.[108] Business custom and negotiations inform resolution, but courts reject strained readings; in Pacific Gas & Electric Co. v. G.W. Thomas Drayage & Rigging Co. (1968), the California Supreme Court emphasized holistic intent over literalism.[108] Unlike statutes, contract canons yield to expressed intent, with ambiguities rarely voiding agreements absent unconscionability.[109]Psychological and Social Dimensions
Ambiguity Tolerance and Personality
Tolerance for ambiguity (ToA), also known as ambiguity tolerance, refers to an individual's propensity to perceive ambiguous situations—characterized by uncertainty, novelty, complexity, or insolubility—as desirable or challenging rather than threatening or distressing.[110] This trait influences cognitive processing, decision-making, and emotional responses to unclear stimuli, with higher ToA associated with reduced anxiety in unpredictable environments.[111] Empirical assessments, such as the Measure of Ambiguity Tolerance (MAT-50), demonstrate high internal consistency (Cronbach's α = .88) and test-retest reliability (r = .86 over 10-12 weeks), confirming ToA as a stable individual difference.[112] Measurement of ToA typically employs multidimensional scales capturing responses to novelty (unfamiliar information), complexity (multiple interpretations), and insolubility (unsolvable problems).[113] The Tolerance of Ambiguity Scale (TAS), developed by McLain (1993), refines earlier instruments like Rydell and Rosen's (1966) version by addressing psychometric limitations, yielding subscales that correlate with real-world behaviors such as adaptability in dynamic settings.[114] Higher scores on these scales indicate greater comfort with ambiguity, often scored such that results above 44-48 reflect lower intolerance.[115] In relation to broader personality frameworks, ToA aligns closely with the Big Five traits, particularly showing negative associations with Neuroticism—reflecting lower fear reactivity to uncertainty—and positive links to Openness to Experience, which involves attraction to novel and complex ideas.[116] A 2019 study of 303 participants found ToA uniquely predicted by low Neuroticism (β = -.32) and high Extraversion (β = .21), beyond shared variance with Openness, suggesting ToA captures motivational orientations toward ambiguity as either avoidant (fear-based) or approach-oriented (reward-seeking).[117] Additionally, ToA positively correlates with general intelligence (r = .15-.20 across facets), as higher cognitive ability facilitates processing ambiguous information without distress.[118] Empirical evidence underscores ToA's role in adaptive outcomes, including enhanced creativity, where tolerant individuals sustain multiple interpretations longer, fostering divergent thinking (e.g., correlations with creative action r = .25-.35 in longitudinal designs).[119] In a 2023 analysis of 3,836 adults, ToA emerged as a predictor of resilience in transitive societies, interacting with Conscientiousness to buffer stress from rapid change.[120] Low ToA, conversely, predicts rigidity and preference for structure, potentially exacerbating anxiety disorders, though causal directions remain debated due to bidirectional influences between trait stability and environmental feedback.[121] These findings, drawn from diverse samples, highlight ToA's integration with personality architecture while emphasizing its distinct predictive power for ambiguity-specific behaviors.[116]Bystander Effect and Social Diffusion
The bystander effect refers to the phenomenon in which individuals are less likely to provide assistance to a victim or in an emergency situation when other people are present, with the probability of intervention decreasing as the number of bystanders increases.[122] This effect was first systematically studied through experiments by Bibb Latané and John Darley in the late 1960s, including a 1968 study simulating an epileptic seizure over an intercom where participants alone reported the emergency 85% of the time, but only 31% did so when they believed four others were also listening.[122] Another 1968 experiment involved a room filling with smoke; solo participants reported it 75% of the time, but only 38% did when three confederates remained passive.[123] A key mechanism underlying the bystander effect is diffusion of responsibility, where individuals assume that someone else in the group will take action, thereby diluting personal accountability and creating ambiguity about individual obligations.[124] This diffusion is exacerbated in larger groups, as empirical data from meta-analyses show helping rates drop inversely with bystander numbers, from near 100% in solitary conditions to under 20% with five or more observers in ambiguous scenarios.[122] Social diffusion in this context extends to the spread of inaction across the group, where perceived shared responsibility fosters collective hesitation rather than coordinated response. Closely related is pluralistic ignorance, a process where bystanders interpret the ambiguous nature of an event—such as whether it constitutes a true emergency—by observing others' non-reactions, mistakenly inferring that no intervention is warranted despite private concerns.[125] In Latané and Darley's decision model, this occurs during the interpretation stage of emergencies, where ambiguity prompts deference to the group's apparent consensus, inhibiting help unless someone acts first to clarify the situation.[122] Experimental evidence confirms that reducing ambiguity, such as by having a confederate vocalize concern, increases intervention rates by up to 80% compared to passive bystander conditions.[126] These dynamics highlight how social cues amplify interpretive uncertainty, leading to causal chains of inaction rooted in misaligned perceptions rather than indifference.[127]Artistic and Rhetorical Uses
In Literature and Poetry
Ambiguity serves as a deliberate literary device in literature and poetry, enabling authors to layer meanings, evoke emotional depth, and invite readers to participate actively in interpretation by resolving or embracing multiple possibilities.[128] In poetry, it often arises from lexical, syntactic, or metaphorical structures that permit alternative readings, contrasting with prosaic clarity to heighten tension or philosophical nuance.[129] This technique traces back to ancient works, such as Lycophron's Alexandra in Alexandrian Greece, where deliberate obscurity cultivated interpretive complexity.[130] William Empson's 1930 book Seven Types of Ambiguity systematized the concept, classifying poetic ambiguities from basic alternative word senses (Type I) to irreconcilable conflicts resolved only through the poem's full context (Type VII).[24] Empson analyzed English poets like John Donne and John Milton, arguing that such ambiguities generate "alternative reactions to the same piece of language," fueling creative vitality rather than mere confusion.[131] His framework influenced New Criticism by emphasizing close reading to unpack these layers, as seen in his dissection of Shakespeare's Hamlet, where ambiguous soliloquies underscore existential uncertainty.[132][133] In Shakespeare's sonnets, lexical ambiguity obscures truths for ironic effect, as in Sonnet 138 ("When my love swears that she is made of truth"), where words like "line" evoke both honesty and fishing bait, allowing mutual deception between speaker and beloved.[134] Similarly, T.S. Eliot's The Waste Land (1922) employs ambiguity in lines like "April is the cruellest month," breeding lilacs out of the dead land, where "breeding" suggests both renewal and sterile proliferation, mirroring modernist fragmentation.[129] Robert Frost exploited ambiguity in poems like "The Road Not Taken" (1916), where the speaker's retrospective claim of difference invites debate over choice versus illusion, demonstrating how it probes human decision-making.[135] Narrative ambiguity in novels extends these principles, as in Henry James's The Turn of the Screw (1898), where governess perceptions of apparitions remain unresolved, forcing readers to question psychological reliability over supernatural claims.[136] Such uses prioritize interpretive openness, avoiding didactic resolution to reflect life's inherent uncertainties, though overuse risks alienating audiences seeking definitive meaning.[137]In Music and Visual Arts
In music, ambiguity frequently manifests in harmonic, metric, and perceptual structures, enabling multiple interpretive layers that enhance listener engagement. Harmonic ambiguity arises when chord progressions support competing tonal centers, as in passages where a sequence can resolve to different keys, delaying resolution and building tension; for instance, composers in Western art music traditions exploit this to evoke uncertainty, a technique evident in trailer music where unresolved dissonances heighten anticipation before climax.[138] Metric ambiguity, involving conflicting pulse interpretations, further complicates perception, as explored in analyses showing how such overlaps affect analytical pedagogy and real-time listening.[139] These elements draw on auditory scene analysis principles, where perceptual illusions akin to visual bistability allow music to sustain dual stream organizations, mirroring neuroscience findings on how the brain parses ambiguous sound sources.[140] In visual arts, ambiguity is leveraged through perceptual multistability and interpretive openness, prompting viewers to alternate between competing gestalts or meanings. Classic examples include bistable figures like the Necker cube or Rubin's vase, where foreground-background reversals create oscillating perceptions, a device rooted in Gestalt psychology and employed by artists to challenge fixed viewpoints.[141] Empirical studies confirm that moderate ambiguity levels boost aesthetic appreciation by fostering active cognitive involvement, as viewers derive pleasure from resolving or sustaining interpretive challenges, rather than demanding full disambiguation.[142] Surrealists such as René Magritte amplified this via incongruous juxtapositions, as in manipulated paintings that invite dual readings of reality and representation, underscoring ambiguity's role in evoking deeper conceptual engagement without prescriptive closure.[143] Across both domains, ambiguity serves causal functions in artistic intent: it exploits innate perceptual mechanisms to prolong attention and elicit emotional depth, as opposed to clarity's potential for superficiality. Research attributes its appeal to the brain's reward from ambiguity solvability, where partial insights yield satisfaction without exhaustive resolution, a pattern observed in both musical improvisation and visual contemplation.[144] This contrasts with unambiguous forms, which may limit replay value, though excessive ambiguity risks disengagement if it overwhelms interpretive capacity.[145]Scientific and Biological Contexts
Ambiguous Signals in Biology and Evolution
In biological signaling systems, ambiguity arises when a signal does not uniquely correspond to a single state or intent, permitting multiple possible interpretations that depend on context, receiver knowledge, or additional cues. Evolutionary models of sender-receiver games demonstrate that such ambiguity can evolve and stabilize under conditions of partial alignment between sender and receiver interests, where fully honest signaling incurs high costs or risks deception by eavesdroppers. For instance, in context-signaling games incorporating external environmental cues, three strategy types emerge under evolutionary dynamics: perfect signaling (unambiguous and fully informative), partial ambiguity (pooling some states), and full ambiguity (no information transfer), with partial ambiguity often persisting due to its balance of reliability and flexibility.[146] This contrasts with classic handicap principle models, where costly signals enforce honesty, but intermediate-cost scenarios favor partially honest or ambiguous equilibria between cheap talk and reliable indicators.[147] Covert signaling exemplifies adaptive ambiguity, involving transmissions that are accurately decoded by intended recipients but obscured or misinterpreted by unintended observers, such as rivals or predators. Theoretical analyses show covert strategies evolve in populations with low average similarity among individuals and frequent forced interactions, where overt signals provoke costly conflicts (e.g., dislike or aggression penalties), while covert ones enable selective cooperation without alienating dissimilar partners.[148] In agent-based simulations, covert signaling invades neutral populations and resists invasion by overt alternatives when reception accuracy for covert signals is sufficiently high relative to costs, promoting assortment on cooperative norms in diverse groups.[149] Biologically, this mechanism applies to multi-audience communication, as in animal systems where signals must navigate eavesdropping risks; for example, graded alarm calls in meerkats convey threat levels but remain ambiguous without visual context, allowing senders to alert kin while minimizing predator exploitation.[150] Empirical support for ambiguous signaling's evolutionary role comes from studies balancing signal cost, context sensitivity, and receiver discrimination, where less-informative signals prevail over precise ones in noisy or conflicted environments.[151] In cooperative contexts, ambiguity facilitates joint action by offloading precise interpretation to rich contextual information, reducing sender costs while maintaining receiver flexibility across species.[152] However, excessive ambiguity risks signal breakdown, as evolution favors systems where ambiguity is constrained by receiver learning or punishing unreliable senders, ensuring long-term informational value in lineages like primates or social insects.[150]Notation Ambiguities in Physics
In physics literature, mathematical notation frequently employs compact inline expressions that omit parentheses, relying on contextual conventions for precedence and grouping, which introduces ambiguities resolvable only through familiarity or explicit clarification. This practice stems from the need for brevity in derivations and equations but can lead to misinterpretations, particularly for readers from mathematical backgrounds adhering strictly to operator precedence rules like PEMDAS (Parentheses, Exponents, Multiplication/Division, Addition/Subtraction). For instance, the kinetic energy formula is often written as , where juxtaposition of and conventionally implies multiplication with higher precedence than the preceding division, yielding rather than ; this diverges from algebraic norms but aligns with physical intent, as units (e.g., mass in kg) further disambiguate by dimensional consistency.[153] Similar ambiguities arise in slashed fractions without explicit grouping, such as , which may parse as or absent context; physics style guides recommend parentheses to avoid such issues, as in tensor contractions or Lagrangian terms where misparsing alters physical meaning.[154] In practice, physicists often prioritize implied multiplication over division or explicit division, a convention criticized for sloppiness but defended as efficient when units or repeated usage provide cues—e.g., unambiguously means due to the constant's familiarity in angular frequency.[153] This reliance on convention has prompted computational physics efforts, like those by Susskind and Wisdom, to replace ambiguous symbolic notation with fully explicit, machine-readable forms for simulations, revealing errors in planetary orbit derivations traceable to notational oversight.[155] Trigonometric notations compound these problems, particularly powers applied to functions divided by numbers, as in , which oscillates between (common in half-angle formulas for scattering amplitudes or polarization) and (e.g., in time-averaged intensities or probability densities).[156] Such expressions appear routinely in quantum mechanics (e.g., spin-1/2 projections) and electromagnetism, where the intended parsing hinges on whether the argument division precedes or follows the squaring; peer-reviewed journals mitigate this via house styles mandating clarification, yet legacy texts perpetuate the risk.[154] Subscripted symbols exacerbate ambiguity in multivariable contexts, such as tensors denoted , where might represent specific indices, dummy summation variables under Einstein convention, or continuous parameters—e.g., in general relativity's Riemann tensor components versus fluid dynamics stress tensors. Without explicit declaration, this blurs discrete versus continuous interpretations, potentially inverting covariance properties or summation rules; modern treatments standardize Einstein notation but older works assume reader inference, leading to errors in index raising/lowering with metrics.[157] Partial derivative notation introduces further vagueness, as could imply total divergence or component-wise operation absent comma or chain rule specification, a pitfall in field theory Lagrangians where ambiguity affects Noether currents.[158] These issues underscore physics' tolerance for notational imprecision, balanced by empirical validation, though computational verification increasingly demands unambiguous reformulation to prevent propagation of errors in numerical models.[155]Computational Handling
Parsing Algorithms in Computer Science
Parsing algorithms in computer science analyze sequences of tokens derived from input strings to construct parse trees or abstract syntax trees according to a specified grammar, typically a context-free grammar (CFG).[159] A CFG is ambiguous if at least one string in its language admits two or more distinct leftmost derivations or parse trees, leading to potential nondeterminism in structure interpretation.[160] This ambiguity poses challenges for deterministic parsers, which assume unique parses for efficiency, but it can be managed through grammar redesign, conflict resolution heuristics, or specialized nondeterministic algorithms.[161] Deterministic top-down parsers, such as LL(k), and bottom-up parsers, such as LR(k), rely on unambiguous grammars to avoid shift-reduce or reduce-reduce conflicts in their parsing tables.[162] In practice, for programming languages, ambiguity—common in expressions like operator precedence (e.g., whethera/bc parses as (a/b)*c or a/(b*c))—is resolved by declaring operator precedences and associativities, which guide conflict resolution in tools like Yacc or Bison without altering the grammar's inherent ambiguity.[161][163] LR parsers can thus process ambiguous grammars by prioritizing higher-precedence reduces over shifts, ensuring a single parse path.[164]
For cases requiring exploration of all parses, such as in natural language processing or experimental language design, nondeterministic algorithms produce parse forests representing multiple interpretations. The Earley parser, introduced in 1970, uses dynamic programming with three operations—predict, scan, and complete—to track partial parses in state sets across input positions, achieving O(n^3) time in the worst case for ambiguous CFGs while degenerating to linear time for unambiguous ones.[162] Similarly, Generalized LR (GLR) parsers extend LR techniques by forking parser stacks at conflicts, maintaining a graph-structured stack to enumerate all valid parses efficiently, with implementations in tools like Bison's GLR mode for handling nondeterminism without exponential blowup in many practical scenarios.[165][166]
Advanced top-down approaches incorporate memoization and left-recursion handling to parse ambiguous grammars in polynomial time, preserving modularity for maintainable implementations.[167] These methods contrast with backtracking parsers, which may explore exponentially many paths without optimization. In compiler construction, preference for unambiguous or disambiguated grammars stems from the need for predictable, efficient single-pass parsing, whereas in domains like NLP, ambiguity-handling algorithms enable probabilistic selection of the most likely parse via integrated statistical models.[168] Overall, while ambiguity complicates verification and optimization, targeted algorithms ensure robust syntactic analysis across applications.[169]