Probability distribution

A probability distribution is a mathematical description of the probabilities of events, subsets of the sample space. The sample space, often represented in notation by ${\displaystyle \ \Omega \ ,}$ is the set of all possible outcomes of a random phenomenon being observed. The sample space may be any set: a set of real numbers, a set of descriptive labels, a set of vectors, a set of arbitrary non-numerical values, etc. For example, the sample space of a coin flip could be Ω = {"heads", "tails"}.

To define probability distributions for the specific case of random variables (so the sample space can be seen as a numeric set), it is common to distinguish between discrete and continuous random variables. In the discrete case, it is sufficient to specify a probability mass function ${\displaystyle p}$ assigning a probability to each possible outcome (e.g. when throwing a fair die, each of the six digits “1” to “6”, corresponding to the number of dots on the die, has probability ${\displaystyle {\tfrac {1}{6}}).}$ The probability of an event is then defined to be the sum of the probabilities of all outcomes that satisfy the event; for example, the probability of the event "the die rolls an even value" is $${\displaystyle p({\text{“}}2{\text{”}})+p({\text{“}}4{\text{”}})+p({\text{“}}6{\text{”}})={\frac {1}{6}}+{\frac {1}{6}}+{\frac {1}{6}}={\frac {1}{2}}.}$$ In contrast, when a random variable takes values from a continuum then by convention, any individual outcome is assigned probability zero. For such continuous random variables, only events that include infinitely many outcomes such as intervals have probability greater than 0.

For example, consider measuring the weight of a piece of ham in the supermarket, and assume the scale can provide arbitrarily many digits of precision. Then, the probability that it weighs exactly 500 g must be zero because no matter how high the level of precision chosen, it cannot be assumed that there are no non-zero decimal digits in the remaining omitted digits ignored by the precision level.

However, for the same use case, it is possible to meet quality control requirements such as that a package of "500 g" of ham must weigh between 490 g and 510 g with at least 98% probability. This is possible because this measurement does not require as much precision from the underlying equipment.

Continuous probability distributions can be described by means of the cumulative distribution function, which describes the probability that the random variable is no larger than a given value (i.e., P(X ≤ x) for some x. The cumulative distribution function is the area under the probability density function from -∞ to x, as shown in figure 1.^[4]

Most continuous probability distributions encountered in practice are not only continuous but also absolutely continuous. Such distributions can be described by their probability density function. Informally, the probability density ${\displaystyle f}$ of a random variable ${\displaystyle X}$ describes the infinitesimal probability that ${\displaystyle X}$ takes any value ${\displaystyle x}$ — that is ${\displaystyle P(x\leq X<x+\Delta x)\approx f(x)\,\Delta x}$ as ${\displaystyle \Delta x>0}$ becomes is arbitrarily small. The probability that ${\displaystyle X}$ lies in a given interval can be computed rigorously by integrating the probability density function over that interval.^[5]

Let ${\displaystyle (\Omega ,{\mathcal {F}},P)}$ be a probability space, ${\displaystyle (E,{\mathcal {E}})}$ be a measurable space, and ${\displaystyle X:\Omega \to E}$ be a ${\displaystyle (E,{\mathcal {E}})}$-valued random variable. Then the probability distribution of ${\displaystyle X}$ is the pushforward measure of the probability measure ${\displaystyle P}$ onto ${\displaystyle (E,{\mathcal {E}})}$ induced by ${\displaystyle X}$. Explicitly, this pushforward measure on ${\displaystyle (E,{\mathcal {E}})}$ is given by $${\displaystyle X_{*}(P)(B)=P\left(X^{-1}(B)\right)}$$ for ${\displaystyle B\in {\mathcal {E}}.}$

Any probability distribution is a probability measure on ${\displaystyle (E,{\mathcal {E}})}$ (in general different from ${\displaystyle P}$, unless ${\displaystyle X}$ happens to be the identity map).^{[citation needed]}

A probability distribution can be described in various forms, such as by a probability mass function or a cumulative distribution function. One of the most general descriptions, which applies for absolutely continuous and discrete variables, is by means of a probability function ${\displaystyle P\colon {\mathcal {A}}\to \mathbb {R} }$ whose input space ${\displaystyle {\mathcal {A}}}$ is a σ-algebra, and gives a real number probability as its output, particularly, a number in ${\displaystyle [0,1]\subseteq \mathbb {R} }$.

The probability function ${\displaystyle P}$ can take as argument subsets of the sample space itself, as in the coin toss example, where the function ${\displaystyle P}$ was defined so that P(heads) = 0.5 and P(tails) = 0.5. However, because of the widespread use of random variables, which transform the sample space into a set of numbers (e.g., ${\displaystyle \mathbb {R} }$, ${\displaystyle \mathbb {N} }$), it is more common to study probability distributions whose argument are subsets of these particular kinds of sets (number sets),^[6] and all probability distributions discussed in this article are of this type. It is common to denote as ${\displaystyle P(X\in E)}$ the probability that a certain value of the variable ${\displaystyle X}$ belongs to a certain event ${\displaystyle E}$.^[7][8]

The above probability function only characterizes a probability distribution if it satisfies all the Kolmogorov axioms, that is:

1. ${\displaystyle P(X\in E)\geq 0\;\forall E\in {\mathcal {A}}}$, so the probability is non-negative
2. ${\displaystyle P(X\in E)\leq 1\;\forall E\in {\mathcal {A}}}$, so no probability exceeds ${\displaystyle 1}$
3. ${\displaystyle P(X\in \bigcup _{i}E_{i})=\sum _{i}P(X\in E_{i})}$ for any countable disjoint family of sets ${\displaystyle \{E_{i}\}}$

The concept of probability function is made more rigorous by defining it as the element of a probability space ${\displaystyle (X,{\mathcal {A}},P)}$, where ${\displaystyle X}$ is the set of possible outcomes, ${\displaystyle {\mathcal {A}}}$ is the set of all subsets ${\displaystyle E\subset X}$ whose probability can be measured, and ${\displaystyle P}$ is the probability function, or probability measure, that assigns a probability to each of these measurable subsets ${\displaystyle E\in {\mathcal {A}}}$.^[9]

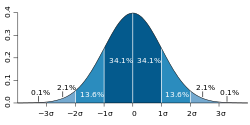
Probability distributions usually belong to one of two classes. A discrete probability distribution is applicable to the scenarios where the set of possible outcomes is discrete (e.g. a coin toss, a roll of a die) and the probabilities are encoded by a discrete list of the probabilities of the outcomes; in this case the discrete probability distribution is known as probability mass function. On the other hand, absolutely continuous probability distributions are applicable to scenarios where the set of possible outcomes can take on values in a continuous range (e.g. real numbers), such as the temperature on a given day. In the absolutely continuous case, probabilities are described by a probability density function, and the probability distribution is by definition the integral of the probability density function.^[7][5][8] The normal distribution is a commonly encountered absolutely continuous probability distribution. More complex experiments, such as those involving stochastic processes defined in continuous time, may demand the use of more general probability measures.

A probability distribution whose sample space is one-dimensional (for example real numbers, list of labels, ordered labels or binary) is called univariate, while a distribution whose sample space is a vector space of dimension 2 or more is called multivariate. A univariate distribution gives the probabilities of a single random variable taking on various different values; a multivariate distribution (a joint probability distribution) gives the probabilities of a random vector – a list of two or more random variables – taking on various combinations of values. Important and commonly encountered univariate probability distributions include the binomial distribution, the hypergeometric distribution, and the normal distribution. A commonly encountered multivariate distribution is the multivariate normal distribution.

Besides the probability function, the cumulative distribution function, the probability mass function and the probability density function, the moment generating function and the characteristic function also serve to identify a probability distribution, as they uniquely determine an underlying cumulative distribution function.^[10]

Some key concepts and terms, widely used in the literature on the topic of probability distributions, are listed below.^[1]

• Random variable: takes values from a sample space; probabilities describe which values and set of values are more likely taken.
• Event: set of possible values (outcomes) of a random variable that occurs with a certain probability.
• Probability function or probability measure: describes the probability ${\displaystyle P(X\in E)}$ that the event ${\displaystyle E,}$ occurs.^[11]
• Cumulative distribution function: function evaluating the probability that ${\displaystyle X}$ will take a value less than or equal to ${\displaystyle x}$ for a random variable (only for real-valued random variables).
• Quantile function: the inverse of the cumulative distribution function. Gives ${\displaystyle x}$ such that, with probability ${\displaystyle q}$, ${\displaystyle X}$ will not exceed ${\displaystyle x}$.

• Discrete probability distribution: for many random variables with finitely or countably infinitely many values.
• Probability mass function (pmf): function that gives the probability that a discrete random variable is equal to some value.
• Frequency distribution: a table that displays the frequency of various outcomes in a sample.
• Relative frequency distribution: a frequency distribution where each value has been divided (normalized) by a number of outcomes in a sample (i.e. sample size).
• Categorical distribution: for discrete random variables with a finite set of values.

• Absolutely continuous probability distribution: for many random variables with uncountably many values.
• Probability density function (pdf) or probability density: function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a relative likelihood that the value of the random variable would equal that sample.

• Support: set of values that can be assumed with non-zero probability (or probability density in the case of a continuous distribution) by the random variable. For a random variable ${\displaystyle X}$, it is sometimes denoted as ${\displaystyle R_{X}}$.
• Tail:^[12] the regions close to the bounds of the random variable, if the pmf or pdf are relatively low therein. Usually has the form ${\displaystyle X>a}$, ${\displaystyle X<b}$ or a union thereof.
• Head:^[12] the region where the pmf or pdf is relatively high. Usually has the form ${\displaystyle a<X<b}$.
• Expected value or mean: the weighted average of the possible values, using their probabilities as their weights; or the continuous analog thereof.
• Median: the value such that the set of values less than the median, and the set greater than the median, each have probabilities no greater than one-half.
• Mode: for a discrete random variable, the value with highest probability; for an absolutely continuous random variable, a location at which the probability density function has a local peak.
• Quantile: the q-quantile is the value ${\displaystyle x}$ such that ${\displaystyle P(X<x)=q}$.
• Variance: the second moment of the pmf or pdf about the mean; an important measure of the dispersion of the distribution.
• Standard deviation: the square root of the variance, and hence another measure of dispersion.
• Symmetry: a property of some distributions in which the portion of the distribution to the left of a specific value (usually the median) is a mirror image of the portion to its right.
• Skewness: a measure of the extent to which a pmf or pdf "leans" to one side of its mean. The third standardized moment of the distribution.
• Kurtosis: a measure of the "fatness" of the tails of a pmf or pdf. The fourth standardized moment of the distribution.

In the special case of a real-valued random variable, the probability distribution can equivalently be represented by a cumulative distribution function instead of a probability measure. The cumulative distribution function of a random variable ${\displaystyle X}$ with regard to a probability distribution ${\displaystyle p}$ is defined as $${\displaystyle F(x)=P(X\leq x).}$$

The cumulative distribution function of any real-valued random variable has the properties:

• ${\displaystyle F(x)}$ is non-decreasing;
• ${\displaystyle F(x)}$ is right-continuous;
• ${\displaystyle 0\leq F(x)\leq 1}$;
• ${\displaystyle \lim _{x\to -\infty }F(x)=0}$ and ${\displaystyle \lim _{x\to \infty }F(x)=1}$; and
• ${\displaystyle \Pr(a<X\leq b)=F(b)-F(a)}$.

Conversely, any function ${\displaystyle F:\mathbb {R} \to \mathbb {R} }$ that satisfies the first four of the properties above is the cumulative distribution function of some probability distribution on the real numbers.^[13]

Any probability distribution can be decomposed as the mixture of a discrete, an absolutely continuous and a singular continuous distribution,^[14] and thus any cumulative distribution function admits a decomposition as the convex sum of the three according cumulative distribution functions.

A discrete probability distribution is the probability distribution of a random variable that can take on only a countable number of values^[15] (almost surely)^[16] which means that the probability of any event ${\displaystyle E}$ can be expressed as a (finite or countably infinite) sum: $${\displaystyle P(X\in E)=\sum _{\omega \in A\cap E}P(X=\omega ),}$$ where ${\displaystyle A}$ is a countable set with ${\displaystyle P(X\in A)=1}$. Thus the discrete random variables (i.e. random variables whose probability distribution is discrete) are exactly those with a probability mass function ${\displaystyle p(x)=P(X=x)}$. In the case where the range of values is countably infinite, these values have to decline to zero fast enough for the probabilities to add up to 1. For example, if ${\displaystyle p(n)={\tfrac {1}{2^{n}}}}$ for ${\displaystyle n=1,2,...}$, the sum of probabilities would be ${\displaystyle 1/2+1/4+1/8+\dots =1}$.

Well-known discrete probability distributions used in statistical modeling include the Poisson distribution, the Bernoulli distribution, the binomial distribution, the geometric distribution, the negative binomial distribution and categorical distribution.^[3] When a sample (a set of observations) is drawn from a larger population, the sample points have an empirical distribution that is discrete, and which provides information about the population distribution. Additionally, the discrete uniform distribution is commonly used in computer programs that make equal-probability random selections between a number of choices.

A real-valued discrete random variable can equivalently be defined as a random variable whose cumulative distribution function increases only by jump discontinuities—that is, its cdf increases only where it "jumps" to a higher value, and is constant in intervals without jumps. The points where jumps occur are precisely the values which the random variable may take. Thus the cumulative distribution function has the form $${\displaystyle F(x)=P(X\leq x)=\sum _{\omega \leq x}p(\omega ).}$$ The points where the cdf jumps always form a countable set; this may be any countable set and thus may even be dense in the real numbers.

A discrete probability distribution is often represented with Dirac measures, also called one-point distributions (see below), the probability distributions of deterministic random variables. For any outcome ${\displaystyle \omega }$, let ${\displaystyle \delta _{\omega }}$ be the Dirac measure concentrated at ${\displaystyle \omega }$. Given a discrete probability distribution, there is a countable set ${\displaystyle A}$ with ${\displaystyle P(X\in A)=1}$ and a probability mass function ${\displaystyle p}$. If ${\displaystyle E}$ is any event, then $${\displaystyle P(X\in E)=\sum _{\omega \in A}p(\omega )\delta _{\omega }(E),}$$ or in short, $${\displaystyle P_{X}=\sum _{\omega \in A}p(\omega )\delta _{\omega }.}$$

Similarly, discrete distributions can be represented with the Dirac delta function as a generalized probability density function ${\displaystyle f}$, where $${\displaystyle f(x)=\sum _{\omega \in A}p(\omega )\delta (x-\omega ),}$$ which means $${\displaystyle P(X\in E)=\int _{E}f(x)\,dx=\sum _{\omega \in A}p(\omega )\int _{E}\delta (x-\omega )=\sum _{\omega \in A\cap E}p(\omega )}$$ for any event ${\displaystyle E.}$^[17]

For a discrete random variable ${\displaystyle X}$, let ${\displaystyle u_{0},u_{1},\dots }$ be the values it can take with non-zero probability. Denote $${\displaystyle \Omega _{i}=X^{-1}(u_{i})=\{\omega :X(\omega )=u_{i}\},\,i=0,1,2,\dots }$$ These are disjoint sets, and for such sets $${\displaystyle P\left(\bigcup _{i}\Omega _{i}\right)=\sum _{i}P(\Omega _{i})=\sum _{i}P(X=u_{i})=1.}$$ It follows that the probability that ${\displaystyle X}$ takes any value except for ${\displaystyle u_{0},u_{1},\dots }$ is zero, and thus one can write ${\displaystyle X}$ as $${\displaystyle X(\omega )=\sum _{i}u_{i}1_{\Omega _{i}}(\omega )}$$ except on a set of probability zero, where ${\displaystyle 1_{A}}$ is the indicator function of ${\displaystyle A}$. This may serve as an alternative definition of discrete random variables.

A special case is the discrete distribution of a random variable that can take on only one fixed value, in other words, a Dirac measure. Expressed formally, the random variable ${\displaystyle X}$ has a one-point distribution if it has a possible outcome ${\displaystyle x}$ such that ${\displaystyle P(X{=}x)=1.}$^[18] All other possible outcomes then have probability 0. Its cumulative distribution function jumps immediately from 0 before ${\displaystyle x}$ to 1 at ${\displaystyle x}$. It is closely related to a deterministic distribution, which cannot take on any other value, while a one-point distribution can take other values, though only with probability 0. For most practical purposes the two notions are equivalent.

An absolutely continuous probability distribution is a probability distribution on the real numbers with uncountably many possible values, such as a whole interval in the real line, and where the probability of any event can be expressed as an integral.^[19] More precisely, a real random variable ${\displaystyle X}$ has an absolutely continuous probability distribution if there is a function ${\displaystyle f:\mathbb {R} \to [0,\infty ]}$ such that for each interval ${\displaystyle I=[a,b]\subset \mathbb {R} }$ the probability of ${\displaystyle X}$ belonging to ${\displaystyle I}$ is given by the integral of ${\displaystyle f}$ over ${\displaystyle I}$:^[20][21] $${\displaystyle P\left(a\leq X\leq b\right)=\int _{a}^{b}f(x)\,dx.}$$ This is the definition of a probability density function, so that absolutely continuous probability distributions are exactly those with a probability density function. In particular, the probability for ${\displaystyle X}$ to take any single value ${\displaystyle a}$ (that is, ${\displaystyle a\leq X\leq a}$) is zero, because an integral with coinciding upper and lower limits is always equal to zero. If the interval ${\displaystyle [a,b]}$ is replaced by any measurable set ${\displaystyle A}$, the according equality still holds: $${\displaystyle P(X\in A)=\int _{A}f(x)\,dx.}$$

An absolutely continuous random variable is a random variable whose probability distribution is absolutely continuous.

There are many examples of absolutely continuous probability distributions: normal, uniform, chi-squared, and others.

Absolutely continuous probability distributions as defined above are precisely those with an absolutely continuous cumulative distribution function. In this case, the cumulative distribution function ${\displaystyle F}$ has the form $${\displaystyle F(x)=P(X\leq x)=\int _{-\infty }^{x}f(t)\,dt}$$ where ${\displaystyle f}$ is a density of the random variable ${\displaystyle X}$ with regard to the distribution ${\displaystyle P}$.

Note on terminology: Absolutely continuous distributions ought to be distinguished from continuous distributions, which are those having a continuous cumulative distribution function. Every absolutely continuous distribution is a continuous distribution but the inverse is not true, there exist singular distributions, which are neither absolutely continuous nor discrete nor a mixture of those, and do not have a density. An example is given by the Cantor distribution. Some authors however use the term "continuous distribution" to denote all distributions whose cumulative distribution function is absolutely continuous, i.e. refer to absolutely continuous distributions as continuous distributions.^[7]

For a more general definition of density functions and the equivalent absolutely continuous measures see absolutely continuous measure.

In the measure-theoretic formalization of probability theory, a random variable is defined as a measurable function ${\displaystyle X}$ from a probability space ${\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}$ to a measurable space ${\displaystyle ({\mathcal {X}},{\mathcal {A}})}$. Given that probabilities of events of the form ${\displaystyle \{\omega \in \Omega \mid X(\omega )\in A\}}$ satisfy Kolmogorov's probability axioms, the probability distribution of ${\displaystyle X}$ is the image measure ${\displaystyle X_{*}\mathbb {P} }$ of ${\displaystyle X}$ , which is a probability measure on ${\displaystyle ({\mathcal {X}},{\mathcal {A}})}$ satisfying ${\displaystyle X_{*}\mathbb {P} =\mathbb {P} X^{-1}}$.^[22][23][24]

Absolutely continuous and discrete distributions with support on ${\displaystyle \mathbb {R} ^{k}}$ or ${\displaystyle \mathbb {N} ^{k}}$ are extremely useful to model a myriad of phenomena,^[7][4] since most practical distributions are supported on relatively simple subsets, such as hypercubes or balls. However, this is not always the case, and there exist phenomena with supports that are actually complicated curves ${\displaystyle \gamma :[a,b]\rightarrow \mathbb {R} ^{n}}$ within some space ${\displaystyle \mathbb {R} ^{n}}$ or similar. In these cases, the probability distribution is supported on the image of such curve, and is likely to be determined empirically, rather than finding a closed formula for it.^[25]

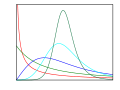
One example is shown in the figure to the right, which displays the evolution of a system of differential equations (commonly known as the Rabinovich–Fabrikant equations) that can be used to model the behaviour of Langmuir waves in plasma.^[26] When this phenomenon is studied, the observed states from the subset are as indicated in red. So one could ask what is the probability of observing a state in a certain position of the red subset; if such a probability exists, it is called the probability measure of the system.^[27][25]

This kind of complicated support appears quite frequently in dynamical systems. It is not simple to establish that the system has a probability measure, and the main problem is the following. Let ${\displaystyle t_{1}\ll t_{2}\ll t_{3}}$ be instants in time and ${\displaystyle O}$ a subset of the support; if the probability measure exists for the system, one would expect the frequency of observing states inside set ${\displaystyle O}$ would be equal in interval ${\displaystyle [t_{1},t_{2}]}$ and ${\displaystyle [t_{2},t_{3}]}$, which might not happen; for example, it could oscillate similar to a sine, ${\displaystyle \sin(t)}$, whose limit when ${\displaystyle t\rightarrow \infty }$ does not converge. Formally, the measure exists only if the limit of the relative frequency converges when the system is observed into the infinite future.^[28] The branch of dynamical systems that studies the existence of a probability measure is ergodic theory.

Note that even in these cases, the probability distribution, if it exists, might still be termed "absolutely continuous" or "discrete" depending on whether the support is uncountable or countable, respectively.

Most algorithms are based on a pseudorandom number generator that produces numbers ${\displaystyle X}$ that are uniformly distributed in the half-open interval [0, 1). These random variates ${\displaystyle X}$ are then transformed via some algorithm to create a new random variate having the required probability distribution. With this source of uniform pseudo-randomness, realizations of any random variable can be generated.^[29]

For example, suppose U has a uniform distribution between 0 and 1. To construct a random Bernoulli variable for some 0 < p < 1, define $${\displaystyle X={\begin{cases}1&{\text{if }}U<p\\0&{\text{if }}U\geq p.\end{cases}}}$$ We thus have $${\displaystyle P(X=1)=P(U<p)=p,\quad P(X=0)=P(U\geq p)=1-p.}$$ Therefore, the random variable X has a Bernoulli distribution with parameter p.^[29]

This method can be adapted to generate real-valued random variables with any distribution: for be any cumulative distribution function F, let F^inv be the generalized left inverse of ${\displaystyle F,}$ also known in this context as the quantile function or inverse distribution function: $${\displaystyle F^{\mathrm {inv} }(p)=\inf\{x\in \mathbb {R} :p\leq F(x)\}.}$$ Then, F^inv(p) ≤ x if and only if p ≤ F(x). As a result, if U is uniformly distributed on [0, 1], then the cumulative distribution function of X = F^inv(U) is F.

For example, suppose we want to generate a random variable having an exponential distribution with parameter ${\displaystyle \lambda }$ — that is, with cumulative distribution function ${\displaystyle F:x\mapsto 1-e^{-\lambda x}.}$ $${\displaystyle {\begin{aligned}F(x)=u&\Leftrightarrow 1-e^{-\lambda x}=u\\[2pt]&\Leftrightarrow e^{-\lambda x}=1-u\\[2pt]&\Leftrightarrow -\lambda x=\ln(1-u)\\[2pt]&\Leftrightarrow x={\frac {-1}{\lambda }}\ln(1-u)\end{aligned}}}$$ so ${\displaystyle F^{\mathrm {inv} }(u)=-{\tfrac {1}{\lambda }}\ln(1-u)}$, and if U has a uniform distribution on [0, 1) then ${\displaystyle X=-{\tfrac {1}{\lambda }}\ln(1-U)}$ has an exponential distribution with parameter ${\displaystyle \lambda .}$^[29]

Although from a theoretical point of view this method always works, in practice the inverse distribution function is unknown and/or cannot be computed efficiently. In this case, other methods (such as the Monte Carlo method) are used.

The concept of the probability distribution and the random variables which they describe underlies the mathematical discipline of probability theory, and the science of statistics. There is spread or variability in almost any value that can be measured in a population (e.g. height of people, durability of a metal, sales growth, traffic flow, etc.); almost all measurements are made with some intrinsic error; in physics, many processes are described probabilistically, from the kinetic properties of gases to the quantum mechanical description of fundamental particles. For these and many other reasons, simple numbers are often inadequate for describing a quantity, while probability distributions are often more appropriate.

The following is a list of some of the most common probability distributions, grouped by the type of process that they are related to. For a more complete list, see list of probability distributions, which groups by the nature of the outcome being considered (discrete, absolutely continuous, multivariate, etc.)

All of the univariate distributions below are singly peaked; that is, it is assumed that the values cluster around a single point. In practice, actually observed quantities may cluster around multiple values. Such quantities can be modeled using a mixture distribution.

• Normal distribution (Gaussian distribution), for a single such quantity; the most commonly used absolutely continuous distribution

• Log-normal distribution, for a single such quantity whose log is normally distributed
• Pareto distribution, for a single such quantity whose log is exponentially distributed; the prototypical power law distribution

• Discrete uniform distribution, for a finite set of values (e.g. the outcome of a fair dice)
• Continuous uniform distribution, for absolutely continuously distributed values

• Basic distributions:
  • Bernoulli distribution, for the outcome of a single Bernoulli trial (e.g. success/failure, yes/no)
  • Binomial distribution, for the number of "positive occurrences" (e.g. successes, yes votes, etc.) given a fixed total number of independent occurrences
  • Negative binomial distribution, for binomial-type observations but where the quantity of interest is the number of failures before a given number of successes occurs
  • Geometric distribution, for binomial-type observations but where the quantity of interest is the number of failures before the first success; a special case of the negative binomial distribution
• Related to sampling schemes over a finite population:
  • Hypergeometric distribution, for the number of "positive occurrences" (e.g. successes, yes votes, etc.) given a fixed number of total occurrences, using sampling without replacement
  • Beta-binomial distribution, for the number of "positive occurrences" (e.g. successes, yes votes, etc.) given a fixed number of total occurrences, sampling using a Pólya urn model (in some sense, the "opposite" of sampling without replacement)

• Categorical distribution, for a single categorical outcome (e.g. yes/no/maybe in a survey); a generalization of the Bernoulli distribution
• Multinomial distribution, for the number of each type of categorical outcome, given a fixed number of total outcomes; a generalization of the binomial distribution
• Multivariate hypergeometric distribution, similar to the multinomial distribution, but using sampling without replacement; a generalization of the hypergeometric distribution

• Poisson distribution, for the number of occurrences of a Poisson-type event in a given period of time
• Exponential distribution, for the time before the next Poisson-type event occurs
• Gamma distribution, for the time before the next k Poisson-type events occur

• Rayleigh distribution, for the distribution of vector magnitudes with Gaussian distributed orthogonal components. Rayleigh distributions are found in RF signals with Gaussian real and imaginary components.
• Rice distribution, a generalization of the Rayleigh distributions for where there is a stationary background signal component. Found in Rician fading of radio signals due to multipath propagation and in MR images with noise corruption on non-zero NMR signals.

• Chi-squared distribution, the distribution of a sum of squared standard normal variables; useful e.g. for inference regarding the sample variance of normally distributed samples (see chi-squared test)
• Student's t distribution, the distribution of the ratio of a standard normal variable and the square root of a scaled chi squared variable; useful for inference regarding the mean of normally distributed samples with unknown variance (see Student's t-test)
• F-distribution, the distribution of the ratio of two scaled chi squared variables; useful e.g. for inferences that involve comparing variances or involving R-squared (the squared correlation coefficient)

• Beta distribution, for a single probability (real number between 0 and 1); conjugate to the Bernoulli distribution and binomial distribution
• Gamma distribution, for a non-negative scaling parameter; conjugate to the rate parameter of a Poisson distribution or exponential distribution, the precision (inverse variance) of a normal distribution, etc.
• Dirichlet distribution, for a vector of probabilities that must sum to 1; conjugate to the categorical distribution and multinomial distribution; generalization of the beta distribution
• Wishart distribution, for a symmetric non-negative definite matrix; conjugate to the inverse of the covariance matrix of a multivariate normal distribution; generalization of the gamma distribution^[30]

• The cache language models and other statistical language models used in natural language processing to assign probabilities to the occurrence of particular words and word sequences do so by means of probability distributions.
• In quantum mechanics, the probability density of finding the particle at a given point is proportional to the square of the magnitude of the particle's wavefunction at that point (see Born rule). Therefore, the probability distribution function of the position of a particle is described by ${\textstyle P_{a\leq x\leq b}(t)=\int _{a}^{b}dx\,|\Psi (x,t)|^{2}}$, probability that the particle's position x will be in the interval a ≤ x ≤ b in dimension one, and a similar triple integral in dimension three. This is a key principle of quantum mechanics.^[31]
• Probabilistic load flow in power-flow study explains the uncertainties of input variables as probability distribution and provides the power flow calculation also in term of probability distribution.^[32]
• Prediction of natural phenomena occurrences based on previous frequency distributions such as tropical cyclones, hail, time in between events, etc.^[33]

• Conditional probability distribution
• Empirical probability distribution
• Histogram
• Joint probability distribution
• Probability measure
• Quasiprobability distribution
• Riemann–Stieltjes integral application to probability theory

• List of probability distributions
• List of statistical topics