Hubbry Logo
Scientific modellingScientific modellingMain
Open search
Scientific modelling
Community hub
Scientific modelling
logo
8 pages, 0 posts
0 subscribers
Be the first to start a discussion here.
Be the first to start a discussion here.
Scientific modelling
Scientific modelling
Scientific modelling
View on Wikipedia
from Wikipedia

Example scientific modelling. A schematic of chemical and transport processes related to atmospheric composition.
Part of a series on
Research
A laptop computer next to archival materials
Research design
Research strategy
Philosophical schools
Methodology
Methods
Tools and software
Philosophy portal

Scientific modelling is an activity that produces models representing empirical objects, phenomena, and physical processes, to make a particular part or feature of the world easier to understand, define, quantify, visualize, or simulate. It requires selecting and identifying relevant aspects of a situation in the real world and then developing a model to replicate a system with those features. Different types of models may be used for different purposes, such as conceptual models to better understand, operational models to operationalize, mathematical models to quantify, computational models to simulate, and graphical models to visualize the subject.

Modelling is an essential and inseparable part of many scientific disciplines, each of which has its own ideas about specific types of modelling.[1][2] The following was said by John von Neumann.[3]

... the sciences do not try to explain, they hardly even try to interpret, they mainly make models. By a model is meant a mathematical construct which, with the addition of certain verbal interpretations, describes observed phenomena. The justification of such a mathematical construct is solely and precisely that it is expected to work—that is, correctly to describe phenomena from a reasonably wide area.

There is also an increasing attention to scientific modelling[4] in fields such as science education,[5] philosophy of science, systems theory, and knowledge visualization. There is a growing collection of methods, techniques and meta-theory about all kinds of specialized scientific modelling.

Overview

[edit]

A scientific model seeks to represent empirical objects, phenomena, and physical processes in a logical and objective way. All models are in simulacra, that is, simplified reflections of reality that, despite being approximations, can be extremely useful.[6] Building and disputing models is fundamental to the scientific enterprise. Complete and true representation may be impossible, but scientific debate often concerns which is the better model for a given task, e.g., which is the more accurate climate model for seasonal forecasting.[7]

Attempts to formalize the principles of the empirical sciences use an interpretation to model reality, in the same way logicians axiomatize the principles of logic. The aim of these attempts is to construct a formal system that will not produce theoretical consequences that are contrary to what is found in reality. Predictions or other statements drawn from such a formal system mirror or map the real world only insofar as these scientific models are true.[8][9]

For the scientist, a model is also a way in which the human thought processes can be amplified.[10] For instance, models that are rendered in software allow scientists to leverage computational power to simulate, visualize, manipulate and gain intuition about the entity, phenomenon, or process being represented. Such computer models are in silico. Other types of scientific models are in vivo (living models, such as laboratory rats) and in vitro (in glassware, such as tissue culture).[11]

Basics

[edit]

Modelling as a substitute for direct measurement and experimentation

[edit]

Models are typically used when it is either impossible or impractical to create experimental conditions in which scientists can directly measure outcomes. Direct measurement of outcomes under controlled conditions (see Scientific method) will always be more reliable than modeled estimates of outcomes.

Within modeling and simulation, a model is a task-driven, purposeful simplification and abstraction of a perception of reality, shaped by physical, legal, and cognitive constraints.[12] It is task-driven because a model is captured with a certain question or task in mind. Simplifications leave all the known and observed entities and their relation out that are not important for the task. Abstraction aggregates information that is important but not needed in the same detail as the object of interest. Both activities, simplification, and abstraction, are done purposefully. However, they are done based on a perception of reality. This perception is already a model in itself, as it comes with a physical constraint. There are also constraints on what we are able to legally observe with our current tools and methods, and cognitive constraints that limit what we are able to explain with our current theories. This model comprises the concepts, their behavior, and their relations informal form and is often referred to as a conceptual model. In order to execute the model, it needs to be implemented as a computer simulation. This requires more choices, such as numerical approximations or the use of heuristics.[13] Despite all these epistemological and computational constraints, simulation has been recognized as the third pillar of scientific methods: theory building, simulation, and experimentation.[14]

Simulation

[edit]
Climate models apply knowledge in various sciences to process extensive sets of input climate data, executing differential equations among grid elements in a three-dimensional model of Earth's climate system. The models produce simulated climates having an array of climatic and weather elements, such as heatwaves and storms. Each element may be described by several attributes, including intensity, frequency, and impacts. Climate models support adaptation to projected climate change, and enable extreme event attribution to explain specific weather events.

A simulation is a way to implement the model, often employed when the model is too complex for the analytical solution. A steady-state simulation provides information about the system at a specific instant in time (usually at equilibrium, if such a state exists). A dynamic simulation provides information over time. A simulation shows how a particular object or phenomenon will behave. Such a simulation can be useful for testing, analysis, or training in those cases where real-world systems or concepts can be represented by models.[15]

Structure

[edit]

Structure is a fundamental and sometimes intangible notion covering the recognition, observation, nature, and stability of patterns and relationships of entities. From a child's verbal description of a snowflake, to the detailed scientific analysis of the properties of magnetic fields, the concept of structure is an essential foundation of nearly every mode of inquiry and discovery in science, philosophy, and art.[16]

Systems

[edit]

A system is a set of interacting or interdependent entities, real or abstract, forming an integrated whole. In general, a system is a construct or collection of different elements that together can produce results not obtainable by the elements alone.[17] The concept of an 'integrated whole' can also be stated in terms of a system embodying a set of relationships which are differentiated from relationships of the set to other elements, and form relationships between an element of the set and elements not a part of the relational regime. There are two types of system models: 1) discrete in which the variables change instantaneously at separate points in time and, 2) continuous where the state variables change continuously with respect to time.[18]

Generating a model

[edit]

Modelling is the process of generating a model as a conceptual representation of some phenomenon. Typically a model will deal with only some aspects of the phenomenon in question, and two models of the same phenomenon may be essentially different—that is to say, that the differences between them comprise more than just a simple renaming of components.

Such differences may be due to differing requirements of the model's end users, or to conceptual or aesthetic differences among the modelers and to contingent decisions made during the modelling process. Considerations that may influence the structure of a model might be the modeler's preference for a reduced ontology, preferences regarding statistical models versus deterministic models, discrete versus continuous time, etc. In any case, users of a model need to understand the assumptions made that are pertinent to its validity for a given use.

Building a model requires abstraction. Assumptions are used in modelling in order to specify the domain of application of the model. For example, the special theory of relativity assumes an inertial frame of reference. This assumption was contextualized and further explained by the general theory of relativity. A model makes accurate predictions when its assumptions are valid, and might well not make accurate predictions when its assumptions do not hold. Such assumptions are often the point with which older theories are succeeded by new ones (the general theory of relativity works in non-inertial reference frames as well).

Evaluating a model

[edit]
See also: Models of scientific inquiry § Choice of a theory

A model is evaluated first and foremost by its consistency to empirical data; any model inconsistent with reproducible observations must be modified or rejected. One way to modify the model is by restricting the domain over which it is credited with having high validity. A case in point is Newtonian physics, which is highly useful except for the very small, the very fast, and the very massive phenomena of the universe. However, a fit to empirical data alone is not sufficient for a model to be accepted as valid. Factors important in evaluating a model include:[citation needed]

  • Ability to explain past observations
  • Ability to predict future observations
  • Cost of use, especially in combination with other models
  • Refutability, enabling estimation of the degree of confidence in the model
  • Simplicity, or even aesthetic appeal

People may attempt to quantify the evaluation of a model using a utility function.

Visualization

[edit]

Visualization is any technique for creating images, diagrams, or animations to communicate a message. Visualization through visual imagery has been an effective way to communicate both abstract and concrete ideas since the dawn of man. Examples from history include cave paintings, Egyptian hieroglyphs, Greek geometry, and Leonardo da Vinci's revolutionary methods of technical drawing for engineering and scientific purposes.

Space mapping

[edit]

Space mapping refers to a methodology that employs a "quasi-global" modelling formulation to link companion "coarse" (ideal or low-fidelity) with "fine" (practical or high-fidelity) models of different complexities. In engineering optimization, space mapping aligns (maps) a very fast coarse model with its related expensive-to-compute fine model so as to avoid direct expensive optimization of the fine model. The alignment process iteratively refines a "mapped" coarse model (surrogate model).

Types

[edit]

Applications

[edit]

Modelling and simulation

[edit]

One application of scientific modelling is the field of modelling and simulation, generally referred to as "M&S". M&S has a spectrum of applications which range from concept development and analysis, through experimentation, measurement, and verification, to disposal analysis. Projects and programs may use hundreds of different simulations, simulators and model analysis tools.

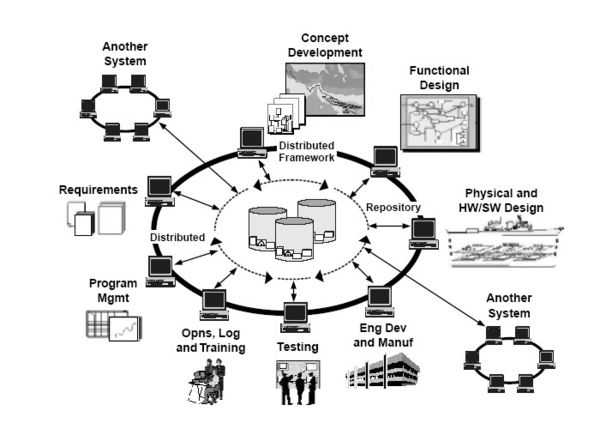
Example of the integrated use of Modelling and Simulation in Defence life cycle management. The modelling and simulation in this image is represented in the center of the image with the three containers.[15]

The figure shows how modelling and simulation is used as a central part of an integrated program in a defence capability development process.[15]

See also

[edit]

References

[edit]

Further reading

[edit]
[edit]
Revisions and contributorsEdit on WikipediaRead on Wikipedia

Scientific modelling

View on Grokipedia
from Grokipedia
Scientific modelling is the practice of developing simplified, abstract representations of real-world systems, phenomena, or processes to make their key features explicit, enabling explanations and predictions that would otherwise be challenging due to complexity, scale, or inaccessibility. These models abstract and focus on essential elements while omitting extraneous details, serving as tools to test hypotheses, communicate ideas, and advance scientific understanding across disciplines such as physics, , and sciences. The primary purposes of scientific modelling include visualizing phenomena that are too small, large, or intricate to observe directly, such as atomic structures or planetary orbits, and generating testable predictions to validate or refine theories. Models facilitate iterative processes where scientists construct, evaluate, and revise representations based on empirical data, thereby contributing to knowledge building and . For instance, models must account for their inherent limitations, as no representation can fully capture every aspect of the target system, ensuring users recognize both strengths and approximations. Scientific models take various forms, broadly categorized into physical, conceptual, and mathematical types, each suited to different investigative needs. Physical models, like scale replicas of molecules or globes, provide tangible demonstrations of spatial relationships. Conceptual models, often diagrams or analogies, emphasize qualitative relationships and ideas, such as flowcharts depicting ecological interactions. Mathematical and computer-based models employ equations or simulations to quantify dynamics and forecast outcomes, as seen in projections or algorithms. This diversity allows modelling to integrate domain-specific knowledge with computational methods, enhancing predictive power in fields like and .

Definition and Overview

Core Definition

Scientific modelling is the process of creating abstract representations of real-world systems to describe, explain, predict, or control phenomena through simplified structures that capture essential features. These representations, often termed scientific models, serve as tools for understanding target systems by depicting selected aspects rather than the entirety of reality. For instance, a of an atom illustrates atomic structure without replicating every subatomic interaction, while equations for planetary motion approximate gravitational dynamics to forecast orbits. Key characteristics of scientific models include their as approximations that balance fidelity to observed phenomena with tractability for and manipulation. This trade-off involves idealizations and simplifications to make complex systems manageable, ensuring the model remains useful despite not being a perfect replica. Such models enable scientists to explore patterns in data and test implications under controlled conditions. The term "model" originates from the Latin modulus, meaning a small measure or standard, which evolved through Middle French modelle and Italian modello to denote scaled likenesses and patterns by the 16th century, later extending to representational uses in scientific contexts. In distinction from related concepts, scientific models differ from theories—formalized sets of general propositions—or hypotheses—tentative, testable explanations—by providing specific, often visual or structural, interpretations of systems or data patterns. Scientific models often substitute for direct experimentation in studying inaccessible or large-scale systems, facilitating indirect investigation.

Importance in Scientific Inquiry

Scientific modeling plays a central role in scientific inquiry by enabling the testing of hypotheses through simulated scenarios rather than requiring full-scale physical experiments, which may be impractical or impossible. For instance, models allow researchers to evaluate competing explanations by integrating experimental data with theoretical assumptions, fostering creative reasoning and iterative refinement of ideas. In cases of inaccessible phenomena, such as the behavior of black holes, computational models based on provide predictions that can be tested against observational data from or emissions, confirming or challenging theoretical hypotheses without direct intervention. Additionally, models facilitate the integration of interdisciplinary data, synthesizing insights from diverse fields to construct coherent representations of complex systems. The benefits of scientific modeling extend to cost-effective exploration of potential outcomes, reducing the need for resource-intensive trials while still yielding reliable insights into . By abstracting key variables, models reveal underlying mechanisms that drive observed phenomena, such as causal pathways in biological processes or environmental interactions, thereby deepening conceptual understanding. In policy contexts, epidemiological models have proven instrumental during pandemics like , simulating the impacts of interventions such as testing and isolation to guide and decisions, ultimately supporting evidence-based strategies that mitigate widespread harm. As a prerequisite for robust scientific practice, modeling bridges empirical observations with theoretical frameworks, operationalizing abstract ideas into testable forms that align with the . This process ensures by standardizing assumptions and procedures for verification across studies, while also promoting through precise, refutable predictions that can be confronted with new evidence. Without such models, many theories would remain untestable, hindering the advancement of knowledge.

Historical Development

Early Conceptual Foundations

The origins of scientific modelling trace back to ancient civilizations, where early attempts to represent natural phenomena laid the groundwork for more systematic approaches. In , around the 5th century BCE, astronomers developed mathematical models to predict celestial events, employing a geocentric framework that positioned at the center of the universe. These models relied on arithmetic progressions and periodic cycles, such as the Saros cycle for eclipses, to forecast planetary positions with reasonable accuracy based on accumulated observations. This predictive emphasis marked an initial shift from mere description toward quantifiable representations of motion. Greek philosophers further advanced qualitative conceptual models, particularly in understanding terrestrial motion. , in the 4th century BCE, proposed a framework in his Physics where motion was categorized into natural and violent types: heavy elements like naturally fall toward the center of the , while light elements like fire rise, and unnatural motions require an external cause. These ideas, though not mathematical, provided a structured of change and locomotion, influencing subsequent thought by emphasizing teleological explanations over empirical . Building on this, Ptolemy's (circa 150 CE) synthesized Greek and into a refined geocentric model using epicycles and deferents to account for retrograde planetary motion, enabling detailed tables for celestial predictions that endured for centuries. The Renaissance and Scientific Revolution transformed these foundations into more empirical and mathematical models, emphasizing prediction through experimentation and observation. Nicolaus Copernicus's De revolutionibus orbium coelestium (1543) introduced a heliocentric system, relocating the Sun at the center and simplifying planetary paths, which shifted modeling from purely descriptive geocentric schemes to predictive frameworks aligned with observed data. Galileo Galilei's inclined plane experiments (circa 1604–1608), detailed in Two New Sciences (1638), served as proto-models by slowing free fall to measurable speeds, revealing uniform acceleration and challenging Aristotelian notions through quantitative results. Johannes Kepler, using Tycho Brahe's precise observations, formulated empirical laws in Astronomia Nova (1609), including elliptical orbits with the Sun at one focus, providing a data-driven geometric model that accurately predicted planetary positions. Isaac Newton's (1687) culminated these developments with the first comprehensive mathematical framework for motion, unifying terrestrial and celestial phenomena through three laws. The second law, expressed as F=maF = ma, where FF produces aa proportional to mass mm, integrated with dynamics, enabling predictive models of diverse systems from falling bodies to orbiting planets. This era's innovations highlighted a profound from qualitative descriptions to predictive, mathematically rigorous models, setting the stage for modern scientific inquiry.

Evolution in the 20th and 21st Centuries

In the early , scientific modeling advanced significantly through the integration of quantum theory, exemplified by Niels Bohr's 1913 atomic model, which quantized orbits to explain hydrogen's spectral lines, marking a shift from classical to quantum descriptions of atomic structure. Concurrently, Albert Einstein's 1915 formulation of revolutionized gravitational modeling by describing curvature as a geometric framework for mass and energy interactions, enabling predictions of phenomena like black holes and . These developments were complemented by the emergence of , with and Albert Einstein's 1924 derivation of Bose-Einstein statistics providing a probabilistic framework for indistinguishable particles, foundational for modeling quantum gases and later Bose-Einstein condensates. By the mid-20th century, modeling evolved with interdisciplinary approaches like and , as articulated in Norbert Wiener's 1948 book Cybernetics: Or Control and Communication in the Animal and the Machine, which formalized feedback loops and for dynamic systems in and . Ludwig von Bertalanffy's general , systematized in his 1968 work, emphasized open systems and holistic interactions across disciplines, influencing ecological and organizational models by transcending reductionist paradigms. The advent of electronic computing further propelled simulations; the , completed in 1945 for U.S. Army ballistic calculations during , demonstrated programmable digital modeling of trajectories, reducing computation times from hours to seconds and paving the way for broader scientific applications. In the late 20th and early 21st centuries, enabled complex global simulations, such as those in the Intergovernmental Panel on Change's (IPCC) 1990 First Assessment , which used coupled atmosphere-ocean general circulation models to project impacts, establishing quantitative scenarios for policy-making. The integration of and transformed modeling precision; DeepMind's , introduced in 2020 and detailed in its 2021 publication, achieved near-atomic accuracy in using on sequences, revolutionizing . Subsequent updates, including AlphaFold 3 in 2024, extended predictions to biomolecular complexes and interactions, incorporating diffusion-based architectures for enhanced multimodal modeling. Parallel advancements in have begun addressing classical limitations in molecular simulations; by the mid-2020s, hybrid quantum-classical algorithms demonstrated feasibility for simulating multi-million-atom systems and chemical dynamics, as surveyed in 2025 reviews, promising exponential speedups for challenges like .

Fundamental Concepts

Abstraction and Simplification

Abstraction in scientific modeling refers to the process of creating representations that range from concrete physical replicas, such as scale models of aircraft or hydraulic analogs of electrical circuits, to more abstract symbolic equations that capture essential dynamics without replicating every detail. At the concrete end, physical models mimic the target system's geometry and behavior to allow direct observation and experimentation, while at the symbolic level, mathematical formulations like differential equations represent relationships among variables in a generalized form. The primary purpose of these abstraction levels is to isolate key variables—such as population sizes in ecological systems or velocities in fluid dynamics—while deliberately ignoring extraneous noise or minor influences that do not significantly affect the core phenomena, thereby enabling focused analysis and prediction. Simplification techniques further refine these abstractions by reducing complexity in targeted ways. Scaling involves normalizing variables to dimensionless forms or adjusting time and space scales to highlight dominant processes, such as treating fast chemical reactions as instantaneous in reaction-diffusion models. Linearization approximates nonlinear relationships with linear ones around operating points, facilitating analytical solutions; for instance, in control systems, it replaces curved trajectories with lines to simplify stability analysis. Compartmentalization divides systems into discrete units or "compartments" with properties, lumping similar elements together to model flows between them, as seen in pharmacokinetic models where the body is segmented into plasma, tissue, and elimination compartments. A classic example is the Lotka-Volterra predator-prey model, which simplifies ecological interactions by assuming two populations—prey (x) and predators (y)—with growth rates governed by: dxdt=ax−bxy,dydt=−cy+dxy\frac{dx}{dt} = ax - bxy, \quad \frac{dy}{dt} = -cy + dxy Here, a represents the prey's intrinsic growth rate, b the predation rate, c the predator's death rate, and d the predator's growth efficiency from consuming prey, abstracting away factors like spatial heterogeneity or multiple species to focus on oscillatory dynamics. These abstraction and simplification strategies involve inherent trade-offs. Over-simplification, by excessively stripping details, can lead to inaccuracies, such as failing to predict real-world bifurcations in population models due to omitted environmental variables. Conversely, under-simplification retains too much complexity, resulting in computationally intractable models that are difficult to solve or generalize, as in high-fidelity simulations requiring prohibitive resources for parameter estimation. Balancing these requires context-specific judgments, often validated through sensitivity analysis, to ensure the model remains both tractable and sufficiently representative of the system's behavior.

Deterministic versus Stochastic Approaches

Deterministic models in scientific modelling assume that system outcomes are precisely predictable given fixed initial conditions and parameters, without incorporating randomness. These models rely on differential equations or algebraic relations that yield unique solutions for any input, treating variables as continuous and deterministic. A classic example is found in , where Newton's second law of motion, F=maF = ma, describes the relationship between (FF), (mm), and (aa), assuming no random fluctuations in the forces or particle behavior. This law underpins models of planetary motion or , where the absence of elements allows exact trajectory predictions under ideal conditions. In contrast, stochastic models account for inherent variability and uncertainty by integrating probability distributions into the , producing a range of possible outcomes rather than a single . These models are essential for systems where random or noise significantly influence behavior, such as in processes. For instance, Albert Einstein's 1905 theory of models the erratic path of suspended particles in a as resulting from random collisions with surrounding molecules, described by a that follows the . This approach captures the statistical nature of microscopic fluctuations, which deterministic models overlook. To solve stochastic models, particularly for estimating integrals or simulating paths, the employs repeated random sampling from probability distributions to approximate expected values, providing numerical solutions where analytical ones are infeasible. The choice between deterministic and stochastic approaches depends on the system's characteristics and the scale of observation. Deterministic models are preferred for large-scale, controlled environments where noise is negligible, such as designs or macroscopic physical systems, offering computational and precise predictions. Stochastic models are more appropriate for noisy or small-scale systems, like biological reactions or atmospheric phenomena, where variability must be quantified to reflect real-world ; for example, relies on parametrizations to represent sub-grid scale processes and improve predictions. Hybrid approaches, combining deterministic frameworks with elements, are increasingly used to balance accuracy and tractability in complex systems.

Model Development Process

Steps in Constructing a Model

The construction of a scientific model begins with Phase 1: Problem and scoping, where the modeler clearly identifies the objectives and delineates the boundaries of the under study. This involves articulating the specific question or the model aims to explain or predict, such as understanding the dynamics of a in an , and determining the scope by deciding what aspects to include or exclude to maintain focus and feasibility. For instance, in modeling, this step includes defining the model's purpose for a particular audience and brainstorming initial components to categorize them as endogenous (internally determined) or exogenous (externally driven). Effective scoping prevents overcomplication by limiting the model to relevant scales, time frames, and interactions. Following this, Phase 2: Conceptualization entails formulating hypotheses about the system's behavior and selecting key variables and processes. This qualitative stage builds a preliminary framework by identifying causal relationships and interactions, often represented through diagrams or verbal descriptions. The process can be outlined in sequential steps akin to a : first, gather observations and prior knowledge to generate hypotheses; second, list potential variables (e.g., like and flows like birth rates); third, sketch relationships between them, such as feedback loops; and fourth, refine the structure based on initial plausibility checks. In biosciences, for example, conceptualization might involve diagramming a to hypothesize how concentrations influence reaction rates. This phase emphasizes collaboration with domain experts to ensure the captures essential mechanisms without unnecessary detail. Phase 3: Formalization translates the into a precise representation, such as mathematical equations, algorithms, or diagrams, to enable quantitative analysis. This step requires applying fundamental principles to derive the model's structure; for a simple mass-spring system, the process starts by considering a mm attached to a spring with constant kk, displaced by position xx from equilibrium on a frictionless surface. Using Hooke's law, the restoring force is F=−kxF = -kx. Applying Newton's second law (F=maF = ma), where acceleration a=d2xdt2a = \frac{d^2x}{dt^2}, yields: md2xdt2=−kxm \frac{d^2x}{dt^2} = -kx Rearranging gives the differential equation: md2xdt2+kx=0m \frac{d^2x}{dt^2} + kx = 0 This equation formalizes the oscillatory behavior from physical principles, providing a basis for further simulation. In general, formalization ensures the model is logically consistent and amenable to testing. Throughout these phases, the model development process is inherently iterative, incorporating feedback loops for refinement. Initial formulations are tested against observations, leading to revisions in objectives, variables, or equations as discrepancies arise; for example, new data might prompt boundary adjustments or reformulation. This cyclical approach, often visualized as recursive arrows between stages, enhances model robustness and alignment with real-world phenomena.

Parameter Estimation and Calibration

Parameter estimation in scientific modeling involves determining the values of model parameters that best align the model's predictions with empirical data, while calibration refines these parameters through systematic adjustment to improve model fidelity. This process typically follows the initial formulation of a model structure, where parameters represent unknown quantities such as physical constants or coefficients in equations. Accurate estimation is crucial for ensuring the model's reliability across applications, from climate simulations to biological systems. One foundational technique for parameter estimation is the method, which minimizes the sum of squared residuals between observed data and model predictions. The objective is to find parameter values θ\theta that solve the : min⁡θ∑i=1n(yi−y^i(θ))2\min_{\theta} \sum_{i=1}^n (y_i - \hat{y}_i(\theta))^2 where yiy_i are the observed values, y^i(θ)\hat{y}_i(\theta) are the predicted values from the model, and nn is the number of data points. This approach assumes errors are normally distributed and provides point estimates that are efficient under these conditions, as originally developed for astronomical data fitting and widely applied in regression-based modeling. In contrast, treats parameters as random variables and estimates their posterior distributions by incorporating prior knowledge with likelihood from data, using : p(θ∣y)∝p(y∣θ)p(θ)p(\theta | y) \propto p(y | \theta) p(\theta). This probabilistic framework quantifies uncertainty in estimates, making it suitable for models with sparse data or complex dependencies, such as in or environmental simulations. Bayesian methods often employ sampling to compute posteriors, enabling robust inference even when parameters are correlated. The process begins with initial guesses, often derived from theoretical bounds, expert knowledge, or preliminary simulations, to seed the optimization. Iterative adjustment then refines these values, typically through gradient-based methods for or sampling algorithms for Bayesian approaches, converging toward optimal fits. To prevent —where the model captures noise rather than underlying patterns— includes validation against holdout data sets not used in estimation, ensuring generalizability. Challenges arise in high-dimensional spaces, where local minima can trap iterative searches, necessitating robust starting points and regularization techniques. Regression analysis serves as a core tool for linear and generalized linear models, extending least squares to handle heteroscedasticity or non-normal errors via techniques like weighted or . For nonlinear or multimodal problems, genetic algorithms provide a alternative, evolving a of sets through selection, crossover, and to minimize an objective function, often outperforming local methods in complex landscapes like pharmacokinetic modeling. These evolutionary strategies are particularly effective when analytical gradients are unavailable, though they require computational resources proportional to problem dimensionality.

Types of Models

Conceptual Models

Conceptual models are qualitative representations that emphasize ideas, relationships, and processes without relying on numerical computations or physical constructions. They often take the form of diagrams, flowcharts, analogies, or verbal descriptions to simplify complex phenomena and facilitate understanding. For example, a diagram illustrates predator-prey interactions in an , highlighting energy flow and dependencies. Another common instance is the model, depicted as a series of arrows connecting , , , and runoff to explain hydrological processes. These models are essential in early stages of scientific inquiry for generation and communication, particularly in fields like and , though they lack the precision of quantitative approaches and may oversimplify interactions.

Physical and Analog Models

Physical models are tangible, scaled representations of real-world systems constructed to replicate their physical behaviors under controlled conditions, allowing engineers and scientists to test hypotheses and predict performance without the risks or costs of full-scale prototypes. A prominent example is the use of scale replicas of in wind tunnels, where airflow over the model reveals aerodynamic forces such as lift and drag that inform full-size design. These models rely on principles of to ensure that the scaled version accurately mirrors the prototype's dynamics, encompassing geometric similarity (proportional shapes and dimensions), kinematic similarity (corresponding motion patterns), and dynamic similarity (balanced forces and moments). A critical aspect of dynamic similarity in is matching dimensionless parameters like the , defined as Re=ρvdμRe = \frac{\rho v d}{\mu}, where ρ\rho is fluid density, vv is , dd is a , and μ\mu is dynamic ; this ratio governs the relative influence of inertial and viscous forces, enabling valid extrapolation from model to prototype despite scale differences. Analog models, in contrast, employ one physical system to imitate another through structural or functional analogies, often translating mechanical or fluid phenomena into electrical equivalents for easier manipulation and measurement. For instance, electrical circuits can simulate mechanical systems by using resistors to represent , inductors for (mass), and capacitors for springs (compliance), with operational amplifiers (op-amps) configured as integrators to model time-dependent behaviors like oscillations in vibrating structures. This approach was particularly vital in the pre-digital computer era, when solved differential equations representing complex systems; early op-amps, developed in the using vacuum tubes, powered simulations for applications such as WWII directors, where they computed mechanical trajectories by electrically mimicking ballistic motion. Both physical and analog models offer intuitive advantages, such as direct visualization of phenomena and empirical validation of theoretical predictions, making them valuable for initial design iterations in where conceptual understanding precedes detailed analysis. They facilitate low-risk experimentation, as seen in hydraulic laboratories where scaled physical models of spillways and outlet works predict flow patterns, scour, and to optimize and efficiency. However, limitations include challenges in achieving complete across all parameters—such as simultaneously matching Reynolds and Froude numbers in models—which can lead to inaccuracies in scaling results, alongside high material and construction costs that restrict scalability for very large or intricate systems. Additionally, analog electrical models suffer from component tolerances and , reducing precision compared to modern alternatives, though their historical role underscores their enduring heuristic value in bridging physical and quantitative insight.

Mathematical and Analytical Models

Mathematical and analytical models represent scientific phenomena through mathematical equations that admit exact, closed-form solutions, enabling precise predictions without computational approximation. These models are particularly valuable in scenarios where the underlying system can be described by relatively simple relationships, allowing researchers to derive explicit expressions for variables as functions of , or other parameters. Unlike empirical or simulation-based approaches, analytical models emphasize manipulation and theoretical insight, often rooted in fundamental laws of physics or other disciplines. A primary type of analytical model involves algebraic equations, which relate variables through polynomial or other explicit functional forms without derivatives. For instance, in , in static equilibrium is modeled algebraically as F=−kxF = -kx, where FF is , kk is the spring constant, and xx is displacement, providing a direct relationship for . Algebraic models are straightforward to solve and interpret, making them suitable for steady-state problems in , such as supply-demand equilibrium P=f(Q)P = f(Q), or basic under constant rates. However, they are limited to non-dynamic systems and may oversimplify interactions involving change over time or space. Differential equations form another cornerstone of analytical modeling, capturing dynamic evolution through rates of change. Ordinary differential equations (ODEs) describe systems varying in a single independent variable, typically time, as in one-dimensional motion. Partial differential equations (PDEs) extend this to multiple variables, such as time and space, for phenomena like wave propagation or heat diffusion. These equations are derived from conservation principles or physical laws and solved to yield analytical expressions that reveal qualitative behaviors, such as stability or periodicity. A classic example is the simple harmonic oscillator, modeling oscillatory motion in systems like pendulums or springs under restoring forces. The governing arises from Newton's second law: for a mm attached to a spring with constant kk, the force balance yields md2xdt2=−kx,m \frac{d^2 x}{dt^2} = -k x, or equivalently, d2xdt2+ω2x=0,\frac{d^2 x}{dt^2} + \omega^2 x = 0, where ω=k/m\omega = \sqrt{k/m}
Add your contribution
Related Hubs
User Avatar
No comments yet.